Bouncing Cosmology in Modified Gravity with Higher-Order Gauss–Bonnet Curvature Term
Abstract
1. Introduction
2. Gravity and Field Equations
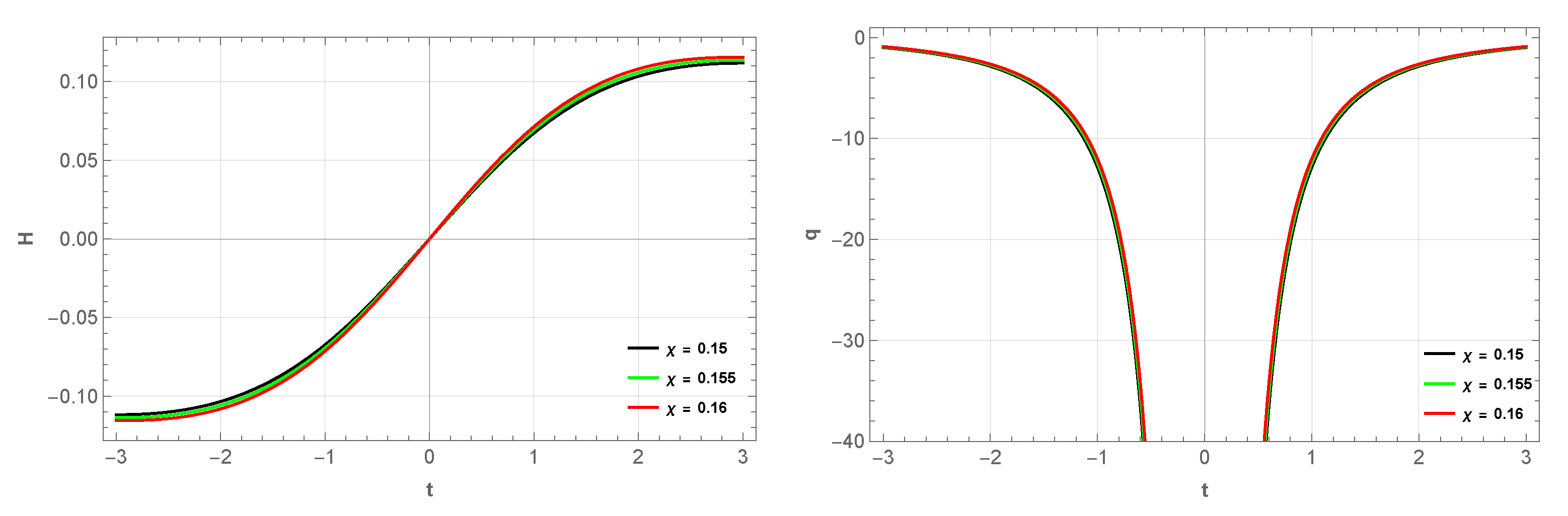
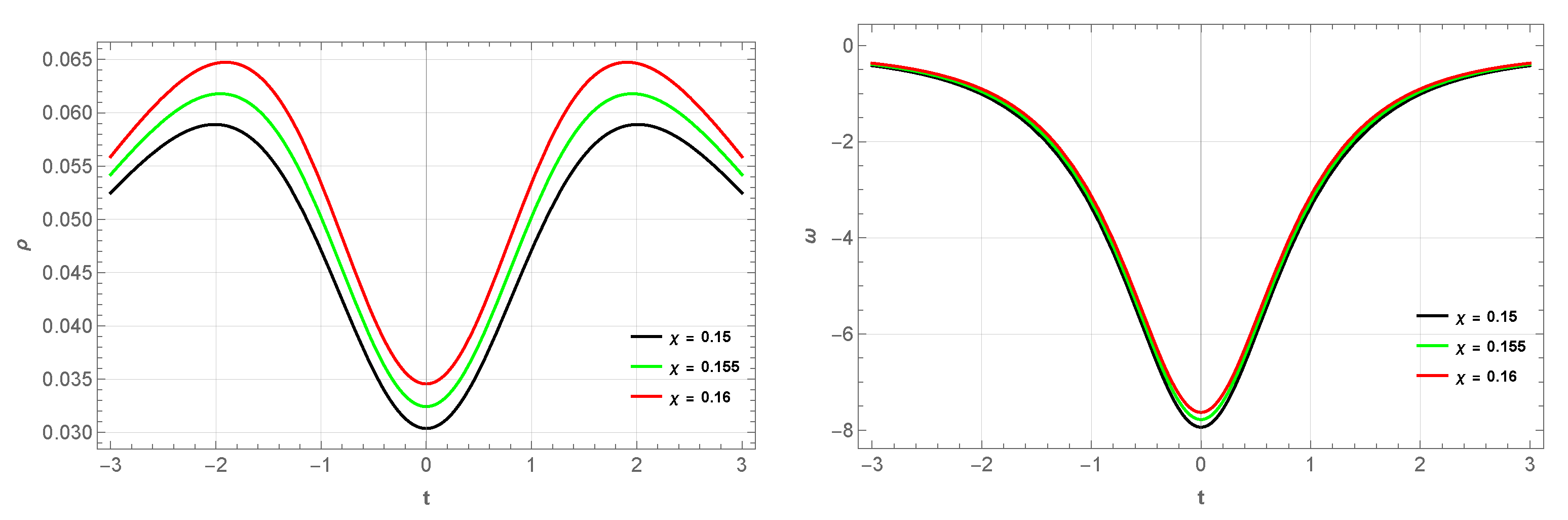
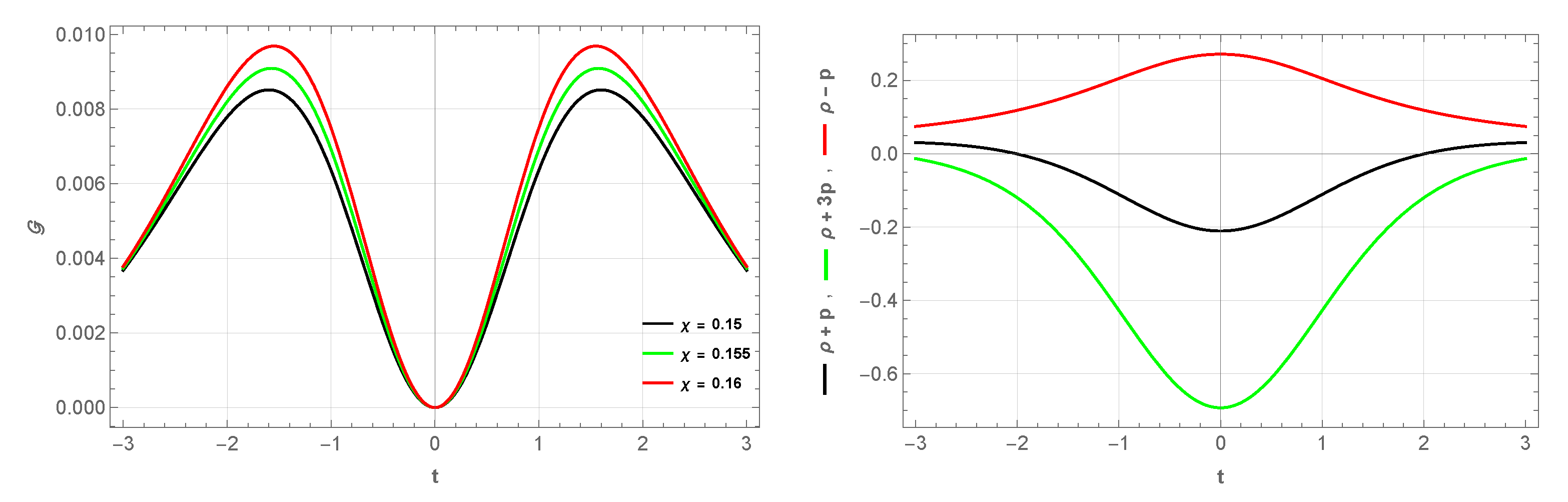
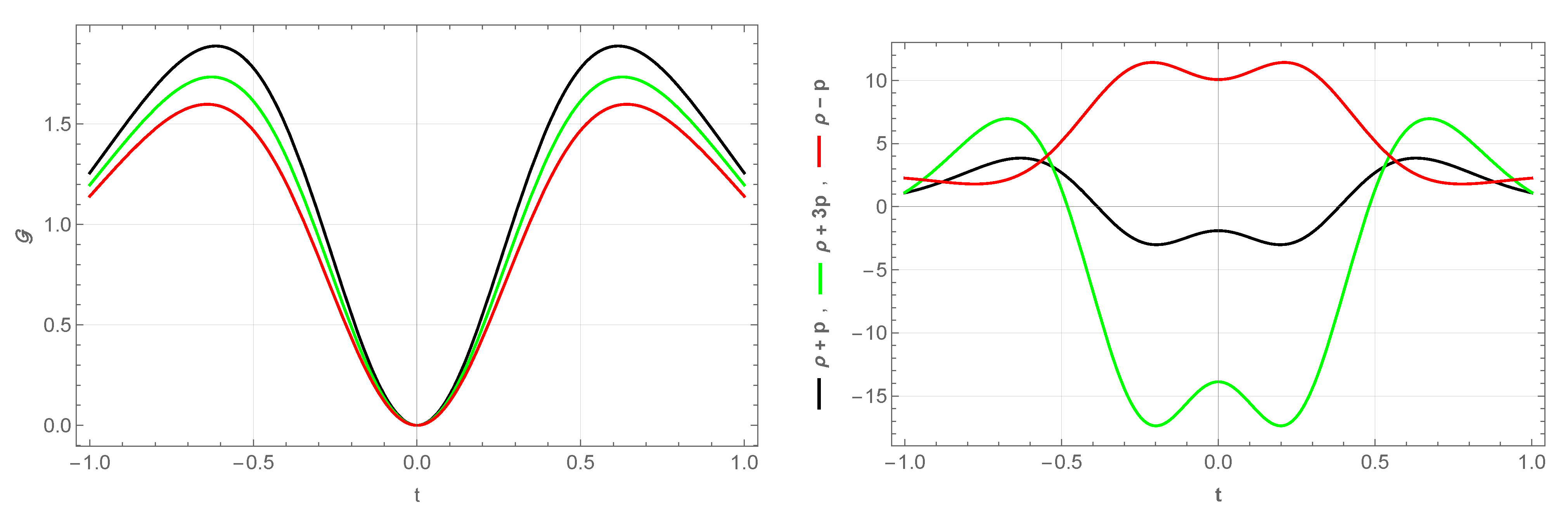
3. Bouncing Model I
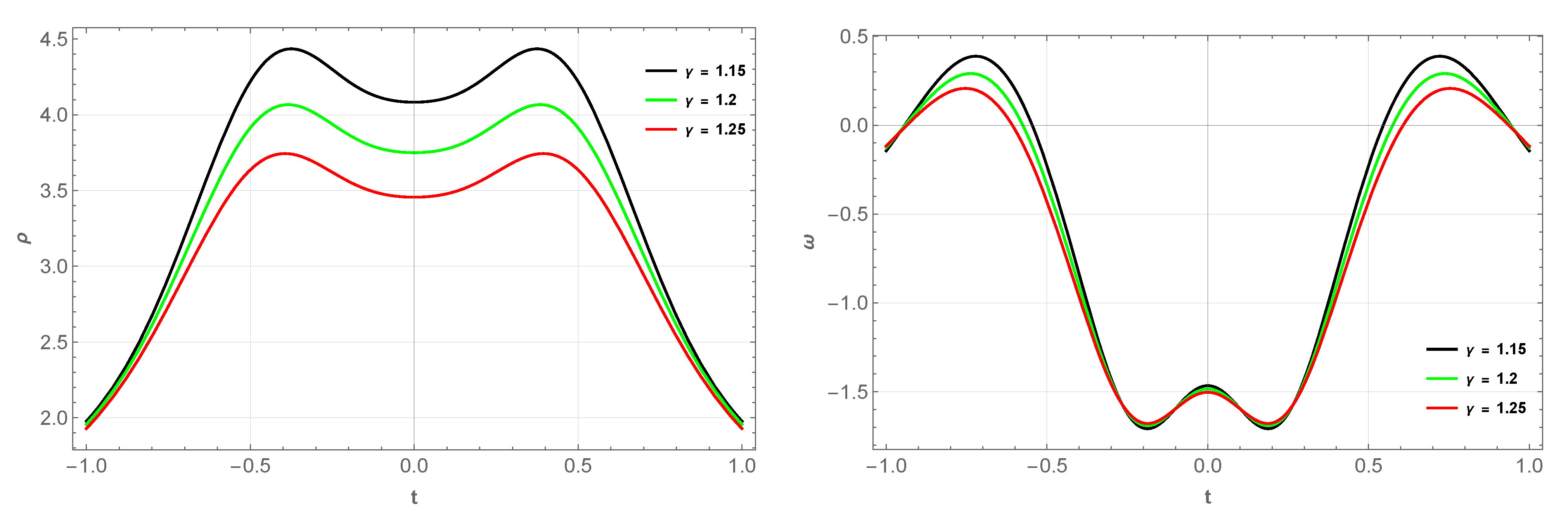
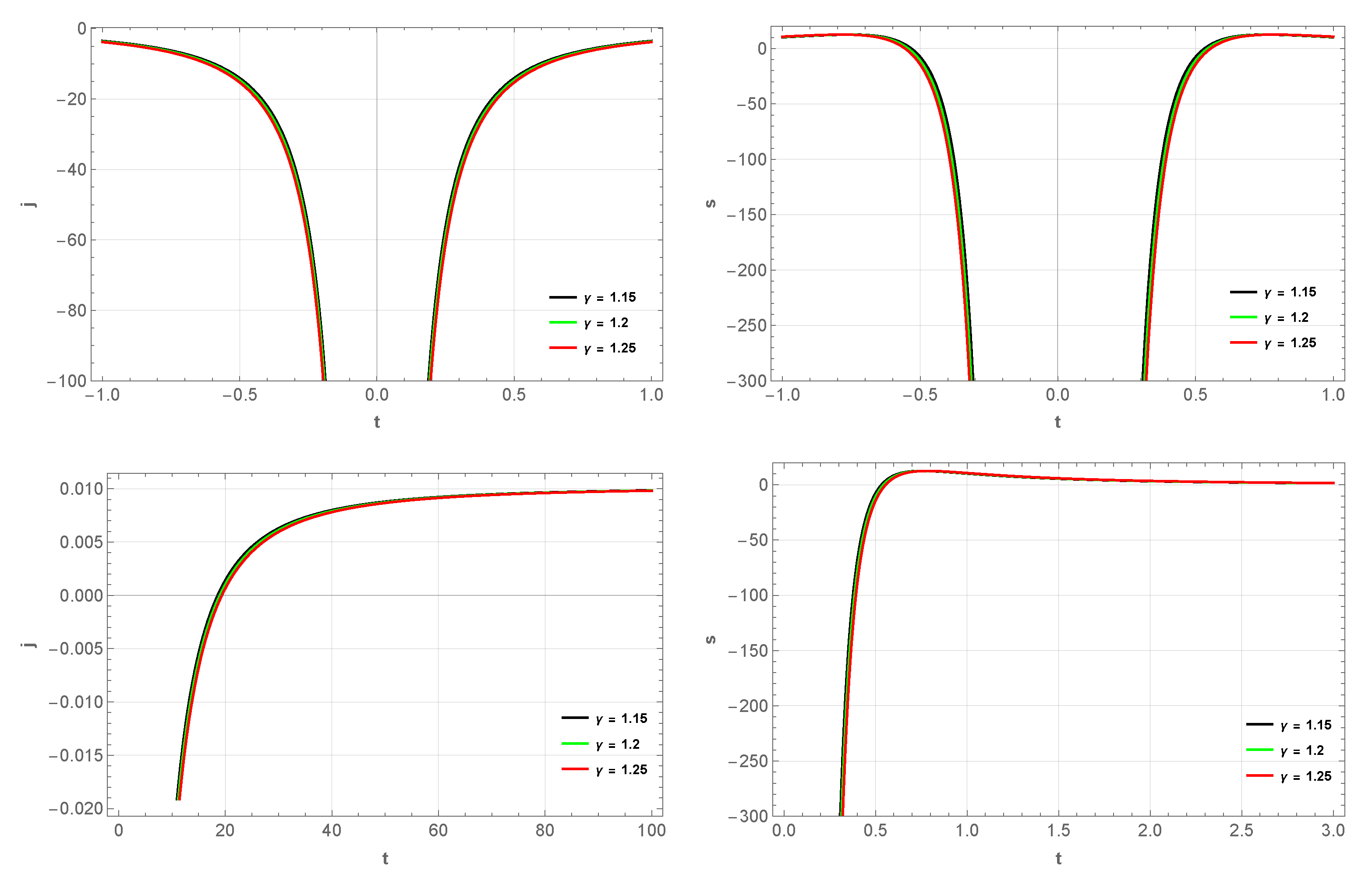
4. Bouncing Model II
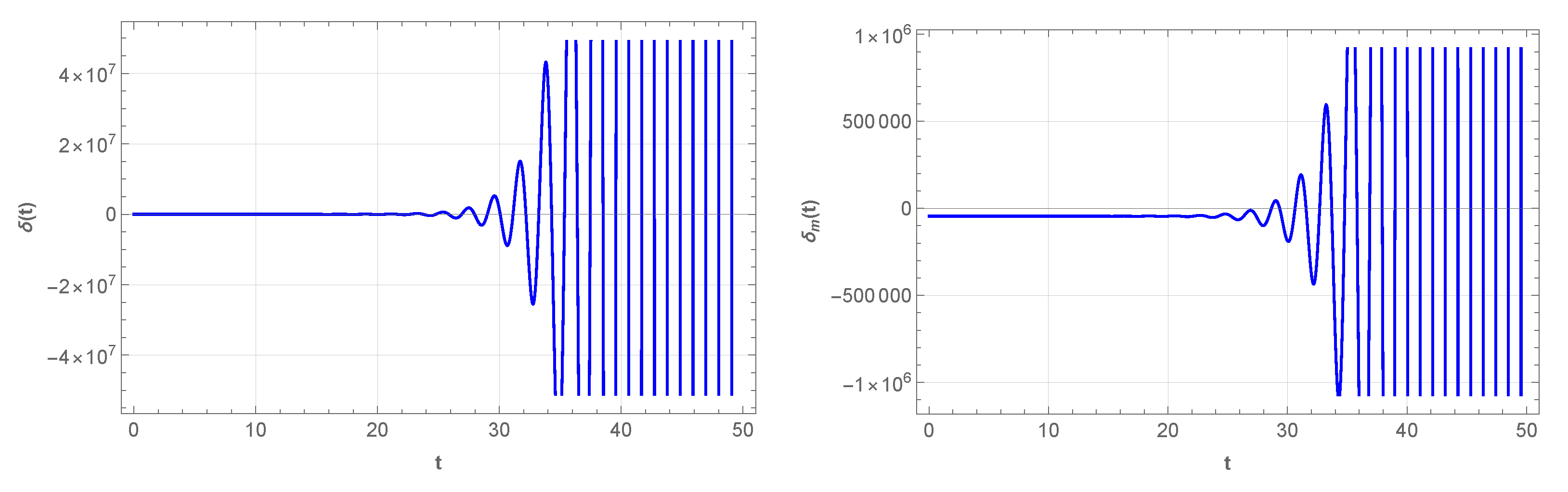
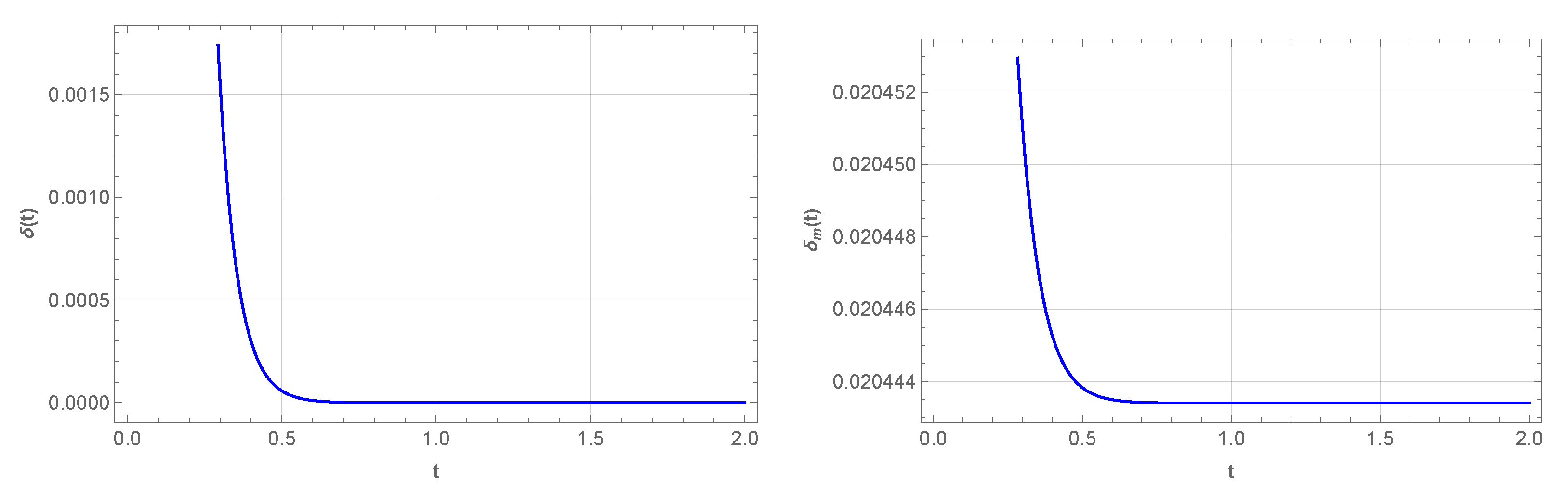
5. Scalar Perturbations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Riess, A.G.; Filippenko, A.V.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; Leibundgut, B.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Bennett, C.L.; Hill, R.S.; Hinshaw, G.; Nolta, M.R.; Odegard, N.; Page, L.; Spergel, D.N.; Weiland, J.L.; Wright, E.L.; Halpern, M.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP)* Observations: Foreground Emission. Astrophys. J. Suppl. Ser. 2003, 148, 1. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP)* Observations: Determination of Cosmological Parameters. Astrophys. J. 2003, 148, 175. [Google Scholar] [CrossRef]
- Spergel, D.N.; Bean, R.; Doré, O.; Nolta, M.R.; Bennett, C.L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; Komatsu, E.; Page, L.; et al. Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology. Astrophys. J. 2007, 170, 377. [Google Scholar] [CrossRef]
- Percival, W.J.; Reid, B.A.; Eisenstein, D.J.; Bahcall, N.A.; Budavari, T.; Frieman, J.A.; Fukugita, M.; Gunn, J.E.; Ivezić, Z.; Knapp, G.R.; et al. Baryon acoustic oscillations in the Sloan Digital Sky Survey Data Release 7 galaxy sample. Mon. Not. R. Astron. Soc. 2010, 401, 2148. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aikin, R.W.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Brevik, J.A.; Buder, I.; Bullock, E.; Dowell, C.D.; et al. Detection of B-Mode Polarization at Degree Angular Scales by BICEP2. Phys. Rev. Lett. 2014, 112, 241101. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- Barragán, C.; Olmo, G.J.; Sanchis-Alepuz, H.; Olmo, G.J.; Sanchis-Alepuz, H. Bouncing cosmologies in Palatini f(R) gravity. Phys. Rev. D 2019, 80, 024016. [Google Scholar] [CrossRef]
- Harko, T.; Francisco Lobo, S.N.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Cai, Y.F.; Chen, S.H.; Dent, J.B.; Dutta, S.; Saridakis, E.N. Matter bounce cosmology with the f(T) gravity. Class. Quant. Grav. 2011, 28, 215011. [Google Scholar] [CrossRef]
- Abedi, H.; Capozziello, S.; D’Agostino, R.; Luongo, O. Effective gravitational coupling in modified teleparallel theories. Phys. Rev. D 2018, 97, 084008. [Google Scholar] [CrossRef]
- Xu, Y.; Li, G.; Harko, T.; Liang, S.D. f(Q,T) gravity. Eur. Phys. J. C 2019, 79, 708. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gauss–Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 6. [Google Scholar] [CrossRef]
- Cai, Y.F.; Qiu, T.; Zhang, X.; Piao, Y.S.; Li, M. Bouncing universe with Quintom matter. J. High Energy Phys. 2007, 10, 071. [Google Scholar] [CrossRef]
- Peter, P.; Pinto-Neto, N. Primordial perturbations in a nonsingular bouncing universe model. Phys. Rev. D 2002, 66, 063509. [Google Scholar] [CrossRef]
- Lin, C.; Brandenberger, R.H.; Perreault, L.L. A matter bounce by means of ghost condensation. J. Cosmol. Astropart. Phys. 2011, 04, 019. [Google Scholar] [CrossRef]
- Fabris, J.C.; Furtado, R.G.; Peter, P.; Pinto-Neto, N. Regular cosmological bouncing solutions in low energy effective action from string theories. Phys. Rev. D 2003, 67, 124003. [Google Scholar] [CrossRef]
- Qiu, T.; Evslin, J.; Cai, Y.F.; Li, M.; Zhang, X. Bouncing Galileon cosmologies. J. Cosmol. Astropart. Phys. 2011, 10, 036. [Google Scholar] [CrossRef]
- Kounnas, C.; Partouche, H.; Toumbas, N. Thermal duality and non-singular cosmology in d-dimensional superstrings. Nucl. Phys. B 2012, 855, 280. [Google Scholar] [CrossRef]
- Novello, M.; Perez Bergliaffa, S.E. Bouncing cosmologies. Phys. Rep. 2008, 463, 127. [Google Scholar] [CrossRef]
- Elizalde, E.; Haro, J.; Odintsov, S.D. Quasimatter domination parameters in bouncing cosmologies. Phys. Rev. D 2015, 90, 063522. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Yu, J.T. Primeval Adiabatic Perturbation in an Expanding Universe. Astrophys. J. 1970, 162, 815. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. Small-scale fluctuations of relic radiation. Astrophys. Space Sci. 1970, 7, 3. [Google Scholar] [CrossRef]
- Battefeld, D.; Peter, P. A critical review of classical bouncing cosmologies. Phys. Rep. 2015, 571, 1. [Google Scholar] [CrossRef]
- Barrau, A.; Bolliet, B.; Schutten, M.; Vidotto, F. Bouncing black holes in quantum gravity and the Fermi gamma-ray excess. Phys. Lett. B 2017, 772, 58. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of a Singularity in Loop Quantum Cosmology. Phys. Rev. Lett. 2011, 86, 5227. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Matter Bounce Loop Quantum Cosmology from F(R) Gravity. Phys. Rev. D 2014, 90, 124083. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. Ekpyrotic universe: Colliding branes and the origin of the hot big bang. Phys. Rev. D 2001, 64, 123522. [Google Scholar] [CrossRef]
- Gasperini, M.; Giovannini, M.; Veneziano, G. Perturbations in a non-singular bouncing Universe. Phys. Lett. B 2003, 569, 113. [Google Scholar] [CrossRef]
- Nojiri, S.; Saridakis, E.N. Phantom without ghost. Astrophys. Space Sci. 2003, 347, 221. [Google Scholar] [CrossRef]
- Saridakis, E.N. Cyclic universes from general collisionless braneworld models. Nucl. Phys. B 2009, 808, 224. [Google Scholar] [CrossRef]
- Brandenberger, R. Matter bounce in Hořava-Lifshitz cosmology. Phys. Rev. D 2009, 80, 043516. [Google Scholar] [CrossRef]
- Cai, Y.F.; Saridakis, E.N. Non-singular cosmology in a model of non-relativistic gravity. J. Cosmol. Astropart. Phys. 2009, 10, 020. [Google Scholar] [CrossRef]
- Agrawal, A.S.; Pati, L.; Tripathy, S.K.; Mishra, B. Matter bounce scenario and the dynamical aspects in f(Q,T) gravity. Phys. Dark Universe 2021, 33, 100863. [Google Scholar] [CrossRef]
- Cai, Y.F.; Duplessis, F.; Easson, D.A.; Wang, D.G. Searching for a matter bounce cosmology with low redshift observations. Phys. Rev. D 2016, 93, 043546. [Google Scholar] [CrossRef]
- Shabani, H.; Ziaie, A.H. Bouncing cosmological solutions from f(R,T) gravity. Eur. Phys. J. C 2018, 78, 397. [Google Scholar] [CrossRef]
- Mishra, B.; Ribeiro, G.; Moraes, P.H.R.S. De Sitter and bounce solutions from anisotropy in extended gravity cosmology. Mod. Phys. Lett. A 2019, 34, 1950321. [Google Scholar] [CrossRef]
- Tripathy, S.K.; Mishra, B.; Ray, S.; Sengupta, R. Bouncing universe models in an extended gravity theory. Chin. J. Phys. 2021, 71, 610. [Google Scholar] [CrossRef]
- Agrawal, A.S.; Tripathy, S.K.; Pal, S.; Mishra, B. Role of extended gravity theory in matter bounce dynamics. Phys. Scr. 2022, 97, 025002. [Google Scholar] [CrossRef]
- Agrawal, A.S.; Tello-Ortiz, F.; Mishra, B.; Tripathy, S.K. Bouncing Cosmology in Extended Gravity and Its Reconstruction as Dark Energy Model. Fortschr. Phys. 2022, 70, 2100065. [Google Scholar] [CrossRef]
- Amani, A.R. The bouncing cosmology with F(R) gravity and its reconstructing. Int. J. Mod. Phys. D 2016, 25, 1650071. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Bounce universe history from unimodular F(R) gravity. Phys. Rev. D 2016, 93, 084050. [Google Scholar] [CrossRef]
- Ilyas, M.; Rahman, W.U. Bounce cosmology in f(R) gravity. Eur. Phys. J. C 2021, 81, 160. [Google Scholar] [CrossRef]
- Amoros, J.; de Haro, J.; Odintsov, S.D. Bouncing loop quantum cosmology from F(T) gravity. Phys. Rev. D 2013, 87, 104037. [Google Scholar] [CrossRef]
- Caruana, M.; Farrugia, G.; Levi Said, J. Cosmological bouncing solutions in f(T,B) gravity. Eur. Phys. J. C 2020, 80, 640. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Paul, T. Bottom-up reconstruction of non-singular bounce in F(R) gravity from observational indices. Nucl. Phys. B 2020, 959, 115159. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Shojaee, R. Phantom-Like Behavior in Modified Teleparallel Gravity. Adv. High Energy Phys. 2019, 8, 4026856. [Google Scholar] [CrossRef]
- Duchaniya, L.K.; Lohakare, S.V.; Mishra, B.; Tripathy, S.K. Dynamical stability analysis of accelerating f(T) gravity models. Eur. Phys. J. C 2022, 82, 448. [Google Scholar] [CrossRef]
- Barrow, J.D.; Cotsakis, S. Inflation and the conformal structure of higher-order gravity theories. Phys. Lett. B 1988, 214, 515. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Carloni, S.; Troisi, A. Can higher order curvature theories explain rotation curves of galaxies? Phys. Lett. A 2004, 326, 292. [Google Scholar] [CrossRef]
- Elizalde, E.; Myrzakulov, R.; Obukhov, V.V.; Sáez-Gómez, D. ΛCDM epoch reconstruction from F(R,G) and modified Gauss–Bonnet gravities. Class. Quantum Grav. 2010, 27, 095007. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, A.; Saez-Gomez, D. On the stability of the cosmological solutions in f(R,G) gravity. Class. Quantum Grav. 2012, 29, 245014. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Zerbini, S. Dark energy in modified Gauss–Bonnet gravity: Late-time acceleration and the hierarchy problem. Phys. Rev. D 2006, 73, 084007. [Google Scholar] [CrossRef]
- De Felice, A.; Suyama, T. Vacuum structure for scalar cosmological perturbations in modified gravity models. J. Cosmol. Astropart. Phys. 2009, 0906, 034. [Google Scholar] [CrossRef]
- De Felice, A.; Gerard, J.M.; Suyama, T. Cosmological perturbation in f(R,G) theories with a perfect fluid. Phys. Rev. D 2010, 82, 063526. [Google Scholar] [CrossRef]
- De Felice, A.; Suyama, T.; Tanaka, T. Stability of Schwarzschild-like solutions in f(R,G) gravity models. Phys. Rev. D 2011, 83, 104035. [Google Scholar] [CrossRef]
- Makarenko, A.N.; Obukhov, V.V.; Kirnos, I.V. From Big to Little Rip in modified F(R,G) gravity. Astrophys. Space Sci. 2013, 343, 481. [Google Scholar] [CrossRef]
- De Laurentis, M.; Paolella, M.; Capozziello, S. Cosmological inflation in F(R,G) gravity. Phys. Rev. D 2015, 91, 083531. [Google Scholar] [CrossRef]
- De Martino, I.; de Laurentis, M.; Capozziello, S. Tracing the cosmic history by Gauss–Bonnet gravity. Phys. Rev. D 2020, 102, 063508. [Google Scholar] [CrossRef]
- Haro, J. Future singularity avoidance in phantom dark energy models. J. Cosmol. Astropart. Phys. 2012, 07, 007. [Google Scholar] [CrossRef]
- Haro, J.; Amorós, J. Viability of the matter bounce scenario in F(T) gravity and Loop Quantum Cosmology for general potentials. J. Cosmol. Astropart. Phys. 2014, 12, 031. [Google Scholar] [CrossRef]
- Cai, Y.F.; Saridakis, E.N.; Setare, M.R.; Xia, J.Q. Quintom cosmology: Theoretical implications and observations. Phys. Rep. 2010, 493, 1. [Google Scholar] [CrossRef]
- Caldwell, R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23. [Google Scholar] [CrossRef]
- Steinhardt, P.; Wang, L.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59, 123504. [Google Scholar] [CrossRef]
- Wang, B.; Gong, Y.; Abdalla, E. Thermodynamics of an accelerated expanding universe. Phys. Rev. D 2006, 74, 083520. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59. [Google Scholar] [CrossRef]
- Capozziello, S.; de Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167. [Google Scholar] [CrossRef]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder—A new geometrical diagnostic of dark energy. JETP Lett. 2003, 77, 201. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Saini, T.D.; Starobinsky, A.A. Exploring the expanding Universe and dark energy using the statefinder diagnostic. Mon. Not. R. Astron. Soc. 2003, 344, 1057. [Google Scholar] [CrossRef]
- Abdussattar; Prajapati, S.R. Role of deceleration parameter and interacting dark energy in singularity avoidance. Astrophys. Space Sci. 2011, 331, 657. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lohakare, S.V.; Tello-Ortiz, F.; Tripathy, S.K.; Mishra, B. Bouncing Cosmology in Modified Gravity with Higher-Order Gauss–Bonnet Curvature Term. Universe 2022, 8, 636. https://doi.org/10.3390/universe8120636
Lohakare SV, Tello-Ortiz F, Tripathy SK, Mishra B. Bouncing Cosmology in Modified Gravity with Higher-Order Gauss–Bonnet Curvature Term. Universe. 2022; 8(12):636. https://doi.org/10.3390/universe8120636
Chicago/Turabian StyleLohakare, Santosh V., Francisco Tello-Ortiz, S. K. Tripathy, and B. Mishra. 2022. "Bouncing Cosmology in Modified Gravity with Higher-Order Gauss–Bonnet Curvature Term" Universe 8, no. 12: 636. https://doi.org/10.3390/universe8120636
APA StyleLohakare, S. V., Tello-Ortiz, F., Tripathy, S. K., & Mishra, B. (2022). Bouncing Cosmology in Modified Gravity with Higher-Order Gauss–Bonnet Curvature Term. Universe, 8(12), 636. https://doi.org/10.3390/universe8120636










