Pasta Phases in Neutron Star Mantle: Extended Thomas–Fermi vs. Compressible Liquid Drop Approaches
Abstract
1. Introduction
2. Basic Formalism
2.1. Extended Thomas–Fermi Calculations
2.2. Compressible Liquid Drop Model
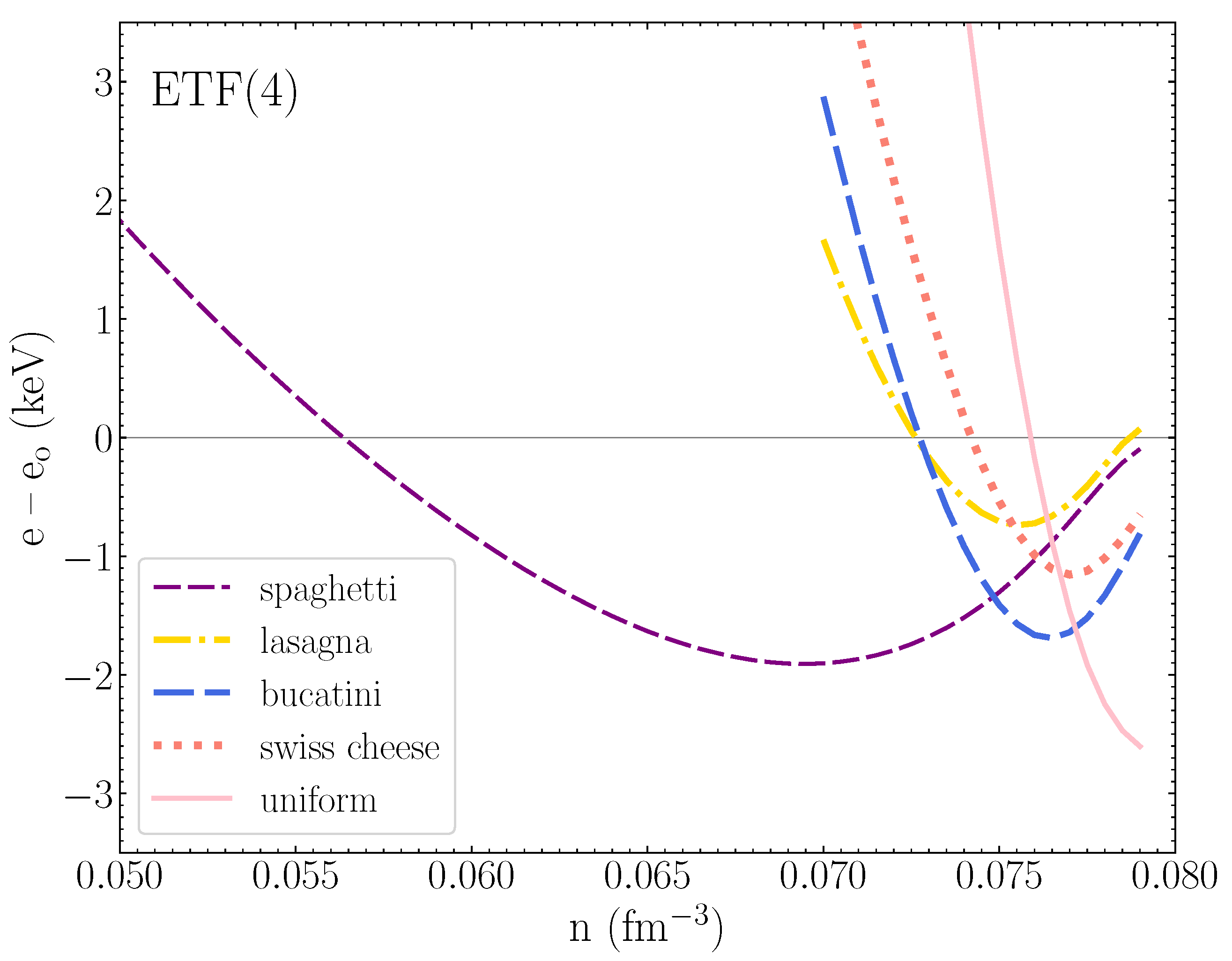
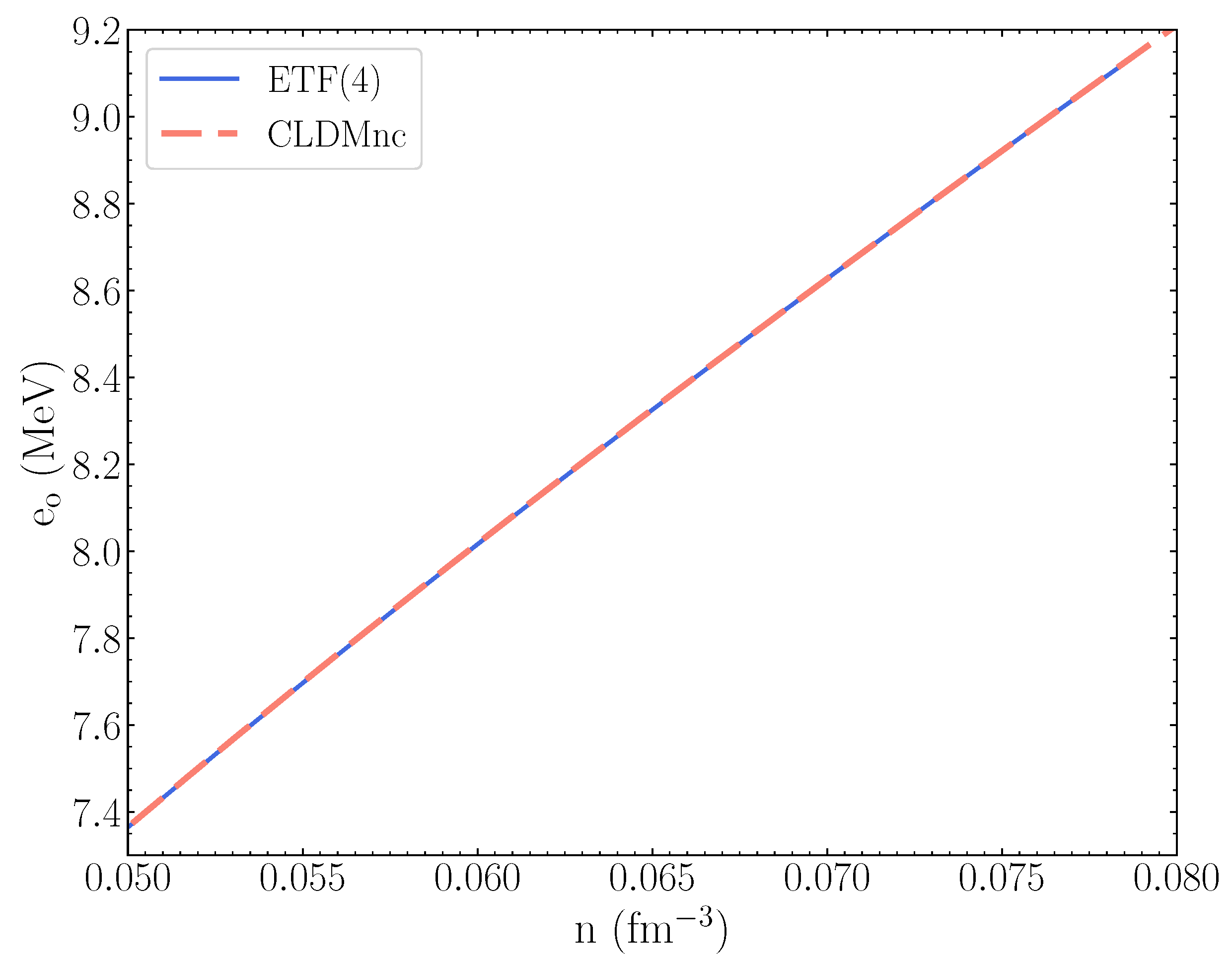
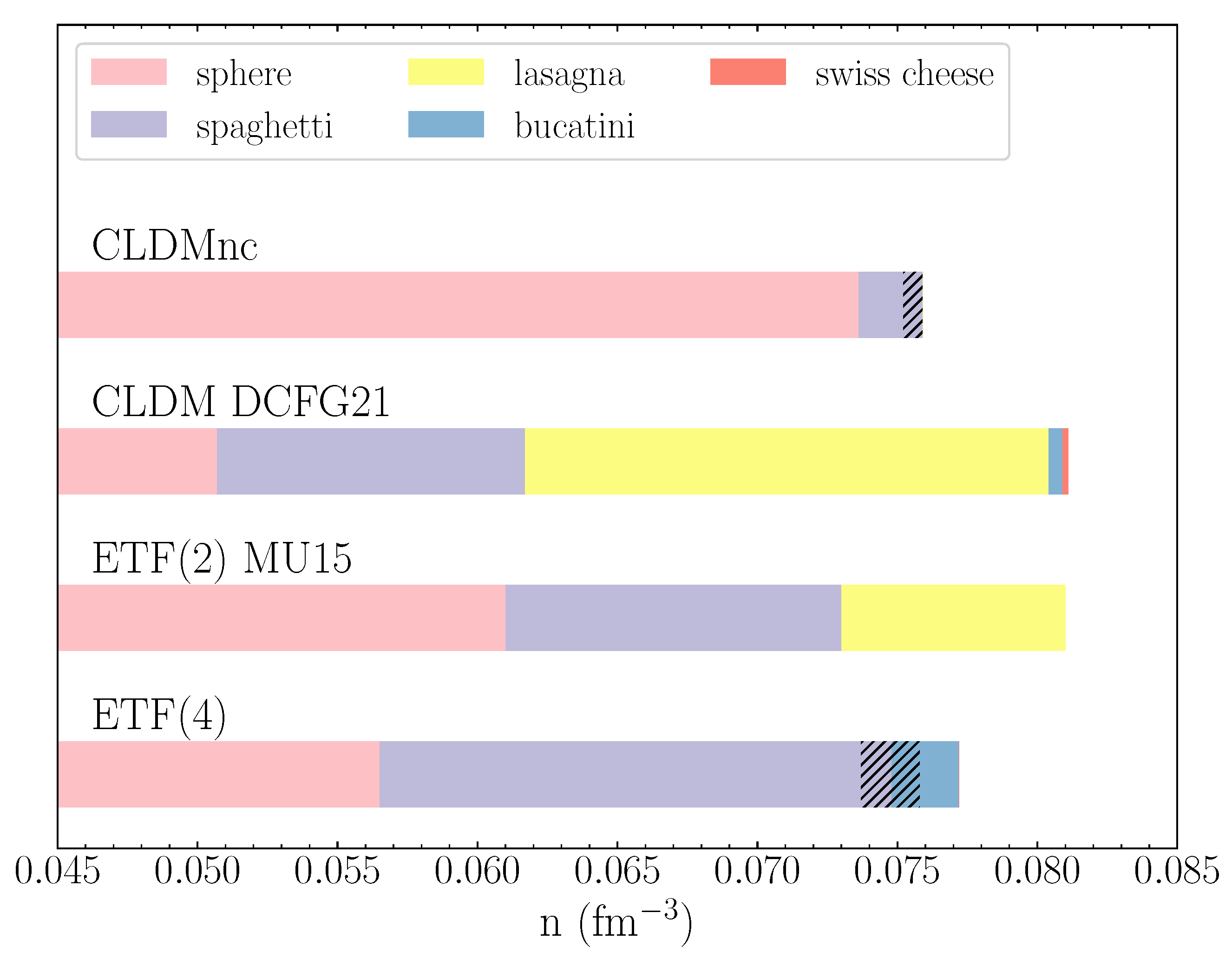
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | |
| 2 | According to [34], the NS temperatures of few keV can allow for a mixture of different phases. |
| 3 | Numerical results do not coincide with [43], which were based on surface tension calculated by the second-order ETF approach with a modified coefficient of the Weizsacker term. |
References
- Zdunik, J.L.; Fortin, M.; Haensel, P. Neutron star properties and the equation of state for the core. Astron. Astrophys. 2017, 599, A119. [Google Scholar] [CrossRef]
- Newton, W.G.; Balliet, L.; Budimir, S.; Crocombe, G.; Douglas, B.; Blake Head, T.; Langford, Z.; Rivera, L.; Sanford, J. Ensembles of unified crust and core equations of state in a nuclear-multimessenger astrophysics environment. arXiv 2021, arXiv:2112.12108. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Yakovlev, D.G.; Haensel, P.; Gnedin, O.Y. Direct Urca process in a neutron star mantle. Astron. Astrophys. 2004, 421, 1143–1148. [Google Scholar] [CrossRef]
- Yakovlev, D.G. Electron transport through nuclear pasta in magnetized neutron stars. Mon. Not. R Astron. Soc. 2015, 453, 581–590. [Google Scholar] [CrossRef]
- Schmitt, A.; Shternin, P. Reaction rates and transport in neutron stars. arXiv 2017, arXiv:1711.06520. [Google Scholar]
- Yakovlev, D.G.; Gusakov, M.E.; Haensel, P. Bulk viscosity in a neutron star mantle. Mon. Not. R Astron. Soc. 2018, 481, 4924–4930. [Google Scholar] [CrossRef]
- Lin, Z.; Caplan, M.E.; Horowitz, C.J.; Lunardini, C. Fast neutrino cooling of nuclear pasta in neutron stars: Molecular dynamics simulations. Phys. Rev. C 2020, 102, 045801. [Google Scholar] [CrossRef]
- Pethick, C.J.; Potekhin, A.Y. Liquid crystals in the mantles of neutron stars. Phys. Lett. B 1998, 427, 7–12. [Google Scholar] [CrossRef]
- Caplan, M.E.; Schneider, A.S.; Horowitz, C.J. Elast. Nucl. Pasta. Phys. Rev. Lett. 2018, 121, 132701. [Google Scholar] [CrossRef]
- Pethick, C.J.; Zhang, Z.W.; Kobyakov, D.N. Elastic properties of phases with nonspherical nuclei in dense matter. Phys. Rev. C 2020, 101, 055802. [Google Scholar] [CrossRef]
- Xia, C.J.; Maruyama, T.; Yasutake, N.; Tatsumi, T.; Zhang, Y.X. Elastic properties of nuclear pasta in a fully three-dimensional geometry. arXiv 2022, arXiv:2209.13310. [Google Scholar]
- Piekarewicz, J.; Fattoyev, F.J.; Horowitz, C.J. Pulsar glitches: The crust may be enough. Phys. Rev. C 2014, 90, 015803. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Berry, D.K.; Briggs, C.M.; Caplan, M.E.; Cumming, A.; Schneider, A.S. Disordered Nuclear Pasta, Magnetic Field Decay, and Crust Cooling in Neutron Stars. Phys. Rev. Lett. 2015, 114, 031102. [Google Scholar] [CrossRef]
- Pons, J.A.; Viganò, D.; Rea, N. A highly resistive layer within the crust of X-ray pulsars limits their spin periods. Nat. Phys. 2013, 9, 431–434. [Google Scholar] [CrossRef]
- Gearheart, M.; Newton, W.G.; Hooker, J.; Li, B.A. Upper limits on the observational effects of nuclear pasta in neutron stars. Mon. Not. R Astron. Soc. 2011, 418, 2343–2349. [Google Scholar] [CrossRef]
- Merritt, R.L.; Cackett, E.M.; Brown, E.F.; Page, D.; Cumming, A.; Degenaar, N.; Deibel, A.; Homan, J.; Miller, J.M.; Wijnands, R. The Thermal State of KS 1731-260 after 14.5 years in Quiescence. Astrophys. J. 2016, 833, 186. [Google Scholar] [CrossRef]
- Ootes, L.S.; Wijnands, R.; Page, D. Long-term temperature evolution of neutron stars undergoing episodic accretion outbursts. Astron. Astrophys. 2019, 630, A95. [Google Scholar] [CrossRef]
- Lalit, S.; Meisel, Z.; Brown, E.F. Crust-cooling Models Are Insensitive to the Crust-Core Transition Pressure for Realistic Equations of State. Astrophys. J. 2019, 882, 91. [Google Scholar] [CrossRef]
- Ravenhall, D.G.; Pethick, C.J.; Wilson, J.R. Structure of Matter below Nuclear Saturation Density. Phys. Rev. Lett. 1983, 50, 2066–2069. [Google Scholar] [CrossRef]
- Hashimoto, M.; Seki, H.; Yamada, M. Shape of nuclei in the crust of a neutron star. Prog. Theor. Phys. 1984, 71, 320–326. [Google Scholar] [CrossRef]
- Lorenz, C.P.; Ravenhall, D.G.; Pethick, C.J. Neutron star crusts. Phys. Rev. Lett. 1993, 70, 379–382. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P.; Meyer, J. Nuclear surface and curvature properties for SLy Skyrme forces and nuclei in the inner neutron-star crust. Nucl. Phys. A 2000, 665, 419–446. [Google Scholar] [CrossRef]
- Newton, W.G.; Gearheart, M.; Li, B.A. A Survey of the Parameter Space of the Compressible Liquid Drop Model as Applied to the Neutron Star Inner Crust. Astrophys. J. Suppl. Ser. 2012, 204, 9. [Google Scholar] [CrossRef]
- Newton, W.G.; Preston, R.; Balliet, L.; Ross, M. From neutron skins and neutron matter to the neutron star crust. arXiv 2021, arXiv:2111.07969. [Google Scholar] [CrossRef]
- Caplan, M.E.; Horowitz, C.J. Colloquium: Astromaterial science and nuclear pasta. Rev. Mod. Phys. 2017, 89, 041002. [Google Scholar] [CrossRef]
- Oyamatsu, K. Nuclear shapes in the inner crust of a neutron star. Nucl. Phys. A 1993, 561, 431–452. [Google Scholar] [CrossRef]
- Sharma, B.K.; Centelles, M.; Viñas, X.; Baldo, M.; Burgio, G.F. Unified equation of state for neutron stars on a microscopic basis. Astron. Astrophys. 2015, 584, A103. [Google Scholar] [CrossRef]
- Martin, N.; Urban, M. Liquid-gas coexistence versus energy minimization with respect to the density profile in the inhomogeneous inner crust of neutron stars. Phys. Rev. C 2015, 92, 015803. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. II. Pasta phases in semiclassical approximation. Phys. Rev. C 2020, 101, 015802. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. III. Inclusion of microscopic corrections to pasta phases. Phys. Rev. C 2022, 105, 015803. [Google Scholar] [CrossRef]
- Ji, F.; Hu, J.; Shen, H. Nuclear pasta and symmetry energy in the relativistic point-coupling model. Phys. Rev. C 2021, 103, 055802. [Google Scholar] [CrossRef]
- Schuetrumpf, B.; Nazarewicz, W. Twist-averaged boundary conditions for nuclear pasta Hartree-Fock calculations. Phys. Rev. C 2015, 92, 045806. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Horowitz, C.J.; Schuetrumpf, B. Quantum nuclear pasta and nuclear symmetry energy. Phys. Rev. C 2017, 95, 055804. [Google Scholar] [CrossRef]
- Newton, W.G.; Cantu, S.; Wang, S.; Stinson, A.; Kaltenborn, M.A.; Stone, J.R. Glassy quantum nuclear pasta in neutron star crusts. Phys. Rev. C 2022, 105, 025806. [Google Scholar] [CrossRef]
- Schneider, A.S.; Berry, D.K.; Briggs, C.M.; Caplan, M.E.; Horowitz, C.J. Nuclear “waffles”. Phys. Rev. C 2014, 90, 055805. [Google Scholar] [CrossRef]
- Berry, D.K.; Caplan, M.E.; Horowitz, C.J.; Huber, G.; Schneider, A.S. “Parking-garage” structures in nuclear astrophysics and cellular biophysics. Phys. Rev. C 2016, 94, 055801. [Google Scholar] [CrossRef]
- Schneider, A.S.; Caplan, M.E.; Berry, D.K.; Horowitz, C.J. Domains and defects in nuclear pasta. Phys. Rev. C 2018, 98, 055801. [Google Scholar] [CrossRef]
- Viñas, X.; Gonzalez-Boquera, C.; Sharma, B.K.; Centelles, M. Pasta-phase Transitions in the Inner Crust of Neutron Stars. Acta Phys. Pol. B Proc. Suppl. 2017, 10, 259. [Google Scholar]
- Gusakov, M.E.; Chugunov, A.I. Thermodynamically Consistent Equation of State for an Accreted Neutron Star Crust. Phys. Rev. Lett. 2020, 124, 191101. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Carreau, T.; Fantina, A.F.; Gulminelli, F. Uncertainties in the pasta-phase properties of catalysed neutron stars. Astron. Astrophys. 2021, 654, A114. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Fantina, A.F.; Gulminelli, F. The effect of the energy functional on the pasta-phase properties of catalysed neutron stars. Eur. Phys. J. A 2021, 57, 296. [Google Scholar] [CrossRef]
- Balliet, L.E.; Newton, W.G.; Cantu, S.; Budimir, S. Prior Probability Distributions of Neutron Star Crust Models. Astrophys. J. 2021, 918, 79. [Google Scholar] [CrossRef]
- Zemlyakov, N.A.; Chugunov, A.I.; Shchechilin, N.N. Non-spherical nucleon clusters in the mantle of a neutron star: CLDM based on Skyrme-type forces. J. Phys. Conf. Ser. 2021, 2103, 012004. [Google Scholar] [CrossRef]
- Pethick, C.; Ravenhall, D.; Lattimer, J. Effect of nuclear curvature energy on the transition between nuclei and bubbles in dense matter. Phys. Lett. B 1983, 128, 137–140. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.; Yakovlev, D. Neutron Stars 1: Equation of State and Structure. In Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Carreau, T.; Gulminelli, F.; Chamel, N.; Fantina, A.F.; Pearson, J.M. Crystallization of the inner crust of a neutron star and the influence of shell effects. Astron. Astrophys. 2020, 635, A84. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Chabrier, G. Crust structure and thermal evolution of neutron stars in soft X-ray transients. Astron. Astrophys. 2021, 645, A102. [Google Scholar] [CrossRef]
- Pais, H.; Bertolino, B.; Fang, J.; Wang, X.; Providência, C. Strong magnetic fields: Neutron stars with an extended inner crust. Eur. Phys. J. A 2021, 57, 193. [Google Scholar] [CrossRef]
- Bao, S.S.; Hu, J.N.; Shen, H. Impact of strong magnetic fields on the inner crust of neutron stars. Phys. Rev. C 2021, 103, 015804. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densitiesPart II. Nuclei far from stabilities. Nucl. Phys. A 1998, 635, 231–256. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. CVII. The nuclear surface. Philos. Mag. 1956, 1, 1043–1054. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D.M. Hartree-Fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei. Phys. Rev. C 1972, 5, 626–647. [Google Scholar] [CrossRef]
- Brack, M.; Guet, C.; Håkansson, H.B. Selfconsistent semiclassical description of average nuclear properties—A link between microscopic and macroscopic models. Phys. Rep. 1985, 123, 275–364. [Google Scholar] [CrossRef]
- Shelley, M.; Pastore, A. How accurately can the Extended Thomas–Fermi method describe the inner crust of a neutron star? J. Phys. Conf. Ser. 2020, 1668, 012037. [Google Scholar] [CrossRef]
- Shelley, M.; Pastore, A. Comparison between the Thomas–Fermi and Hartree-Fock-Bogoliubov Methods in the Inner Crust of a Neutron Star: The Role of Pairing Correlations. Universe 2020, 6, 206. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels-Montreal functionals - I. Role of symmetry energy. Mon. Not. R Astron. Soc. 2018, 481, 2994–3026. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Cornell University: Ithaca, NY, USA, 1983. [Google Scholar]
- Centelles, M.; Del Estal, M.; Viñas, X. Semiclassical treatment of asymmetric semi-infinite nuclear matter: Surface and curvature properties in relativistic and non-relativistic models. Nucl. Phys. A 1998, 635, 193–230. [Google Scholar] [CrossRef]
- Shchechilin, N.N.; Chugunov, A.I. Surface energy of nuclear matter above and below neutron drip with the Skyrme-type effective interactions. In Proceedings of the Journal of Physics Conference Series. J. Phys. Conf. Ser. 2020, 1697, 012025. [Google Scholar] [CrossRef]
- Furtado, U.J.; Gulminelli, F. Parametrization of the surface energy in the ETF approximation. J. Phys. G Nucl. Phys. 2021, 48, 015102. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Pethick, C.J.; Ravenhall, D.G.; Lamb, D.Q. Physical properties of hot, dense matter: The general case. Nucl. Phys. A 1985, 432, 646–742. [Google Scholar] [CrossRef]
- Carreau, T.; Gulminelli, F.; Margueron, J. General predictions for the neutron star crustal moment of inertia. Phys. Rev. C 2019, 100, 055803. [Google Scholar] [CrossRef]
- Carreau, T.; Gulminelli, F.; Margueron, J. Bayesian analysis of the crust-core transition with a compressible liquid-drop model. Eur. Phys. J. A 2019, 55, 188. [Google Scholar] [CrossRef]
- Mackie, F.D.; Baym, G. Compressible liquid drop nuclear model and mass formula. Nucl. Phys. A 1977, 285, 332–348. [Google Scholar] [CrossRef]
- Wang, M.; Audi, G.; Kondev, F.G.; Huang, W.J.; Naimi, S.; Xu, X. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2017, 41, 030003. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Goriely, S.; Ducoin, C. Inner crust of neutron stars with mass-fitted Skyrme functionals. Phys. Rev. C 2012, 85, 065803. [Google Scholar] [CrossRef]
- Chamel, N.; Naimi, S.; Khan, E.; Margueron, J. Validity of the Wigner-Seitz approximation in neutron star crust. Phys. Rev. C 2007, 75, 055806. [Google Scholar] [CrossRef]
- Baldo, M.; Saperstein, E.E.; Tolokonnikov, S.V. The role of the boundary conditions in the Wigner Seitz approximation applied to the neutron star inner crust. Nucl. Phys. A 2006, 775, 235–244. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shchechilin, N.N.; Zemlyakov, N.A.; Chugunov, A.I.; Gusakov, M.E. Pasta Phases in Neutron Star Mantle: Extended Thomas–Fermi vs. Compressible Liquid Drop Approaches. Universe 2022, 8, 582. https://doi.org/10.3390/universe8110582
Shchechilin NN, Zemlyakov NA, Chugunov AI, Gusakov ME. Pasta Phases in Neutron Star Mantle: Extended Thomas–Fermi vs. Compressible Liquid Drop Approaches. Universe. 2022; 8(11):582. https://doi.org/10.3390/universe8110582
Chicago/Turabian StyleShchechilin, Nikolai N., Nikita A. Zemlyakov, Andrey I. Chugunov, and Mikhail E. Gusakov. 2022. "Pasta Phases in Neutron Star Mantle: Extended Thomas–Fermi vs. Compressible Liquid Drop Approaches" Universe 8, no. 11: 582. https://doi.org/10.3390/universe8110582
APA StyleShchechilin, N. N., Zemlyakov, N. A., Chugunov, A. I., & Gusakov, M. E. (2022). Pasta Phases in Neutron Star Mantle: Extended Thomas–Fermi vs. Compressible Liquid Drop Approaches. Universe, 8(11), 582. https://doi.org/10.3390/universe8110582






