On General-Relativistic Lagrangian Perturbation Theory and Its Non-Perturbative Generalization
Abstract
1. Introduction
1.1. A Brief History of Lagrangian Perturbation Theory for Newtonian Flows
1.2. Relativistic Generalization of Lagrangian Perturbation Theory
1.2.1. Lagrange–Newton System
1.2.2. Lagrange–Einstein System
1.3. Summary of Results on Relativistic Lagrangian Perturbations
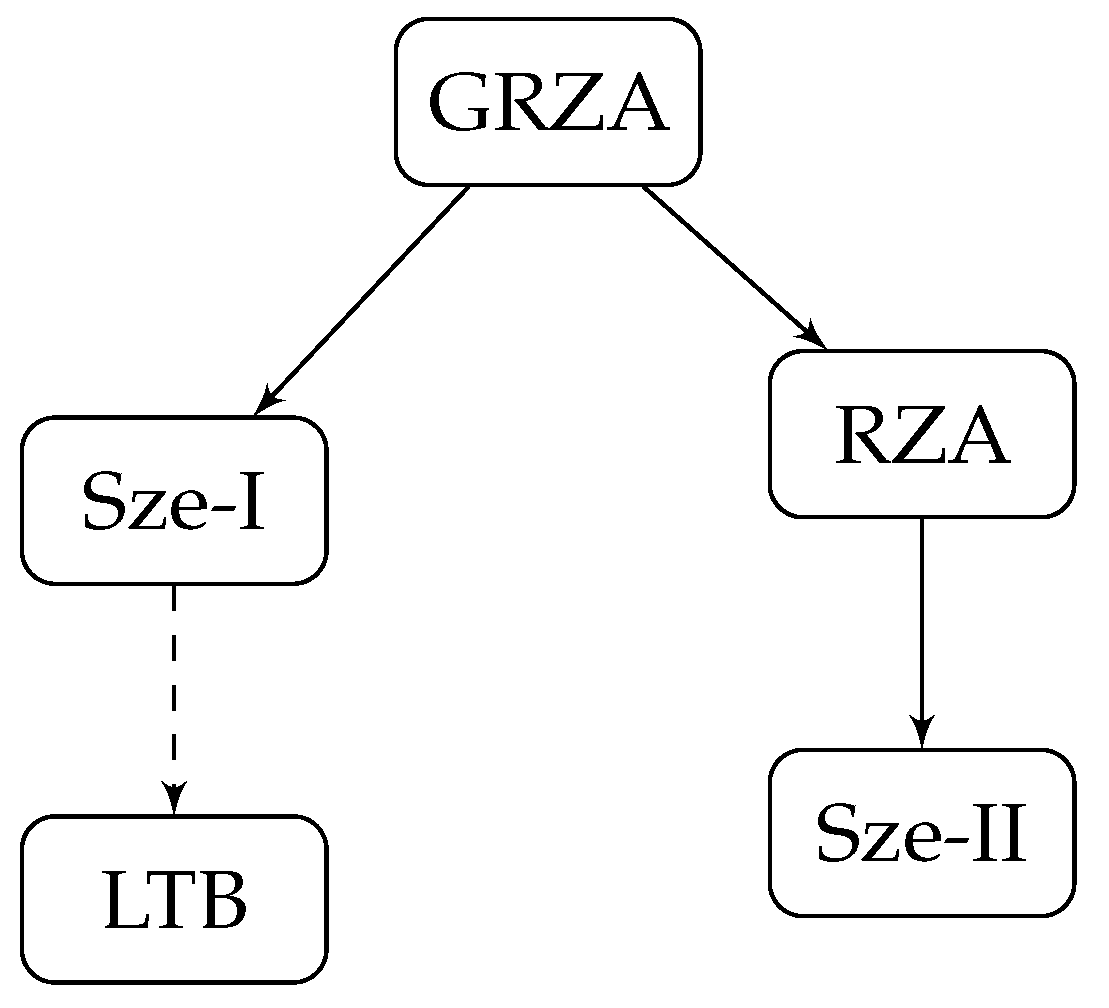
2. Non-Perturbative Generalization of Relativistic Lagrangian Perturbation Theory
2.1. Szekeres Solutions in the Goode and Wainwright Parameterization
- Class I:, , , and where is the time of the initial singularity and is an arbitrary function.
- Class II:, , , .
2.2. Szekeres Models and Lagrangian Perturbation Theory
2.2.1. Class II Models as the Exact Limit of RZA
2.2.2. Class I Models and Lagrangian Perturbation Theory
2.2.3. Rescaled Class I Solution
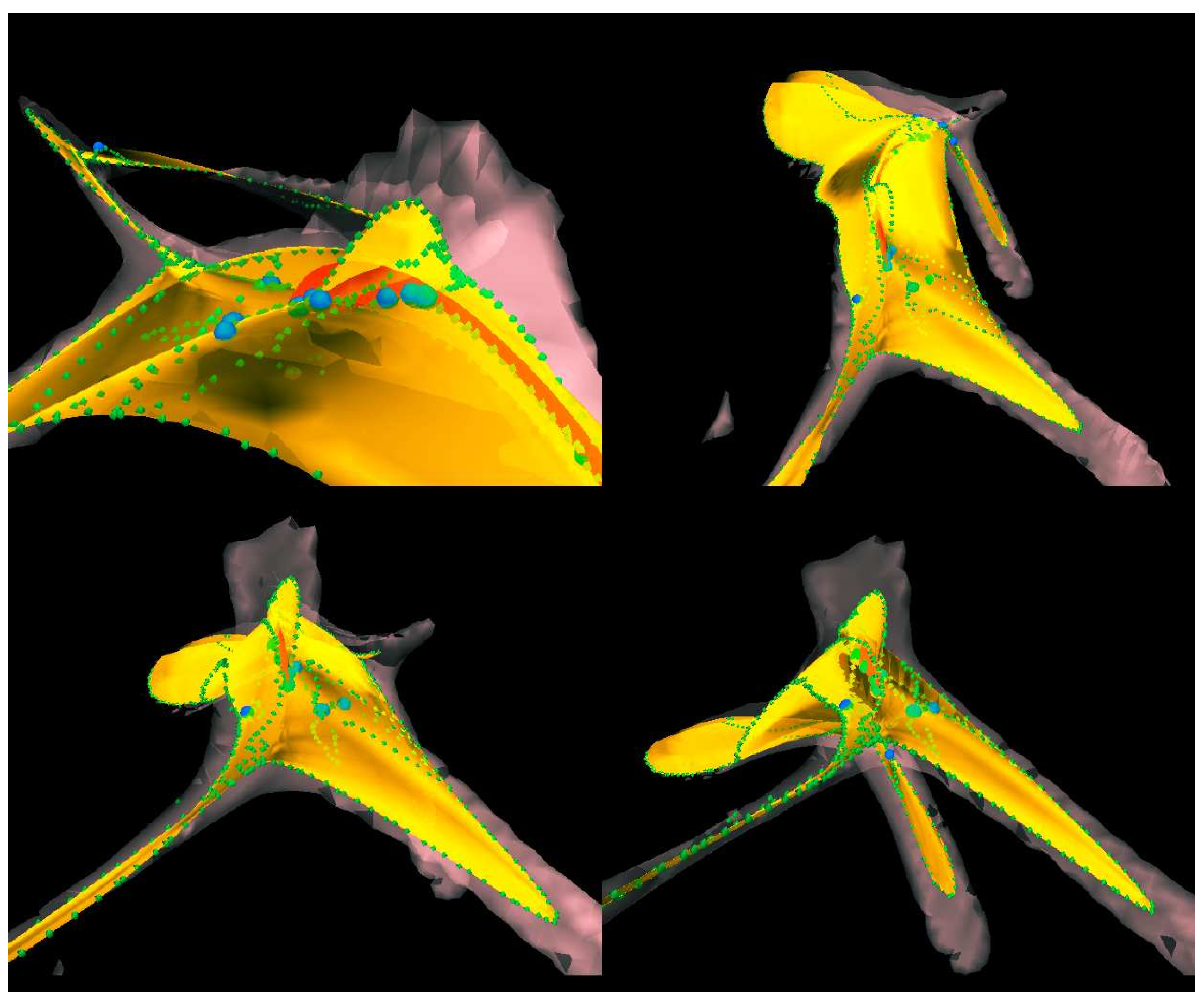
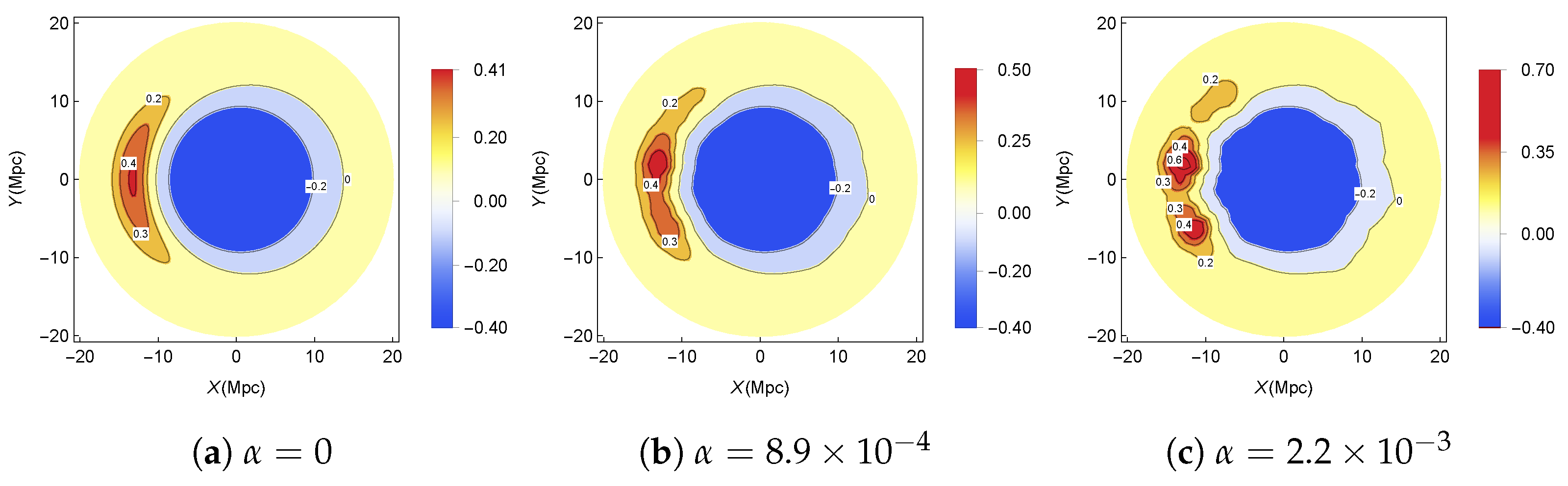
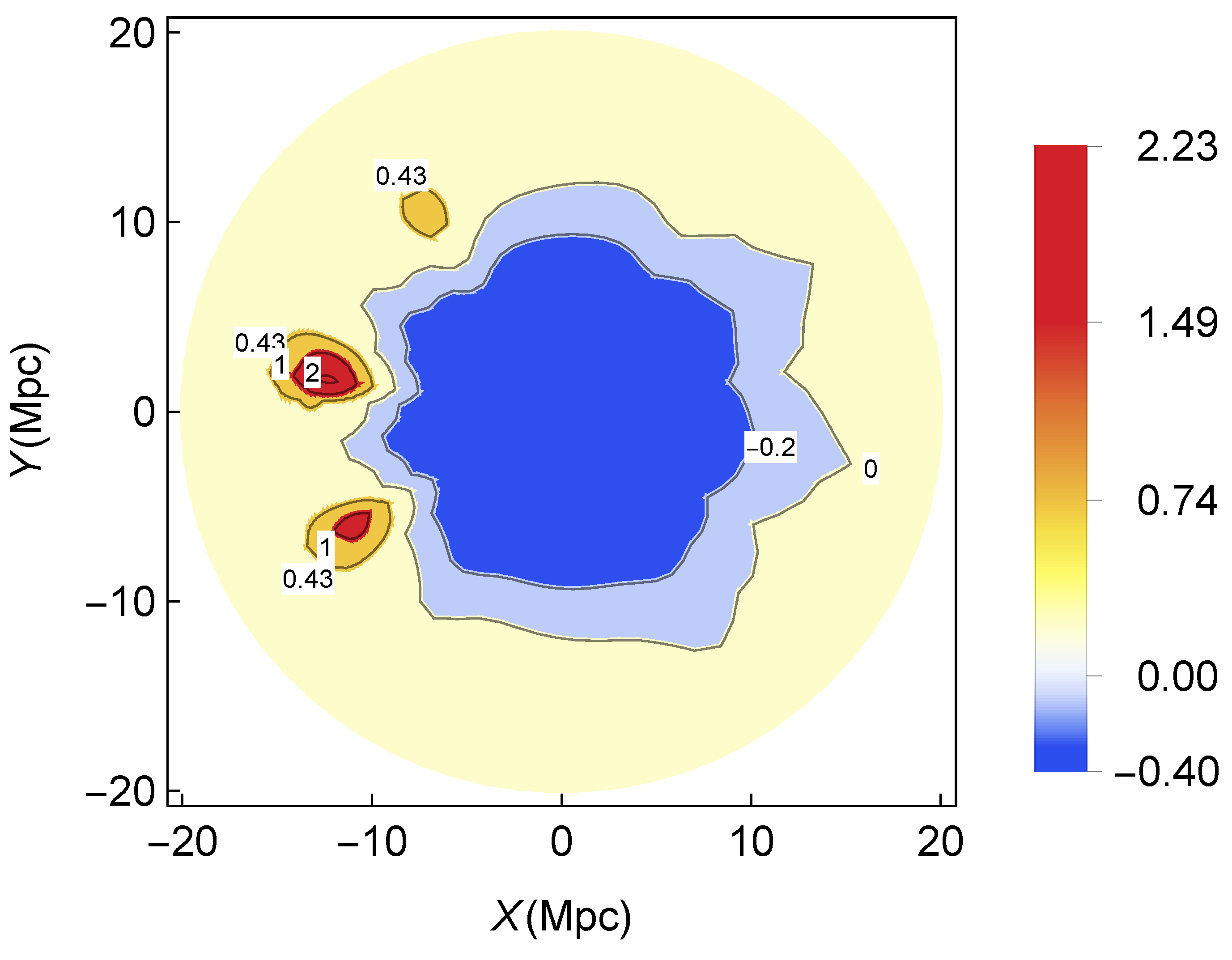
2.3. Generalized RZA: An Exact-Solution-Controlled Model of Structure Formation11
An Example of GRZA Numerical Simulation
3. Summary, Discussion and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | For further discussion of and references to the singularity problem, see [55], Section VB. |
| 2 | In this context, it is important to remark that the best numerical methods are simulations in phase space that provide a controlled and detailed access of the formation of structure via a projection into space [60]. Since the phase space is six-dimensional, this, however, provides limits of resolution. For recent simulations, see [61,62] and the review [63]. For a discussion of eigenvalues of the deformation tensor, see [64]. |
| 3 | In order to achieve even higher resolution, it is possible to interpolate initial data, since they are smooth and the analytical scheme maps any (calculated or interpolated) point to the nonlinear stage. |
| 4 | |
| 5 | We have distinguished counter-indices , here counting vector components, from coordinate indices . We shall later see that this is convenient when a coordinate basis does not exist; here, the vector components are also coordinate indices in the Eulerian basis. |
| 6 | Starting with Paper II in the series, we employ the metric form coefficients , using Gram’s matrix instead of for orthonormal co-frames. It has the advantage that the initial deformation can be set to be undeformed and therefore provides a closer correspondence to Newtonian solutions. The initial metric is then not encoded in initial deformations but in Gram’s matrix (for details, see [136,137]; for the Euclidean restriction (integrable limit) of Gram’s matrix, see Appendix A [136]), and for the integrable limit of the gravito-magnetic part, see Sect. III.A.2 [55].Note also that Equations (6a) imply . |
| 7 | |
| 8 | |
| 9 | Henceforth, we use units where . |
| 10 | To avoid confusion, we use to refer to the deformation field with respect a generic reference model and reserve for the deformation with respect to the FLRW background. |
| 11 | In this section, we highlight some of the salient results of a detailed investigation [189]. |
References
- Brustein, R.; Gasperini, M.; Giovannini, M.; Mukhanov, V.F.; Veneziano, G. Metric perturbations in dilaton-driven inflation. Phys. Rev. D 1995, 51, 6744. [Google Scholar] [CrossRef] [PubMed]
- Gasperini, M. Tensor perturbations in high-curvature string backgrounds. Phys. Rev. D 1997, 56, 4815. [Google Scholar] [CrossRef]
- Lifshitz, E.M. On the gravitational stability of the expanding universe. J. Phys. 1946, 10, 116–129, reprinted in Gen. Rel. Grav. 2017, 49, 18. [Google Scholar] [CrossRef]
- Hawking, S.W. Perturbations of an Expanding Universe. Astrophys. J. 1966, 145, 544. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Khalatnikov, I.M. Investigations in relativistic cosmology. Adv. Phys. 1963, 12, 185–249, reprinted in Sov. Phys. Usp. 1964, 6, 522. [Google Scholar] [CrossRef]
- Tomita, K. Non-Linear Theory of Gravitational Instability in the Expanding Universe. Prog. Theor. Phys. 1967, 37, 831–846. [Google Scholar] [CrossRef]
- Durrer, R. Gauge Invariant Cosmological Perturbation Theory: A General Study and It’s Application to the Texture Scenario of Structure Formation. Fundam. Cosm. Phys. 1994, 15, 209. [Google Scholar]
- Kodama, H.; Sasaki, M. Cosmological Perturbation Theory. Prog. Theor. Phys. Suppl. 1984, 78, 1. [Google Scholar] [CrossRef]
- Malik, K.A.; Wands, T. Cosmological perturbations. Phys. Rep. 2009, 475, 1. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Phys. Rep. 1992, 215, 203. [Google Scholar] [CrossRef]
- Ehlers, J. Beiträge zur relativistischen Mechanik kontinuierlicher Medien. Abh. Math.-Naturwissenschaftlichen Kl. 1961, 793–836, Translated: Contributions to the relativistic mechanics of continuous media. Gen. Rel. Grav. 1993, 25, 1225–1266. [Google Scholar] [CrossRef]
- Bardeen, J.M. Gauge-invariant cosmological perturbations. Phys. Rev. D 1980, 22, 1882. [Google Scholar] [CrossRef]
- Stewart, J.M. Perturbations of Friedmann-Robertson-Walker cosmological models. Class. Quant. Grav. 1990, 7, 1169. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Bruni, M. Covariant and gauge-invariant approach to cosmological density fluctuations. Phys. Rev. D 1989, 40, 1804. [Google Scholar] [CrossRef] [PubMed]
- Buchert, T.; Mourier, P.; Roy, X. On cosmological backreaction and its dependence on spacetime foliation. Class. Quant. Grav. 2018, 35, 24LT02. [Google Scholar] [CrossRef]
- Buchert, T.; Mourier, P.; Roy, X. On average properties of inhomogeneous fluids in general relativity III: General fluid cosmologies. Gen. Rel. Grav. 2020, 52, 27. [Google Scholar] [CrossRef]
- Vitenti, S.D.P.; Falciano, F.T.; Pinto-Neto, N. Covariant Bardeen perturbation formalism. Phys. Rev. D 2014, 89, 103538. [Google Scholar] [CrossRef]
- Roy, X.; Buchert, T. Relativistic cosmological perturbation scheme on a general background: Scalar perturbations for irrotational dust. Class. Quant. Grav. 2012, 29, 115004. [Google Scholar] [CrossRef][Green Version]
- Combi, L. Spacetime is material. In Contemporary Materialism. Its Ontology and Epistemology; Romero, E.G., Pérez Jara, J., Camprubí, L., Eds.; Synthese Library, Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Buchert, T.; Ehlers, J. Averaging inhomogeneous Newtonian cosmologies. Astron. Astrophys. 1997, 320, 1. [Google Scholar]
- Ellis, G.F.R.; Buchert, T. The universe seen at different scales. Phys. Lett. A 2005, 347, 38. [Google Scholar] [CrossRef]
- Buchert, T.; Carfora, M. Regional averaging and scaling in relativistic cosmology. Class. Quant. Grav. 2002, 19, 6109. [Google Scholar] [CrossRef]
- Carfora, M.; Piotrkowska, K. A Renormalization Group Approach to Relativistic Cosmology. Phys. Rev. D 1995, 52, 4393. [Google Scholar] [CrossRef] [PubMed]
- Buchert, T. On average properties of inhomogeneous fluids in general relativity I: Dust cosmologies. Gen. Rel. Grav. 2000, 32. [Google Scholar] [CrossRef]
- Buchert, T. On average properties of inhomogeneous fluids in general relativity II: Perfect fluid cosmologies. Gen. Rel. Grav. 2001, 33, 1381. [Google Scholar] [CrossRef]
- Buchert, T.; van Elst, H.; Heinesen, A. The averaging problem on the past null cone in inhomogeneous dust cosmologies. Gen. Rel. Grav. 2022, submitted.
- Gasperini, M.; Marozzi, G.; Veneziano, G. A covariant and gauge invariant formulation of the cosmological ‘backreaction’. J. Cosmol. Astropart. Phys. 2010, 2, 009. [Google Scholar] [CrossRef]
- Gasperini, M.; Marozzi, G.; Nugier, F.; Veneziano, G. Light-cone averaging in cosmology: Formalism and applications. J. Cosmol. Astropart. Phys. 2011, 7, 008. [Google Scholar] [CrossRef]
- Heinesen, A.; Mourier, P.; Buchert, T. On the covariance of scalar averaging and backreaction in relativistic inhomogeneous cosmology. Class. Quant. Grav. 2019, 36, 075001. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Myshkis, A.D. Elements of Mathematical Physics, Medium of Non-Interacting Particles; Nauka: Moscow, Russia, 1973. [Google Scholar]
- Dawson, J.M. Nonlinear Electron Oscillations in a Cold Plasma. Phys. Rev. 1959, 113, 383. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The Large-Scale Structure of the Universe; Princeton University Press: Princeton, JS, USA, 1980; ISBN 9780691209838. [Google Scholar]
- Zel’dovich, Y.B. Gravitational instability: An approximate theory for large density perturbations. Astron. Astrophys. 1970, 5, 84. [Google Scholar]
- Zel’dovich, Y.B. Fragmentation of a homogeneous medium under the action of gravitation. Astrofizika 1970, 6, 319, Translated in Astrophysics 1973, 6, 164–174. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. The Large Scale Structure of the Universe. In International Astronomical Union Symposia; Longair, M.S., Einasto, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1978; Volume 79, p. 409. ISBN 978-94-009-9843-8. [Google Scholar]
- Zel’dovich, Y.B.; Shandarin, S.F. Maximum density in heavy-neutrino clouds. Sov. Astron. Lett. 1982, 8, 139, Translated in Pis’ma Astron. Zh. 1982, 8, 259–262. [Google Scholar]
- Doroshkevich, A.G.; Ryabenkii, V.S.; Shandarin, S.F. Non-linear theory of development of potential perturbations. Astrofizika 1975, 9, 257, Translated in Astrophysics 1973, 9, 144. [Google Scholar]
- Bartelmann, M.; Schneider, P. A large-scale structure model for gravitational lensing. Astron. Astrophys. 1992, 259, 413. [Google Scholar]
- Doroshkevich, A.G. The space structure of perturbations and the origin of rotation of galaxies in the theory of fluctuation. Astrofizika 1973, 6, 581–600, Translated in Astrophysics 1970, 6, 320–330. [Google Scholar] [CrossRef]
- Grinstein, B.; Wise, M.B. On the validity of the Zel’dovich Approximation. Astrophys. J. 1987, 320, 448, Erratum in Astrophys. J. 1989, 337, 579. [Google Scholar] [CrossRef]
- Fillmore, J.A.; Goldreich, P. Self-similar gravitational collapse in an expanding Universe. Astrophys. J. 1984, 281, 1. [Google Scholar] [CrossRef]
- Bartelmann, M. Trajectories of point particles in cosmology and the Zel’dovich approximation. Phys. Rev. D 2014, 91, 083524. [Google Scholar] [CrossRef]
- Buchert, T. A class of solutions in Newtonian cosmology and the pancake theory. Astron. Astrophys. 1989, 223, 9. [Google Scholar]
- Shandarin, S.F.; Zel’dovich, Y.B. The large-scale structure of the universe: Turbulence, intermittency, structures in a self-gravitating medium. Rev. Mod. Phys. 1989, 61, 185. [Google Scholar] [CrossRef]
- Lin, C.C.; Mestel, L.; Shu, F.H. The Gravitational Collapse of a Uniform Spheroid. Astrophys. J. 1965, 142, 1431. [Google Scholar] [CrossRef]
- Goodman, J.; Binney, J. Gravitational collapse of pressureless inhomogeneous spheroids. Mon. Not. R. Astron. Soc. 1983, 203, 265. [Google Scholar] [CrossRef][Green Version]
- Yoshisato, A.; Matsubara, T.; Morikawa, M. Accuracy of Nonlinear Approximations in Spheroidal Collapse: Why Are Zeldovich-Type Approximations Good? Astrophys. J. 1998, 498, 48. [Google Scholar] [CrossRef]
- Doroshkevich, A.G.; Kotok, E.V.; Novikov, I.D.; Polyudov, A.N.; Shandarin, S.F.; Sigov, Y.S. Two-dimensional simulation of the gravitational system dynamics and formation of the large-scale structure of the universe. Mon. Not. R. Astron. Soc. 1980, 192, 321. [Google Scholar] [CrossRef]
- Klypin, A.A.; Shandarin, S.F. Three-dimensional numerical model of the formation of large-scale structure in the Universe. Mon. Not. R. Astron. Soc. 1983, 204, 891. [Google Scholar] [CrossRef]
- Melott, A.L.; Shandarin, S.F. Gravitational Instability with High Resolution. Astrophys. J. 1989, 343, 26. [Google Scholar] [CrossRef]
- Arnol’d, V.I.; Shandarin, S.F.; Zel’dovich, Y.B. The large-scale structure of the Universe. I. General properties. One- and two-dimensional models. Geophys. Astrophys. Fluid Dyn. 1982, 20, 111. [Google Scholar] [CrossRef]
- Arnol’d, V.I.; Gusein-Sade, S.M.; Varchenko, A.N. Singularities of Differentiable Maps; Birkhäuser: Boston, MA, USA, 1985; USSR Academy of Sciences: Moscow, Russia, 1982; Volume I. [Google Scholar]
- Shandarin, S.F. Evolution of Perturbations in Friedmann Models of the Universe. Astrofizika 1980, 16, 769–779, Translated in Astrophysics 1980, 16, 439–445. [Google Scholar] [CrossRef]
- Zentsova, A.S.; Chernin, A.D. Evolution of entropy perturbations in the post-recombination epoch II—Nonlinear stage. Astrofizika 1980, 16, 169–177, Translated in Astrophysics 1980, 16, 108–113. [Google Scholar] [CrossRef]
- Buchert, T.; Ostermann, M. Lagrangian theory of structure formation in relativistic cosmology. I. Lagrangian framework and definition of a nonperturbative approximation. Phys. Rev. D 2012, 86, 023520. [Google Scholar] [CrossRef]
- Shukurov, A.M. Nonlinear growth of density perturbations in an expanding collisionless medium. Astrofizika 1981, 17, 469, Translated in Astrophysics 1982, 17, 263. [Google Scholar] [CrossRef]
- Gurbatov, S.N.; Saichev, A.I.; Shandarin, S.F. The large-scale structure of the universe in the frame of the model equation of non-linear diffusion. Mon. Not. R. Astron. Soc. 1989, 236, 385. [Google Scholar] [CrossRef]
- Buchert, T.; Domínguez, A. Modeling multi-stream flow in collisionless matter: Approximations for large-scale structure beyond shell-crossing. Astron. Astrophys. 1998, 335, 395. [Google Scholar]
- Buchert, T.; Domínguez, A. Adhesive Gravitational Clustering. Astron. Astrophys. 2005, 438, 443. [Google Scholar] [CrossRef]
- Afshordi, N.; Mohayaee, R.; Bertschinger, E. Hierarchical phase space structure of dark matter haloes: Tidal debris, caustics, and dark matter annihilation. Phys. Rev. D 2009, 79, 083526. [Google Scholar] [CrossRef]
- Hahn, O.; Abel, T.; Kaehler, R. Tracing the Dark Matter sheet in phase space. Mon. Not. R. Astron. Soc. 2012, 427, 61. [Google Scholar] [CrossRef]
- Hahn, O.; Abel, T.; Kaehler, R. A new approach to simulating collisionless dark matter fluids. Mon. Not. R. Astron. Soc. 2013, 434, 1171. [Google Scholar] [CrossRef]
- Angulo, R.E.; Hahn, O. Large-scale dark matter simulations. Living Rev. Comput. Astrophys. 2022, 8, 1. [Google Scholar] [CrossRef]
- Nadkarni-Ghosh, S.; Singhal, A. Phase Space dynamics of triaxial collapse: Joint density-velocity evolution. Mon. Not. R. Astron. Soc. 2016, 457, 2773. [Google Scholar] [CrossRef]
- Buchert, T.; Domínguez, A.; Pérez-Mercader, J. Extending the scope of models for large-scale structure formation in the Universe. Astron. Astrophys. 1999, 349, 343. [Google Scholar]
- Buchert, T. The non-perturbative regime of cosmic structure formation. Astron. Astrophys. 2006, 454, 415. [Google Scholar] [CrossRef]
- Bildhauer, S.; Buchert, T.; Kasai, M. Solutions in Newtonian cosmology—The pancake theory with cosmological constant. Astron. Astrophys. 1992, 263, 23. [Google Scholar]
- Buchert, T.; Götz, G. A class of solutions for self-gravitating dust in Newtonian gravity. J. Math. Phys. 1987, 28, 2714. [Google Scholar] [CrossRef]
- Buchert, T. Lagrangian theory of gravitational instability of Friedmann–Lemaître cosmologies and the ‘Zel’dovich approximation’. Mon. Not. R. Astron. Soc. 1992, 254, 729. [Google Scholar] [CrossRef]
- Buchert, T.; Ehlers, J. Lagrangian theory of gravitational instability of Friedmann–Lemaître cosmologies—Second-order approach: An improved model for nonlinear clustering. Mon. Not. R. Astron. Soc. 1993, 264, 375. [Google Scholar] [CrossRef]
- Buchert, T. Lagrangian theory of gravitational instability of Friedmann–Lemaître cosmologies—A generic third–order model for nonlinear clustering. Mon. Not. R. Astron. Soc. 1994, 267, 811. [Google Scholar] [CrossRef]
- Rampf, C.; Buchert, T. Lagrangian perturbations and the matter bispectrum I: Fourth-order model for non-linear clustering. J. Cosmol. Astropart. Phys. 2012, 06, 021. [Google Scholar] [CrossRef]
- Ehlers, J.; Buchert, T. Newtonian cosmology in Lagrangian formulation: Foundations and perturbation theory. Gen. Rel. Grav. 1997, 29, 733. [Google Scholar] [CrossRef]
- Matsubara, T. Recursive solutions of Lagrangian perturbation theory. Phys. Rev. D 2015, 92, 023534. [Google Scholar] [CrossRef]
- Rampf, C. The recursion relation in Lagrangian perturbation theory. J. Cosmol. Astropart. Phys. 2012, 12, 004. [Google Scholar] [CrossRef]
- Rampf, C.; Villone, B.; Frisch, U. How smooth are particle trajectories in a ΛCDM Universe? Mon. Not. R. Astron. Soc. 2015, 452, 1421. [Google Scholar] [CrossRef]
- Zheligovsky, V.; Frisch, U. Time-analyticity of Lagrangian particle trajectories in ideal fluid flow. J. Fluid Mech. 2014, 749, 404. [Google Scholar] [CrossRef]
- Bouchet, F.R.; Juszkiewicz, R.; Colombi, S.; Pellat, R. Weakly nonlinear gravitational instability for arbitrary Omega. Astrophys. J. 1992, 394, L5. [Google Scholar] [CrossRef]
- Bouchet, F.R.; Colombi, S.; Hivon, E.; Juszkiewicz, R. Perturbative Lagrangian approach to gravitational instability. Astron. Astrophys. 1995, 296, 575. [Google Scholar]
- Moutarde, F.; Alimi, J.-M.; Bouchet, F.R.; Pellat, R.; Ramani, A. Precollapse scale invariance in gravitational instability. Astrophys. J. 1991, 382, 377. [Google Scholar] [CrossRef]
- Sahni, V.; Coles, P. Approximation methods for nonlinear gravitational clustering. Phys. Rep. 1995, 262, 1. [Google Scholar] [CrossRef]
- Buchert, T. Lagrangian perturbation theory—A key-model for large-scale structure. Astron. Astrophys. 1993, 267, L51. [Google Scholar]
- Buchert, T. Lagrangian perturbation approach to the formation of large-scale structure. In Proceedings of the International School of Physics “Enrico Fermi”; IOS Press: Amsterdam, The Netherlands, 1995; pp. 543–564. [Google Scholar] [CrossRef]
- Bertschinger, E. Cosmological Dynamics. (Les Houches Summer School Lectures on Cosmology, August 1993); Massachusetts Institute of Technology: Cambridge, MA, USA, 1995. [Google Scholar] [CrossRef]
- Bernardeau, F.; Colombi, S.; Gaztanaga, E.; Scoccimarro, R. Large-scale structure of the Universe and cosmological perturbation theory. Phys. Rep. 2002, 367, 1–248. [Google Scholar] [CrossRef]
- Adler, S.; Buchert, T. Lagrangian theory of structure formation in pressure-supported cosmological fluids. Astron. Astrophys. 1999, 343, 317. [Google Scholar] [CrossRef]
- Buchert, T.; Melott, A.L.; Weiß, A. Testing higher-order Lagrangian perturbation theory against numerical simulations—1. pancake models. Astron. Astrophys. 1994, 288, 349. [Google Scholar]
- Coles, P.; Melott, A.L.; Shandarin, S.F. Testing approximations for nonlinear gravitational clustering. Mon. Not. R. Astron. Soc. 1993, 260, 765. [Google Scholar] [CrossRef]
- Melott, A.L.; Buchert, T.; Weiß, A.G. Testing higher-order Lagrangian perturbation theory against numerical simulations—2. hierarchical models. Astron. Astrophys. 1995, 294, 345. [Google Scholar]
- Melott, A.L.; Pellman, T.F.; Shandarin, S.F. Optimizing the Zel’dovich approximation. Mon. Not. R. Astron. Soc. 1994, 269, 626. [Google Scholar] [CrossRef]
- Weiß, A.G.; Gottlöber, S.; Buchert, T. Optimizing higher-order Lagrangian perturbation theory for standard CDM and BSI models. Mon. Not. R. Astron. Soc. 1996, 278, 953. [Google Scholar] [CrossRef]
- Weinberg, D.H.; Gunn, J.E. Large-scale Structure and the Adhesion Approximation. Mon. Not. R. Astron. Soc. 1990, 247, 260. [Google Scholar]
- Michaux, M.; Hahn, O.; Rampf, C.; Angulo, R.E. Accurate initial conditions for cosmological N-body simulations: Minimizing truncation and discreteness errors. Mon. Not. R. Astron. Soc. 2021, 500, 663. [Google Scholar] [CrossRef]
- Schmidt, F. An n-th order Lagrangian forward model for large-scale structure. J. Cosmol. Astropart. Phys. 2021, 04, 033. [Google Scholar] [CrossRef]
- Buchert, T.; Karakatsanis, G.; Klaffl, R.; Schiller, P. The performance of Lagrangian perturbation schemes at high resolution. Astron. Astrophys. 1997, 318, 1. [Google Scholar]
- Yano, T.; Koyama, H.; Buchert, T.; Gouda, N. Universality in the distribution of caustics in the expanding Universe. Astrophys. J. Suppl. 2004, 151, 185. [Google Scholar] [CrossRef][Green Version]
- Rampf, C. Cosmological Vlasov-Poisson equations for dark matter. Rev. Mod. Plasma Phys. 2021, 5, 10. [Google Scholar] [CrossRef]
- Rampf, C.; Frisch, U. Shell-crossing in quasi-one-dimensional flow. Mon. Not. R. Astron. Soc. 2017, 471, 671. [Google Scholar] [CrossRef]
- Rampf, C.; Hahn, O. Shell-crossing in a ΛCDM Universe. Mon. Not. R. Astron. Soc. 2021, 501, L71. [Google Scholar] [CrossRef]
- Rampf, C.; Frisch, U.; Hahn, O. Unveiling the singular dynamics in the cosmic large-scale structure. Mon. Not. R. Astron. Soc. 2021, 505, L90. [Google Scholar] [CrossRef]
- Ray, S.S.; Frisch, U.; Nazarenko, S.; Matsumoto, T. Resonance phenomenon for the Galerkin-truncated Burgers and Euler equations. Phys. Rev. E 2011, 84, 016301. [Google Scholar] [CrossRef] [PubMed]
- Saga, S.; Taruya, A.; Colombi, S. Lagrangian Cosmological Perturbation Theory at Shell Crossing. Phys. Rev. Lett. 2018, 121, 241302. [Google Scholar] [CrossRef] [PubMed]
- Saga, S.; Taruya, A.; Colombi, S. Cold dark matter protohalo structure around collapse: Lagrangian cosmological perturbation theory versus Vlasov simulations. Astron. Astrophys. 2022, 664, A3. [Google Scholar] [CrossRef]
- Kitaura, F.-S.; Hess, S. Cosmological structure formation with augmented Lagrangian perturbation theory. Mon. Not. R. Astron. Soc. 2013, 435, L78. [Google Scholar] [CrossRef]
- Kitaura, F.-S.; Balaguera-Antolínez, A.; Sinigaglia, F.; Pellejero-Ibàñez, M. The cosmic web connection to the dark matter halo distribution through gravity. Mon. Not. R. Astron. Soc. 2022, 512, 2245. [Google Scholar] [CrossRef]
- Kokron, N.; Chen, S.F.; White, M.; DeRose, J.; Maus, M. Accurate predictions from small boxes: Variance suppression via the Zel’dovich approximation. J. Cosmol. Astropart. Phys. 2022, 09, 059. [Google Scholar] [CrossRef]
- Monaco, P. Approximate methods for the generation of dark matter halo catalogs in the age of precision cosmology. Galaxies 2016, 4, 53. [Google Scholar] [CrossRef]
- Monaco, P.; Sefusatti, E.; Borgani, S.; Crocce, M.; Fosalba, P.; Sheth, R.K.; Theuns, T. An accurate tool for the fast generation of dark matter halo catalogues. Mon. Not. R. Astron. Soc. 2013, 433, 2389. [Google Scholar] [CrossRef]
- Munari, E.; Monaco, P.; Sefusatti, E.; Castorina, E.; Mohammad, F.G.; Anselmi, S.; Borgani, S. Improving fast generation of halo catalogs with higher-order Lagrangian perturbation theory. Mon. Not. R. Astron. Soc. 2017, 465, 4658. [Google Scholar] [CrossRef]
- Buchert, T.; Bartelmann, M. High-spatial resolution in three dimensions: A challenge for large-scale structure formation models. Astron. Astrophys. 1991, 251, 389. [Google Scholar]
- Hidding, J.; Shandarin, S.F.; van de Weygaert, R. The Zel’dovich approximation: Key to understanding cosmic web complexity. Mon. Not. R. Astron. Soc. 2014, 437, 3442. [Google Scholar] [CrossRef]
- Buchert, T.; Shandarin, S.F.; Weiß, A. Building Blocks of Large-Scale Structure in the Universe. Three-Dimensional Singularities and Metamorphoses. 1995; unpublished. [Google Scholar]
- Susperregi, M.; Buchert, T. Cosmic density and velocity fields in Lagrangian perturbation theory. Astron. Astrophys. 1997, 323, 295. [Google Scholar]
- Doumler, T.; Hoffman, Y.; Courtois, H.; Gottlöber, S. Reconstructing cosmological initial conditions from galaxy peculiar velocities. I. Reverse Zel’dovich Approximation. Mon. Not. R. Astron. Soc. 2013, 430, 888. [Google Scholar] [CrossRef]
- Brenier, Y.; Frisch, U.; Henon, M.; Loeper, G.; Matarrese, S.; Mohayaee, R.; Sobolevskii, A. Reconstruction of the early Universe as a convex optimization problem. Mon. Not. R. Astron. Soc. 2003, 346, 501–524. [Google Scholar] [CrossRef]
- Nadkarni-Ghosh, S.; Chernoff, D.F. Extending the domain of validity of the Lagrangian approximation. Mon. Not. R. Astron. Soc. 2011, 410, 1454. [Google Scholar] [CrossRef][Green Version]
- Nadkarni-Ghosh, S.; Chernoff, D.F. Modelling non-linear evolution using Lagrangian Perturbation Theory (LPT) re-expansions. Mon. Not. R. Astron. Soc. 2013, 431, 799. [Google Scholar] [CrossRef]
- Crocce, M.; Scoccimarro, R. Renormalized cosmological perturbation theory. Phys. Rev. D 2006, 73, 063519. [Google Scholar] [CrossRef]
- Matsubara, T. Resumming cosmological perturbations via the Lagrangian picture: One-loop results in real space and in redshift space. Phys. Rev. D 2008, 77, 063530. [Google Scholar] [CrossRef]
- Hivon, E.; Bouchet, F.R.; Colombi, S.; Juszkiewicz, R. Redshift distortions of clustering: A Lagrangian approach. Astron. Astrophys. 1995, 298, 643. [Google Scholar]
- Percival, W.J.; White, M. Testing cosmological structure formation using redshift-space distortions. Mon. Not. R. Astron. Soc. 2009, 393, 29712. [Google Scholar] [CrossRef]
- Desjacques, V.; Jeong, D.; Schmidt, F. Large-scale galaxy bias. Phys. Rep. 2018, 733, 1–193. [Google Scholar] [CrossRef]
- Serrin, I. Mathematical Principles of Classical Fluid Mechanics. In Encyclopedia of Physics; Springer: Berlin/Heidelberg, Germany, 1959; Volume VIII.1, pp. 125–263. [Google Scholar] [CrossRef]
- Kasai, M. Inhomogeneous cosmological models which are homogeneous and isotropic on average. Phys. Rev. D 1993, 47, 3214. [Google Scholar] [CrossRef]
- Matarrese, S.; Pantano, O.; Saez, D. General relativistic dynamics of irrotational dust: Cosmological implications. Phys. Rev. Lett. 1994, 72, 320. [Google Scholar] [CrossRef]
- Matarrese, S.; Pantano, O.; Saez, D. A Relativistic Approach to Gravitational Instability in the Expanding Universe—Second-Order Lagrangian Solutions. Mon. Not. R. Astron. Soc. 1994, 271, 513. [Google Scholar] [CrossRef]
- Matarrese, S.; Terranova, D. Post-Newtonian cosmological dynamics in Lagrangian coordinates. Mon. Not. R. Astron. Soc. 1996, 283, 400. [Google Scholar] [CrossRef]
- Russ, H.; Morita, M.; Kasai, M.; Börner, G. Zel’dovich-type approximation for an inhomogeneous universe in general relativity: Second-order solutions. Phys. Rev. D 1996, 53, 6881. [Google Scholar] [CrossRef]
- Russ, H.; Soffel, M.H.; Kasai, M.; Börner, G. Age of the universe: Influence of the inhomogeneities on the global expansion factor. Phys. Rev. D 1997, 56, 2044. [Google Scholar] [CrossRef]
- Parry, J.; Salopek, D.S.; Stewart, J.M. Solving the Hamilton-Jacobi equation for general relativity. Phys. Rev. D 1994, 49, 2872. [Google Scholar] [CrossRef]
- Salopek, D.S.; Stewart, J.M. Hamilton-Jacobi theory for general relativity with matter fields. Class. Quant. Grav. 1992, 9, 1943. [Google Scholar] [CrossRef]
- Rampf, C.; Rigopoulos, G. Initial conditions for cold dark matter particles and general relativity. Phys. Rev. D 2013, 87, 123525. [Google Scholar] [CrossRef]
- Rigopoulos, G.; Valkenburg, W. Nonlinear approximation for perturbations in ΛCDM. Phys. Rev. D 2012, 86, 043523. [Google Scholar] [CrossRef]
- Buchert, T.; Mädler, T. Editorial Note to: On the Newtonian Limit of Einstein’s Theory of Gravitation (by Jürgen Ehlers). Gen. Rel. Grav. 2019, 51, 162. [Google Scholar] [CrossRef]
- Vigneron, Q. The 1+3-Newton-Cartan system and Newton-Cartan cosmology. Phys. Rev. D 2021, 103, 064064. [Google Scholar] [CrossRef]
- Alles, A.; Buchert, T.; Al Roumi, F.; Wiegand, A. Lagrangian theory of structure formation in relativistic cosmology. III. Gravitoelectric perturbation and solution schemes at any order. Phys. Rev. D 2015, 92, 023512. [Google Scholar] [CrossRef]
- Buchert, T.; Nayet, C.; Wiegand, A. Lagrangian theory of structure formation in relativistic cosmology. II. Average properties of a generic evolution model. Phys. Rev. D 2013, 87, 123503. [Google Scholar] [CrossRef]
- Buchert, T. Dark Energy from structure: A status report. Gen. Rel. Grav. 2008, 40, 467. [Google Scholar] [CrossRef]
- Buchert, T. Toward physical cosmology: Focus on inhomogeneous geometry and its non-perturbative effects. Class. Quant. Grav. 2011, 28, 164007. [Google Scholar] [CrossRef]
- Buchert, T.; Räsänen, S. Backreaction in Late-Time Cosmology. Annu. Rev. Nucl. Part. Sci. 2012, 62, 57. [Google Scholar] [CrossRef]
- Buchert, T.; Larena, J.; Alimi, J.M. Correspondence between kinematical backreaction and scalar field cosmologies—The ‘morphon field’. Class. Quant. Grav. 2006, 23, 6379. [Google Scholar] [CrossRef]
- Buchert, T.; Obadia, N. Effective inhomogeneous inflation: Curvature inhomogeneities of the Einstein vacuum. Class. Quant. Grav. 2011, 28, 162002. [Google Scholar] [CrossRef]
- Vigneron, Q.; Buchert, T. Dark Matter from Backreaction? Collapse models on galaxy cluster scales. Class. Quant. Grav. 2019, 36, 175006. [Google Scholar] [CrossRef]
- Krasiński, A. Inhomogeneous Cosmological Models; Cambridge University Press: Cambridge, UK, 1997; ISBN 0521481805. [Google Scholar]
- Lemaître, G. The expanding universe. Ann. Soc. Sci. Brux. A 1933, 53, 51. [Google Scholar] [CrossRef]
- Plebański, J.; Krasiński, A. An Introduction to General Relativity and Cosmology; Cambridge University Press: Cambridge, UK, 2006; ISBN 0-521-85623-X. [Google Scholar]
- Tolman, R.C. Effect of inhomogeneity on cosmological models. Proc. Natl. Acad. Sci. USA 1934, 20, 169. [Google Scholar] [CrossRef]
- Morita, M.; Nakamura, K.; Kasai, M. Relativistic Zel’dovich approximation in a spherically symmetric model. Phys. Rev. D 1998, 57, 6094. [Google Scholar] [CrossRef]
- Desgrange, C.; Heinesen, A.; Buchert, T. Dynamical spatial curvature as a fit to type Ia supernovae. Int. J. Mod. Phys. D 2019, 28, 1950143. [Google Scholar] [CrossRef]
- Heinesen, A.; Buchert, T. Solving the curvature and Hubble parameter inconsistencies through structure formation-induced curvature. Class. Quant. Grav. 2020, 37, 164001. [Google Scholar] [CrossRef]
- Roukema, B.F.; Ostrowski, J.J.; Borkowska, J. inhomog: Biscale Kinematical Backreaction Analytical Evolution. Astrophysics Source Code Library. 2017. Available online: https://ui.adsabs.harvard.edu/abs/2017ascl.soft11002R (accessed on 26 September 2022).
- Buchert, T.; Kerscher, M.; Sicka, C. Backreaction of inhomogeneities on the expansion: The evolution of cosmological parameters. Phys. Rev. D 2000, 62, 043525. [Google Scholar] [CrossRef]
- Al Roumi, F.; Buchert, T.; Wiegand, A. Lagrangian theory of structure formation in relativistic cosmology. IV. Lagrangian approach to gravitational waves. Phys. Rev. D 2017, 96, 123538. [Google Scholar] [CrossRef]
- Li, Y.Z.; Mourier, P.; Buchert, T.; Wiltshire, D.L. Lagrangian theory of structure formation in relativistic cosmology. V. Irrotational fluids. Phys. Rev. D 2018, 98, 043507. [Google Scholar] [CrossRef]
- Delgado Gaspar, I.; Buchert, T. Lagrangian theory of structure formation in relativistic cosmology. VI. Comparison with Szekeres exact solutions. Phys. Rev. D 2021, 103, 023513. [Google Scholar] [CrossRef]
- Kasai, M. Tetrad-based perturbative approach to inhomogeneous universes: A general relativistic version of the Zel’dovich approximation. Phys. Rev. D 1995, 52, 5605. [Google Scholar] [CrossRef] [PubMed]
- Buchert, T.; Carfora, M. On the curvature of the present-day Universe. Class. Quant. Grav. 2008, 25, 195001. [Google Scholar] [CrossRef]
- Szekeres, P. Quasispherical Gravitational Collapse. Phys. Rev. D 1975, 12, 2941. [Google Scholar] [CrossRef]
- Szafron, D.A. Inhomogeneous cosmologies: New exact solutions and their evolution. J. Math. Phys. 1977, 18, 1673. [Google Scholar] [CrossRef]
- Spero, A.; Szafron, D.A. Spatial conformal flatness in homogeneous and inhomogeneous cosmologies. J. Math. Phys. 1978, 19, 1536. [Google Scholar] [CrossRef]
- Delgado Gaspar, I.; Sussman, R.A.; McNutt, D.D.; Coley, A.A. Comment on ‘Szekeres universes with homogeneous scalar fields’. Eur. Phys. J. C 2021, 81, 310. [Google Scholar] [CrossRef]
- Bonnor, W.B.; Sulaiman, A.H.; Tomimura, N. Szekeres’s Space-Times Have No Killing Vectors. Gen. Rel. Grav. 1977, 8, 549. [Google Scholar] [CrossRef]
- Bolejko, K. Structure formation in quasispherical Szekeres model. Phys. Rev. D 2006, 73, 123508. [Google Scholar] [CrossRef]
- Bolejko, K. Evolution of cosmic structures in different environments in the quasispherical Szekeres model. Phys. Rev. D 2007, 75, 043508. [Google Scholar] [CrossRef]
- Bolejko, K. The Szekeres Swiss Cheese model and the CMB observations. Gen. Rel. Grav. 2009, 41, 1737. [Google Scholar] [CrossRef]
- Bolejko, K.; Célérier, M.N. Szekeres Swiss-Cheese model and supernova observations. Phys. Rev. D 2010, 82, 103510. [Google Scholar] [CrossRef]
- Bolejko, K.; Sussman, R.A. Cosmic spherical void via coarse-graining and averaging non-spherical structures. Phys. Lett. B 2011, 697, 265. [Google Scholar] [CrossRef]
- Buckley, R.G.; Schlegel, E.M. CMB dipoles and other low-order multipoles in the quasispherical Szekeres model. Phys. Rev. D 2013, 87, 023524. [Google Scholar] [CrossRef]
- Coley, A.A.; Layden, N.; McNutt, D. An invariant characterization of the quasi-spherical Szekeres dust models. Gen. Rel. Grav. 2019, 51, 164. [Google Scholar] [CrossRef]
- Delgado Gaspar, I.; Hidalgo, J.C.; Sussman, R.A.; Quiros, I. Black hole formation from the gravitational collapse of a nonspherical network of structures. Phys. Rev. D 2018, 97, 104029. [Google Scholar] [CrossRef]
- Hellaby, C. The null and KS limits of the Szekeres model. Class. Quant. Grav. 1996, 13, 2537. [Google Scholar] [CrossRef]
- Hellaby, C.; Krasiński, A. You can’t get through Szekeres wormholes: Or, regularity, topology and causality in quasispherical Szekeres models. Phys. Rev. D 2002, 66, 084011. [Google Scholar] [CrossRef]
- Hellaby, C.; Krasiński, A. Physical and geometrical interpretation of the ϵ ≤ 0 Szekeres models. Phys. Rev. D 2008, 77, 023529. [Google Scholar] [CrossRef]
- Ishak, M.; Richardson, J.; Garred, D.; Whittington, D.; Nwankwo, A.; Sussman, R.A. Dark energy or apparent acceleration due to a relativistic cosmological model more complex than the Friedmann-Lemaître-Robertson Walker model? Phys. Rev. D 2011, 84, 089902. [Google Scholar] [CrossRef]
- Koksbang, S.M.; Hannestad, S. Methods for studying the accuracy of light propagation in N-body simulations. Phys. Rev. D 2015, 91, 043508. [Google Scholar] [CrossRef]
- Koksbang, S.M.; Hannestad, S. Studying the precision of ray tracing techniques with Szekeres models. Phys. Rev. D 2015, 92, 023532. [Google Scholar] [CrossRef]
- Koksbang, S.M. Light propagation in Swiss-cheese models of random close-packed Szekeres structures: Effects of anisotropy and comparisons with perturbative results. Phys. Rev. D 2017, 95, 063532. [Google Scholar] [CrossRef]
- Sussman, R.A.; Bolejko, K. A Novel approach to the dynamics of Szekeres dust models. Class. Quant. Grav. 2012, 29, 065018. [Google Scholar] [CrossRef]
- Sussman, R.A.; Delgado Gaspar, I. Multiple nonspherical structures from the extrema of Szekeres scalars. Phys. Rev. D 2015, 92, 083533. [Google Scholar] [CrossRef]
- Sussman, R.A.; Delgado Gaspar, I.; Hidalgo, J.C. Coarse-grained description of cosmic structure from Szekeres models. J. Cosmol. Astropart. Phys. 2016, 03, 012. [Google Scholar] [CrossRef][Green Version]
- Vrba, D.; Svítek, O. Modelling inhomogeneity in Szekeres spacetime. Gen. Rel. Grav. 2014, 46, 1808. [Google Scholar] [CrossRef]
- Walters, A.; Hellaby, C. Constructing realistic Szekeres models from initial and final data. Phys. Rev. D 2012, 1212, 001. [Google Scholar] [CrossRef][Green Version]
- Goode, S.W.; Wainwright, J. Singularities and evolution of the Szekeres cosmological models. Phys. Rev. D 1982, 26, 3315. [Google Scholar] [CrossRef]
- Meures, N.; Bruni, M. Exact nonlinear inhomogeneities in ΛCDM cosmology. Phys. Rev. D 2011, 83, 123519. [Google Scholar] [CrossRef]
- Meures, N.; Bruni, M. Redshift and distances in a ΛCDM cosmology with non-linear inhomogeneities. Mon. Not. R. Astron. Soc. 2012, 419, 3. [Google Scholar] [CrossRef]
- Bolejko, K. Relativistic numerical cosmology with Silent Universes. Class. Quant. Grav. 2017, 35, 024003. [Google Scholar] [CrossRef]
- Bruni, M.; Matarrese, S.; Pantano, O. Dynamics of silent universes. Astrophys. J. 1995, 445, 958. [Google Scholar] [CrossRef]
- van Elst, H.; Ellis, G.F.R. The Covariant approach to LRS perfect fluid space-time geometries. Class. Quant. Grav. 1996, 13, 1099. [Google Scholar] [CrossRef]
- Delgado Gaspar, I.; Buchert, T.; Ostrowski, J.J. Beyond relativistic Lagrangian perturbation theory. I. An exact-solution controlled model for structure formation. Phys. Rev. D 2022. submitted. [Google Scholar]
- Wiegand, A.; Buchert, T. Multiscale cosmology and structure-emerging Dark Energy: A plausibility analysis. Phys. Rev. D 2010, 82, 023523. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buchert, T.; Delgado Gaspar, I.; Ostrowski, J.J. On General-Relativistic Lagrangian Perturbation Theory and Its Non-Perturbative Generalization. Universe 2022, 8, 583. https://doi.org/10.3390/universe8110583
Buchert T, Delgado Gaspar I, Ostrowski JJ. On General-Relativistic Lagrangian Perturbation Theory and Its Non-Perturbative Generalization. Universe. 2022; 8(11):583. https://doi.org/10.3390/universe8110583
Chicago/Turabian StyleBuchert, Thomas, Ismael Delgado Gaspar, and Jan Jakub Ostrowski. 2022. "On General-Relativistic Lagrangian Perturbation Theory and Its Non-Perturbative Generalization" Universe 8, no. 11: 583. https://doi.org/10.3390/universe8110583
APA StyleBuchert, T., Delgado Gaspar, I., & Ostrowski, J. J. (2022). On General-Relativistic Lagrangian Perturbation Theory and Its Non-Perturbative Generalization. Universe, 8(11), 583. https://doi.org/10.3390/universe8110583





