Does Lorentz Relativistic Mass Make Dark Energy Superfluous?

Abstract

This paper shows that a simple and relativistic extension of Newtonian gravity that takes into account Lorentz relativistic mass leads to predictions that fit supernova observations of magnitude versus redshift without the need to introduce dark energy. To test the concept, we look at 580 supernova data points from the Union2 database. Some relativistic extensions of Newtonian gravity have been investigated in the past, but we have reason to believe the efforts were rejected prematurely before their full potential was investigated. Our model suggests that mass, as related to gravity, is also affected by Lorentz relativistic effects, something that is not the case in standard gravity theory, and this adjustment gives supernova predictions that fit the observations. Our model seems very robust with respect to supernova data, as no arbitrary parameters are introduced. Since recent investigations of Lorentz’s relativistic mass also seem to solve other challenges in physics, we think it is worthwhile for the physics community to look into this more carefully, at least before rejecting it based on prejudice. After all, no one has been able to detect dark energy despite massive efforts to do so. Until dark energy is really confirmed, other alternative models should be worth investigating further.

1. History of Relativistic Mass

Before we discuss gravity, it is important to understand the history of relativistic mass, why it was rejected, and why its potential was never fully investigated. Relativistic mass, as we know it from a series of university textbooks [1,2,3,4], today is given by:

$$\mathrm{relativistic} \mathrm{mass}=m\gamma =\frac{m}{\sqrt{1-\frac{v^2}{c^2}}}$$

(1)

where m is the rest-mass. However, when it comes to gravity, relativistic mass is never mentioned as it was abandoned by the time general relativity theory was developed; something we will soon get back to.

The formula above was first derived and published by Lorentz [5] in 1899. Lorentz [6], in 1904 again, published a relativistic mass formula; this time, with an additional constant: L.

$$\mathrm{relativistic} \mathrm{mass}=\frac{Lm}{\sqrt{1-\frac{v^2}{c^2}}}$$

(2)

It was shown by Henri Poincaré [7] in 1905 that this additional constant L should always be set to one, thus, returning us to the original 1899 Lorentz relativistic mass formula. Lorentz had derived a separate relativistic mass formula for transverse mass (the formula above) and another formula for longitudinal mass: $m{\gamma }^3$.

Einstein [8], at the end of his famous 1905 paper introducing special relativity, gave two formulas for relativistic mass:

$$\mathrm{longitudinal} \mathrm{mass}=m{\gamma }^3=\frac{m}{{\sqrt{1-\frac{v^2}{c^2}}}^3}$$

(3)

and for transverse mass, he suggested:

$$\mathrm{transverse} \mathrm{mass}=m{\gamma }^2=\frac{m}{1-\frac{v^2}{c^2}}$$

(4)

Einstein’s longitudinal mass formula is the same as had been suggested by Lorentz before him, but Einstein made no reference to Lorentz so he was likely not aware of Lorentz’s papers on this. None of Einstein’s formulas were accepted by the physics community over time, and none of them are used today. Einstein was indeed the first to introduce relativistic energy:

$$E=m{c}^2\gamma$$

(5)

and he could just have divided this by $c^2$ to get the Lorentz relativistic mass (transverse), but instead, he speculated on other formulas for relativistic mass (m in the formula above is rest-mass). In 1906, Einstein wrote a paper exploring ideas to distinguish which relativistic mass formula was the correct one [9]. This paper led to little, if anything. At this point, Einstein still also held on to transverse and longitudinal mass.

Max Planck [10], in 1906, introduced relativistic momentum: $p=mv\gamma$. In a paper in 1907, Einstein [11] wrote, “Thus, a system of moving mass points is—taken as a whole—has the more inertia, the faster the mass points move relative to the other”. So Einstein, as late as 1907, thought the mass was affected by velocity, as did most physicists of the time.

At least as late as in the 1920s, some physicists still thought Einstein’s transverse mass was the correct one, perhaps because Einstein had attained a big influence by this time. For example, Wien [12] in 1921 referred to Einstein’s transverse mass as $\frac{m}{1-\frac{v^2}{c^2}}$ without also mentioning the alternative: Lorentz’s relativistic mass. In addition, Wien was a very prominent physicist, best known today for Wien’s law.

Tolman [13], in 1934 argued that only the transverse mass: $m\gamma$ of Lorentz makes sense: “since this is the quantity that will give momentum multiplied by the velocity of the particle. It is the quantity that is conserved when particles interact by collision”. This view was held by several physicists at that time; for example, Vereide [14], and after this point, the relativistic mass was referred to as the formula given by Lorentz in 1899.

Minkowski [15] invented a geometrical set-up for special relativity theory in 1908. With the four-dimensional space-time idea of that time period, the standard relativistic momentum did not fit well. After all, standard momentum is zero when $v=0$; in other words, when an object stands still and only time goes by. A new type of momentum was needed, namely fourth momentum $\overrightarrow{p}=\left(\frac{E}{c},p_x,p_y,p_z\right)$ for which the so-called time component was $\frac{E}{c}$. Several authoritative physicists claimed the relativistic mass was not really compatible with four-dimensional space-time, even if this was not obvious. Einstein decided sometime after the invention of Minkowski space-time to abandon relativistic mass altogether. There could be several reasons for this. First, relativistic mass perhaps did not seem to fit well into the four-dimensional Minkowski space-time, as it would not necessarily be compatible with the time component of the four-momentum. One should also not ignore that there was still competition between Lorentz’s relativity theory and Einstein’s relativity theory. Einstein was well aware that Lorentz had derived relativistic mass before him, and it was preferred by most physicists who still thought there was something to relativistic mass; to give credit to it could perhaps reduce the prestige of his special-relativity theory. However, we do not know if this played a role in Einstein’s abandonment of relativistic mass or not.

In a letter to the American journalist Lincoln Barnett, dated 19 June 1948, Einstein wrote:

“It is not good to introduce the concept of the mass $M=m/\sqrt{1-\frac{v^2}{c^2}}$ of a moving body for which no clear definition can be given. It is better to introduce no other mass concept than the “rest mass," m. Instead of introducing M, it is better to mention the expression for the momentum and energy of a body in motion."

In other words, he preferred the new fourth momentum. In particular, this letter by Einstein has given fuel to other researchers to ignore relativistic mass. For example, Okun and Hecht [16,17] have published papers very critical of relativistic mass; also, Adler [18] was very critical and, in 1987, wrote:

“It should also be pointed out that there is no reason to introduce relativistic mass in general relativity theory.”

Taylor and Wheeler [19] have spoken out against relativistic mass, but we will claim their arguments against it are rather weak, and we cannot see that any of these researchers have fully investigated what relativistic mass leads to if we incorporate it into gravitational theory. It can be surmised that they have decided that Minkowski’s space-time must be fully correct and that, therefore, no further investigation of relativistic mass is needed, but we think this is a big mistake.

Other prominent physicists, like Rindler [20,21], that are supportive of special relativity theory, have defended the relativistic mass concept but have not investigated its potential in terms of what it leads to in predictions of gravity if one incorporates it; see also Jammer [22].

Gravitational theory, including the Lambda–CDM model, therefore, does not contain relativistic mass at all. The same is naturally the case with Newtonian gravity, which is partly the weak field limit of general relativity theory. We will claim that the negativity against relativistic mass has led to relativistic mass not even being fully investigated before being rejected. We think before a concept is rejected, it should be more carefully investigated, in particular when suggested by such a prominent researcher as Lorentz.

Relativistic mass has gotten more attention in the past few years. Haug and Spavieri [23,24] have shown that general relativity theory, when it comes to micro black holes, can match only, at maximum, one or two properties of the Planck scale at the same time. With properties of the Planck scale, we think about such things as the Planck mass, Planck length, Planck time, Planck energy, and Planck acceleration. This is also why a series of different masses close to the Planck mass, and not only the exact Planck mass, have been suggested as candidates for micro black holes in general relativity theory. On the other hand, if one considers relativistic mass, then the Planck mass fits the properties of a micro black hole with respect to all aspects of the Planck scale.

Recently Haug [25] has also shown that incorporating Lorentz’s relativistic mass leads to a new universe model that is very similar to the Friedman model, but in which there seems to be simpler logic. This has recently been shown to be compatible with a 3D space-time theory, which is where we have three space and three time dimensions; see Haug [26]. So instead of simply rejecting Lorentz’s relativistic mass, one should perhaps instead ask what it leads to in terms of predictions, and could it be that four-dimensional space-time is not the ideal geometry of our universe? We naturally do not expect the reader to take this idea, in recently published papers, for granted, as new ideas and theories should be scrutinized by a series of researchers over time and perhaps be improved upon or even rejected. All we ask is that readers not have prejudice before carefully investigating the implications of predictions from Lorentz’s relativistic mass.

2. Relativistic Newton Extension

Somewhat ad hoc relativistic extensions of Newtonian gravity have been suggested in the past. In the 1980s, Bagge [27] and Phipps [28], for example, both suggested the following relativistic extension of Newtonian gravity

$$F=G\frac{M\frac{m}{\sqrt{1-\frac{v^2}{c^2}}}}{R^2}$$

(6)

where M and m are the rest mass of the large and small mass.

It seems like both Bagge and Phipps were not aware that Einstein had also abandoned relativistic mass in his special relativity theory (not only in general relativity theory) and that relativistic mass as we know it today was actually invented by Lorentz. However, Phipps mentioned that authorities had, perhaps prematurely, been too negative towards relativistic mass; he then tried to incorporate it into Newtonian gravity theory. The idea behind the relativistic modified Newton gravity by these authors is that the small mass is moving relative to the larger gravitational mass and, therefore, appears to be relativistic from the perspective of the larger gravitational mass. In other words, they incorporated Lorentz relativistic mass for the small mass m in the Newton formula.

Phipps initially claimed that his relativistic Newton extension led to a prediction of the perihelion precession of Mercury that was equal to the predictions from Einstein’s [29] general relativity, which has been confirmed by experiments. In 1986, Peters [30] claimed that Phipps had made a mistake in his calculations and that, in reality, the Phipps extension only predicted half of the needed perihelion precession of Mercury. Shortly after that revelation, Phipps [31] acknowledged the mistake but claimed that the approach was still interesting and should be investigated further. The Phipps and Bagge model were, for similar reasons, also criticized by Ghosal [32] and Chow [33]. However, recently Corda [34,35] has suggested that one gets the correct Mercury perihelion precession from Newton if one correctly analyzes the situation in the framework of the two-body problem without neglecting the mass of Mercury in addition to relativistic effects. However, this should naturally be scrutinized by researchers over time before being fully accepted or rejected. Further, in the astronomical system, it is mainly the sun that acts on Mercury, and naturally, both the sun and the Mercury are moving relative to Earth. In this case, Haug [36] has, therefore, suggested that the relativistic model should be extended as follows:

$$F=G\frac{\frac{M}{\sqrt{1-\frac{v_M^2}{c^2}}}\frac{m}{\sqrt{1-\frac{v_m^2}{c^2}}}}{R^2\left(1-\frac{v_M^2}{c^2}\right)}$$

(7)

That is, we are simply using standard logic from relativity but incorporating Lorentz relativistic mass and length contraction. We are standing in a third reference frame, Earth, and are observing two masses moving relative to us, namely the sun and Mercury. Clearly, both masses, not only one of them, must be relativistic, according to Lorentz. Further, R must represent the center-to-center distance between Mercury and the sun, and this length, as seen by an observer outside this system (Earth), will undergo Lorentz length contraction (that is also incorporated in special relativity theory as well as in Lorentz theory). Previous researchers may have missed the point that, in the case of the sun’s effect on Mercury, we are outside observers. Our point is simply that to conclude that Newton’s gravity theory, even when adjusted for relativistic effects, cannot explain the perihelion precession of Mercury is a premature conclusion made before full investigation. The precession of Mercury is far from the main topic of this paper, so we only mention it in passing.

A central issue in such investigations is that relativistic extensions of Newtonian gravity must follow the logic in a realistic manner. If we are standing on Earth, for example, and are completing gravitational predictions about the moon, then the large mass is Earth, and we are at rest with respect to Earth. The moon is a relativistic mass relative to Earth, and the radius, center to center, from Earth to the moon is observed from the rest frame, that is, from Earth. This means that the relativistic effects will only be present for the small mass, and in this case, we should have the Bagge and Philips formula:

$$F=G\frac{M\frac{m}{\sqrt{1-\frac{v^2}{c^2}}}}{R^2}$$

(8)

Another case to consider would be to address a different phenomenon—observing the redshift of a supernova as viewed from Earth, for example. In this case, the large mass M is the supernova, the lab frame is the small mass (the photon we observe at Earth), and the relativistic Newton formula must actually be:

$$F=G\frac{\frac{M}{\sqrt{1-\frac{v^2}{c^2}}}m}{R^2}$$

(9)

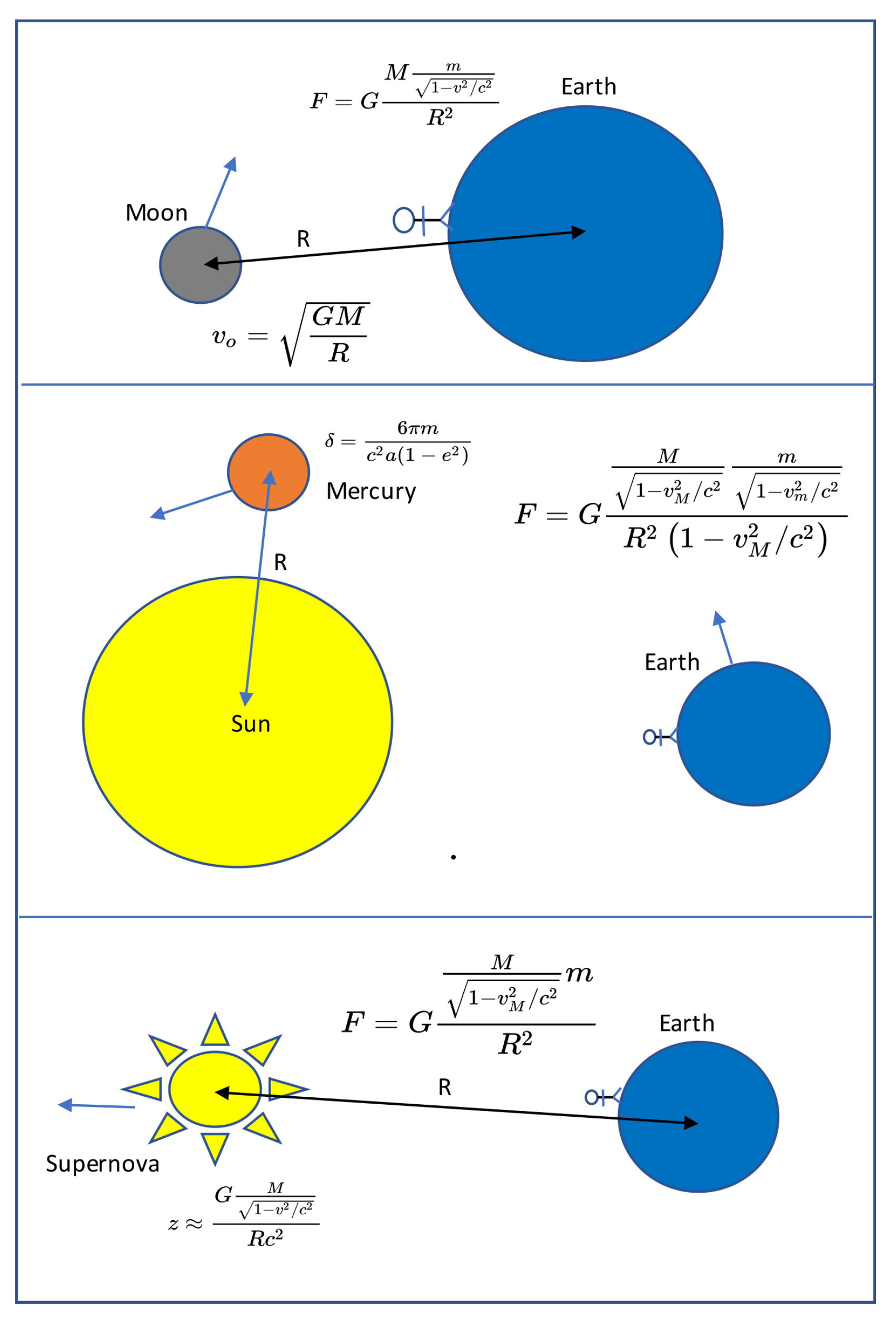
In this case, the large gravity mass is the supernova that is moving relative to Earth. Further, the distance R runs from the center of the supernova to Earth, and this distance is not undergoing length contraction because the distance between Earth and the supernova itself is not moving, even though it is expanding due to the supernova moving relative to us. It seems we must have three versions of the relativistic Newton formula, depending on the situation. These three situations are illustrated in Figure 1. In the upper panel, Earth is the laboratory frame and at the same time, it is the mass M, and the moon is the mass m. Here, the small mass is relativistic relative to the lab frame. In the middle panel, we are studying the sun’s gravitational effect on Mercury from Earth. That is, both the sun and Mercury must be moving relative to the observer frame (Earth). Here, both of the masses in the Newton formula must be relativistic. In the lower panel, we are observing the gravity effect on light sent out from a supernova from our base on Earth. That is, the large mass M is the supernova, and the supernova is moving relative to Earth. These all follow from the most logical steps in relativity theory as applied to Newtonian gravity. To our surprise, even after an extensive “library” search, only the formula in the upper panel has been discussed in the physics literature, and it was, in our view, incorrectly applied to the situation in the second panel. This led to an incorrect prediction and may have caused researchers to abandon the further investigation of relativistic Newton extensions prematurely.

Using the correct relativistic extension, based on relativistic logic in relation to Lorentz relativistic mass combined with Newtonian gravity, even fits supernova redshift data very well, using baryonic matter only. We will look at this in the next sections and show a striking result: that no dark energy is needed.

3. Do We Need Dark Energy to Explain Supernovae Data?

Here we will look at our Newton relativistic model to see if it predicts supernova data correctly. Our model needs to take into account Newton’s relativistic effects, Lorentz’s relativistic mass, and also Einstein’s special relativistic Doppler effects. The Einstein special relativistic Doppler shift is given by

$$z=\frac{1-\frac{v}{c}}{\sqrt{1-\frac{v^2}{c^2}}}-1=\sqrt{\frac{1-\frac{v}{c}}{1+\frac{v}{c}}}-1$$

(10)

Solved with respect to v, this gives the well-known formula:

$$v_{pec}\left(z\right)=c\frac{{(1+z)}^2-1}{{(1+z)}^2+1}$$

(11)

where the luminous distance (as a first approximation) is given by

$$D\approx \frac{c}{H_o}\frac{{(1+z)}^2-1}{{(1+z)}^2+1}$$

(12)

where $H_o$ is the Hubble constant. However, in the time that light takes to travel the distance D, that is $t_D=\frac{D}{c}$, then the emitting object will move away $t_D{v}_{pec}$. This was not taken into account by Davis and Lineweaver [37], for example, as first pointed out by MacLeod [38] and also discussed by Brissender [39]. The corrected emitter time is, therefore, given by

$$t_e=t_D+\frac{t_D{v}_{pec}}{c}=t_D(1+v_{pec}/c)$$

(13)

This means the relationship between the proper time at the emitter $t_e$ and the proper time at the observer $t_o$ is given by

$$t_o=\frac{t_e}{\sqrt{1-\frac{v_{pec}^2}{c^2}}}=\frac{t_D(1+v_{pec}/c)}{\sqrt{1-\frac{v_{pec}^2}{c^2}}}=t_D\sqrt{\frac{1-v_{pec}/c}{1+v_{pec}/c}}=t_D(1+z)$$

(14)

This means the luminous distance is actually given by

$$D=t_{D}c=\frac{c}{H_o}\frac{{(1+z)}^2-1}{{(1+z)}^2+1}(1+z)$$

(15)

The effective magnitude is found by using the following formula (see for example [37,40]):

$$m_B\left(z\right)=5log{H}_{o}D+M_B$$

(16)

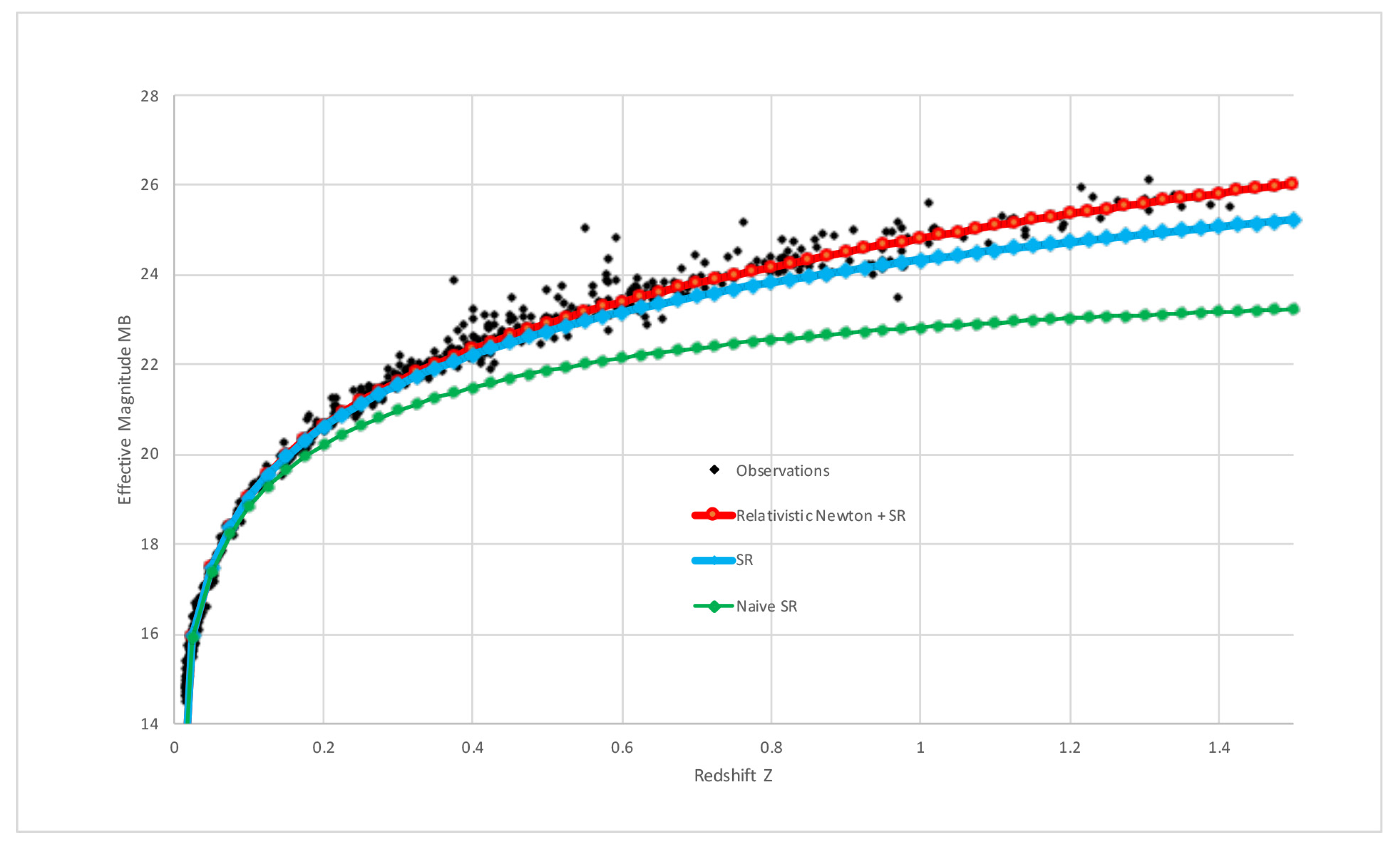
where $M_B$ is the absolute magnitude in the B-band at the maximum light curve and log is the log with base 10. Be aware that the Hubble constant cancels out with the Hubble constant in the distance formula, so the formula is, in reality, not dependent on the Hubble constant. Davis and Lineweaver suggested that $M_B$ should have a value of around $3.45$, as found from the data; we will use the same value here. We can say this is what special relativity (SR) alone will predict. Davis and Lineweaver compared the SR model with supernova data and concluded, “SR fails this observational test dramatically being $23\sigma$ from the general relativistic ΛCDM model?”. The SR model Davis and Lineweaver used is the one before taking into account that the supernova moves during the time it takes for the light to travel from the supernova to the observer, so it is better than they claimed, as also pointed out by Brissenden [39]. Still, we agree that SR cannot explain the supernova data alone. In addition, we need to take Lorentz’s relativistic mass effects in Newton’s theory into consideration. The supernova is the large mass M in the Newton formula, and we are observing it from Earth. If the supernova is moving, the mass will be a relativistic mass in relation to us and is not mathematically identical to the rest mass, as it is in the standard Newton formula. That is, the following formula is relevant:

$$F=G\frac{M\gamma m}{R^2}=G\frac{\frac{M}{\sqrt{1-\frac{v^2}{c^2}}}m}{R^2}$$

(17)

This again leads to a gravitational redshift (as observed from a weak gravitational field) of approximately:

$$z_{gr}\approx \frac{G\frac{M}{\sqrt{1-\frac{v_{pec}^2}{c^2}}}}{R{c}^2}$$

(18)

This is equal to the standard GR gravitational redshift multiplied by ${\gamma }_z=\frac{1}{\sqrt{1-v_{pec}^2/c^2}}$. It is important that gravitational redshift can be derived independent of GR, as shown by researchers in the past; something we discuss in more detail in Appendix A. We must adjust our luminous distance with this factor to get the correct prediction. This will then give what we can call an apparent distance that, in addition to distance, reflects the missing relativistic mass adjustment for the supernova. Our model will, therefore, simply be

$$m_B\left(z\right)=5log\left(H_{o}D{\gamma }_z\right)+M_B$$

(19)

The difference between this and pure SR is the additional ${\gamma }_z$ factor due to Lorentz relativistic mass. Our result is the mathematical “equivalent” to a theory recently suggested by Brissender [39]. However, in his theory, the $\gamma$ factor comes from a speculative idea that proper velocity is what is relevant and not the velocity, so he claimed $v_{pec}\gamma$ is relevant. Proper velocity is defined as taking the distance, as measured from the laboratory frame (“stationary” frame), divided by the time traveled as measured in the moving frame. Brissender has shown that this fits very well with supernova observations. However, there is no deep theory as to why we should use proper velocity here rather than the velocity, and, in fact, we will claim the logic falls in the opposite direction; that it is the velocity that should be used and not the proper velocity.

In the naive case where we do not take into account that the supernova has moved in the time for the light to reach us, and as the Hubble constant cancels out, we end up with:

$$m_B\left(z\right)=5log\left[v_{pec}\right]+M_B$$

(20)

In addition, also taking into account also when the supernova has moved during the time it took for the light to arrive at us, we get:

$$m_B\left(z\right)=5log\left[v_{pec}(1+z)\right]+M_B$$

(21)

and when, in addition, taking into account Lorentz relativistic mass, we get:

$$m_B\left(z\right)=5log\left[v_{pec}\gamma (1+z)\right]+M_B$$

(22)

In other approaches, Kipreos [41] has what we would call a structural equivalent mathematical model, arguing that his $\gamma$ factor adjustment relative to SR is due to the need for a suggested time-contraction ratio. In order to get a $\gamma$ factor here, he needed to use the Mansouri and Sexl [42] transformation rather than the Lorentz transformation. So, Kipreos’s work is basically mathematical and very similar to ours in that the time must be adjusted by a ${\gamma }_z=1/\sqrt{1-v_{pec}^2/c^2}$. However, again, there is no deep theory for why he had to do this suggested time-contraction ratio (by this, we do not mean the lack of a solid transformation theory, but rather, why he needed the time-contraction in the first place).

We propose that we may have found the correct explanation: namely, because we also need to do relativistic adjustments for the mass in the Newtonian gravity formula. In short, we need to take into account that masses moving relative to an observer are observed as relativistic masses and not rest masses. We will discuss this further in the coming sections.

4. Testing the Model against 580 Supernova 1A Data Points

To assess the prediction power of our model, we tested it against 580 data points from the Union-2 supernova 1A database [43]. Figure 2 shows the observations in black points. The red line corresponds to our Newton relativistic model adjusted for relativistic mass in addition to SR doppler shift, that is, using Equation (22). It is important to understand we have not used any fit parameter (apart from the well-known $M_B$ that also is used in the standard cosmological model); this is since $v_{per}$ is a function of z already, and so this seems to make this model considerably simpler than other explanatory models (The red line will also be the predictions from the Brissender model and from the Kipreos model. However, these approaches have very different interpretations than our model.) The blue line is when we are only taking standard SR into account; that is, only relativistic doppler shift, Equation (21). As stated previously, our model is simply a logical extension of SR where we, in addition, take into account relativistic mass, as suggested by Lorentz. That is, we assume any mass when moving relative to us, is a relativistic mass.

The green line is an even more naive use of SR, where we neglect to take into account that the supernova has moved even further away in the time it takes for light to travel the distance from the supernova to the observer (Earth); this corresponds to using formula Equation (20).

Outline of How the Plots Were Made

To make the plots for the three prediction models, we first calculated the predicted velocity from Equation (11), which is identical to the three models. This we have done for redshifts going from $z=0.001$ with step size $0.025$ all the way to $z=1.5$. This was done so as to be able to compare our predictions to all types of Ia supernovas in the Union-2 database, where the lowest redshift observation is $z=0.015$ and the highest redshift observation in the database is $z=1.414$.

It is important to be aware that the velocity from Equation (11) needs no free or estimated parameter. It does not need to be calibrated to any observation, as it only requires the redshift we want to look at; in this case, the whole range from close to 0 (0.01) to $z=1.5$, and also the speed of light c that is well known.

To get the predictions from the three different models, we now input this velocity into, respectively, Equations (20)–(22). Actually, the calculated velocity is multiplied by $\frac{1}{1000}$ to get it in km/s, as this is normally used in such magnitude calculations. It is a logarithm with base 10 that has been used in several other papers and that we also have used here. In the equation, we also need the B-band, $M_B$, which should have a value of around $-3.45$, according to Davis and Lineweaver. In other words, our predictions from the two first models are the same as given by previous literature, and our new model needs no additional input. All these models need only the redshift we are interested in plus the estimated absolute magnitude in the B-band and the speed of light c. There are, in other words, no flexible curve fitting parameters, something that makes the model very robust if it fits the observation, as the model takes into account Lorentz relativistic mass.

Next, these model predictions are compared to the observations given in the Union-2 database. The black dots that represent these observations are simply the third column in the Union-2 database plus the M (h = 0.7, with systematic) minus 19.31 that is given at the top of the table in the database. These values are then plotted together using the corresponding redshift (z values in column 1); see the end of the paper for a link to the Union-2 database.

5. Do We Need Global Inertial Frames to Introduce Lorentz Relativistic Mass in Newtonian Gravity?

Special relativity requires that we have global inertial frames, in other words, flat space-time. This is naturally not the case under the influence of gravity, where we, for example, will observe gravitational redshift that is in conflict with flat space-time. First, including Lorentz relativistic mass is not directly part of special relativity, as pointed out in Section 1. The Michelson Morley [44] experiment published in 1897 clearly showed that the ether theory at that time was wrong. Length contraction was introduced by FitzGerald [45] in 1899 and was further formalized by Lorentz [46] in 1892. Time dilation was introduced by Larmor [47] in 1900. Each of these was introduced after the Michelson–Morley experiment to make the theory consistent with observational results, but these prominent researchers still believed that there existed a unique reference frame. The question, however, was if this unique reference could still be detected, as the old ether theory clearly no longer held up against experiments. Poincaré [48] in 1898 pointed out that it is likely impossible to measure the one-way speed of light and to detect anisotropy in the one-way speed of light is closely linked to detecting a unique reference frame. His reasoning was likely that, when taking into account length contraction, one would need two synchronized clocks over distance to measure the one-way speed of light. However, to synchronize two clocks apart over distance, in general, requires knowledge of the one-way speed of light, so this led to a circular problem that, to this day, has been discussed; see, for example [49,50,51].

Einstein, in 1905, went one step further and assumed that since one could not measure the one-way speed of light, and since the round-trip speed of light experimentally was clearly isotropic and c, then why not simply abandon the ether altogether, to make a simpler but still consistent theory? However, when Einstein also came up with a gravitational theory, it became clear that global inertial reference frames were no longer valid in this context (see [29,52,53] ), also based on experiments. When considering gravity, it only assumed inertial frames held locally due to curved space-time. This is likely why Einstein in 1920 said:

“Recapitulating, we may say that according to the general theory of relativity, space is endowed with physical qualities; in this sense, therefore, there exists an ether. According to the general theory of relativity, space without ether is unthinkable; for in such space there not only would be no propagation of light, but also no possibility of existence for standards of space and time …"

This was not to return to the pre-Michelson–Morley ether theory but likely rooted in Einstein’s understanding very well that taking into account gravity was not consistent with flat space-time and that gravity was something quite special.

For us to simply multiply the mass in Newton’s theory with the Lorentz factor, therefore, at first glance, looks inconsistent due to gravity not being consistent with global inertial frames. There is, however, a new possibility here that is linked to recent progress in understanding the Planck scale as well as quantum gravity but let us first quickly go back to the history of quantum gravity.

In 1916, in one of his most famous papers on general relativity, Einstein [29] already suggested the next step in gravity was to unify gravity with quantum mechanics. Eddington [54], in 1918, was likely the first to suggest that gravity would need to be linked to the Planck length, that is, the Planck scale; see also Mead [55]. Since the introduction of the Planck [10,56] units in 1899, there has been extensive research into creating experiments that can detect the Planck scale. Parts of the Planck scale, such as the Planck length and the Planck time, are considered far below the detection level for any modern apparatus. For example, the best current clocks (see [57]) can measure time intervals down to approximately ${10}^{-19}$ seconds while the Planck time is of the order ${10}^{-44}$ seconds. The Planck energy, on the other hand, is far above what can be achieved in the Large Hadron Collider or even any foreseeable much stronger collider. Extensive research into even indirectly detecting weaker effects of the Planck energy have been attempted without success as mentioned by, for example, Hees et al [58].

Recent research, however, opens up a new possibility here as it has recently been demonstrated that the Planck length and the Planck time can be extracted from a series of gravity phenomena without knowledge of G or ℏ or even c (see [59,60]). This is in strong contrast to what has been assumed.

Already in 1987, it was pointed out by Cohen [61] that trying to rely on Planck units rather than calculate them through G just led to a circular problem as one first had to know G to find the Planck units. This is a view that has been repeated at least until 2016 (see [62]). However, since we now know we can measure the Planck units without knowledge of G or ℏ, then we should ask why this is the case?

We have suggested that the reason is that to detect the effects of gravity is, surprisingly, to detect the effects of the Planck scale. We have recently shown that Newtonian theory is consistent with a newly suggested quantum gravity theory [26] rooted in the Planck scale but that it looks like one needs to adjust it for relativistic mass, as we have done here.

Planck energies are traditionally considered extremely high ($E_p=m_p{c}^2$), but, as we have explained, this may be due to an incomplete understanding of the relations between time and mass. Thus, the Planck energy we should look for is extremely small, as the Planck mass particle only lasts the Planck time. This is not based purely on the theoretical assumption but on calibrating such a quantum gravity model to gravity phenomena. We then get out that the Planck mass only lasts the Planck time; see [26,36]. In this new quantum gravity theory, the Planck scale, when detected at time scales we are able to do direct measurements for, shows that the Planck energy is surprisingly equivalent to a very weak (low) energy that corresponds to observed gravitational phenomena.

To detect gravity is, in this new view, to detect the Planck scale and, therefore, it is no surprise that when we incorporate gravity into Lorentz-modified Einstein “special relativity”, which global inertial frames no longer hold. This can be seen as modified special relativity at the Planck scale. For a long time, it has been expected that special relativity will likely need modifications at the Planck scale, and we agree with this. By simply combining Lorentz relativistic mass in relation to gravity, one has, surprisingly, incorporated the Planck scale. It would take many pages to go into much detail about this here, and we do not ask the readers to take this for granted, but ask them kindly to study recent publications on this new quantum gravity theory before making up their minds. See in particular [25,26,63].

In an addition to the question about global inertial frames, which seems to be solved due to what we mentioned above, there are likely additional effects here. We are observing the supernova gravitational redshifts from Earth (Union2 database). At the surface of Earth, we have a very weak gravity field that will have effects on the light we also observe from heavenly objects, but this effect is typically very small compared to redshift caused by the massive stars (supernovas) sending out the light that we are observing in this case.

Earth is, in addition, rotating around its own axis and around the sun. This should naturally lead to additional minor adjustments, even if we expect these to be very small, as the rotational velocity of Earth, for example, around the sun is approximately 30,000 km/s, that is approximately 0.01% of the speed of light, while the whole solar system is likely moving at approximately 0.1% as measured from CMB anisotropy by Henry [64] and with muon flux anisotropy by Monstein and Wesley [65] and also several other methods, such as relative to the average of observations related to galaxies; see [66]. It would be interesting to look into whether there are some small seasonal variations in cosmological redshifts from different directions, as the velocity in Equation (11) should then alter in some directions relative to Earth, dependent on the time of the year. This we will leave for future research, but we expect adjusting for any such effect will be minuscule for, in particular, relatively high z supernovas, as the rotational velocity effects from Earth are so low compared to the speed of light.

6. Summary and Discussion

In this paper, we have introduced three basically mathematical and very similar models that all predict supernova observations without relying on dark energy. Naturally, there may be some debate on whether or not they are very similar mathematically, as the inputs and assumptions are not at all the same for these models. To be clear, these are then three considerably different models in their assumptions and interpretation of explanatory causes that give the correct prediction of supernovas. However, these models are very similar from a structural mathematical point of view. We summarize the three alternatives plus the standard GR Newton model below.

(1)

The relativistic modified Newtonian model presented here simply states that we need to take into account relativistic masses for moving objects, as suggested by Lorentz. Gravitational masses are no exception. Since the standard model does not do this, we get a correction factor of ${\gamma }_z=1/\sqrt{1-v_{pec}^2/c^2}$. This gives a nice fit to supernova observations without the need for dark energy. This model is also fully consistent with Haug’s [26,67] recently presented quantum gravity theory, which claims to unify gravity with quantum mechanics. We do not ask the reader to take such a new model for granted, but to be interested enough to understand this could be of interest to the research community to look at more closely.

(2)

The model presented by Brissender in 2019 in relation to predicting supernovas is mathematically very similar to the model above, but it has a very different interpretation. In the Brissender model, the $\gamma$ adjustment factor is due to what we would claim is a speculative idea: that it is the proper supernova velocity that is relevant and not the standard velocity. We strongly doubt this explanation. That said, the Brissender paper, together with the Kipreos model, made us think more deeply about the need for a $\gamma$ correction to get the correct supernova predictions. Taken together with our view that we must also have relativistic masses in the Newton gravity model, this helps to develop a new perspective.

(3)

The Kipreos [41] model published in 2014 has an end result that is mathematically very similar to the two models described above. This model also has a $\gamma$ factor that it claims is a correction factor for the time dilation of the signal sent in the past versus the one received in the present. The explanation for exactly why this should be the case seems to be the weakness of this approach. Still, this paper strongly indicated that something might be missing in the standard theory and pointed us toward the need for further research.

(4)

The standard Lambda–CDM model. This model needs dark energy in order to be consistent with supernova data, but we strongly suspect that dark energy is simply a “fudge factor” to get general relativity theory to fit observations. It should be investigated whether Lorentz’s relativistic mass could also be incorporated into general relativity theory or if it is only consistent with a new alternative theory.

The Kipreos [41] interpretation relies on the absolute transformation by Mansouri and Sexl [42] that again is linked to absolute simultaneity rather than relativity of simultaneity, something that has been supported by some recent research [49,50,68,69], but that still is up for discussion. The Mansouri and Sexl transformation has the same length transformation as the Lorentz transformation, but the time transformation is just $t^{\prime }=t\gamma$ compared to the Lorentz time transformation of $t^{\prime }=(t-vx/c^2)\gamma$. The suggested interpretation in this paper seems to be compatible both with SR and with the Mansouri and Sexel transformation. This is because it does not rely on any time transformation; the same seems to be the case with the Brissender interpretation. Therefore, the essential question is: what is the most likely cause for the $\gamma$ adjustment that leads to a good fit of supernova predictions? Is it the time adjustment suggested by Kipreos? Is it that we should rely on proper velocity? Or is it simply that the masses in the Newton gravity formula are also relativistic? We believe that the last suggestion, as presented in this paper, makes the most sense. In particular, this is true since incorporating relativistic mass also seems to lead to an escape velocity that is compatible with a Planck mass particle and is, in general, a more consistent and logical theory; see [25,26,36].

It is worth pointing out that recent research indicates there are strong parallels between mass and clocks. Elementary particles are likely “ticking" at the Compton time interval, as suggested by [36]. That mass is linked to the Compton frequency and also has some recent observational support; see [36,70,71].

7. Conclusions

Both Kipreos [41] and Brissender [39] have recently suggested basically similar mathematical models that seem to predict supernova 1A data very well without relying on dark energy. However, we question the assumptions behind their models. Here we have shown a third alternative that is mathematically very similar to the two other models but provides a very different explanation for why this adjustment is needed. We claim that the mass in gravity and, more precisely, in the Newton formula is not excluded from velocity-related Lorentz relativistic effects, the so-called Lorentz relativistic mass, as first suggested by Lorentz in 1899 and again in 1904. By taking into account relativistic mass, we create a model that predicts supernova 1A data and that addresses redshift versus magnitude correctly without relying on dark energy.

This also shows the importance of letting speculative ideas be published and circulated, even if they are in conflict with mainstream models, such as the dark energy hypothesis and the Lambda–CDM model. We will claim the Kipreos model and the Brissender model, for example, are much more speculative than our model. Still, they both show how a small adjustment to SR doppler shift leads to the correct prediction of supernovas without relying on dark energy. Instead of ignoring this work, we have investigated these lines of thought further and have developed a robust and sound explanatory model for both simple multi-body planetary systems and also for supernovas. It is logical and consistent to say that there is only one type of mass at the most fundamental level and that this mass is affected by velocity from the perspective of the observer as well as in relation to gravity. Further study is merited. Can this lead to modifications of the Lambda–CDM model, or will quantum gravity models, in which relativistic mass plays a role, be what we need to move forward in gravity research?