Scalar Weak Gravity Conjecture in Super Yang-Mills Inflationary Model
Abstract
1. Introduction
2. Overview of Inflationary Models
2.1. Model I: NJLI
2.2. Model II: GI
2.3. Model III: SYMI
2.4. Model IV: OI
3. SWGC and SSWGC on Inflation Models
3.1. Model I
3.2. Model II
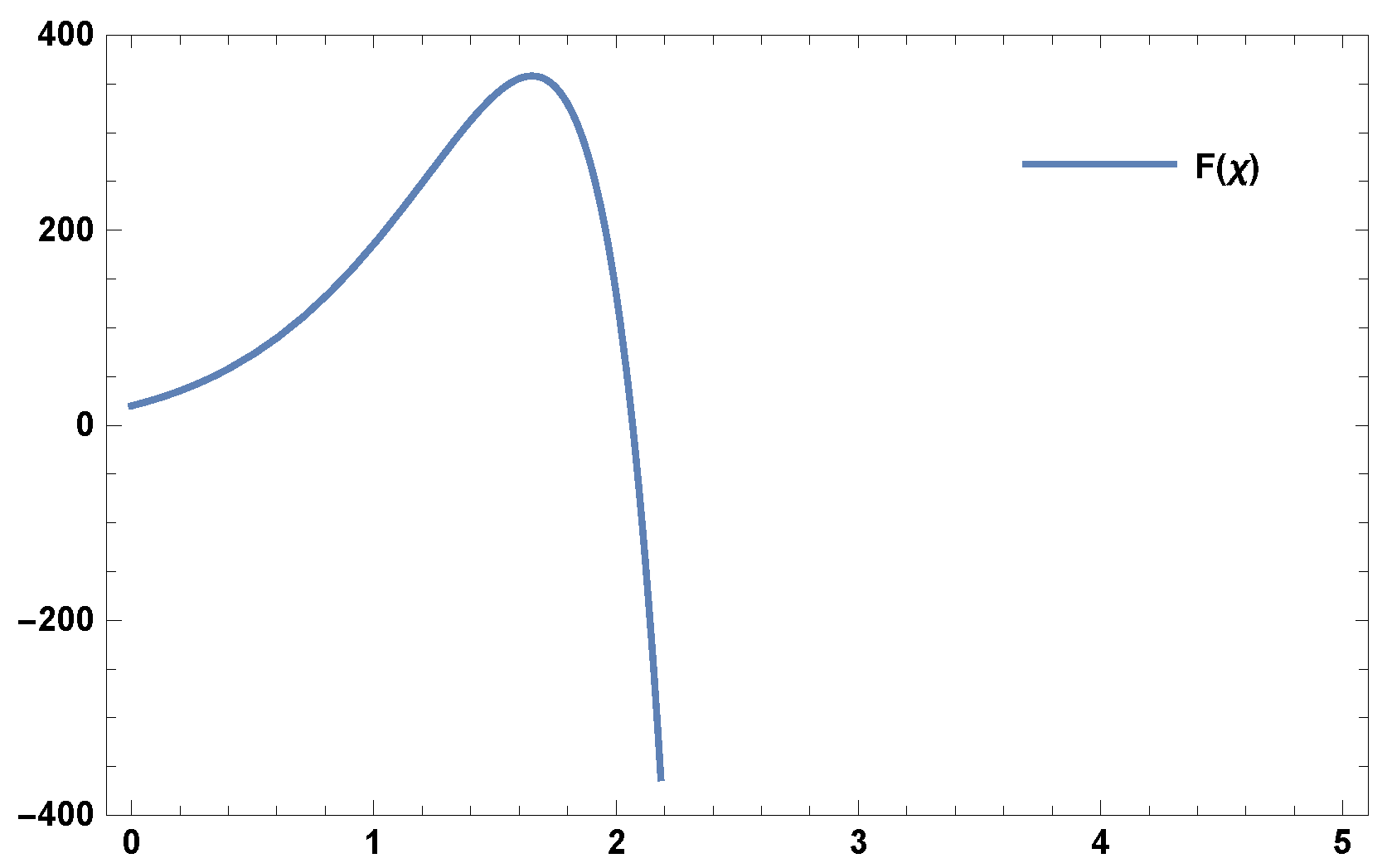
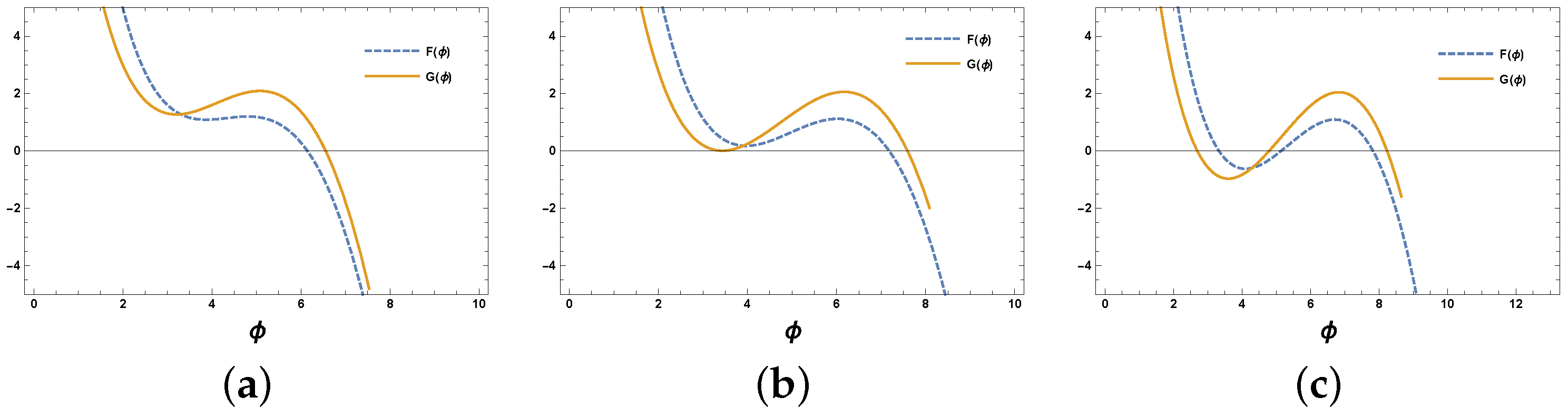
3.3. Model III
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vafa, C. The string landscape and the swampland. arXiv 2005, arXiv:hep-th/0509212. [Google Scholar]
- Ooguri, H.; Vafa, C. On the Geometry of the String Landscape and the Swampland. Nucl. Phys. B 2007, 766, 21. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Motl, L.; Nicolis, A.; Vafa, C. The string landscape, black holes and gravity as the weakest force. J. High Energy Phys. 2007, 2007, 060. [Google Scholar] [CrossRef]
- Montero, M.; Vafa, C.; Valenzuela, I. The Dark Dimension and the Swampland. arXiv 2022, arXiv:2205.12293. [Google Scholar]
- Yuennan, J.; Channuie, P. Composite Inflation and further refining dS swampland conjecture. arXiv 2022, arXiv:2208.09842. [Google Scholar]
- Kadota, K.; Shin, C.S.; Terada, T.; Tumurtushaa, G. Trans-Planckian censorship and single-field inflaton potential. J. Cosmol. Astropart. Phys. 2020, 2020, 008. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Rescaled Einstein-Hilbert gravity from f(R) gravity: Inflation, dark energy, and the swampland criteria. Phys. Rev. D 2021, 103, 124028. [Google Scholar] [CrossRef]
- Trivedi, O. Rejuvenating the hope of a swampland consistent inflated multiverse with tachyonic inflation in the high-energy RS-II braneworld. Mod. Phys. Lett. A 2022, 37, 2250162. [Google Scholar] [CrossRef]
- Das, S. Distance, de Sitter and trans-Planckian censorship conjectures: The status quo of Warm inflation. Phys. Dark Universe 2020, 27, 100432. [Google Scholar] [CrossRef]
- Mohammadi, A.; Golanbari, T.; Saaidi, K. Beta-function formalism for k-essence constant-roll inflation. Phys. Dark Universe 2020, 28, 100505. [Google Scholar] [CrossRef]
- Sadeghi, J.; Pourhassan, B.; Gashti, S.N.; Upadhyay, S. Swampland conjecture and inflation model from brane perspective. Phys. Scr. 2021, 96, 125317. [Google Scholar] [CrossRef]
- Sadeghi, J.; Pourhassan, B.; Gashti, S.N.; Upadhyay, S. Weak gravity conjecture, black branes and violations of universal thermodynamics relation. Ann. Phys. 2022, 447, 168168. [Google Scholar] [CrossRef]
- Shokri, M.; Sadeghi, J.; Herrera, R.; Gashti, S.N. Warm inflation with bulk viscous pressure for different solutions of an anisotropic universe. arXiv 2021, arXiv:2112.12309. [Google Scholar]
- Gashti, S.N. Two-field inflationary model and swampland de Sitter conjecture. J. Hologr. Appl. Phys. 2022, 2, 13. [Google Scholar]
- Kinney, W.H. Eternal Inflation and the Refined Swampland Conjecture. Phys. Rev. Lett. 2019, 122, 081302. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.Y.; Wen, W.Y. Cosmic censorship and Weak Gravity Conjecture in the Einstein–Maxwell-dilaton theory. Phys. Lett. B 2018, 781, 713–718. [Google Scholar] [CrossRef]
- Sadeghi, J.; Mezerji, E.N.; Gashti, S.N. Study of some cosmological parameters in logarithmic corrected f(R) gravitational model with swampland conjectures. Mod. Phys. Lett. A 2021, 36, 2150027. [Google Scholar] [CrossRef]
- Silk, J.; Cassé, M. Swampland Revisited. Found. Phys. 2022, 52, 86. [Google Scholar] [CrossRef]
- Sadeghi, J.; Gashti, S.N.; Mezerji, E.N. The investigation of universal relation between corrections to entropy and extremality bounds with verification WGC. Phys. Dark Universe 2021, 30, 100626. [Google Scholar] [CrossRef]
- Mezerji, E.N.; Sadeghi, J.; Pourhassan, B. The effect of the WGC condition on the maximal energy extracted from black holes. Eur. Phys. J. Plus 2022, 137, 1145. [Google Scholar] [CrossRef]
- Mezerji, E.N.; Sadeghi, J. The correlation of WGC and hydrodynamics bound with R4 correction in the charged AdSd+2 black brane. Nucl. Phys. D 2022, 981, 115858. [Google Scholar] [CrossRef]
- Sadeghi, J.; Gashti, S.N. Anisotropic constant-roll inflation with noncommutative model and swampland conjectures. Eur. Phys. J. C 2021, 81, 301. [Google Scholar] [CrossRef]
- Montero, M.; Muñoz, J.B.; Obied, G. Swampland Bounds on Dark Sectors. arXiv 2022, arXiv:2207.09448. [Google Scholar] [CrossRef]
- Gashti, S.N.; Sadeghi, J.; Pourhassan, B. Pleasant behavior of swampland conjectures in the face of specific inflationary models. Astropart. Phys. 2022, 139, 102703. [Google Scholar] [CrossRef]
- Anchordoqui, L.; Antoniadis, I.; Lust, D. Dark dimension, the swampland, and the dark matter fraction composed of primordial black holes. Phys. Rev. D 2022, 106, 086001. [Google Scholar] [CrossRef]
- Sadeghi, J.; Gashti, S.N. Investigating the logarithmic form of f(R) gravity model from brane perspective and swampland criteria. Pramana 2021, 95, 198. [Google Scholar] [CrossRef]
- Alvarez-García, R.; Blumenhagen, R.; Kneissl, C.; Makridou, A.; Schlechter, L. Swampland conjectures for an almost topological gravity theory. Phys. Lett. B 2022, 825, 136861. [Google Scholar] [CrossRef]
- Gashti, S.N.; Sadeghi, J. Constraints on cosmological parameters in light of the scalar–tensor theory of gravity and swampland conjectures. Mod. Phys. Lett. A 2022, 37, 2250110. [Google Scholar] [CrossRef]
- Gonzalo, E.; Ibáñez, L.E.; Valenzuela, I. Swampland constraints on neutrino masses. J. High Energy Phys. 2022, 2022, 88. [Google Scholar] [CrossRef]
- Gashti, S.N.; Sadeghi, J.; Upadhyay, S.; Alipour, M.R. Swampland dS conjecture in mimetic f(R, T) gravity. Commun. Theor. Phys. 2022, 74, 085402. [Google Scholar] [CrossRef]
- Conlon, J.P.; Ning, S.; Revello, F. Exploring the holographic Swampland. J. High Energy Phys. 2022, 2022, 117. [Google Scholar] [CrossRef]
- Sadeghi, J.; Gashti, S.N.; Darabi, F. Swampland conjectures in hybrid metric-Palatini gravity. Phys. Dark Universe 2022, 37, 101090. [Google Scholar] [CrossRef]
- Hamada, Y.; Montero, M.; Vafa, C.; Valenzuela, I. Finiteness and the swampland. J. Phys. Math. Theor. 2022, 55, 224005. [Google Scholar] [CrossRef]
- Gashti, S.N.; Sadeghi, J. Inflation, swampland and landscape. Int. J. Mod. Phys. A 2022, 37, 2250006. [Google Scholar] [CrossRef]
- Mishra, R.K. Confinement in de Sitter Space and the Swampland. arXiv 2022, arXiv:2207.12364. [Google Scholar]
- Gashti, S.N.; Sadeghi, J. Refined swampland conjecture in warm vector hybrid inflationary scenario. Eur. Phys. J. Plus 2022, 137, 1. [Google Scholar] [CrossRef]
- Cribiori, N.; Dierigl, M.; Gnecchi, A.; Lust, D.; Scalisi, M. Large and Small Non-extremal Black Holes, Thermodynamic Dualities, and the Swampland. arXiv 2022, arXiv:2202.04657. [Google Scholar] [CrossRef]
- Shokri, M.; Setare, M.R.; Capozziello, S.; Sadeghi, J. Constant-roll f(R) inflation compared with cosmic microwave background anisotropies and swampland criteria. Eur. Phys. J. Plus 2022, 137, 639. [Google Scholar] [CrossRef]
- Sadeghi, J.; Shokri, M.; Alipour, M.R.; Gashti, S.N. Weak Gravity Conjecture from Conformal Field Theory: A Challenge from Hyperscaling Violating and Kerr-Newman-AdS Black Holes. Chin. Phys. C 2022, 47, 015103. [Google Scholar] [CrossRef]
- Obied, G.; Ooguri, H.; Spodyneiko, L.; Vafa, C. De Sitter Space and the Swampland. arXiv 2018, arXiv:1806.08362. [Google Scholar]
- Andriot, D.; Roupec, C. Further Refining the de Sitter Swampland Conjecture. Fortschritte Phys. 2019, 67, 1800105. [Google Scholar] [CrossRef]
- Liu, Y. Higgs inflation and its extensions and the further refining dS swampland conjecture. Eur. Phys. J. C 2021, 81, 1122. [Google Scholar] [CrossRef]
- Garg, S.K.; Krishnan, C. Bounds on slow roll and the de Sitter Swampland. J. High Energy Phys. 2019, 11, 075. [Google Scholar] [CrossRef]
- Ooguri, H.; Palti, E.; Shiu, G.; Vafa, C. Distance and de Sitter conjectures on the Swampland. Phys. Lett. B 2019, 788, 180. [Google Scholar] [CrossRef]
- Palti, E. The weak gravity conjecture and scalar fields. J. High Energy Phys. 2017, 8, 034. [Google Scholar] [CrossRef]
- Palti, E. The Swampland: Introduction and Review. Fortschritte Phys. 2019, 67, 1900037. [Google Scholar] [CrossRef]
- Gonzalo, E.; Ibáñez, L. A Strong Scalar Weak Gravity Conjecture and some implications. J. High Energy Phys. 2019, 8, 118. [Google Scholar] [CrossRef]
- Channuie, P.; Xiong, C. Unified composite scenario for inflation and dark matter in the Nambu-Jona-Lasinio model. Phys. Rev. D 2017, 95, 043521. [Google Scholar] [CrossRef]
- Samart, D.; Pongkitivanichkul, C.; Channuie, P. Composite dynamics and cosmology: Inflation. Eur. Phys. J. Spec. Top. 2022, 231, 1325. [Google Scholar] [CrossRef]
- Channuie, P.; Jorgensen, J.J.; Sannino, F. Composite inflation from super Yang-Mills theory, orientifold, and one-flavor QCD. Phys. Rev. D 2012, 86, 125035. [Google Scholar] [CrossRef]
- Bezrukov, F.; Channuie, P.; Joergensen, J.J.; Sannino, F. Composite inflation setup and glueball inflation. Phys. Rev. D 2012, 86, 063513. [Google Scholar] [CrossRef]
- Feo, A.; Merlatti, P.; Sannino, F. Information on the Super Yang-Mills spectrum. Phys. Rev. D 2004, 70, 096004. [Google Scholar] [CrossRef]
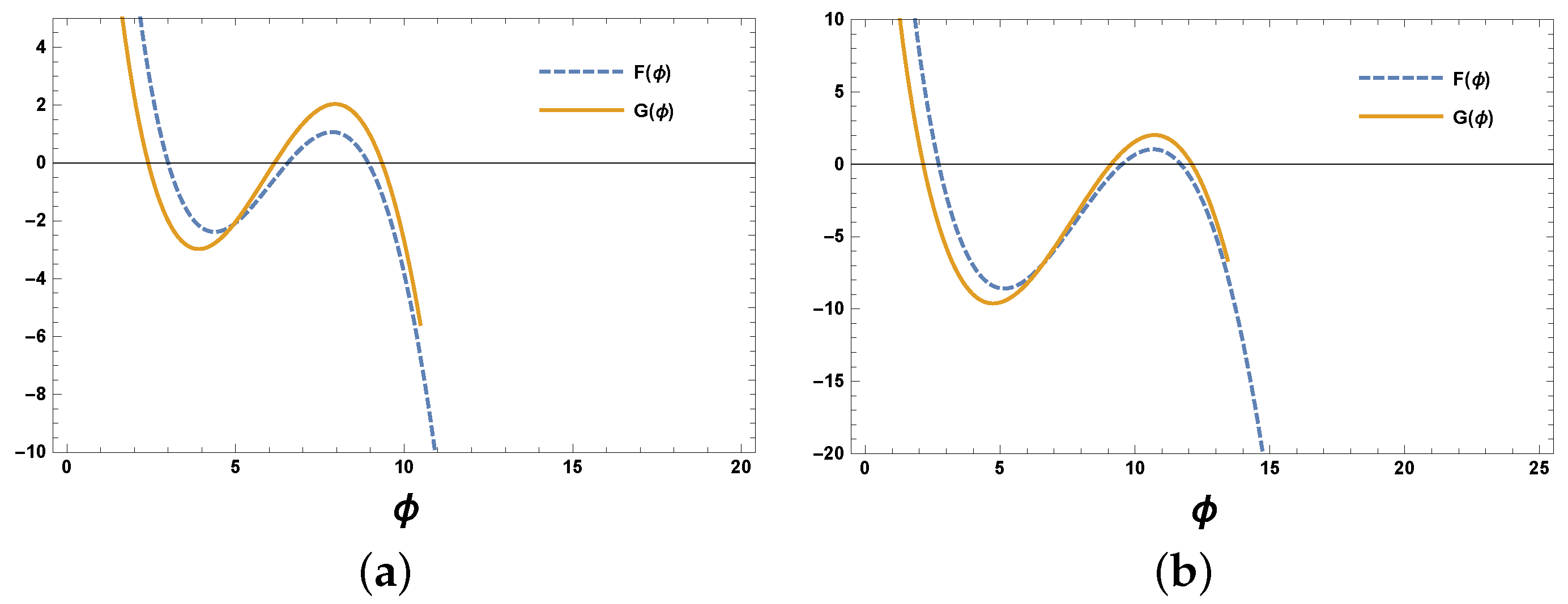
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghi, J.; Alipour, M.R.; Noori Gashti, S. Scalar Weak Gravity Conjecture in Super Yang-Mills Inflationary Model. Universe 2022, 8, 621. https://doi.org/10.3390/universe8120621
Sadeghi J, Alipour MR, Noori Gashti S. Scalar Weak Gravity Conjecture in Super Yang-Mills Inflationary Model. Universe. 2022; 8(12):621. https://doi.org/10.3390/universe8120621
Chicago/Turabian StyleSadeghi, Jafar, Mohammad Reza Alipour, and Saeed Noori Gashti. 2022. "Scalar Weak Gravity Conjecture in Super Yang-Mills Inflationary Model" Universe 8, no. 12: 621. https://doi.org/10.3390/universe8120621
APA StyleSadeghi, J., Alipour, M. R., & Noori Gashti, S. (2022). Scalar Weak Gravity Conjecture in Super Yang-Mills Inflationary Model. Universe, 8(12), 621. https://doi.org/10.3390/universe8120621











