Study of Intra-Day Flux Distributions of Blazars Using XMM-Newton Satellite
Abstract
1. Introduction
2. Sample Selection and Data Analysis
3. Analysis Techniques
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
| 1 | (https://heasarc.gsfc.nasa.gov/docs/archive.html, accessed on 9 September 2022). |
References
- Blandford, R.D.; Königl, A. Relativistic jets as compact radio sources. Astrophys. J. 1979, 232, 34–48. [Google Scholar] [CrossRef]
- Urry, C.M.; Padovani, P. Unified Schemes for Radio-Loud Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1995, 107, 803. [Google Scholar] [CrossRef]
- Fan, J.H.; Yang, J.H.; Liu, Y.; Luo, G.Y.; Lin, C.; Yuan, Y.H.; Xiao, H.B.; Zhou, A.Y.; Hua, T.X.; Pei, Z.Y. The spectral energy distributions of Fermi blazars. Astrophys. J. Suppl. Ser. 2016, 226, 20. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Agudo, I.; Ajello, M.; Aller, H.D.; Aller, M.F.; Angelakis, E.; Arkharov, A.A.; Axelsson, M.; Bach, U.; et al. The Spectral Energy Distribution of Fermi Bright Blazars. Astrophys. J. 2010, 716, 30–70. [Google Scholar] [CrossRef]
- Yang, W.X.; Xiao, H.B.; Wang, H.G.; Yang, J.H.; Pei, Z.Y.; Wu, D.X.; Yuan, Y.H.; Fan, J.H. Correlation between Brightness Variability and Spectral Index Variability for Fermi Blazars. Res. Astron. Astrophys. 2022, 22, 085002. [Google Scholar] [CrossRef]
- Romero, G.E.; Boettcher, M.; Markoff, S.; Tavecchio, F. Relativistic Jets in Active Galactic Nuclei and Microquasars. Space Sci. Rev. 2017, 207, 5–61. [Google Scholar] [CrossRef]
- Dermer, C.D.; Schlickeiser, R.; Mastichiadis, A. High-energy gamma radiation from extragalactic radio sources. Astron. Astrophys. 1992, 256, L27–L30. [Google Scholar]
- Sikora, M.; Begelman, M.C.; Rees, M.J. Comptonization of Diffuse Ambient Radiation by a Relativistic Jet: The Source of Gamma Rays from Blazars? Astrophys. J. 1994, 421, 153. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F. Canonical high-power blazars. Mon. Not. R. Astron. Soc. 2009, 397, 985–1002. [Google Scholar] [CrossRef]
- Böttcher, M.; Reimer, A.; Sweeney, K.; Prakash, A. Leptonic and Hadronic Modeling of Fermi-detected Blazars. Astrophys. J. 2013, 768, 54. [Google Scholar] [CrossRef]
- Atoyan, A.M.; Dermer, C.D. Neutral Beams from Blazar Jets. Astrophys. J. 2003, 586, 79–96. [Google Scholar] [CrossRef]
- Sembay, S.; Warwick, R.S.; Urry, C.M.; Sokoloski, J.; George, I.M.; Makino, F.; Ohashi, T.; Tashiro, M. The X-ray Spectral Variability of the BL Lacertae Type Object PKS 2155-304. Astrophys. J. 1993, 404, 112. [Google Scholar] [CrossRef]
- Wagner, S.J.; Witzel, A. Intraday Variability In Quasars and BL Lac Objects. Annu. Rev. Astron. Astrophys. 1995, 33, 163–198. [Google Scholar] [CrossRef]
- Ulrich, M.H.; Maraschi, L.; Urry, C.M. Variability of active galactic nuclei. Annu. Rev. Astron. Astrophys. 1997, 35, 445–502. [Google Scholar] [CrossRef]
- Gaur, H.; Gupta, A.C.; Bachev, R.; Strigachev, A.; Semkov, E.; Wiita, P.J.; Kurtanidze, O.M.; Darriba, A.; Damljanovic, G.; Chanishvili, R.G.; et al. Optical variability of TeV blazars on long time-scales. Mon. Not. R. Astron. Soc. 2019, 484, 5633–5644. [Google Scholar] [CrossRef]
- Gaskell, C.M. Lognormal X-ray Flux Variations in an Extreme Narrow-Line Seyfert 1 Galaxy. Astrophys. J. 2004, 612, L21–L24. [Google Scholar] [CrossRef][Green Version]
- Uttley, P.; McHardy, I.M.; Vaughan, S. Non-linear X-ray variability in X-ray binaries and active galaxies. Mon. Not. R. Astron. Soc. 2005, 359, 345–362. [Google Scholar] [CrossRef]
- McHardy, I.M. Lecture Notes in Physics; Belloni, T., Ed.; Springer: Berlin, Germany, 2010; Volume 794, p. 203. [Google Scholar]
- Giebels, B.; Degrange, B. Lognormal variability in BL Lacertae. Astron. Astrophys. 2009, 503, 797–799. [Google Scholar] [CrossRef]
- Chevalier, J.; Kastendieck, M.A.; Rieger, F.M.; Maurin, G.; Lenain, J.P.; Lamanna, G. Long term variability of the blazar PKS 2155-304. arXiv 2015, arXiv:1509.03104. [Google Scholar]
- Sinha, A.; Shukla, A.; Saha, L.; Acharya, B.S.; Anupama, G.C.; Bhattacharjee, P.; Britto, R.J.; Chitnis, V.R.; Prabhu, T.P.; Singh, B.B.; et al. Long-term study of Mkn 421 with the HAGAR Array of Telescopes. Astron. Astrophys. 2016, 591, A83. [Google Scholar] [CrossRef]
- Sinha, A.; Sahayanathan, S.; Acharya, B.S.; Anupama, G.C.; Chitnis, V.R.; Singh, B.B. On the Spectral Curvature of VHE Blazar 1ES 1011+496: Effect of Spatial Particle Diffusion. Astrophys. J. 2017, 836, 83. [Google Scholar] [CrossRef]
- Sinha, A.; Khatoon, R.; Misra, R.; Sahayanathan, S.; Mandal, S.; Gogoi, R.; Bhatt, N. The flux distribution of individual blazars as a key to understand the dynamics of particle acceleration. Mon. Not. R. Astron. Soc. 2018, 480, L116–L120. [Google Scholar] [CrossRef]
- Kushwaha, P.; Chandra, S.; Misra, R.; Sahayanathan, S.; Singh, K.P.; Baliyan, K.S. Evidence for Two Lognormal States in Multi-wavelength Flux Variation of FSRQ PKS 1510-089. Astrophys. J. 2016, 822, L13. [Google Scholar] [CrossRef]
- Kushwaha, P.; Pal, M. Short-Term X-ray Variability during Different Activity Phases of Blazars S5 0716+714 and PKS 2155-304. Galaxies 2020, 8, 66. [Google Scholar] [CrossRef]
- Shah, Z.; Mankuzhiyil, N.; Sinha, A.; Misra, R.; Sahayanathan, S.; Iqbal, N. Log-normal flux distribution of bright Fermi blazars. Res. Astron. Astrophys. 2018, 18, 141. [Google Scholar] [CrossRef]
- Biteau, J.; Giebels, B. The minijets-in-a-jet statistical model and the rms-flux correlation. Astron. Astrophys. 2012, 548, A123. [Google Scholar] [CrossRef]
- Giannios, D.; Uzdensky, D.A.; Begelman, M.C. Fast TeV variability in blazars: Jets in a jet. Mon. Not. R. Astron. Soc. 2009, 395, L29–L33. [Google Scholar] [CrossRef]
- Gaur, H.; Mohan, P.; Wierzcholska, A.; Gu, M. Signature of inverse Compton emission from blazars. Mon. Not. R. Astron. Soc. 2018, 473, 3638–3660. [Google Scholar] [CrossRef]
- Pavana Gowtami, G.S.; Gaur, H.; Gupta, A.C.; Wiita, P.J.; Liao, M.; Ward, M. X-ray intraday variability and power spectral density profiles of the blazar 3C 273 with XMM-Newton during 2000–2021. Mon. Not. R. Astron. Soc. 2022, 511, 3101–3112. [Google Scholar] [CrossRef]
- Strüder, L.; Briel, U.; Dennerl, K.; Hartmann, R.; Kendziorra, E.; Meidinger, N.; Pfeffermann, E.; Reppin, C.; Aschenbach, B.; Bornemann, W.; et al. The European Photon Imaging Camera on XMM-Newton: The pn-CCD camera. Astron. Astrophys. 2001, 365, L18–L26. [Google Scholar] [CrossRef]
- Vaughan, S.; Edelson, R.; Warwick, R.S.; Uttley, P. On characterizing the variability properties of X-ray light curves from active galaxies. Mon. Not. R. Astron. Soc. 2003, 345, 1271–1284. [Google Scholar] [CrossRef]
- Edelson, R.A.; Krolik, J.H.; Pike, G.F. Broad-Band Properties of the CfA Seyfert Galaxies. III. Ultraviolet Variability. Astrophys. J. 1990, 359, 86. [Google Scholar] [CrossRef]
- Rodríguez-Pascual, P.M.; Alloin, D.; Clavel, J.; Crenshaw, D.M.; Horne, K.; Kriss, G.A.; Krolik, J.H.; Malkan, M.A.; Netzer, H.; O’Brien, P.T.; et al. Steps toward Determination of the Size and Structure of the Broad-Line Region in Active Galactic Nuclei. IX. Ultraviolet Observations of Fairall 9. Astrophys. J. Suppl. Ser. 1997, 110, 9–20. [Google Scholar] [CrossRef][Green Version]
- Knuth, K.H. Optimal data-based binning for histograms and histogram-based probability density models. Digit. Signal Process. 2019, 95, 102581. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. Asymptotic Theory of Certain “Goodness of Fit” Criteria Based on Stochastic Processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]
- Stephens, M.A. Goodness of fit for the extreme value distribution. Biometrika 1977, 64, 583–588. [Google Scholar] [CrossRef]
- Mohorian, M.; Bhatta, G.; Adhikari, T.P.; Dhital, N.; Pánis, R.; Dinesh, A.; Chaudhary, S.C.; Bachchan, R.K.; Stuchlík, Z. X-ray timing and spectral variability properties of blazars S5 0716+714, OJ 287, Mrk 501, and RBS 2070. Mon. Not. R. Astron. Soc. 2022, 510, 5280–5301. [Google Scholar] [CrossRef]
- Khatoon, R.; Shah, Z.; Misra, R.; Gogoi, R. Study of long-term flux and photon index distributions of blazars using RXTE observations. Mon. Not. R. Astron. Soc. 2020, 491, 1934–1940. [Google Scholar] [CrossRef]
- Bhatta, G. Characterizing Long-term Optical Variability Properties of γ-Ray-bright Blazars. Astrophys. J. 2021, 923, 7. [Google Scholar] [CrossRef]
- Bhatta, G.; Dhital, N. The Nature of γ-ray Variability in Blazars. Astrophys. J. 2020, 891, 120. [Google Scholar] [CrossRef]
- Duda, J.; Bhatta, G. Gamma-ray blazar variability: New statistical methods of time-flux distributions. Mon. Not. R. Astron. Soc. 2021, 508, 1446–1458. [Google Scholar] [CrossRef]
- McHardy, I.M.; Koerding, E.; Knigge, C.; Uttley, P.; Fender, R.P. Active galactic nuclei as scaled-up Galactic black holes. Nature 2006, 444, 730–732. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, K.; Mori, M. Time Series Analysis of Gamma-Ray Blazars and Implications for the Central Black-hole Mass. Astrophys. J. 2013, 773, 177. [Google Scholar] [CrossRef]
- Sobolewska, M.A.; Siemiginowska, A.; Kelly, B.C.; Nalewajko, K. Stochastic Modeling of the Fermi/LAT γ-Ray Blazar Variability. Astrophys. J. 2014, 786, 143. [Google Scholar] [CrossRef]
- Tluczykont, M.; Bernardini, E.; Satalecka, K.; Clavero, R.; Shayduk, M.; Kalekin, O. Long-term lightcurves from combined unified very high energy γ-ray data. Astron. Astrophys. 2010, 524, A48. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Becerra Gonzalez, J.; Bellazzini, R.; Bissaldi, E.; et al. The Third Catalog of Active Galactic Nuclei Detected by the Fermi Large Area Telescope. Astrophys. J. 2015, 810, 14. [Google Scholar] [CrossRef]
- Narayan, R.; Piran, T. Variability in blazars: Clues from PKS 2155-304. Mon. Not. R. Astron. Soc. 2012, 420, 604–612. [Google Scholar] [CrossRef]
- Marscher, A.P.; Gear, W.K. Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273. Astrophys. J. 1985, 298, 114–127. [Google Scholar] [CrossRef]
- Böttcher, M.; Dermer, C.D. Timing Signatures of the Internal-Shock Model for Blazars. Astrophys. J. 2010, 711, 445–460. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F. Rapid variability in TeV blazars: The case of PKS2155-304. Mon. Not. R. Astron. Soc. 2008, 386, L28–L32. [Google Scholar] [CrossRef]
- Giannios, D.; Uzdensky, D.A.; Begelman, M.C. Fast TeV variability from misaligned minijets in the jet of M87. Mon. Not. R. Astron. Soc. 2010, 402, 1649–1656. [Google Scholar] [CrossRef]
- Marscher, A.P. Turbulent, Extreme Multi-zone Model for Simulating Flux and Polarization Variability in Blazars. Astrophys. J. 2014, 780, 87. [Google Scholar] [CrossRef]
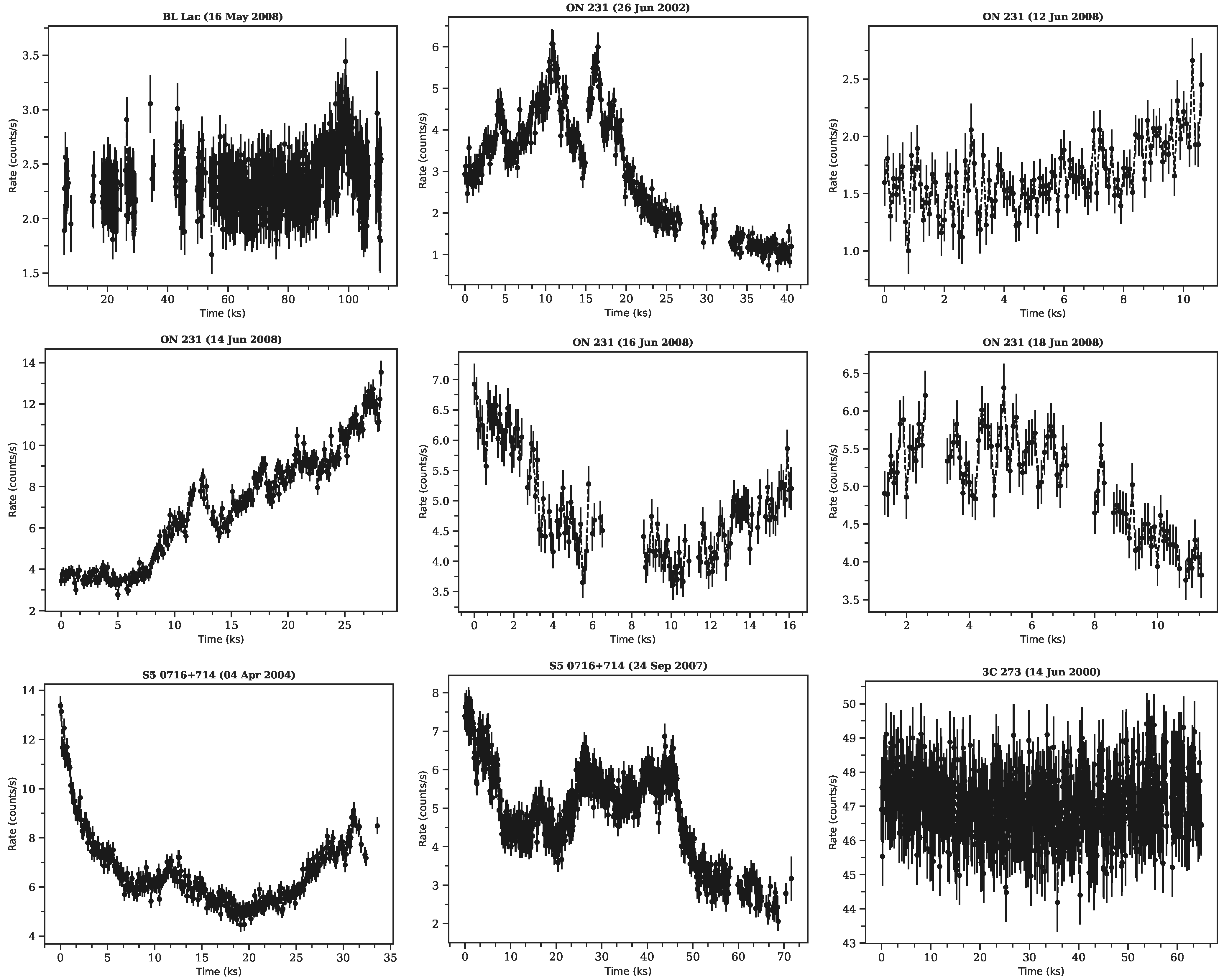
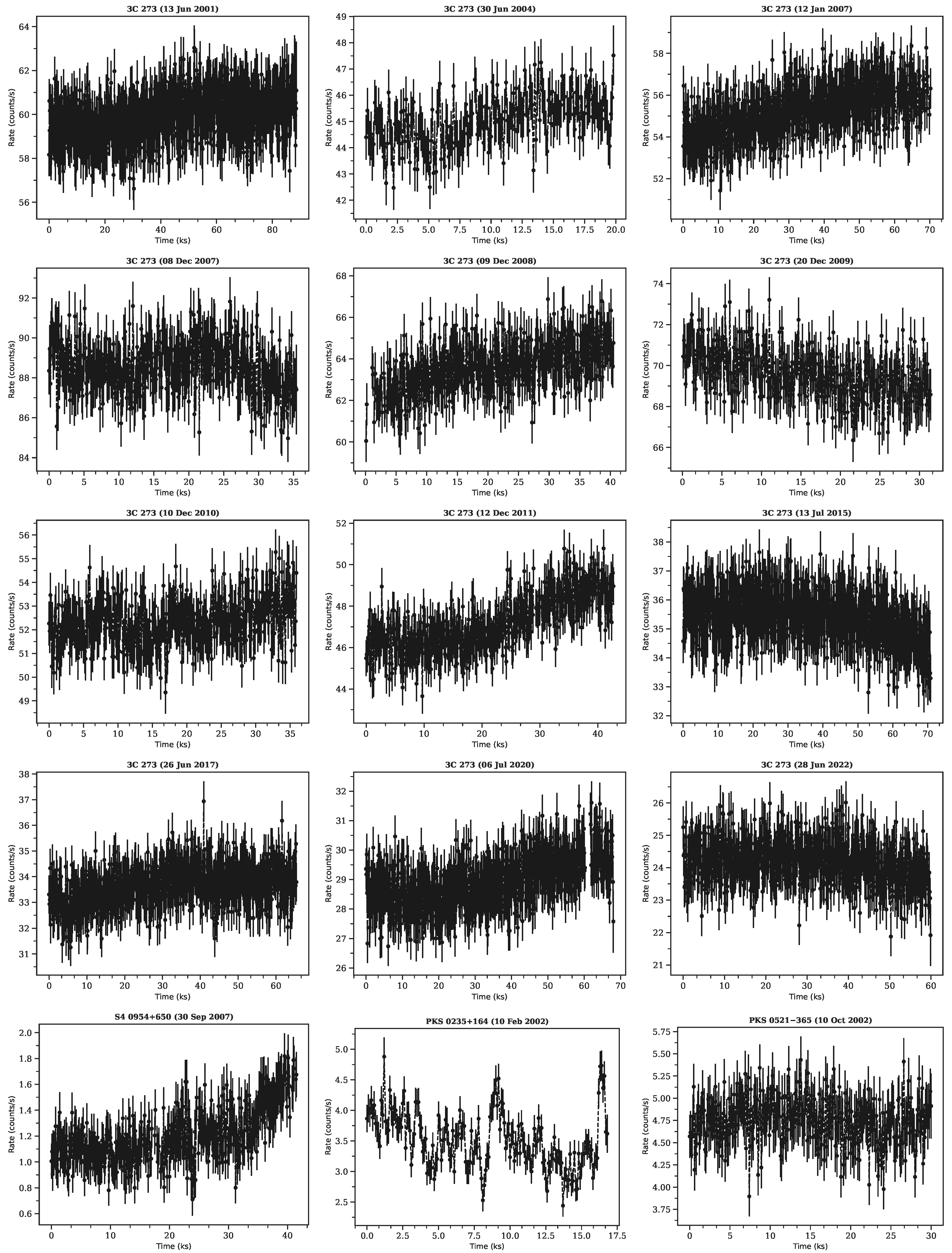
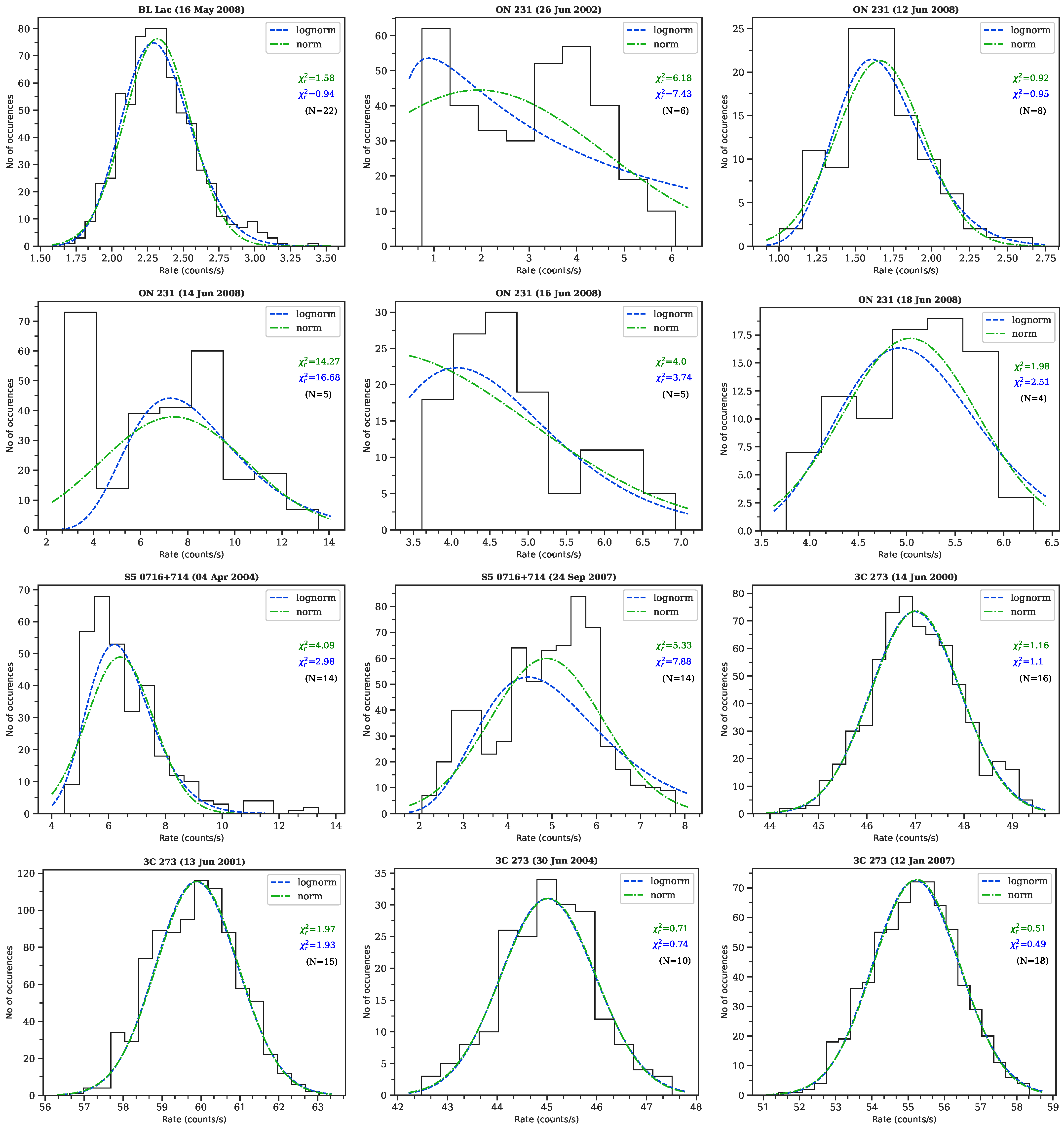

| Object | Source Class | Redshift | Observation Date | N | Lognormal | Normal | RMS-Flux Relation | Preferred Model | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (p-Value) | (prob) | (p-Value) | (prob) | -Value) | -Value) | |||||||
| BL Lac | ISP | 0.069 | 16 May 2008 | 22 | 7.26 (0.42) | 0.32 (0.52) | 0.94 (0.54) | 2.93 (<0.01) | 1.58 (0.04) | 0.22 (0.26) | 0.36 (0.18) | Lognormal |
| ON 231 | ISP | 0.102 | 26 June 2002 | 6 | 44.54 (0.44) | 5.59 (<0.01) | 7.43 (<0.01) | 5.04 (<0.01) | 6.18 (<0.01) | 0.66 (<0.01) | 0.74 (<0.01) | - |
| ON 231 | ISP | 0.102 | 12 June 2008 | 8 | 14.15 (1.21) | 0.29 (0.60) | 0.95 (0.48) | 0.46 (0.26) | 0.92 (0.50) | −0.05 (0.91) | 0.75 (0.14) | None |
| ON 231 | ISP | 0.102 | 14 June 2008 | 5 | 38.42 (0.30) | 5.95 (<0.01) | 16.68 (<0.01) | 4.69 (<0.01) | 14.27 (<0.01) | 0.83 (<0.01) | 0.41 (0.24) | - |
| ON 231 | ISP | 0.102 | 16 June 2008 | 5 | 15.89 (0.54) | 0.59 (0.12) | 3.74 (<0.01) | 2.82 (<0.01) | 4.00 (<0.01) | 0.05 (0.93) | −0.49 (0.40) | - |
| ON 231 | ISP | 0.102 | 18 June 2008 | 4 | 11.08 (0.67) | 1.05 (0.01) | 2.51 (0.04) | 0.98 (0.01) | 1.98 (0.09) | −0.09 (0.89) | −0.94 (0.22) | - |
| S5 0716+714 | ISP | 0.3 | 4 April 2004 | 14 | 22.00 (0.25) | 0.26 (0.70) | 2.98 (<0.01) | 9.68 (<0.01) | 4.09 (<0.01) | 0.83 (<0.01) | 0.87 (<0.01) | - |
| S5 0716+714 | ISP | 0.3 | 24 September 2007 | 14 | 24.09 (0.24) | 3.63 (<0.01) | 7.88 (<0.01) | 3.49 (<0.01) | 5.33 (<0.01) | 0.52 (<0.01) | 0.52 (0.02) | - |
| 3C 273 * | LSP | 0.1575 | 14 June 2000 | 16 | 0.64 (0.17) | 0.22 (0.84) | 1.10 (0.35) | 0.27 (0.68) | 1.16 (0.29) | 0.09 (0.67) | 0.07 (0.82) | None |
| 3C 273 | LSP | 0.1575 | 13 June 2001 | 15 | 0.63 (0.12) | 0.77 (0.04) | 1.93 (0.02) | 0.72 (0.06) | 1.97 (0.01) | −0.06 (0.78) | −0.21 (0.54) | - |
| 3C 273 | LSP | 0.1575 | 30 June 2004 | 10 | 0.91 (0.24) | 0.17 (0.93) | 0.74 (0.68) | 0.16 (0.96) | 0.71 (0.71) | 0.23 (0.66) | 1.00 (1.00) | None |
| 3C 273 | LSP | 0.1575 | 12 January 2007 | 18 | 1.29 (0.09) | 0.39 (0.38) | 0.50 (0.96) | 0.35 (0.48) | 0.51 (0.95) | −0.13 (0.64) | 0.59 (0.06) | - |
| 3C 273 | LSP | 0.1575 | 8 December 2007 | 11 | 0.49 (0.16) | 0.29 (0.60) | 0.94 (0.50) | 0.32 (0.54) | 0.98 (0.46) | 0.09 (0.76) | 0.20 (0.67) | None |
| 3C 273 | LSP | 0.1575 | 9 December 2008 | 12 | 1.05 (0.12) | 0.13 (0.98) | 0.61 (0.83) | 0.14 (0.98) | 0.63 (0.82) | 0.07 (0.80) | −0.73 (0.06) | - |
| 3C 273 | LSP | 0.1575 | 20 December 2009 | 12 | 0.89(0.14) | 0.20 (0.87) | 1.09 (0.36) | 0.25 (0.75) | 1.07 (0.38) | 0.10 (0.77) | 0.66 (0.15) | None |
| 3C 273 | LSP | 0.1575 | 10 December 2010 | 14 | 0.73 (0.19) | 0.28 (0.63) | 1.30 (0.20) | 0.55 (0.16) | 1.36 (0.16) | 0.43 (0.13) | 0.82 (0.05) | None |
| 3C 273 | LSP | 0.1575 | 12 December 2011 | 12 | 2.11 (0.11) | 0.62 (0.11) | 1.91 (0.03) | 1.54 (<0.01) | 2.11 (0.01) | 0.19 (0.51) | 0.04 (0.92) | - |
| 3C 273 | LSP | 0.1575 | 13 July 2015 | 12 | 1.06 (0.14) | 0.46 (0.27) | 0.98 (0.46) | 0.43 (0.31) | 0.95 (0.49) | −0.18 (0.40) | −0.45 (0.11) | None |
| 3C 273 | LSP | 0.1575 | 26 June 2017 | 21 | 0.73 (0.20) | 0.33 (0.52) | 1.27 (0.18) | 0.28 (0.63) | 1.20 0.24) | 0.64 (<0.01) | 0.44 (0.38) | None |
| 3C 273 | LSP | 0.1575 | 6 July 2020 | 16 | 1.79 (0.13) | 0.17 (0.93) | 0.41 (0.98) | 0.38 (0.40) | 0.47 (0.96) | −0.02 (0.92) | −0.41 (0.21) | - |
| 3C 273 | LSP | 0.1575 | 28 June 2022 | 18 | 1.03 (0.22) | 0.24 (0.78) | 1.33 (0.16) | 0.25 (0.73) | 1.32 (0.16) | 0.25 (0.24) | 0.30 (0.34) | None |
| S4 0954+650 | LSP | 0.367 | 30 September 2007 | 13 | 12.57 (0.75) | 0.74 (0.05) | 1.55 (0.09) | 3.92 (<0.01) | 3.35 (<0.01) | 0.39 (0.19) | 0.61 (0.20) | Lognormal |
| PKS 0235+164 | LSP | 0.94 | 10 February 2002 | 8 | 11.60 (0.50) | 0.23 (0.80) | 1.50 (0.15) | 0.60 (0.12) | 1.75 (0.08) | 0.36 (0.22) | 0.32 (0.49) | None |
| PKS 0521-365 | LSP | 0.055 | 10 October 2002 | 9 | 2.06 (0.62) | 0.36 (0.45) | 1.30 (0.23) | 0.33 (0.51) | 1.15 (0.33) | 0.42 (0.14) | 0.32 (0.44) | None |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wani, K.; Gaur, H. Study of Intra-Day Flux Distributions of Blazars Using XMM-Newton Satellite. Universe 2022, 8, 578. https://doi.org/10.3390/universe8110578
Wani K, Gaur H. Study of Intra-Day Flux Distributions of Blazars Using XMM-Newton Satellite. Universe. 2022; 8(11):578. https://doi.org/10.3390/universe8110578
Chicago/Turabian StyleWani, Kiran, and Haritma Gaur. 2022. "Study of Intra-Day Flux Distributions of Blazars Using XMM-Newton Satellite" Universe 8, no. 11: 578. https://doi.org/10.3390/universe8110578
APA StyleWani, K., & Gaur, H. (2022). Study of Intra-Day Flux Distributions of Blazars Using XMM-Newton Satellite. Universe, 8(11), 578. https://doi.org/10.3390/universe8110578






