Abstract
Neutrinos are a powerful tool for searching physics beyond the standard model of elementary particles. In this review, we present the status of the research on charge-parity-time (CPT) symmetry and Lorentz invariance violations using neutrinos emitted from the collapse of stars such as supernovae and other astrophysical environments, such as gamma-ray bursts. Particularly, supernova neutrino fluxes may provide precious information because all neutrino and antineutrino flavors are emitted during a burst of tens of seconds. Models of quantum gravity may allow the violation of Lorentz invariance and possibly of CPT symmetry. Violation of Lorentz invariance may cause a modification of the dispersion relation and, therefore, in the neutrino group velocity as well in the neutrino wave packet. These changes can affect the arrival time signal registered in astrophysical neutrino detectors. Direction or time-dependent oscillation probabilities and anisotropy of the neutrino velocity are manifestations of the same kind of new physics. CPT violation, on the other hand, may be responsible for different oscillation patterns for neutrino and antineutrino and unconventional energy dependency of the oscillation phase or of the mixing angles. Future perspectives for possible CPT and Lorentz violating systems are also presented.
1. Introduction
The standard model of elementary particles, Standard Model (SM) for short, is a quantum field theory in which symmetries play an essential role [1]. For example, the invariance of the Poincarè-Lorentz space-time symmetry guarantees that the laboratory orientation and its velocity do not affect the experimental results. There are also discrete symmetries, such as the time reversal (T), parity transformation (P), and charge conjugation (C) that are crucial in the SM formulation.
However, it is of fundamental importance that P is a broken symmetry in the weak interactions of the SM. The combination of C and P result in symmetry, but it is broken in the SM quark sector. This symmetry breaking could explain the asymmetry between matter and antimatter in the Universe. Nevertheless, it is insufficient, so that looking for symmetry breaking in other sectors of the SM becomes desirable. Why the Universe is constituted by an overwhelming abundance of matter over antimatter is still a topic of research. Finally, the combination of the three discrete symmetries mentioned above forms the symmetry, which is invariant in flat spacetimes [2]. The SM is structured on the pillars of symmetry and Lorentz invariance [3]. If symmetry is conserved, particles and their respective antiparticles are predicted to have, for example, the same mass and lifetime.
O. W. Greenberg proved that if violation occurs, Lorentz symmetry violation occurs [4]. However, there are other scenarios where violation is found such as, for example, when locality is broken instead of Lorentz invariance [5]. Quoting Tasson [6]: “there are two main reasons to consider Lorentz invariance violation (LIV): (i) considering our current detectors and the foreseeable ones, there is always the possibility to probe new physics at very high energy scale, the Planck scale (∼ GeV); (ii) also it is very important to do a very rigorous testing on the fundamental basis of our fundamental theories, such as general relativity and the SM”.
Neutrinos may be a useful tool to explore physics on the Planck energy scale. They are already one step beyond the standard model because neutrino flavor oscillations are described through the interference of mass eigenstates, which are not predicted in the original theory [7]. Furthermore, given that their mass scale is small, that their charge and magnetic moment are robustly constrained, and that their only coupling with matter in the standard model is the weak interaction, effects of new physics on neutrinos may be relatively strong. Therefore, they are natural candidates to explore possible violations of Lorentz and symmetries [8]. One very general effective field theory that incorporates the SM and general relativity and breaks Lorentz invariance, with possible violation of symmetry, is the Standard Model Extension (SME) [9].
Neutrinos have different production sources, such as the Sun, particle accelerators, nuclear reactors, secondary reactions after cosmic ray interactions in the upper atmosphere, relics of the Big-Bang. Together with photons and charged cosmic rays, neutrinos are in the present a real source of data in astronomy and astrophysics. The first detection of an astrophysical neutrino, particularly a solar neutrino, was realized by the Homestake experiment [10]. Neutrinos are abundantly produced in extreme phenomena, such as the collapse of stars. The first detection of supernova (SN) neutrinos happened with the SN1987A [11,12,13,14]. The IceCube experiment, at the South Pole, detected for the first time in history events of energy in the range TeV to PeV with astrophysical origin [15,16], rejecting at 5.7 the atmospheric origin explanation [17].
The combination of very long distances and high energy increases the possibility of exploring the Planck energy scale. In Ref. [18], the reader can find a review of the state-of-the-art recent observations and challenges coming from neutrino astronomy, particularly with neutrino telescopes.
The literature on Lorentz violation is extensive. There are numerous works discussing model building and the use of experimental results to restrict Lorentz and symmetry violations. Various analysis frameworks are explored, from terrestrial to astrophysical experiments [19]. For example, the neutrino sector is explored in the context of the SME in Ref. [20]. This short review focuses on astrophysical sources of neutrinos that can provide tests of LIV and CPT violation.
This article is organized as follows: Section 2 describes aspects of models that introduce LIV and violation, and also how the SME introduces both effects. Section 3 presents limits on LIV and violations in SN environments. Section 4 discusses limits in astrophysical environments with higher energies when compared with SN. Section 5 states our conclusions and future perspectives.
2. Lorentz Invariance and CPT Symmetry Violations
Even though and LIV can be associated, there is the possibility of LIV without violation. In order to preserve CPT symmetry, besides preserving Lorentz invariance, weak local commutativity is a necessary and sufficient condition, as pointed out in Ref. [19] and demonstrated in Ref. [21]. symmetry implies that , where represents the parameter of violation in the neutrino sector and for antineutrinos. Besides , other parameters in neutrino oscillation physics, that is, mass squared differences and mixing angles, must be constrained independently for neutrinos and antineutrinos if one considers the possibility of symmetry violation.
In this sense, a few analyses were conducted looking for discrepancies between neutrino and antineutrino correspondent parameters, with no discovery of violation. Other attempts tried to explain the so-called neutrino anomalies [22,23,24,25,26,27,28], such as the LSND one.
However, even though there is good agreement under the current experimental uncertainties, between neutrino and antineutrino parameters, there is still room to explore novel effects and several new analyses and previous works are relevant [29,30,31,32].
Antineutrino oscillation parameters—, , , , —are explored mainly by reactor, atmospheric and accelerator neutrino experiments. Reactor experiments measure the survival probability of at different baselines: KamLAND, with a baseline of approximately 100 km [33]; Daya-Bay, RENO and Double-Chooz with baselines of order 1 km [34,35,36]. Super-Kamiokande detected atmospheric neutrinos [37]. MINOS [38] and T2K [39] are accelerator experiments and extracted data of the disappearance for around eV.
Constraints on the neutrino oscillation parameters, on the other hand, are provided by solar neutrino experiments [40,41,42,43,44,45], the Super-Kamiokande atmospheric neutrino data [37] and accelerator data from MINOS [46], T2K [39] and NOA (NuMI Off-Axis Appearance Experiment) [47]. The situation of , the parameter related to violation, is still uncertain and the discussion of the most recent results on violation is not on the scope of this article. From Ref. [48], (), for normal (inverted) ordering. In the normal ordering the mass eigenstate is the lightest: ; for inverted ordering is the lightest one: .
Table 1 summarizes results on neutrino and antineutrino parameters obtained directly from the above experiments or from a combined analysis of them [48,49].

Table 1.
Neutrino and antineutrino mass squared differences and mixing angles.
One of the most traditional models which introduces the break of CPT and LIV is the Standard Model Extension (SME) [9]. This formulation guarantees the Dirac equation and the Schrodinger equation for non-relativistic scenarios and its construction is made preserving gauge symmetries and microcausality. A few remarks are in order to understand the SME fundamental ideas and here we follow the notation and ideas presented in Ref. [20]. SME is an effective field theory and is constructed from the basis of General Relativity and the Standard Model. It contains operators for Lorentz violation and these operators are controlled by coefficients that introduce Lorentz violation, with or without breaking. Generally, in the SME we can say that the Lorentz violation terms are constructed by coupling Standard Model operators with Lorentz violation coefficients (tensor or vector). The SME Lagrangian density for the neutrino sector is:
where represents all neutrino fields; M is the mass matrix associated with the seesaw mechanism [51]; are the Dirac matrices (); is the operator related to Lorentz violation:
where consists of matrices that can be decomposed in blocks of Dirac and Majorana components. At leading order the scalar, , and pseudo-scalar, , components cannot be observed. The vector, , and axial, , terms modify propagation and mixing of left-handed neutrinos and right-handed antineutrinos independently by their Dirac components. Mixing between neutrinos and antineutrinos is introduced by the Majorana component of the tensor . Finally, and .
When we convert the Lagrangian in Equation (1) into a Hamiltonian, we have two diagonal blocks of matrices, for neutrinos and for antineutrinos, where a and b are flavor indexes. The remaining two off diagonal blocks, and , mix neutrinos and antineutrinos and represent a Lorentz violation effect. The above matrices are written as:
and
In Equations (3) and (4), is the momentum, and are the mass matrix ( = ). The a and c are, respectively, the CPT-odd and CPT-even Lorentz violation coefficients. and for and , 0 for and . In Equation (5), and are, respectively, the coefficients for CPT-odd and CPT-even Lorentz violation for the case where there is mixing between neutrinos and antineutrinos. See Ref. [52] for details. The left- and right-handed coefficients for CPT-odd Lorentz violation are related by and CPT-even Lorentz violation are related by the following relation: . and represents the polarization state. The introduction of operators with higher dimensions will lead to higher powers of the neutrino energy in the Hamiltonian.
Violation of Lorentz invariance and CPT for neutrino physics provide two general effects. The first one does not change oscillations, as opposed to the second.
Concerning the first one, in the context of SME, the neutrino velocity compared with the speed of light, in natural units, can be expressed as:
In Equation (6), the sum indicates that several non-related coefficients produce the effect of non-oscillation Lorentz violation. The is the real mass parameter and does not alter the oscillation pattern in the neutrino path to the detector. The energy dependence is contained in the neutrino momentum ; d is the dimension of the operators and and are, respectively, the coefficients for CPT-odd and CPT-even Lorentz violation. contains the orientation of the experiment related to the neutrino direction in the Sun-centered frame. It involves the location of the detector and it is expanded in spherical harmonics, , in the laboratory frame. The index m controls the harmonics of the sidereal phase . The time dependence describes the Earth’s rotation in the Sun-centered reference frame. For the neutrino velocity is isotropic. When the neutrino velocity becomes time dependent. For d odd, neutrinos and anti-neutrinos have different speeds. For , neutrinos have different dispersion with different energies, including different time delays that can be explored in a variety of astrophysical phenomena.
Concerning the second type of symmetry violation effect, the SME coefficients modify the mixing angles and then, consequently, neutrino oscillations. For example, neutrino appearance probability in short baseline experiments is written as:
where L is the baseline, E is the neutrino energy, and . For antineutrinos one substitutes and . For long baseline experiments the probability can be described perturbatively [53], where the zero-order term is the standard oscillation probability. The first order conversion probability can be written as:
where the amplitudes, , contain Lorentz violating coefficients, important in the studies involving neutrino energy, neutrino beam direction, and the location of the experiment. For the complete expressions, see [53].
In the SME, for a relativistic, oscillation-free, and CPT-even framework, the dispersion relation for a high energy neutrino or antineutrino with energy E and momentum p is [8]:
where is the mass dimension of the underlying operator in the field theoretical action, j and m are indices related to the conventional angular momentum , and are the coefficients directly related to Lorentz violation. This equation introduces a new energy dependence and a possible modification depending on the particle propagation direction. Equation (9) does not consider the contribution of d odd coefficients, , related to CPT-odd operators which introduce CPT symmetry breaking. It also neglects mass terms for the very high energy regime, for example, neutrinos detected at IceCube.
There are models considering the possibility of Lorentz violation [54,55]. These models can be compatible with and reconstructed using the SME formalism [56,57].
It is possible to introduce LIV without CPT violation on phenomenological grounds through a modified dispersion relation [19]. For instance, 1. Very Special Relativity [58], where the particle with mass m, energy E, and momentum p, interacts with the quantum background producing the dispersion relation,
where is the parameter accounting for the violation. 2. Doubly Special Relativity [59,60]. In this model, apart from the speed of light invariance, the Planck length is invariant. For a particle with momentum p and mass m the modified dispersion relation becomes:
where is a function of p and E, in contrast with a constant in Equation (10). 3. Homogeneously Modified Special Relativity [61], where the author geometrizes the interaction of massive particles with the background. In order to do so Lorentz symmetry is modified and the Lorentz group changes to preserve covariance. Then,
where perturbation preserves rotation invariance and can assume different values for different particles. Notice, however, that the aforementioned models are particular types of quantum gravity that may predict modified dispersion relations. For other models such as non critical strings, Finsler geometries, and so forth, we refer to the review [62].
In the next two Sections, we present some of the main results in the low energy regime of SN and the high energy regime of other astrophysical sources, for example, gamma-ray bursts (GRBs).
3. Limits from Supernova Events
Supernovae are among the most powerful sources of neutrino emission in the Universe. During an SN explosion, 99% of the emitted energy is released by neutrinos and antineutrinos of all flavors. Neutrinos from these explosions have energy ranging from a few MeV to hundreds of MeV. They play the role of astrophysical messengers, escaping almost freely from the SN core. The SN neutrino flux has been extensively studied as a probe of the fundamental properties of the neutrinos and of the physics that seeks to explain the collapse of the nucleus. Therefore, SN neutrino research represents a truly interdisciplinary field of research encompassing particle physics, nuclear physics, and astrophysics. For a recent review, we suggest Ref. [63].
Although SN explosions in our galaxy are rare, large existing neutrino detectors will allow us to capture a large number of neutrino events. The detection of SN neutrinos will be crucial to test models explaining the explosion mechanisms, providing empirical information for the sophistication of such models. Certainly, such stellar collapse models will be scrutinized with the data generated in the explosion. However, we can also think about neutrino physics itself and how supernovae can contribute to the construction and understanding of the still incomplete, but more than relevant, neutrino physics.
Originating inside the nucleus, neutrinos are affected by flavor conversions on their way through the star mantle and envelope. In this path, the SN matter is extremely dense. Under these conditions, neutrinos may experience, in addition to the usual interaction with matter via the MSW effect, autointeractions causing new oscillation effects [64]. Therefore, the neutrino fluxes arriving at the detectors may carry signatures of oscillation effects in the deeper regions of supernovae. Such conversions also depend on the mass ordering of the neutrino eigenstates. In this sense, the dense interior of supernovae represents a unique laboratory for probing the mixture of neutrino flavors under high-density conditions.
Neutrinos from stellar collapse were first observed in 1987 originated in the Large Magellanic Cloud, 51 kpc away. Two Cherenkov detectors in water of the order of kilotons of effective mass observed the event: Kamiokande-II [14] and Irvine-Michigan-Brookhaven (IMB) [11] observed approximately 20 neutrino events in 13 seconds. This time interval is consistent with the optical observation of the SN1987A. Two smaller scintillator-type detectors, Baksan [12] and Mont Blanc Liquid Scintillation Detector (LSD) [13] reported several events.
The detection of SN1987A neutrinos is regarded as a key milestone in understanding the phenomenon of core collapse and the associated neutrino emission [65]. The observation of SN1987A allowed us to place strong restrictive limits on the exotic properties of neutrinos, like neutrino decay [66,67]. From the other side, the total energy of the and the neutron protostar’s cooling time scale of the order of a few seconds put severe limits on the unusual cooling mechanisms that can be associated with new particles emitted from the nucleus [68]. Even though there are good attempts to point out directions [65], given the small number of events of SN1987A, determining, at the same time, the astrophysical parameters associated with the SN mechanism and the parameters of neutrino physics is difficult [65].
Among the various experiments that are being prepared for the detection of stellar collapse neutrinos, we highlight the Deep Underground Neutrino Experiment (DUNE) [69] and the Hyper–Kamiokande [70]. Both will investigate, through different detection channels, the neutronization peak via and aspects of stellar cooling via .
3.1. CPT Violation Measurements from Supernovae
CPT violation impacts neutrino and antineutrino masses and mixing angles, influencing the energy spectra of the different flavors [71].
The neutrino flux after propagation from the source is [72],
where , and are, respectively, the fluxes of electronic neutrinos, electronic antineutrinos and the other neutrino flavors at the source; , and are the corresponding neutrino flavor fluxes after propagation; p and are, respectively, the survival probabilities for and .
Each p and are functions that depend on the values of the elements of the Pontecorvo–Maki –Nakagawa–Sakata (PMNS) mixing matrix [7], on the values of the transition probabilities at the high and low level crossings, and , respectively, and on the mass ordering. Level crossings refer to the transition probability of one mass eigenstate into another. In the SN environment, is the high resonance probability linked to the scale and is the low resonance probability linked to scale.
Figure 1 represents the evolution of the mass eigenstates for antineutrinos inside the star. There are several possibilities when considering CPT violation, besides the usual normal ordering and inverted ordering. In this Figure 1 we can notice the low density, , and high density, , level crossings for mass eigenstate transitions in SN environment. Figure 1a corresponds to normal ordering (N), , and ; Figure 1b corresponds to inverted ordering (I), , and ; Figure 1c corresponds to normal ordering (N), , and ; and Figure 1d corresponds to inverted ordering (I), and . For the usual neutrino level crossing diagram with normal and inverted ordering see Figure 5 of Ref. [72].
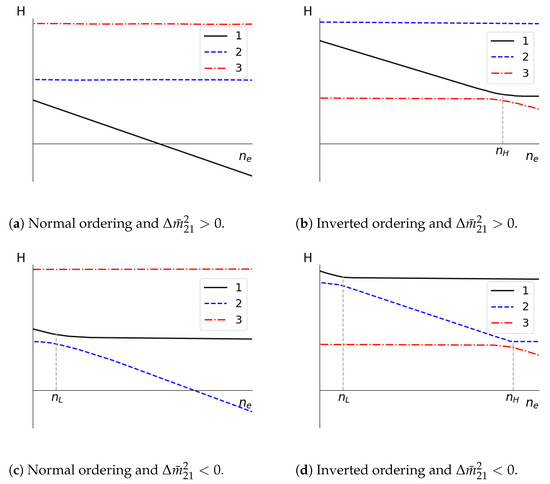
Figure 1.
Level crossing diagrams for mass eigenstates transitions in SN environment for antineutrinos. The vertical axes, H, represent the eigenvalue of the eigenstates (1,2,3) from the evolution Hamiltonian as a function of the electronic density, , of the medium. and are the high and low resonance densities, respectively. Figure adapted from Ref. [71].
For neutrinos and normal ordering, we have [71]:
For the ≈ eV under consideration, , since the level crossings are adiabatic. Then Equation (14) simplifies to .
For antineutrinos there are two different orderings for the mass eigenstates 1 and 2: and . Then, for each of these orderings, there are different transitions probabilities: () and (), where N stands for normal ordering and is related to the fact that . See Figure 1. Then and are represented by the following:
Equations (14)–(16) above show the possibility to probe CPT violation with SN neutrinos. With different p and it would be possible, for different eigenstate orderings, to generate distinctive neutrino and antineutrino signals.
We can write the survival probabilities for all these situations now considering the inverted ordering, . For neutrinos:
For antineutrinos—see Figure 1—where I stands for and () represents the transition probability when ().
We do not take into account the Earth matter effects, because they are very small and cannot disentangle the degeneracy between CPT-odd and CPT-even [71,72].
However, as pointed out by Minakata and Ushinami, the investigation has a “flux model dependence” and “a concern with its weakness at the precision test” [71]. Because the test is based on the difference between and mixing angles, it is important that SN neutrino detection is sensitive to those parameters.
3.2. LIV Measurements from Supernovae
The main constraints on CPT-conserving LIV from SN are related to modifications of the dispersion relation in a phenomenological framework. This is related to the fact that spacetime should have a foamy structure due to quantum-gravitational effects [73,74]. The fundamental idea is that matter particles interact with the spacetime foam medium and this affects the dispersion relation. This happens in string models, where electrically neutral particles, such as neutrinos and photons, recoil in the presence of a space-time defect. It is a non-usual interaction with the open-string which is a particle excitation in a brane universe. For example, photons feel a different refractive index in vacuum and have a subluminal propagation. Something similar happens with neutrinos due to their small masses.
The modification of the particle velocity in this context can be described by:
where v is the particle velocity, c is the speed of light, E is the energy of the particle and is the mass of the quantum gravity scale. The + and − signal represents, respectively, superluminal and subluminal particle propagation.
From SN1987A, Stodolsky compared the delay of a few hours between and and obtained a bound of [75]. Using Equation (20), for , GeV and for , GeV, considering MeV a representative energy for SN neutrinos.
In Ref. [76], the neutronization burst with a peak of duration 25 ms is explored. The presence of LIV spread the time of the expected events related to the SN luminosity curve when no LIV effects are taken into account - see Equation (20). Then, for a Mton Cerenkov detector and a galactic SN at 10 kpc Ref. [76] find a sensitivity of around ∼ GeV for a linear effect, in Equation (20), and ∼ GeV for a quadratic effect, in Equation (20), either for superluminal or subluminal neutrinos and independent of the mass ordering.
The experimentally observed duration of SN1987A was approximately 10 seconds. Considering the signal of Kamiokande-II [14], Irvine-MichiganBrookhaven (IMB) [11] and Baksan detectors [12], Ellis et al [77] found for , GeV and for , GeV, at of C.L. Also they considered a Super-Kamiokande-type of detector, with 22.5 kton and for a SN distance of 10 kpc, and estimated, for subluminal (superluminal) neutrinos and ; GeV, for , GeV, taking into account neutrino oscillation, but with the same LIV effect for all flavors.
Quantum gravity models predict a modification of the neutrino group velocities given by Equation (20). In Ref. [78], considering a scale of millisecond, differences in time variations from 2D simulations, limits with two orders of magnitude better could be obtained comparing to the previous ones found in Ref. [77]. However, this small millisecond differences could be detected only in SN simulation for a distance of 2 kpc [79].
In Ref. [78], an effect induced by quantum-gravity foam models, the spread of the wave packet width, is analysed using the wavelet technique. The spread is dependent on the neutrino energy and arises from energy-dependent neutrino group velocity.
The spread of the wave packet, with Gaussian shape, , is given by,
where is the spread at s, , where k is the amplitude of the spatial momentum and it is related to the dispersion relation . A few comments about are in order. If neutrinos are massless, linear order corrections are independent of the neutrino energy. However, if neutrinos have a small mass (), contributes in the form of . Hence, there will be a competition between this term and the term that corresponds to quantum gravity effects: the former decreases with neutrino energy, while the latter may be constant or increase with energy, as it depends on whether the refractive index is linear or quadratic in energy. The spread in can be parameterized as:
where or .
An stochastic process at fixed energy could reproduce the effects above, such as the spread of the wave packet, however, distinct from the spread caused by the modification of the refractive index.
These fluctuations have the form,
where is related to the string scale, is the string coupling constant, E is the average energy of the massless particle, or with very small mass. In this particular case there is a spread in the arrival times of photons and neutrinos of the order,
where L is the distance of the detector to the source and , where is defined in Equation (23). These fluctuations can be thought as a time independent spread in the wave packet. With the wavelet technique in the two dimensional SN simulation that exhibit signal variation of a few milliseconds in time, Ellis et al. obtained, at 95% confidence level, sensitivities to the quantum mass gravity scale of ∼ GeV () and ∼ GeV () [78].
For SN1987A data, in the context of the SME, there are several coefficients to be constrained. For example, for operators with dimension , is related to LIV with CPT-even coefficients. These are non isotropic coefficients and have dependence on propagation direction. For the isotropic case, the isotropic coefficient is represented by . We list on Table 2 a few upper limits on dimension operators for renormalizable model [8]. For more details, see Ref. [80], where measured and derived limits on coefficients of Lorentz and CPT violation in the SME are presented.

Table 2.
Neutrino upper bounds on LIV from SN1987A for SME with dimension four operators. Data from [8].
4. High Energy Astrophysical Environments
Neutrinos with energies higher than GeV, from astrophysical sources, are good tools to probe the Planck scale. These neutrinos can be produced from GRBs, Active Galactic Nuclei (AGN), microquasars, SN remnants, star clusters, and X-ray binaries. The most relevant experiment and the only one that collected high energy neutrino data is IceCube. It has observed extragalactic neutrinos [15,16] and is an important source of studies on Lorentz and CPT violation symmetry. The large astrophysical distances allow in general the effects of new physics to be maximized. Furthermore, the higher the energies of neutrinos the better is to investigate the symmetry-breaking scale.
High energy neutrinos are important tools for testing Lorentz violation models. Considering an effective theory, non-renormalizable operators that violate Lorentz symmetry may or may not violate the CPT symmetry, which may be CPT event or CPT odd. These operators cause deviation from the maximum attainable velocity c that a standard model particle may achieve. Superluminal neutrinos can lose their energy, during vacuum propagation, via vacuum pair emission or neutrino splitting.
4.1. LIV Limit Measurements
In addition to studies that involve modification in the dispersion relation, we can have new processes that are not allowed in standard physics. This can be explored when we join high energy neutrinos and astrophysical sources. Typical studies of isotropic events can be extended to explore effects that depend on the direction between production and detection [81]. In this section we present some of these studies in astrophysical sources and very high energy regime.
In GRBs, ultra high energy protons are accelerated in shock waves on which they photoproduce pions which in turn decay in muons and neutrinos, and the muons decay in electrons and neutrinos, from where the high energy neutrinos come. GRBs are natural sources of very high energy neutrinos [82,83], that can reach energies from dozens of TeV until dozens of PeV. Ref. [84] considered the generic context of LIV introduced in the time-of-flight (Equation (20)) comparing the neutrino arrival time with the prompt low-energy photons emitted from the redshift GRB. They obtained eV, for , and eV, for . A possible time-of-flight difference between the PeV neutrino and gamma-ray photons from blazar flares PKS B1424-418 at redshift was analyzed considering LIV and the following constraints on the LIV energy scale were obtained: , for , and for [85].
Neutrinos traveling with a superluminal speed can suffer new effects that would not be kinematically allowed with standard speed in vacuum [86]. There are three main effects: (i) Cherenkov radiation () [87]; (ii) neutrino splitting () [88]; and (iii) bremssthralung of electron-positron pairs () [89]. They all cause a depletion in neutrino fluxes.
For the bremsstrahlung of electron-positron pairs the energy loss per unity of length can be written, in natural units, as [89]:
where ≈ GeV is the Fermi coupling constant, ( ) is the speed deviation of neutrinos and electrons, where is the deviation from the speed of light (), represented generically by . The same representation can be used for electrons: [90]. This , with a LIV parameter related to a quantum gravity mass scale , can be represented in the following equation:
In order to lose energy and attain a terminal energy, , after traveling a distance, L, a superluminal neutrino must satisfy . Then,
From the neutrino event IceCube-170922A, which can be associated with blazar TXS 0506+056, considering the process in Equations (25)–(27), Wang et al. constrained , for , and for , where eV [91].
With the first two neutrino-induced events detected at IceCube [15] with estimated energies of PeV and PeV, ≲ [90] was obtained. Later, this limit improved to ≲ [92], where the authors assumed that the distribution of the star formation rate dictates the distribution of neutrino sources. For the two PeV scale IceCube events, Ref. [93] obtained ≲ and using Equation (26), , for , and ≳, for .
A tracklike neutrino event, IceCube-170922A, with energy 290 TeV in coincident with the blazar TXS 0506+056 with redshift z≈ [94,95] was used in several works to constraint neutrino velocity, and, as consequence, constrain also LIV. The IceCube-170922A event was also used to put constraints on LIV parameters using directly the time-of-flight [96,97,98]: ≲ [96]; ≳ GeV [97]; and – GeV () and GeV () [98].
Very high energy neutrinos observed by IceCube were analyzed in the context of SME [81] using Equation (9) to constrain the coefficients with dimension 4, ), related to LIV but CPT even. They are non isotropic coefficients and have dependence on propagation direction. For the isotropic case, the isotropic coefficient is represented by . See Table 3 for several constraints on these operators. They are obtained in Ref. [81], except for the last two lines, which are from [99,100]. For other constraints on other coefficients of higher dimension and also nonrenormalizable SME models, see [80].

Table 3.
IceCube neutrino bounds on LIV for dimension four operators from the SME. Limits extracted from Ref. [81], except where noted.
4.2. CPT Limit Measurements
To our knowledge, the production of articles involving only CPT violation and high energy neutrinos is not very extensive. We point out Ref. [101], where the CPT violation bound is obtained from the loss of unitarity that leads to quantum decoherence, a damping factor in oscillation probabilities.
In this context, space-time has a topologically discrete nature and there will be creation of quantum black holes in vacuum. These black holes have a radius of dimension of the Planck scale. They are created and evaporate continuously, leaving a trace of space-time that has a foamy nature. In nonstandard models that involve quantum mechanics, some pure quantum states may evolve into mixed quantum states because of the loss of information in these black holes.
The creation of these mixed quantum states modifies the standard mixing of neutrinos, and this can modify the flavor ratios of neutrinos in very high energy regimes. The CPT violation associated with the quantum decoherence, regardless of the source of emission, result in a flavor ratio of :: = 1/3:1/3:1/3 [101]. For more on CPT violation with decoherence effects see [102].
5. Outlook and Future Perspectives
This review presented a brief description of some aspects of the research in LIV and CPT violation in astrophysical environments. Astrophysical environments offer effective possibilities for the discovery of new physics in the Planck scale, since they combine large distances and high energies. Neutrinos are emitted in sources such as supernovae, and higher energy sources like GRBs or active galactic nuclei. Neutrinos are excellent candidates for new physics search, since there are possibly many neutrino properties yet to be discovered, besides the ones currently under scrutiny.
We present, besides the SME, other phenomenological approaches on LIV and CPT violation, based on, for example, quantum gravity effects that lead to superluminal or subluminal neutrinos. In the very high energy regime, new experiments of neutrinos, such as KM3NeT [103] and IceCube-GEN2 [104], will be very important to improve sensitivities in Planck scale searches. Ref. [52] shows an overview of searches related to neutrinos from astronomical and astrophysical origin, performed within the framework of the SME.
Concerning CPT violation, it can also be obtained from the loss of unitarity that leads to quantum decoherence, as mentioned in Section 4.2. Neutrino telescopes can be excellent instruments for investigating this kind of new physics in very high energy regimes [105,106]. For a low energy regime, a limit was obtained from SN1987A, which is at a distance of 50 kpc. In this case, the damping decoherence parameter found is GeV [107].
The detection of the next galactic SN with a real time structured events and the total characterization of the neutrino flavors with the DUNE far detector [108] and Hyper–Kamiokande [70] will provide more hints on possible differences in oscillation channels for the neutrinos and their respective antineutrinos, showing possible effective hints of CPT violation. Concerning LIV only effects, the precise characterization of time delays in future detectors can provide valuable information about the nature of this new physics. However, the complication in modeling astrophysical aspects of neutrinos and antineutrinos emission and the stellar collapse can impair the perception of the new physics introduced either by LIV or CPT violation.
Author Contributions
The authors C.A.M. and F.R.-T. contributed equally to this article. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
CAM acknowledges support from FAPESP Grant Process No. 2014/19164-6. F.R.-T. thanks UFABC for the hospitality.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SM | The Standard Model of Elementary Particles |
| SME | Standard Model Extension |
| LIV | Lorentz Invariance Violation |
| PMNS | Pontecorvo–Maki–Nakagawa–Sakata |
| SN | Supernova |
| GRB | Gamma-Ray Burst |
References
- Rosner, J.L. Resource letter: The Standard model and beyond. Am. J. Phys. 2003, 71, 302. [Google Scholar] [CrossRef]
- Luders, G. Proof of the TCP theorem. Ann. Phys. 1957, 2, 1. [Google Scholar] [CrossRef]
- Srednicki, M. Quantum Field Theory; Cambridge University Press: New York, NY, USA, 2007; pp. 543–561. [Google Scholar]
- Greenberg, O.W. CPT violation implies violation of Lorentz invariance. Phys. Rev. Lett. 2002, 89, 231602. [Google Scholar] [CrossRef] [PubMed]
- Chaichian, M.; Dolgov, A.D.; Novikov, V.A.; Tureanu, A. CPT Violation Does Not Lead to Violation of Lorentz Invariance and Vice Versa. Phys. Lett. B 2011, 699, 177. [Google Scholar] [CrossRef]
- Tasson, J.D. Gravity Effects on Antimatter in the Standard-Model Extension. Int. J. Mod. Phys. Conf. Ser. 2014, 30, 1460273. [Google Scholar] [CrossRef]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Kostelecky, A.; Mewes, M. Neutrinos with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2012, 85, 096005. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecky, V.A. Lorentz violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Davis, R., Jr.; Harmer, D.S.; Hoffman, K.C. Search for neutrinos from the sun. Phys. Rev. Lett. 1968, 20, 1205. [Google Scholar] [CrossRef]
- Bionta, R.M.; Blewitt, G.; Bratton, C.B.; Casper, D.; Ciocio, A.; Claus, R.; Cortez, B.; Crouch, M.; Dye, S.T.; Errede, S.; et al. Observation of a Neutrino Burst in Coincidence with Supernova SN 1987a in the Large Magellanic Cloud. Phys. Rev. Lett. 1987, 58, 1494. [Google Scholar] [CrossRef]
- Alekseev, E.N.; Alekseeva, L.N.; Volchenko, V.I.; Krivosheina, I.V. Detection of the Neutrino Signal From SN1987A in the LMC Using the Inr Baksan Underground Scintillation Telescope. Phys. Lett. B 1988, 205, 209. [Google Scholar] [CrossRef]
- Aglietta, M.; Badino, G.; Bologna, G.; Castagnoli, C.; Castellina, A.; Fulgione, W.; Galeotti, P.; Saavedra, O.; Trinchero, G.; Vernetto, S.; et al. On the event observed in the Mont Blanc Underground Neutrino observatory during the occurrence of Supernova 1987a. Europhys. Lett. 1987, 3, 1315. [Google Scholar] [CrossRef]
- Hirata, K. et al. [Kamiokande-II Collaboration] Observation of a Neutrino Burst from the Supernova SN 1987a. Phys. Rev. Lett. 1987, 58, 1490. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] First observation of PeV-energy neutrinos with IceCube. Phys. Rev. Lett. 2013, 111, 021103. [Google Scholar] [CrossRef] [PubMed]
- Aartsen, M.G. et al. [IceCube Collaboration] Evidence for High-Energy Extraterrestrial Neutrinos at the IceCube Detector. Science 2013, 342, 1242856. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Observation of High-Energy Astrophysical Neutrinos in Three Years of IceCube Data. Phys. Rev. Lett. 2014, 113, 101101. [Google Scholar] [CrossRef]
- Greus, F.S.; Losa, A.S. Multimessenger Astronomy with Neutrinos. Universe 2021, 7, 397. [Google Scholar] [CrossRef]
- Antonelli, V.; Miramonti, L.; Torri, M.D.C. Phenomenological Effects of CPT and Lorentz Invariance Violation in Particle and Astroparticle Physics. Symmetry 2020, 12, 1821. [Google Scholar] [CrossRef]
- Diaz, J.S. Testing Lorentz and CPT invariance with neutrinos. Symmetry 2016, 8, 105. [Google Scholar] [CrossRef]
- Greaves, H.; Thomas, T. On the CPT theorem. Stud. Hist. Phil. Sci. B 2014, 45, 46. [Google Scholar] [CrossRef][Green Version]
- Murayama, H.; Yanagida, T. LSND, SN1987A, and CPT violation. Phys. Lett. B 2001, 520, 263. [Google Scholar] [CrossRef]
- Barenboim, G.; Borissov, L.; Lykken, J.D.; Smirnov, A.Y. Neutrinos as the Messengers of CPT Violation. J. High Energy Phys. 2002, 10, 1. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, M.C.; Maltoni, M.; Schwetz, T. Status of the CPT violating interpretations of the LSND signal. Phys. Rev. D 2003, 68, 053007. [Google Scholar] [CrossRef]
- De Gouvêa, A.; Kelly, K.J. Neutrino vs. Antineutrino Oscillation Parameters at DUNE and Hyper-Kamiokande. Phys. Rev. D 2017, 96, 095018. [Google Scholar] [CrossRef]
- De Gouvea, A.; Pena-Garay, C. Probing new physics by comparing solar and KamLAND data. Phys. Rev. D 2005, 71, 093002. [Google Scholar] [CrossRef]
- Giunti, C.; Laveder, M. Hint of CPT Violation in Short-Baseline Electron Neutrino Disappearance. Phys. Rev. D 2010, 82, 113009. [Google Scholar] [CrossRef]
- Barenboim, G.; Beacom, J.F.; Borissov, L.; Kayser, B. CPT Violation and the Nature of Neutrinos. Phys. Lett. B 2002, 537, 227. [Google Scholar] [CrossRef]
- Moura, C.A.; on behalf of the DUNE Collaboration. Physics Beyond the Standard Model with DUNE: Prospects for Exploring Lorentz and CPT Violation. In Proceedings of the Eighth Meeting on CPT and Lorentz Symmetry, Bloomington, IN, USA, 12–16 May 2019; Lehnert, R., Ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2020; pp. 150–153. [CrossRef]
- Barenboim, G.; Ternes, C.A.; Tórtola, M. “Neutrinos, DUNE and the world best bound on CPT invariance. Phys. Lett. B 2018, 780, 631. [Google Scholar] [CrossRef]
- Carrasco, J.C.; Díaz, F.N.; Gago, A.M. Probing CPT breaking induced by quantum decoherence at DUNE. Phys. Rev. D 2019, 99, 075022. [Google Scholar] [CrossRef]
- Majhi, R.; Singha, D.K.; Deepthi, K.N.; Mohanta, R. Constraining CPT violation with Hyper-Kamiokande and ESSnuSB. Phys. Rev. D 2021, 104, 055002. [Google Scholar] [CrossRef]
- Gando, A. et al. [KamLAND Collaboration] Reactor On-Off Antineutrino Measurement with KamLAND. Phys. Rev. D 2013, 88, 033001. [Google Scholar] [CrossRef]
- Adey, D. et al. [Daya Bay Collaboration] Measurement of the Electron Antineutrino Oscillation with 1958 Days of Operation at Daya Bay. Phys. Rev. Lett. 2018, 121, 241805. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.H. et al. [RENO Collaboration] Observation of Energy and Baseline Dependent Reactor Antineutrino Disappearance in the RENO Experiment. Phys. Rev. Lett. 2016, 116, 211801. [Google Scholar] [CrossRef] [PubMed]
- Abe, Y. et al. [Double Chooz Collaboration] Improved measurements of the neutrino mixing angle θ13 with the Double Chooz detector. J. High Energy Phys. 2014, 10, 086, Erratum in J. High Energy Phys. 2015, 2, 74. [Google Scholar] [CrossRef]
- Abe, K. et al. [Super-Kamiokande Collaboration] Search for Differences in Oscillation Parameters for Atmospheric Neutrinos and Antineutrinos at Super-Kamiokande. Phys. Rev. Lett. 2011, 107, 241801. [Google Scholar] [CrossRef]
- Adamson, P. et al. [MINOS Collaboration] Measurement of Neutrino and Antineutrino Oscillations Using Beam and Atmospheric Data in MINOS. Phys. Rev. Lett. 2013, 110, 251801. [Google Scholar] [CrossRef] [PubMed]
- Abe, K. et al. [T2K Collaboration] T2K measurements of muon neutrino and antineutrino disappearance using 3.13 × 1021 protons on target. Phys. Rev. D 2021, 103, L011101. [Google Scholar] [CrossRef]
- Hampel, W. et al. [GALLEX Collaboration] Final results of the Cr-51 neutrino source experiments in GALLEX. Phys. Lett. B 1998, 420, 114. [Google Scholar] [CrossRef]
- Altmann, M. et al. [GNO Collaboration] Complete results for five years of GNO solar neutrino observations. Phys. Lett. B 2005, 616, 174. [Google Scholar] [CrossRef]
- Abdurashitov, J.N. et al. [SAGE Collaboration] Measurement of the solar neutrino capture rate with gallium metal. III: Results for the 2002–2007 data-taking period. Phys. Rev. C 2009, 80, 015807. [Google Scholar] [CrossRef]
- Aharmim, B. et al. [SNO Collaboration] Combined Analysis of all Three Phases of Solar Neutrino Data from the Sudbury Neutrino Observatory. Phys. Rev. C 2013, 88, 025501. [Google Scholar] [CrossRef]
- Bellini, G. et al. [Borexino Collaboration] Final results of Borexino Phase-I on low energy solar neutrino spectroscopy. Phys. Rev. D 2014, 89, 112007. [Google Scholar] [CrossRef]
- Abe, K. et al. [Super-Kamiokande Collaboration] Solar Neutrino Measurements in Super-Kamiokande-IV. Phys. Rev. D 2016, 94, 052010. [Google Scholar] [CrossRef]
- Adamson, P. et al. [MINOS Collaboration] Combined analysis of νμ disappearance and νμ→νe appearance in MINOS using accelerator and atmospheric neutrinos. Phys. Rev. Lett. 2014, 112, 191801. [Google Scholar] [CrossRef] [PubMed]
- Adamson, P. et al. [NOvA Collaboration] Constraints on Oscillation Parameters from νe Appearance and νμ Disappearance in NOvA. Phys. Rev. Lett. 2017, 118, 231801. [Google Scholar] [CrossRef]
- Esteban, I.; Gonzalez-Garcia, M.C.; Maltoni, M.; Schwetz, T.; Zhou, A. The fate of hints: Updated global analysis of three-flavor neutrino oscillations. J. High Energy Phys. 2020, 9, 178. [Google Scholar] [CrossRef]
- De Salas, P.F.; Forero, D.V.; Gariazzo, S.; Martínez-Miravé, P.; Mena, O.; Ternes, C.A.; Tórtola, M.; Valle, J.W.F. 2020 global reassessment of the neutrino oscillation picture. J. High Energy Phys. 2021, 2, 71. [Google Scholar] [CrossRef]
- Abe, K. et al. [T2K Collaboration] Improved constraints on neutrino mixing from the T2K experiment with 3.13 × 1021 protons on target. Phys. Rev. D 2021, 103, 112008. [Google Scholar] [CrossRef]
- Guo, W.L.; Xing, Z.Z.; Zhou, S. Neutrino Masses, Lepton Flavor Mixing and Leptogenesis in the Minimal Seesaw Model. Int. J. Mod. Phys. E 2007, 16, 1. [Google Scholar] [CrossRef]
- Roberts, Á. Astrophysical Neutrinos in Testing Lorentz Symmetry. Galaxies 2021, 9, 47. [Google Scholar] [CrossRef]
- Diaz, J.S.; Kostelecky, V.A.; Mewes, M. Perturbative Lorentz and CPT violation for neutrino and antineutrino oscillations. Phys. Rev. D 2009, 80, 076007. [Google Scholar] [CrossRef]
- Mattingly, D. Modern tests of Lorentz invariance. Living Rev. Rel. 2005, 8, 5. [Google Scholar] [CrossRef]
- Liberati, S. Tests of Lorentz invariance: A 2013 update. Class. Quant. Grav. 2013, 30, 133001. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Mewes, M. Electrodynamics with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2009, 80, 015020. [Google Scholar] [CrossRef]
- Kostelecký, A.; Mewes, A. Fermions with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2013, 88, 096006. [Google Scholar] [CrossRef]
- Coleman, S.R.; Glashow, S.L. High-energy tests of Lorentz invariance. Phys. Rev. D 1999, 59, 116008. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Doubly special relativity. Nature 2002, 418, 34. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Doubly special relativity: First results and key open problems. Int. J. Mod. Phys. D 2002, 11, 1643. [Google Scholar] [CrossRef]
- Torri, M.D.C.; Antonelli, V.; Miramonti, L. Homogeneously Modified Special relativity (HMSR): A new possible way to introduce an isotropic Lorentz invariance violation in particle standard model. Eur. Phys. J. C 2019, 79, 808. [Google Scholar] [CrossRef]
- Addazi, A.; Alvarez-Muniz, J.; Batista, R.A.; Amelino-Camelia, G.; Antonelli, V.; Arzano, M.; Asorey, M.; Atteia, J.L.; Bahamonde, S.; Bajardi, F.; et al. Quantum gravity phenomenology at the dawn of the multi-messenger era—A review. arXiv 2021, arXiv:2111.05659. [Google Scholar]
- Mirizzi, A.; Tamborra, I.; Janka, H.T.; Saviano, N.; Scholberg, K.; Bollig, R.; Hudepohl, L.; Chakraborty, S. Supernova Neutrinos: Production, Oscillations and Detection. Riv. Nuovo Cim. 2016, 39, 1. [Google Scholar] [CrossRef]
- Duan, H.; Fuller, G.M.; Qian, Y.Z. Collective Neutrino Oscillations. Ann. Rev. Nucl. Part. Sci. 2010, 60, 569. [Google Scholar] [CrossRef]
- Vissani, F. Comparative analysis of SN1987A antineutrino fluence. J. Phys. G 2015, 42, 013001. [Google Scholar] [CrossRef]
- Jaffe, A.H.; Turner, M.S. Gamma-rays and the decay of neutrinos from SN1987A. Phys. Rev. D 1997, 55, 7951. [Google Scholar] [CrossRef]
- Schmid, H.; Raffelt, G.; Leike, A. The Bremsstrahlung process tau-neutrino —> electron-neutrino e+ e− gamma. Phys. Rev. D 1998, 58, 113004. [Google Scholar] [CrossRef]
- Raffelt, G.G. What Have We Learned From SN 1987A? Mod. Phys. Lett. A 1990, 5, 2581. [Google Scholar] [CrossRef]
- Abi, B. et al. [DUNE Collaboration] Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report, Volume II: DUNE Physics. arXiv 2020, arXiv:2002.03005. [Google Scholar]
- Abe, K.; Abe, T.; Aihara, H.; Fukuda, Y.; Hayato, Y.; Huang, K.; Ichikawa, A.K.; Ikeda, M.; Inoue, K.; Ishino, H.; et al. Letter of Intent: The Hyper-Kamiokande Experiment—Detector Design and Physics Potential. arXiv 2011, arXiv:1109.3262. [Google Scholar]
- Minakata, H.; Uchinami, S. Testing CPT symmetry with supernova neutrinos. Phys. Rev. D 2005, 72, 105007. [Google Scholar] [CrossRef]
- Dighe, A.S.; Smirnov, A.Y. Identifying the neutrino mass spectrum from the neutrino burst from a supernova. Phys. Rev. D 2000, 62, 033007. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Ellis, J.R.; Mavromatos, N.E.; Nanopoulos, D.V.; Sarkar, S. Tests of quantum gravity from observations of gamma-ray bursts. Nature 1998, 393, 763. [Google Scholar] [CrossRef]
- Garay, L.J. Thermal properties of space-time foam. Phys. Rev. D 1998, 58, 124015. [Google Scholar] [CrossRef]
- Stodolsky, L. The Speed of Light and the Speed of Neutrinos. Phys. Lett. B 1998, 201, 353. [Google Scholar] [CrossRef]
- Chakraborty, S.; Mirizzi, A.; Sigl, G. Testing Lorentz invariance with neutrino bursts from supernova neutronization. Phys. Rev. D 2013, 87, 017302. [Google Scholar] [CrossRef]
- Ellis, J.R.; Harries, N.; Meregaglia, A.; Rubbia, A.; Sakharov, A. Probes of Lorentz Violation in Neutrino Propagation. Phys. Rev. D 2008, 78, 033013. [Google Scholar] [CrossRef]
- Ellis, J.; Janka, H.T.; Mavromatos, N.E.; Sakharov, A.S.; Sarkisyan, E.K.G. Probing Lorentz Violation in Neutrino Propagation from a Core-Collapse Supernova. Phys. Rev. D 2012, 85, 045032. [Google Scholar] [CrossRef]
- Lund, T.; Wongwathanarat, A.; Janka, H.T.; Muller, E.; Raffelt, G. Fast time variations of supernova neutrino signals from 3-dimensional models. Phys. Rev. D 2012, 86, 105031. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Russell, N. Data Tables for Lorentz and CPT Violation. arXiv 2008, arXiv:0801.0287. [Google Scholar]
- Diaz, J.S.; Kostelecky, A.; Mewes, M. Testing Relativity with High-Energy Astrophysical Neutrinos. Phys. Rev. D 2014, 89, 043005. [Google Scholar] [CrossRef]
- Waxman, E.; Bahcall, J.N. High-energy neutrinos from cosmological gamma-ray burst fireballs. Phys. Rev. Lett. 1997, 78, 2292. [Google Scholar] [CrossRef]
- Vietri, M. On the energy of neutrinos from gamma-ray bursts. Astrophys. J. 1998, 507, 40. [Google Scholar] [CrossRef]
- Jacob, U.; Piran, T. Neutrinos from gamma-ray bursts as a tool to explore quantum-gravity-induced Lorentz violation. Nat. Phys. 2007, 3, 87. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Liu, R.Y.; Wang, X.Y. Testing the equivalence principle and Lorentz invariance with PeV neutrinos from blazar flares. Phys. Rev. Lett. 2016, 116, 151101. [Google Scholar] [CrossRef]
- Maccione, L.; Liberati, S.; Mattingly, D.M. Violations of Lorentz invariance in the neutrino sector after OPERA. J. Cosmol. Astropart. Phys. 2013, 3, 39. [Google Scholar] [CrossRef]
- Jentschura, U.D.; Nándori, I.; Ehrlich, R. Calculation of the decay rate of tachyonic neutrinos against charged-lepton-pair and neutrino-pair Cerenkov radiation. J. Phys. G 2017, 44, 105201. [Google Scholar] [CrossRef]
- Somogyi, G.; Nándori, I.; Jentschura, U.D. Neutrino Splitting for Lorentz-Violating Neutrinos: Detailed Analysis. Phys. Rev. D 2019, 100, 035036. [Google Scholar] [CrossRef]
- Cohen, A.G.; Glashow, S.L. Pair Creation Constrains Superluminal Neutrino Propagation. Phys. Rev. Lett. 2011, 107, 181803. [Google Scholar] [CrossRef]
- Stecker, F.W. Limiting superluminal electron and neutrino velocities using the 2010 Crab Nebula flare and the IceCube PeV neutrino events. Astropart. Phys. 2014, 56, 16. [Google Scholar] [CrossRef]
- Wang, K.; Xi, S.Q.; Shao, L.; Liu, R.Y.; Li, Z.; Zhang, Z.K. Limiting Superluminal Neutrino Velocity and Lorentz Invariance Violation by Neutrino Emission from the Blazar TXS 0506+056. Phys. Rev. D 2020, 102, 063027. [Google Scholar] [CrossRef]
- Stecker, F.W.; Scully, S.T.; Liberati, S.; Mattingly, D. Searching for Traces of Planck-Scale Physics with High Energy Neutrinos. Phys. Rev. D 2015, 91, 045009. [Google Scholar] [CrossRef]
- Borriello, E.; Chakraborty, S.; Mirizzi, A.; Serpico, P.D. Stringent constraint on neutrino Lorentz-invariance violation from the two IceCube PeV neutrinos. Phys. Rev. D 2013, 87, 116009. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration, Fermi-LAT, MAGIC, AGILE, ASAS-SN, HAWC, H.E.S.S., INTEGRAL, Kanata, Kiso, Kapteyn, Liverpool Telescope, Subaru, Swift NuSTAR, VERITAS and VLA/17B-403] Multimessenger observations of a flaring blazar coincident with high-energy neutrino IceCube-170922A. Science 2018, 361, 1378. [Google Scholar] [CrossRef]
- Paiano, S.; Falomo, R.; Treves, A.; Scarpa, R. The redshift of the BL Lac object TXS 0506+056. Astrophys. J. Lett. 2018, 854, L32. [Google Scholar] [CrossRef]
- Laha, R. Constraints on neutrino speed, weak equivalence principle violation, Lorentz invariance violation, and dual lensing from the first high-energy astrophysical neutrino source TXS 0506+056. Phys. Rev. D 2019, 100, 103002. [Google Scholar] [CrossRef]
- Ellis, J.; Mavromatos, N.E.; Sakharov, A.S.; Sarkisyan-Grinbaum, E.K. Limits on Neutrino Lorentz Violation from Multimessenger Observations of TXS 0506+056. Phys. Lett. B 2019, 789, 352. [Google Scholar] [CrossRef]
- Wei, J.J.; Zhang, B.B.; Shao, L.; Gao, H.; Li, Y.; Yin, Q.Q.; Wu, X.F.; Wang, X.Y.; Zhang, B.; Dai, Z.G. Multimessenger tests of Einstein’s weak equivalence principle and Lorentz invariance with a high-energy neutrino from a flaring blazar. J. High Energy Astrophys. 2019, 22, 1. [Google Scholar] [CrossRef]
- Stecker, F.W.; Scully, S.T. Propagation of Superluminal PeV IceCube Neutrinos: A High Energy Spectral Cutoff or New Constraints on Lorentz Invariance Violation. Phys. Rev. D 2014, 90, 043012. [Google Scholar] [CrossRef]
- Stecker, F.W. Tests of Lorentz Invariance Using High Energy Astrophysics Observations. In CPT and Lorentz Symmetry, Proceedings of the Sixth Meeting, Bloomington, IN, USA, 17–21 June 2013; Kostelecky, V.A., Ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2014; pp. 73–76. [Google Scholar] [CrossRef]
- Hooper, D.; Morgan, D.; Winstanley, E. Lorentz and CPT invariance violation in high-energy neutrinos. Phys. Rev. D 2005, 72, 065009. [Google Scholar] [CrossRef]
- Buoninfante, L.; Capolupo, A.; Giampaolo, S.M.; Lambiase, G. Revealing neutrino nature and CPT violation with decoherence effects. Eur. Phys. J. C 2020, 80, 1009. [Google Scholar] [CrossRef]
- Adrian-Martinez, S. et al. [KM3Net Collaboration] Letter of intent for KM3NeT 2.0. J. Phys. G 2016, 43, 084001. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube-Gen2 Collaboration] IceCube-Gen2: The window to the extreme Universe. J. Phys. G 2021, 48, 060501. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Goldberg, H.; Gonzalez-Garcia, M.C.; Halzen, F.; Hooper, D.; Sarkar, S.; Weiler, T.J. Probing Planck scale physics with IceCube. Phys. Rev. D 2005, 72, 065019. [Google Scholar] [CrossRef]
- Mehta, P.; Winter, W. Interplay of energy dependent astrophysical neutrino flavor ratios and new physics effects. J. Cosmol. Astropart. Phys. 2011, 3, 41. [Google Scholar] [CrossRef]
- Klapdor-Kleingrothaus, H.V.; Pas, H.; Sarkar, U. Effects of quantum space-time foam in the neutrino sector. Eur. Phys. J. A 2000, 8, 577. [Google Scholar] [CrossRef]
- Abi, B. et al. [DUNE Collaboration] Supernova neutrino burst detection with the Deep Underground Neutrino Experiment. Eur. Phys. J. C 2021, 81, 423. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).