Analyzing the Time Spectrum of Supernova Neutrinos to Constrain Their Effective Mass or Lorentz Invariance Violation
Abstract
1. Introduction
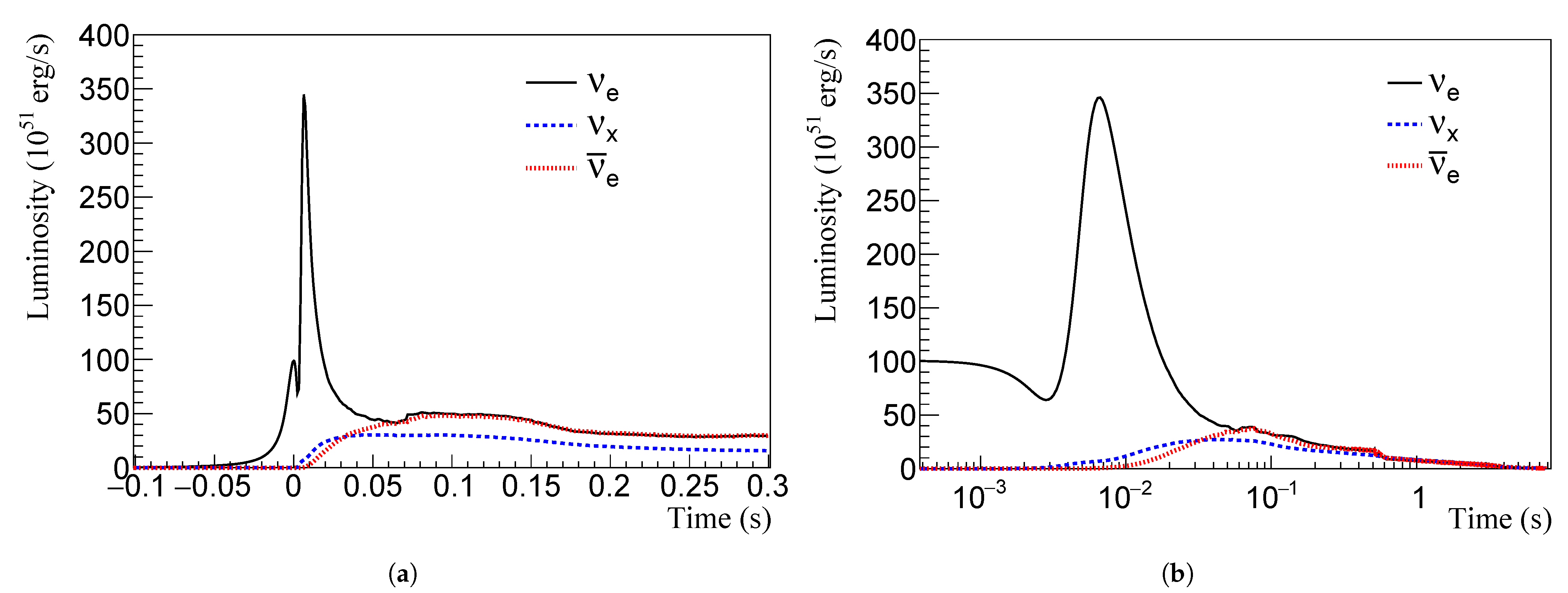
2. Neutrino Fluxes
3. Methodology
3.1. Number of Events
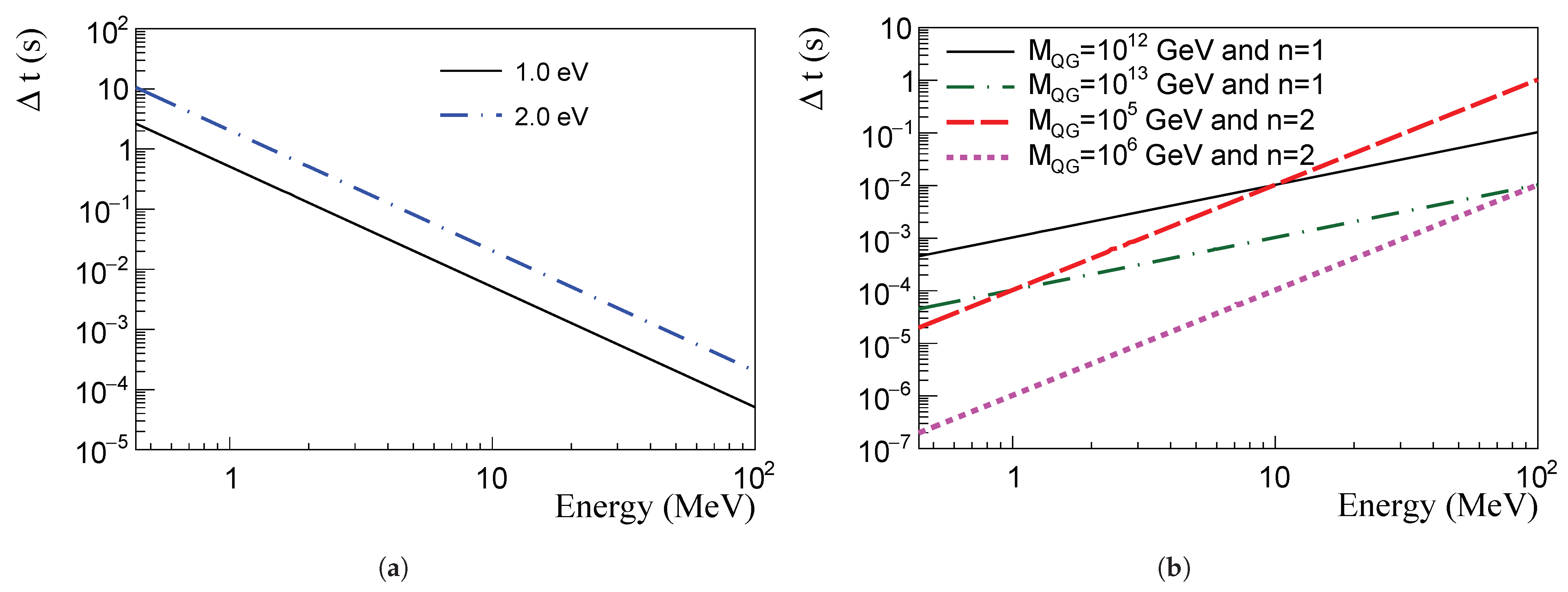
3.2. Time Delay
4. Detection Techniques
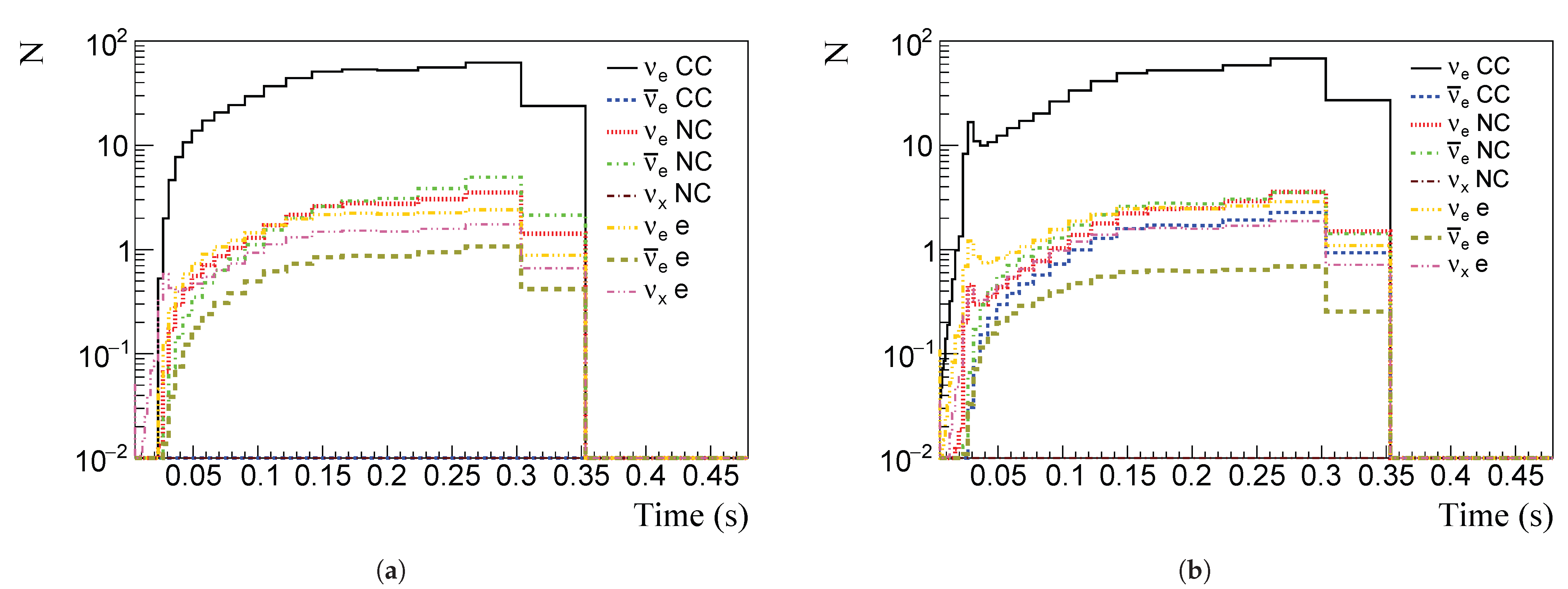
4.1. Liquid Argon TPC
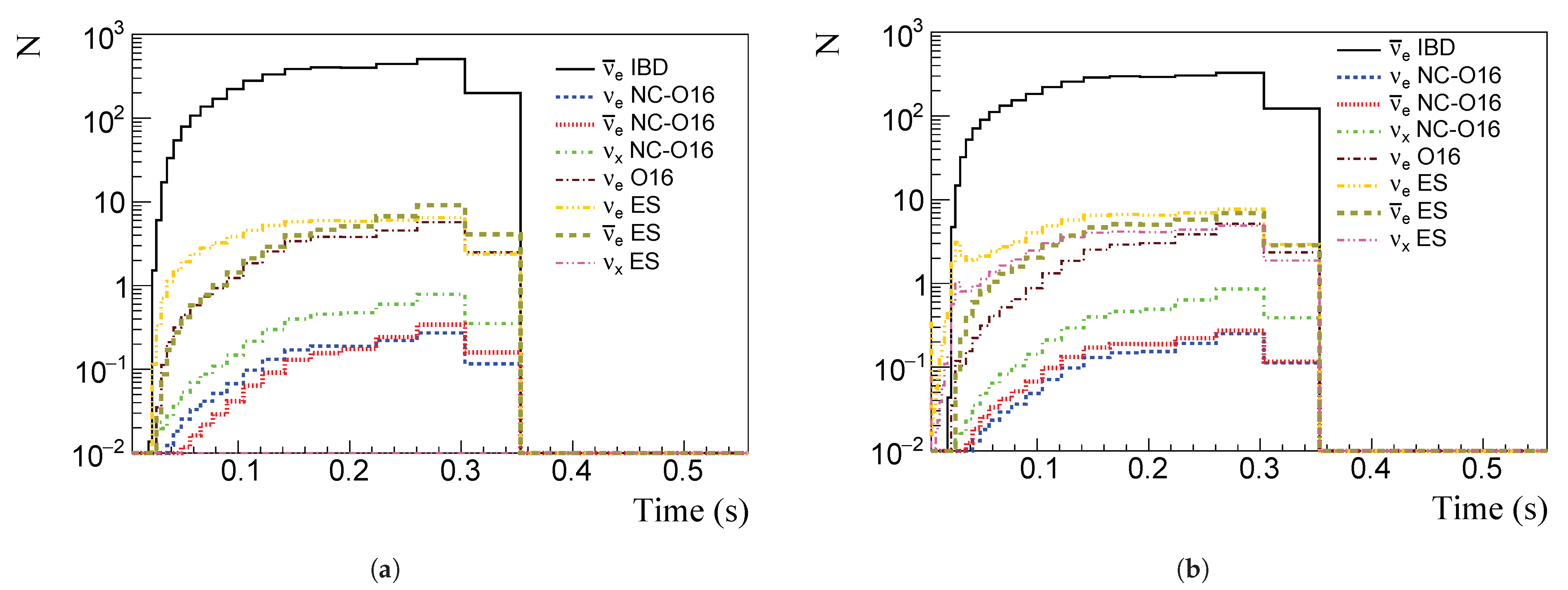
4.2. Water Cherenkov Detector
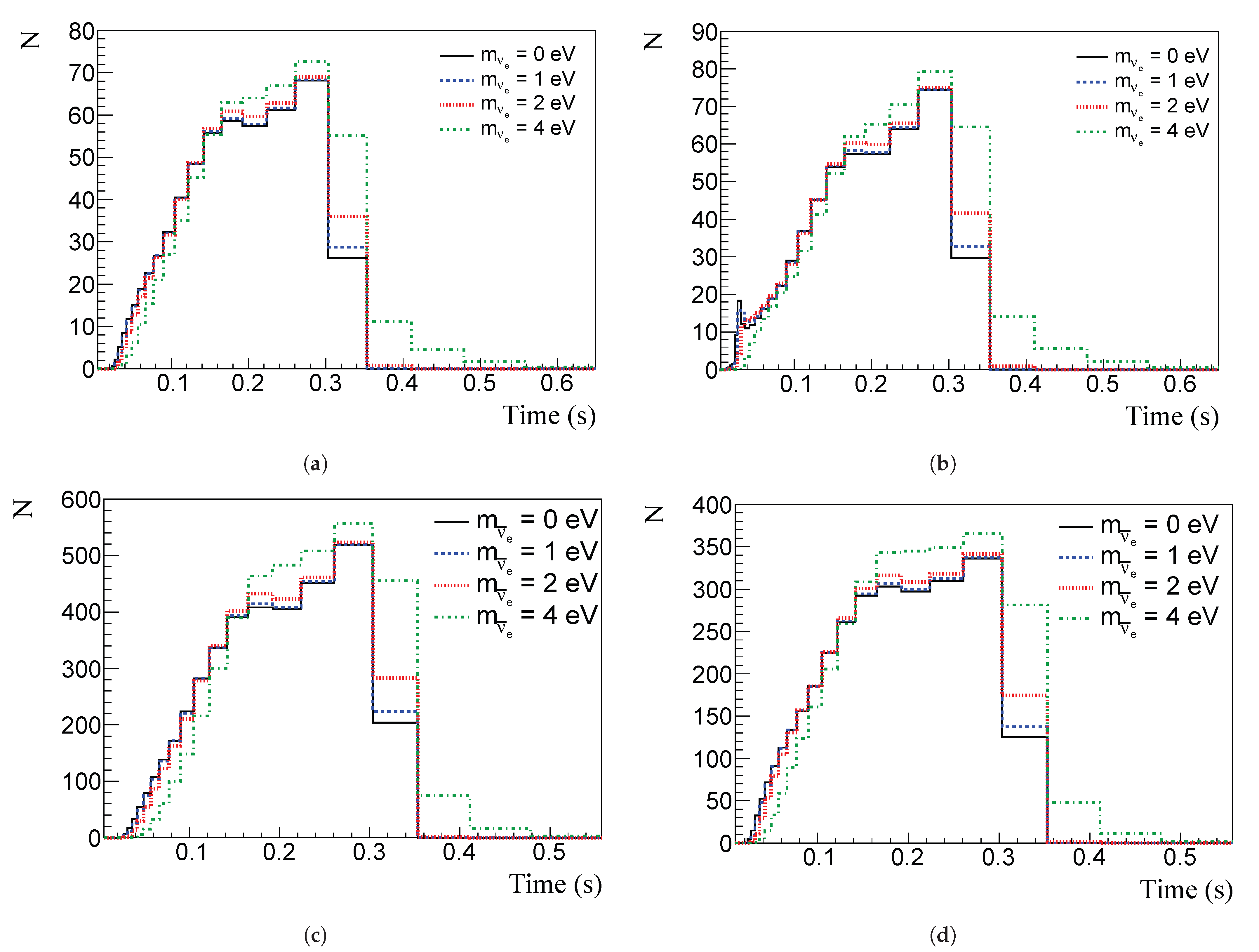
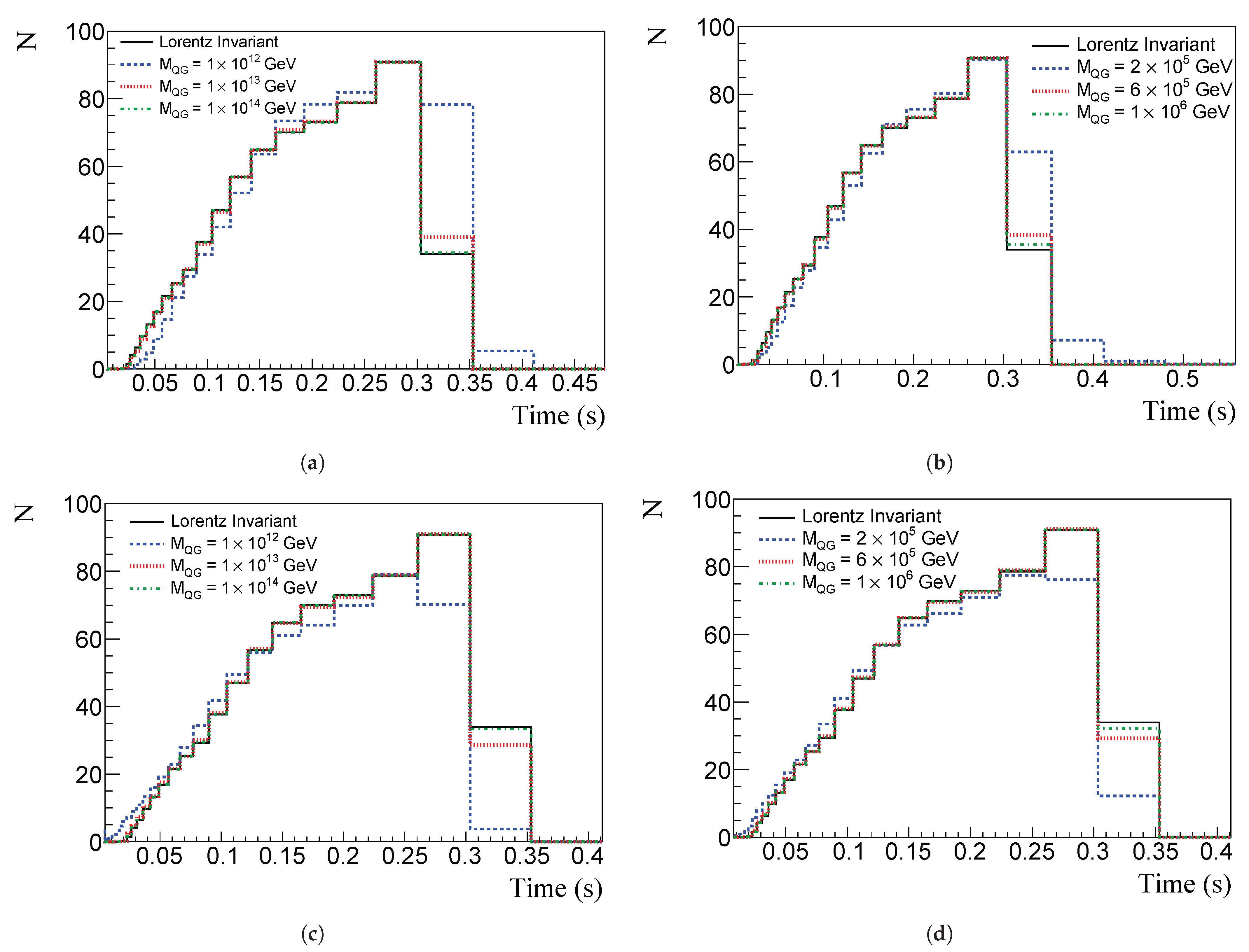
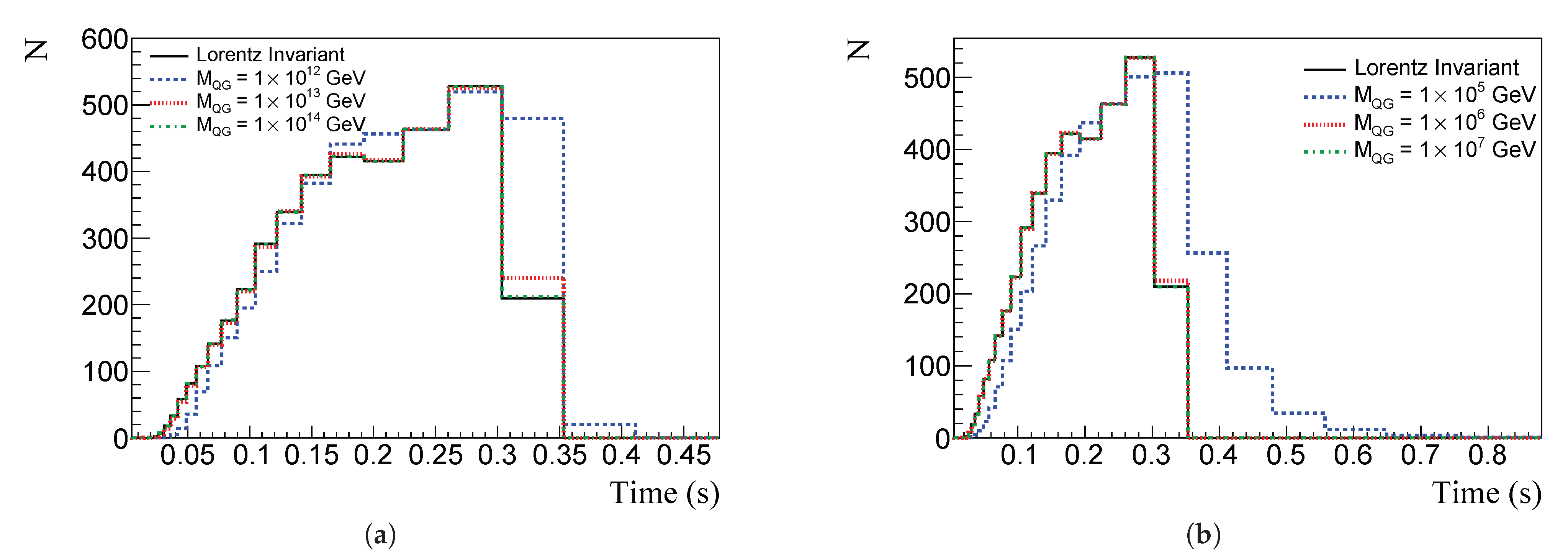
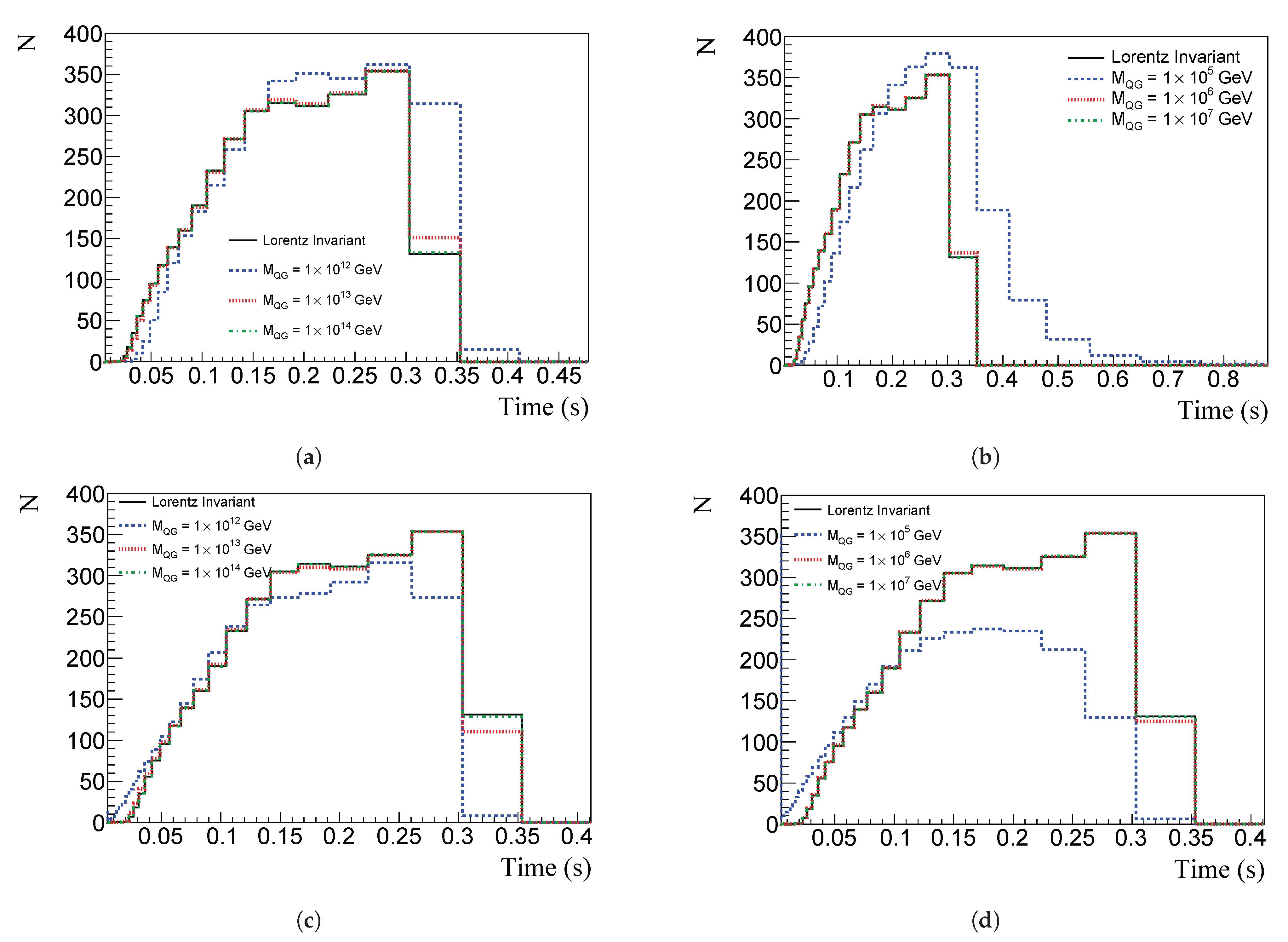
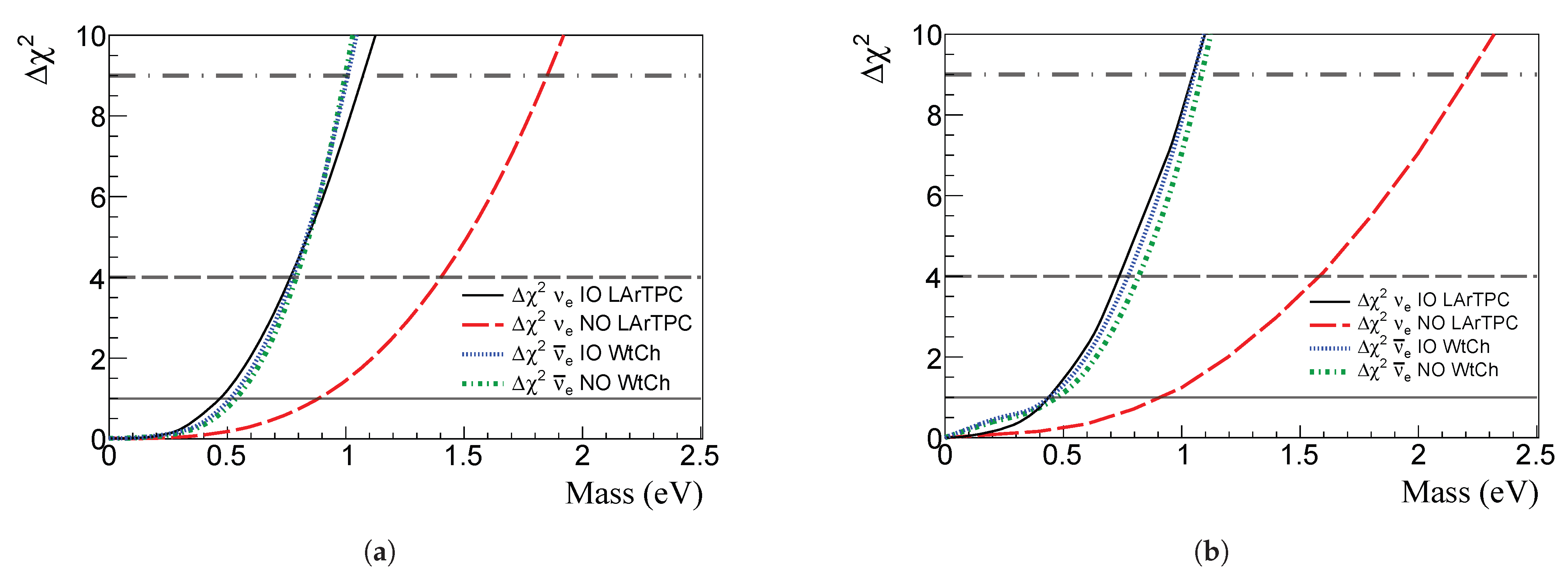
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SN | Supernova |
| NO | Normal ordering |
| IO | Inverted ordering |
| LIV | Lorentz Invariant Violation |
| CC | Charged Current |
| NC | Neutral Current |
| ES | Elastic Scattering |
| IBD | Inverse Beta Decay |
| DUNE | Deep Underground Neutrino Experiment |
| HyperK | Hyper-Kamiokande |
| SK | Super-Kamiokande |
| MSW | Mikheyev–Smirnov–Wolfenstein |
| LArTPC | Liquid Argon Time Projection Chamber |
| PMNS | Pontecorvo–Maki–Nakagawa–Sakata |
| WtCh | Water Cherenkov |
| 1 | The experiment performed in this work has no specific name, so we refer in this table to the first name author. |
| 2 | See Ref. [52] for a more precise discussion about the theory of neutrino detection. |
| 3 | See Ref. [1] for a recent value of and other neutrino oscillation parameters. |
| 4 | Other analysis using WtCh detectors such as HyperK showed that it is possible to distinguish between SN simulation models with different neutrino emission mechanisms considering times of neutrino emission up to s [54]. They did not consider MSW on the neutrino propagation. |
References
- Gonzalez-Garcia, M.C.; Maltoni, M.; Schwetz, T. NuFIT: Three-Flavour Global Analyses of Neutrino Oscillation Experiments. Universe 2021, 7, 459. [Google Scholar] [CrossRef]
- Kharusi, S.A.; et al.; [SNEWS] SNEWS 2.0: A next-generation supernova early warning system for multi-messenger astronomy. New J. Phys. 2021, 23, 031201. [Google Scholar] [CrossRef]
- Mirizzi, A.; Tamborra, I.; Janka, H.T.; Saviano, N.; Scholberg, K.; Bollig, R.; Hudepohl, L.; Chakraborty, S. Supernova Neutrinos: Production, Oscillations and Detection. Riv. Nuovo Cim. 2016, 39, 1–112. [Google Scholar] [CrossRef]
- Janka, H.T. Neutrino-driven Explosions. arXiv 2017, arXiv:1702.08825. [Google Scholar]
- Scholberg, K. Supernova Signatures of Neutrino Mass Ordering. J. Phys. G 2018, 45, 014002. [Google Scholar] [CrossRef]
- Aker, M.; et al.; [KATRIN] Direct neutrino-mass measurement with sub-electronvolt sensitivity. Nat. Phys. 2022, 18, 160–166. [Google Scholar] [CrossRef]
- Drexlin, G.; Hannen, V.; Mertens, S.; Weinheimer, C. Current direct neutrino mass experiments. Adv. High Energy Phys. 2013, 2013, 293986. [Google Scholar] [CrossRef]
- Springer, P.T.; Bennett, C.L.; Baisden, P.A. Measurement of the Neutrino Mass Using the Inner Bremsstrahlung Emitted in the Electron-Capture Decay og 163Ho. Phys. Rev. A 1987, 35, 679–689. [Google Scholar] [CrossRef]
- Yasumi, S.; Maezawa, H.; Shima, K.; Inagaki, Y.; Mukoyama, T.; Mizogawa, T.; Sera, K.; Kishimoto, S.; Fujioka, M.; Ishii, K.; et al. The Mass of the electron-neutrino from electron capture in Ho-163. Phys. Lett. B 1994, 334, 229–233. [Google Scholar] [CrossRef]
- Gatti, F. Microcalorimeter measurements. Nucl. Phys. B Proc. Suppl. 2001, 91, 293–296. [Google Scholar] [CrossRef]
- Sisti, M.; Arnaboldi, C.; Brofferio, C.; Ceruti, G.; Cremonesi, O.; Fiorini, E.; Giuliani, A.; Margesin, B.; Martensson, L.; Nucciotti, A.; et al. New limits from the Milano neutrino mass experiment with thermal microcalorimeters. Nucl. Instrum. Meth. A 2004, 520, 125–131. [Google Scholar] [CrossRef]
- Esfahani, A.A.; et al.; [Project 8] Tritium Beta Spectrum and Neutrino Mass Limit from Cyclotron Radiation Emission Spectroscopy. arXiv 2022, arXiv:2212.05048. [Google Scholar]
- Giuliani, A.; Poves, A. Neutrinoless Double-Beta Decay. Adv. High Energy Phys. 2012, 2012, 857016. [Google Scholar] [CrossRef]
- Gando, A.; et al.; [KamLAND-Zen] Search for Majorana Neutrinos near the Inverted Mass Hierarchy Region with KamLAND-Zen. Phys. Rev. Lett. 2016, 117, 082503. [Google Scholar] [CrossRef]
- Anton, G.; et al.; [EXO-200] Search for Neutrinoless Double-β Decay with the Complete EXO-200 Dataset. Phys. Rev. Lett. 2019, 123, 161802. [Google Scholar] [CrossRef]
- Klapdor-Kleingrothaus, H.V.; Krivosheina, I.V. The evidence for the observation of 0nu beta beta decay: The identification of 0nu beta beta events from the full spectra. Mod. Phys. Lett. A 2006, 21, 1547–1566. [Google Scholar] [CrossRef]
- Valentino, E.D.; Gariazzo, S.; Mena, O. Most constraining cosmological neutrino mass bounds. Phys. Rev. D 2021, 104, 083504. [Google Scholar] [CrossRef]
- Lesgourgues, J.; Pastor, S. Neutrino mass from Cosmology. Adv. High Energy Phys. 2012, 2012, 608515. [Google Scholar] [CrossRef]
- Zatsepin, G.T. On the possibility of determining the upper limit of the neutrino mass by means of the flight time. Pisma Zh. Eksp. Teor. Fiz. 1968, 8, 333–334. [Google Scholar]
- Pakvasa, S.; Tennakone, K. Neutrinos of Non-zero Rest Mass. Phys. Rev. Lett. 1972, 28, 1415. [Google Scholar] [CrossRef]
- Hirata, K.S.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. Observation in the Kamiokande-II Detector of the Neutrino Burst from Supernova SN 1987a. Phys. Rev. D 1988, 38, 448–458. [Google Scholar] [CrossRef]
- Bratton, C.B.; et al.; [IMB] Angular Distribution of Events From Sn1987a. Phys. Rev. D 1988, 37, 3361. [Google Scholar] [CrossRef] [PubMed]
- Alekseev, E.N.; Alekseeva, L.N.; Volchenko, V.I.; Krivosheina, I.V. Possible Detection of a Neutrino Signal on 23 February 1987 at the Baksan Underground Scintillation Telescope of the Institute of Nuclear Research. JETP Lett. 1987, 45, 589–592. [Google Scholar]
- Pagliaroli, G.; Rossi-Torres, F.; Vissani, F. Neutrino mass bound in the standard scenario for supernova electronic antineutrino emission. Astropart. Phys. 2010, 33, 287–291. [Google Scholar] [CrossRef]
- Ianni, A.; Pagliaroli, G.; Strumia, A.; Torres, F.R.; Villante, F.L.; Vissani, F. The Likelihood for supernova neutrino analyses. Phys. Rev. D 2009, 80, 043007. [Google Scholar] [CrossRef]
- Loredo, T.J.; Lamb, D.Q. Bayesian analysis of neutrinos observed from supernova SN-1987A. Phys. Rev. D 2002, 65, 063002. [Google Scholar] [CrossRef]
- Lu, J.S.; Cao, J.; Li, Y.F.; Zhou, S. Constraining Absolute Neutrino Masses via Detection of Galactic Supernova Neutrinos at JUNO. J. Cosmol. Astropart. Phys. 2015, 5, 044. [Google Scholar] [CrossRef]
- Hansen, R.S.L.; Lindner, M.; Scholer, O. Timing the neutrino signal of a Galactic supernova. Phys. Rev. D 2020, 101, 123018. [Google Scholar] [CrossRef]
- Pitik, T.; Heimsoth, D.J.; Suliga, A.M.; Balantekin, A.B. Exploiting stellar explosion induced by the QCD phase transition in large-scale neutrino detectors. Phys. Rev. D 2022, 106, 103007. [Google Scholar] [CrossRef]
- Fischer, T.; Bastian, N.U.F.; Wu, M.R.; Baklanov, P.; Sorokina, E.; Blinnikov, S.; Typel, S.; Klähn, T.; Blaschke, D.B. Quark deconfinement as a supernova explosion engine for massive blue supergiant stars. Nat. Astron. 2018, 2, 980–986. [Google Scholar] [CrossRef]
- Abi, B.; et al.; [DUNE] Deep Underground Neutrino Experiment (DUNE), far detector technical design report, Volume II: DUNE physics. arXiv 2020, arXiv:2002.03005. [Google Scholar]
- Abi, B.; et al.; [DUNE] Deep Underground Neutrino Experiment (DUNE), far detector technical design report, Volume I: Introduction to DUNE. J. Instrum. 2020, 15, T08008. [Google Scholar] [CrossRef]
- Abi, B.; et al.; [DUNE] Supernova neutrino burst detection with the Deep Underground Neutrino Experiment. Eur. Phys. J. C 2021, 81, 423. [Google Scholar] [CrossRef]
- Rossi-Torres, F.; Guzzo, M.M.; Kemp, E. Boundaries on Neutrino Mass from Supernovae Neutronization Burst by Liquid Argon Experiments. arXiv 2015, arXiv:1501.00456. [Google Scholar]
- Abi, K.; et al.; [Hyper-Kamiokande] Hyper-Kamiokande Design Report. arXiv 2018, arXiv:1805.04163. [Google Scholar]
- Amelino-Camelia, G.; Ellis, J.R.; Mavromatos, N.E.; Nanopoulos, D.V.; Sarkar, S. Tests of quantum gravity from observations of gamma-ray bursts. Nature 1998, 393, 763–765. [Google Scholar] [CrossRef]
- Garay, L.J. Thermal properties of space-time foam. Phys. Rev. D 1998, 58, 124015. [Google Scholar] [CrossRef]
- Moura, C.A.; Rossi-Torres, F. Searches for Violation of CPT Symmetry and Lorentz Invariance with Astrophysical Neutrinos. Universe 2022, 8, 42. [Google Scholar] [CrossRef]
- Antonelli, V.; Miramonti, L.; Torri, M.D.C. Phenomenological Effects of CPT and Lorentz Invariance Violation in Particle and Astroparticle Physics. Symmetry 2020, 12, 1821. [Google Scholar] [CrossRef]
- Chakraborty, S.; Mirizzi, A.; Sigl, G. Testing Lorentz invariance with neutrino bursts from supernova neutronization. Phys. Rev. D 2013, 87, 017302. [Google Scholar] [CrossRef]
- Serpico, P.D.; Chakraborty, S.; Fischer, T.; Hudepohl, L.; Janka, H.T.; Mirizzi, A. Probing the neutrino mass hierarchy with the rise time of a supernova burst. Phys. Rev. D 2012, 85, 085031. [Google Scholar] [CrossRef]
- Hudepohl, L. Neutrinos from the Formation, Cooling and Black Hole Collapse of Neutron Stars. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2014. [Google Scholar]
- Keil, M.T.; Raffelt, G.G.; Janka, H.T. Monte Carlo study of supernova neutrino spectra formation. Astrophys. J. 2003, 590, 971–991. [Google Scholar] [CrossRef]
- Wolfenstein, L. Neutrino Oscillations in Matter. Phys. Rev. D 1978, 17, 2369–2374. [Google Scholar] [CrossRef]
- Mikheyev, S.P.; Smirnov, A.Y. Resonance Amplification of Oscillations in Matter and Spectroscopy of Solar Neutrinos. Sov. J. Nucl. Phys. 1985, 42, 913–917. [Google Scholar]
- Mikheev, S.P.; Smirnov, A.Y. Resonant amplification of neutrino oscillations in matter and solar neutrino spectroscopy. Nuovo Cim. C 1986, 9, 17–26. [Google Scholar] [CrossRef]
- Dighe, A.S.; Smirnov, A.Y. Identifying the neutrino mass spectrum from the neutrino burst from a supernova. Phys. Rev. D 2000, 62, 033007. [Google Scholar] [CrossRef]
- Pompa, F.; Capozzi, F.; Mena, O.; Sorel, M. Absolute ν Mass Measurement with the DUNE Experiment. Phys. Rev. Lett. 2022, 129, 121802. [Google Scholar] [CrossRef]
- Capozzi, F.; Saviano, N. Neutrino Flavor Conversions in High-Density Astrophysical and Cosmological Environments. Universe 2022, 8, 94. [Google Scholar] [CrossRef]
- Available online: http://webhome.phy.duke.edu/~schol/snowglobes/ (accessed on 27 May 2023).
- Rubbia, C. The Liquid Argon Time Projection Chamber: A New Concept for Neutrino Detectors. CERN-EP-INT-77-08. CERN Internal Report 77-8. 1977. Available online: http://cdsweb.cern.ch/record/117852/files/CERN-EP-INT-77-8.pdf (accessed on 27 May 2023).
- Porto-Silva, Y.P.; de Oliveira, M.C. Theory of Neutrino Detection—Flavor Oscillations and Weak Values. Eur. Phys. J. C 2021, 81, 330. [Google Scholar] [CrossRef]
- Kayser, B. On the Quantum Mechanics of Neutrino Oscillation. Phys. Rev. D 1981, 24, 110. [Google Scholar] [CrossRef]
- Olsen, J.; Qian, Y.Z. Prospects for distinguishing supernova models using a future neutrino signal. Phys. Rev. D 2022, 105, 083017. [Google Scholar] [CrossRef]
- Kachelriess, M.; Tomas, R.; Buras, R.; Janka, H.T.; Marek, A.; Rampp, M. Exploiting the neutronization burst of a galactic supernova. Phys. Rev. D 2005, 71, 063003. [Google Scholar] [CrossRef]
- Janka, H.T. Neutrino Emission from Supernovae. arXiv 2017, arXiv:1702.08713. [Google Scholar]



| Experiment | Method | Mass Limit |
|---|---|---|
| Katrin [6] | Tritium beta decay | 0.8 eV |
| Springer et al. [8]1 | capture decays of Ho | 225 eV at 95% C.L |
| MANU [10] | Re decay | 26 eV at 95% C.L. |
| MiBeta [11] | Re decay | 15 eV |
| Project 8 [12] | CRES | 152 eV |
| KamLAND-ZEN [14] | 0.061–0.165 eV | |
| EXO-200 [15] | 0.093–0.286 eV | |
| Planck [17] | Cosmic microwave | 0.09 eV at 95% C.L. |
| Mass (eV) | ||||
|---|---|---|---|---|
| Mass Ordering | Flavor | |||
| NO | 0.52 (1.23) | 0.79 (1.93) | 1.00 (2.83) | |
| IO | 0.49 (1.29) | 0.77 (2.11) | 1.01 (3.08) | |
| NO | 1.71 (0.88) | 1.90 (1.40) | 2.64 (1.85) | |
| IO | 0.68 (0.47) | 1.25 (0.77) | 2.01 (1.07) | |
| (GeV) | ||||
|---|---|---|---|---|
| Mass Ordering | ||||
| subluminal | NO | 2.9 (1.5) | 1.7 (0.6) | 0.9 (0.4) |
| subluminal | IO | 3.1 (2.9) | 1.7 (1.3) | 0.9 (0.7) |
| superluminal | NO | 3.1 (1.7) | 1.8 (0.8) | 1.1 (0.6) |
| superluminal | IO | 3.2 (2.3) | 1.8 (1.3) | 1.2 (0.8) |
| ( GeV) | ||||
|---|---|---|---|---|
| Mass Ordering | ||||
| subluminal | NO | 8.5 (5.9) | 5.9 (4.0) | 4.9 (3.3) |
| subluminal | IO | 8.6 (7.5) | 5.9 (4.8) | 4.8 (3.7) |
| superluminal | NO | 8.8 (6.2) | 6.3 (4.6) | 5.2 (3.9) |
| superluminal | IO | 8.8 (6.9) | 6.3 (5.0) | 5.2 (4.2) |
| Mass (eV) | ||||
|---|---|---|---|---|
| Mass Ordering | Flavor | |||
| NO | 0.45 (1.71) | 0.82 (3.13) | 1.08 (4.64) | |
| IO | 0.43 (1.66) | 0.77 (3.27) | 1.05 (5.05) | |
| NO | 1.31 (0.92) | 2.43 (1.58) | 3.71 (2.22) | |
| IO | 0.65 (0.44) | 1.23 (0.74) | 2.43 (1.04) | |
| ( GeV) | ||||
|---|---|---|---|---|
| Mass Ordering | ||||
| subluminal | NO | 4.1 (1.3) | 1.4 (0.4) | 0.6 (0.2) |
| subluminal | IO | 8.7 (3.8) | 2.0 (1.4) | 1.2 (0.7) |
| superluminal | NO | 11.0 (1.9) | 1.7 (0.7) | 0.9 (0.5) |
| superluminal | IO | 5.1 (3.2) | 1.8 (1.7) | 0.9 (0.9) |
| ( GeV) | ||||
|---|---|---|---|---|
| Mass Ordering | ||||
| subluminal | NO | 8.6 (4.7) | 4.6 (2.9) | 3.4 (2.1) |
| subluminal | IO | 14.6 (7.7) | 6.1 (4.7) | 4.4 (3.2) |
| superluminal | NO | 9.9 (5.6) | 5.4 (4.0) | 4.5 (3.7) |
| superluminal | IO | 9.4 (7.9) | 5.5 (5.3) | 4.7 (4.4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moura, C.A.; Quintino, L.; Rossi-Torres, F. Analyzing the Time Spectrum of Supernova Neutrinos to Constrain Their Effective Mass or Lorentz Invariance Violation. Universe 2023, 9, 259. https://doi.org/10.3390/universe9060259
Moura CA, Quintino L, Rossi-Torres F. Analyzing the Time Spectrum of Supernova Neutrinos to Constrain Their Effective Mass or Lorentz Invariance Violation. Universe. 2023; 9(6):259. https://doi.org/10.3390/universe9060259
Chicago/Turabian StyleMoura, Celio A., Lucas Quintino, and Fernando Rossi-Torres. 2023. "Analyzing the Time Spectrum of Supernova Neutrinos to Constrain Their Effective Mass or Lorentz Invariance Violation" Universe 9, no. 6: 259. https://doi.org/10.3390/universe9060259
APA StyleMoura, C. A., Quintino, L., & Rossi-Torres, F. (2023). Analyzing the Time Spectrum of Supernova Neutrinos to Constrain Their Effective Mass or Lorentz Invariance Violation. Universe, 9(6), 259. https://doi.org/10.3390/universe9060259







