Heating in Magnetar Crusts from Electron Captures
Abstract
1. Introduction
2. Microphysics of Magnetar Crusts
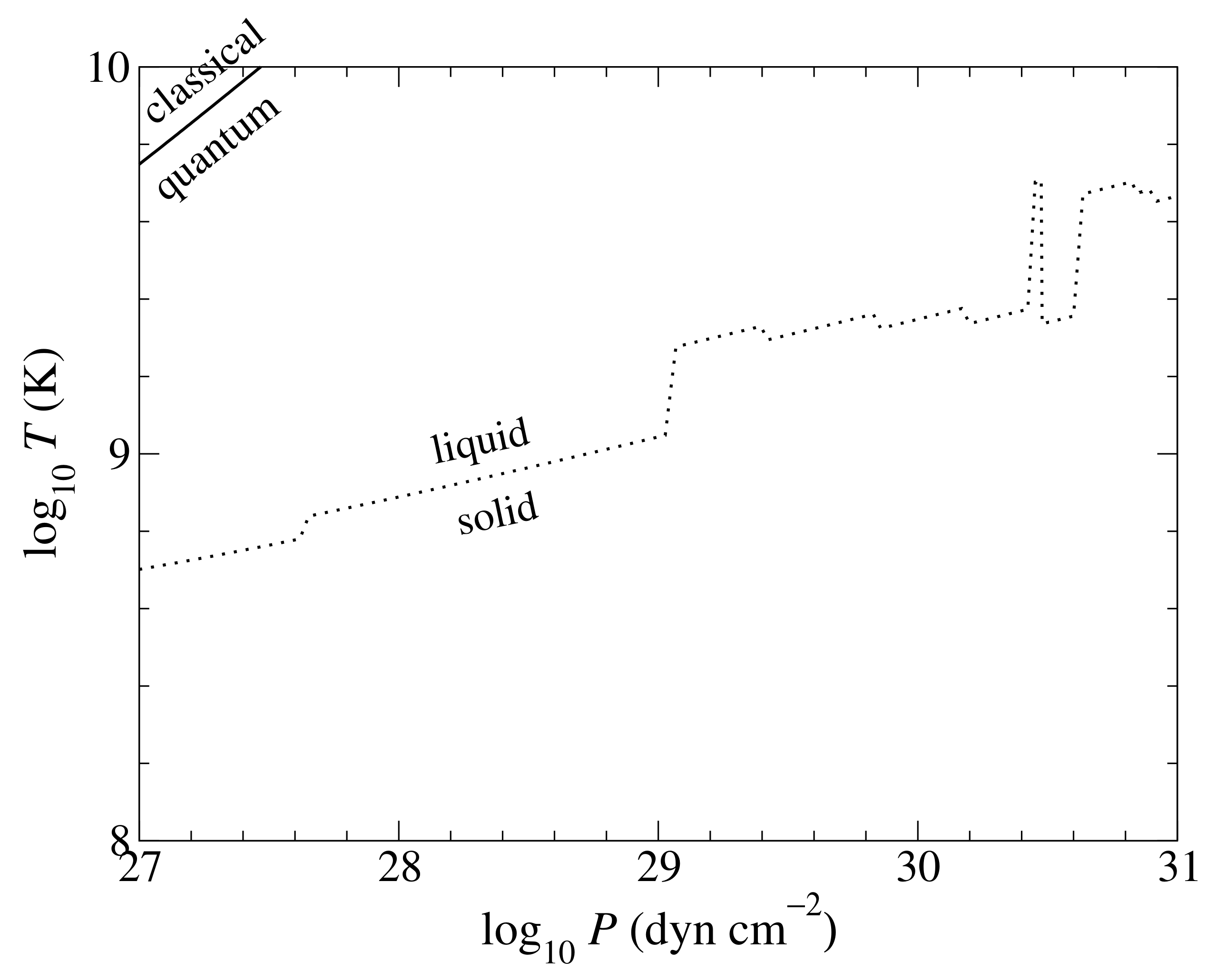
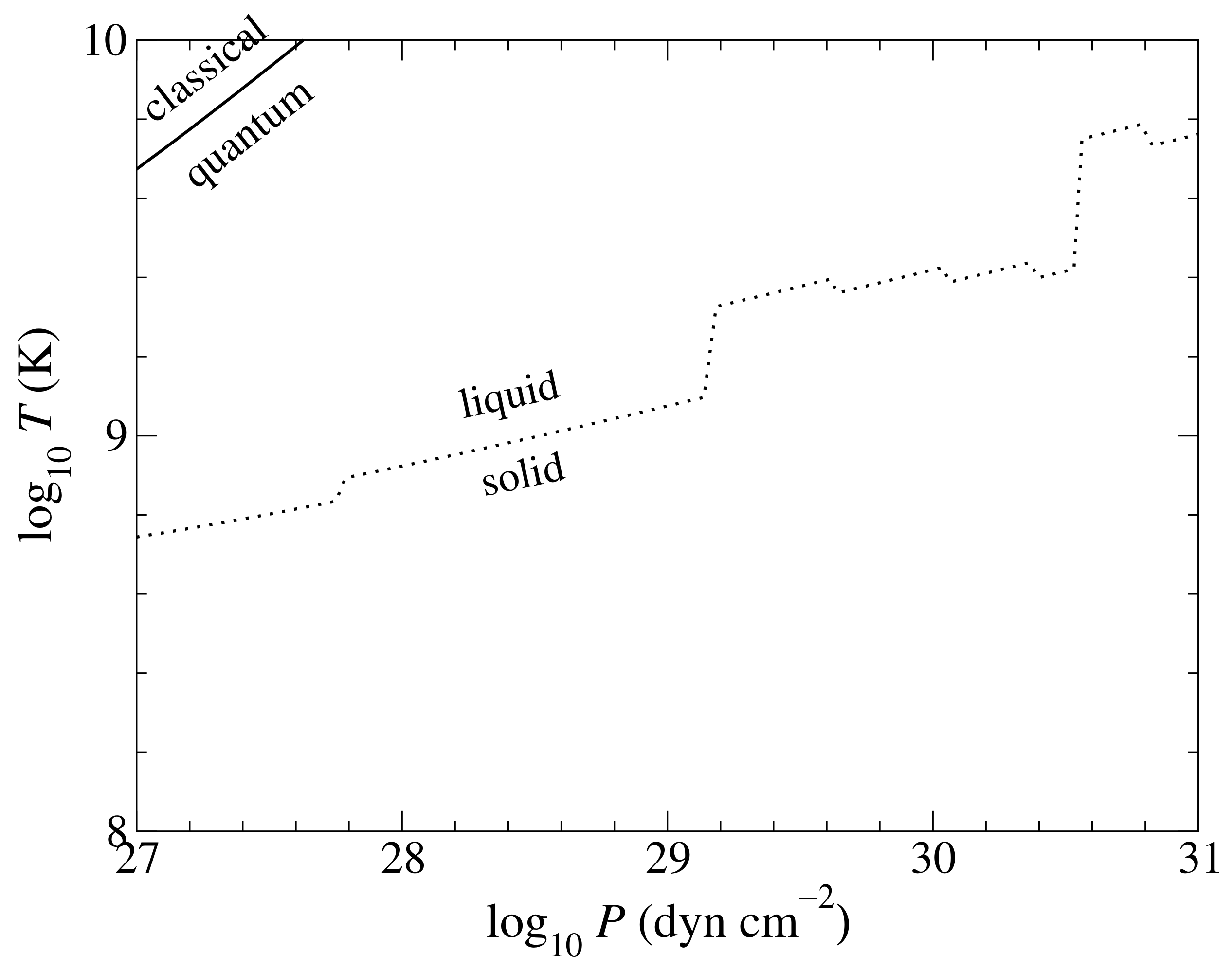
2.1. Thermodynamic Conditions
2.2. Compression-Induced Nuclear Processes
2.3. Baryon Chemical Potential and Matter Pressure
2.4. Onset of Electron Captures
3. Crustal Heating
3.1. Heat Released by Electron Captures
3.2. Heat Released by Pycnonuclear Fusions
3.3. Results and Discussions
4. Astrophysical Implications
4.1. Equilibrium of Self-Gravitating Magnetized Stars
4.2. Heating Induced by Magnetic Field Decay
4.3. Heating Induced by Spin-Down
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | http://www.physics.mcgill.ca/~pulsar/magnetar/main.html, accessed on 7 May 2021. |
| 2 | The demonstration follows directly from the definitions and , where denotes the energy density of the electron Fermi gas. |
| 3 | http://www.astro.ulb.ac.be/bruslib/, accessed on 7 May 2021. |
| 4 | https://www-nds.iaea.org/relnsd/NdsEnsdf/QueryForm.html, accessed on 7 May 2021. |
| 5 | http://magnetars.ice.csic.es, accessed on 7 May 2021. |
References
- Duncan, R.C.; Thompson, C. Formation of Very Strongly Magnetized Neutron Stars: Implications for Gamma-ray Bursts. Astrophys. J. Lett. 1992, 392, L9. [Google Scholar] [CrossRef]
- Esposito, P.; Rea, N.; Israel, G.L. Magnetars: A Short Review and Some Sparse Considerations. In Astrophysics and Space Science Library; Belloni, T.M., Méndez, M., Zhang, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 461, pp. 97–142. [Google Scholar] [CrossRef]
- Olausen, S.A.; Kaspi, V.M. The McGill Magnetar Catalog. Astrophys. J. Suppl. Ser. 2014, 212, 6. [Google Scholar] [CrossRef]
- Coti Zelati, F.; Rea, N.; Pons, J.A.; Campana, S.; Esposito, P. Systematic study of magnetar outbursts. Mon. Not. R. Astron. Soc. 2018, 474, 961–1017. [Google Scholar] [CrossRef]
- De Grandis, D.; Turolla, R.; Wood, T.S.; Zane, S.; Taverna, R.; Gourgouliatos, K.N. Three-dimensional Modeling of the Magnetothermal Evolution of Neutron Stars: Method and Test Cases. Astrophys. J. 2020, 903, 40. [Google Scholar] [CrossRef]
- Beloborodov, A.M.; Li, X. Magnetar Heating. Astrophys. J. 2016, 833, 261. [Google Scholar] [CrossRef]
- Kaminker, A.D.; Yakovlev, D.G.; Potekhin, A.Y.; Shibazaki, N.; Shternin, P.S.; Gnedin, O.Y. Magnetars as cooling neutron stars with internal heating. Mon. Not. R. Astron. Soc. 2006, 371, 477–483. [Google Scholar] [CrossRef]
- Kaminker, A.D.; Potekhin, A.Y.; Yakovlev, D.G.; Chabrier, G. Heating and cooling of magnetars with accreted envelopes. Mon. Not. R. Astron. Soc. 2009, 395, 2257–2267. [Google Scholar] [CrossRef][Green Version]
- Cooper, R.L.; Kaplan, D.L. Magnetic Field-Decay-Induced Electron Captures: A Strong Heat Source in Magnetar Crusts. Astrophys. J. Lett. 2010, 708, L80–L83. [Google Scholar] [CrossRef]
- Fantina, A.F.; Zdunik, J.L.; Chamel, N.; Pearson, J.M.; Haensel, P.; Goriely, S. Crustal heating in accreting neutron stars from the nuclear energy-density functional theory. I. Proton shell effects and neutron-matter constraint. Astron. Astrophys. 2018, 620, A105. [Google Scholar] [CrossRef]
- Koliopanos, F.; Vasilopoulos, G.; Godet, O.; Bachetti, M.; Webb, N.A.; Barret, D. ULX spectra revisited: Accreting, highly magnetized neutron stars as the engines of ultraluminous X-ray sources. Astron. Astrophys. 2017, 608, A47. [Google Scholar] [CrossRef]
- Tong, H.; Wang, W. Accreting magnetars: Linking ultraluminous X-ray pulsars and the slow pulsation X-ray pulsars. Mon. Not. R. Astron. Soc. 2019, 482, 4956–4964. [Google Scholar] [CrossRef]
- Doroshenko, V.; Santangelo, A.; Suleimanov, V.F.; Tsygankov, S.S. An observational argument against accretion in magnetars. Astron. Astrophys. 2020, 643, A173. [Google Scholar] [CrossRef]
- Brice, N.; Zane, S.; Turolla, R.; Wu, K. Super-Eddington Emission from Accreting, Highly Magnetised Neutron Stars with a Multipolar Magnetic Field. Mon. Not. R. Astron. Soc. 2021, 504, 701–715. [Google Scholar] [CrossRef]
- Iida, K.; Sato, K. Spin Down of Neutron Stars and Compositional Transitions in the Cold Crustal Matter. Astrophys. J. 1997, 477, 294–312. [Google Scholar] [CrossRef]
- Chamel, N.; Fantina, A.F.; Zdunik, J.L.; Haensel, P. Experimental constraints on shallow heating in accreting neutron star crusts. Phys. Rev. C 2020, 102, 015804. [Google Scholar] [CrossRef]
- Rabi, I.I. Das freie Elektron im homogenen Magnetfeld nach der Diracschen Theorie. Z. Phys. 1928, 49, 507–511. [Google Scholar] [CrossRef]
- Landau, L. Diamagnetismus der Metalle. Z. Phys. 1930, 64, 629–637. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars. 1. Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Chamel, N.; Stoyanov, Z.K.; Mihailov, L.M.; Mutafchieva, Y.D.; Pavlov, R.L.; Velchev, C.J. Role of Landau quantization on the neutron-drip transition in magnetar crusts. Phys. Rev. C 2015, 91, 065801. [Google Scholar] [CrossRef]
- Mutafchieva, Y.D.; Chamel, N.; Stoyanov, Z.K.; Pearson, J.M.; Mihailov, L.M. Role of Landau–Rabi quantization of electron motion on the crust of magnetars within the nuclear energy density functional theory. Phys. Rev. C 2019, 99, 055805. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Chabrier, G. Equation of state for magnetized Coulomb plasmas. Astron. Astrophys. 2013, 550, A43. [Google Scholar] [CrossRef]
- Blandford, R.D.; Hernquist, L. Magnetic susceptibility of a neutron star crust. J. Phys. C Solid State Phys. 1982, 15, 6233–6243. [Google Scholar] [CrossRef]
- Chamel, N.; Fantina, A.F. Electron capture instability in magnetic and nonmagnetic white dwarfs. Phys. Rev. D 2015, 92, 023008. [Google Scholar] [CrossRef]
- Hollerbach, R.; Rüdiger, G. Hall drift in the stratified crusts of neutron stars. Mon. Not. R. Astron. Soc. 2004, 347, 1273–1278. [Google Scholar] [CrossRef]
- Pons, J.A.; Geppert, U. Magnetic field dissipation in neutron star crusts: From magnetars to isolated neutron stars. Astron. Astrophys. 2007, 470, 303–315. [Google Scholar] [CrossRef]
- Viganò, D.; Rea, N.; Pons, J.A.; Perna, R.; Aguilera, D.N.; Miralles, J.A. Unifying the observational diversity of isolated neutron stars via magneto-thermal evolution models. Mon. Not. R. Astron. Soc. 2013, 434, 123–141. [Google Scholar] [CrossRef]
- Geppert, U.; Viganò, D. Creation of magnetic spots at the neutron star surface. Mon. Not. R. Astron. Soc. 2014, 444, 3198–3208. [Google Scholar] [CrossRef][Green Version]
- Gourgouliatos, K.N.; Cumming, A. Hall Attractor in Axially Symmetric Magnetic Fields in Neutron Star Crusts. Phys. Rev. Lett. 2014, 112, 171101. [Google Scholar] [CrossRef] [PubMed]
- Wood, T.S.; Hollerbach, R. Three Dimensional Simulation of the Magnetic Stress in a Neutron Star Crust. Phys. Rev. Lett. 2015, 114, 191101. [Google Scholar] [CrossRef]
- Bransgrove, A.; Levin, Y.; Beloborodov, A. Magnetic field evolution of neutron stars-I. Basic formalism, numerical techniques and first results. Mon. Not. R. Astron. Soc. 2018, 473, 2771–2790. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Hollerbach, R.; Wood, T.; Gourgouliatos, K.N. Strong toroidal magnetic fields required by quiescent X-ray emission of magnetars. Nat. Astron. 2021, 5, 145–149. [Google Scholar] [CrossRef]
- Kojima, Y.; Kisaka, S.; Fujisawa, K. Evolution of magnetic deformation in neutron star crust. Mon. Not. R. Astron. Soc. 2021, 502, 2097–2104. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Dussan, H.; Berry, D.K. Fusion of neutron-rich oxygen isotopes in the crust of accreting neutron stars. Phys. Rev. C 2008, 77, 045807. [Google Scholar] [CrossRef]
- Rashdan, M. Sub-barrier fusion calculations for the neutron star crust using the microscopic Brueckner G -matrix and Skyrme energy density functionals. Phys. Rev. C 2015, 91, 054613. [Google Scholar] [CrossRef]
- Chatterjee, P.; Hernquist, L.; Narayan, R. An Accretion Model for Anomalous X-ray Pulsars. Astrophys. J. 2000, 534, 373–379. [Google Scholar] [CrossRef]
- Alpar, M.A. On Young Neutron Stars as Propellers and Accretors with Conventional Magnetic Fields. Astrophys. J. 2001, 554, 1245–1254. [Google Scholar] [CrossRef]
- Ertan, Ü.; Erkut, M.H.; Ekşi, K.Y.; Alpar, M.A. The Anomalous X-Ray Pulsar 4U 0142+61: A Neutron Star with a Gaseous Fallback Disk. Astrophys. J. 2007, 657, 441–447. [Google Scholar] [CrossRef][Green Version]
- Fantina, A.F.; Chamel, N.; Mutafchieva, Y.D.; Stoyanov, Z.K.; Mihailov, L.M.; Pavlov, R.L. Role of the symmetry energy on the neutron-drip transition in accreting and nonaccreting neutron stars. Phys. Rev. C 2016, 93, 015801. [Google Scholar] [CrossRef]
- Chamel, N.; Pavlov, R.L.; Mihailov, L.M.; Velchev, C.J.; Stoyanov, Z.K.; Mutafchieva, Y.D.; Ivanovich, M.D.; Pearson, J.M.; Goriely, S. Properties of the outer crust of strongly magnetized neutron stars from Hartree-Fock-Bogoliubov atomic mass models. Phys. Rev. C 2012, 86, 055804. [Google Scholar] [CrossRef]
- Salpeter, E.E. Electrons Screening and Thermonuclear Reactions. Aust. J. Phys. 1954, 7, 373. [Google Scholar] [CrossRef]
- Chamel, N.; Fantina, A.F.; Zdunik, J.L.; Haensel, P. Neutron drip transition in accreting and nonaccreting neutron star crusts. Phys. Rev. C 2015, 91, 055803. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Gasques, L.R.; Afanasjev, A.V.; Beard, M.; Wiescher, M. Fusion reactions in multicomponent dense matter. Phys. Rev. C 2006, 74, 035803. [Google Scholar] [CrossRef]
- Wang, M.; Audi, G.; Kondev, F.G.; Huang, W.J.; Naimi, S.; Xu, X. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2017, 41, 030003. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XIII. The 2012 atomic mass evaluation and the symmetry coefficient. Phys. Rev. C 2013, 88, 024308. [Google Scholar] [CrossRef]
- Xu, Y.; Goriely, S.; Jorissen, A.; Chen, G.L.; Arnould, M. Databases and tools for nuclear astrophysics applications. BRUSsels Nuclear LIBrary (BRUSLIB), Nuclear Astrophysics Compilation of REactions II (NACRE II) and Nuclear NETwork GENerator (NETGEN). Astron. Astrophys. 2013, 549, A106. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Heinke, C.O. A neutron star with a carbon atmosphere in the Cassiopeia A supernova remnant. Nature 2009, 462, 71–73. [Google Scholar] [CrossRef]
- Lunney, D.; Pearson, J.M.; Thibault, C. Recent trends in the determination of nuclear masses. Rev. Mod. Phys. 2003, 75, 1021–1082. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels-Montreal functionals-I. Role of symmetry energy. Mon. Not. R. Astron. Soc. 2018, 481, 2994–3026. [Google Scholar] [CrossRef]
- Ingraham, R.L.; Wilkes, J.M. Inhibition of Degeneracy by Intense Magnetic Fields-Derivation and Astrophysical Application. Astrophys. Space Sci. 1987, 135, 87–104. [Google Scholar] [CrossRef]
- Chatterjee, D.; Elghozi, T.; Novak, J.; Oertel, M. Consistent neutron star models with magnetic field-dependent equations of state. Mon. Not. R. Astron. Soc. 2015, 447, 3785–3796. [Google Scholar] [CrossRef]
- Chatterjee, D.; Fantina, A.F.; Chamel, N.; Novak, J.; Oertel, M. On the maximum mass of magnetized white dwarfs. Mon. Not. R. Astron. Soc. 2017, 469, 95–109. [Google Scholar] [CrossRef]
- Braithwaite, J. Axisymmetric magnetic fields in stars: Relative strengths of poloidal and toroidal components. Mon. Not. R. Astron. Soc. 2009, 397, 763–774. [Google Scholar] [CrossRef]
- Tiengo, A.; Esposito, P.; Mereghetti, S.; Turolla, R.; Nobili, L.; Gastaldello, F.; Götz, D.; Israel, G.L.; Rea, N.; Stella, L.; et al. A variable absorption feature in the X-ray spectrum of a magnetar. Nature 2013, 500, 312–314. [Google Scholar] [CrossRef]
- Makishima, K.; Enoto, T.; Hiraga, J.S.; Nakano, T.; Nakazawa, K.; Sakurai, S.; Sasano, M.; Murakami, H. Possible Evidence for Free Precession of a Strongly Magnetized Neutron Star in the Magnetar 4U 0142+61. Phys. Rev. Lett. 2014, 112, 171102. [Google Scholar] [CrossRef]
- Borghese, A.; Rea, N.; Coti Zelati, F.; Tiengo, A.; Turolla, R. Discovery of a Strongly Phase-variable Spectral Feature in the Isolated Neutron Star RX J0720.4-3125. Astrophys. J. Lett. 2015, 807, L20. [Google Scholar] [CrossRef]
- Rodríguez Castillo, G.A.; Israel, G.L.; Tiengo, A.; Salvetti, D.; Turolla, R.; Zane, S.; Rea, N.; Esposito, P.; Mereghetti, S.; Perna, R.; et al. The outburst decay of the low magnetic field magnetar SWIFT J1822.3-1606: Phase-resolved analysis and evidence for a variable cyclotron feature. Mon. Not. R. Astron. Soc. 2016, 456, 4145–4155. [Google Scholar] [CrossRef]
- Makishima, K.; Enoto, T.; Yoneda, H.; Odaka, H. A NuSTAR confirmation of the 36 ks hard X-ray pulse-phase modulation in the magnetar 1E 1547.0-5408. Mon. Not. R. Astron. Soc. 2021, 502, 2266–2284. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Prendergast, K.H. The Equilibrium of Magnetic Stars. Proc. Natl. Acad. Sci. USA 1956, 42, 5–9. [Google Scholar] [CrossRef]
- Pearson, J.M.; Goriely, S.; Chamel, N. Properties of the outer crust of neutron stars from Hartree-Fock-Bogoliubov mass models. Phys. Rev. C 2011, 83, 065810. [Google Scholar] [CrossRef]
- Sur, A.; Haskell, B. The impact of superconductivity and the Hall effect in models of magnetized neutron stars. arXiv 2021, arXiv:2104.14908. [Google Scholar]
- Gusakov, M.E.; Kantor, E.M.; Reisenegger, A. Rotation-induced deep crustal heating of millisecond pulsars. Mon. Not. R. Astron. Soc. Lett. 2015, 453, L36–L40. [Google Scholar] [CrossRef]
- Peña Arteaga, D.; Grasso, M.; Khan, E.; Ring, P. Nuclear structure in strong magnetic fields: Nuclei in the crust of a magnetar. Phys. Rev. C 2011, 84, 045806. [Google Scholar] [CrossRef]
- Stein, M.; Maruhn, J.; Sedrakian, A.; Reinhard, P.G. Carbon-oxygen-neon mass nuclei in superstrong magnetic fields. Phys. Rev. C 2016, 94, 035802. [Google Scholar] [CrossRef]
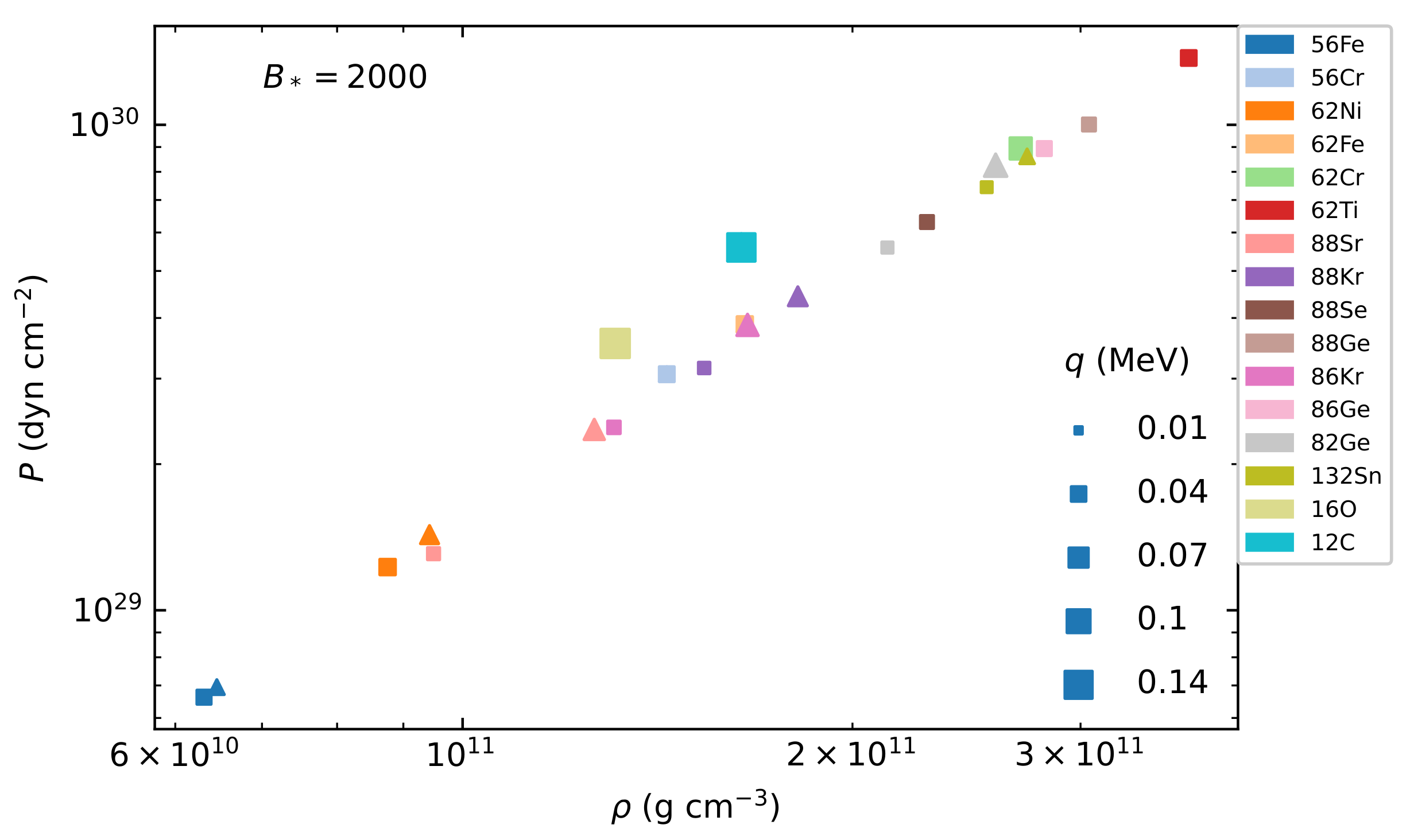

| (dyn cm−2) | (g cm−3) | Reactions | q (MeV) |
|---|---|---|---|
| 0.037 | |||
| 0.041 | |||
| 0.041 | |||
| 0.023 | |||
| 0.045 | |||
| 0.061 | |||
| 0.044 | |||
| 0.086 | |||
| 0.041 | |||
| 0.027 | |||
| 0.078 | |||
| 0.025 | |||
| 0.068 | |||
| 0.031 | |||
| 0.031 | |||
| 0.029 | |||
| 0.086 | |||
| 0.023 | |||
| 0.037 | |||
| 0.027 | |||
| 0.029 | |||
| 0.029 | |||
| 0.029 | |||
| 0.023 | |||
| 0.096 | |||
| 0.019 | |||
| 0.026 | |||
| 0.022 | |||
| 0.040 | |||
| 0.017 | |||
| 0.022 | |||
| 0.005 | |||
| 0.026 | |||
| 0.018 | |||
| 0.015 | |||
| 0.024 | |||
| 0.007 |
| (dyn cm−2) | (g cm−3) | Reactions | q (MeV) |
|---|---|---|---|
| 0.037 | |||
| 0.041 | |||
| 0.042 | |||
| 0.023 | |||
| 0.045 | |||
| 0.062 | |||
| 0.044 | |||
| 0.086 | |||
| 0.041 | |||
| 0.027 | |||
| 0.078 | |||
| 0.025 | |||
| 0.068 | |||
| 0.031 | |||
| 0.032 | |||
| 0.029 | |||
| 0.086 | |||
| 0.023 | |||
| 0.037 | |||
| 0.027 | |||
| 0.029 | |||
| 0.029 | |||
| 0.029 | |||
| 0.023 | |||
| 0.096 | |||
| 0.019 | |||
| 0.026 | |||
| 0.022 | |||
| 0.040 | |||
| 0.017 | |||
| 0.023 | |||
| 0.018 | |||
| 0.015 | |||
| 0.024 | |||
| 0.007 |
| (dyn cm−2) | (g cm−3) | Reactions | q (MeV) |
|---|---|---|---|
| 0.143 | |||
| 0.153 |
| (dyn cm−2) | (g cm−3) | Reactions | q (MeV) |
|---|---|---|---|
| 0.143 | |||
| 0.154 |
| (dyn cm−2) | (g cm−3) | Reactions | (MeV) |
|---|---|---|---|
| 1.42 (0.65) | |||
| 1.17 (0.60) |
| (dyn cm−2) | (g cm−3) | Reactions | (MeV) |
|---|---|---|---|
| 1.42 (0.67) | |||
| 1.18 (0.61) |
| Reactions | |
|---|---|
| Reactions | |
|---|---|
| Reactions | |
|---|---|
| Reactions | |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamel, N.; Fantina, A.F.; Suleiman, L.; Zdunik, J.-L.; Haensel, P. Heating in Magnetar Crusts from Electron Captures. Universe 2021, 7, 193. https://doi.org/10.3390/universe7060193
Chamel N, Fantina AF, Suleiman L, Zdunik J-L, Haensel P. Heating in Magnetar Crusts from Electron Captures. Universe. 2021; 7(6):193. https://doi.org/10.3390/universe7060193
Chicago/Turabian StyleChamel, Nicolas, Anthea Francesca Fantina, Lami Suleiman, Julian-Leszek Zdunik, and Pawel Haensel. 2021. "Heating in Magnetar Crusts from Electron Captures" Universe 7, no. 6: 193. https://doi.org/10.3390/universe7060193
APA StyleChamel, N., Fantina, A. F., Suleiman, L., Zdunik, J.-L., & Haensel, P. (2021). Heating in Magnetar Crusts from Electron Captures. Universe, 7(6), 193. https://doi.org/10.3390/universe7060193







