Nonlinear Actuation of Casimir Oscillators toward Chaos: Comparison of Topological Insulators and Metals
Abstract
1. Introduction
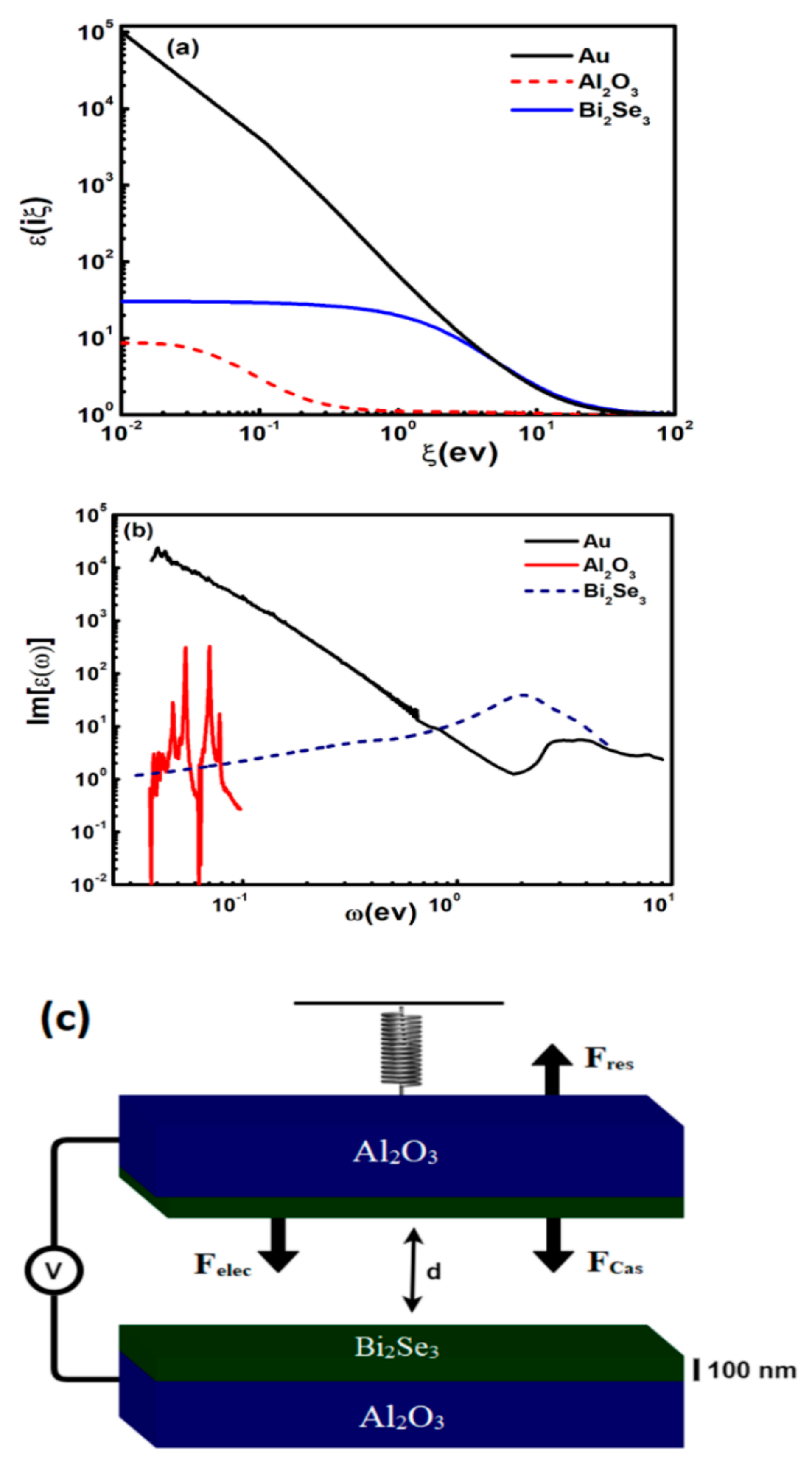
2. Optical Properties of Materials and Device Actuation
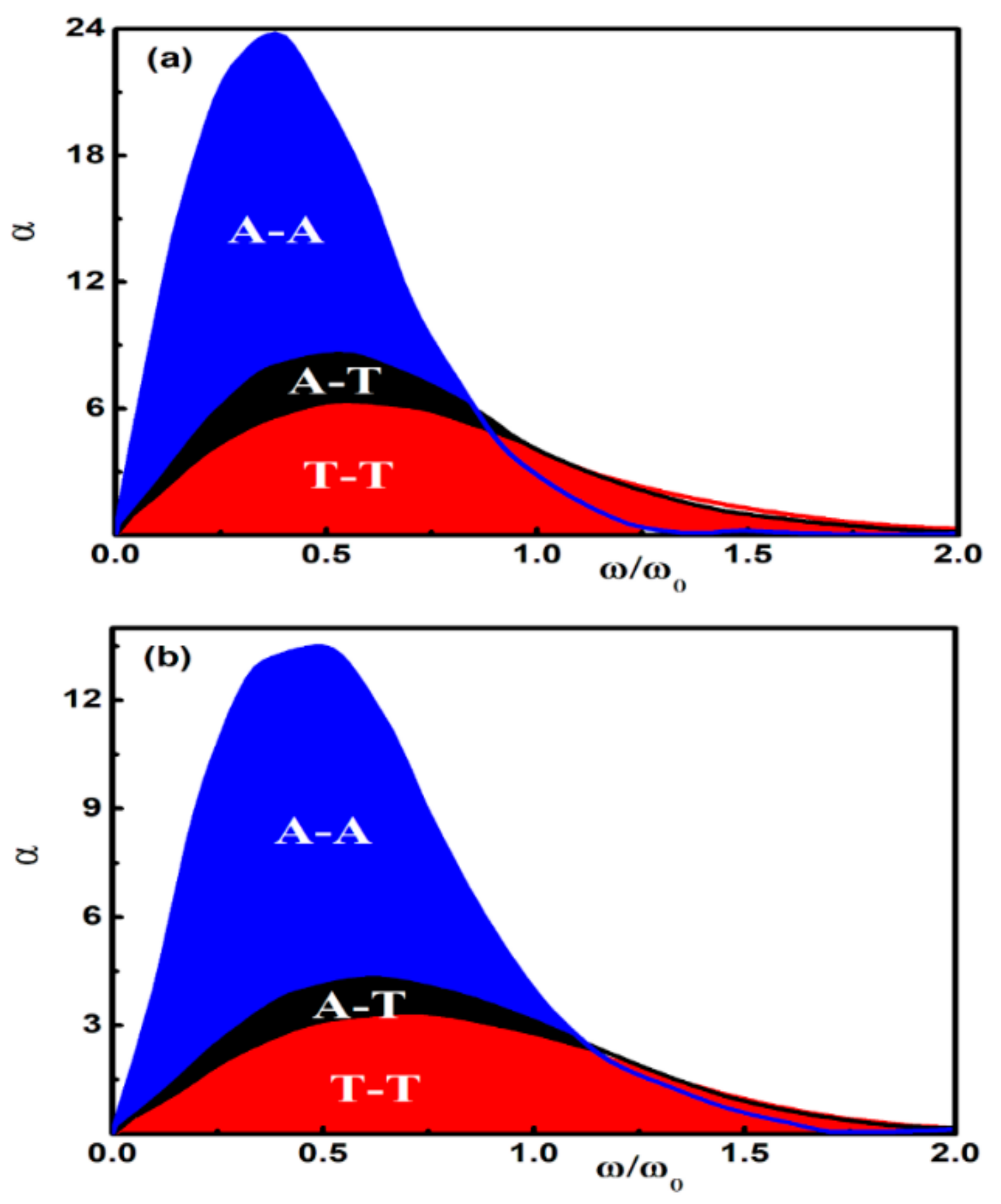
3. Results and Discussion
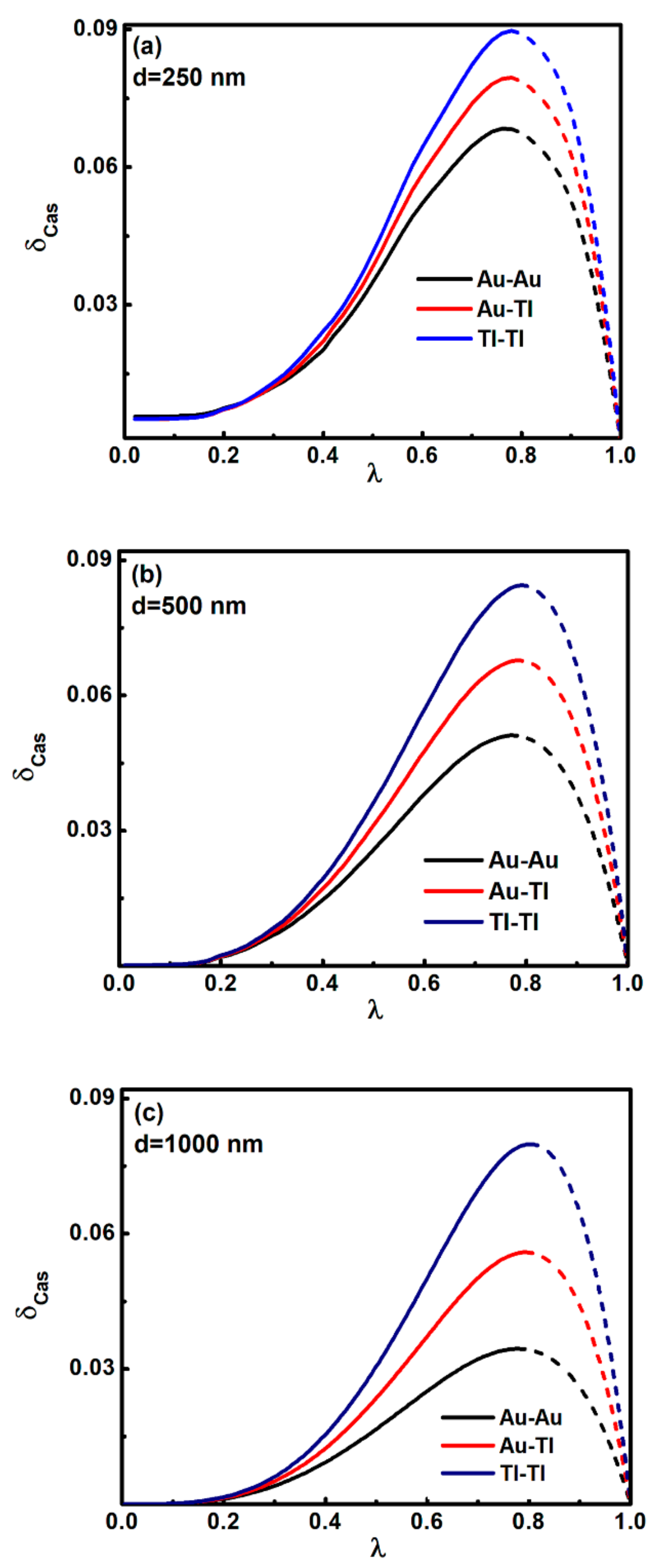
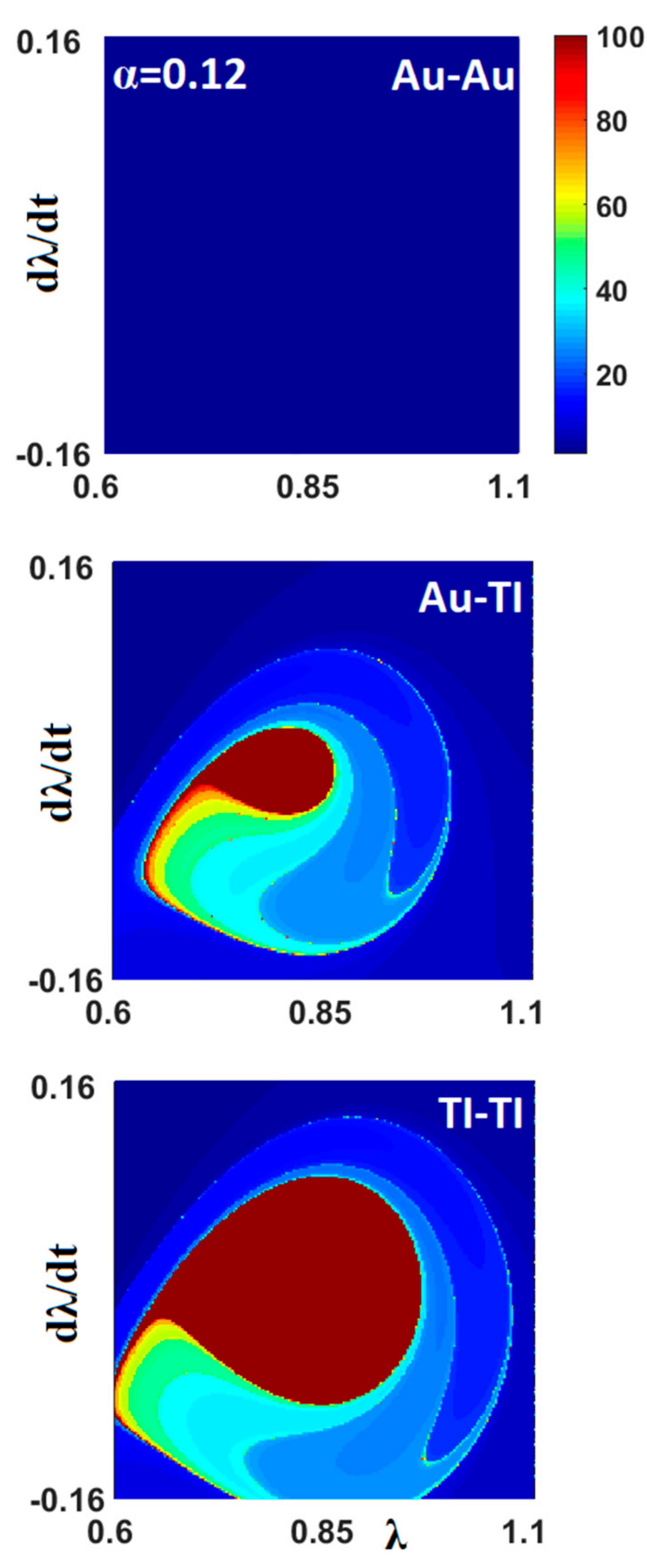
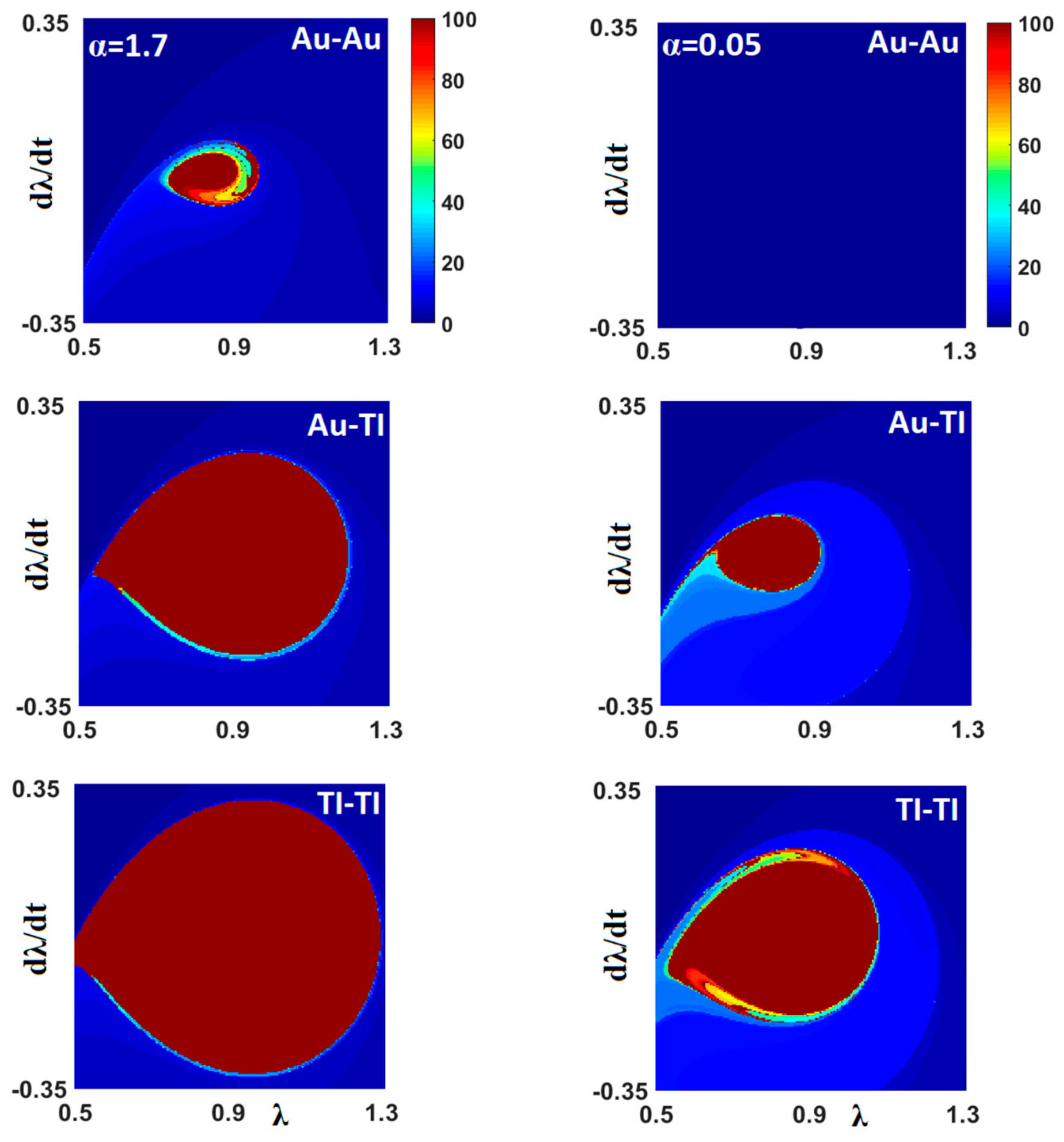
3.1. Conservative Actuating System (ε = 0)
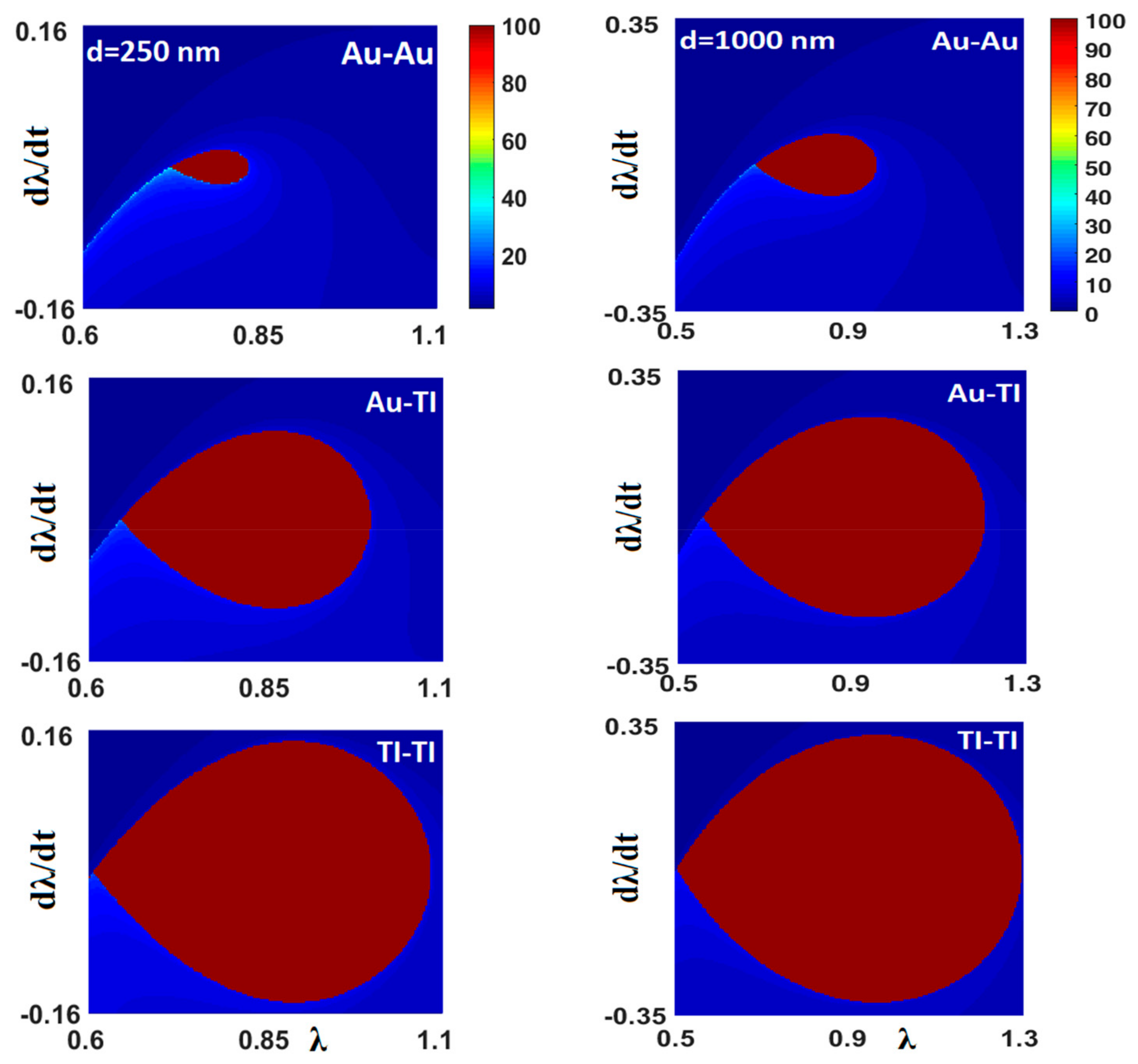
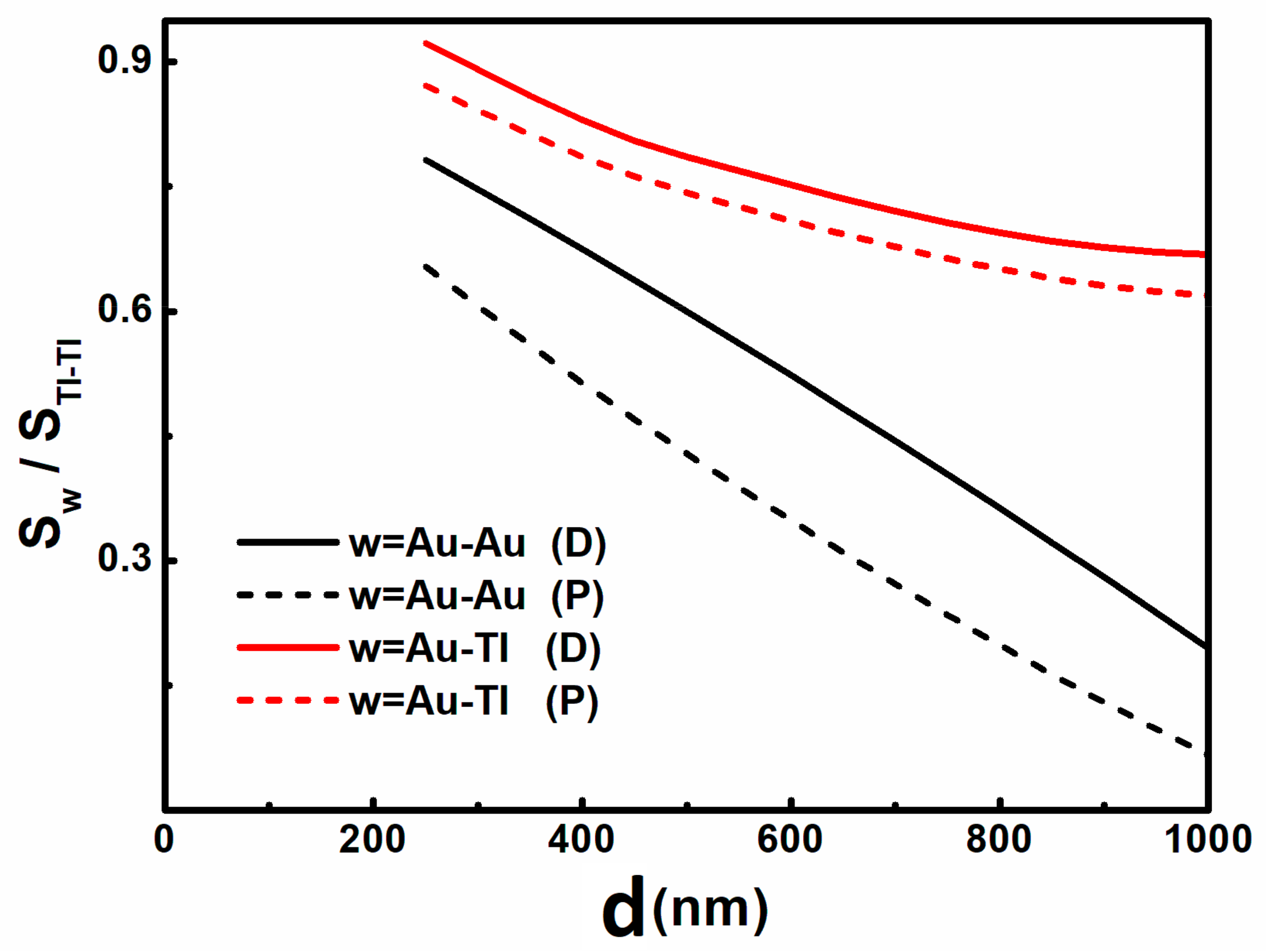
3.2. Nonconservative Driven System (ε = 1)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Lifshitz Theory for Stratified Media
Appendix B. Dielectric Function of Materials with Extrapolations
References
- Rodriguez, A.W.; Capasso, F.; Johnson, S.G. The Casimir effect in microstructured geometries. Nat. Photonics 2011, 5, 211. [Google Scholar] [CrossRef]
- Capasso, F.; Munday, J.N.; Iannuzzi, D.; Chan, H.B. Casimir Forces and Quantum Electrodynamical Torques: Physics and Nanomechanics. IEEE J. Sel. Top. Quant. Electron. 2007, 13, 400. [Google Scholar] [CrossRef]
- Ball, P. Fundamental physics: Feel the force. Nature 2007, 447, 77. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Tajik, F.; Sedighi, M.; Palasantzas, G. Sensitivity on materials optical properties of single beam torsional Casimir actuation. J. Appl. Phys. 2017, 121, 174302. [Google Scholar] [CrossRef]
- Tajik, F.; Sedighi, M.; Khorrami, M.; Masoudi, A.A.; Palasantzas, G. Chaotic behavior in Casimir oscillators: A case study for phase-change materials. Phys. Rev. E 2017, 96, 042215. [Google Scholar] [CrossRef] [PubMed]
- Tajik, F.; Sedighi, M.; Khorrami, M.; Masoudi, A.A.; Waalkens, H.; Palasantzas, G. Dependence of chaotic behavior on optical properties and electrostatic effects in double-beam torsional Casimir actuation. Phys. Rev. E 2018, 98, 02210. [Google Scholar] [CrossRef]
- Casimir, H.B.G. Zero Point Energy Effects on Quantum Electrodynamics. Proc. K. Ned. Akad. Wet. 1948, 51, 793. [Google Scholar]
- Lifshitz, E.M. The Theory of Molecular Attractive Forces between Solids. Sov. Phys. JETP 1956, 2, 73. [Google Scholar]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. General theory of van der waals forces. Sov. Phys. Uspekhi 1961, 4, 153. [Google Scholar] [CrossRef]
- Decca, R.S.; L’opez, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Novel constraints on light elementary particles and extra-dimensional physics from the Casimir effect. Eur. Phys. J. C 2007, 51, 963. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Tests of new physics from precise measurements of the Casimir pressure between two gold-coated plates. Phys. Rev. D 2007, 75, 077101. [Google Scholar] [CrossRef]
- Craighead, H.G. Nanoelectromechanical systems. Science 2000, 290, 1532. [Google Scholar] [CrossRef] [PubMed]
- Bochobza-Degani, O.; Nemirovsky, Y. Modeling the pull-in parameters of electrostatic actuators with a novel lumped two degrees of freedom pull-in model. Sens. Actuators A 2002, 97–98, 659. [Google Scholar]
- Sedighi, M.; Broer, W.H.; Palasantzas, G.; Kooi, B.J. Sensitivity of micromechanical actuation on amorphous to crystalline phase transformations under the influence of Casimir forces. Phys. Rev. B 2013, 88, 165423. [Google Scholar] [CrossRef]
- Sedighi, M.; Palasantzas, G. Casimir and hydrodynamic force influence on microelectromechanical system actuation in ambient conditions. Appl. Phys. Lett. 2014, 104, 074108. [Google Scholar] [CrossRef]
- Sedighi, M.; Svetovoy, V.B.; Broer, W.H.; Palasantzas, G. Casimir forces from conductive silicon carbide surfaces. Phys. Rev. B 2014, 89, 195440. [Google Scholar] [CrossRef]
- Tajik, F.; Sedighi, M.; Babamahdi, Z.; Masoudi, A.A.; Waalkense, H.; Palasantzas, G. Dependence of non-equilibrium Casimir forces on material optical properties towards chaotic motion during device actuation. Chaos 2019, 29, 093126. [Google Scholar] [CrossRef] [PubMed]
- Tajik, F.; Sedighi, M.; Babamahdi, Z.; Masoudi, A.A.; Waalkense, H.; Palasantzas, G. Sensitivity of non-equilibrium Casimir forces on low frequency optical properties towards chaotic motion of microsystems. Chaos 2020, 30, 023108. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Moore, J.E. The birth of topological insulators. Nature 2010, 464, 194. [Google Scholar] [CrossRef]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.; Cava, R.J.; Hasan, M. A Topological Dirac insulator in a quantum spin Hall phase. Nature 2008, 452, 970. [Google Scholar]
- Grushin, A.G.; Corteijo, A. Tunable Casimir Repulsion with Three-Dimensional Topological Insulators. Phys. Rev. Lett. 2011, 106, 020403. [Google Scholar] [CrossRef]
- Grushin, A.G.; Rodriguez-Lopez, P.; Corteijo, A. Effect of finite temperature and uniaxial anisotropy on the Casimir effect with three-dimensional topological insulators. Phys. Rev. B 2011, 84, 045119. [Google Scholar] [CrossRef]
- Martinez, J.C.; Jalil, M.B.A. Tuning the Casimir force via modification of interface properties of three-dimensional topological insulators. J. Appl. Phys. 2013, 113, 204302. [Google Scholar] [CrossRef]
- Babamahdi, Z.; Svetovoy, V.B.; Yimam, D.T.; Kooi, B.J.; Banerjee, T.; Moon, J.; Enache, S.; Oh, M.; Stöhr, M.; Palasantzas, G. Casimir and electrostatic forces from Bi2Se3 thin films of varying thickness. Phys. Rev. B Lett. 2021, 103, L161102. [Google Scholar]
- Svetovoy, V.B.; van Zwol, P.J.; Palasantzas, G.; de Hosson, J.T.M. Optical properties of gold films and the Casimir force. Phys. Rev. B 2008, 77, 035439. [Google Scholar] [CrossRef]
- Pelesko, J.A.; Bernstein, D.H. Modeling MEMS and NEMS; Chapman & Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Garcıa, R.; Perez, R. Dynamic atomic force microscopy methods. Surf. Sci. Rep. 2002, 47, 197. [Google Scholar] [CrossRef]
- Li, M.; Tang, H.X.; Roukes, M.L. Ultra-sensitive NEMS-based cantilevers for sensing, scanned probe and very high-frequency applications. Nat. Nanotechnol. 2007, 2, 114. [Google Scholar] [CrossRef] [PubMed]
- Mamin, H.J.; Rugar, D. Sub-attonewton force detection at millikelvin temperatures. Appl. Phys. Lett. 2011, 79, 3358. [Google Scholar] [CrossRef]
- Torricelli, G.; van Zwol, P.J.; Shpak, O.; Palasantzas, G.; Svetovoy, V.B.; Binns, C.; Kooi, B.J.; Jost, P.; Wuttig, M. Casimir force contrast between Amorphous and Crystalline Phases of AIST. Adv. Funct. Mater. 2012, 22, 3729. [Google Scholar] [CrossRef]
- Broer, W.; Waalkens, H.; Svetovoy, V.B.; Knoester, J.; Palasantzas, G. Nonlinear actuation dynamics of driven Casimir oscillators with rough surfaces. Phys. Rev. Appl. 2015, 4, 054016. [Google Scholar] [CrossRef]
- Hirsch, M.W.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos; Elsevier Academic Press: San Diego, CA, USA, 2004. [Google Scholar]
- Sedighi, M.; Svetovoy, V.B.; Palasantzas, G. Casimir force measurements from silicon carbide surfaces. Phys. Rev. B 2016, 93, 085434. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tajik, F.; Babamahdi, Z.; Sedighi, M.; Palasantzas, G. Nonlinear Actuation of Casimir Oscillators toward Chaos: Comparison of Topological Insulators and Metals. Universe 2021, 7, 123. https://doi.org/10.3390/universe7050123
Tajik F, Babamahdi Z, Sedighi M, Palasantzas G. Nonlinear Actuation of Casimir Oscillators toward Chaos: Comparison of Topological Insulators and Metals. Universe. 2021; 7(5):123. https://doi.org/10.3390/universe7050123
Chicago/Turabian StyleTajik, Fatemeh, Zahra Babamahdi, Mehdi Sedighi, and George Palasantzas. 2021. "Nonlinear Actuation of Casimir Oscillators toward Chaos: Comparison of Topological Insulators and Metals" Universe 7, no. 5: 123. https://doi.org/10.3390/universe7050123
APA StyleTajik, F., Babamahdi, Z., Sedighi, M., & Palasantzas, G. (2021). Nonlinear Actuation of Casimir Oscillators toward Chaos: Comparison of Topological Insulators and Metals. Universe, 7(5), 123. https://doi.org/10.3390/universe7050123






