Vacuum Polarization in a Zero-Width Potential: Self-Adjoint Extension
Abstract
1. Introduction
2. Perturbation Theory over Potential
- (i)
- may appear as a solution for some kernel of the subsequent integration (like in the Green’s function); in this case the definition of actual usage of is formulated in terms of some continuous functional acting on the proper test function (a source);
- (ii)
- may be considered as limiting state of locally integrable ”common” functions (the delta-like sequences);
- (iii)
- may be considered just as a rule, which extracts the locus of delta from consideration but sets some requirements on the admissible solutions and/or their derivatives (like in Quantum Mechanics).
2.1. Abstract Static Potential
2.2. First-Order VEVs for Static Potential
2.3. Weak-Field Approximation for Zero-Range Potential
- The effect vanishes in the limit , hence the weak-field approximation works at least at very high (with respect to some lengthy constant) distances;
- The only such a constant for the problem-at-hand is , deduced above;
- From dimensional consideration, the 2nd-order correction to is expected to be of order . In other words, the parameter of formal series is .
3. Self-Adjoint Extension
3.1. Eigenfunctions and the Green’s Function
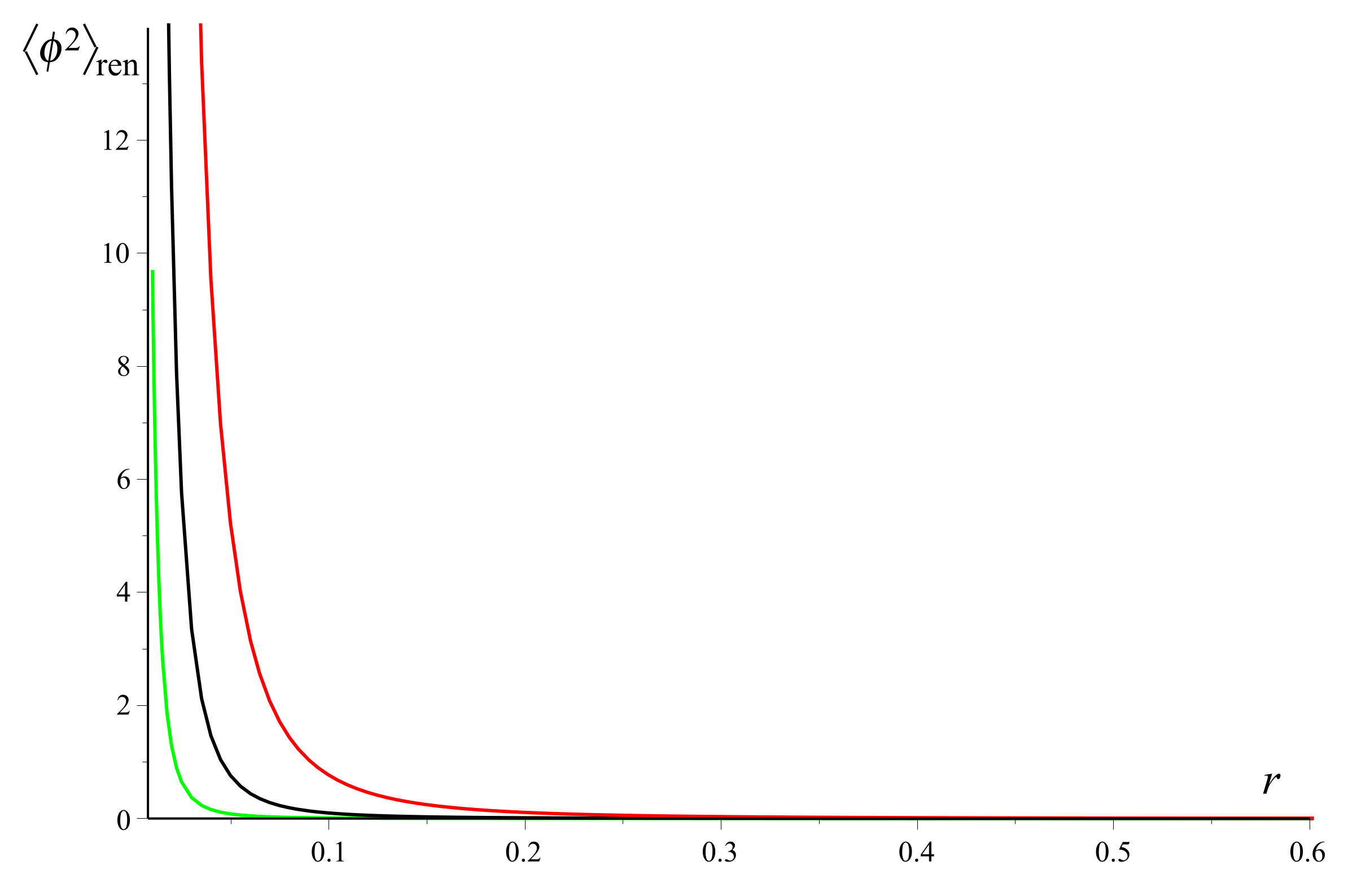
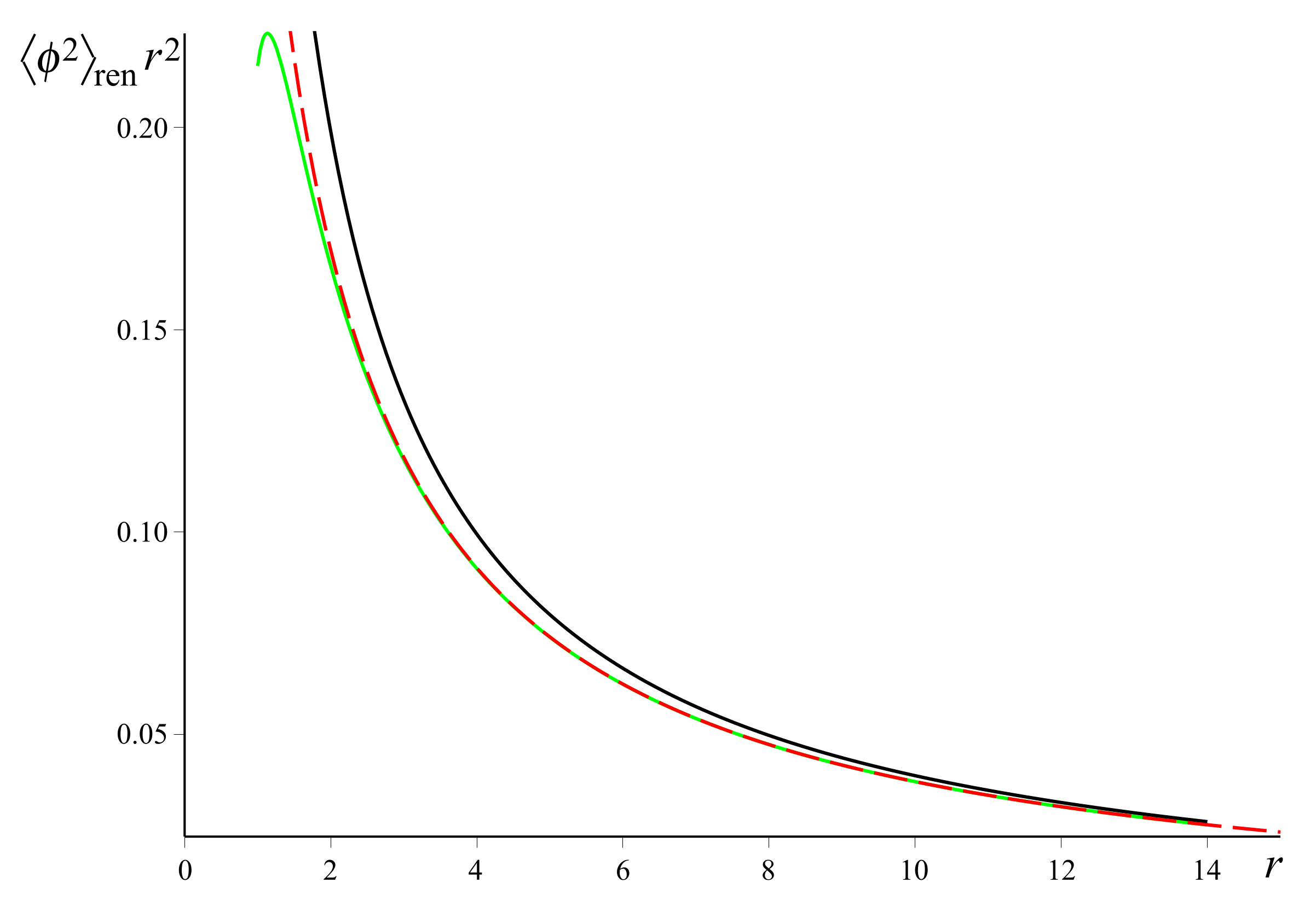
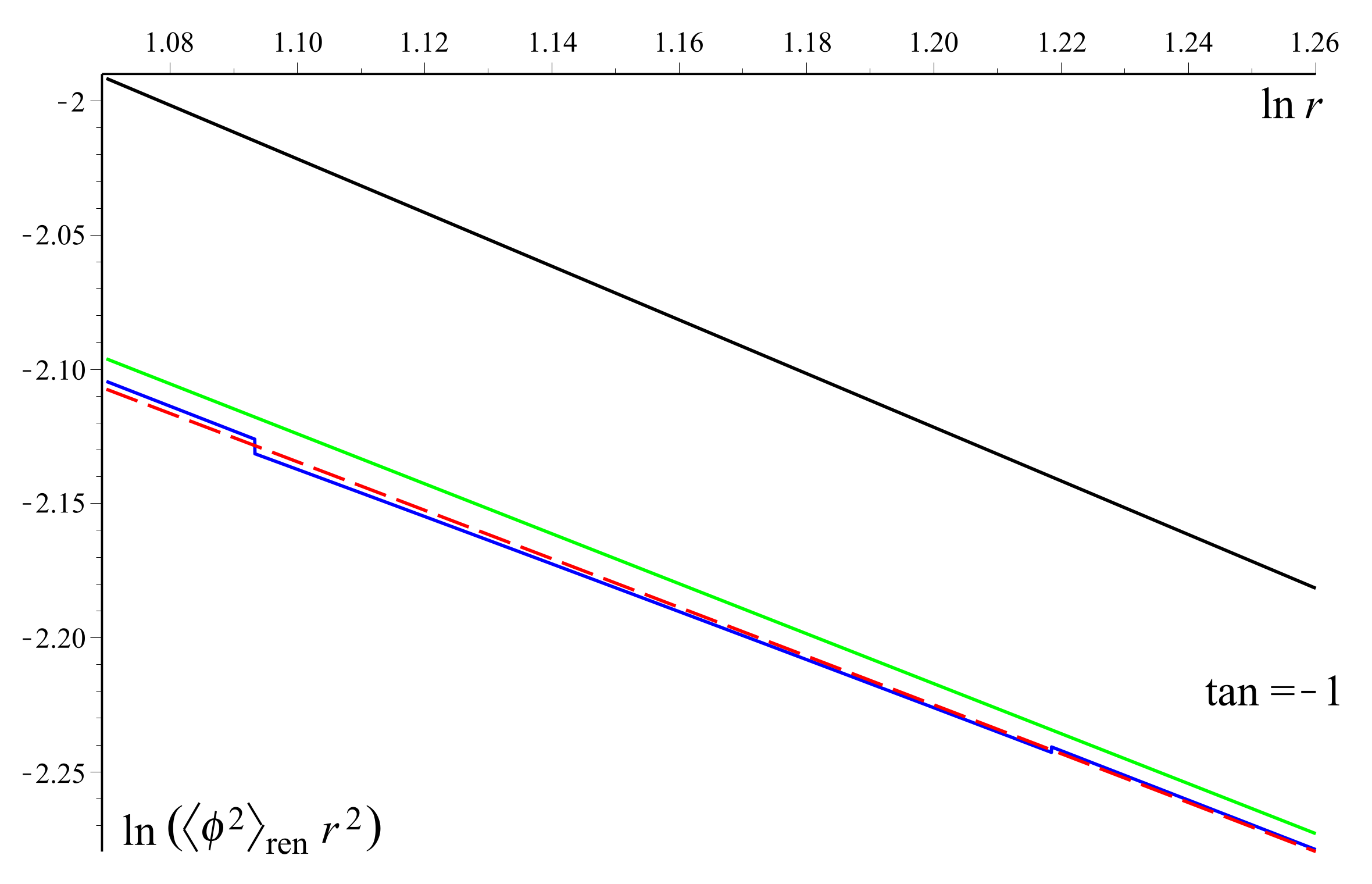
3.2. Field-Square VEV
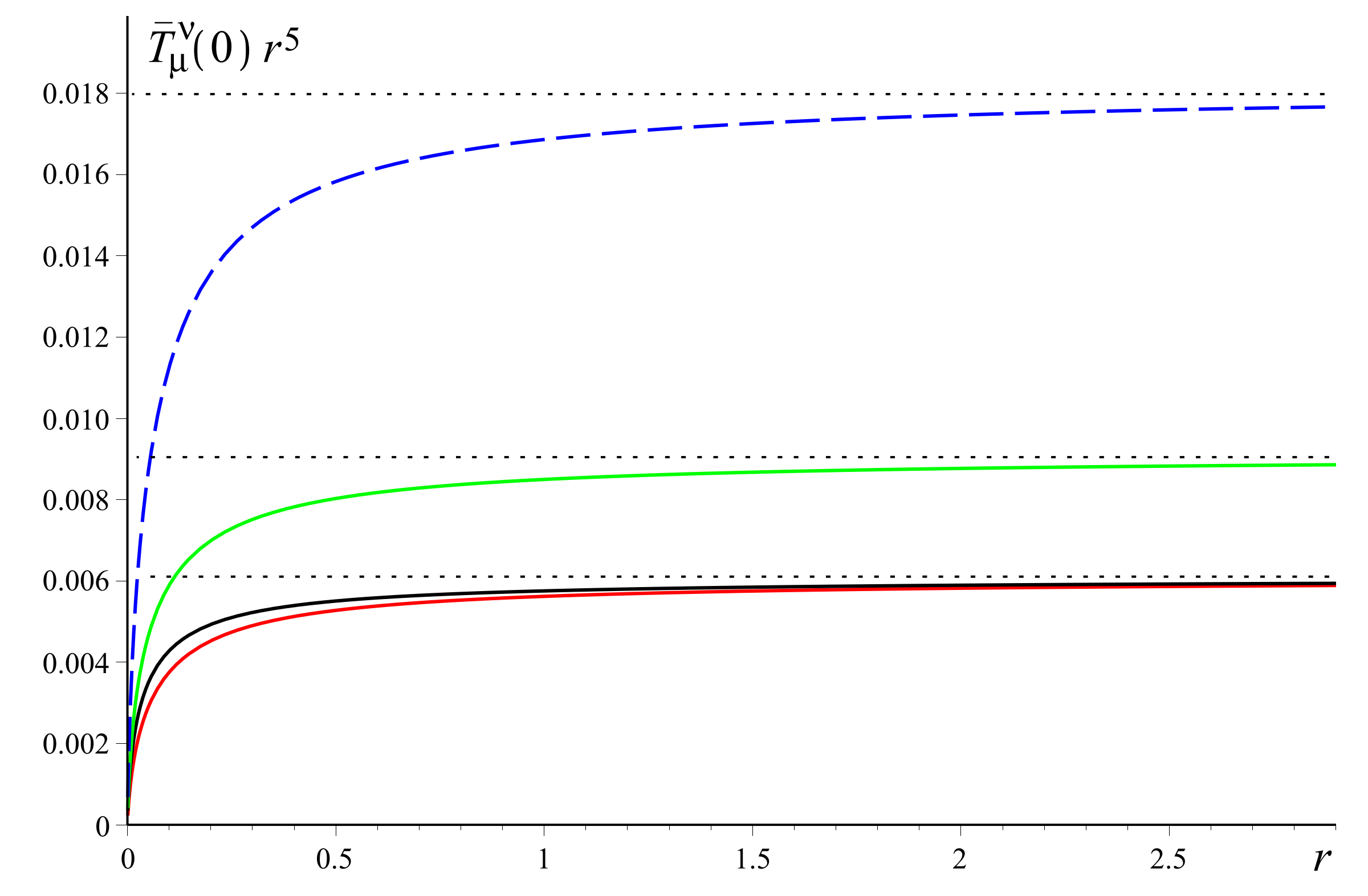
3.3. Vacuum Energy-Momentum Tensor
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FT | Field Theory |
| QFT | Quantum Field Theory |
| QM | Quantum Mechanics |
| PT | Perturbation Theory |
| SAE | Self-Adjoint Extension |
| EMT | Energy-Momentum Tensor |
| VEV | Vacuum Expectation Value |
References
- Kronig, R.L.; Penney, W.R. Quantum Mechanics of Electrons in Crystal Lattices. Proc. Roy. Soc. A 1931, 130, 499. [Google Scholar]
- Demkov, Y.N.; Ostrovskii, V.N. The Usage of Zero-Range Potentials in Atomic Physics; Nauka: Moscow, Russia, 1975. (In Russian) [Google Scholar]
- Mamaev, S.G.; Trunov, N.N. Vacuum Expectation Values of the Energy Momentum Tensor of Quantized Fields on Manifolds with Different Topologies and Geometries III. Sov. Phys. J. 1980, 23, 551. [Google Scholar] [CrossRef]
- Mamaev, S.G.; Trunov, N.N. Quantum Effects in the External Fields Determined by the Potentials with Point-like Support. Yad. Fiz. 1982, 35, 1049. (In Russian) [Google Scholar]
- Bordag, M.; Henning, D.; Robaschik, D. Vacuum energy in quantum field theory with external potentials concentrated on planes. J. Phys. A 1992, 25, 4483. [Google Scholar] [CrossRef]
- Bordag, M.; Mohideen, U.; Mostepanenko, V.M. New developments in the Casimir effect. Phys. Rep. 2001, 353, 1205. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Muños-Castañeda, J.M.; Moteos Guilarte, J.; Moreno Mosquera, A. Quantum vacuum energies and Casimir forces between partially transparent δ-function plates. Phys. Rev. D 2013, 87, 105020. [Google Scholar] [CrossRef]
- Grats, Y.V. Casimir Energy in Contact-Interaction Models. Phys. Atom. Nucl. 2018, 81, 253–256. [Google Scholar] [CrossRef]
- Fermi, D.; Pizzocchero, L. Local Casimir Effect for a Scalar Field in Presence of a Point Impurity. Symmetry 2018, 10, 38. [Google Scholar] [CrossRef]
- Fermi, D.; Pizzocchero, L. Local Zeta Regularization and the Scalar Casimir Effect. A General Approach Based on Integral Kernels; World Scientific Publishing Co.: Singapore, 2017. [Google Scholar]
- Fermi, D. Vacuum Polarization with Zero-Range Potentials on a Hyperplane. Universe 2021, 7, 92. [Google Scholar] [CrossRef]
- Grats, Y.V. Vacuum Polarization in a Zero-Range Potential Field. Phys. Atom. Nucl. 2019, 82, 153–157. [Google Scholar] [CrossRef]
- Sokolov, D.D.; Starobinsky, A.A. The structure of the curvature tensor at conical singularities. Sov. Phys. Dokl. 1977, 22, 312. [Google Scholar]
- Grats, Y.V.; Spirin, P. Vacuum polarization and classical self-action near higher-dimensional defects. Eur. Phys. J. C 2017, 77, 101. [Google Scholar] [CrossRef]
- Grats, Y.V.; Spirin, P. Vacuum polarization in the background of conical singularity. Int. J. Mod. Phys. A 2020, 35, 2040030. [Google Scholar] [CrossRef]
- Jackiw, R. Delta function potentials in two-dimensional and three-dimensional quantum mechanics. In M. A. Beg Memorial Volume; Ali, A., Hoodbhoy, P., Eds.; World Scientific: Singapore, 1991; 15p. [Google Scholar]
- Jackiw, R.W. Diverse Topics in Theoretical and Mathematical Physics; World Scientific: Singapore, 1995. [Google Scholar]
- Allen, B.; Ottewill, A.C. Effects of curvature couplings for quantum fields on cosmic string space-times. Phys. Rev. D 1990, 42, 2669. [Google Scholar] [CrossRef] [PubMed]
- Kay, B.; Studer, U.M. Boundary conditions for quantum mechanics on cones and fields around cosmic strings. Comm. Math. Phys. 1991, 139, 103. [Google Scholar] [CrossRef]
- Allen, B.; Kay, B.S.; Ottewill, A.C. Long range effects of cosmic string structure. Phys. Rev. D 1996, 53, 6829. [Google Scholar] [CrossRef]
- Khusnutdinov, N.R.; Khabibullin, A.R. Zero point energy of a massless scalar field in the cosmic string space-time. Gen. Rel. Grav. 2004, 36, 1613. [Google Scholar] [CrossRef]
- Berezin, F.A.; Faddeev, L.D. Remark on the Schrödinger equation with singular potential. Soviet. Math. Dokl. 1961, 2, 372. [Google Scholar]
- Zel’dovich, Y.B. Scattering by a singular potential in perturbation theory and in the momentum representation. JETP 1960, 11, 594. [Google Scholar]
- Solodukhin, S.N. Exact solution for a quantum field with delta-like interaction. Nucl. Phys. B 1999, 541, 461. [Google Scholar] [CrossRef]
- Spreafico, M.; Zerbini, S. Finite temperature quantum field theory on noncompact domains and application to delta interactions. Rep. Math. Phys. 2009, 63, 163. [Google Scholar] [CrossRef]
- Scardicchio, A. Casimir Dynamics: Interactions of Surfaces with Codimension > 1 Due to Quantum Fluctuations. Phys. Rev. D 2005, 72, 065004. [Google Scholar] [CrossRef]
- Albeverio, S.; Cognola, G.; Spreafico, M.; Zerbini, S. Singular perturbations with boundary conditions and the Casimir effect in the half space. J. Math. Phys. 2010, 51, 063502. [Google Scholar] [CrossRef]
- Fermi, D. The Casimir energy anomaly for a point interaction. Mod. Phys. Lett. A 2020, 35, 2040008. [Google Scholar] [CrossRef]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics. II. Fourier Analysis. Self-Adjointness; Academic-Press: New York, NY, USA; London, UK, 1975. [Google Scholar]
- Albeverio, S.; Gesztesy, R.; Hoegh-Krohn, R.; Holden, H. Solvable Models in Quantum Mechanics; World Scientific: Singapore, 1995. [Google Scholar]
- Gitman, D.M.; Tyutin, I.V.; Voronov, B.L. Self-Adjoint Extensions in Quantum Mechanics; Springer: New York, NY, USA, 2012. [Google Scholar]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Itzykson, C.; Zuber, J.B. Quantum Field Theory; Mcgraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Gel’fand, I.M.; Shilov, G.E. Generalized Functions: Properties and Operations; Academic Press: Waltham, MA, USA, 1964. [Google Scholar]
- Christensen, S.M. Vacuum expectation value of the stress tensor in an arbitrary curved background: The covariant point-separation method. Phys. Rev. D 1976, 14, 2490. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Westview Press: Pod, FL, USA, 1995. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; U.S. Government Printing Office: Washington, DC, USA, 1964.
- Park, D.K. Green’s-function approach to two- and three-dimensional delta-function potentials and application to the spin-1/2 Aharonov-Bohm problem. J. Math. Phys. 1995, 36, 5453. [Google Scholar] [CrossRef]
| 1 | In what follows we define the Feynman propagator as . |
| 2 | Hereafter the 4- and 3-dimensional direct Fourier-transforms are defined as
|
| 3 | Here is n-dimensional Euclidean vector and stands for its i-th component. In Equation (18) the monomial (or, equivalently, ) is constructed from the components of the Minkowski vector , where the sign changes in dependence of the index kind. But since q enters quadratically, the lowercase Minkowski tensor is identical to the Euclidean , where is the spatial sector of with uppercase index. This equality does not give rise to any confusion. |
| 4 | Excepting the conformal field. |
| 5 | |
| 6 | Notice, we use the definitions of [39]. Not to be confused with the 1st Euler’s polynomial. |
| 7 | Namely, the actual non-vanishing Christoffels for us will be and . |
| 8 | Here we are not interested in the problem whether the potential, being an energy source, produces own gravitational field. |
| 9 | What represents a goal of our issue. |
| 10 | The parameter appears from reexpressing (21) as
|



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grats, Y.V.; Spirin, P. Vacuum Polarization in a Zero-Width Potential: Self-Adjoint Extension. Universe 2021, 7, 127. https://doi.org/10.3390/universe7050127
Grats YV, Spirin P. Vacuum Polarization in a Zero-Width Potential: Self-Adjoint Extension. Universe. 2021; 7(5):127. https://doi.org/10.3390/universe7050127
Chicago/Turabian StyleGrats, Yuri V., and Pavel Spirin. 2021. "Vacuum Polarization in a Zero-Width Potential: Self-Adjoint Extension" Universe 7, no. 5: 127. https://doi.org/10.3390/universe7050127
APA StyleGrats, Y. V., & Spirin, P. (2021). Vacuum Polarization in a Zero-Width Potential: Self-Adjoint Extension. Universe, 7(5), 127. https://doi.org/10.3390/universe7050127




