Abstract
We derive modified reflection coefficients for electromagnetic waves in the THz and far infrared range. The idea is based on hydrodynamic boundary conditions for metallic conduction electrons. The temperature-dependent part of the Casimir pressure between metal plates is evaluated. The results should shed light on the “thermal anomaly,” where measurements deviate from the standard fluctuation electrodynamics for conducting metals.
1. Introduction
The Universe is mainly filled with matter and radiation. While the former makes up a mass of roughly one Hydrogen atom per cubic meter, averaged over cosmological scales, quantum theory has predicted, since about one century ago, that the zero-point energy of radiation, one half photon energy per electromagnetic mode, sums up to an energy per unit volume of [1]
where the factor 2 accounts for two transverse polarizations, and is a cutoff of the k-space available to the modes. Choosing this at the Planck length , one obtains an energy density factor ∼ above the energy equivalent of the matter content—the “wrongest formula in physics”. It is intriguing to handle this discrepancy with an argument familiar from renormalization theory (and also used by Casimir [2]): the vacuum energy scales in leading order with the volume of the system and can be subtracted by comparing two situations with the same volume—but differing in boundary conditions. However, what should set boundary conditions for the Universe as a whole and where?—perhaps the cosmological horizon, effectively considering the Universe as a bubble with Hubble radius . Subtracting the energies, a term remains, which scales with the surface of the bubble. Taking the short-wavelength cutoff for k-vectors parallel to the horizon, the vacuum energy density in our Universe bubble becomes
The subtraction has removed ℏ from the formula (if the Hubble constant H is considered a given parameter), and it has reduced the radiation energy by a factor , leading to an estimate comparable to the observed mass-energy. For other estimates about the cosmological horizon and its role in the possibly accelerated expansion, see Easson et al. [3]. An analysis of the self-gravitation of the huge vacuum energy density has been given by Wang et al. [4].
The Casimir effect predicts a (generally) attractive force between macroscopic objects, due to quantum fluctuations of the surrounding fields [5]. Direct measurements of these so-called dispersion forces are often popularised as improving our understanding of vacuum fluctuations—see, however, the viewpoint of Jaffe [6] who recalls the tracing-back to zero-point fluctuations of charges and currents in matter. A related motivation drives experiments searching for fundamental corrections to short-range forces that arise from axion fields or compactified dimensions [7,8]. Advances in this field are somehow stalled, however, by the relatively down-to-Earth issue of how to characterize precisely the electromagnetic Casimir forces between real metallic conductors. Metallic objects have obvious advantages because electric forces can be avoided, which typically mask the weaker dispersion interactions. The problem arises, however, that the Casimir force under realistic conditions also contains a temperature-dependent contribution (sometimes this is attributed to “real” rather than “virtual” particles) whose relevant frequencies peak in the infrared ( at room temperature, for example, Wien’s displacement law) [9,10]. Its evaluation requires the knowledge of the infrared conductivity of a metal, but this has been the subject of great discussions—the “Drude vs. plasma” controversy [11,12,13,14,15].
The bulk conductivity, however, provides only half the answer to the response of a conducting object to an external field—its surface and its geometry play equally important roles. The controversy has taught us that frequencies in the thermal range do give a significant contribution to the Casimir force, on the one hand. On the other hand, from experience with calculations, the k-vectors of the relevant field modes are set by the (smallest) distance d between the objects, typically much shorter than the thermal wavelength (at room temperature ∼). We are facing a curious combination of k and : contrary to our intuition about infrared frequencies, the relevant length scales are below , being determined by d. This calls for a reappraisal of methods that have been developed over the last century. Those coming from the context of infrared spectroscopy do not address the range of parameters , since one is dealing with the response to long wavelengths . More relevant is work on electron energy loss spectroscopy [16] where the fields correspond to the Coulomb potential of a moving charge. In that context, however, the focus has been on rather high frequencies (energies), even the surface plasmon resonance (in the visible or UV) being considered a low-energy feature [17]. The situation is exacerbated by experiments addressing, in the distance range d∼10, …, 300 nm, the Casimir force [7,18] and non-contact heat transfer [19,20]: they give results that disagree with the standard theory of the fluctuating electromagnetic field [21,22].
We outline in this paper an improved, hydrodynamic approximation for the electromagnetic response of conduction electrons at a metallic surface. It is shown in particular that the classical Fresnel formulas based on a local dielectric function apply only in a specific range in the -plane, as it happens also with other models including spatial dispersion [23,24]. In our context, a kind of conspiration of scales has to be addressed. To fix a relevant set of parameters, consider the commonly used local Drude dielectric function and conductivity
Here, (possibly frequency-dependent, too) describes the response of bound electrons, the plasma frequency scales with the root of the conduction electron density, and is the scattering time. The latter can be determined from the DC conductivity . Typical parameters for gold at room temperature are and (wavelength , in the far infrared). The scattering rate separates the classical Hagen-Rubens regime (low frequencies) from the so-called relaxation regime (see Sievers [25] and Appendix E of Dressel and Grüner [24] for more details). The first coincidence is that the typical thermal frequency is quite close to the Drude scattering rate (gold at room temperature). (For a detailed study of the behaviour of Casimir pressure and entropy at low temperatures, see References [14,26].) The second coincidence is one of length scales. Recall that an electromagnetic field in the thermal frequency band penetrates into a metal in a diffusive way, leading to the characteristic length where ( being the permeability) is the diffusion constant for magnetic fields [27]. The scale ∼20 nm explains the “thermal anomaly” of the Casimir pressure, namely that temperature-dependent corrections appear already at distances d much shorter than [28,29]. The hydrodynamic model introduces another length in the same range, namely the electronic mean free path ℓ. From the Fermi velocity (gold: ), we have . This scale appeared already in the anomalous skin effect [24] that occurs when ℓ is larger than the classical penetration depth . Its impact on the Casimir pressure has been studied using generalisations of the Fresnel reflection amplitudes [30,31], although the modifications were found to occur only for p-polarized field modes. This polarization contains an electric field component perpendicular to the surface and probes the charge density profile at a metallic surface, whose characteristic scale is the Fermi wavelength or the Thomas-Fermi screening length [32,33].
We focus our hydrodynamic approach on the response to s-polarized fields whose electric field is parallel to the surface. To understand the basic idea, recall the Maxwell matching conditions for the tangential electric field in vacuum and metal, . Using Ohm’s law in local form , a nonzero current density right at the metal surface appears. This is not consistent with the no-slip boundary condition typical for the hydrodynamics of viscous fluids [34]. For electrons moving parallel to a surface, the no-slip condition takes into account, on length scales much larger than the Fermi wavelength, the scattering by surface roughness and by amorphous reconstructions of the sub-surface material. Note that this would not apply for atomically clean samples, but rather for metals kept in ambient conditions, as also suggested by experiments in the THz range [35]. Our hydrodynamic calculations indeed predict that the electronic current density varies significantly in the sub-surface region on the scale of the mean free path ℓ.
A key parameter is the shear viscosity of the electron fluid. We use the observation of Conti and Vignale [36] that the hydrodynamic (Navier-Stokes) equations can be phrased in the language of a visco-elastic medium. An elastic modulus and the viscosity are related, at finite frequencies, to the real and imaginary parts of the same mechanical response. It turns out that this response is encoded in the longitudinal and transverse dielectric functions of the charged Fermi gas. These are well-known within Lindhard theory [37] in the self-consistent field (or random-phase) approximation. By matching the long-wavelength expansion of these functions, extended to take into account collisions [36,38,39], we find a kinematic shear viscosity that scales, below the collision rate , with . This is formally a diffusion coefficient comparable in magnitude to the magnetic one because of the coincidence between the (reduced) plasma wavelength and the mean free path ℓ.
An overview of our results is shown in Figure 1 where the Casimir pressure (left) and the heat transfer (right) due to s-polarized modes is plotted. These modes give a sizeable thermal correction to the Casimir force [9,28,29] and reduce the attraction prevailing between ideal reflectors. The p-polarisation does not contribute because of the efficient charge build-up at the metal surfaces (in the infrared, the dielectric screening is ). Note in particular that the s-polarized modes alone account for nearly the entire difference between the measured Casimir force and the theory based on the local Drude approximation (open dots with error bars [40]). In the no-slip model, their repulsive contribution drops significantly compared to the local Drude model, so that the difference to observations gets smaller [15]. The radiative heat current in Figure 1 (right) is also reduced, but the data are well below the levels observed in Refs. [19,20].
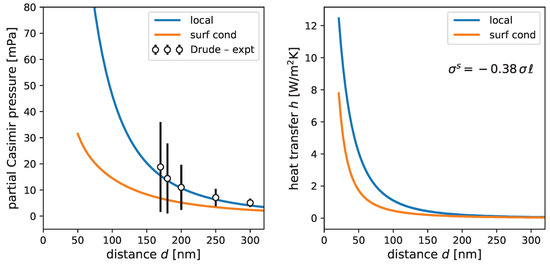
Figure 1.
(Left) Partial Casimir pressure (only s-polarized waves are included) between two thick plates as a function of distance d. The solid lines give the repulsive thermal contribution (the limit subtracted) for two response functions of the metal. The open black symbols with error bars give the absolute difference between the observed pressure and the full theoretical calculation based on the local Drude approximation (data from Ref. [40]). (Right) Heat transfer coefficient [see Equations (7) and (8)], as the temperature difference . The results are dominated by evanescent waves with , propagating waves giving a negligible contribution. Local: Formula (9) for reflection coefficient ; surf cond: model of Section 3.3 with surface conductivity . Material parameters for gold as given in the main text, temperature .
The outline of the paper is as follows—in Section 2, we motivate the formulas for the Casimir pressure between metallic plates at nonzero temperature and for the radiative heat transfer. After an introduction to the hydrodynamic approximation (Navier-Stokes equation) in Section 3.1, we solve the reflection/transmission problem at a conducting surface using the no-slip boundary condition (Section 3.2) and a modified surface current density (Section 3.3). A discussion of the reflection coefficients and the impact on the Casimir pressure is given in Section 4. Appendix A presents the derivation of the viscosity for conduction electrons based on the wave vector- and frequency-dependent longitudinal and transverse dielectric functions.
2. Casimir Pressure and Boundary Conditions
The famous formula by Casimir for the force per unit area between two ideally reflecting plates (Figure 2) reads
where d is the distance and the negative sign denotes an attractive force. This formula ignores the physical properties of the plates, although its derivation requires that they become transparent in the far UV—to regularise the UV divergent vacuum energy.
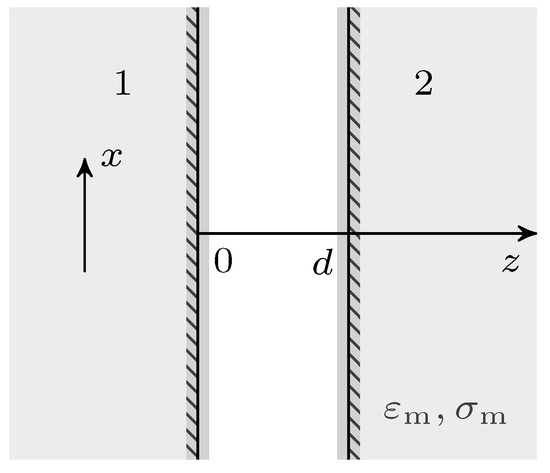
Figure 2.
Simple system setup: two metallic plates (1 and 2) separated by a vacuum gap of distance d. In the sub-surface regions (hatched), the hydrodynamic and local models give different profiles for the current density.
A more complete description is provided by the theory of dispersion forces. It describes electromagnetic fluctuations, both in the quantum and thermal regime, in and between macroscopic bodies and the ensuing interactions. If we restrict the discussion to distances , it seems appropriate to use a continuum description and to describe the objects with the help of material equations, using the framework of macroscopic electrodynamics. This has been developed over the last twenty years into macroscopic quantum electrodynamics [5,22,41,42,43]. Its basic idea is that the macroscopic response functions also determine the strength of the fluctuations produced by the bodies. By the very construction of this approach, there is no distinction to be made between virtual or real fields—the body’s material is responding to an external field.
We focus on the simple geometry of two thick parallel plates a distance d apart, with the z-axis normal to the surfaces. They are kept at temperature T so that for a given (angular) frequency , the mean energy per photon mode is given by defining the Bose-Einstein distribution . Due to translational and rotational symmetry parallel to the plates, the electromagnetic modes may be labelled by a two-dimensional k-vector . Between the plates (vacuum), these modes vary with the wave vector
In the second case, the modes are called evanescent and they are localised to the vicinity of their sources. (Klimchitskaya and Mostepanenko [15] use the words “on-shell” (“off-shell”) for propagating (evanescent) modes, respectively.) There are two transverse polarisations, usually called p (or TM) and s (TE). When a wave with polarisation is incident on the metal plate, it is reflected with amplitude . Multiple reflections between plate 1 and 2 can be represented by a geometric series
At each reflection, a propagating photon imparts a recoil momentum of order onto the plate. Taking into account the reflection amplitudes and summing over all photon modes and their thermal occupation numbers, the electromagnetic stress normal to the surfaces yields the Lifshitz formula for the Casimir force per unit area [44]
This also contains the contribution of evanescent waves via the -shaped path of the integral—it runs along the imaginary axis from to 0 and then to (recall the convention: negative P gives an attractive force).
Formula (5) is not suitable for calculating the pressure because its zero-temperature limit is plagued by the rapid oscillating factor at high frequencies (along the real “leg” of the -integral). (The integral is physically cut off around the the plasma frequency where tabulated optical data rather than the Drude permittivity must be used.) Lifshitz shifted the -integration in the complex frequency plane to the imaginary axis , which is possible because the integrand is built from response functions that are analytic in the upper half plane. The -integral is then taken from to so that all exponentials become real and decay at large . For finite temperatures, the integration is replaced by a summation over the Matsubara frequencies , the poles of , with the term counting only one half:
We have used here that the integrand becomes a real function along the imaginary axis.
Similar considerations have led Polder and Van Hove [45] and Loomis and Maris [46] to a formula for the heat current between two planar bodies of temperatures , separated by a vacuum gap of width d [43]. For small gaps, the important contribution comes from evanescent waves, that is, imaginary :
where is the difference of Bose distributions. The contribution from real looks a bit different,
Physical properties of the reflection coefficients, namely energy conservation for real () and passivity for imaginary (), ensure that the heat current is always oriented from hot to cold, consistent with the Second Law of thermodynamics. Note that in this approach, the concept of temperature has shifted from the field itself to its sources, namely currents and charges in the two bodies. A detailed discussion when the simple picture of two uniform temperatures is applicable, has been given by Eckhardt [47]. The basic idea is that the material’s heat capacity and thermal conductivity are sufficiently large so that the absorption of electromagnetic energy does not change its temperature. Similar arguments have been used to model transport in semiconductors at high fields [48]. Additional bodies in thermal contact are obviously also instrumental in maintaining the non-equilibrium setting.
In the following, our focus will be on the temperature-dependent part of the Casimir pressure and the radiative heat transfer. This is why we do not use the Matsubara sum—the thermal correction would be hidden in the difference between sum and integral [see Equation (6)]. Using the argument principle rather than the Euler-MacLaurin formula to evaluate that difference, brings us back to the real-frequency integral (5). This makes one essential difference with respect to Klimchitskaya and Mostepanenko [15] where a modified surface response was also proposed, but the focus was on the behaviour of the zero’th Matsubara frequency . Further comparison to that paper will be drawn in the Conclusion. Since we also focus on distances d much smaller than the thermal wavelength , the -integral is dominated by its imaginary leg (evanescent modes), thus providing numerically tractable expressions. A typical scale for the imaginary wavenumber is set by the inverse distance .
It remains in the following to analyse the reflection coefficients. If the plates are characterized by a local dielectric function , the Fresnel formulas can be used
where
is the decay constant inside the metal. (We take .) These expressions arise from the dispersion relation in the metal and by matching the tangential components of the electric and magnetic fields at the vacuum-metal interface. In the following section, we derive a generalisation of these expressions using a hydrodynamic picture where the conduction electrons are modelled as a charged, visco-elastic medium.
3. Visco-Elastic Electron Dynamics
3.1. Bulk
The key concepts for a hydrodynamic description are the density n and the velocity field for carriers with mass m and charge e. The dynamics of the latter is given by with the Navier-Stokes force density [34]
Here, is the Drude scattering rate (see discussion in Appendix A), the compressibility is expressed via the velocity , and the kinematic shear and bulk viscosities are , with . (This force density can be interpreted as a gradient expansion, assuming that n and vary on large scales only. The hydrodynamic description does not resolve a microscopic scale like the Fermi wavelength.)
We are interested in the linear response of conduction electrons to the electric field that splits naturally into a longitudinal (L) and transverse (T) part (Coulomb gauge: ). Using the equation of continuity , assuming all fields to evolve at a given frequency with , and dropping second-order terms from the Navier-Stokes Equation (11), we obtain
The complex combination can be interpreted as a dynamic modulus, using the language of visco-elastic media [36]. In a homogeneous medium where the fields vary with the wave vector , these equations produce the longitudinal and transverse conductivities in the hydrodynamic approximation according to :
where is the DC conductivity and the equilibrium charge density. Note from the poles of these expressions for how determines the speed of longitudinal sound waves, while the transverse current behaves in a diffusive way with diffusion constant .
The expressions (14) and (15) provide a framework to actually find the hydrodynamic parameters for the electron fluid. In this paper, we focus on the seminal results of Lindhard [37] for the conductivities in the self-consistent field (or random-phase) approximation, leaving a detailed study of exchange-correlation effects for later work (see Conti and Vignale [36] for this more general approach). We incorporate collisions into the Lindhard functions in such a way that charge excitations relax to local equilibrium set by the electrochemical potential and their static limit is correctly reproduced [36,38,39]. The Lindhard conductivities are not restricted by the hydrodynamic approximation and can be expanded for small q-vectors. As outlined in Appendix A, this procedure gives
The expression (16) recovers the longitudinal speed of sound derived by Halevi [49]. Its real part crosses over from at low frequencies to at high frequencies (isentropic limit). Its imaginary part is attributed here to the viscosities of the electron fluid. The shear viscosity (17) is plotted in Figure 3 (black dashed lines). Its low-frequency limit is set by the value . The lower part of the Figure gives the corresponding shear velocity , defined from . It scales at low frequencies, consistent with the picture that a liquid does not support low-frequency shear waves. Around the collision frequency, the response to shear changes from viscous to elastic, and for . The gray dashed lines correspond approximately to the longitudinal elastic parameters (see discussion of de Andrés et al. [50] in Appendix A.2.3). The other curves in Figure 3 illustrate corrections beyond hydrodynamics that appear when the dimensionless parameter . They become relevant on scales shorter than the mean free path, that is, .
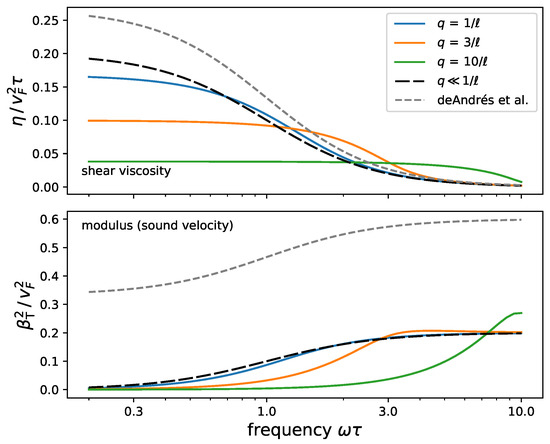
Figure 3.
Shear viscosity (top) and modulus (bottom) for the Fermi gas with collisions, based on the transverse Lindhard dielectric function modified according to Conti and Vignale [36]. We plot the kinematic viscosity and the square of the shear wave sound velocity . The thick black dashed line corresponds to the hydrodynamic limit (small q). The gray dashed line is the result of de Andrés et al. [50] (see Appendix A.2.3). The solid colored lines are obtained from the inverse conductivity computed according to Kliewer and Fuchs [38] and Conti and Vignale [36], by subtracting the local limit and dividing by [see Equation (15) and Appendix A.2.2]. The kinks appearing at signal the onset of Landau damping (creation of electron-hole pairs).
We finally note a close coincidence of parameters. The penetration of s-polarised evanescent fields into a metal follows the decay constant where the DC conductivity can be expressed as a diffusion constant that governs the spatio-temporal behaviour of low-frequency magnetic fields [27]. The kinematic shear viscosity has also the dimension of a diffusion coefficient [see Equation (15)] . For the noble metal parameters, we have , and the diffusive behaviour of both types overlaps in space. The only way to formally isolate the local Drude model is the “dirty limit,” where at fixed , . A discussion of the opposite case, that is typical for low temperatures, is provided by Reiche et al. [14], Intravaia et al. [26].
3.2. Sub-Surface Region
We now apply the Navier-Stokes equations to the response of a metallic half-space to an s-polarized field and compute the reflection amplitude . We assume that all fields vary ∼ with the x-axis parallel to the surface and the metal occupying the region . It is easy to see that the s-polarisation gives transverse fields senkrecht (orthogonal) to the -plane, we denote by and the corresponding components of and . The no-slip boundary condition thus pertains to the tangential velocity of the electron fluid, while A, proportional to the tangential electric field, is actually continuous across the surface. This rule has the advantage of not needing a dimensional parameter (apart from the bulk viscosity fixed from the bulk behaviour). It nevertheless provides an “additional boundary condition” in the language of optics in spatially dispersive media [24]. The approach of Klimchitskaya and Mostepanenko [15] is very different since they modify the -dependence of the bulk dielectric function. Compared to Equations (14) and (15), their corrections are linear in k rather than quadratic, the anisotropy being justified by the presence of the surface. Our approach is quite the opposite, since an explicit boundary condition enters into the description of the surface, while (deep) inside the metal, the bulk dielectric functions are applied, keeping their spatial dispersion within the scope of hydrodynamics.
Equation (13) and the Maxwell equations yield the following equations of motion
where we used the link between electron density and plasma wavelength to re-write the current density (first term of Equation (19)). In , the displacement current will give a negligibly small contribution. Since the fields must decay deep into the bulk metal, this system can be solved with the Ansatz
and similar for A. The decay constants are given by
The ratio between the eigenmode amplitudes , () is [Equation (19)]. It is essential to have two decay modes here, otherwise the boundary conditions would make the velocity vanish everywhere. For typical good conductors and , the two terms under the root are comparable. If the mean free path is not resolved, diverges (thin boundary layer) and is the decay constant in the local Drude model and the Fresnel Equation (9).
The no-slip boundary condition fixes from Equation (20) the ratio , so that only one free parameter remains. It is fixed by the amplitude of the field incident from the vacuum side. A convenient quantity is the ratio (a length) evaluated at the surface. Since is a tangential electric field and a tangential magnetic field, the ratio Z is actually proportional to the surface impedance of the metallic half-space. A quick calculation gives
The “impedance” Z matches with the incident and reflected fields on the vacuum side, . This yields the beautiful formula for the s-polarised reflection amplitude
the main result of this section. (The second form becomes exact for .) In the local limit (vanishing viscosity), diverges [Equation (21)], and goes into the Fresnel Formula (9). Corrections to this thus depend on the ratio .
The hydrodynamic description is illustrated by the results in Figure 4 where the current profile is shown for different choices of parameters. The values of the reflection coefficients are also given and compared to the local (Drude-Fresnel) result.
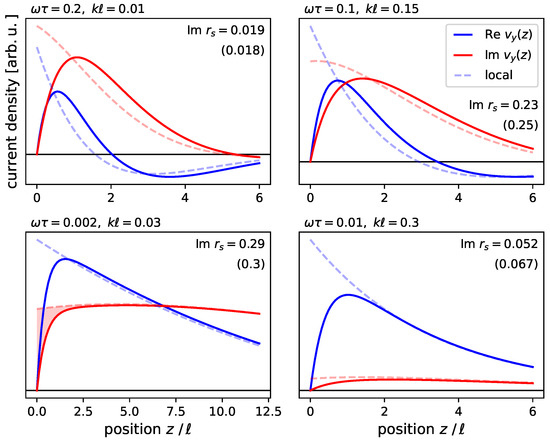
Figure 4.
Sub-surface distribution of current density for different choices in the -plane (marked by white dots in Figure 5). The shaded area in the bottom left illustrates the concept of an excess current (Section 3.3). The numbers for correspond to the hydrodynamic no-slip model and the local Drude model (in parentheses). The data are based on a unit amplitude (real-valued) electric field incident from the vacuum side ().
3.3. Reduced Boundary Layer Conductivity
It is remarkable in Figure 4 (bottom left) how the current distribution is “missing” a sub-surface sheet a few ℓ thick, when comparing to the local model that does not apply the no-slip boundary condition (light dashed lines). We outline in this section how this can be included into a modified boundary condition for the electromagnetic fields, using the excess field technique developed by Bedeaux and Vlieger [51]. This is actually a paradigmatic example of boundary layer approximations or multiple-scale expansions [52,53]. The response of the charge density at a conducting surface has been recently analyzed in the same spirit by Mortensen et al. [54].
The excess field approach lumps the details about the behaviour of fields and currents in the surface region into a small number of response functions. The idea is based on a separation of scales where deviations from a homogeneous bulk material only occur in a thin region near the surface (sometimes called the selvedge [55]). For simplicity, we focus on non-magnetic materials and neglect spatial dispersion in the bulk (far away from the interface). In the following, we provide a closer look at p-polarized waves because the calculations are more involved.
The central concept of an excess field is based on taking the difference between a smooth, microscopic field , say, and its approximation that extrapolates the local-medium values down to the surface,
Bedeaux and Vlieger [51] define the “total excess” as the integral of this difference, . The integral typically converges even before the variation with depth of sets in, a manifestation of a separation of length scales. The excess may still depend on the coordinates in the surface. In Figure 4 (bottom left), the excess current would be the shaded area between the no-slip hydrodynamic and the local current profiles.
It now remains to connect the excesses to the fields outside the surface layer. Excess quantities play similar roles as surface charges and currents in macroscopic electrodynamics and determine jumps of the coarse-grained electromagnetic fields. For a non-magnetic system and a fixed frequency, an integration of the macroscopic Maxwell equations across the interface yields the boundary conditions [51]:
where is the displacement field, tangential components carry the index ‖, and is the unit normal pointing into the metal. For simplicity, the surface coordinates x, y have been suppressed everywhere. Note certain jumps that are absent from the ordinary Maxwell boundary conditions.
Finally, material relations specific to the surface are needed to express the surface excesses by the bulk fields [51]. We focus here on the surface conductivity and the surface resistivity , in order to capture the conductive properties of the selvedge. Introducing as the average on both sides, one obtains the relations
The time derivative of gives, of course, the excess current tangential to the surface, while expresses a potential drop due to the normal displacement current.
We proceed to solving the reflection and transmission problem for a p-polarized wave incident from the vacuum side. A plane-wave Ansatz as in Section 3.2 leads to complex amplitudes and that away from the surface vary according to
where is the amplitude of the incident field, the complex refractive index inside the metal, and given in Equation (10). The coefficients and are the reflection and transmission amplitudes. The corresponding magnetic fields can be obtained by using the relation with the Snell-Descartes law giving the wave vectors on both sides of the surface.
The excess boundary conditions (29), (30) yield the set of equations
which is solved for the reflection amplitude
Compared with the Fresnel Formula (9), this expression features three additional terms. The familiar Fresnel terms are paired with a mixed term containing surface conductivity and resistivity. Both contribute additional corrections as well. Interestingly, the terms including the resistivity are paired with the parallel component k of the wave vector, suggesting that this may be a minor correction in the long-wavelength limit ( much longer than the selvedge thickness).
The same calculations can be done for the s-polarisation and lead to
which depends only on the surface conductivity, since there is no normal electric field component in this case.
For the surface quantities and , we propose a Drude-like model with a relaxation time and a length that captures the thickness of the selvedge region:
By comparing to the no-slip viscous model, we estimate , the negative sign translating the “missing” current due to the boundary condition (Figure 4). The behaviour of the reflection coefficients in the far infrared is illustrated in Figure 6—we note a reduction compared to the local approximation for . This may be attributed to a better impedance matching when the jump of the current density at the surface is reduced. A good agreement with the hydrodynamic model is found in the long-wavelength limit for the parameter combination and . At larger k-vectors, some discrepancies occur. The p-polarization does not contribute significantly in the evanescent wave sector (away from the light line ).
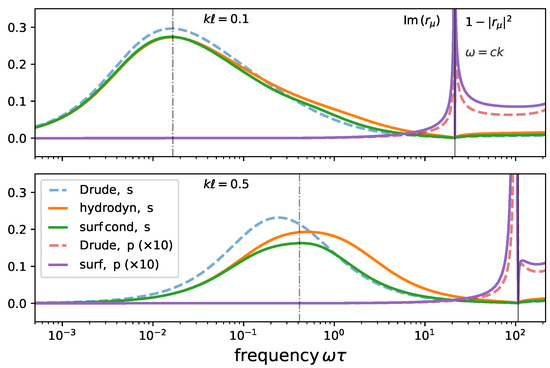
Figure 6.
Reflection amplitudes computed with three different models for two values of k (top and bottom). Both s- and p-polarizations are shown. The light line (vertical line at ) divides each panel into evanescent (left) and propagating (right) waves. On the left of it, the imaginary part of the reflection amplitude is shown, on the right the absorption. The low-frequency maximum in the s-polarization appears at (dash-dotted lines). The p-polarization (scaled up by a factor 10) gives negligible contributions, except for a surface-plasmon-like pole near the light line. Material parameters for gold (see main text).
4. Discussion and Conclusions
In Figure 5, we plot in the -plane a “spectral representation” of the Casimir pressure (left) and the radiative heat transfer (right). Only the thermal contribution of the s-polarization is shown. The data are normalized to the maximum value (in the chosen domain) of the local (Drude-Fresnel) approximation. One notes for both quantities an upper limit , as expected from the Bose-Einstein distribution. The heat transfer data are shifted upwards in frequency due to the additional factor under the integrals (7) and (8). The maximum in the -plane is set by the magnetic diffusion constant (dashed gray lines). A reduction of the pressure appears notably in the range set by the kinematic viscosity (dash-dotted line), when compared to the local approximation. For both quantities, the hydrodynamic and the surface conductivity models give qualitatively the same distributions with the parameters , [Equation (37)] mentioned before [see Figure 5 (right)].
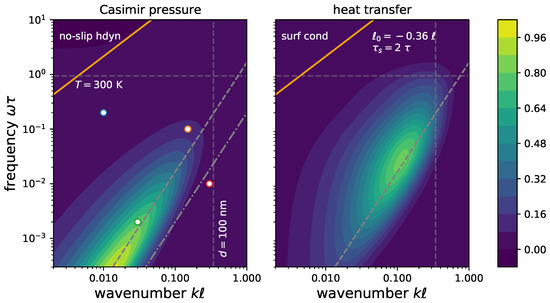
Figure 5.
Integrand of the Casimir pressure (left) and heat transport (right) in the -plane. In the left (right) panel, the hydrodynamic (surface conductivity) model is used to compute the reflection coefficients. Only s-polarized modes are taken into account. Propagating modes appear above the orange line. The gray dashed lines mark relevant parameters—temperature (), distance (), maximum contribution of magnetic diffusion (diagonal dashed) at , diffusive behaviour due to the low-frequency kinematic viscosity (dot-dashed). The data are scaled to the maximum values computed in the local (Drude-Fresnel) approximation. The white dots in the left mark the values chosen in Figure 4.
To summarize, in this paper we have extended the classic Fresnel formulas for the reflection of electromagnetic waves by a metal surface. Two methods have been used—a hydrodynamic description that captures the spatial dispersion of the metal’s dielectric function, and a boundary layer technique introducing surface layers of charges and currents. Both methods build on the assumption that the electric current density right at the surface vanishes. This boundary condition corresponds to the behaviour of a viscous fluid, and mirrors the impact of surface roughness on the few-nm scale. The viscosity of conduction electrons was derived from a modification of the well-known Lindhard dielectric functions, taking into account collisions with impurities, but neglecting exchange-correlation effects [36]. Note that the no-slip condition is needed to solve the hydrodynamic Navier-Stokes equation that involves higher derivatives of the electronic velocity field. It corrects the spatial profile of the current density right below the surface, and the “missing current” is mapped in the boundary layer technique onto a tangential surface current sheet. An interesting consequence is a modification of the s-polarized reflection coefficient such that repulsive contributions to the Casimir pressure between metallic plates are reduced in both models. This brings theoretical predictions closer to the observed values, possibly pointing towards a physically motivated solution of the so-called “plasma vs. Drude” controversy.
Among similar attempts to modify the reflection amplitudes by taking spatial dispersion into account, we mention Reiche et al. [14] and Klimchitskaya and Mostepanenko [15]. For both, the starting point are the surface impedances of a metallic half-space based on a specular reflection boundary condition [23,56] where the longitudinal and transverse dielectric functions appear. Reference [14] uses the nonlocal Lindhard theory corrected for collisions as in Appendix A, but also focuses on the impact of Landau damping and the low-temperature behaviour of Casimir interactions. The authors have also stressed that surface roughness on the scale of the mean free path may conflict with the specular reflection assumption. Reference [15] invokes the breaking of translational symmetry due to the surface to introduce an anisotropic -dependence into the dielectric function. This correction uses the same small parameter as our hydrodynamic approximation, but is otherwise quite different in form. The analysis presented here complements both approaches. The Navier-Stokes model allows to resolve spatial non-locality on scales larger than the mean free path and predicts nontrivial variations in the sub-surface current when the no-slip boundary condition is applied. The excess field (boundary layer) technique collects some of the non-locality into a modified surface response, while allowing for a simpler, local description of the bulk. This illustrates that the term ‘surface’ depends on the choice of length scales implicit in the formulation of fields and boundary conditions.
We conclude with a few remarks. The hydrodynamic model has been used in metals long before, but the focus was almost exclusively on the longitudinal response (charge density waves). The corresponding speed of sound was derived by Halevi [49]. Our analysis links it to complex visco-elastic moduli [36] and provides an additional interpretation. The dispersion of is actually due to the complex shear modulus of the collisional electron gas in the Navier-Stokes equation, while the bulk viscosity vanishes completely in the hydrodynamic approximation (Stokes hypothesis).
Finally, we expect that the boundary conditions considered here will also modify the surface plasmon dispersion relation (that appears as a peak in in Figure 6). This is probably irrelevant to radiative heat transfer because it appears in the frequency range where thermal occupation is negligible. The plasmon dispersion has been studied since a long time [23,49] and depends on the spatial profile of the surface charge on the Thomas-Fermi scale . We thus do not expect large modifications since the no-slip condition changes the current density on the much longer scale of the mean free path , but a quantitative analysis is beyond the scope of this paper.
Author Contributions
Conceptualization, C.H. and G.W.; software, M.H. and C.H.; validation, M.H., C.H. and G.W.; formal analysis, G.W.; writing—original draft preparation, C.H.; writing—review and editing, M.H., C.H. and G.W. All authors have read and agreed to the published version of the manuscript.
Funding
G.W. gratefully acknowledges funding by the German Research Foundation (DFG) in the framework of the Collaborative Research Center 1375 “Nonlinear Optics down to Atomic Scales (NOA)”.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
C.H. is indebted to L. P. Pitaevskii for suggesting the dirty limit as a meaningful simplification of material parameters. We thank K. Busch for a careful, constructive reading of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Derivation of Hydrodynamic Parameters
For the ease of comparison to other work, we first write down the dielectric functions that follow from the hydrodynamic expressions obtained with the Navier-Stokes model (11) of the electronic liquid:
(For simplicity, we put the background dielectric constant in this appendix.) We expect the hydrodynamic description to be accurate in the semiclassical and long-wavelength limits. This requires at least the regime , the Fermi momentum. It is also apparent that the inverses are polynomials in . We shall fix their complex coefficients by a corresponding expansion of the dielectric functions of the electron gas. For simplicity, we focus on the degenerate case (temperature much smaller than the Fermi energy ) and on the self-consistent field (or random phase) approximation where the dielectric functions are given by Lindhard theory [24,37].
A technical challenge is to take into account collisions, since we expect their rate ∼ to be comparable to . We apply results from Kliewer and Fuchs [38], Mermin [39], and Conti and Vignale [36] who combined the relaxation-time approximation with the longitudinal and transverse Lindhard functions. The same dielectric functions have been used by Reiche et al. [14]. Let us recall that collisions may involve different scenarios. Our focus is on impurity scattering that does not conserve total momentum, while carrier-carrier collisions do. Electron-phonon scattering is probably some intermediate case due to Umklapp processes [57]. These mechanisms lead to distinct temperature dependences of . For an overview of the implications for Casimir-Polder interactions, see Refs. [14,58].
We match in the following the hydrodynamic parameters to the power series for the inverse susceptibilities
where . Multiplying these expressions with , we obtain the normalized inverse conductivities given in Equations (14) and (15).
Appendix A.1. Expansion of Lindhard Functions
We collect here, for the convenience of the reader, the Lindhard formulas with the dielectric functions of the homogeneous degenerate electron gas [37]. Lindhard introduced the dimensionless variables
The longitudinal dielectric function takes the form
and the transverse is
The (natural) logarithms are to be evaluated on their principal branchs, approaching the real frequency axis from above. This can also be denoted by (hence the superscript 0 in Equations (A6) and (A8). The resulting imaginary parts appear in the domains and (and are positive there); they vanish for .
For the matching with the hydrodynamic expressions (A3) and (A4), we perform a double expansion in the Lindhard variables: small z and large u. In this limit, the imaginary parts do not play a role, and we obtain a regular power series whose first few terms are
Among the last two terms, the first one dominates if we restrict to frequencies , well justified for and a collisional width . This result is consistent with Lindhard’s Equations (3.5) and (3.10) apart from the order which has been obtained, however, by Arista and Brandt [59] in the same limit (see Table 1 there). The corresponding expansion of the transverse dielectric function yields
Lindhard’s Equation (3.19) contains a term (which vanishes in our calculations) and stops before the order . We conclude that the small parameter for corrections beyond the hydrodynamic approximation is if we focus on . Fortunately enough, they appear with relatively small numerical coefficients. Klimchitskaya and Mostepanenko [15] have also used the small parameter to add correction terms to the local dielectric function of the Drude model. Their correction is, however, of the first order and is anisotropic (the wavevector k parallel to the metal surface is used in place of q).
Appendix A.2. Including Collisions
Appendix A.2.1. Longitudinal Dielectric Function
Kliewer and Fuchs [38], Mermin [39], and Conti and Vignale [36] have constructed the collisional form of based on the requirement that the electron gas relaxes to a state defined by a shifted electrochemical potential where is computed self-consistently from the induced charge density. This argument can be carried out for a broad class of dielectric functions, and for the Lindhard function introduced above, it gives the formula
We denote by the superscript the collisional form. In the first term on the rhs, the electric susceptibility is evaluated at the complex frequency , while the second one involves the static susceptibility that is responsible for the screening of a static charge density. The latter is evaluated from the Lindhard Formula (A6) by taking the limit (approaching zero from the upper half of the complex plane), yielding
Expanding for small q, one obtains
Note that this treatment of collisions is necessary to match the zero’th order term. The quadratic term yields the complex combination spelled out in Equation (16). Its low-frequency limit arises from the static susceptibility in Equation (A12). The second term of order is again negligible compared to the one before.
Halevi [49] found his formula for the speed of longitudinal sound waves by a similar hydrodynamic argument. The present formalism provides a visco-elastic view with a splitting into elastic moduli and viscosities, a connection also made in Ref. [36]. In particular, the shear viscosity appears in the imaginary part of Halevi’s , and the frequency dispersion of the speed of sound originates entirely from the nonzero shear modulus , see Equation (A18) below.
Appendix A.2.2. Transverse Dielectric Function
To include collisions into the self-consistent field approximation, similar considerations are applied by Conti and Vignale [36]. If we assume that the total carrier momentum is not conserved (as it happens for impurity scattering), then the resulting susceptibility takes a form slightly simpler than (A12)
The power series for the comparison to the hydrodynamic form (A4) is thus
and its quadratic term yields the complex shear viscosity given in Equation (17).
It is interesting to subtract the contribution of the shear viscosity from . It turns out that only the static term survives
The bulk modulus (as expressed by the real part ) is thus determined by the static density response, as expected for a compressibility. Its frequency dependence is negligible, consistent with the remark of Ref. [36] that the relevant frequency scale is the much larger Fermi frequency . The bulk viscosity , however, vanishes: collisions do not contribute any losses when compressing the electron gas. This has been observed also for other models of the dielectric response by Conti and Vignale [36]. In particular, they went beyond the random phase approximation and included exchange correlation (xc) effects by dynamic local field factors. Apart from the self-consistent field, the Coulomb interaction between electrons is neglected when using Lindhard’s transverse dielectric function. A residual footprint of xc effects may be encoded in the electronic lifetime , however, as soon as the Lindhard functions are generalized to a collisional model.
Appendix A.2.3. Argument Based on Magnetic Charge Conservation
De Andrés et al. [50] have argued that the construction of Kliewer and Fuchs [38] for the collisional transverse dielectric function was in error because Equation (A16) could not reproduce, in the static limit, the weak diamagnetism of the electron gas. Their reasoning is based on the relation
between the relative permeability and the dielectric functions. They apply Equation (A12) with the substitution to derive a collisional permeability . The strict analogy between electric and magnetic response relies on the assumption that magnetic charges be conserved. It turns out that is for frequencies close to its static value much smaller than unity. (The spin contribution to the magnetic response would only give small corrections [37,50].) Relation (A19) then predicts that are practically the same. We obtain a complex shear viscosity
where the last term is negligible for . This is plotted in dashed gray in Figure 3. Note that the pole would yield a finite velocity for acoustic shear waves, quite unexpected for a liquid. Also the bulk viscosity [see Equation (A18)] would be nonzero in disagreement with the general observations of Ref. [36]. We thus believe that the close analogy between electric and magnetic responses put forward by de Andrés et al. [50] (magnetic charge conservation) is not warranted, at least in the low-frequency region.
References
- Adler, R.J.; Casey, B.; Jacob, O.C. Vacuum catastrophe: An elementary exposition of the cosmological constant problem. Am. J. Phys. 1995, 63, 620–626, Comment by Ovshinsky, S.R.; Fritzsche, H. Am. J. Phys. 1997, 65, 927; Reply by Ovshinsky, S.R.;Fritzsche, H. Am. J. Phys. 1997, 65, 928. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On the attraction between two perfectly conducting plates. Proc. Kon. Ned. Akad. Wet. 1948, 51, 793–795. [Google Scholar]
- Easson, D.A.; Frampton, P.H.; Smoot, G.F. Entropic accelerating universe. Phys. Lett. B 2011, 696, 273–277. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, Z.; Unruh, W.G. How the huge energy of quantum vacuum gravitates to drive the slow accelerating expansion of the Universe. Phys. Rev. D 2017, 95, 103504. [Google Scholar] [CrossRef]
- Sernelius, B.E. Fundamentals of van der Waals and Casimir Interactions; Series on Atomic, Optical, and Plasma Physics; Springer: Cham, Switzerland, 2018; Volume 102. [Google Scholar]
- Jaffe, R.L. Casimir effect and the quantum vacuum. Phys. Rev. D 2005, 72, 021301. [Google Scholar] [CrossRef]
- Chen, Y.J.; Tham, W.K.; Krause, D.E.; Lopez, D.; Fischbach, E.; Decca, R.S. Stronger Limits on Hypothetical Yukawa Interactions in the 30–8000 nm Range. Phys. Rev. Lett. 2016, 116, 221102. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L. Constraints on Theoretical Predictions beyond the Standard Model from the Casimir Effect and Some Other Tabletop Physics. Universe 2021, 7, 47. [Google Scholar] [CrossRef]
- Torgerson, J.R.; Lamoreaux, S.K. Low-frequency character of the Casimir force between metallic films. Phys. Rev. E 2004, 70, 047102. [Google Scholar] [CrossRef]
- Bimonte, G. Bohr–van Leeuwen theorem and the thermal Casimir effect for conductors. Phys. Rev. A 2009, 79, 042107. [Google Scholar] [CrossRef]
- Mostepanenko, V.M. How to confirm and exclude different models of material properties in the Casimir effect. J. Phys. Condens. Matter 2015, 27, 214013. [Google Scholar] [CrossRef][Green Version]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Recent measurements of the Casimir force: Comparison between experiment and theory. Mod. Phys. Lett. A 2020, 35, 2040007. [Google Scholar] [CrossRef]
- Henkel, C. Thermally Excited Quasiparticles in Metals, Dispersion Forces, and the Thermal Anomaly. Mod. Phys. Lett. A 2020, 35, 2040009. [Google Scholar] [CrossRef]
- Reiche, D.; Busch, K.; Intravaia, F. Quantum thermodynamics of overdamped modes in local and spatially dispersive materials. Phys. Rev. A 2020, 101, 012506. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. An alternative response to the off-shell quantum fluctuations: A step forward in resolution of the Casimir puzzle. Eur. Phys. J. C 2020, 80, 900. [Google Scholar] [CrossRef]
- Verbeeck, J.; Hens, S.; Potapov, P.; Schryvers, D. Electron Energy Loss Spectrometry. In Encyclopedia of Analytical Science, 2nd ed.; Worsfold, P., Townshend, A., Poole, C., Eds.; Elsevier: Oxford, UK, 2005; pp. 324–331. [Google Scholar] [CrossRef]
- Zangwill, A. Optical properties. In Physics at Surfaces; Cambridge University Press: Cambridge, UK, 1988; Chapter 7; pp. 163–182. [Google Scholar] [CrossRef]
- Bimonte, G.; López, D.; Decca, R.S. Isoelectronic determination of the thermal Casimir force. Phys. Rev. B 2016, 93, 184434. [Google Scholar] [CrossRef]
- Kloppstech, K.; Könne, N.; Biehs, S.A.; Rodriguez, A.W.; Worbes, L.; Hellmann, D.; Kittel, A. Giant heat transfer in the crossover regime between conduction and radiation. Nat. Commun. 2017, 8, 14475. [Google Scholar] [CrossRef]
- Cui, L.; Jeong, W.; Fernández-Hurtado, V.; Feist, J.; García-Vidal, F.J.; Cuevas, J.C.; Meyhofer, E.; Reddy, P. Study of radiative heat transfer in Ångström- and nanometre-sized gaps. Nat. Commun. 2017, 8, 14479. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Pitaevskii, L.P. Statistical Physics (Part 2), 2nd ed.; Landau and Lifshitz, Course of Theoretical Physics; Pergamon: Oxford, UK, 1980; Volume 9. [Google Scholar]
- Rytov, S.M.; Kravtsov, Y.A.; Tatarskii, V.I. Elements of Random Fields; Principles of Statistical Radiophysics; Springer: Berlin, Germany, 1989; Volume 3. [Google Scholar]
- García-Moliner, F.; Flores, F. Introduction to the Theory of Solid Surfaces; Cambridge Monographs on Physics; Cambridge University Press: Cambridge, UK, 1979. [Google Scholar]
- Dressel, M.; Grüner, G. Electrodynamics of Solids—Optical Properties of Electrons in Matter; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Sievers, A.J. Thermal radiation from metal surfaces. J. Opt. Soc. Am. 1978, 68, 1505–1516. [Google Scholar] [CrossRef]
- Intravaia, F.; Ellingsen, S.A.; Henkel, C. Casimir-Foucault interaction: Free energy and entropy at low temperature. Phys. Rev. A 2010, 82, 032504. [Google Scholar] [CrossRef]
- Jackson, J.D. Klassische Elektrodynamik; De Gruyter Studium; De Gruyter: Berlin, Germany, 2014. [Google Scholar]
- Boström, M.; Sernelius, B.E. Thermal Effects on the Casimir Force in the 0.1–5 m Range. Phys. Rev. Lett. 2000, 84, 4757–4760. [Google Scholar] [CrossRef]
- Intravaia, F.; Henkel, C. Casimir interaction from magnetically coupled eddy currents. Phys. Rev. Lett. 2009, 103, 130405. [Google Scholar] [CrossRef] [PubMed]
- Esquivel, R.; Villarreal, C.; Mochán, W.L. Exact surface impedance formulation of the Casimir force: Application to spatially dispersive metals. Phys. Rev. A 2003, 68, 052103. [Google Scholar] [CrossRef]
- Svetovoy, V.B.; Esquivel, R. The Casimir free energy in high- and low-temperature limits. J. Phys. A 2006, 39, 6777–6784. [Google Scholar] [CrossRef]
- Feibelman, P.J. Surface electromagnetic fields. Progr. Surf. Sci. 1982, 12, 287–408. [Google Scholar] [CrossRef]
- Wegner, G.; Henkel, C. Remarks about surface plasmons and their stability. arXiv 2020, arXiv:2005.03716. [Google Scholar]
- Landau, L.; Lifshitz, E. Fluid Mechanics: Volume 6, 2nd ed.; Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Laman, N.; Grischkowsky, D. Reduced conductivity in the terahertz skin-depth layer of metals. Appl. Phys. Lett. 2007, 90, 122115. [Google Scholar] [CrossRef]
- Conti, S.; Vignale, G. Elasticity of an electron liquid. Phys. Rev. B 1999, 60, 7966–7980. [Google Scholar] [CrossRef]
- Lindhard, J. On the properties of a gas of charged particles. Dan. Mat. Fys. Medd. 1954, 28, 1–57. [Google Scholar]
- Kliewer, K.L.; Fuchs, R. Lindhard Dielectric Functions with a Finite Electron Lifetime. Phys. Rev. 1969, 181, 552–558. [Google Scholar] [CrossRef]
- Mermin, N.D. Lindhard Dielectric Function in the Relaxation-Time Approximation. Phys. Rev. B 1970, 1, 2362–2363. [Google Scholar] [CrossRef]
- Decca, R.S.; Lopez, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Precise comparison of theory and new experiment for the Casimir force leads to stronger constraints on thermal quantum effects and long-range interactions. Ann. Phys. 2005, 318, 37–80. [Google Scholar] [CrossRef]
- Buhmann, S.Y. Dispersion Forces I—Macroscopic Quantum Electrodynamics and Ground-State Casimir, Casimir–Polder and van der Waals Forces; Springer Tracts in Modern Physics; Springer: Heidelberg, Germany, 2012; Volume 247. [Google Scholar] [CrossRef]
- Buhmann, S.Y. Dispersion Forces II—Many-Body Effects, Excited Atoms, Finite Temperature and Quantum Friction; Springer Tracts in Modern Physics; Springer: Heidelberg, Germany, 2012; Volume 247. [Google Scholar] [CrossRef]
- Volokitin, A.I.; Persson, B.N. Electromagnetic Fluctuations at the Nanoscale; NanoScience and Technology; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Lifshitz, E.M. The Theory of Molecular Attractive Forces between Solids. Sov. Phys. JETP 1956, 2, 73–83, [J. Exper. Theoret. Phys. USSR 1955, 29, 94]. [Google Scholar]
- Polder, D.; Van Hove, M. Theory of Radiative Heat Transfer between Closely Spaced Bodies. Phys. Rev. B 1971, 4, 3303–3314. [Google Scholar] [CrossRef]
- Loomis, J.J.; Maris, H.J. Theory of heat transfer by evanescent electromagnetic waves. Phys. Rev. B 1994, 50, 18517–18524. [Google Scholar] [CrossRef]
- Eckhardt, W. First and second fluctuation-dissipation-theorem in electromagnetic fluctuation theory. Opt. Commun. 1982, 41, 305–309. [Google Scholar] [CrossRef]
- Ancona, M.G. Hydrodynamic Models of Semiconductor Electron Transport at High Fields. VLSI Des. 1995, 3, 085107. [Google Scholar] [CrossRef]
- Halevi, P. Hydrodynamic model for the degenerate free-electron gas: Generalization to arbitrary frequencies. Phys. Rev. B 1995, 51, 7497–7499. [Google Scholar] [CrossRef] [PubMed]
- De Andrés, P.; Monreal, R.; Flores, F. Relaxation-time effects in the transverse dielectric function and the electromagnetic properties of metallic surfaces and small particles. Phys. Rev. B 1986, 34, 7365–7366. [Google Scholar] [CrossRef]
- Bedeaux, D.; Vlieger, J. Optical Properties of Surfaces; Imperial College Press: London, UK, 2002. [Google Scholar]
- Nayfeh, A.H. Introduction to Perturbation Techniques; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers; International Series in Pure and Applied Mathematics; McGraw-Hill Inc.: New York, NY, USA, 1978. [Google Scholar]
- Mortensen, N.A.; Gonçalves, P.A.D.; Shuklin, F.A.; Cox, J.D.; Tserkezis, C.; Ichikawa, M.; Wolff, C. Surface-response functions obtained from equilibrium electron-density profiles. arXiv 2021, arXiv:2103.00162. [Google Scholar]
- Sipe, J.E. Bulk-selvedge coupling theory for the optical properties of surfaces. Phys. Rev. B 1980, 22, 1589–1599. [Google Scholar] [CrossRef]
- Ford, G.W.; Weber, W.H. Electromagnetic interactions of molecules with metal surfaces. Phys. Rep. 1984, 113, 195–287. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders: Philadelphia, PA, USA, 1976. [Google Scholar]
- Bordag, M. Casimir and Casimir-Polder forces with dissipation from first principles. Phys. Rev. A 2017, 96, 062504. [Google Scholar] [CrossRef]
- Arista, N.R.; Brandt, W. Dielectric response of quantum plasmas in thermal equilibrium. Phys. Rev. A 1984, 29, 1471–1480. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).