Superfluid Neutron Matter with a Twist
Abstract
1. Introduction
2. Superfluid Neutron Matter: A Strongly Interacting Fermionic System
2.1. The Variety of Approaches in Superfluid Neutron Matter
2.2. The BCS and PBCS Theories for Neutron Matter
2.2.1. Even-Particle-Number Superfluid
2.2.2. Odd-Particle-Number Systems
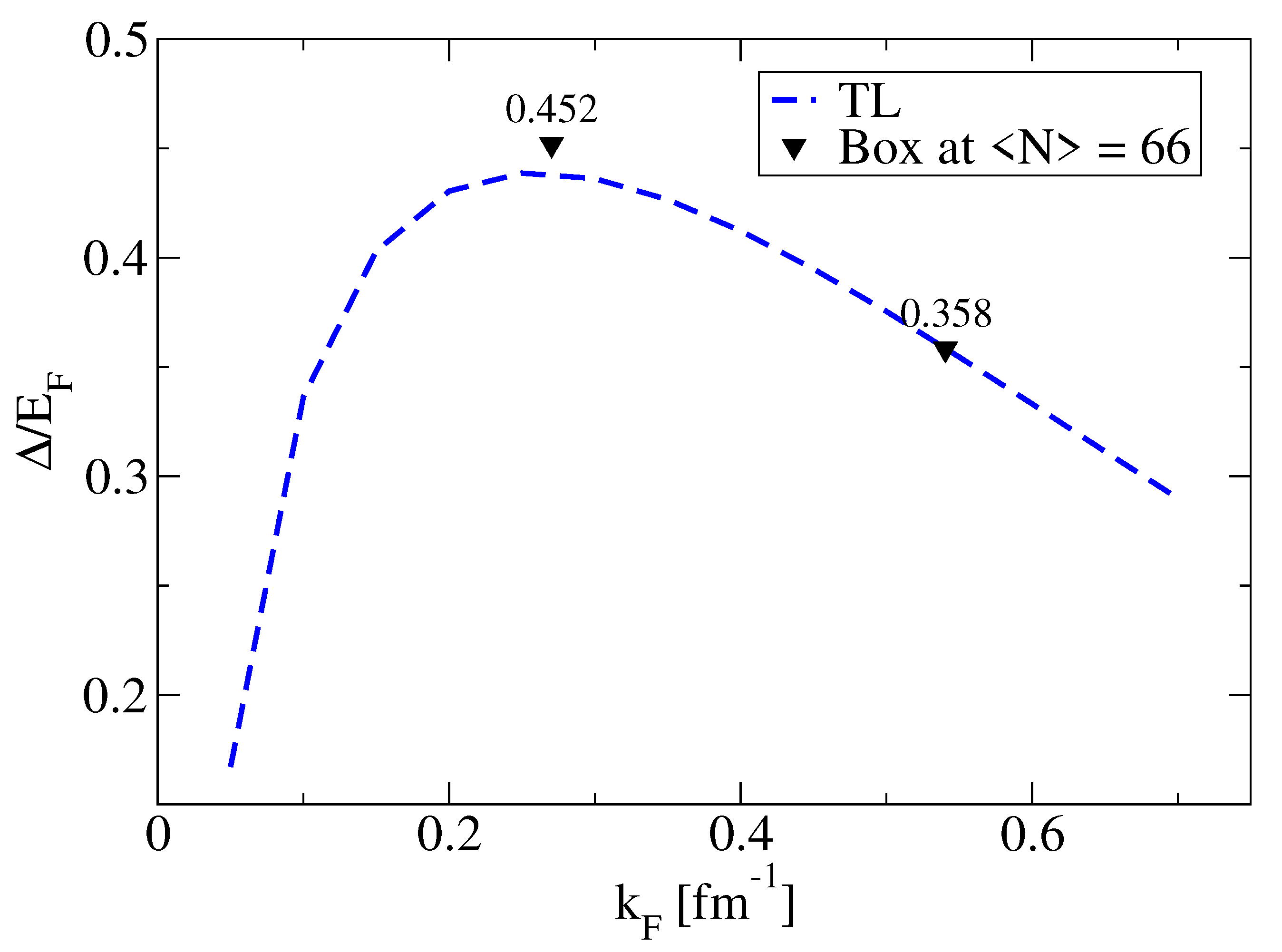
2.2.3. The Thermodynamic Limit
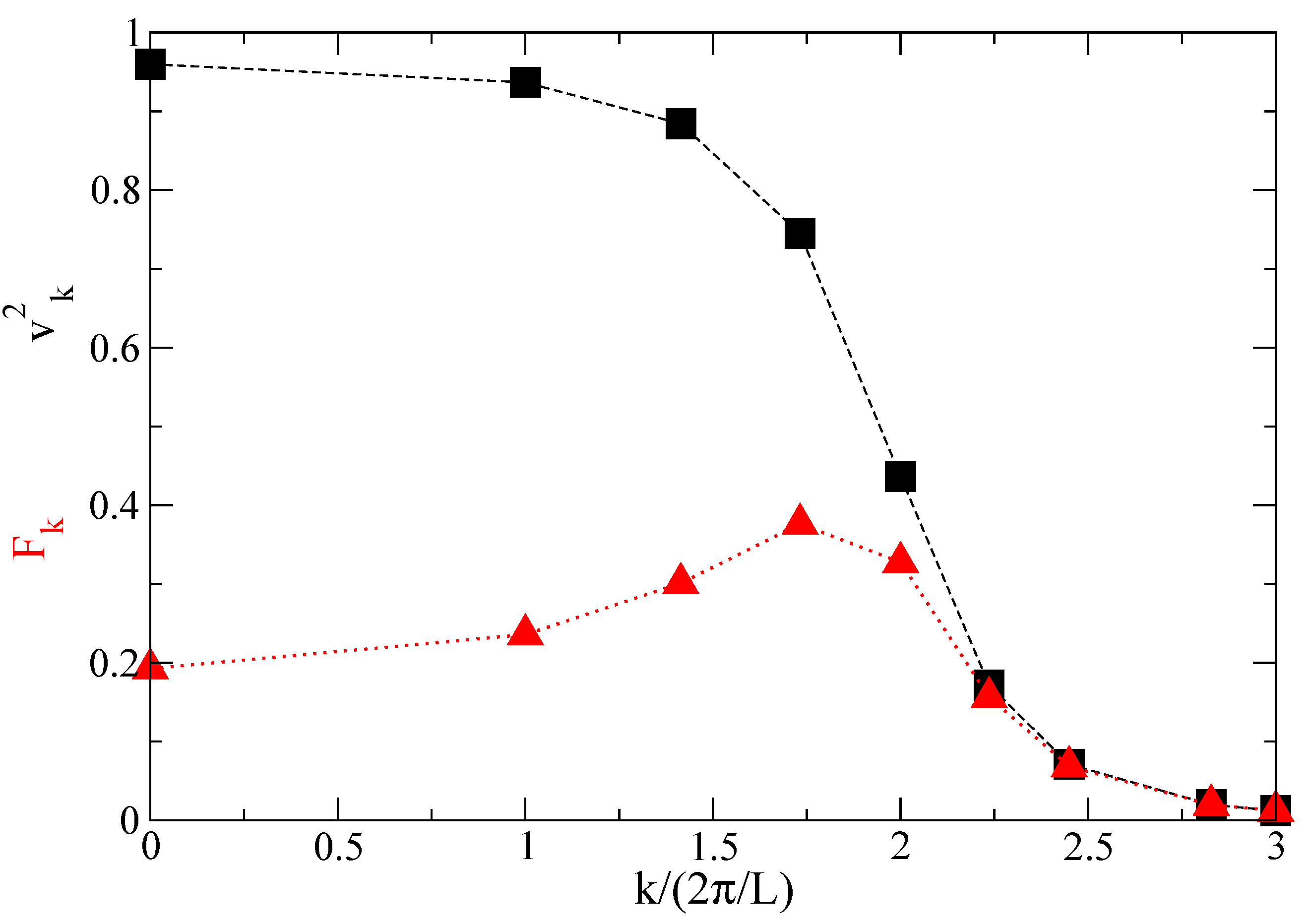
2.2.4. The Solution of the BCS Gap Equations
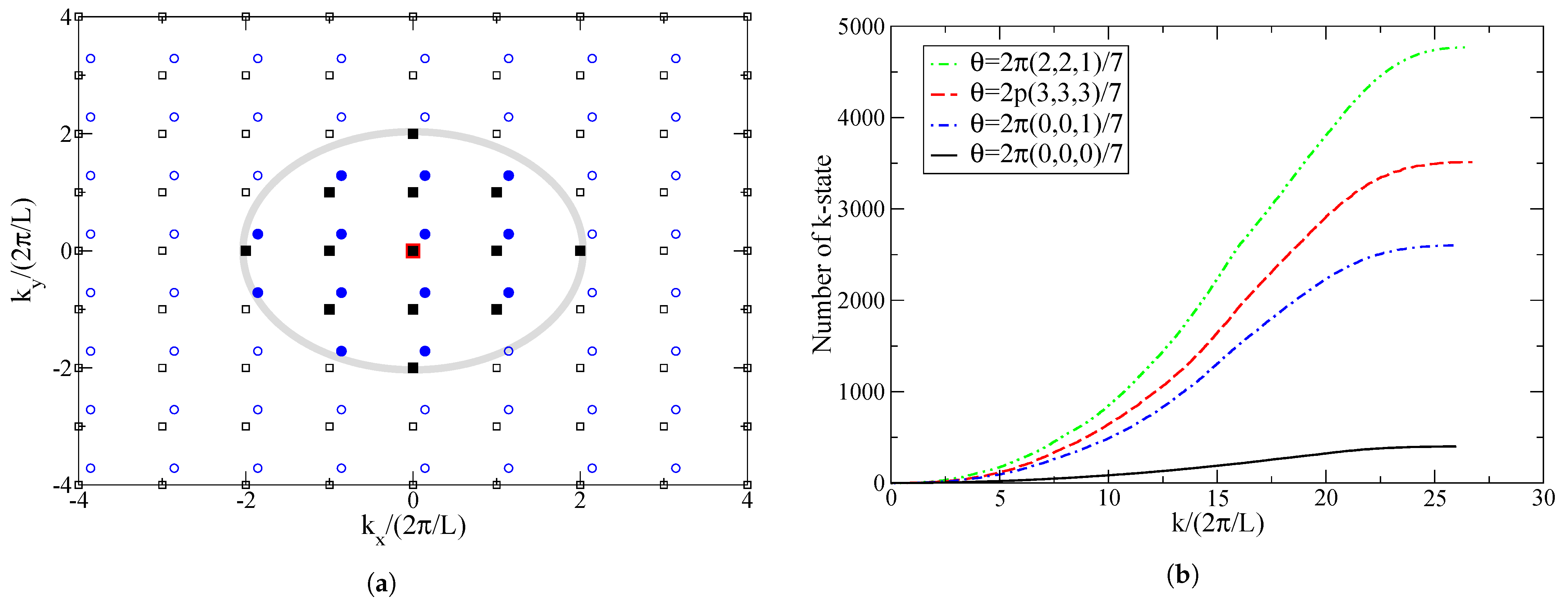
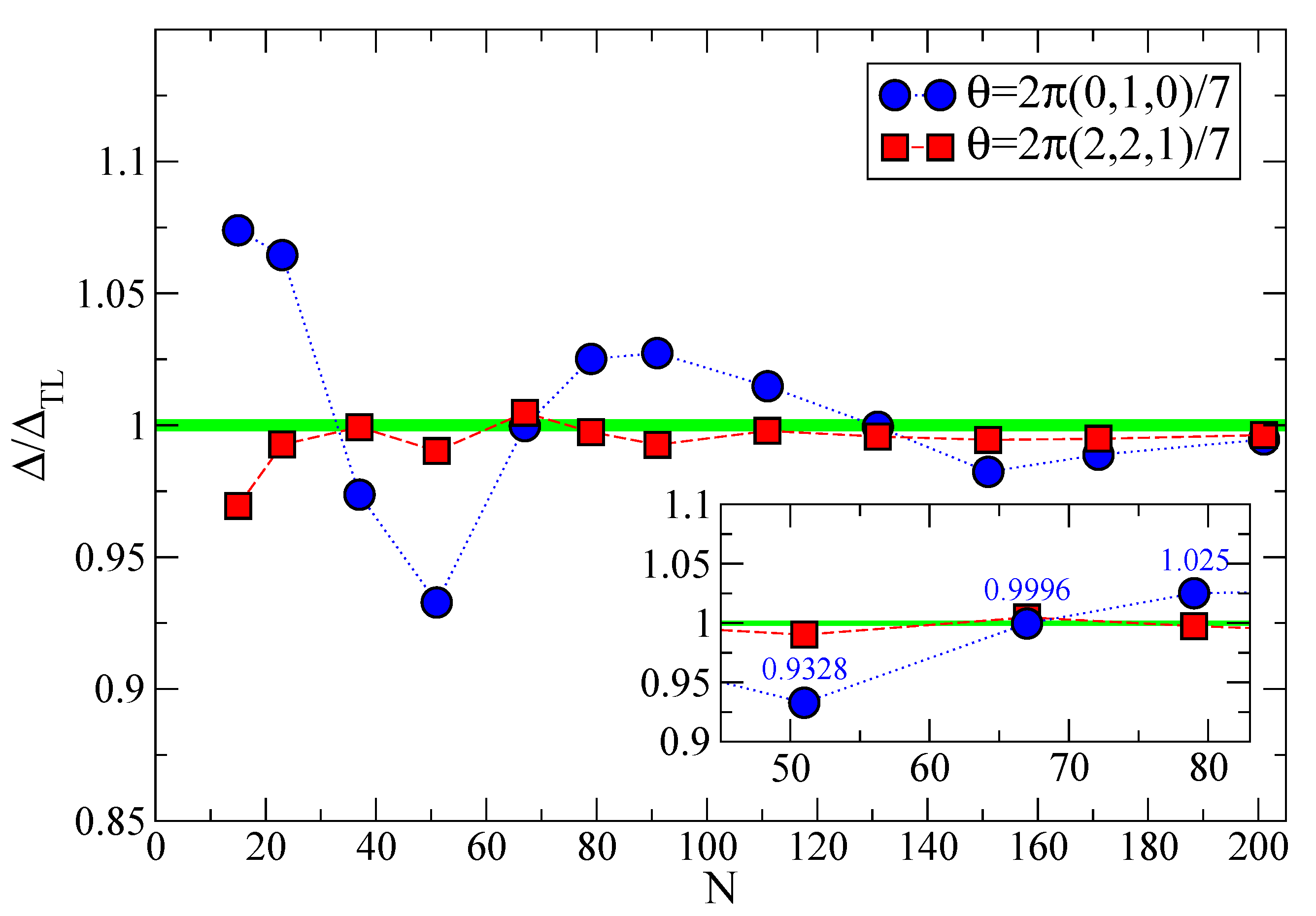
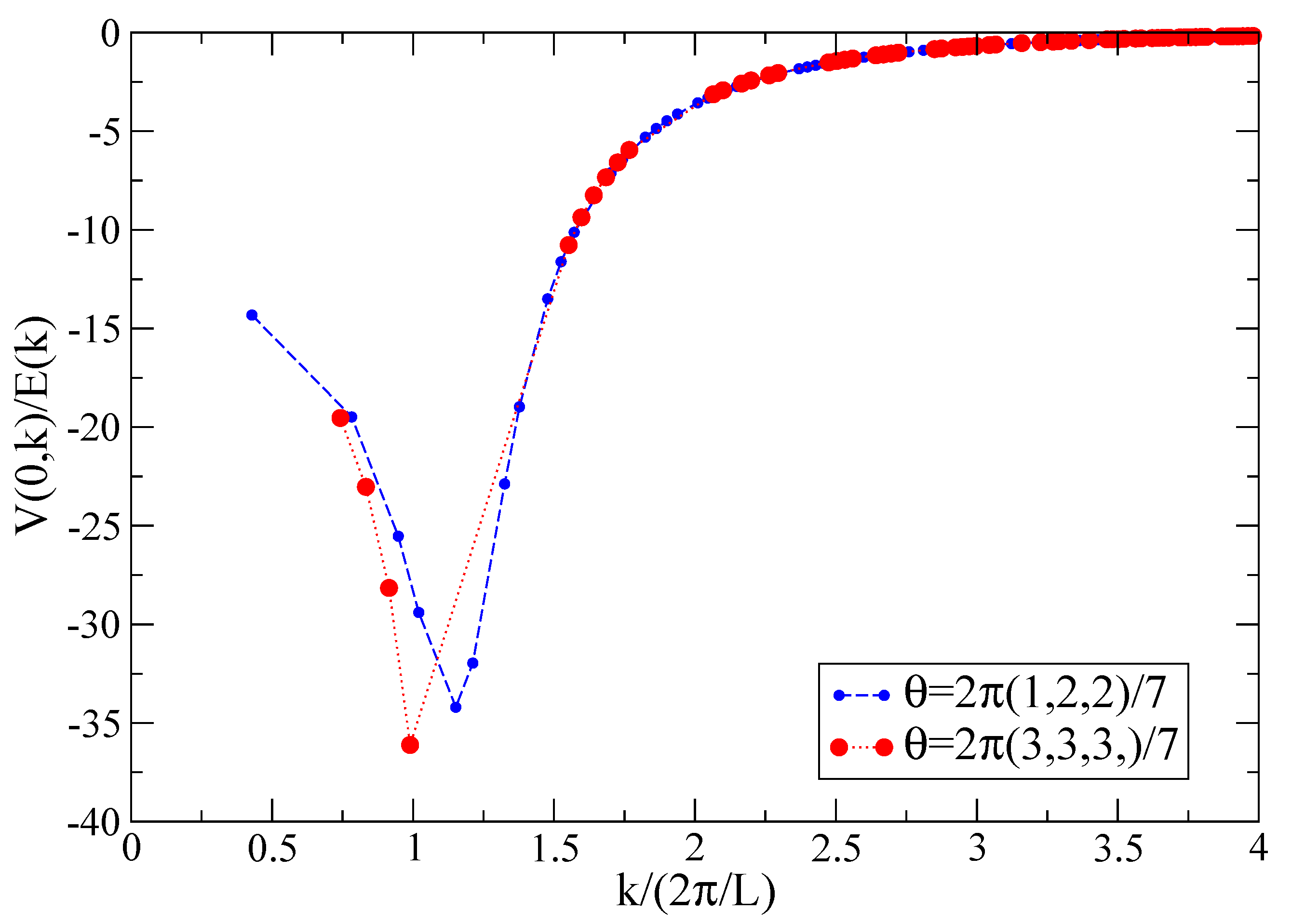
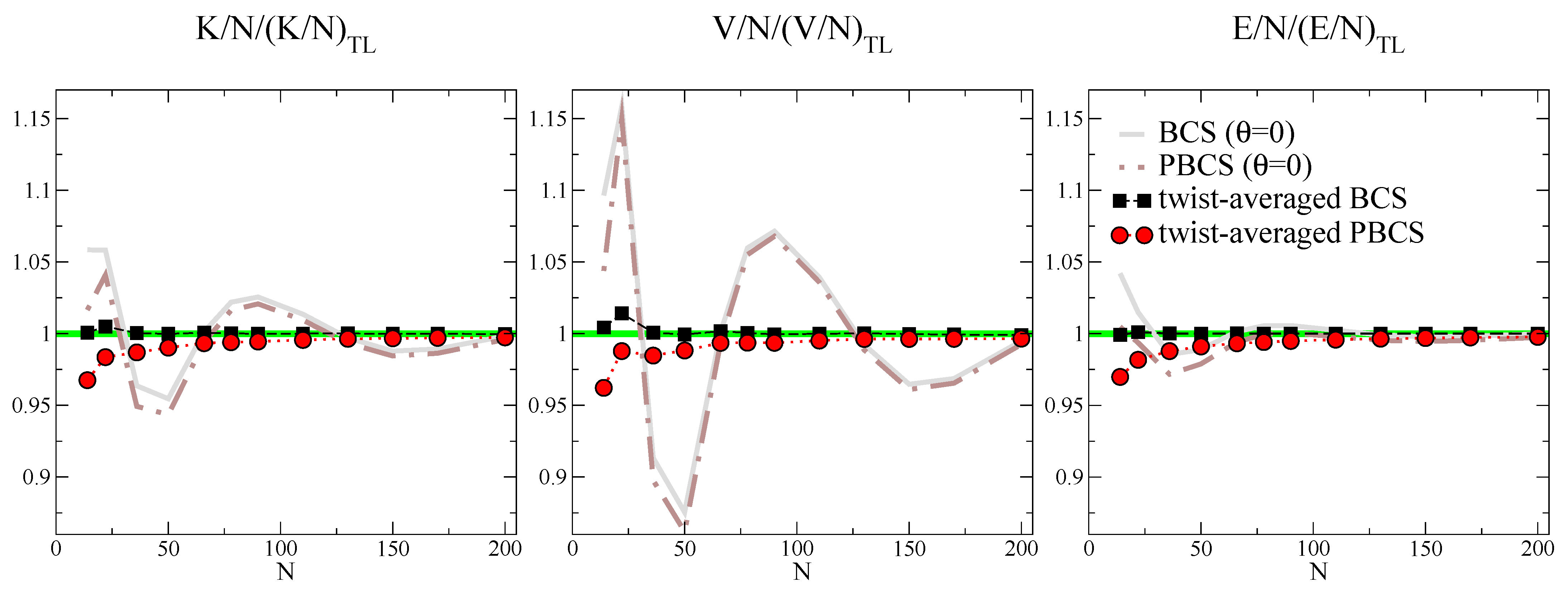
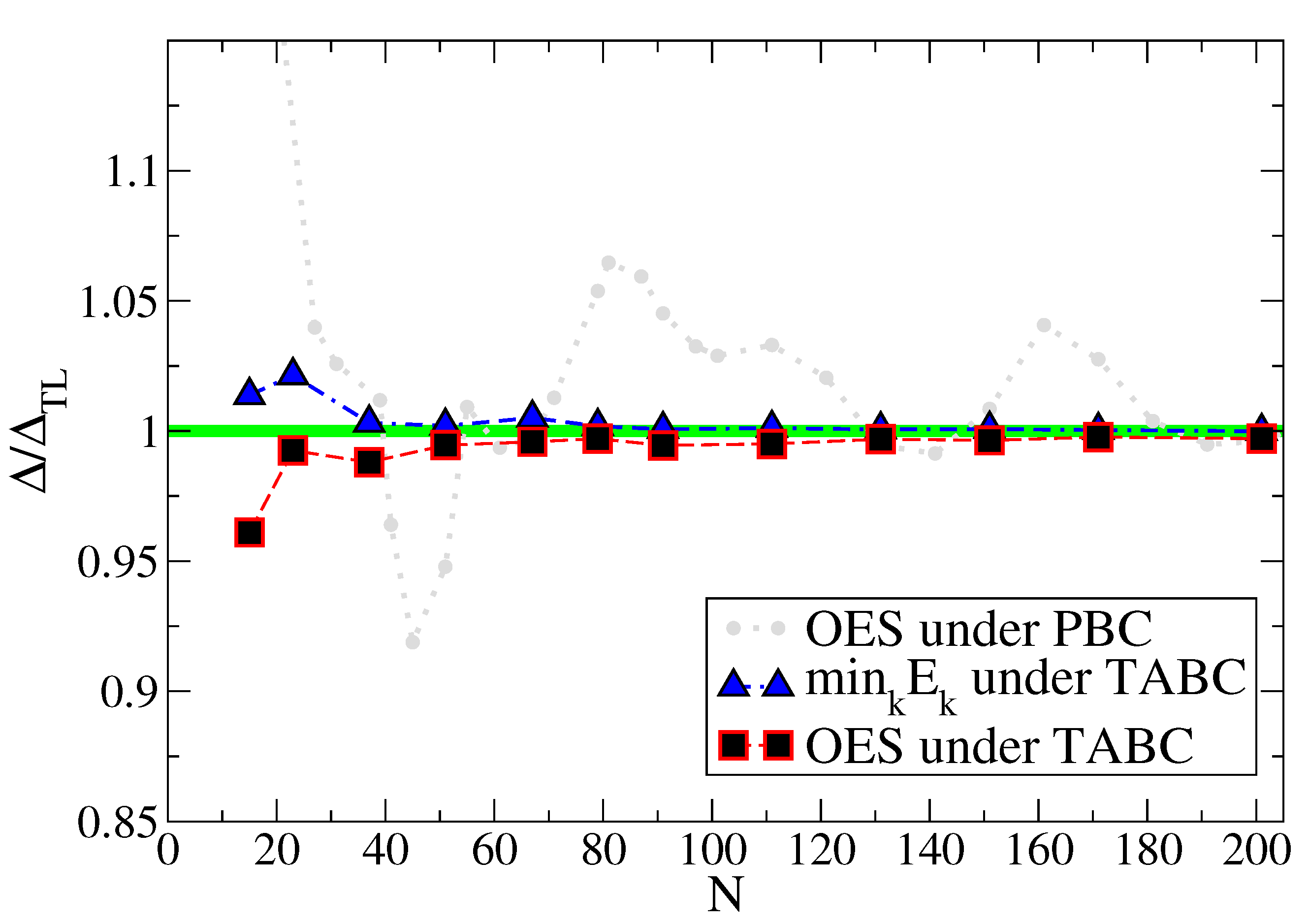
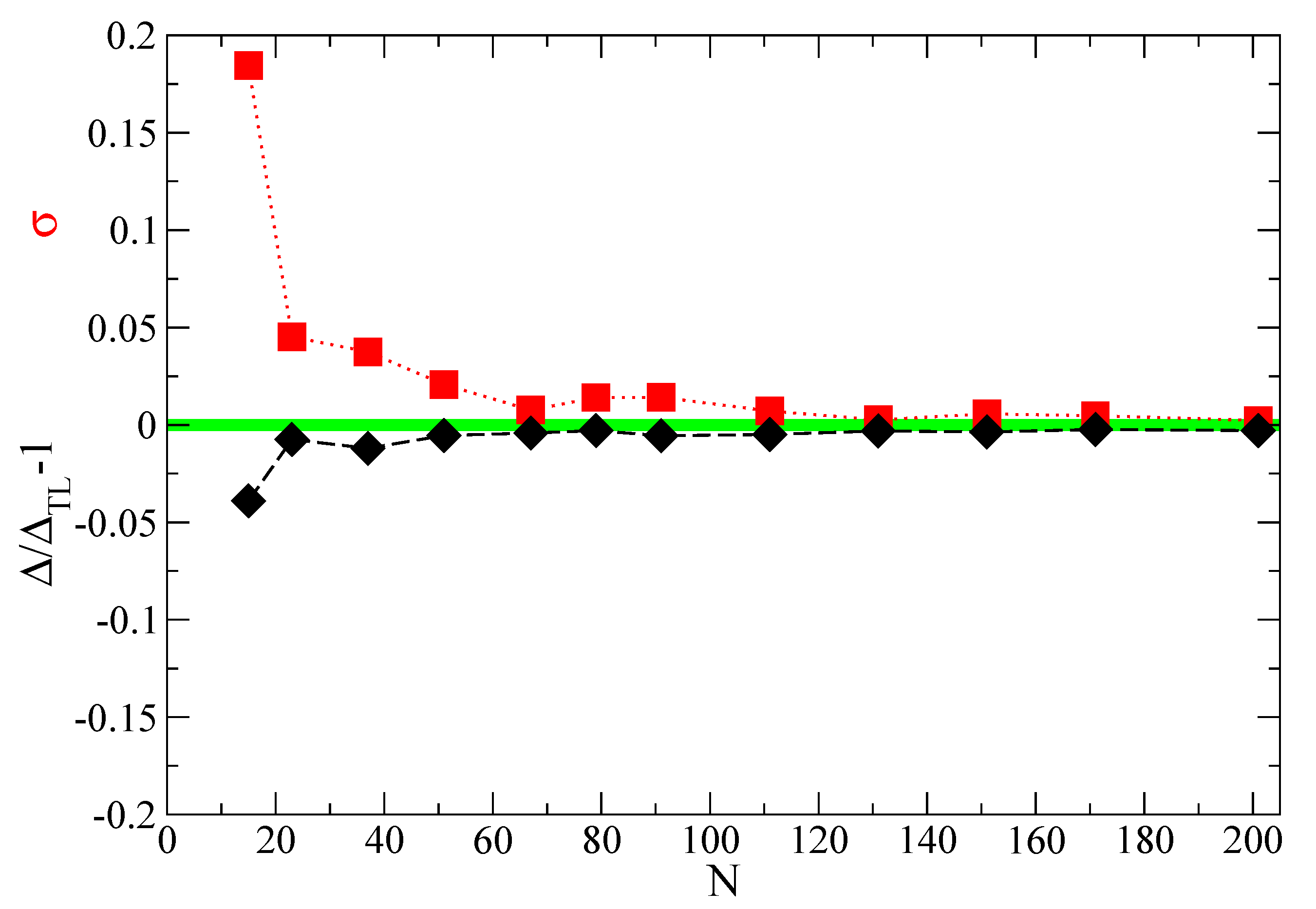
3. Finite-Size Effects and Twisted Boundary Conditions
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NS | Neutron star |
| NN | Neutron–neutron |
| NM | Neutron matter |
| BCS | Bardeen–Cooper–Schrieffer |
| OES | Odd–even staggering |
| PBCS | Projected BCS |
| FBCS | Full BCS |
| RG | Renormalization group |
| QMC | Quantum Monte Carlo |
| TL | Thermodynamic Limit |
| PT | Pöschl–Teller |
| CBF | Correlated basis functions |
| FSE | Finite-size effect |
| BC | Boundary condition |
| TBC | Twisted boundary condition |
| TABC | Twist-averaged boundary condition |
References
- Landau, L.D. Phys. Z. On the theory of stars. Phys. Z. Sowjetunion 1932, 1, 152. [Google Scholar]
- Yakovlev, D.G.; Haensel, P.; Baym, G.; Pethick, C. Lev Landau and the concept of neutron stars. Phys. Uspekhi 2013, 56, 289. [Google Scholar] [CrossRef]
- Chadwick, J. Possible existence of a neutron. Nature 1932, 129, 312. [Google Scholar] [CrossRef]
- Baade, W.; Zwicky, F. Remarks on super-novae and cosmic rays. Phys. Rev. 1934, 45, 138. [Google Scholar]
- Baade, W.; Zwicky, F. On super-novae. Proc. Natl. Acad. Sci. USA 1934, 20, 254. [Google Scholar] [CrossRef]
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a rapidly pulsating radio source. Nature 1968, 217, 709–713. [Google Scholar] [CrossRef]
- Gold, T. Rotating neutron stars and the nature of pulsars. Nature 1969, 221, 25–27. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B.R.; Pines, D. Possible analogy between the excitation spectra of nuclei and those of the superconducting metallic state. Phys. Rev. 1958, 110, 936. [Google Scholar] [CrossRef]
- Migdal, A.B. Superfluidity and the moments of inertia of nuclei. Nucl. Phys. 1959, 13, 655–674. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Durel, D.; Urban, M. BCS-BEC Crossover Effects and Pseudogap in Neutron Matter. Universe 2020, 6, 208. [Google Scholar] [CrossRef]
- Shelley, M.; Pastore, A. Comparison between the Thomas-Fermi and Hartree-Fock-Bogoliubov Methods in the Inner Crust of a Neutron Star: The Role of Pairing Correlations. Universe 2020, 6, 206. [Google Scholar] [CrossRef]
- Wei, J.B.; Burgio, F.; Schulze, H.J. Nuclear Pairing Gaps and Neutron Star Cooling. Universe 2020, 6, 115. [Google Scholar] [CrossRef]
- Kobyakov, D.; Pethick, C.J. Towards a metallurgy of neutron star crusts. Phys. Rev. Lett. 2014, 112, 112504. [Google Scholar] [CrossRef] [PubMed]
- Kobyakov, D.; Pethick, C.J. Nucleus-nucleus interactions in the inner crust of neutron stars. Phys. Rev. C 2016, 94, 055806. [Google Scholar] [CrossRef]
- Blaschke, D.; Chamel, N. Phases of dense matter in compact stars. Astrophys. Space Sci. Libr. 2018, 457, 337–400. [Google Scholar]
- Chamel, N.; Fantina, A.F.; Zdunik, J.L.; Haensel, P. Neutron drip transition in accreting and nonaccreting neutron star crusts. Phys. Rev. C 2015, 91, 055803. [Google Scholar] [CrossRef]
- Stoks, V.G.J.; Klomp, R.A.M.; Rentmeester, M.C.M.; Swart, J.J. Partial-wave analysis of all nucleon-nucleon scattering data below 350 MeV. Phys. Rev. C 1993, 48, 792–815. [Google Scholar] [CrossRef]
- Pastore, A.; Margueron, J.; Schuck, P.; Viñas, X. Pairing in exotic neutron-rich nuclei near the drip line and in the crust of neutron stars. Phys. Rev. C 2013, 88, 034314. [Google Scholar] [CrossRef]
- Sedrakian, A.; Clark, J.W. Superfluidity in nuclear systems and neutron stars. Eur. Phys. J. A 2019, 55, 167. [Google Scholar] [CrossRef]
- Martin, N.; Urban, M. Collective modes in a superfluid neutron gas within the quasiparticle random-phase approximation. Phys. Rev. C 2014, 90, 065805. [Google Scholar] [CrossRef]
- Martin, N.; Urban, M. Superfluid hydrodynamics in the inner crust of neutron stars. Phys. Rev. C 2016, 94, 065801. [Google Scholar] [CrossRef]
- Chamel, N.; Goriely, S.; Pearson, J.M.; Onsi, M. Unified description of neutron superfluidity in the neutron-star crust with analogy to anisotropic multiband BCS superconductors. Phys. Rev. C 2010, 81, 045804. [Google Scholar] [CrossRef]
- Chamel, N.; Page, D.; Reddy, S. Low-energy collective excitations in the neutron star inner crust. Phys. Rev. C 2013, 87, 035803. [Google Scholar] [CrossRef]
- Chamel, N. Entrainment in Superfluid Neutron-Star Crusts: Hydrodynamic Description and Microscopic Origin. J. Low Temp. Phys. 2017, 189, 328–360. [Google Scholar] [CrossRef]
- Inakura, T.; Matsuo, M. Anderson-Bogoliubov phonons in the inner crust of neutron stars: Dipole excitation in a spherical Wigner-Seitz cell. Phys. Rev. C 2017, 96, 025806. [Google Scholar] [CrossRef]
- Inakura, T.; Matsuo, M. Coexistence of Anderson-Bogoliubov phonon and quadrupole cluster vibration in the inner crust of neutron stars. Phys. Rev. C 2019, 99, 045801. [Google Scholar] [CrossRef]
- Durel, D.; Urban, M. Long-wavelength phonons in the crystalline and pasta phases of neutron-star crusts. Phys. Rev. C 2018, 97, 065805. [Google Scholar] [CrossRef]
- Watanabe, G.; Pethick, C.J. Superfluid density of neutrons in the inner crust of neutron stars: New life for pulsar glitch models. Phys. Rev. Lett. 2017, 119, 062701. [Google Scholar] [CrossRef]
- Baym, G.A.; Bethe, H.A.; Pethick, C.J. Neutron star matter. Nucl. Phys. A 1971, 175, 225–271. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455. [Google Scholar] [CrossRef]
- Takatsuka, T.; Tamagaki, R. Superfluidity in neutron star matter and symmetric nuclear matter. Prog. Theor. Phys. Suppl. 1993, 112, 27–65. [Google Scholar] [CrossRef]
- Pethick, C.J.; Schaefer, T.; Schwenk, A. Bose-Einstein condensates in neutron stars. arXiv 2015, arXiv:1507.05839. [Google Scholar]
- Yakovlev, D.G.; Pethick, C.J. Neutron star cooling. Ann. Rev. Astron. Astrophys. 2004, 42, 169–210. [Google Scholar] [CrossRef]
- Page, D.; Prakash, M.; Lattimer, J.M.; Steiner, A.W. Rapid cooling of the neutron star in Cassiopeia A triggered by neutron superfluidity in dense matter. Phys. Rev. Lett. 2011, 106, 081101. [Google Scholar] [CrossRef] [PubMed]
- Page, D.; Reddy, S. Neutron Star Crust; Bertulani, C., Piekarewicz, J., Eds.; Nova Science Publishers: New York, NY, USA, 2012. [Google Scholar]
- Haskell, B.; Melatos, A. Models of Pulsar Glitches. Int. J. Mod. Phys. D 2015, 24, 1530008. [Google Scholar] [CrossRef]
- Andersson, N. A Superfluid Perspective on Neutron Star Dynamics. Universe 2021, 7, 17. [Google Scholar] [CrossRef]
- Gandolfi, S.; Illarionov, A.Y.; Fantoni, S.; Pederiva, F.; Schmidt, K.E. Equation of state of superfluid neutron matter and the calculation of the 1S0 pairing gap. Phys. Rev. Lett. 2008, 101, 132501. [Google Scholar] [CrossRef]
- Sedrakian, A. Axion cooling of neutron stars. Phys. Rev. D 2016, 93, 065044. [Google Scholar] [CrossRef]
- Dean, D.J.; Hjorth-Jensen, M. Pairing in nuclear systems: From neutron stars to finite nuclei. Rev. Mod. Phys. 2003, 75, 607. [Google Scholar] [CrossRef]
- Bertsch, G.F. Recent Progress in Many-body Theories. In Proceedings of the Tenth International Conference on Recent Progress in Many-Body Theories, Seattle, WA, USA, 10–15 September 1999. [Google Scholar]
- Baker, G.A., Jr. Neutron matter model. Phys. Rev. C 1999, 60, 054311. [Google Scholar] [CrossRef]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215. [Google Scholar] [CrossRef]
- Strinati, G.; Pieri, P.; Röpke, G.; Schuck, P.; Urban, M. The BCS–BEC crossover: From ultra-cold Fermi gases to nuclear systems. Phys. Rep. 2018, 738, 1–76. [Google Scholar] [CrossRef]
- Carlson, J.; Chang, S.-Y.; Pandharipande, V.R.; Schmidt, K.E. Superfluid Fermi gases with large scattering length. Phys. Rev. Lett. 2003, 91, 050401. [Google Scholar] [CrossRef] [PubMed]
- Heiselberg, H. Fermi systems with long scattering lengths. Phys. Rev. A 2001, 63, 043606. [Google Scholar] [CrossRef]
- Sà de Melo, C.A.R.; Randeria, M.; Engelbrecht, J.R. Crossover from BCS to Bose superconductivity: Transition temperature and time-dependent Ginzburg-Landau theory. Phys. Rev. Lett. 1993, 71, 3202. [Google Scholar] [CrossRef]
- Gezerlis, A.; Carlson, J. Strongly paired fermions: Cold atoms and neutron matter. Phys. Rev. C 2008, 77, 032801. [Google Scholar] [CrossRef]
- Regal, C.; Ticknor, C.; Bohn, J.L.; Jin, D.S. Creation of ultracold molecules from a Fermi gas of atoms. Nature 2003, 424, 47–50. [Google Scholar] [CrossRef]
- Bourdel, T.; Cubizolles, J.; Khaykovich, L.; Magalhães, K.M.F.; Kokkelmans, S.J.J.M.F.; Shlyapnikov, G.V.; Salomon, C. Measurement of the Interaction Energy near a Feshbach Resonance in a 6Li Fermi Gas. Phys. Rev. Lett. 2003, 91, 020402. [Google Scholar] [CrossRef]
- Tajima, H. Generalized Crossover in Interacting Fermions within the Low-Energy Expansion. J. Phys. Soc. Jpn. 2019, 88, 093001. [Google Scholar] [CrossRef]
- Regal, C.A.; Greiner, M.; Jin, D.S. Observation of resonance condensation of fermionic atom pairs. Phys. Rev. Lett. 2004, 92, 040403. [Google Scholar] [CrossRef]
- Bartenstein, M.; Altmeyer, A.; Riedl, S.; Jochim, S.; Chin, C.; Denschlag, J.H.; Grimm, R. Crossover from a Molecular Bose-Einstein Condensate to a Degenerate Fermi Gas. Phys. Rev. Lett. 2004, 92, 120401. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225. [Google Scholar] [CrossRef]
- Partridge, G.B.; Strecker, K.E.; Kamar, R.I.; Jack, M.W.; Hulet, R.G. Molecular probe of pairing in the BEC-BCS crossover. Phys. Rev. Lett. 2005, 95, 020404. [Google Scholar] [CrossRef] [PubMed]
- Gandolfi, S.; Gezerlis, A.; Carlson, J. Neutron matter from low to high density. Annu. Rev. Nucl. Part. Sci. 2015, 65, 303–328. [Google Scholar] [CrossRef]
- Gezerlis, A.; Pethick, C.J.; Schwenk, A. Novel Superfluids: Volume 2; International Series of Monographs on Physics; Bennemann, K.-H., Ketterson, J.B., Eds.; Oxford University Press: Oxford, UK, 2014; Volume 157. [Google Scholar]
- Hebeler, K.; Schwenk, A.; Friman, B. Dependence of the BCS 1S0 superfluid pairing gap on nuclear interactions. Phys. Lett. B 2007, 648, 176–180. [Google Scholar] [CrossRef][Green Version]
- Gezerlis, A.; Carlson, J. Low-density neutron matter. Phys. Rev. C 2010, 81, 025803. [Google Scholar] [CrossRef]
- Schulze, H.-J.; Polls, A.; Ramos, A. Pairing with polarization effects in low-density neutron matter. Phys. Rev. C 2001, 63, 044310. [Google Scholar] [CrossRef]
- Gorkov, L.P.; Melik-Barkhudarov, T.K. Contribution to the theory of superfluidity in an imperfect Fermi gas. JETP 1961, 40, 1452. [Google Scholar]
- Ding, D.; Rios, A.; Dussan, H.; Dickhoff, W.H.; Witte, S.J.; Carbone, A.; Polls, A. Publisher’s Note: Pairing in high-density neutron matter including short-and long-range correlations. Phys. Rev. C 2016, 94, 029901. [Google Scholar] [CrossRef]
- Cao, L.G.; Lombardo, U.; Schuck, P. Screening effects in superfluid nuclear and neutron matter within Brueckner theory. Phys. Rev. C 2006, 74, 064301. [Google Scholar] [CrossRef]
- Schwenk, A.; Friman, B.; Brown, G.E. Renormalization group approach to neutron matter: Quasiparticle interactions, superfluid gaps and the equation of state. Nucl. Phys. A 2003, 713, 191–216. [Google Scholar] [CrossRef]
- Wambach, J.; Ainsworth, T.; Pines, D. Quasiparticle interactions in neutron matter for applications in neutron stars. Nucl. Phys. A 1993, 555, 128–150. [Google Scholar] [CrossRef]
- Pavlou, G.E.; Mavrommatis, E.; Moustakidis, C.; Clark, J.W. Microscopic study of 1S0 superfluidity in dilute neutron matter. Eur. Phys. J. A 2017, 53, 96. [Google Scholar] [CrossRef]
- Maurizio, S.; Holt, J.W.; Finelli, P. Nuclear pairing from microscopic forces: Singlet channels and higher-partial waves. Phys. Rev. C 2014, 90, 044003. [Google Scholar] [CrossRef]
- Foulkes, W.M.C.; Mitas, L.; Needs, R.J.; Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 2001, 73, 33. [Google Scholar] [CrossRef]
- Machleidt, R.; Sammarruca, F.; Song, Y. Nonlocal nature of the nuclear force and its impact on nuclear structure. Phys. Rev. C 1996, 53, R1483. [Google Scholar] [CrossRef]
- Stoks, V.G.J.; Klomp, R.A.M.; Terheggen, C.P.F.; de Swart, J.J. Construction of high-quality NN potential models. Phys. Rev. C 1994, 49, 2950. [Google Scholar] [CrossRef]
- Gezerlis, A.; Tews, I.; Epelbaum, E.; Freunek, M.; Gandolfi, S.; Hebeler, K.; Nogga, A.; Schwenk, A. Local chiral effective field theory interactions and quantum Monte Carlo applications. Phys. Rev. C 2014, 90, 054323. [Google Scholar] [CrossRef]
- Duguet, T.; Bonche, P.; Heenen, P.-H.; Meyer, J. Pairing correlations. II. Microscopic analysis of odd-even mass staggering in nuclei. Phys. Rev. C 2001, 65, 014311. [Google Scholar] [CrossRef]
- Palkanoglou, G.; Diakonos, F.K.; Gezerlis, A. From odd-even staggering to the pairing gap in neutron matter. Phys. Rev. C 2020, 102, 064324. [Google Scholar] [CrossRef]
- Dietrich, K.; Mang, H.J.; Pradal, J.H. Conservation of particle number in the nuclear pairing model. Phys. Rev. 1964, 135, B22. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many Body Problem; Springer: New York, NY, USA, 1980. [Google Scholar]
- Baldereschi, A. Mean-value point in the Brillouin zone. Phys. Rev. B 1973, 7, 5212. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Gros, C. The boundary condition integration technique: Results for the Hubbard model in 1D and 2D. Z. Phys. B 1992, 86, 359–365. [Google Scholar] [CrossRef]
- Gammel, J.T.; Campbell, D.K.; Loh, E.Y., Jr. Extracting infinite system properties from finite size clusters: “phase randomization/boundary condition averaging”. Synth. Met. 1993, 57, 4437–4442. [Google Scholar] [CrossRef]
- Hagen, G.; Papenbrock, T.; Ekström, A.; Wendt, K.A.; Baardsen, G.; Gandolfi, S.; Hjorth-Jensen, M.; Horowitz, C.J. Coupled-cluster calculations of nucleonic matter. Phys. Rev. C 2014, 89, 014319. [Google Scholar] [CrossRef]
- Schuetrumpf, B.; Zhang, C.; Nazarewicz, W. Time-dependent density functional theory with twist-averaged boundary conditions. Phys. Rev. C 2016, 93, 054304. [Google Scholar] [CrossRef]
- Byers, N.; Yang, C.N. Theoretical considerations concerning quantized magnetic flux in superconducting cylinders. Phys. Rev. Lett. 1961, 7, 46. [Google Scholar] [CrossRef]
- Lin, C.; Zong, F.H.; Ceperley, D.M. Twist-averaged boundary conditions in continuum quantum Monte Carlo algorithms. Phys. Rev. E 2001, 64, 016702. [Google Scholar] [CrossRef]
- Buraczynski, M.; Gezerlis, A. Static response of neutron matter. Phys. Rev. Lett. 2016, 116, 152501. [Google Scholar] [CrossRef]
- Buraczynski, M.; Martinello, S.; Gezerlis, A. Satisfying the compressibility sum rule in neutron matter. arXiv 2020, arXiv:2007.06589. [Google Scholar]
- Perot, L.; Chamel, N.; Sourie, A. Role of the crust in the tidal deformability of a neutron star within a unified treatment of dense matter. Phys. Rev. C 2020, 101, 015806. [Google Scholar] [CrossRef]
- Perot, L.; Chamel, N.; Sourie, A. Role of the symmetry energy and the neutron-matter stiffness on the tidal deformability of a neutron star with unified equations of state. Phys. Rev. C 2019, 100, 035801. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palkanoglou, G.; Gezerlis, A. Superfluid Neutron Matter with a Twist. Universe 2021, 7, 24. https://doi.org/10.3390/universe7020024
Palkanoglou G, Gezerlis A. Superfluid Neutron Matter with a Twist. Universe. 2021; 7(2):24. https://doi.org/10.3390/universe7020024
Chicago/Turabian StylePalkanoglou, Georgios, and Alexandros Gezerlis. 2021. "Superfluid Neutron Matter with a Twist" Universe 7, no. 2: 24. https://doi.org/10.3390/universe7020024
APA StylePalkanoglou, G., & Gezerlis, A. (2021). Superfluid Neutron Matter with a Twist. Universe, 7(2), 24. https://doi.org/10.3390/universe7020024






