Abstract
It was conjectured by Maldacena, Shenker and Stanford that the classical chaos can be diagnosed in thermal quantum systems by using an out-of-time-order correlation function. The Artin dynamical system defined on the fundamental region of the modular group SL(2,Z) represents a well defined example of a highly chaotic dynamical system in its classical regime. We investigated the influence of the classical chaotic behaviour on the quantum–mechanical properties of the Artin system calculating the corresponding out-of-time-order thermal quantum–mechanical correlation functions. We demonstrated that the two- and four-point correlation functions of the Liouiville-like operators decay exponentially with temperature dependent exponents and that the square of the commutator of the Liouiville-like operators separated in time grows exponentially.
1. Introduction
The hyperbolic Anosov C-systems have exponential instability of their trajectories and as such represent the most natural chaotic dynamical systems [1]. Of special interest are C-systems that are defined on closed surfaces of the Lobachevsky plane of constant negative curvature1. An example of such a system has been introduced in a brilliant article published in 1924 by the mathematician Emil Artin [6]. The dynamical system is defined on the fundamental region of the Lobachevsky plane which is obtained by the identification of points congruent with respect to the modular group , a discrete subgroup of the Lobachevsky plane isometries [7,8,9]. The fundamental region in this case is a hyperbolic triangle in Figure 1. The geodesic trajectories are bounded to propagate on the fundamental hyperbolic triangle. The geodesic flow in this fundamental region represents a highly chaotic dynamical system with exponential instability of its trajectories, has mixing of all orders, Lebesgue spectrum and non-zero Kolmogorov entropy [1,2,3,4,5,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].
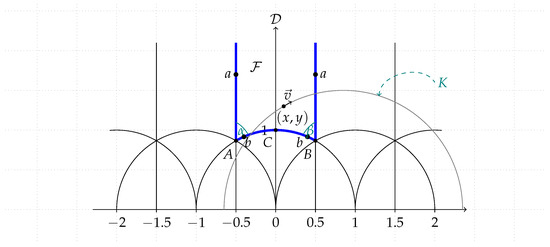
Figure 1.
The non-compact fundamental region of a finite area is represented by the hyperbolic triangle . The vertex is at infinity of the y axis and corresponds to a cusp. The edges of the triangle are the arc , the rays and . The points on the edges and and the points of the arcs with should be identified by the transformations and in order to form a closed non-compact surface by “gluing” the opposite edges of the modular triangle together. The hyperbolic triangle can be considered equally well as the fundamental region. The modular transformations of the fundamental region create a regular tessellation of the whole Lobachevsky plane by congruent hyperbolic triangles. The trajectory K is geodesic passing through the point () of in the direction.
In the classical regime the correlation functions are defined as an integral over a pair of functions/observables A and B in which the first one is stationary and the second one evolves with the geodesic flow :
Earlier investigation of the classical correlation functions of the geodesic flows was performed in [17,18,19,20,29] by using different approaches including Fourier series for the group, zeta functions for the geodesic flows, relating the poles of the Fourier transform of the correlation functions to the spectrum of an associated Ruelle operator, the methods of unitary representation theory, spectral properties of the corresponding Laplacian and other approaches. In recent articles [30,31] the authors demonstrated exponential decay of the correlation functions with time on the classical phase space. The result was derived using differential geometry, the group-theoretical methods of Gelfand and Fomin, the time evolution equations, and the properties of automorphic functions on . The exponential decay rate was expressed in terms of the entropy of the system:
where M and K are constants depending on the smoothness of the functions. In the classical regime the exponential divergence of the geodesic trajectories results in the universal exponential decay of its classical correlation functions [30,31].
In the present article, we are interested to study the quantum–mechanical correlation functions of highly chaotic Artin system. The interest in studying the quantum–mechanical behaviour of highly chaotic systems is rooted in the fact that the fundamental interactions, electroweek and strong interactions are described by the Yang–Mills gauge theory which is highly chaotic in its classical regime [21,22,27,32,33,34,35]. In recent years the quantum–mechanical properties of highly chaotic systems were widely discussed in series of publications [26,27,33,34,36]. The investigation was initiated by the analysis of black holes evaporation thermodynamics [26,27,36]. Therefore, there is a great interest in the quantisation of the highly chaotic dynamical systems and investigation of their quantum–mechanical properties. It is important to learn how and to what extent the classical chaos influences the quantum–mechanical behaviour. Our main focus in this article is to study the behaviour of the quantum–mechanical correlation functions of the Artin system because on the one hand it is highly chaotic and on the other hand it has a deep mathematical origin. It was conjectured by Maldacena, Shenker and Stanford [26] that the classical chaos influences the thermal properties of the corresponding quantum–mechanical system and can be traced by investigation of out-of-time-order correlation functions, as well as of the square of the commutator of the operators separated in time.
In order to investigate the behaviour of the correlation functions in the quantum–mechanical regime it is necessary to know the spectrum of the system and the corresponding wave functions. In the case of the modular group the energy spectrum has a continuous part, which originates from the asymptotically free motion inside an infinitely long vertical “y-channel” extended in the vertical direction of the fundamental region, as well as infinitely many discrete energy states corresponding to bounded motion at the “bottom” of the fundamental triangle. The spectral problem has a deep number-theoretical origin and was partially solved in a series of pioneering articles [37,38,39,40]. It was only partially solved because the discrete spectrum and the corresponding wave functions are not known analytically. The general properties of the discrete spectrum have been derived using the Selberg trace formula [39,40,41,42,43,44]. Numerical calculations of the discrete energy levels were performed for many energy states [45,46,47].
In the next section we shall describe the geometry of Lobachevsky hyperbolic plane and of the fundamental region which corresponds to the modular group , the geodesic flow on that region and the quantisation of the system. The derivation of the Maass wave functions [37] for the continuous spectrum will be reviewed in detail. We shall use the Poincaré representation for the Maass non-holomorphic automorphic wave functions. We introduce a natural physical variable for the distance in the vertical direction2 on the fundamental triangle and the corresponding momentum in order to represent the Maass wave functions (54) in a physically insightful manner
where the functions , and will be defined precisely in Section 3 and are given by the Formulas (48), (44) and (41). Indeed, the first two terms describe the incoming and outgoing plane waves. The plane wave incoming from infinity of the y axis in Figure 2 (the vertex ) elastically scatters on the boundary of the fundamental triangle shown in Figure 1. The reflection amplitude is a pure phase and is given by the expression in front of the outgoing plane wave :
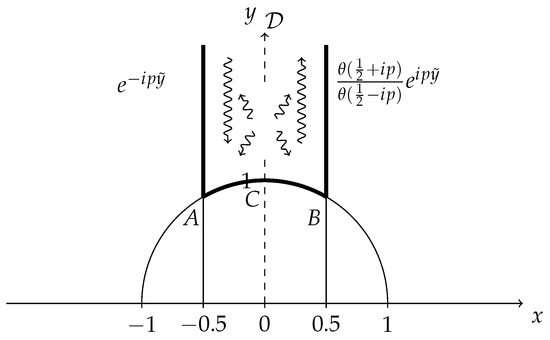
Figure 2.
The incoming and outgoing plane waves (3). The plane wave incoming from infinity of the y axis (the vertex ) elastically scatters on the boundary of the fundamental triangle which defines the fundamental region (see also Figure 1). The reflection amplitude is a pure phase and is given by the expression in front of the outgoing plane wave . The rest of the wave function describes the standing waves in the x direction between boundaries with the amplitudes, which are exponentially decreasing.
The rest of the wave function describes the standing waves in the x direction between boundaries with the amplitudes , which are exponentially decreasing with index l Figure 2. The continuous energy spectrum is given by the formula
The wave functions of the discrete spectrum have the following form [37,38,39,40,45,46,47]:
where the spectrum and the coefficients are not known analytically, but were computed numerically for many values of n [45,46,47].
Having in hand the explicit expression of the wave function one can analyze a quantum–mechanical behaviour of the correlation functions defined in [26,48]:
where in our case the operators A and B are chosen to be of the Liouiville type:
Analyzing the basic matrix elements of the Liouiville-like operators (9) we shall demonstrate that all two- and four-point correlation functions (7) decay exponentially with time:
with exponents and that depend on temperature. These exponents define the dissipation time and reflect the fact that with increasing temperature the correlation functions will universally decay. Their behaviour is shown in Figure 3 and Figure 4.
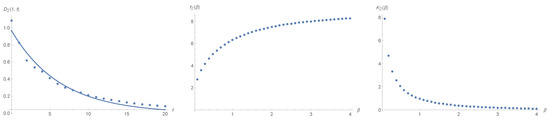
Figure 3.
The exponential decay of the two-point correlation function as a function of time at temperature . The points are fitted by the curve . The exponent has a well defined high and low temperature limits. The limiting values in dimensionless units are and . The temperature dependence of is shown at the far right.
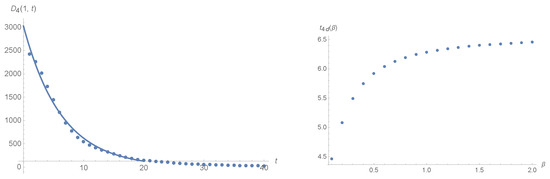
Figure 4.
The exponential decay of the correlation function as a function of time at . The rest of the functions demonstrate a similar exponential decay . The temperature dependence of the exponent have a well defined high and low temperature limits and is shown at far right. The corresponding limiting values of the function in dimensionless units are and . The behaviour of the exponent of the two-point correlation function is shown in Figure 3.
Alternatively to the exponential decay of the correlation functions (7), the square of the commutator of the Liouiville-like operators separated in time (8) grows exponentially Figure 5. This growth is reminiscent to the local exponential divergence of trajectories in the Artin system when it is considered in the classical regime [30,31]. At short time scales the exponential growth of the commutator (8) shown in Figure 5 has the following form:
where the behaviour of the exponent is presented in Figure 5. The temperature dependence of the exponent is smooth and there are no signs of any kind of phase transitions.
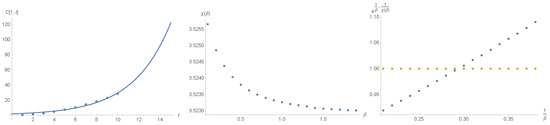
Figure 5.
Time evolution of the correlation function (84) at temperature . For the short time intervals the function exponentially increases with time. This behaviour is reminiscent to the exponential divergence of the classical trajectories in hyperbolic dynamical systems. As one can see, the exponent which defines the behaviour of the correlation function of the operators separated in time in the commutator (84), (85) slowly decreases with . The temperature dependence of relative to the maximum growth is shown by blue dots at the far right figure.
In our calculation of the quantum–mechanical correlation functions we shall use a perturbative expansion in which the high-mode Bessel function in (54) and (59) will be considered as perturbations. We found that our calculations are stable with respect to these perturbations and do not influence the final results. The reason is that in the integration region of the matrix elements (62) the high-mode Bessel functions are exponentially small.
2. Quantisation of Artin System
Let us start with Poincare model of the Lobachevsky plane, i.e., the upper half of the complex plane: H = , supplied with the metric (we set )
which has Ricci scalar . Isometries of this space are given by transformations. The matrix (a, b, c, d are real and )
acts on a point z by linear fractional substitutions:
Note also that g and give the same transformation, hence the effective group is . We’ll be interested in the space of orbits of a discrete subgroup in H. Our main example will be the modular group . A nice choice of the fundamental region of is displayed in Figure 1. The fundamental region of the modular group consists of those points between the lines and that lie outside the unit circle in Figure 1. The modular triangle has two equal angles and the third one at equal to zero, , thus . The area of the fundamental region is finite and equal to and has the topology of sphere due to “gluing” the opposite edges of the triangle. The invariant area element on the Lobachevsky plane is proportional to the square root of the determinant of the metric (12): , thus
Consider geodesic flow on , which is conveniently described by the least action principle , where (cf. (12)):
By varying the action, we get the equations of motion
Notice the invariance of the action and of the equations of motion under time reparametrizations . Presence of a local (“gauge”) symmetry indicates that we have a constrained dynamical system. One particularly convenient choice of gauge fixing specifying the time parameter t proportional to the proper time, is archived by imposing the condition
where H is a constant. In this gauge the Equation (15) will take the following form [49]:
Defining the canonical momenta , conjugate to the coordinates x, y as
we shall get the geodesic Equation (17) in the Hamiltonian form:
Indeed, after defining the Hamiltonian as
the corresponding equations will take the following form:
and coincide with (18) and (19). The advantage of the gauge (16) is that the Hamiltonian (20) coincides with the constraint. Now it is fairly standard to quantize this Hamiltonian system. We simply replace in (20)
and consider the (time independent) Schrödinger equation
The resulting equation explicitly reads:
On the left hand side one recognises the Laplace operator (with an extra minus sign) in Poincare metric (12). It is easy to see that the Hamiltonian is a positive semi-definite Hermitian operator. Indeed, for any quadratically integrable function that fulfills the periodic boundary condition (26)
It is convenient to introduce parametrization of the energy and to rewrite this equation as
As far as E is real and semi-positive and parametrisation is symmetric with respect to it follows that the parameter s should be chosen within the range
One should impose the “periodic” boundary condition on the wave function with respect to the modular group
in order to have the wave function which is properly defined on the fundamental region shown in Figure 1. Taking into account that the transformation belongs to , one has to impose the periodicity condition . Thus we have a Fourier expansion
Inserting this into Equation (24), for the Fourier component we get
For the case the solution which exponentially decays at large y reads
and for one simply gets
Thus the solution can be represented in the following form:
where the coefficients should be defined so that the wave function fulfills the boundary conditions (26). Thus one should impose also the invariance with respect to the second generator of the modular group , that is, with respect to the transformation :
This functional equation defines the coefficients . We found that it is much easier to resolve it by using the full group of transformations acting on a particular solution (30) in order to derive the eigenfunctions obtained by Maass [37]. The wave function generated in this way will be invariant with respect to the transformations. We shall follow this approach in the next section.
3. Continuous Spectrum and the Reflection Amplitude
As we just mentioned above in order to get invariant solutions, one should define the coefficients and in (31). Another option is to start from a particular solution and perform summation over all nonequivalent shifts of the argument by the elements of , that is, by using the Poincaré series representation [7,8]. We will demonstrate this strategy by using the simplest solution (30), (31) with :
Let us denote by the subgroup of , generating shifts , . Explicitly the elements of are given by matrices:
Since is already invariant with respect to , we should perform summation over the conjugacy classes . Let us define these conjugacy classes. If two matrices
belong to the same class, then by definition for some
so that , , and . Since , it follows that a and c do not have a common devisor. In fact, the opposite is also true. Given a pair of mutually prime integers it is always possible to find a pair of integers such that . For any other pair satisfying the same condition , the relations and are satisfied for some integer n. Thus we established a bijection between the set of mutually prime pairs with and the set of conjugacy classes . The fact that the integers are mutually prime integers means that their greatest common divisor (gcd) is equal to one: . As a result, it is defined by the classical Poincaré series representation [7,8] and for the sum of our interest we get3
where, as explained above, the sum on the r.h.s. is taken over all mutually prime pairs . The series (34) is convergent when . We used also the simple relation
To simplify further the sum let us multiply both sides of the Equation (34) by [37]
so that we shall get
It is easy to be convinced now that the set of all pairs with n a positive integer and mutually prime coincides with the set of all pairs of integers which are not simultaneously zero. Indeed, given a pair we can factor out the greatest common divisor n and represent it as with mutually prime . Thus we arrive at the Eisenstein series representation of the wave function:
Since the r.h.s. of this equation is periodic in x with period 1, we can expand it in Fourier series. Our next goal is to find the coefficients of this expansion:
First let us handle the term with :
For the sum over non-zero m’s let us note that we may drop the factor and sum over . Indeed, the sum over negative m’s can be reverted to a sum over positive ones through redefinition . For fixed positive m it is instructive to represent k as thus splitting the initial sum over into double sum over and . In this way after few simple manipulations we get
The last integral is expressed in terms of modified Bessel K function:
A useful alternative representation of modified Bessel K function which makes its properties more transparent is given by
This expression allows analytical continuation of the wave function from the region in (34) into the whole complex plane s because the Bessel functions are well defined for any s. Besides, an easy examination shows that the finite sum is:
Thus we recovered the second solution in (31) and calculated the coefficient in front of it. Thus the invariant solution (36) takes the following form:
Using Riemann’s reflection relation
and introducing the notation
we arrive at the elegant final expression for the energy eigenfunctions obtained by Maas [37]:
This wave function is well defined in the complex s plane and has a simple pole at . The physical continuous spectrum was defined in (25), where , so that
The continuous spectrum wave functions are delta function normalisable [37,38,39,40,41,42]. The wave function (49) can be conveniently represented also in the form
where
The physical interpretation of the wave function becomes more transparent when we introduce the new variables
as well as an alternative normalisation of the wave function:
Indeed, the first two terms describe the incoming and outgoing plane waves. The plane wave incoming from infinity of the y axis in Figure 1 and Figure 2 (the vertex ) elastically scatters on the boundary of the fundamental region in Figure 1. The reflection amplitude is a pure phase and is given by the expression in front of the outgoing plane wave :
The rest of the wave function describes the standing waves in the x direction between boundaries with the amplitudes , which are exponentially decreasing with index l.
In addition to the continuous spectrum, the system (24) has a discrete spectrum [37,38,39,40,41,42]. The number of discrete states is infinite: , the spectrum is extended to infinity—unbounded from above—and lacks any accumulation point except infinity. Let us denote the wave functions of the discrete spectrum by so that the expansion into the full set of basis vectors will take the form
and the Parseval identity will be
and
The wave functions of the discrete spectrum have the following form [37,38,39,40,45,46,47]:
where the spectrum and the coefficients are not known analytically, but were computed numerically for many values of n [45,46,47]. Having explicit expressions of the wave functions one can analyze the quantum–mechanical behaviour of the correlation functions, which we shall investigate in the next sections.
4. Correlation Functions
First let us calculate the two-point correlation function:
The energy eigenvalues (50) are parametrised by , and , , thus
where the complex conjugate function is . Defining the basic matrix element as
for the two-point correlation function we shall get
The matrix elements (62) and (64) play a fundamental role in the investigation of the correlation functions because all correlations can be expressed through it. One should also choose appropriate observables A and B. The operator seems very appropriate for two reasons. Firstly, the convergence of the integrals over the fundamental region will be well defined. Secondly, this operator is reminiscent of the exponentiated Liouiville field since . Thus we are interested in calculating the matrix element (64) for the observables in the form of the Liouiville-like operators 4:
We shall get
To calculate the above matrix elements we shall use a perturbative expansion in which the part of the wave function (54) containing the Bessel functions and the contribution of the discrete spectrum (59) will be considered as perturbation. As we shall demonstrate below, these terms of the perturbative expansion are small and do not influence our results. The reason behind this fact is that in the integration region of the matrix element (62) the Bessel function decays exponentially, as one can be convinced by inspecting (41). Therefore, the contribution of these high modes is small (analogues to the so called mini-superspace approximation in the Liouville theory). Thus we shall consider the perturbative expansion over high frequency modes in (54) and (59). In the first approximation of the wave function (54) for the matrix element we shall get
where we used (55). Integration over x can be performed exactly with the result for the basic matrix element of the following form:
where the reflation phase was defined in (55). Thus for the two-point correlation function we shall get
The correlation function is between two Liouiville-like fields in the power N and M respectively. This expression is very convenient for analytical and numerical analyses. It is expected that the two-point correlation function should decay exponentially [26], therefore we fitted the points by the curve
The is the dissipation time and defines one of the characteristic time scales in the quantum–mechanical system5. The exponential decay of the two-point correlation function with time and the dependence of the exponent and of the prefactor as a function of temperature are presented in Figure 3. As one can see, at high and low temperatures the dissipation time tends to the fixed values. These limiting values we have calculated by using the expressions (71) and (72). At large the main contribution came from the zero momentum region :
and at from the region :
The corresponding limiting values in dimensionless units are shown on the l.h.s. of Figure 3.
Four-Point Correlation Function
It was conjectured by Maldacena, Shenker and Stanford [26] that the classical chaos can be diagnosed in thermal quantum systems by using an out-of-time-order correlation functions as well as by the square of the commutator of the operators which are separated in time. The out-of-time four-point correlation function of interest was defined in [26,48] as follows:
The other important observable which we shall consider here is the square of the commutator of the Liouiville-like operators separated in time [26]
The energy eigenvalues we shall parametrise as , , and , thus from (73) we shall get
In terms of the variables (53) the four-point correlation function (75) will take the following form:
In order to compute the square of the commutator (74), one should also consider the following four-point correlation function:
As it was suggested in [26], the most important correlation function indicating the traces of the classical chaotic dynamics in quantum regime is (74)
where in the case of the Artin system these correlation functions in the momentum space representation have the form:
and
Figure 4 shows the behaviour of the four-point correlations as a function of temperature and time. All of the four-point correlation functions decay exponentially:
Now we can turn to the investigation of the commutator (74), (80) which can be represented in the following form:
where we used (81) and (82). Due to the sinus functions the vanishes at and is proportional to at the very short time scale: , . Generally the commutator between operators at different moments of time is not vanishing because the operator and the time dependent operator do not coincide, for example in the case of a simple oscillator, where . For larger time intervals the value of the matrix elements (66) plays a crucial role and essentially influences the behaviour of the .
In contrast to the exponential decay of the correlation functions the square of the commutator of the operators separated in time grows exponentially, Figure 5. This growth is reminiscent to the local exponential divergence of trajectories in the Artin system when it is considered in the classical [30,31] and in quasi-classical limits. In the quasi-classical limit the commutator changes proportionally to the square of trajectory deviation which grows exponentially [30,31]. The growth of the commutator has been parameterised in the following form:
where the behaviour of the exponent and ratio with respect to the maximal growth exponent is presented in Figure 5. This beautifully confirms the fact that the correlation function indeed grows exponentially with time, as it takes place in its classical counterpart. As one can see, the exponent defining the behaviour of the commutator in (84) and (85) slowly decreases with .
5. Discussion
In order to check if the results are sensitive to the truncation of the high modes of the Maass wave function (49), as well as to the contribution of the discrete energy levels (59), we included the corresponding terms into the integration of the basic matrix element in (62). The first discrete energy level is at and has the wave function given in (59) [46]. The value of the corresponding matrix element (62) at is of order . In comparison, the contribution from continuous energy spectrum to the same matrix element is varying in the interval . We also included two consecutive terms of the discrete sum of the Maass wave function (54) with in our calculation of the basic matrix element and found that the changes are of the same order. Thus we found that their influence on the behaviour of the correlation functions is negligible mainly because the Bessel function (41) is exponentially small in the fundamental region. The numerical values of the exponents are changing in the range of a few percentage points and do not influence the results. In summary, all two- and four-point correlation functions decay exponentially. The commutator in (84) and (85) grows exponentially with an exponent that is almost constant, Figure 5.
Author Contributions
Writing—review and editing, G.S., H.B. and R.P. All authors have read and agreed to the published version of the manuscript.
Funding
This project received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skĺodowska-Curie grant agreement No 644121.
Acknowledgments
R.P. is thankful to the NCSR”Demokritos” for hospitality during June–July 2018 when this work was completed. H.B. would like to thank NCSR“Demokritos” for kind hospitality and generous financial support of the MIXMAX project. The work of H.B. and R.P. was partially supported also by the Armenian State Committee of Science in the framework of the research project 18T-1C-340. G.S. would like to thank Luis Alvarez-Gaume for stimulating discussions of automorphic functions, the references [41,44] and kind hospitality at the Simon Center for Geometry and Physics where part of this work was completed. We would like to thank T. Akutagawa, K. Hashimoto, T. Sasaki and R. Watanabe for correspondence and discussion of temperature dependent exponents.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anosov, D.V. Geodesic flows on closed Riemannian manifolds with negative curvature. Trudy Mat. Inst. Steklov. 1967, 90, 3–210. [Google Scholar]
- Kolmogorov, A.N. New metrical invariant of transitive dynamical systems and automorphisms of Lebesgue spaces. Dokl. Acad. Nauk SSSR 1958, 119, 861–865. [Google Scholar]
- Kolmogorov, A.N. On the entropy per unit time as a metrical invariant of automorphism. Dokl. Acad. Nauk SSSR 1959, 124, 754–755. [Google Scholar]
- Sinai, Y.G. On the Notion of Entropy of a Dynamical System. Dokl. Russ. Acad. Sci. 1959, 124, 768–771. [Google Scholar]
- Savvidy, G. Anosov C-systems and random number generators. Theor. Math. Phys. 2016, 188, 1155. [Google Scholar] [CrossRef]
- Artin, E. Ein mechanisches system mit quasiergodischen bahnen. Abh. Math. Semin. Univ. Hambg. 1924, 3, 170. [Google Scholar] [CrossRef]
- Poincaré, H. Théorie des Groupes Fuchsiennes. Acta Math. 1882, 1, 1–62. [Google Scholar] [CrossRef]
- Poincaré, H. Mémoire sur les Fonctions Fuchsiennes. Acta Math. 1882, 1, 193–294. [Google Scholar] [CrossRef]
- Fuchs, L. Ueber eine Klasse von Funktionen mehrerer Variablen, welche durch Umkehrung der Integrale von Lösungen der linearen Differentialgleichungen mit rationalen Coeffizienten entstehen. J. Reine Angew. Math. 1880, 89, 151–169. [Google Scholar]
- Hadamard, J. Les surfaces á courbures opposées et leur linges geodesiques. Liouville J. Mathématique 1898, 4, 27. [Google Scholar]
- Hedlund, G. The dynamics of geodesic flow. Bull. Am. Math. Soc. 1939, 45, 241–246. [Google Scholar] [CrossRef]
- Bowen, R. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms; Lecture Notes in Mathematics, no. 470; Dold, A., Eckmann, B., Eds.; Springer: Heidelberg, Germany, 1975; 108p. [Google Scholar]
- Ruelle, D. Thermodynamic Formalism; Addison-Wesley: Reading, MA, USA, 1978. [Google Scholar]
- Hopf, E. Statistik der Lösungen geodätischer Probleme vom unstabilen Typus. II. Math. Ann. 1940, 117, 590–608. [Google Scholar] [CrossRef]
- Hopf, E. Ergodic theory and the geodesic flow on surfaces of constant negative curvature. Bull. Am. Math. Soc. 1971, 77, 863–877. [Google Scholar] [CrossRef]
- Gelfand, I.M.; Fomin, S.V. Geodesic flows on manifolds of constant negative curvature. Uspekhi Mat. Nauk 1952, 7, 118–137. [Google Scholar]
- Collet, P.; Epstein, H.; Gallavotti, G. Perturbations of Geodesic Flows on Surfaces of Constant Negative Curvature and Their Mixing Properties. Commun. Math. Phys. 1984, 95, 61–112. [Google Scholar] [CrossRef]
- Moore, C.C. Exponential Decay of Correlation Coefficients for Geodesic Flows; Group Representations, Ergodic Theory, Operator Algebras, and Mathematical Physics (Berkeley, Calif., 1984), Math. Sci. Res. Inst. Publ.; Springer: New York, NY, USA, 1987; Volume 6, pp. 163–181. [Google Scholar]
- Dolgopyat, D. On Decay of Correlations in Anosov Flows. Ann. Math. Second. Ser. 1998, 147, 357–390. [Google Scholar] [CrossRef]
- Chernov, N.I. Markov Approximations and Decay of Correlations for Anosov Flows. Ann. Math. Second. Ser. 1998, 147, 269–324. [Google Scholar] [CrossRef]
- Savvidy, G. The Yang-Mills mechanics as a Kolmogorov K-system. Phys. Lett. B 1983, 130, 303. [Google Scholar] [CrossRef]
- Savvidy, G. Classical and Quantum Mechanics of non-Abelian Gauge Fields. Nucl. Phys. B 1984, 246, 302. [Google Scholar] [CrossRef]
- Savvidy, G.; Ter-Arutyunyan-Savvidy, N. On the Monte Carlo simulation of physical systems. J. Comput. Phys. 1991, 97, 566. [Google Scholar] [CrossRef]
- Savvidy, K. The MIXMAX random number generator. Comput. Phys. Commun. 2015, 196, 161–165. [Google Scholar] [CrossRef]
- Savvidy, K.; Savvidy, G. Spectrum and Entropy of C-systems. MIXMAX random number generator. Chaos Solitons Fractals 2016, 91, 33. [Google Scholar] [CrossRef]
- Maldacena, J.; Shenker, S.H.; Stanford, D. A bound on chaos. J. High Energy Phys. 2016, 2016, 106. [Google Scholar] [CrossRef]
- Gur-Ari, G.; Hanada, M.; Shenker, S.H. Chaos in Classical D0-Brane Mechanics. J. High Energy Phys. 2016, 2016, 91. [Google Scholar] [CrossRef]
- Hanada, M.; Shimada, H.; Tezuka, M. Universality in Chaos: Lyapunov Spectrum and Random Matrix Theory. Phys. Rev. E 2018, 97, 022224. [Google Scholar] [CrossRef] [PubMed]
- Pollicott, M. On the rate of mixing of Axiom A flows. Invent. Math. 1985, 81, 413–426. [Google Scholar] [CrossRef]
- Savvidy, G.; Savvidy, K. Exponential decay of correlations functions in MIXMAX generator of pseudorandom numbers. Chaos Solitons Fractals 2018, 107, 244. [Google Scholar] [CrossRef]
- Poghosyan, H.; Babujian, H.; Savvidy, G. Artin Billiard Exponential Decay of Correlation Functions. arXiv 2018, arXiv:1802.04543. [Google Scholar] [CrossRef]
- Akutagawa, T.; Hashimoto, K.; Sasaki, T.; Watanabe, R. Out-of-time-order correlator in coupled harmonic oscillators. arXiv 2020, arXiv:2004.04381. [Google Scholar]
- Aref’eva, I.Y.; Koshelev, A.S.; Medvedev, P.B. On stable sector in supermembrane matrix mode. Nucl. Phys. B 2000, 579, 411. [Google Scholar] [CrossRef][Green Version]
- Aref’eva, I.Y.; Volovich, I.V. Holographic thermalization. Theor. Math. Phys. 2013, 174, 186–196. [Google Scholar] [CrossRef]
- Anous, T.; Cogburn, C. Mini-BFSS matrix model in silico. Phys. Rev. D 2019, 100, 066023. [Google Scholar] [CrossRef]
- Shenker, S.H.; Stanford, D. Black holes and the butterfly effect. J. High Energy Phys. 2014, 2014, 67. [Google Scholar] [CrossRef]
- Maass, H. Über eine neue Art von nichtanalytischen automorphen Funktionen. Math. Ann. 1949, 121, 141–183. [Google Scholar] [CrossRef]
- Roelcke, W. Über die Wellengleichung bei Grenzkreisgruppen Erster Art; Springer: Berlin/Heidelberg, Germany, 1956; Volume 4, pp. 161–267. [Google Scholar]
- Selberg, A. Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series. Indian J. Math. Soc. 1956, 20, 47–87. [Google Scholar]
- Selberg, A. Discontinuous groups and harmonic analysis. In Proceedings of the Stockholm Mathematical Congress, Stockholm, Sweden, 15–22 August 1962. [Google Scholar]
- Bump, D. Automorphic Forms and Representations; Cambridge Studies in Advance Mathematics: 55; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Faddeev, L.D. Expansion in eigenfunctions of the Laplace operator on the fundamental domain of a discrete group on the Lobachevsky plane. Trans. Mosc. Math. Soc. 1967, 17, 357–386. [Google Scholar]
- Faddeev, L.D.; Venkov, A.B.; Kalinin, V.L. A non-arithmetic derivation of the Selberg trace formula. J. Sov. Math. 1977, 8, 171–199. [Google Scholar]
- Hejhal, D.A. The Selberg Trace Formula for PSL(2, R); Lecture Notes in Mathematics 548; Springer: Berlin/Heidelberg, Germany, 1976; Volume 1. [Google Scholar]
- Winkler, A. Cusp forms and Hecke groups. J. Reine Angew. Math. 1988, 386, 187. [Google Scholar]
- Hejhal, D.A. Eigenvalues of the Laplacian for PSL(2,Z): Some new results and computational techniques. In International Symposium in Memory of Hua Loo-Keng; Gong, S., Lu, Q., Wang, Y., Yang, L., Eds.; Science Press and Springer: Berlin/Heidelberg, Germany, 1991; Volume 1, pp. 59–102. [Google Scholar]
- Hejhal, D.A.; Berg, B. Some New Results Concerning Eigenvalues of the non-Euclidean Laplacian for PSL(2,Z); Report No. 82-172; University of Minnesota: Minneapolis, MN, USA, 1982; 7p. [Google Scholar]
- Larkin, A.; Ovchinnikov, Y. Nonuniform state of superconductors. Zh. Eksp. Teor. Fiz. 1964, 47, 1136–1146. [Google Scholar]
- Faddeev, L.D. Feynman integral for singular Lagrangians. Theor. Math. Phys. 1969, 1, 1. [Google Scholar] [CrossRef]
| 1. | The definition of the Anosov C-systems can be found in his excellent work [1]. In order to provide this definition one should use such mathematical concepts as tangent vector bundle, derivative mapping, contracting and expanding linear spaces and others. The properties of the C-systems [1], of the Kolmogorov entropy [2,3,4] and the description of their periodic trajectories can be found in the recent review article [5]. |
| 2. | Physical distances are obtained by integration of the metric (12) along the trajectories. |
| 3. | The factor below is introduced for removing the double degeneracy due to the fact that elements both act on z in the same way. |
| 4. | Another interesting observable is . As a consequence of the chaotic nature of the system it is expected that the behaviour of the correlation functions will have a universal character. |
| 5. | We would like to thank Gabriel Poghosyan for numerical calculation of the two-point correlation function presented in Figure 3. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).