Langer Modification, Quantization Condition and Barrier Penetration in Quantum Mechanics
Abstract
1. Introduction
2. Uniform Asymptotic Approximation Method
2.1. Wave Functions in the Uniform Asymptotic Approximation
2.1.1. For Single Turning Point
2.1.2. A Pair of Turning Points
2.2. Second-Order Pole and Langer Modification
2.3. Extreme Point and the Elimination of the Error Term
3. Improved Quantization Conditions and Potential Barrier Transmission Coefficients
3.1. Improved Quantization Condition
3.1.1. Hydrogen Atoms
3.1.2. Harmonic Oscillators
3.1.3. Morse Potential
3.1.4. Pöschl-Teller Potential
3.1.5. Eckart Potential
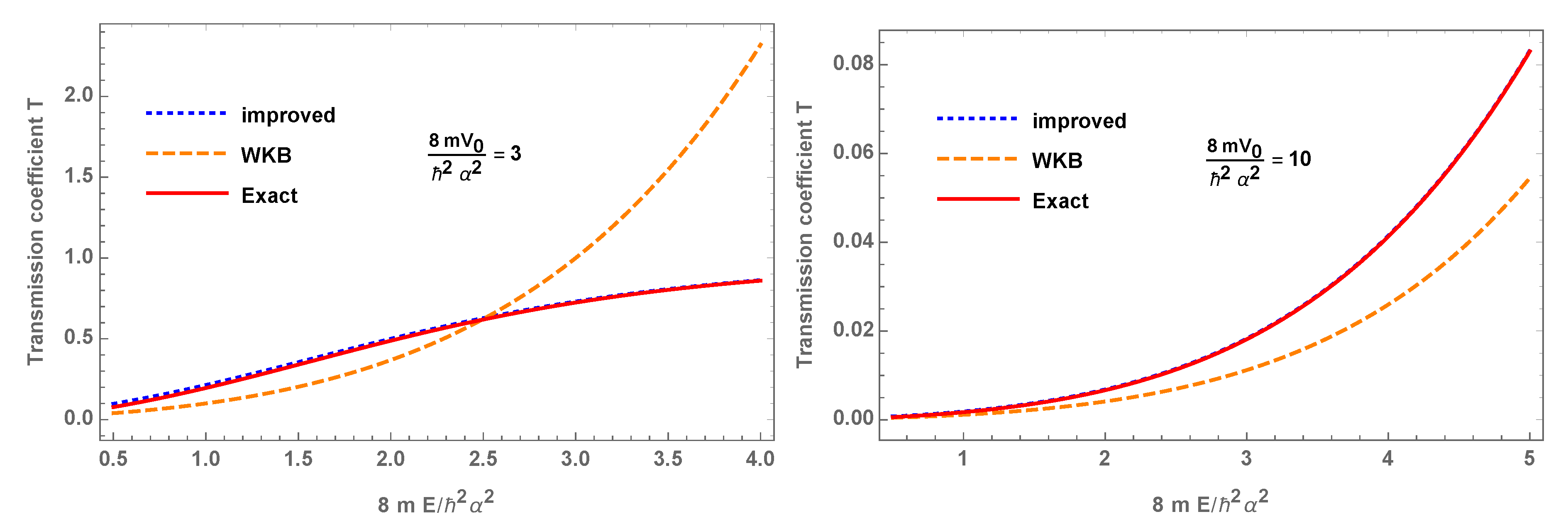
3.2. Potential Barrier Transmission
4. Summary and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Berry, M.V.; Mount, K.E. Semiclassical approximations in wave mechanics. Rep. Prog. Phys. 1972, 35, 315. [Google Scholar] [CrossRef]
- Friedrich, H.; Trost, J. Working with WKB waves far from the semiclassical limit. Phys. Rep. 2004, 397, 359. [Google Scholar] [CrossRef]
- Price, T.J.; Greene, C.H. Semiclassical Treatment of High-Lying Electronic States of . J. Phys. Chem. A 2018, 122, 8565. [Google Scholar] [CrossRef]
- Hyouguchi, T.; Adachi, S.; Ueda, M. Divergence-Free WKB Method. Phys. Rev. Lett. 2002, 88, 170404. [Google Scholar] [CrossRef] [PubMed]
- Karnakov, B.M.; Krainov, V.P. WKB Approximation in Atomic Physics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Fröman, N.; Fröman, P.O. JWKB Approximation: Contributions to the Theory; North Holland Publishing Company: Amsterdam, The Netherlands, 1965. [Google Scholar]
- Dong, S.-H. Wave Equations in Higher Dimensions; Springer: Dordrecht, The Netherlands; New York, NY, USA, 2011. [Google Scholar]
- Young, L.A.; Uhlenbeck, G.E. On the Wentzel-Brillouin-Kramers Approximate Solution of the Wave Equation. Phys. Rev. 1930, 36, 1154. [Google Scholar] [CrossRef]
- Langer, R.E. On the Connection Formulas and the Solutions of the Wave Equation. Phys. Rev. 1937, 51, 669. [Google Scholar] [CrossRef]
- Zwaan, A. Intensitäten im Ca Funkenspectrum. Ph.D. Thesis, Universiteitsbibliotheek Utrecht, Utrecht, The Netherlands, 1929. Available online: https://dspace.library.uu.nl/handle/1874/294713 (accessed on 30 June 2020).
- Langer, R. The Asymptotic Solutions of Linear Ordinary Differential Equations with Reference to the Stokes Phenomenon. Bull. Am. Math. Soc. 1934, 40, 545–582. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics (Non-Relativistic Theory), 3rd ed.; Butterworth-Heinemann: Beijing, China, 1997; pp. 46–53. [Google Scholar]
- Berry, M.V. Waves near Stokes lines. Proc. R. Soc. Lond. A 1990, 427, 265–280. [Google Scholar]
- Delabaere, E.; Dillinger, H.; Pham, F. Exact semiclassical expansions for one-dimensional quantum oscillators. J. Math. Phys. 1997, 38, 6126. [Google Scholar] [CrossRef]
- Miller, S.G.; Good, R.H. A WKB Type Approximation to the Schroedinger Equation. Phys. Rev. 1953, 91, 174–179. [Google Scholar] [CrossRef]
- Dingle, R.B. The method of comparison equations in the solution of linear second-order differential equations (generalized W.K.B. method). Appl. Sci. Res. B 1956, 5, 345. [Google Scholar] [CrossRef]
- Álvarez, G. Langer-Cherry derivation of the multi-instanton expansion for the symmetric double well. J. Math. Phys. 2004, 45, 3095. [Google Scholar] [CrossRef]
- Dunne, G.V.; Ünsal, M. Uniform WKB, multi-instantons, and resurgent trans-series. Phys. Rev. D 2014, 89, 105009. [Google Scholar] [CrossRef]
- Zinn-Justin, J. Quantum Field Theory and Critical Phenomena; Clarendon: Oxford, UK; New York, NY, USA, 2002. [Google Scholar]
- Slavyanov, S.Y. Asymptotic Solutions of the One-Dimensional Schrödinger Equation; American Mathematical Society: Providence, RI, USA, 1996. [Google Scholar]
- Fröman, N.; Fröman, P.O. Phase-Integral Method; Springer: New York, NY, USA, 1996. [Google Scholar]
- Olver, F.W.J. Second-Order Linear Differential Equations with Two Turning Points. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 1975, 278, 137. [Google Scholar]
- Olver, F.W.J. Asymptotics and Special Functions; A K Peters, Ltd.: Wellesley, MA, USA, 1997. [Google Scholar]
- Habib, S.; Heitmann, K.; Jungman, G.; Molina-Paris, C. The Inflationary perturbation spectrum. Phys. Rev. Lett. 2002, 89, 281301. [Google Scholar] [CrossRef]
- Habib, S.; Heinen, A.; Heitmann, K.; Jungman, G.; Molina-Paris, C. Characterizing inflationary perturbations: The Uniform approximation. Phys. Rev. D 2004, 70, 083507. [Google Scholar] [CrossRef]
- Wang, A. Vector and tensor perturbations in Horava-Lifshitz cosmology. Phys. Rev. 2010, 82, 124063. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Power spectra and spectral indices of k-inflation: High-order corrections. Phys. Rev. D 2014, 90, 103517. [Google Scholar] [CrossRef]
- Alinea, A.L.; Kubota, T.; Naylor, W. Logarithmic divergences in the k-inflationary power spectra computed through the uniform approximation. J. Cosmol. Astropart. Phys. 2016, 2, 028. [Google Scholar] [CrossRef][Green Version]
- Wu, Q.; Zhu, T.; Wang, A. Primordial Spectra of slow-roll inflation at second-order with the Gauss-Bonnet correction. Phys. Rev. D 2018, 97, 103502. [Google Scholar] [CrossRef]
- Alinea, A.L.; Kubota, T.; Nakanishi, Y.; Naylor, W. Adiabatic regularisation of power spectra in k-inflation. JCAP 2015, 6, 019. [Google Scholar] [CrossRef]
- Alinea, A.L. Adiabatic regularization of power spectra in nonminimally coupled chaotic inflation. J. Cosmol. Astropart. Phys. 2016, 10, 02. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Constructing analytical solutions of linear perturbations of inflation with modified dispersion relations. Int. J. Mod. Phys. A 2014, 29, 1450142. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Inflationary cosmology with nonlinear dispersion relations. Phys. Rev. D 2014, 89, 043507. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A. Gravitational quantum effects in light of BICEP2 results. Phys. Rev. D 2014, 90, 027304. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Gravitational quantum effects on power spectra and spectral indices with higher-order corrections. Phys. Rev. D 2014, 90, 063503. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Kirsten, K.; Cleaver, G.; Sheng, Q. High-order Primordial Perturbations with Quantum Gravitational Effects. Phys. Rev. D 2016, 93, 123525. [Google Scholar] [CrossRef]
- Qiao, J.; Ding, G.H.; Wu, Q.; Zhu, T.; Wang, A. Inflationary perturbation spectrum in extended effective field theory of inflation. J. Cosmol. Astropart. Phys. 2019, 1909, 064. [Google Scholar] [CrossRef]
- Ding, G.H.; Qiao, J.; Wu, Q.; Zhu, T.; Wang, A. Inflationary perturbation spectra at next-to-leading slow-roll order in effective field theory of inflation. Eur. Phys. J. C 2020, 101, 043528. [Google Scholar] [CrossRef]
- Qiao, J.; Zhu, T.; Zhao, W.; Wang, A. Polarized primordial gravitational waves in the ghost-free parity-violating gravity. Phys. Rev. D 2019, 79, 976. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Kirsten, K.; Cleaver, G.; Sheng, Q.; Wu, Q. Inflationary spectra with inverse-volume corrections in loop quantum cosmology and their observational constraints from Planck 2015 data. J. Cosmol. Astropart. Phys. 2016, 1603, 046. [Google Scholar] [CrossRef][Green Version]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q.; Wu, Q. Scalar and tensor perturbations in loop quantum cosmology: High-order corrections. J. Cosmol. Astropart. Phys. 2015, 1510, 052. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q.; Wu, Q. Detecting quantum gravitational effects of loop quantum cosmology in the early universe? Astrophys. J. 2015, 807, L17. [Google Scholar] [CrossRef]
- Li, B.F.; Zhu, T.; Wang, A.; Kirsten, K.; Cleaver, G.; Sheng, Q. Pre-inflationary perturbations from deformed algebra approach in loop quantum cosmology. Phys. Rev. D 2019, 99, 103536. [Google Scholar] [CrossRef]
- Zhu, T.; Wu, Q.; Wang, A. An analytical approach to the field amplification and particle production by parametric resonance during inflation and reheating. Phys. Dark Univ. 2019, 26, 100373. [Google Scholar] [CrossRef]
- Miller, W.H. Classical S Matrix: Numerical Application to Inelastic Collisions. J. Chem. Phys. 1970, 53, 3578. [Google Scholar] [CrossRef]
- Cooper, F.; Khare, A.; Sukhatme, U.P. Supersymmetry in Quantum Mechanics; World Scientific: River Edge, NJ, USA; Singapore, 2001. [Google Scholar]
- Qiang, W.-C.; Dong, S.-H. Proper quantization rule. Europhys. Lett. 2010, 89, 10003. [Google Scholar] [CrossRef]
- Serrano, F.A.; Gu, X.-Y.; Dong, S.-H. Qiang-Dong proper quantization rule and its applications to exactly solvable quantum systems. J. Math. Phys. 2010, 51, 082103. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys. 2011, 83, 793. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quantum Gravity 2009, 26, 163001. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, T.; Wang, A. Nonadiabatic evolution of primordial perturbations and non-Gaussinity in hybrid approach of loop quantum cosmology. Phys. Rev. D 2018, 98, 103528. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Kirsten, K.; Cleaver, G.; Sheng, Q. Primordial non-Gaussianity and power asymmetry with quantum gravitational effects in loop quantum cosmology. Phys. Rev. D 2018, 97, 043501. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Pre-inflationary universe in loop quantum cosmology. Phys. Rev. D 2017, 96, 083520. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Kirsten, K.; Cleaver, G.; Sheng, Q. Universal features of quantum bounce in loop quantum cosmology. Phys. Lett. B 2017, 773, 196. [Google Scholar] [CrossRef]
- Gottfried, K.; Yan, T.-M. Quantum Mechanics: Fundamentals, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Rosen, M.; Yennie, D.R. A Modified WKB Approximation for Phase Shifts. J. Math. Phys. 1964, 5, 1505. [Google Scholar] [CrossRef]
- Bassett, B.A.; Tsujikawa, S.; Wands, D. Inflation dynamics and reheating. Rev. Mod. Phys. 2006, 78, 537. [Google Scholar] [CrossRef]
- Dumlu, C.K.; Dunne, G.V. Stokes Phenomenon and Schwinger Vacuum Pair Production in Time-Dependent Laser Pulses. Phys. Rev. Lett. 2010, 104, 250402. [Google Scholar] [CrossRef]
| 1. | It should be noted that the integration of the form, , by using the method of stationary phase, is well-established, see, for example, [45], where there are two roots, and , of the equation . When is small, the method leads to the solution, , where is the value of x for which , , and so on. However, to our current purpose, we find that the expression of (17) is more suitable. |
| 2. | It should be noted that in general the expansion should be carried out in terms of in the complex x plane [12]. However, we find that for the analysis of the error control function defined by (17) near the turning point, the expansion alone the real axis is sufficient. In particular, it is only involved with the choice of the zeroth-order term , as can be seen from (19) and (20). |
| Potentials | ||
|---|---|---|
| Hydrogen | ||
| Harmonic oscillator | ||
| Morse potential | 0 | |
| Pöschl-Teller potential | ||
| Eckart potential |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.-F.; Zhu, T.; Wang, A. Langer Modification, Quantization Condition and Barrier Penetration in Quantum Mechanics. Universe 2020, 6, 90. https://doi.org/10.3390/universe6070090
Li B-F, Zhu T, Wang A. Langer Modification, Quantization Condition and Barrier Penetration in Quantum Mechanics. Universe. 2020; 6(7):90. https://doi.org/10.3390/universe6070090
Chicago/Turabian StyleLi, Bao-Fei, Tao Zhu, and Anzhong Wang. 2020. "Langer Modification, Quantization Condition and Barrier Penetration in Quantum Mechanics" Universe 6, no. 7: 90. https://doi.org/10.3390/universe6070090
APA StyleLi, B.-F., Zhu, T., & Wang, A. (2020). Langer Modification, Quantization Condition and Barrier Penetration in Quantum Mechanics. Universe, 6(7), 90. https://doi.org/10.3390/universe6070090







