Abstract
Power spectra play an important role in the theory of inflation, and their ability to reproduce current observational data to high accuracy is often considered a triumph of inflation, largely because of a lack of credible alternatives. In previous work we introduced an alternative picture for the cosmological power spectra based on the nonperturbative features of the quantum version of Einstein’s gravity, instead of currently popular inflation models based on scalar fields. The key ingredients in this new picture are the appearance of a nontrivial gravitational vacuum condensate (directly related to the observed cosmological constant), and a calculable renormalization group running of Newton’s G on cosmological scales. More importantly, one notes the absence of any fundamental scalar fields in this approach. Results obtained previously were largely based on a semi-analytical treatment, and thus, while generally transparent in their implementation, often suffered from the limitations of various approximations and simplifying assumptions. In this work, we extend and refine our previous calculations by laying out an updated and extended analysis, which now utilizes a set of suitably modified state-of-the-art numerical programs (ISiTGR, MGCAMB and MGCLASS) developed for observational cosmology. As a result, we are able to remove some of the approximations employed in our previous studies, leading to a number of novel and detailed physical predictions. These should help in potentially distinguishing the vacuum condensate picture of quantum gravity from that of other models such as scalar field inflation. Here, besides the matter power spectrum , we work out, in detail, predictions for what are referred to as the TT, TE, EE, BB angular spectra, as well as their closely related lensing spectra. However, the current limited precision of observational data today (especially on large angular scales) does not allow us yet to clearly prove or disprove either set of ideas. Nevertheless, by exploring in more details the relationship between gravity and cosmological matter and radiation both analytically and numerically, together with an expected future influx of increasingly accurate observational data, one can hope that the new quantum gravitational picture can be subjected to further stringent tests in the near future.
1. Introduction
In cosmology, we know that the Universe is not perfectly homogeneous and isotropic, but rather comprises of fluctuations in matter and energy densities. Furthermore, these fluctuations are congregated and correlated in a rather specific manner. Detailed measurements reveals fluctuations of various sizes follows a well-defined patterns, which can be quantified with correlation functions and power spectra [1,2,3,4]. The question of why these density fluctuations are distributed the way they are is thus an important one in cosmology. The conventional explanation for the shape of these power spectra is provided by inflation models, which are based on hypotheses of additional primordial scalar fields called inflatons [5,6,7]. The shape of the observed power spectra are then derived from quantum fluctuation of these primordial inflaton fields, and the agreement of this prediction with observations to high accuracy has been widely regarded as a great triumph and confirmation for inflation [8].
In our previous works [9,10], we have offered an alternative explanation based on gravitational fluctuations alone without inflation, which to our knowledge is the first-of-its-kind. While the theory of quantum gravity remains speculative in the short-distance regime—due to both the infinite number of allowed higher-order operators consistent with general covariance together with a lack of experimental results in this regime, the long-distance or infrared limit of the theory is however in principle well-defined and unique, governed primarily by the concept of universality. Nevertheless, this long-distance quantum theory of gravity still suffers from being perturbatively nonrenormalizable, rendering perturbation theory useless for calculating any quantum corrections in gravity. However, in the past decades, well known field theory techniques have been extensively developed, applied and even tested to high accuracy in various disciplines of physics where perturbation theory fails (e.g., non-linear sigma model, Heisenberg magnets). It is thus highly conceivable that these nonperturbative techniques may find use in deriving physical consequences for another perturbatively nonrenormalizable theory such as gravity.
From previous efforts [11,12], it was shown that quantum effects of gravity may manifest themselves not only on the extreme small (UV) scales, but also on the extreme large (IR), cosmological scales. In particular, our works [9,10] have shown that, utilizing nonperturbative field theory methods, much of the cosmological matter power spectrum can be derived and reproduced purely from Einstein gravity and standard CDM cosmology alone, without the need of any additional scalar fields as advocated by inflation. We have shown that not only the predictions agree quite well with recent data by the Planck Collaboration [13], but also that additional quantum effects predict subtle deviations from the classical picture, which allows this approach to be testable in the near future with increasingly powerful cosmological experiments.
In this paper, we extended our analysis in two major areas. First, we utilized a number of current numerical cosmological programs, such as ISiTGR, MGCAMB and MGCLASS. Secondly, with the help of these numerical programs, we generated predictions for all other cosmologically significant spectra, including polarizations (, etc.) and lensing spectra (, etc.). The paper is organized as follows. In Section 2, we summarize the theoretical basis as relevant to present discussion. Section 3 introduces the numerical programs we use. Section 4 presents the numerical results and analysis. Finally, key points and future work are summarized in the conclusion.
2. Background
In this section, we will provide a brief review of the quantum theory of gravity and how it is related to various power spectra that can be measured in cosmology. More detailed accounts of the nonperturbative approach to quantum gravity and the derivation of the spectra can be found in previous work [9,10,11,12]. The following will therefore only serve to summarize the key points and main results that are relevant for the subsequent discussion.
Quantum gravity, the covariantly quantized theory of a massless spin-two particles, is in principle a unique theory, as shown by Feynman some time ago [14,15], much like the Yang–Mills theory and QED are for massless spin-one particles. In the covariant Feynman path integral approach, only two key ingredients are needed to formulate the quantum theory—the gravitational action and the functional measure over metrics , leading to the generating function
where all physical observables could in principle be derived from. For gravity the action is given by the Einstein–Hilbert term appended by a cosmological constant
where R is the scalar curvature, g being the determinant of the metric , G Newton’s constant and is the scaled cosmological constant (where a lower case is used here, as opposed to the more popular upper case in cosmology, so as not to confuse it with the ultraviolet-cutoff in quantum field theories that is commonly associated with ). The other key ingredient is the functional measure for the metric field, which in the case of gravity describes an integration over all four metrics, with weighting determined by the celebrated DeWitt form [16]. There are two important subtleties worth noting here. Firstly, in principle, additional higher derivative terms that are consistent with general covariance could be allowed in the action, but nevertheless will only affect physics at very short distances and will not be relevant nor needed here for studying large-distance cosmological effects. Secondly, as in most cases that the Feynman path integral can be written down, from non-relativistic quantum mechanics to field theories, the formal definition of integrals requires the introduction of a lattice, in order to properly account for the known fact that quantum paths are nowhere differentiable. It is therefore a remarkable aspect that the theory, in a nonperturbative context, does not, at least in principle, seem to require any additional extraneous ingredients, besides the standard ones mentioned above, to properly define a quantum theory of gravity.
At the same time, gravity does present some rather difficult and fundamentally inherent challenges, such as its well-known perturbatively nonrenormalizable feature due to a badly divergent series in Newton’s constant G, the intensive computational power needed for any numerical calculation due to it being a highly nonlinear theory, the conformal instability which makes the Euclidean path integral potentially divergent, and further genuinely gravitational-specific technical complications such as the fact that physical distances between spacetime points—which depend on the metric which is a quantum entity—fluctuate.
Although these hurdles will ultimately need to be addressed in a complete and satisfactory way, a comprehensive account is of course far beyond the scope of this paper. However, regarding the perturbatively nonrenormalizable nature, some of the most interesting phenomena in physics often stem from non-analytic behavior in the coupling constant and the existence of nontrivial quantum condensates, which are hidden from and impossible to probe within perturbation theory alone. It is therefore possible that certain challenges encountered in the case of gravity are likely the result of inadequate perturbative treatments, and not necessarily a reflection of some fundamentally insurmountable problem with the theory itself. Here, we shall take this as a motivation to utilize the plethora of well-established nonperturbative methods to deal with other quantum field theories where perturbation theory fails, and attempt to derive sensible physical predictions that can hopefully be tested against observations. More detailed accounts on the other various issues associated with the theory of quantum gravity can be found for example in [11,12], and references therein.
For our present discussion, we will mention several main results and ingredients from this perspective. The nonperturbative treatments of quantum gravity via both Wilson’s double expansion (both in G and the spacetime dimension) and the Regge–Wheeler lattice path integral formulation [17] reveal the existence of a new quantum phase, involving a nontrivial gravitational vacuum condensate [11]. Along with this comes a nonperturbative characteristic correlation length scale, , and a new set of non-trivial scaling exponents such as , as is common for well-studied perturbatively non-renormalizable theories [18,19,20,21,22,23]. Together, these two parameters characterize the quantum corrections to physical observables such as the long-distance behavior of invariant correlation functions, as well as the renormalization group (RG) running of Newton’s constant G, which in coordinate space leads to a covariant with [12]. In particular, in can be shown [11,24] that for , the connected correlation function of the scalar curvature over large geodesic separation scales as
where d here refers to the dimension of spacetime, and is the fluctuation in the scalar curvature. Furthermore, the RG running of Newton’s constant can be expressed as
where is a characteristic nonperturbative mass scale, and a nonperturbative amplitude, which (unlike the universal exponent ) cannot be obtained in perturbation theory, and thus requires a genuinely nonperturbative approach, such as the Regge–Wheeler lattice formulation of gravity [25,26,27,28,29,30,31].
Here we note the important roles played by the quantum parameters and . The appearance of a gravitational condensate is viewed as analogous to the (equally nonperturbative) gluon and chiral condensates known to describe the physical vacuum of QCD, so that the genuinely nonperturbative scale (or equivalently ) is in many ways analogous to the scaling violation parameter of QCD (Note that gravitons nevertheless stay massless the same way gluons do in QCD, and there is no explicit violation of gauge or coordinate invariance). Similarly, the overall magnitude of such a scale cannot be established from first principles, but should instead be linked with other length scales in the theory, such as the observed cosmological constant scale , or equivalently the (scalar) curvature vacuum expectation value
The latter is related to the observed cosmological constant via the Einstein field equations
It follows that the observed cosmological constant can be used to infer the magnitude of the gravitational vacuum condensate scale . More specifically, the combination most natural to be identified with is
such that for the observed value of [11,32,33]. On the other hand, the other key quantity—the universal scaling dimension , can be extracted via a number of methods, many of which are summarized in [29,30,31,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51]. Multiple avenues (including a simple geometric argument that suggests for spacetime dimension of [12]) point to a value of , which will serve as a sufficiently good working value for this parameter in the following.
It should be noted that the nonperturbative scale should also act as an infrared (IR) regulator, such that, like in other quantum field theories, expressions in the “infrared” (i.e., as , or equivalently ) should be augmented by
where the quantity , expressed in the dimensionless Hubble constant for later convenience. Consequently, the augmented expression for the running of Newton’s constant G becomes
The aim here is therefore to explore areas where these predictions can be put to a test. The cosmological power spectra, which are closely related to correlation functions, and thus take effects over large distances, provide a great testing ground for these quantum gravity effects.
To make contact with cosmological observations, the gravitational correlation function in Equation (3) has to be related to the cosmologically observed matter density correlation
where , and
is the matter density contrast, which measures the fractional overdensity, or fluctuation, of matter density above the average background density . In the literature, this correlation is more often studied in Fourier-, or wavenumber-space, , via a Fourier transform. It is also common to bring these measurements to the same time, say , so that one can compare density fluctuations of different scales as they are measured and appear today. The resultant object is referred to as the matter power spectrum,
where . The factor then simply follows the standard GR evolution formulas as governed by the Friedmann–Robertson–Walker (FRW) metric. As a result, can be related to, and extracted from, the real-space measurements via the inverse transform
It is often convenient to parameterize these correlators by a so-called scale-invariant spectrum, which includes an amplitude and a scaling index, conventionally written as
It is then straightforward to relate the scaling indices using Equation (13), giving . Note that is sometimes referred to as in the literature, but we will use the former to avoid confusion with the fundamental gravitational correlation length .
To arrive at a prediction for the matter density fluctuations , from gravitational fluctuations , we make use of the Einstein field equations
In a matter dominated era, such as the one where galaxies and clusters are formed, the energy momentum tensor follows a perfect pressureless fluid to first approximation. Hence, the trace equation reads
(For a perfect fluid the trace gives , and thus for a non-relativistic fluid.) Since is a constant, the variations and hence correlations, are directly related as in
As described above, quantum gravity predicts that, over large distances, the scalar curvature- fluctuations scale as . This implies that the matter density fluctuations follow an analogous scaling relation
as , within the matter dominated era, and thus . From the Fourier transform in Equation (13), we get
as in wavenumber-space, in the matter dominated regime. This result of linear scaling is a well-tested and well-supported result from decades of cosmological measurements of galaxy correlations functions [52].
It should be noted that the scaling relation of Equation (3) with , and as a result or , does not follow from simple dimensional arguments, (indeed the relevant correlation function is dimensionless), and is instead a non-trivial result based on anomalous scaling dimensions associated with quantum gravity in four dimensions. Indeed (as discussed for example in [11]) in the weak field expansion the scaling result of Equation (3) would be rather different. In fact the approximate value of for galaxy matter density correlations has been a long standing puzzle in observational cosmology, see for example the cosmology monograph [1].
To extend beyond the linear matter dominated regime, the trace equation alone becomes insufficient (since the trace of the energy momentum tensor for radiation vanishes), and the full tensor equation has to be used. Furthermore, in a real universe with multiple fluid components, interactions and transient behaviors have to be taken into account, which are governed by coupled Boltzmann equations. However, these classical procedures are fully worked out in standard cosmology texts [53,54]. Following [53], the matter power spectrum can be written in two parts—an initial condition known as a primordial spectrum , and an interpolating function between the domains known as a transfer function . Thus, the full beyond the galaxy domain will take the form
where is a constant of cosmological parameters, and the factor for convenience. The transfer function is usually written in terms of , a scaled dimensionless wavenumber, with being the wavenumber at matter-radiation-equality. With this decomposition, the transfer function is a fully classical solution of the set of Friedmann and Boltzmann equations, capturing the nonlinear dynamics. This leaves the initial primordial function, which can be parameterized as a scale-invariant spectrum
which is only parameterized by an amplitude and a spectral index . is referred to as the “pivot scale”, and is simply a reference scale, conventionally taken to be .
While the transfer function —the solution to the highly-coupled and nonlinear set of Friedmann, Boltzmann and continuity differential equations—is difficult to solve, it is in principle fully determined from classical dynamics. Moreover, assuming standard CDM cosmology dynamics and evolution, a semi-analytical interpolating formula for [53] is known. As a result, if the initial spectrum , or more specifically the parameters N and , is set, then is fully determined. To find N and , it can be done by matching. Since Equation (20) is known to be valid in the galaxy and cluster domains, and Equation (21) is supposed to account for all wavenumber-scales, these equations should overlap in the galaxy domain. So by matching Equation (20), which is fixed by the scaling of curvature correlation functions, with Equation (21) in the overlapping region, N and can be found, thus fully normalizing . More precise details of this procedure, as well as detailed comparison plots with the latest observational data, can be found in our previous work [9]. The key resultant analytical prediction for from this procedure is also reproduced here in the later plot as the solid blue curve in Figure 1, showing almost perfect fit to all observational data for .
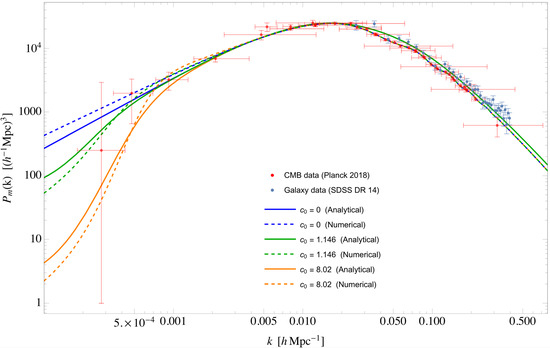
Figure 1.
Comparison between the analytical vs. numerical predictions of the RG running of Newton’s constant’s effect on the matter power spectrum . The solid curves represent the analytical predictions, with the top (blue), middle (green) and bottom (orange) representing the quantum amplitude quantum amplitudes (see Equation (9)) , respectively (see Equation (9)), of which their detailed derivations can be found in [9,10]. The corresponding dashed curves represent the corresponding the numerical predictions generated by ISiTGR, showing very good general consistency with the trend derived from analytical methods. The observational CMB and galaxy data points, taken from the Planck (2018) collaboration [13] and Sloan Digital Sky Survey (SDSS)’s 14th Data Release (DR14) [52] are also shown.
Finally for scales of k comparable to , additional quantum effects are expected to become significant, due to the nontrivial vacuum condensation nature of gravity, enough to cause deviations from the classical CDM result of . This scale is already hinted in for example Equation (4). These modification can again be done either analytically or relying on a program numerically. Analytically, the effect of the RG running of Newton’s constant (Equation (4)) can be included via dimensional analysis for the correct factors of G to include,
and IR regulations rather straightforwardly as per Equation (8), as is done in other similar quantum condensate theories such as QCD or condensed matter theories. More details can again be found in [10]. These results are reproduced as a plot later (Figure 1) to compare with the fully-numerical results, showing great agreement between them. Obtaining the latter, i.e., the numerical results, shall form the focus and the remaining of this paper. Following similar analysis to determining , other spectra such as the angular temperature spectrum , should be fully derivable from the primordial function , or specifically , which is set by the scaling of gravitational curvature fluctuations . In fact, many spectra are only various variations of integral transforms with different physical observable quantities, say, photon temperature and polarization, instead of mass density . A brief review of that is given in Section 4.2. Finally, it should be re-emphasized that in this picture, a scalar field is not an essential ingredient to determine .
It should be noted that there are intrinsic uncertainties in some of the theoretical parameters of this analytical approach as well—such as the value of the scaling dimensions of from Equation (3), or the amplitude of the first order quantum corrections for the RG running of Newton’s G from Equation (4). These values have to be extracted from the highly nonlinear gravitational Feynman path integral, and have to be done through either various analytical approximations, or more precisely through numerical simulations. For example, from the latest lattice simulations results of the path integral, it is found and , with the latter an error that is estimated at around . Other methods, summarized in [11], including observational data as studied in [10], all support the value . As eluded in this paper as well, this concordance for the value of with various methods is not surprising, given the universality nature of this index . On the other hand, the amplitude for quantum corrections cannot be claimed to the same degree of confidence as , other than an intuition that it should be some order-1 parameter. For example, from a comparison with latest observational data for in [10], the data seem to best fit a value roughly 7 times smaller () than that suggested by lattice simulation. So the agreement for is less precise compared to , and is only up to the order of magnitude. However, it should also be pointed out the theoretical expression defining possesses a slight degeneracy with the correlation length scale (Equation (4)). Hence, the data can also be interpreted as suggested as a value of 14,000 Mpc, around times larger than the expected , or, some combination of both instead. In principle, the inclusion of IR regulation to the final expressions (Equation (9)) changes the shape of the curve and can in principle break the degeneracy, but the current crudeness of the observational data in those regimes of k is much too uncertain to make any conclusions as to the more favorable possibility. While we will continue to primarily refer to studying the constraints on for simplicity for the rest of this paper, it should be kept in mind the possibility of this degeneracy. It is also hopeful that with increasingly precise observational data in the future, complimented with looking at independent and orthogonal observables that we are to present in this paper, a better constraint on these theoretical parameters can be found.
Finally, it should be noted that the current most popular approach to explain the shape, or more precisely, the index of the matter power spectrum is typically reliant on the fluctuations of postulated primordial scalar fields from inflation models [55]. Given the long interest for understanding this spectral index [56,57,58], the ability to derive this index, as well as the lack of competing theories, is thus championed as a triumph of inflation. The picture reviewed here, where the correlations are explained by nonperturbative critical scaling behaviors of gravitational fluctuations, is thus first-of-its-kind. As discussed in this background, the formulation of this picture is in principle rather constricted with little flexibility. As a result, this gravitational picture makes concrete predictions that can be concretely tested (or falsified), without suffering from the typical flexibilities in scalar-field-driven inflation models, and thus offering a compelling alternative to the canonical inflation picture.
Having reviewed this analytic background, we will next present the numerical programs we used, and the subsequent results for the cosmological spectra from effects of quantum gravity.
3. Numerical Programs
There are a variety of publicly available Einstein–Boltzmann (EB) solvers that have been in use for the past two decades starting with CMBFAST [59]. The main independent programs are CAMB [60] and CLASS [61] which solve the coupled Einstein–Boltzmann equations in a background FRW metric. These codes are computed for CDM cosmology with a limited set of choices for a parameterization of equation of state for the Dark Energy (w). In all our programs we use , which considers dark energy as a vacuum energy.
For modifications of gravity with a scale dependent gravitational constant, there are three EB solvers. We used Integrated Software in Testing General Relativity (ISiTGR) [62] as the primary code to generate power spectra. Then we compare with another two programs Modified Growth with CAMB (MGCAMB) [63] and MGCLASS (CLASS version for phenomenological modified gravity) [64]. ISiTGR and MGCAMB are patches for CAMB and COSMOMC [65] which was written in the FORTRAN language, while MGCLASS is a patch for CLASS written in C. All three programs have implemented the parameterization effective gravitational coupling —gravitation slip parameter which sometimes is denoted as . Those two parameters are defined as and where is the laboratory value of Newton’s gravitational constant and are scalar potentials in the conformal Newtonian gauge. The comparison of the three programs for no RG running of G as in standard CDM cosmology is shown in Figure 2 and Figure 3.
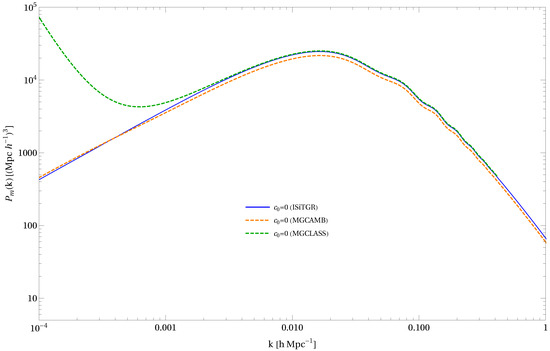
Figure 2.
As an example we illustrate the predictions between the three programs—Integrated Software in Testing General Relativity (ISiTGR) (blue), Modified Growth with CAMB (MGCAMB) (orange) and Modified Growth with CLASS (MGCLASS) (green)—with their corresponding patches for a modified Newton’s constant. This serves as a consistency check between the programs and a validity check for their patches. The solid curves are generated from the respective original CDM programs, while the dashed curves are generated by each program’s modified Newton’s constant patch setting . It can be seen that ISiTGR is the most consistent, and hence reliable program of the three, to investigate the effects of a modified Newton’s constant.
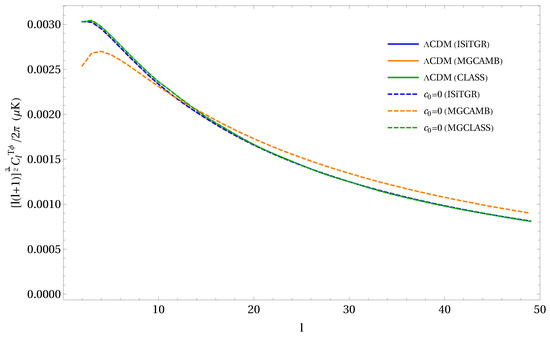
Figure 3.
Comparison of the predictions between the three programs—ISiTGR (blue), MGCAMB (orange) and MGCLASS (green)—with their corresponding patches for a modified Newton’s constant. This serves as a consistency check between the programs and a validity check for their patches. The solid curves are generated from the respective original CDM programs, while the dashed curves are generated by each program’s modified Newton’s constant patch setting . It can be seen that ISiTGR is the most consistent, and hence reliable program of the three, to investigate the effects of a modified Newton’s constant.
One can see that while all three program’s CDM predictions are generally consistent, only ISiTGR’s modified Newton’s constant patch with (or equivalently in Equation (9)) is consistent with its original default-CDM prediction. Matter power spectrum from MGCLASS has a noticeable upper trend for small k from the CDM curve, as shown in the left plot in Figure 2. Figure 3 shows a significant deviation of MGCAMB’s from the CDM curve. Primarily due to this reason we chose ISiTGR over these two other programs.
In the ISiTGR program all times are in conformal time, as is the case for CAMB. The growth equations are written based on a perturbed FLRW metric in the Newtonian gauge,
where and are scalar gravitational potentials, represents comoving coordinates and is scale factor at conformal time . For a flat universe the three dimensional spatial metric in cartesian coordinates is given by
From now on we only discuss cosmology for a spatially flat universe (usually described in the literature as the case ).
There are four built in functional forms for selected modified cosmologies [66] and we used - gravitation slip parameter form. The modified growth equations are
and
where and are respectively the equation of state and density of ith particle species. Generally there are three species which are radiation, non relativistic matter and dark energy. is the gauge-invariant, rest-frame overdensity defined by,
where is the Hubble’s constant in conformal time, fractional overdensity and is the heat flux, related with the peculiar velocity ()
From the conservation of energy-momentum tensor of the perturbed matter fluids and for uncoupled fluid species evolution is given by
Secondary effects considered by ISiTGR are reionization, weak gravitational lensing and the integrated Sachs–Wolfe (ISW) effect. For reionization it uses the same approach as in CAMB [67], namely a simple tanh model for reionization fraction , given by
where , is the red shift value where the , and is the fractional change in y. The latter agrees with a Thomson scattering optical depth for an instantaneous reionzation which occurred at . The treatment of weak lensing is discussed here later in Section 4.
Since the required formulation for , as appropriate for the quantum RG running of Newton’s G described earlier, does not appear as an inbuilt function, we added a part with newly defined functions , for our need in the above equations. In accordance with Equation (9) we have
and .
As secondary effects, ISiTGR considers reionization, weak gravitational lensing and the ISW effect. is assumed since there are no different modifications to the potentials. ISiTGR has two binning methods but here we only used the traditional binning method. For all the power spectra computations we set the tensor part to zero. The program computes 2-point self- and cross-correlation functions for the temperature, E-mode and B-mode polarization and weak lensing potential. Each generated power spectrum appears in two separate files, one with lensing and the other without. In the following we use power spectra with gravitational lensing included. The values of the cosmological parameters we used here as initial conditions are shown in Table 1.

Table 1.
Values used here for cosmological parameters in the CDM model. We have used the Planck-18 68% interval from CMB power spectra, in combination with CMB lensing reconstruction and Baryonic Acoustic Oscillations (BAO).
In a previous paper [9,10] we used semi-analytic methods to solve for the matter power spectra using semi-numerical approximations for the relevant transfer functions. In the current approach the numerical programs solve the full set of Boltzmann equations, and uses integration techniques such as adaptive Runge–Kutta method to integrate all the tightly coupled equations. Secondary effects accounted for like reionization and integrated Sachs–Wolfe (ISW) effect are treated as a more general case compared to our previous work.
4. Numerical Results
In this section we present numerical results for the quantum gravitational corrections to the various cosmological spectra (). This includes both the effects of an RG running of Newton’s constant and the IR regulation, collectively achieved by replacing
For simplicity, of the three numerical programs used for our analysis (ISiTGR, MGCAMB, MGCLASS), only the results from the ISiTGR numerical program shall be plotted. The reason for this choice is that we expect this program to provide better consistency and reliability in the particular region considered (small k, small l), as explained in Section 3. Furthermore, all numerical results presented here are generated using the latest values of the cosmological parameters as given by Planck (2018) [13].
In the above, is the coefficient that governs the amplitude of quantum corrections. For all the following spectra, three different values of and will be plotted. Lattice calculations give . However, being a non-universal parameter, it can depend on specific choices arising from the way an ultraviolet cutoff is imposed. Therefore, not too much weight should not be placed on this specific value, beyond perhaps the order of magnitude. In practice, this value could be further constrained by experiments, which is precisely what these observations of cosmological spectra can achieve. From previous work [10], using the approximate semi-analytical methods, we see that a value of is generally favored.
4.1. Matter Power Spectrum
We start with the matter power spectrum . Recall the definitions
where the variable is the fractional density fluctuations above the average, referred to in cosmology as the mass-density contrast. The numerical results for obtained from the numerical program (ISiTGR), for both the classical CDM (i.e., ) and quantum () results, as well as the respective analytical results (as derived in [9,10]), are shown and compared in Figure 1.
From Figure 1, we see that all the numerical results are generally consistent with the corresponding analytical results from earlier work, which were obtained by following the semi-analytical interpolating formulas from [53], and the implementation of the RG running following dimensional arguments. The small deviations may be attributed to the slightly older values of cosmological parameters [68] and some analytic approximations used by Weinberg and Dicus’ interpolating formula for the transfer function in [53], whereas the numerical results presented here use the latest cosmological parameter values from the Planck collaboration [13]. Despite the small discrepancies, we see that the overall trends, and the extra downwards bend due to the inclusion of the (IR regulated) RG running of Newton’s constant, as predicted analytically using the semi-analytical formulas are in very good agreement with the numerical predictions using the latest fitted cosmological parameters. This overall general agreement between the analytical and numerical result provides a good verification and confidence that the procedure of including a running Newton’s constant as presented above is reliable.
The same numerical analysis has now been repeated with the other two numerical programs MGCAMB and MGCLASS, besides ISiTGR. The result of MGCAMB is in extremely good agreement with ISiTGR, with its predictions for all three values of almost completely overlapping with ISiTGR’s result, giving additional confidence to the latter. However, while MGCLASS is relatively consistent with ISiTGR for most of the angular spectrum results (as we will discuss later), its prediction for shows a rather radical upturn below , which is at odds with both ISiTGR and MGCAMB, as well as the analytical predictions (also shown and discussed earlier in Figure 2 and then in Section 3), even for the CDM case. The pathological upturn at small-k and resultant disagreement of MGCLASS (even with CLASS, the original CDM program that MGCLASS is based on, when setting ) suggests some potentially unresolved issues in MGCLASS’s prediction for , while the consistent results between ISiTGR, MGCAMB and the analytical predictions should be treated in our opinion with a higher reliability.
Given the more confident, and in principle more accurate, predictions from the numerical programs as shown in Figure 1, it can be seen that the value of is a better overall fit to the observational data from Planck, which is a consistent conclusion from our previous work that was based exclusively on the early analytical results. Armed with the new tools of numerical programs, we will now move on to present the numerical results for the other various correlation functions, which will hopefully shed new insights to the validity of the quantum gravity effects in cosmology.
It should be noted that there is a slight degeneracy between and in the original expression for the RG running of Newton’s G, as in Equation (9). A support of a smaller from the observational data can equivalently be mimicked by an increase in the vacuum condensate scale . In fact, the apparently better fit value of , seven times smaller than the lattice predicted value of ≈8.0 ± 3.1, can be mimicked by simply a factor of ∼1.9 larger in . Technically, including IR regulation will change the shape of the curve and break the degeneracy, which in principle could be fitted sophisticated say with a Monte Carlo simulation. However, not only is that currently beyond the scope of this paper, the lack of and crudeness of data points in the small-k regime will not render the exercise fruitful.
On the other hand, it may be instructive, amongst other physical motivations, to look at the quantum effects on a variety of other spectra of cosmological significance with these numerical programs. With independent quantities and measurements, the new plots may either provide additional constraints to these quantum gravitational parameters, but also potential insights to the physics.
4.2. Angular Temperature Power Spectrum
The TT power spectrum is one of the most important cosmological spectrum since it is measured to high degree of accuracy, thus allowing for great insights in constraining various cosmological models. Figure 4 shows the numerical predictions for the temperature-temperature (TT) angular power spectrum with and without the quantum effects. We will first briefly recall the definitions for and how theoretical predictions for it can be obtained, and then compare them against observational data. Following notations in Weinberg [53], the temperature fluctuations can first be resolved into spherical harmonics ’s,
where is the temperature in the direction , the average temperature over the sky and the coefficients quantifying the fluctuation for each harmonic. Since ’s are real, and the products of s are rotationally invariant, one has
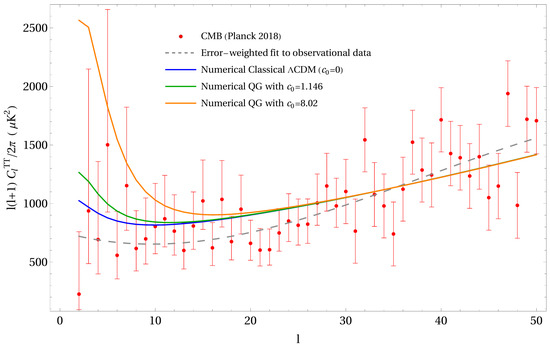
Figure 4.
Comparison of the numerical prediction of the classical CDM program vs. the numerical predictions of the renormalization group (RG) running of Newton’s constant’s effect on the temperature (TT) power spectrum . The solid curves represent the numerical predictions generated by the ISiTGR program, with the bottom (blue), middle (green) and top (orange) representing quantum amplitudes (see Equation (9)) , respectively (see Equation (9)), showing a higher trend at large angular scales () as compared to the classical CDM (no running) numerical curve. The dashed curve represents an error-weighted cubic fit to the observational CMB data, from the Planck (2018) collaboration [13].
Here the are the Legendre polynomials, and is defined as
the 2-point correlation functions of , the temperature fluctuation in “l”-space. Or equivalently,
by inverting the transformation. As a result, the correlations for temperature-temperature fluctuations are fully quantified with the s. (Note that here we use instead of the usual notation for the Legendre polynomials, in order to avoid confusion with the matter power spectra.)
Theoretically, since CMB photon temperatures and matter density are coupled, the s are therefore related to the matter power spectrum , via integral transforms that involve spherical Bessel functions and appropriate form factors and transfer functions. However, from transforming the predictions from one set of observable to another, new insights, and potential constraints to the theory, can be derived.
To do so, one can first use the Friedmann and continuity equations to relate the temperature fluctuations to the metric perturbations, via suitable form factors , through
where the latter are defined as
Here the B and E functions are suitable decompositions of the metric perturbations, and is the velocity potential for the CMB photons. It is known that these form factors simplify in certain gauge choices. In the synchronous gauge, one has , whereas in the Newtonian gauge and , which then gives
(Note that and are referred to as “” and “”, respectively in [53]. Here we will use the former in order to avoid confusion with the expression for the running of Newton’s constant , as it will be implemented below. The above equations also assumed a sudden transition to opacity on the CMB at a time , which nevertheless does not change the form of the basic equations and only some of the details, which are later taken into account fully with the numerical programs, discussed below.)
Hence, given appropriate initial conditions, the functions and , as well as the scale factor and the function , can all be obtained as solutions of the classical Friedmann equations. These are then combined with the Boltzmann transport equations, as is done in standard cosmology, which eventually leads to unambiguous predictions for the s. The solutions for can be parameterized in terms of transfer functions , and , leading to the following expressions for and
where , , Mpc, Mpc, Mpc, Mpc and (the latest set of suitable parameters are taken from Planck 2018 [13]). It is noteworthy at this stage to point out again that all three transfer functions are completely determined by standard measured cosmological parameters, so that the only remaining ingredient to fully determine the coefficient is the initial (or primordial) spectrum , where q is the wavenumber, and “o” refers to outside the horizon. Conventionally, is parameterized by an amplitude N and spectral index ,
Here the reference “pivot scale” is usually taken to be by convention. As a consequence, once the primary function is somehow determined, classical cosmology is then expected to fully determine the form of the spectral coefficients. It is therefore possible to write the s fully, and explicitly, in terms of the primary function . After expanding the plane waves factor in a complete set of spherical harmonics and spherical Bessel functions, from Equation (38) becomes
where , and we have factored out the function explicitly by defining and .
Now, recall that the matter power spectrum is given by
which tells us that we can obtain a direct relation between the matter power spectrum and the angular temperature coefficients ,
where q and k are related by , and the scale factor “today” can be taken to be 1. As a result, the predictions on can be directly transformed into a prediction for . Utilizing the same parameters in the numerical programs, the effects of with and without the RG running of Newton’s constant (with IR regulation) on can then be generated.
Figure 4 shows the numerical result of (no running) , and with the blue, green and orange curve, respectively, generated by ISitGR. The observational CMB data from Planck (2018), as well as an (error-weighted) cubic fit for ence, are also shown. Noticing that the point is anomalously low, with large uncertainty due to cosmic variance, the error-weighted fit shown in this plot has not included the point.
From Figure 4, we see that the effects of a RG running of Newton’s constant generally cause an upturn to the spectrum at low-ls, starting at roughly . It can also be seen that the orange curve with a quantum amplitude (see Equation (9)) (or Mpc) creates a much more dramatic deviation, reaching a maximum of larger in value compared to the blue, classical () CDM curve, while the green curve with (or roughly = 14,000 Mpc) has a milder deviation of ≈24% from the classical result. Again, neglecting the anomalous point, the green curve with is generally consistent with all observational data, arguably also with the desirable feature of marginally going through the error bars of and . On the other hand, the orange curve, while still lying within a few points’ error margins, is less favorably supported by the data in this plot. It is also seen that its deviations starts earlier at a higher value around , which causes it to miss a few more error bars in the low l points. As a result, the numerical results of this plot shows that the green (or 14,000 Mpc) curve is currently a more favorable parameter than the orange one. Note that this is also consistent with the discussion and conclusion from the matter power spectrum plot in Figure 1.
We also investigated the results with all 3 programs. However unlike , the three programs do not agree, despite being supplied with the same RG modified expression for Newton’s constant. Figure 4 displays the result from ISiTGR, which seems to be the most consistent for all plots. MGCAMB produces a much more dramatic upturn effect from the RG running at small ls, roughly having its curve coinciding with ISiTGR’s curve, and the MGCAMB curve even higher. On the other hand, MGCLASS predicts a much milder upturn, with its curve coinciding with ISiTGR’s curve. In other words, MGCAMB seem to predict an upturn around 7 times larger than ISiTGR, while MGCLASS seem to predict an upturn that is 7 times smaller than ISiTGR. Given the blackbox nature of such programs, it is unclear of the cause of this different given that all programs where supplied the same modification in Newton’s G. These programs, designed for modified gravity models, are known to be less well-tested compared to their base program (CAMB, CLASS), and it may not be surprising that two (or all) of them may be incorrect. One consistency is that all three programs predicts an upturn at low l’s, just to a different degree, roughly order of magnitude. Hence, it is at best that we can conclude from these available programs that the RG running of Newton’s G causes an upturn to roughly the order of magnitude presented in Figure 4.
Perhaps even more intriguing is the disagreement with a naive analytical analysis. From Equation (49), the first order estimate is that since is the (weighted) integral of over all k, a smaller caused by an RG running (c.f. Figure 1) should cause a smaller value of . In fact, if one assumes the transfer functions are not affected by the quantum corrections, the integral Equation (49) can be performed numerically (as done in [10]), since the classical interpolating formulas for the transfer functions are known, which does show a downturn, as naively expected, instead of an upturn. This work utilizes programs that in principle modifies the initial Friedmann and Boltzmann equations from the beginning, and includes any effects of the RG modified Newton’s G into the solutions, and thus in principle more trustworthy. Given the opaque nature of such programs, it remains further investigations through a more detailed study of the entangled initial set of coupled differential equations to fully understand the disagreements between the programs and the first-order analytical result, as well as the disagreement, and hence the reliability, within the numerical programs.
Nevertheless, given that these programs represents the most sophisticated tools currently, it is still constructive to look at their predictions of the quantum effects on other modes and variables of the CMB. For example, the theoretical predictions for the percentage deviations for curve with the classical curve is ∼37% on at its further available data point, while only ∼24% on . This reveals the fact that the quantum effects maybe more significant in different physical variables. So by studying the predictions for different auto- and cross-correlations of different variables, and comparing them to potentially independent data (e.g., ground-based measurements of E- and B-mode polarizations as opposed to space-based measurements of CMB temperature), new constraints and insight may be deduced. We will present the analysis and results of the other spectra of interest to cosmology in the remaining of this section.
4.3. Temperature-E-Mode Power Spectrum
The next few most popularly studied correlations on the CMB are the so-called E- and B-type polarization modes. Here we will give a brief recap of the physics, and present the numerical results of the quantum corrections from a RG running Newton’s constant, later compared with the observational data.
Recall that observations of the CMB photons not only reveal their intensity (i.e., temperature) from various directions, but also the photons’ polarizations, which can result from scattering on free electrons either at the time of recombination, or during the later period of reionization. Measurements on polarizations then reveal extra information in constraining the parameters arising from a running of Newton’s constant.
Following notations in [53], CMB photon distributions are fully described through a number density matrices , or, more usefully, the dimensionless version of its perturbation (referred to as the dimensionless photon intensity perturbation matrix), related to via
In a line-of-sight direction , can be parameterized via
where and V are three real functions of direction (with units of temperature), known as the Stokes parameters, describing the photon’s polarizations. Notice that the photon temperature perturbations are given by the trace
It is these Stokes parameters that are measured in current observations of the CMB. Since the scattering of light by non-relativistic electrons does not produce circular polarization, one expects that all CMB photons will be linearly polarized, so that is real, and therefore V = 0. For further convenience in comparing with observations of 2-point functions, which respect spherical symmetry, it is useful to expand the Stokes parameters and seen in a direction in a series of functions
where the subscript “P” in the coefficient stands for “polarization”, is the angular part of the gradient operator and are the polarization vectors in the direction . To further satisfy the reality condition, one defines the amplitudes
so that their correlation functions
are real and rotationally invariant. The above relations define the various angular power spectrum functions , where . The superscripts E and B are referred to as E- and B-type polarization, respectively, since under spatial-parity inversion, , and similarly for , whereas . As a result of parity, there are no bilinear correlations between B with either E or T. (i.e., .)
With this background, we shall present the numerical predictions for the corresponding spectra with and without an RG running of Newton’s G, compared against the latest observational data. We start with the spectrum. Figure 5 shows the numerical results with the observational data for . The lowest solid (blue) curve represents the classical () spectrum, while the solid middle (green) and top (orange) curve represents the effect of a RG running Newton’s constant with and , respectively.
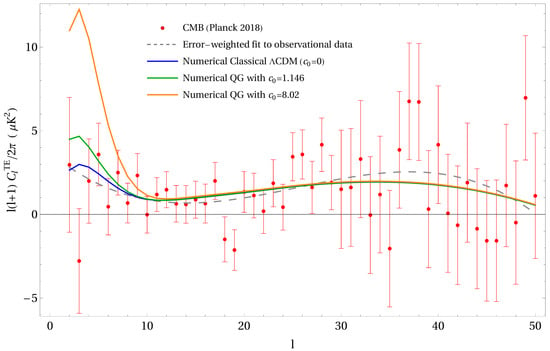
Figure 5.
Comparison of the numerical prediction of the classical CDM program vs. the numerical predictions of the RG running of Newton’s constant’s effect on the cross-temperature-E-mode-polarization (TE) power spectrum . The solid curves represent the numerical predictions generated by the ISiTGR program, with the bottom (blue), middle (green) and top (orange) representing quantum amplitudes (see Equation (9)) quantum amplitudes (see Equation (9)) , respectively. Here again one finds higher trends at large angular scales () as compared to the classical (no running) numerical CDM curve. The dashed curve represents an error-weighted cubic fit to the observational CMB data from Planck (2018) [13].
It turns out new constraints for the RG running parameter can be deduced with this new plot. With the inclusion of the E-type polarization data, we see that this has further constraints on some of the error bars in the low-l data points. This is due to the smaller error bars from the observational data in the E-type polarization correlations in the low-l regime (see Figure 6). As a result, one sees that the top curve (orange) is strongly disfavored by this plot. Another observation is that the difference between the and the classical CDM () curve is about in this plot, which is a larger percentage deviation compared to ≈24% for the plot.
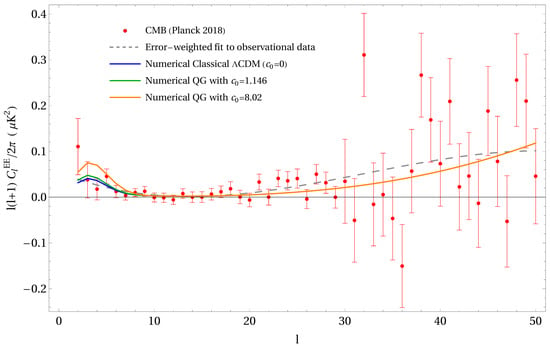
Figure 6.
Comparison of the numerical prediction of the classical CDM program vs. the numerical predictions of the RG running of Newton’s constant’s effect on the E-mode (EE) power spectrum . The solid curves represent the numerical predictions generated by ISiTGR, with the bottom (blue), middle (green) and top (orange) representing quantum amplitudes quantum amplitudes (see Equation (9)) , respectively, showing slightly higher trends for large angular scales () as compared to the classical (no running) numerical CDM curve. The dashed curve represents error-weighted cubic fit for observational CMB data from the Planck (2018) collaboration [13].
We also compared the results from the other two programs (MGCLASS and MGCAMB, not shown on Figure 5). All the resultant curves of MGCLASS agree with ISiTGR for . But for , the curve of MGCLASS is about lower than the corresponding ISiTGR curve. All two curves with RG running from MGCLASS are within the error bars but due to the mismatch as shown in the Figure 2, MGCLASS results should be investigated further. For MGCAMB, the curves with RG running are significantly higher than ISiTGR, making them disfavored. In addition, there is a slight horizontal shift for MGCAMB in l-space compared to the other two program, which should be investigated further.
4.4. EE- Power Spectrum
We move on to the spectrum. Figure 6 shows the numerical results with the observational data for . We also plotted an error-weighted cubic fit (dashed line) for the classical () spectrum (solid blue), as well as the quantum RG running of G for the above values for (green and orange). It can be seen that there is no significant deviation from standard CDM prediction like in temperature power spectra and all the curves are well within the data point error bars. We can see that in the large scales () the errors are significantly small which makes T-E spectrum having smaller error bars in the scale of interest in this paper.
When the other two programs are compared, there is no significant deviation to rule out any any curve. There is no noticeable deviation for MGCAMB curves from ISiTGR for but there is a slight upward deviation for . With MGCLASS, the RG curves are smaller than ISiTGR making smaller deviation from CDM curve.
4.5. BB- Power Spectrum
Next we discuss about B-mode polarization power spectrum, here shown in Figure 7. We have plotted an error-weighted quadratic fit (dashed line) for the classical () spectrum (solid blue), as well as the RG varying of Newton’s G for (green). It can be seen that there is no noticeable deviation from standard CDM prediction like in the temperature power spectra, and all the curves are well within the data point error bars. As a result of the unnoticeable deviation, we did not include the curve. In standard cosmology, due to weak lensing there is a partial conversion of the E-mode to the B-mode polarization and it’s predicted to be considerable around scale which leaves large scale () close to zero. Due to limitations in dust modeling and telescopes limitations there are only data up to .
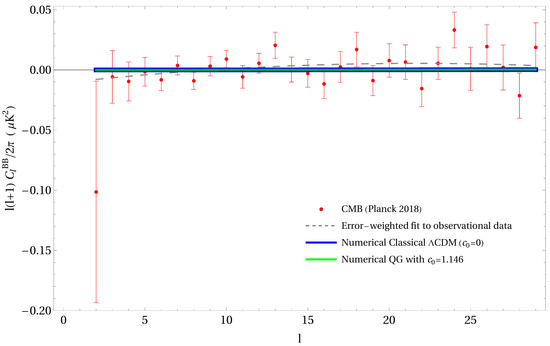
Figure 7.
Comparison of the numerical prediction of the classical CDM program vs. the numerical prediction of the RG running of Newton’s constant’s effect on the B-mode (BB) power spectrum . The solid curves represent the numerical predictions generated by ISiTGR, with the top (blue) and bottom (green) representing respectively, showing no significant deviation with the classical no running numerical CDM curve. The dashed curve represents error-weighted quadratic fit for observational CMB data from the Planck (2018) collaboration [13]. The other curve, like the (green) curve, is consistent with zero (to around 1 part in 10,000). So any deviations from the classical and curve are too insignificant to be seen, and negligible relative to the size of the error bars from the current latest data. Hence the curve is not included in this plot for clarity.
4.6. Lensing Power Spectrum
The theory of CMB lensing is a vast topic on its own. Here, we will try to present the key defining equations of the lensing spectrum, and then look at the numerical results of quantum gravitational effects on the lensing potential spectra. A more complete account for the physics and observations can be found in [53,69,70].
Consider a small deflection angle from the undeflected direction of a CMB photon, with describing perpendicular direction to , and . Define the shear matrix as
where run over the directions orthogonal to , is the radial distance of the source from earth in a Robertson–Walker coordinate system and is the amount of deflection of . From standard general relativistic calculations, the shear matrix can be related to the Newtonian potential of the lens source (), via
where is a small perpendicular deflection vector to , and is the time for a photon that that just reached us from radial coordinate r. Hence, the measurements of the shear matrix can yield information about perturbations to the gravitational potential () by masses spread along the line of sight. Define the so-called lensing convergence field as
is particularly useful because, if the lensing is due to a collection of bodies all at about the same radial coordinate , it can be directly related to the matter perturbations . More explicitly, falls off rapidly for large distances, so that the factor can be replaced in a first approximation with and similarly the second term with can be dropped. Then Poisson’s equation gives
resulting in an expression directly linking to matter density fluctuations . Hence, a measurement of the value of for sources seen in one direction can reveal the total mass density of a cluster of lensing masses that lies along that line of sight at distance (projected onto a plane perpendicular to the line of sight). Since, as we have shown, gravity constraints the scaling of correlations of matter, it should also do so for .
So, to project the convergence field onto the sky, we decompose it in a way that is analogous to the other angular spectra,
with
with quantum noise fluctuation correlation
which defines
Or more explicitly, by inverting the expression in Equation (67),
In the literature [69,70], it is often the correlation for the lensing potential that is plotted, instead of that of the lensing convergence field , related by
Finally, the cross-correlations and can be similarly defined in analogous to Equation (67) with respective expansion coefficients and , similar to Equations (56)–(59). With this background, we will present the numerical results of including a quantum RG running of Newton’s constant for these spectra.
In Figure 8 for we have plotted for the classical () spectrum (solid blue), with as well as for an RG running of G with the previously used values for (green and orange). One can see that there are a significant deviation which is up to for , but only for , compared to the standard CDM prediction. Due to current observational limitations there are only three data points which lie inside our region of interest (). Apart from Planck collaboration (2018) data other projects such as the South Pole Telescope (SPT) [71] and the Atacama Cosmology Telescope (ACT) [72] have few observational data points which mostly lie in the region .
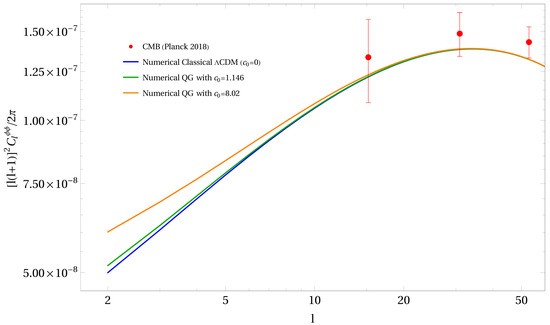
Figure 8.
Comparison of the numerical prediction of the classical CDM program vs. the numerical predictions of the RG running of Newton’s constant’s effect on the deflection lensing () power spectrum . The solid curves represent the numerical predictions generated by ISiTGR, with the bottom (blue), middle (green) and top (orange) representing the quantum amplitudes (see Equation (9)) , respectively, showing just slightly higher trends at the very large angular scales () as compared to the classical (no quantum running) numerical CDM curve. Only limited observational data is available currently, especially at large angular scales (below ).
4.7. Temperature-Lensing Power Spectrum
For the and power spectra there are no observational data points so far, and given having limited number of data points we do not expect to have any in the large scale region (). In Figure 9 we show and we have plotted the classical () spectrum (solid blue) with RG with the above values for (green and orange). It can be seen that there is significant deviation for which drops to negative values. The deviation begins for scales corresponding to . For it drops up to of standard CDM prediction.
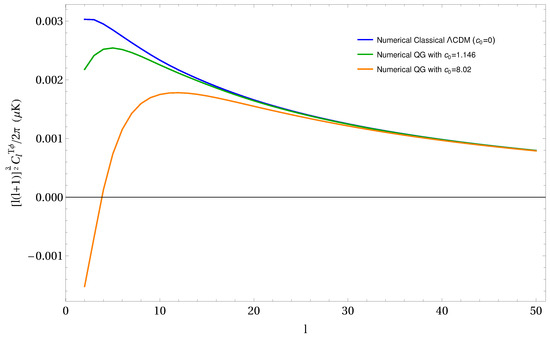
Figure 9.
Comparison of the numerical prediction of the classical CDM program vs. numerical predictions of the RG running of Newton’s constant’s effect on the cross-temperature-lensing (T) power spectrum . The solid curves represent the numerical predictions generated by ISiTGR, with the bottom (blue), middle (green) and top (orange) representing quantum amplitudes (see Equation (9)) , respectively, showing again just slightly higher trends at large angular scales () as compared to the classical no running numerical CDM curve. No data with reasonable errors are found so far for .
4.8. Lensing-E-Mode Power Spectrum
In Figure 10 we show the results for , and we have plotted the classical CDM () spectrum (solid blue) compared with the RG running of Newton’s G spectrum with the above values for (green and orange). It can be seen that there is significant deviation for which drops by more than which gets ruled out. The deviation begins around scales corresponding to . For it drops within of the standard CDM prediction. Since for now there are limited observational data points for nothing can be done about ruling out any specific model. In the near future with CMB-S4 (The next generation "Stage-4" ground-based CMB experiment) [73] more data on , might provide a good test for the models.
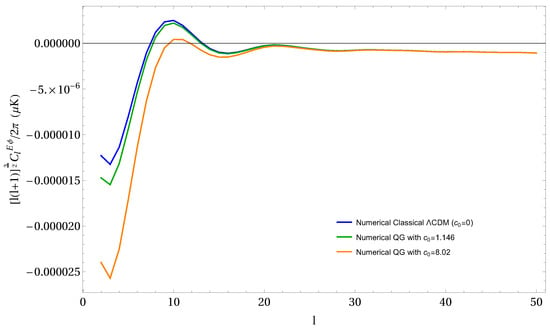
Figure 10.
Comparison of the numerical prediction of the classical CDM program vs. numerical predictions of the RG running of Newton’s constant’s effect on the cross-E-mode-lensing (E) power spectrum . The solid curves represent the numerical predictions generated by ISiTGR, with the top (blue), middle (green) and bottom (orange) representing quantum amplitudes (see Equation (9)) quantum amplitudes (see Equation (9)) , respectively. showing this time smaller trends at the large angular scales () as compared to the classical no running numerical CDM curve. No data with reasonable errors are found so far for .
5. Conclusions
In this paper, we have revisited the derivation of the matter and temperature power spectra from the quantum theory of gravity without invoking any additional scalar fields from inflation, which, to our knowledge, is the first of its kind. We reviewed that while the short-distance quantum theory of gravity remains speculative, the long-distance behaviors are well known and primarily governed by the renormalization group (RG) behaviors near its critical point. In particular, we reviewed how the critical scaling dimension “s” of the correlation function of the scalar curvature fluctuations at large distances directly governs the scalar spectral index “” of the cosmological spectra, as well as the additional quantum gravitational effects, such as the (IR-regulated) renormalization group running of the coupling constant (Newton’s constant) G, that will affect these spectra subtly at large distances. We then presented the various numerical programs that we used in this work, and their main results, to complement the previous mainly analytical analysis. We then utilized these programs to further study other cosmological spectra of different modes. We compared these with latest available observational data, and provided new constraints and insights to the parameters () of the quantum theory. We also discussed the possibility of verifying, or falsifying, some of these hypothesis with increasingly powerful observational cosmology experiments in the future.
Using the numerical results, we find that especially the plots of the matter power spectrum , the angular temperature spectrum , and the angular temperature-E-mode spectrum - all play an important role in revealing new insight to constraining the quantum amplitude , a parameter that governs the size of quantum corrections due to the RG running of Newton’s constant. We find that all three plots agreeably favor a value of closer to around , rather than the naive estimate of ∼8.0. This is particularly obvious in the new plot from this work, with the curve showing a ∼60% deviation from the classical CDM (no quantum running) curve. On the other hand, the angular E-mode spectrum and angular angular B-mode spectrum plots are the least useful in distinguishing the running effect, with the plot showing only a mild deviation of about 15% from the classical prediction for the curve, and the deviations on the plot are basically consistent with zero. The three angular lensing spectra, and , are potentially feasible candidates in providing further insights and constraints. Especially for the plot, showing around 20% and almost 150% deviation for the and curve respectively, from the classical curve. However, all these latter spectra suffer from a lack of observational data in the low-l regime, making it impossible to draw any conclusion about the favorability of the parameter or the RG running in general at this stage.
However, although the percentage differences between the spectra with and without quantum corrections are decently significant for scales below —ranging from ∼15–60% even with the milder value of for , the uncertainties from current observational data in those ranges are unfortunately even larger. As a result, it is not yet possible to conclude at this stage the visibility of these effects. At best, one can claim the slight hints of RG running from the smallest data point in , as well as the last few points (, ignoring the anomalous point) of . Nevertheless, with technology and precision of cosmological experiments improving at a rapid pace, better observational data in this regime perhaps forms one of the most promising area where quantum effects of gravity can be revealed and tested for the first time. This is a consequence of the concrete predictions of the long-distance quantum effects, based on well-established renormalization group analysis, as opposed to the still rather speculative short-distance theories of gravity.
From a theoretical perspective, the numerical results from this work also serve an important purpose in ruling out the less favorable value of for the quantum amplitude, but instead suggesting a value around seven times smaller, closer to . We also noted that the uncertainties in the observational data at low-ls cannot yet fully constrain the precise shape of the RG running, allowing for the possibility that these various deviations can all be mimicked instead by a modified value of 14,000 Mpc, or around 2.5 times larger than the naive estimate . As we discussed in the theory section (Section 2), unlike the universal critical scaling index (shown from various method to have a value very closed to ), the parameters and do not necessarily follow from universality, but are instead confident only up to order of magnitudes. While the observational data at this stage cannot yet exhibit the effects of RG running, they do provide a useful constraint to the possible values of these theoretical parameters. In particular, as studied in detail in our earlier work [10], even with the current observational data’s precision, they provide an extremely stringent constraint on the allowed values of , down to at most a 1–2% deviation from . This result not only provides a great verification of the values obtained from various theoretical methods such as the Regge lattice calculations of the path integral, but perhaps the first phenomenological test of the quantum theory of gravity in cosmology. It is thus hopeful that as observational technology continues to improve, more insights can be gained regarding the values for and . With more data and smaller error bars, one can further narrow down a best fit value for the quantum amplitude or vacuum condensate scale by Markov Chain Monte Carlo (MCMC) sampling in the ISiTGR program. In addition, ISiTGR is also capable of calculating tensor perturbations, which can be used to test this quantum gravitational picture as soon as more observational data on that becomes available. As a fundamentally tensor theory, this gravitational fluctuation picture is expected to produce nontrivial predictions to those of scalar field based inflation models.
It should also be noted that the numerical programs show a very encouraging agreement with the analytical results on the matter power spectrum , as shown here in Figure 1. This agreement provides great confidence in the analytical methodology used in [9], or as summarized here in Section 2. The concordance between numerical and analytical results provides extra support on how the quantum fluctuations of the gravitational field are linked to the fluctuations of the matter density field. However, the numerical results for the effects of a RG running of G, suggesting an upturn at low ls, seem to disagree with the analytical intuition that a lower should give a lower , as suggested in Equation (49). Since the derivation of Equation (49) is purely classical and does not involve any quantum gravitation input, this suggests a lack of analytical understanding of the effects of a having a modified RG running Newton’s constant on the Boltzmann equations, and thus their solutions of the form factors and (Equations (44) and (45)). It is unclear analytically from the coupled differential equations how the running of Newton’s G from Equation (33) affects their solutions, making it difficult to translate the predictions on , which agrees with the numerical results, to . This is an area under active further theoretical investigations, and will be addressed in future work. Nevertheless, armed with the supposedly more comprehensive and reliable numerical programs, new insights should be gained regarding the various quantum effects of gravity on the different cosmological spectra.
At first, the results presented in this paper might appear puzzling, since one usually associates quantum fluctuations with microscopic, very short distance phenomena. This is in fact generally incorrect, with superconductors, superfluids, phase transitions and white dwarf stars appearing as well known examples of condensation and macroscopic quantum cooperative behavior. The point here is that experience shows that the magnitude and scale for quantum fluctuations in quantum field theory is instead generally related to an intrinsic dynamical length scale, here the gravitational correlation length , or equivalently the vacuum condensate connected to it. In this QCD-like picture, supported by extensive nonperturbative calculations on the lattice and in the continuum, quantum fluctuations exist on all length scales and propagate from the microscopic to the macroscopic regime, all the way up to the cosmological domain (since in the quantum theory the only relevant scale is the vacuum condensate , which we know from observation is exceedingly small). This is not unexpected, as the graviton is massless, and macroscopic effects thus arise because of strong infrared divergences, again in a way that is similar to what happens in QCD, where perturbation also fails completely in the infrared regime. Consequently, quantum fluctuations of the gravitational field are not just primordial () or microscopic () in nature, instead they occur on all length scales (including infrared scales) at all times, with specific features (such as a weak running of G) predicted by the existence of those scale invariant quantum fluctuations, and with the parameter setting the scale for those very subtle quantum effects, again, in close analogy to QCD. Of course, such effects are entirely missed in ordinary perturbation theory, which is badly divergent due to a (largely invisible) nontrivial vacuum condensation.
In conclusion, we have presented in this paper a compelling alternative picture for the various observed cosmological spectra that is motivated by gravitational fluctuations. In this work, we provided updated and extended analysis utilizing numerical programs in cosmology, as well as new physical predictions that can potentially distinguish this perspective from that of standard scalar field inflation. To this day inflation still forms one of the more popular approaches, but its full acceptance has remained controversial [74,75,76]. While there exists a number of alternatives to the standard horizon and flatness problems [77,78], the ability to explain the various cosmological power spectra has long been one of the unique predictions from inflation-motivated models, and thus often considered as one of the “major successes” for inflation. It is thus significant that this work provides an entirely new alternative, which is in principle arguably more elegant as it only uses Einstein gravity and standard (and well established) nonperturbative quantum field theory methods, without the usual burden of flexibilities associated with inflation. Nevertheless, because of the limited precision of current observational data, it is not yet possible to clearly prove or disprove either idea. In addition, a complete address of various other cosmological problems such as the horizon and flatness problem, the issue of cosmological initial conditions, quantum coherence of the initial state, etc. are out of the scope of this paper, but are certainly interesting and important. It would remain as future work to see how those can be integrated into the picture. Still, the possibility of an alternative explanation without invoking the artificial machinery of scalar fields is significant, as it suggests that the observed power spectra may not be a direct consequence nor a solid confirmation of inflation, as some literature may suggest. By exploring in more details the relationship between gravity and cosmological matter and radiation both analytically and numerically, together with the influx of new and increasingly accurate observational data, one can hope that this hypothesis can be subjected to further stringent tests in the future.
Author Contributions
Supervision, H.W.H.; conceptualization, H.W.H., L.H.S.Y. and H.E.P.K.; investigation, H.W.H., L.H.S.Y. and H.E.P.K.; writing, H.W.H., L.H.S.Y. and H.E.P.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University of California.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peebles, P.J.E. Principles of Physical Cosmology; Princeton Series in Physics; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Peebles, P.J.E. Issues for the Next Generation of Galaxy Surveys. Philos. Trans. R. Soc. Lond. A 1999, 357, 21–34. [Google Scholar] [CrossRef][Green Version]
- Baugh, C. Correlation Function and Power Spectra in Cosmology; Encyclopedia of Astronomy and Astrophysics; IOP: London, UK, 2006; ISBN 0333750888. [Google Scholar]
- Tegmark, M.; Zaldarriaga, M. Separating the Early Universe from the Late Universe: Cosmological parameter estimation beyond the black box. Phys. Rev. D 2002, 66, 103508. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary Universe: A possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A new Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy, and Primordial Monopole Problems. Phys. Lett. B 1982, 108, 389. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiation Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220. [Google Scholar] [CrossRef]
- Liddle, A.R.; Lyth, D.H. Cosmological Inflation and Large-Scale Structure; Cambridge University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Hamber, H.W.; Yu, L.H.S. Gravitational Fluctuations as an Alternative to Inflation. Universe 2019, 5, 31. [Google Scholar] [CrossRef]
- Hamber, H.W.; Yu, L.H.S. Gravitational Fluctuations as an Alternative to Inflation II. CMB Angular Power Spectrum. Universe 2019, 5, 216. [Google Scholar] [CrossRef]
- Hamber, H.W. Vacuum Condensate Picture of Quantum Gravity. Symmetry 2019, 11, 87. [Google Scholar] [CrossRef]
- Hamber, H.W. Quantum Gravitation; Springer Tracts in Modern Physics; Springer: Berlin, Germany; New York, NY, USA, 2009. [Google Scholar]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. I. Overview and the cosmological legacy of Planck. arXiv 2018, arXiv:1807.06205v1. [Google Scholar]
- Feynman, R.P. Quantum Theory of Gravitation. Acta Phys. Polon. 1963, 24, 697–722. [Google Scholar]
- Feynman, R.P. Lectures on Gravitation, Caltech Lecture Notes, 1962–1963; Morinigo, F.B., Wagner, W.G., Hatfield, B., Eds.; Advanced Book Program; Addison-Wesley: Boston, MA, USA, 1995. [Google Scholar]
- DeWitt, B.S. Quantization of Fields with Infinite-Dimensional Invariance Groups. III. Generalized Schwinger-Feynman Theory. J. Math. Phys. 1962, 3, 1073. [Google Scholar] [CrossRef]
- Hamber, H.W. Simplicial Quantum Gravity. In Critical Phenomena, Random Systems and Gauge Theories, 1984 Les Houches Summer School, Session XLIII; Osterwalder, K., Stora, R., Eds.; North-Holland: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Wilson, K.G. Feynman-graph expansion for critical exponents. Phys. Rev. Lett. 1972, 28, 548. [Google Scholar] [CrossRef]
- Wilson, K.G. Quantum field-theory models in less than 4 dimensions. Phys. Rev. D 1973, 7, 2911. [Google Scholar] [CrossRef]
- Parisi, G. On the Renormalizability of not Renormalizable Theories. Lett. Nuovo Cimento 1973, 6, 450–452. [Google Scholar] [CrossRef]
- Parisi, G. Theory of Non-Renormalizable Interactions—The large N Expansion. Nucl. Phys. B 1975, 100, 368. [Google Scholar] [CrossRef]
- Parisi, G. Symanzik’s Improvement Program. Nucl. Phys. B 1985, 254, 58. [Google Scholar] [CrossRef]
- Parisi, G. On Non-Renormalizable Interactions. In Proceedings of the 1976 Cargése NATO Advances Study Institute, on New Developments in Quantum Field Theory and Statistical Mechanics, Cargese, France, 12–31 July 1976; Levy, M., Mitter, P., Eds.; Plenum Press: New York, NY, USA, 1977. [Google Scholar]
- Hamber, H.W. Invariant Correlations in Simplicial Gravity. Phys. Rev. D 1994, 50, 3932. [Google Scholar] [CrossRef] [PubMed]
- Hamber, H.W.; Williams, R.M. Nonlocal effective gravitational field equations and the running of Newton’s G. Phys. Rev. D 2005, 72, 044026. [Google Scholar] [CrossRef]
- Hamber, H.W.; Toriumi, R. Cosmological Density Perturbations with a Scale-Dependent Newton’s G. Phys. Rev. D 2010, 82, 043518. [Google Scholar] [CrossRef]
- Hamber, H.W.; Toriumi, R. Scale-Dependent Newton’s Constant G in the Conformal Newtonian Gauge. Phys. Rev. D 2011, 84, 103507. [Google Scholar] [CrossRef]
- Hamber, H.W.; Toriumi, R. Inconsistencies from a Running Cosmological Constant. Int. J. Mod. Phys. D 2013, 22, 1330023. [Google Scholar] [CrossRef]
- Hamber, H.W. Scaling Exponents for Lattice Quantum Gravity in Four Dimensions. Phys. Rev. D 2015, 92, 064017. [Google Scholar] [CrossRef]
- Hamber, H.W. Phases of Simplicial Quantum Gravity in Four Dimensions: Estimates for the Critical Exponents. Nucl. Phys. B 1993, 400, 347. [Google Scholar] [CrossRef]
- Hamber, H.W. Gravitational Scaling Dimensions. Phys. Rev. D 2000, 61, 124008. [Google Scholar] [CrossRef]
- Hamber, H.W.; Williams, R.M. Gravitational Wilson Loop and Large Scale Curvature. Phys. Rev. D 2007, 76, 084008. [Google Scholar] [CrossRef]
- Gravitational Wilson Loop in Discrete Gravity. Phys. Rev. D 2010, 81, 084048. [CrossRef]
- Weinberg, S. Ultraviolet Divergences in Quantum Gravity. In General Relativity—An Einstein Centenary Survey; Hawking, S.W., Israel, W., Eds.; Cambridge University Press: Cambridge, UK, 1979. [Google Scholar]
- Gastmans, R.; Kallosh, R.; Truffin, C. Quantum Gravity Near Two Dimensions. Nucl. Phys. B 1978, 133, 417. [Google Scholar] [CrossRef]
- Christensen, S.M.; Duff, M.J. Quantum Gravity in 2 + ϵ Dimensions. Phys. Lett. B 1978, 79, 213. [Google Scholar] [CrossRef]
- Kawai, H.; Ninomiya, M. Renormalization Group and Quantum Gravity. Nucl. Phys. B 1990, 336, 115. [Google Scholar] [CrossRef]
- Kawai, H.; Kitazawa, Y.; Ninomiya, M. Scaling Exponents in Quantum Gravity near two Dimensions. Nucl. Phys. B 1993, 393, 280. [Google Scholar] [CrossRef]
- Kitazawa, Y.; Ninomiya, M. Scaling Behavior of Ricci Curvature near two Dimensions. Phys. Rev. D 1997, 55, 2076. [Google Scholar] [CrossRef]
- Aida, T.; Kitazawa, Y. Two Loop Prediction for Scaling Exponents in (2 + ϵ)-dimensional Quantum Gravity. Nucl. Phys. B 1997, 491, 427. [Google Scholar] [CrossRef]
- Hamber, H.W.; Williams, R.M. Quantum Gravity in Large Dimensions. Phys. Rev. D 2006, 73, 044031. [Google Scholar] [CrossRef]
- Hamber, H.W.; Toriumi, R.; Williams, R.M. Wheeler-DeWitt Equation in 2+1 Dimensions. Phys. Rev. D 2012, 86, 084010. [Google Scholar] [CrossRef]
- Reuter, M. Nonperturbative Evolution Equation for Quantum Gravity. Phys. Rev. D 1998, 57, 971. [Google Scholar] [CrossRef]
- Reuter, M.; Weyer, H. The Role of Background Independence for Asymptotic Safety in Quantum Einstein Gravity. Gen. Relativ. Gravit. 2009, 41, 983. [Google Scholar] [CrossRef][Green Version]
- Litim, D.F. Fixed Points of Quantum Gravity. Phys. Rev. Lett. 2004, 92, 201301. [Google Scholar] [CrossRef] [PubMed]
- Fischer, P.; Litim, D.F. Fixed Points of Quantum Gravity in Extra Dimensions. Phys. Lett. B 2006, 638, 497. [Google Scholar] [CrossRef]
- Becker, D.; Reuter, M. En Route to Background Independence: Broken Split-Symmetry, and how to Restore it with Bi-Metric Average Actions. Ann. Phys. 2014, 350, 225. [Google Scholar] [CrossRef]
- Falls, K. Critical scaling in Quantum Gravity from the Renormalisation Group. arXiv 2015, arXiv:1503.06233. [Google Scholar]
- Falls, K.; Litim, D.F.; Nikolakopoulo, K.; Rahmede, C. Further Evidence for Asymptotic Safety of Quantum Gravity. arXiv 2016, arXiv:1501.05331. [Google Scholar] [CrossRef]
- Ohta, N.; Percacci, R.; Pereira, A.D. Gauges and Functional Measures in Quantum Gravity I: Einstein Theory. JHEP 2016, 1606, 115. [Google Scholar] [CrossRef]
- Gies, H.; Knorr, B.; Lippoldt, S. Generalized Parametrization Dependence in Quantum Gravity. Phys. Rev. D 2015, 92, 084020. [Google Scholar] [CrossRef]
- Gil-Marín, H.; Guy, J.; Zarrouk, P.; Burtin, E.; Chuang, C.H.; Percival, W.J.; Ross, A.J.; Ruggeri, R.; Tojerio, R.; Zhao, G.B.; et al. The Clustering of the SDSS-IV Extended Baryon Oscillation Spectroscopic Survey DR14 Quasar Sample: Structure Growth Rate Measurement from the Anisotropic Quasar Power Spectrum in the Redshift Range 0.8 < z < 2.2. Mon. Not. R. Astron. Soc. 2017, 437, 4773–4794. [Google Scholar]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Dodelson, S. Modern Cosmology; Academic Press: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Steinhardt, P.J. Cosmological Perturbations. Mod. Phys. Lett. A 2004, 19, 967–982. [Google Scholar] [CrossRef]
- Harrison, E.R. Fluctuations at the Threshold of Classical Cosmology. Phys. Rev. D 1970, 1, 2726. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. A Hypothesis Unifying the Structure and the Entropy of the Universe. Mon. Not. R. Astron. Soc. 1972, 160, 1P. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Yu, J.T. Primeval Adiabatic Perturbation in an Expanding Universe. Astrophys. J. 1970, 162, 815. [Google Scholar] [CrossRef]
- Bellini, E.; Barreira, A.; Frusciante, N.; Hu, B.; Peirone, S.; Raveri, M.; Zumalacarregui, M.; Avilez-Lopez, A.; Ballardini, M.; Battye, R.A.; et al. Comparison of Einstein-Boltzmann solvers for testing general relativity. Phys. Rev. D 2018, 97, 023520. [Google Scholar] [CrossRef]
- Lewis, A.; Challinor, A.; Lasenby, A. Efficient Computation of CMB anisotropies in closed FRW models. arXiv 1999, arXiv:astro-ph/9911177. [Google Scholar]
- Lesgourgues, J. The Cosmic Linear Anisotropy Solving System (CLASS) I: Overview. arXiv 2011, arXiv:1104.2932. [Google Scholar]
- Garcia-Quintero, C.; Ishak, M. ISiTGR Version 3.1 Released in February 2020 (with Python Wrapper), GitHub Repository. Available online: https://github.com/mishakb/ISiTGR (accessed on 1 April 2020).
- Alex, Z.; Levon, P.; Alessandra, S.; Gong-Bo, Z. MGCAMB with massive neutrinos and dynamical dark energy. arXiv 2019, arXiv:1901.05956. [Google Scholar]
- Tessa, B.; Philip, B. Observational signatures of modified gravity on ultra-large scales. arXiv 2015, arXiv:1506.00641. [Google Scholar]
- Antony, L.; Sarah, B. Cosmological parameters from CMB and other data: A Monte-Carlo approach. arXiv 2020, arXiv:astro-ph/0205436. [Google Scholar]
- Garcia-Quintero, C.; Ishak, M.; Fox, L.; Dossett, J. ISiTGR: Testing deviations from GR at cosmological scales including dynamical dark energy, massive neutrinos, functional or binned parametrizations, and spatial curvature. arXiv 2019, arXiv:1908.00290. [Google Scholar]
- Antony Lewis, CAMB Notes. Available online: https://cosmologist.info/notes/CAMB.pdf (accessed on 1 April 2020).
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. arXiv 2003, arXiv:astro-ph/0302209v3. [Google Scholar] [CrossRef]
- van Engelen, A.; Bhattacharya, S.; Sehgal1, N.; Holder, G.P.; Zahn, O.; Nagai, D. CMB Lensing Power Spectrum Biases from Galaxies and Clusters using High-angular Resolution Temperature Maps. Astrophys. J. 2014, 786, 13. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VIII. Gravitational lensing. arXiv 2018, arXiv:1807.06210v2. [Google Scholar]
- Simard, G.; Omori, Y.; Aylor, K.; Baxter, E.J.; Benson, B.A.; Bleem, L.E.; Carlstrom, J.E.; Chang, C.L.; Cho, H.-M.; Chown, R.; et al. Constraints on Cosmological Parameters from the Angular Power Spectrum of a Combined 2500 deg2 SPT-SZ and Planck Gravitational Lensing Map. Astrophys. J. 2018, 860, 2. [Google Scholar] [CrossRef]
- Das, S.; Louis, T.; Nolta, M.R.; Addison, G.E.; Battistelli, E.S.; Bond, J.R.; Calabrese, E.; Crichton, D.; Devlin, M.J.; Dicker, S.; et al. The Atacama Cosmology Telescope: Temperature and gravitational lensing power spectrum measurements from three seasons of data. Astrophys. J. 2014, 2014, 014. [Google Scholar] [CrossRef]
- Abazajian, K.N.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Arnold, K.S.; Baccigalupi, C.; Bartlett, J.G.; Battaglia, N.; Benson, B.A.; et al. CMB-S4 Science Book, First Edition. arXiv 2016, arXiv:1610.02743. [Google Scholar]
- Boyle, L.A.; Steinhardt, P.J.; Turok, N. Inflationary Predictions for Scalar and Tensor Fluctuations Reconsidered. Phys. Rev. Lett. 2006, 96, 111301. [Google Scholar] [CrossRef]
- Tegmark, M. What does Inflation Really Predict? J. Cosmol. Astropart. Phys. (JCAP) 2005, 4, 001. [Google Scholar] [CrossRef]
- Ijjas, A.; Steinhardt, P.J.; Loeb, A. Inflationary Schism. Phys. Lett. B 2014, 736, 142–146. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. A Cyclic Model of the Universe. Science 2002, 296, 1436–1439. [Google Scholar] [CrossRef] [PubMed]
- Hollands, S.; Wald, R.M. An Alternative to Inflation. arXiv 2002, arXiv:gr-qc/0205058. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).