The Effective Field Theory of Dark Energy Diagnostic of Linear Horndeski Theories After GW170817 and GRB170817A
Abstract
1. Introduction
2. Overview of the EFT of DE Construction
2.1. Spontaneous Symmetry Breaking in Cosmology
2.2. Unitary Gauge and the Action
2.3. Stückelberg Mechanism and Stability of Theories
2.4. Equations and Observables
3. Phenomenology of LSS Observables
3.1. Parameterization, Models and Method
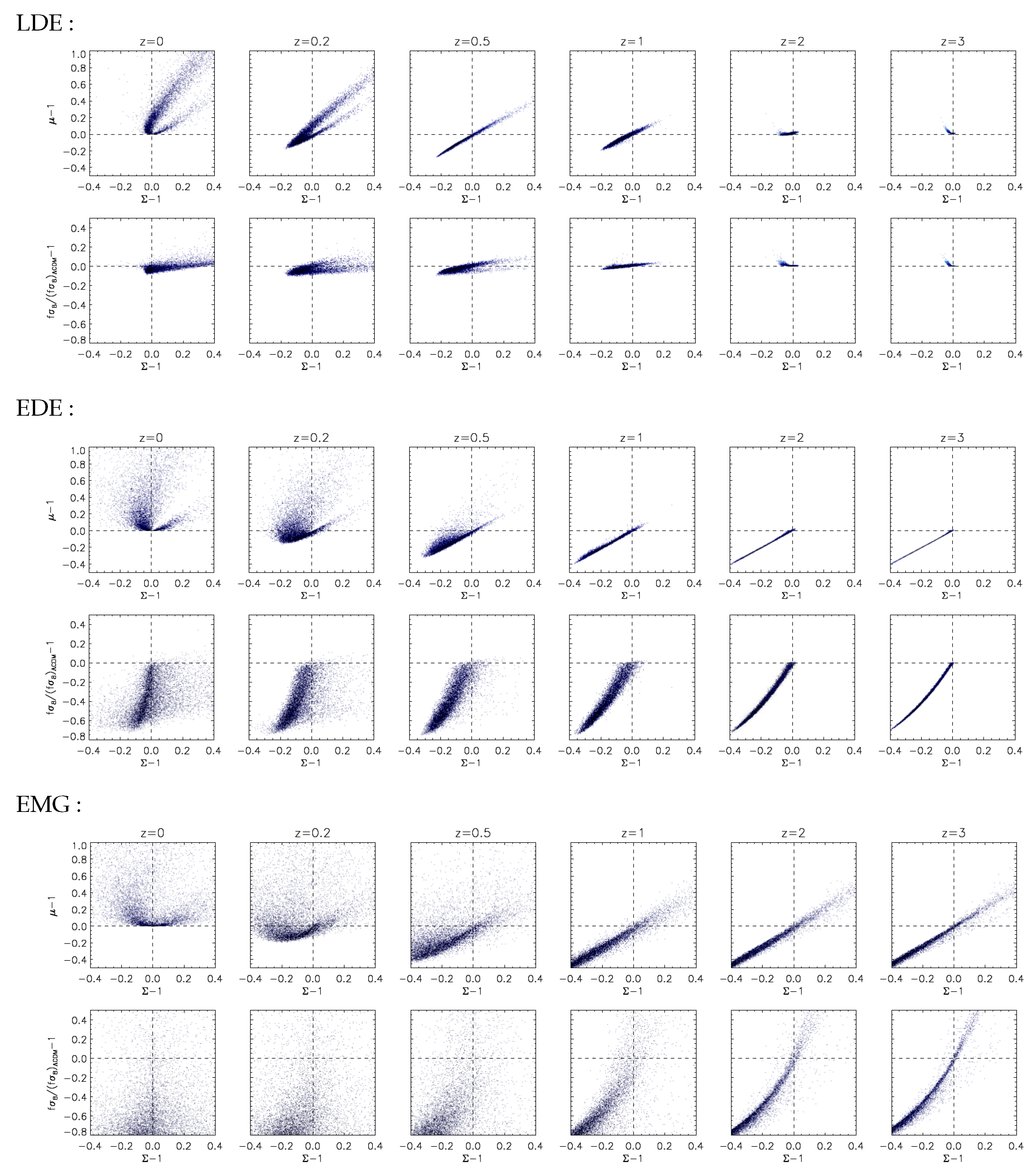
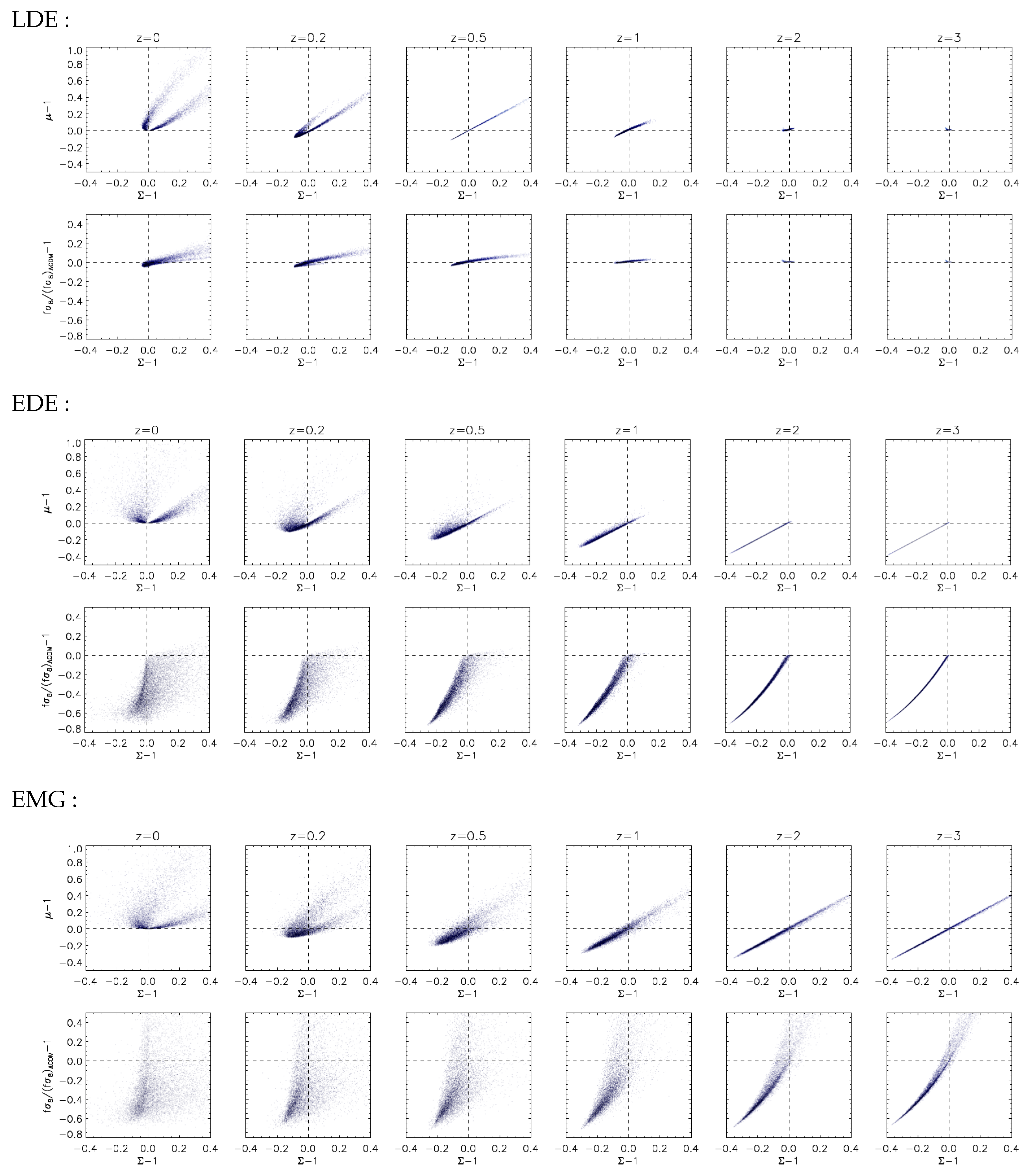
3.2. Correlations of LSS Observables
4. Implications after GW170817 and GRB170817A
4.1. Constraints on the Speed of Gravitational Waves
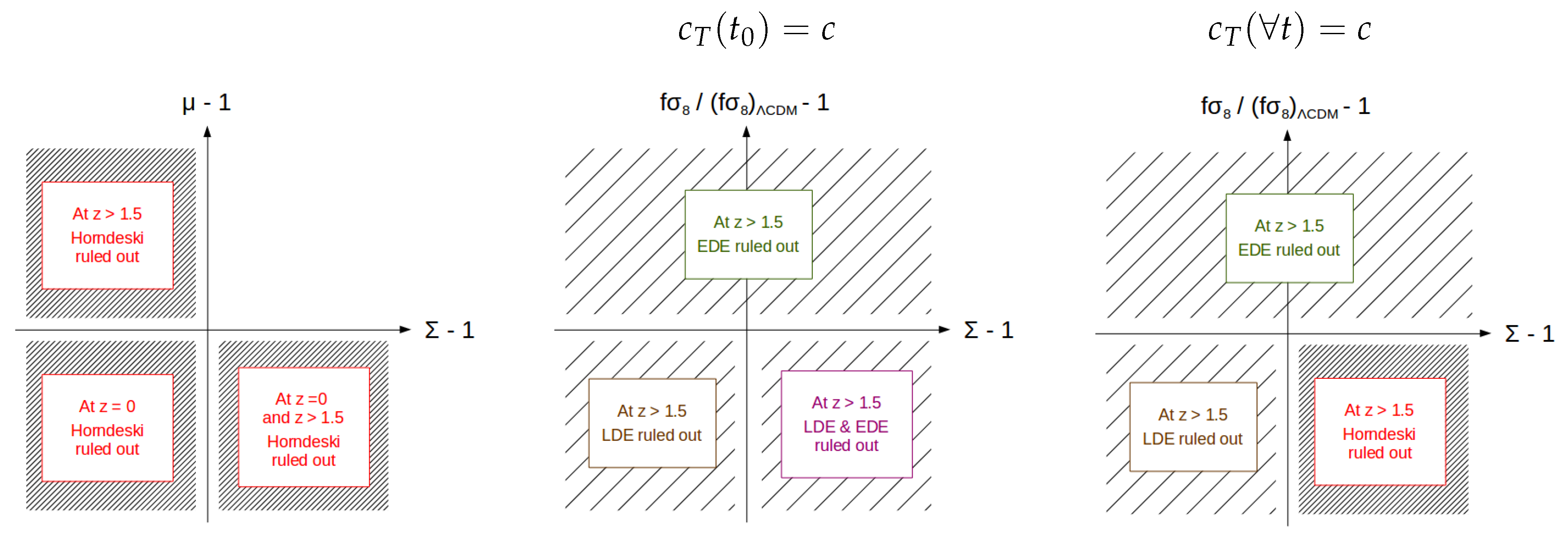
4.2. The Diagnostic of Linear Horndeski Theories
- -
- and of opposite sign for ,
- -
- at .
- -
- the LDE case should be ruled out if at ,
- -
- the EDE case should be ruled out if at or and at .
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Piazza, F.; Steigerwald, H.; Marinoni, C. Phenomenology of dark energy: Exploring the space of theories with future redshift surveys. J. Cosmol. Astropart. Phys. 2014, 2014, 043. [Google Scholar] [CrossRef]
- Raveri, M.; Hu, B.; Frusciante, N.; Silvestri, A. Effective Field Theory of Cosmic Acceleration: Constraining dark energy with CMB data. Phys. Rev. D 2014, 90, 043513. [Google Scholar] [CrossRef]
- Bellini, E.; Cuesta, A.J.; Jimenez, R.; Verde, L. Constraints on deviations from ΛCDM within Horndeski gravity. J. Cosmol. Astropart. Phys. 2016, 2016, 053. [Google Scholar] [CrossRef]
- Salvatelli, V.; Piazza, F.; Marinoni, C. Constraints on modified gravity from Planck 2015: When the health of your theory makes the difference. J. Cosmol. Astropart. Phys. 2016, 2016, 027. [Google Scholar] [CrossRef]
- Perenon, L.; Marinoni, C.; Piazza, F. Diagnostic of Horndeski theories. J. Cosmol. Astropart. Phys. 2017, 2017, 035. [Google Scholar] [CrossRef]
- Perenon, L.; Piazza, F.; Marinoni, C.; Hui, L. Phenomenology of dark energy: general features of large-scale perturbations. J. Cosmol. Astropart. Phys. 2015, 2015, 029. [Google Scholar] [CrossRef]
- Peirone, S.; Koyama, K.; Pogosian, L.; Raveri, M.; Silvestri, A. Large-scale structure phenomenology of viable Horndeski theories. Phys. Rev. D 2018, 97, 043519. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational wave; gamma-rays from a binary neutron star merger: GW17081; GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Lombriser, L.; Taylor, A. Breaking a dark degeneracy with gravitational waves. J. Cosmol. Astropart. Phys. 2016, 2016, 031. [Google Scholar] [CrossRef]
- Lombriser, L.; Lima, N.A. Challenges to self-acceleration in modified gravity from gravitational wave; large-scale structure. Phys. Lett. B 2017, 765, 382–385. [Google Scholar] [CrossRef]
- Creminelli, P.; Vernizzi, F. Dark Energy after GW17081; GRB170817A. Phys. Rev. Lett. 2017, 119, 251302. [Google Scholar] [CrossRef] [PubMed]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark energy after GW170817: Dead end; the road ahead. Phys. Rev. Lett. 2017, 119, 251304. [Google Scholar] [CrossRef] [PubMed]
- Sakstein, J.; Jain, B. Implications of the neutron star merger GW170817 for cosmological scalar-tensor theories. Phys. Rev. Lett. 2017, 119, 251303. [Google Scholar] [CrossRef] [PubMed]
- Langlois, D.; Saito, R.; Yamauchi, D.; Noui, K. Scalar-tensor theorie; modified gravity in the wake of GW170817. Phys. Rev. D 2018, 97, 061501. [Google Scholar] [CrossRef]
- Kase, R.; Tsujikawa, S. Dark energy in Horndeski theories after GW170817: A review. arXiv 2018, arXiv:1809.08735. [Google Scholar]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark Energy in light of Multi-Messenger Gravitational-Wave astronomy. arXiv 2018, arXiv:1807.09241. [Google Scholar] [CrossRef]
- De Rham, C.; Melville, S. Gravitational rainbows: LIG; dark energy at its cutoff. Phys. Rev. Lett. 2018, 121, 221101. [Google Scholar] [CrossRef]
- Gubitosi, G.; Piazza, F.; Vernizzi, F. The effective field theory of dark energy. J. Cosmol. Astropart. Phys. 2013, 2013, 032. [Google Scholar] [CrossRef]
- Gleyzes, J.; Langlois, D.; Piazza, F.; Vernizzi, F. Essential building blocks of dark energy. J. Cosmol. Astropart. Phys. 2013, 2013, 025. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Creminelli, P.; Luty, M.A.; Nicolis, A.; Senatore, L. Starting the universe: Stable violation of the null energy conditio; non-standard cosmologies. J. High Energy Phys. 2006, 2006, 080. [Google Scholar] [CrossRef]
- Cheung, C.; Fitzpatrick, A.L.; Kaplan, J.; Senatore, L.; Creminelli, P. The effective field theory of inflation. J. High Energy Phys. 2008, 2008, 014. [Google Scholar] [CrossRef]
- Creminelli, P.; D’Amico, G.; Norena, J.; Vernizzi, F. The effective theory of quintessence: The w < −1 side unveiled. J. Cosmol. Astropart. Phys. 2009, 2009, 018. [Google Scholar]
- Piazza, F.; Vernizzi, F. Effective field theory of cosmological perturbations. Class. Quant. Grav. 2013, 30, 214007. [Google Scholar] [CrossRef]
- Bloomfield, J.; Flanagan, É.É.; Park, M.; Watson, S. Dark energy or modified gravity? An effective field theory approach. J. Cosmol. Astropart. Phys. 2013, 2013, 010. [Google Scholar] [CrossRef]
- Bloomfield, J. A simplified approach to general scalar-tensor theories. J. Cosmol. Astropart. Phys. 2013, 2013, 044. [Google Scholar] [CrossRef]
- Gleyzes, J.; Langlois, D.; Mancarella, M.; Vernizzi, F. Effective theory of interacting dark energy. J. Cosmol. Astropart. Phys. 2015, 2015, 054. [Google Scholar] [CrossRef]
- Gleyzes, J.; Langlois, D.; Mancarella, M.; Vernizzi, F. Effective theory of dark energy at redshift survey scales. J. Cosmol. Astropart. Phys. 2016, 2016, 056. [Google Scholar] [CrossRef]
- D’Amico, G.; Huang, Z.; Mancarella, M.; Vernizzi, F. Weakening gravity on redshift-survey scales with kinetic matter mixing. J. Cosmol. Astropart. Phys. 2017, 2017, 014. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s principl: A relativistic theory of gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results-xiii. cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Raveri, M.; Bull, P.; Silvestri, A.; Pogosian, L. Priors on the effective dark energy equation of state in scalar-tensor theories. Phys. Rev. D 2017, 96, 083509. [Google Scholar] [CrossRef]
- Brando, G.; Falciano, F.T.; Linder, E.V.; Velten, H.E.S. Modified Gravity Away from a ΛCDM Background. arXiv 2019, arXiv:1904.12903. [Google Scholar]
- Pogosian, L.; Silvestri, A. What can cosmology tell us about gravity? Constraining Horndeski gravity with Σ and μ. Phys. Rev. D 2016, 94, 104014. [Google Scholar] [CrossRef]
- Moore, G.D.; Nelson, A.E. Lower bound on the propagation speed of gravity from gravitational Cherenkov radiation. J. High Energy Phys. 2001, 2001, 023. [Google Scholar] [CrossRef]
- Caves, C.M. Gravitational radiatio: The ultimate speed in Rosen’s bimetric theory of gravity. Ann. Phys. 1980, 125, 35–52. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Piazza, F.; Velten, H. Evading the Vainshtein mechanism with anomalous gravitational wave speed: constraints on modified gravity from binary pulsars. Phys. Rev. Lett. 2016, 116, 061101. [Google Scholar] [CrossRef]
- Saltas, I.D.; Sawicki, I.; Amendola, L.; Kunz, M. Anisotropic stress as a signature of nonstandard propagation of gravitational waves. Phys. Rev. Lett. 2014, 113, 191101. [Google Scholar] [CrossRef]
- Amendola, L.; Ballesteros, G.; Pettorino, V. Effects of modified gravity on B-mode polarization. Phys. Rev. D 2014, 90, 043009. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Cornish, N.; Blas, D.; Nardini, G. Bounding the speed of gravity with gravitational wave observations. Phys. Rev. Lett. 2017, 119, 161102. [Google Scholar] [CrossRef] [PubMed]
- Copeland, E.J.; Kopp, M.; Padilla, A.; Saffin, P.M.; Skordis, C. Dark Energy after GW170817 Revisited. Phys. Rev. Lett. 2019, 122, 061301. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Lombriser, L.; Taylor, A. Reconstructing Horndeski theories from phenomenological modified gravit; dark energy models on cosmological scales. Phys. Rev. D 2018, 98, 044051. [Google Scholar] [CrossRef]
- Battye, R.A.; Pace, F.; Trinh, D. Gravitational wave constraints on dark sector models. Phys. Rev. D 2018, 98, 023504. [Google Scholar] [CrossRef]
- Renk, J.; Zumalacárregui, M.; Montanari, F. Gravity at the horizon: On relativistic effects, CMB-LSS correlation; ultra-large scales in Horndeski’s theory. J. Cosmol. Astropart. Phys. 2016, 2016, 040. [Google Scholar] [CrossRef][Green Version]
- Gleyzes, J.; Langlois, D.; Piazza, F.; Vernizzi, F. Healthy theories beyond Horndeski. arXiv 2014, arXiv:1404.6495. [Google Scholar]
- Gleyzes, J.; Langlois, D.; Piazza, F.; Vernizzi, F. Exploring gravitational theories beyond Horndeski. J. Cosmol. Astropart. Phys. 2015, 2015, 018. [Google Scholar] [CrossRef]
- Langlois, D.; Mancarella, M.; Noui, K.; Vernizzi, F. Effective description of higher-order scalar-tensor theories. J. Cosmol. Astropart. Phys. 2017, 2017, 033. [Google Scholar] [CrossRef]
- Nicolis, A.; Penco, R.; Piazza, F.; Rattazzi, R. Zoology of condensed matter: Framids, ordinary stuff, extra-ordinary stuff. J. High Energy Phys. 2015, 2015, 155. [Google Scholar] [CrossRef]
| 1. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perenon, L.; Velten, H. The Effective Field Theory of Dark Energy Diagnostic of Linear Horndeski Theories After GW170817 and GRB170817A. Universe 2019, 5, 138. https://doi.org/10.3390/universe5060138
Perenon L, Velten H. The Effective Field Theory of Dark Energy Diagnostic of Linear Horndeski Theories After GW170817 and GRB170817A. Universe. 2019; 5(6):138. https://doi.org/10.3390/universe5060138
Chicago/Turabian StylePerenon, Louis, and Hermano Velten. 2019. "The Effective Field Theory of Dark Energy Diagnostic of Linear Horndeski Theories After GW170817 and GRB170817A" Universe 5, no. 6: 138. https://doi.org/10.3390/universe5060138
APA StylePerenon, L., & Velten, H. (2019). The Effective Field Theory of Dark Energy Diagnostic of Linear Horndeski Theories After GW170817 and GRB170817A. Universe, 5(6), 138. https://doi.org/10.3390/universe5060138





