The Geometrical Trinity of Gravity
Abstract
:1. Introduction
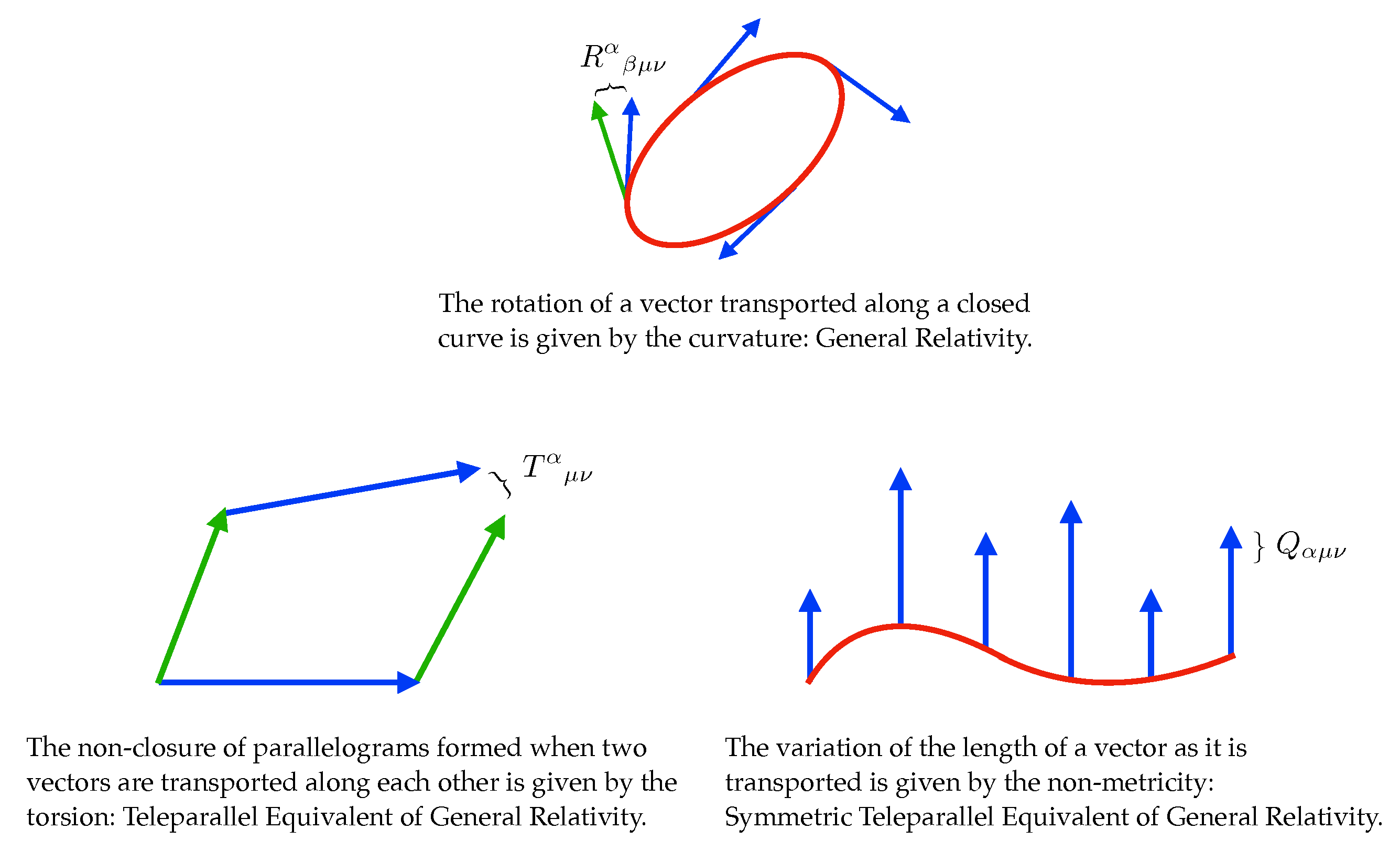
- Metric: the connection is metric-compatible, . Non-metricity measures how much the length of vectors change as we parallel transport them, so in metric spaces the length of vectors is conserved.
- Torsionless: the connection is symmetric, . Torsion gives a measure of the non-closure of the parallelogram formed when two infinitesimal vectors are parallel transported along each other. For this reason, it is usually said that parallelograms do not close in the presence of torsion.
- Flat: the connection is not curved, . Curvature measures the rotation experienced by a vector when it is parallel transported along a closed curve. This represents an obstacle to compare vectors defined at different spacetime points. In flat spaces, however, vectors do not rotate as they are transported so that there is a better notion of parallelism at a distance. This is the reason why theories formulated in these spaces are referred to as teleparallel.
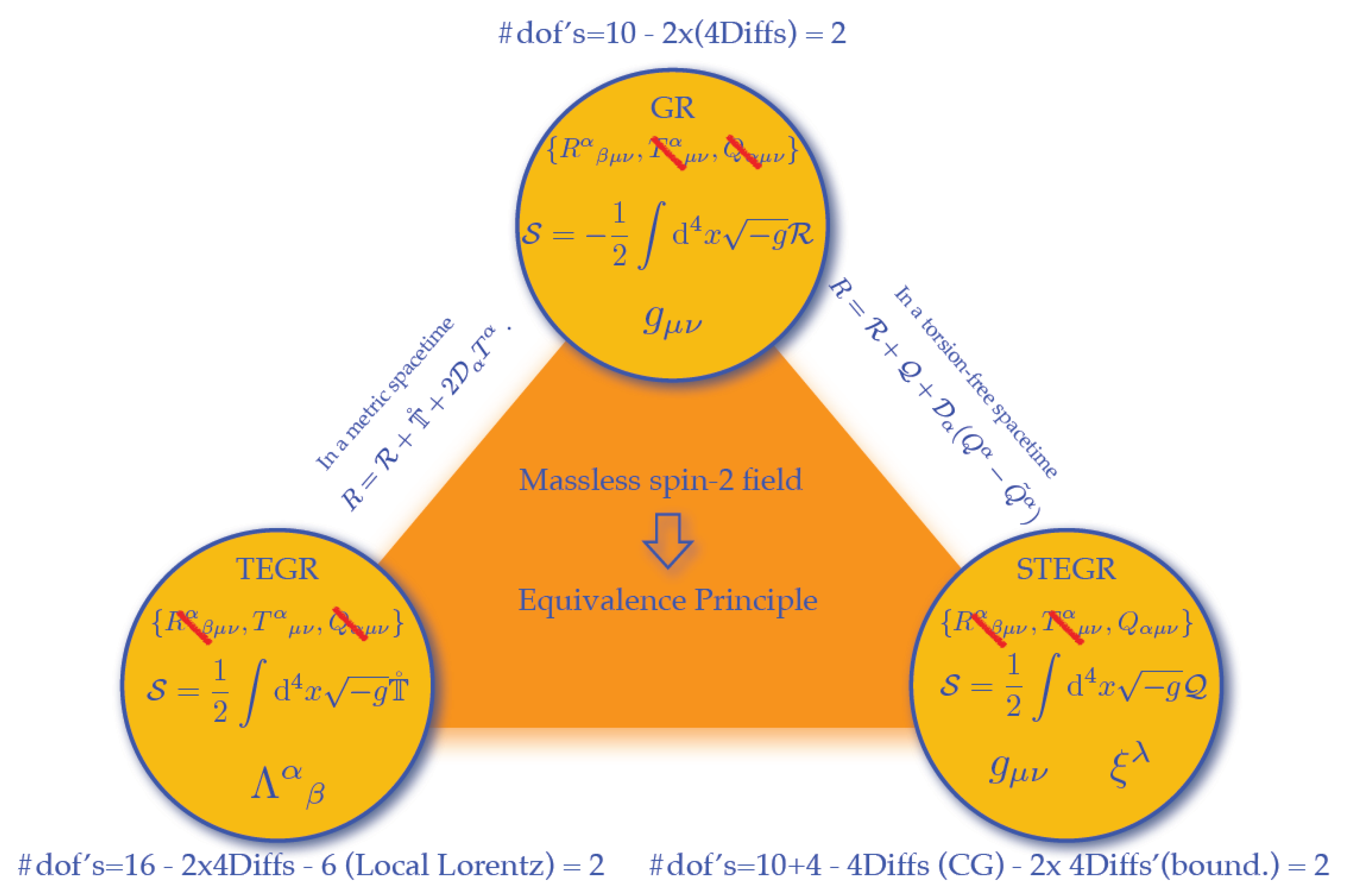
2. General Relativity
3. Metric Teleparallelism
3.1. Vierbein Formulation
3.2. Alternative Theories
4. Symmetric Teleparallelisms
4.1. Symmetric Teleparallel Equivalent of GR: Coincident GR
4.2. General Quadratic Theory
4.3. Extensions
5. Matter Couplings
- generalized geometries give room for ambiguity in the matter coupling,
- crucial differences arise for bosonic and fermionic fields.
5.1. General Relativity
- the matter fields do not couple to the connection, and
- the minimal coupling prescription , with is applied.
5.2. Metric Teleparallelism
5.3. Symmetric Teleparallelisms
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GR | General Relativity |
| DOF | Degree of Freedom |
| GHY | Gibbons–Hawking–York |
| TEGR | Teleparallel Equivalent of GR |
| STEGR | Symmetric Teleparallel Equivalent of GR |
| CGR | Coincident GR |
| Diff | Diffeomorphism |
| TDiff | Transverse Diffeomorphism |
| WTDiff | Weyl Transverse Diffeomorphism |
| Diffs | Diffeomorphism in the coincident gauge |
References
- Schrödinger, E. Space-Time Structure; Cambridge University Press: Cambridge, UK, 1950. [Google Scholar]
- Olmo, G.J. Palatini Approach to Modified Gravity: f(R) Theories and Beyond. Int. J. Mod. Phys. D 2011, 20, 413. [Google Scholar] [CrossRef]
- Heisenberg, L. A systematic approach to generalisations of General Relativity and their cosmological implications. arXiv 2018, arXiv:1807.01725. [Google Scholar] [CrossRef]
- Petrov, A.N.; Kopeikin, S.M.; Lompay, R.R.; Tekin, B. Metric Theories of Gravity: Perturbation and Conservation Laws; De Gryter: Berlin, Germany, 2017; ISBN 978-3110351736. [Google Scholar]
- Dirac, P.A.M. Lectures on Quantum Mechanics; Yeshiva University Press: New York, NY, USA, 1964. [Google Scholar]
- Henneaux, M.; Teitelboim, C. Quantization of Gauge Systems; Princeton University Press: Princeton, NJ, USA, 1992; p. 520. [Google Scholar]
- Jimenez, J.B.; Heisenberg, L.; Olmo, G.J.; Rubiera-Garcia, D. Born-Infeld inspired modifications of gravity. Phys. Rept. 2018, 727, 1–129. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Action Integrals and Partition Functions in Quantum Gravity. Phys. Rev. D 1977, 15, 2752. [Google Scholar] [CrossRef]
- Jimenez, J.B.; Heisenberg, L.; Koivisto, T. Teleparallel Palatini theories. J. Cosmol. Astropart. Phys. 2018, 2018, 039. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Pereira, J.G. Teleparallel Gravity: An Introduction; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Golovnev, A.; Koivisto, T.; Sandstad, M. On the covariance of teleparallel gravity theories. Class. Quantum Gravity 2017, 34, 145013. [Google Scholar] [CrossRef]
- Krssak, M.; van den Hoogen, R.J.; Pereira, J.G.; Boehmer, C.G.; Coley, A.A. Teleparallel Theories of Gravity: Illuminating a Fully Invariant Approach. arXiv 2018, arXiv:1810.12932. [Google Scholar] [CrossRef]
- Hayashi, K.; Shirafuji, T. New General Relativity. Phys. Rev. D 1979, 19, 3524, Addendum in Phys. Rev. D 1982, 24, 3312. [Google Scholar] [CrossRef]
- Ortin, T. Gravity and Strings; Cambridge University Press: Cambridge, UK, 2004; ISBN 9780511616563. [Google Scholar]
- Koivisto, T.; Tsimperis, G. The spectrum of teleparallel gravity. arXiv 2018, arXiv:1810.11847. [Google Scholar]
- Nester, J.M.; Yo, H.J. Symmetric teleparallel general relativity. Chin. J. Phys. 1999, 37, 113. [Google Scholar]
- Einstein, A. The formal foundation of the general theory of relativity. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1914, 1914, 1030–1085. [Google Scholar]
- Jimenez, J.B.; Heisenberg, L.; Koivisto, T. Coincident General Relativity. Phys. Rev. D 2018, 98, 044048. [Google Scholar] [CrossRef]
- Unruh, W.G. A Unimodular Theory of Canonical Quantum Gravity. Phys. Rev. D 1989, 40, 1048. [Google Scholar] [CrossRef]
- Einstein, A. Do Gravitational Fields Play an essential Role in the Structure of Elementary Particles of Matter. In The Principle of Relativity; Dover: NewYork, NY, USA, 1952. [Google Scholar]
- Alvarez, E.; Blas, D.; Garriga, J.; Verdaguer, E. Transverse Fierz-Pauli symmetry. Nucl. Phys. B 2006, 756, 148–170. [Google Scholar] [CrossRef]
- Jimenez, J.B.; Heisenberg, L.; Koivisto, T.S.; Pekar, S. Cosmology in f(Q) geometry. arXiv 2019, arXiv:1906.10027. [Google Scholar]
- Obukhov, Y.N.; Pereira, J.G. Lessons of spin and torsion: Reply to ‘Consistent coupling to Dirac fields in teleparallelism’. Phys. Rev. D 2004, 69, 128502. [Google Scholar] [CrossRef]
- Lehmkuhl, D. Why Einstein did not believe that general relativity geometrizes gravity. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2014, 69, 316–326. [Google Scholar] [CrossRef]
| 1. | |
| 2. | Let us note here the typo in the corresponding Equation (50) in Ref. [9] where the inverse was misplaced. |
| 3. | This simply means that we can identify the tangent space and the curved indices at first order. |
| 4. | Barring possible topological obstructions. |
| 5. | It is noteworthy that Einstein considered these five non-metricity terms with a trivial connection, which corresponds to our coincident gauge [17]. |
| 6. | Of course, in this expression, should be interpreted as the inverse of the matrix . |
| 7. | This gauge is defined up to an affine transformation with a and b constants. Since this residual global symmetry does not vanish at infinity, it might lead to interesting properties of the infrarred structure of the theory. |
| 8. | For the sake of completeness, let us recall that the Stückelberg fields are a set of compensating fields introduced to restore any gauge invariance. In practice, one performs a transformation on the fields and, then, the parameters of the transformation are promoted to fields . The object , which is invariant by construction if the ’s transform according to , is then used to construct the action that is now manifestly gauge invariant at the expense of having introduced the (redundant) compensating fields . The unitary gauge is defined as that in which the transformation is the identity, i.e., in unitary gauge we have . Of course, in this gauge, we recover the original non-gauge invariant action before introducing the compensating fields. |
| 9. | We denote this symmetry Diffs as the Diffs symmetry that arises in the coincident gauge in order to distinguish it from the original Diffs that in turn are used to go to the coincident gauge. |
| 10. | |
| 11. | By nonlinear extension, we refer to the corresponding field equations not being linear in the non-metricity. |
| 12. | Let us stress that all these theories are Diffs invariant by construction and, consequently, the coincident/unitary gauge also exists for them. The gauge symmetries we refer to here are the Diffs that remain in the coincident gauge and that ensure the absence of additional propagating DOFs. |
| 13. | It can happen that a subset of Diffs remains a symmetry. The conditions would be that such a subset of symmetries give rise to a trivial boundary term. We will see an explicit example of this below. |
| 14. | It may be worth stating that, by minisuperspace, we simply mean the homogeneous and isotropic sub-manifold whose only variables are the time-dependent lapse and scale factor , but it does not intend to relate to any quantum gravity scheme. |
| 15. | Another possibility would of course be to re-introduce the connection through and seek for a more convenient gauge involving both metric and connection perturbations. |
| 16. | It is worth stressing that the equation obtained from the covariantization of the Dirac Lagrangian does not give the covariantized version of the Dirac equation in spaces with torsion and/or non-metricity. This subtlety is irrelevant in the case of GR, but it is important when considering more generally connected spacetimes. |
| 17. | To see how this occurs, first generalise the Lorentz basis to the general linear basis, . Thus, only the trace of non-metricity contributes to the covariant derivative of spinors in the first place. Secondly, in the Dirac action, this trace simply cancels due to the Hermitisation. As a result, even though in the coincident gauge we have in the action, effectively we recover in the equations of motion. |
| 18. | See Ref. [24] for an elaboration on this point and references. |
| 19. | Recall indeed from (23) that the theory is the minimal covariantization of the Einstein Lagrangian (1916). |
| 20. | More precisely, the spin connection is an , the affine connection is a transformation. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beltrán Jiménez, J.; Heisenberg, L.; Koivisto, T.S. The Geometrical Trinity of Gravity. Universe 2019, 5, 173. https://doi.org/10.3390/universe5070173
Beltrán Jiménez J, Heisenberg L, Koivisto TS. The Geometrical Trinity of Gravity. Universe. 2019; 5(7):173. https://doi.org/10.3390/universe5070173
Chicago/Turabian StyleBeltrán Jiménez, Jose, Lavinia Heisenberg, and Tomi S. Koivisto. 2019. "The Geometrical Trinity of Gravity" Universe 5, no. 7: 173. https://doi.org/10.3390/universe5070173
APA StyleBeltrán Jiménez, J., Heisenberg, L., & Koivisto, T. S. (2019). The Geometrical Trinity of Gravity. Universe, 5(7), 173. https://doi.org/10.3390/universe5070173






