Abstract
The QCD Lagrangian is based on quark and gluonic fields—not squarks nor gluinos. However, one can show that its hadronic eigensolutions conform to a representation of superconformal algebra, reflecting the underlying conformal symmetry of chiral QCD. The eigensolutions of superconformal algebra provide a unified Regge spectroscopy of meson, baryon, and tetraquarks of the same parity and twist as equal-mass members of the same 4-plet representation with a universal Regge slope. The predictions from light-front holography and superconformal algebra can also be extended to mesons, baryons, and tetraquarks with strange, charm and bottom quarks. The pion eigenstate has zero mass for A key tool is the remarkable observation of de Alfaro, Fubini, and Furlan (dAFF) which shows how a mass scale can appear in the Hamiltonian and the equations of motion while retaining the conformal symmetry of the action. When one applies the dAFF procedure to chiral QCD, a mass scale appears which determines universal Regge slopes, hadron masses in the absence of the Higgs coupling. One also predicts the form of the nonperturbative QCD running coupling: , in agreement with the effective charge determined from measurements of the Bjorken sum rule. One also obtains viable predictions for spacelike and timelike hadronic form factors, structure functions, distribution amplitudes, and transverse momentum distributions. The combination of conformal symmetry, light-front dynamics, its holographic mapping to AdS space, and the dAFF procedure thus provide new insights, not only into the physics underlying color confinement, but also the nonperturbative QCD coupling and the QCD mass scale.
1. Conformal Invariance of QCD and the Principle of Maximum Conformality
Conformal symmetry is a an underlying symmetry of quantum chromodynamics (QCD). If one sets the quark masses to zero in the QCD Lagrangian, the theory has no evident mass scale, and it is manifestly scale invariant. In effect, the classical chiral QCD theory is conformal.
A key tool is the remarkable observation of de Alfaro, Fubini, and Furlan (dAFF) [1] which shows how a mass scale can appear in the Hamiltonian and the equations of motion of a theory while retaining the conformal symmetry of the action. When one applies the dAFF procedure to chiral light-front QCD, a mass scale appears which determines universal Regge slopes and hadron masses in the absence of the Higgs coupling.
Conformal symmetry also leads to a rigorous way to eliminate the renormalization scale ambiguity [2,3,4] A primary problem for perturbative QCD analyses is how to set the renormalization scale of the QCD running coupling in order to achieve precise fixed-order predictions for physical observables. The Principle of Maximal Conformality (PMC) provides a systematic way to set the renormalization scales order-by-order for any perturbative QCD process, eliminating the ambiguities associated with the conventional renormalization scale-setting procedure. The resulting predictions are independent of the choice of renormalization scheme, a requirement of renormalization group invariance. The scales of the QCD couplings and the effective number of quark flavors are set order-by-order by absorbing the nonconformal terms in the pQCD series into the running coupling. The resulting pQCD series then matches the conformal series.The PMC generalizes the BLM procedure to all orders [5] and it reduces to the Gell Mann Low scale setting procedure for Abelian QED in the limit. The divergent renormalon series does not appear. The PMC satisfies renormalization group invariance and all of the other self-consistency conditions derived from the renormalization group. It thus systematically eliminates a major theoretical uncertainty for pQCD predictions and increases the sensitivity of experiment to new physics beyond the Standard Model.
The Crewther relation [6], which was originally derived for conformal theory, provides a remarkable connection in conformal theory between two observables when the function vanishes. Specifically, it connects the non-singlet Adler function to the Bjorken sum rule coefficient for polarized deep-inelastic electron scattering at leading twist. The “Generalized Crewther Relation” [6,7,8] relates these observables for physical QCD with nonzero function. The resulting relation is independent of the choice of the renormalization scheme at any finite order, and the dependence on the choice of the initial scale is negligible. Similar scale-fixed “commensurate scale relations” also connect other physical observables at their physical momentum scales, thus providing new convention-independent precision tests of QCD.
2. The Origin of the QCD Mass Scale and the dAFF Principle
A fundamental question for QCD is the origin of the mass of the proton and other hadrons when the quark masses are zero.
It is often stated that the mass scale of the renormalized perturbative theory generates the nonperturbative QCD mass scale; however, this “dimensional transmutation” solution is problematic since the perturbative scale is renormalization-scheme dependent, whereas hadron masses cannot depend on a theoretical convention. It is conventional to measure hadron masses in MeV units; however, QCD has no knowledge of units such as electron-volts. Thus QCD at can at best only predict ratios of masses such as and other dimensionless quantities. It is often argued that the QCD mass scale reflects the presence of quark and gluon condensates in the QCD vacuum state. However, such condensates lead to a cosmological constant a factor of larger than measured. In fact, nontrivial vacuum structure does not appear in QCD if one defines the vacuum state as the eigenstate of lowest invariant mass of the QCD light-front (LF) Hamiltonian. In fact, in Dirac’s boost invariant “front form” [9], where the time variable is the time along the light-front, the light-front vacuum is both causal and frame-independent; one thus has [10] and zero cosmological constant [11,12]. In the case of the Higgs theory, the traditional Higgs vacuum expectation value (VEV) is replaced by a “zero mode”, in the LF theory, analogous to a classical Stark or Zeeman field [13]. The Higgs LF zero mode [13] has no energy-momentum density, so it also gives zero contribution to the cosmological constant.
The remarkable work of de Alfaro, Fubini, and Furlan (dAFF) [1] provides a novel solution for the origin of the hadron mass scale in QCD. dAFF have shown that one can introduce a nonzero mass scale into the Hamiltonian of a conformal theory without affecting the conformal invariance of the action. The essential step is to add to the Hamiltonian H a term proportional to the dilation operator and/or the special conformal operator. In the case of one-dimensional quantum mechanics, the resulting Hamiltonian acquires a confining harmonic oscillator potential; however, after a redefinition of the time variable, the action remains conformal.
The same principle can be applied to relativistic quantum field theory using light-front (LF) quantization [14]. The application of dAFF then leads in fact to a color-confining LF harmonic oscillator potential, where again the action remains conformal. In fact, De Téramond, Dosch, and I [15] have shown that a mass gap and a fundamental color confinement scale also appear when one extends the dAFF procedure to light-front (LF) Hamiltonian theory in physical 3 + 1 spacetime. The LF equation for bound states for can be systematically reduced to a differential equation in a single LF radial variable :
where is the radial variable of the front form and is the LF orbital angular momentum [16]. This is in analogy to the non-relativistic radial Schrödinger equation for bound states such as positronium in QCD. Thus in the case of QCD(3 + 1)—using the causal, frame-independent light-front Hamiltonian formalism—the LF potential has the unique form , where is the radial variable of the light-front form: where is the boost invariant momentum fraction.
3. Light-Front Holography
As noted by Maldacena [17], anti-deSitter space in five space-time dimensions (AdS) provides a geometrical representation of the conformal group. Thus AdS can be used as a starting point for a conformal theory such as chiral QCD. In fact AdS is holographically dual to gauge theory quantized at fixed light-front time, Dirac’s front form. Exclusive hadron amplitudes, such as elastic and transition form factors are given in terms of convolutions of light-front wavefunctions [18]. The light-front Drell-Yan-West formulae for electromagnetic and gravitational form factors is identical to the Polchinski-Strassler [19] formula for form factors in AdS. This identification (light-front holography also provides a nonperturbative derivation of scaling laws [20,21] for form factors at large momentum transfer. Additional references and reviews of Light-Front Holography may be found in refs. [22,23,24,25,26].
Remarkably, the identical LF potential and the same LF equation of motion are obtained in AdS when one identifies the fifth coordinate z with the LF radial coordinate and introduces a specific modification of the AdS metric—the “dilaton” . This dilaton also leads to Gaussian functional form of the nonperturbative QCD running coupling: , in agreement with the effective charge determined from measurements of the Bjorken sum rule. The soft wall dilaton modification of the conformal AdS action is selected so that the resulting bound state equation in the AdS fifth dimension yields the confining potential and thus the potential in the LF Schrödinger equation, as in the dAFF modification of a conformally-invariant Hamiltonian. Thus this dilaton conforms with the dAFF procedure which shows how a mass scale can appear in a bound state equation while retaining the conformal invariance of the action.
Deur, de Teramond, and I [27,28,29] have also shown how the parameter , which determines the mass scale of hadrons and Regge slopes in the zero quark mass limit, can be connected to the mass scale controlling the evolution of the perturbative QCD coupling. The high momentum transfer dependence of the coupling is predicted by pQCD. The matching of the high and low momentum transfer regimes of —both its value and its slope—then determines a scale GeV which sets the interface between perturbative and nonperturbative hadron dynamics. This connection can be done for any choice of renormalization scheme, such as the scheme, The mass scale underlying hadron masses can thus be connected to the parameter in the QCD running coupling by matching its predicted nonperturbative form to the perturbative QCD regime. The result is an effective coupling defined at all momenta.
This identification of AdS with the light-front Hamiltonian theory automatically introduces an extra spin-dependent constant term in the LF Hamiltonian, where with are the LF spins. The resulting prediction from AdS/QCD is the single variable “LF Schrodinger Equation” in , where and . The synthesis of AdS/QCD with superconformal algebra and the dAFF ansatz is illustrated in Figure 1. The eigenvalues for the meson spectrum are The mesonic spectrum of bound states is thus described as Regge trajectories in both the radial variable n and the orbital angular momentum L with the same slope . Color confinement is a consequence of the light-front potential . Remarkably, the pion is massless: for . Thus light-front holography explains another fundamental question in hadron physics – how a zero mass pseudoscalar pion bound state can emerge, despite its composite structure. The eigensolutions generate both the mass spectrum and the light front wavefunctions for all meson bound state.
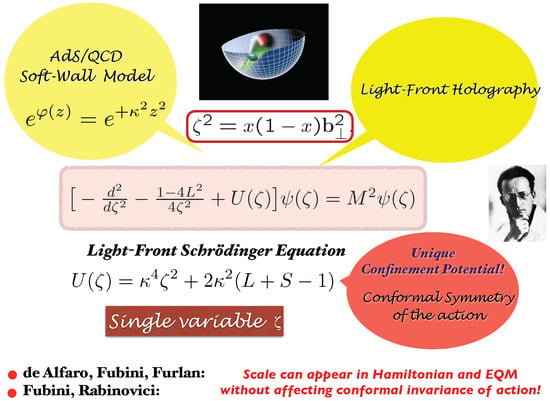
Figure 1.
The convergence of theoretical methods for generating a model of hadron spectroscopy and dynamics with color confinement and meson-baryon supersymmetric relations.
Nonzero quark masses appear in the “LF kinetic energy” (LFKE) contribution to the LF Hamiltonian—the square of the invariant mass of the constituents: . One can identify the the contribution to the LFKE as arising in the Higgs theory from the coupling of each quark to the background zero-mode Higgs field [13] which replaces the usual VEV of the standard time “instant form”. In the heavy quark limit, one recovers the usual confining potential for heavy quarkonium [30].
4. Superconformal Algebra and Supersymmetric Hadron Spectroscopy
Another advance in LF holography is the application of superconformal algebra, a feature of the underlying conformal symmetry of chiral QCD. The conformal group has an elegant Pauli matrix representation called superconformal algebra, originally discovered by Haag, Lopuszanski, and Sohnius [31] (1974) The conformal Hamiltonian operator and the special conformal operators can be represented as anticommutators of Pauli matrices and . As shown by Fubini and Rabinovici, [32], a nonconformal Hamiltonian with a mass scale and universal confinement can then be obtained by shifting , the analog of the dAFF procedure. In effect, one has obtained generalized supercharges of the superconformal algebra [32]. This ansatz extends the predictions for the hadron spectrum to a “4-plet” —consisting of mass-degenerate quark-antiquark mesons, quark-diquark baryons, and diquark-antidiquark tetraquarks, as shown in Figure 2. The 4-plet contains two entries for each baryon, corresponding to internal orbital angular momentum L and . This property of the baryon LFWFs is the analog of the eigensolution of the Dirac-Coulomb equation which has both an upper component and a lower component .

Figure 2.
The 4-plet representation of mass-degenerate hadronic states predicted by superconformal algebra [15]. Mesons are bound states, baryons are quark—antidiquark bound states and tetraquarks are diquark-antidiquark bound states. The supersymmetric ladder operator connects quarks and anti-diquark clusters of the same color.
LF Schrödinger Equations for baryons and mesons can be derived from superconformal algebra. The baryonic eigensolutions correspond to bound states of quarks to a spin-0 or spin-1 diquark cluster; the tetraquarks in the 4-plet are bound states of diquarks and anti-diquarks. The quark-diquark baryons have two amplitudes with equal probability, a feature of “quark chirality invariance”. The proton Fock state component (with parallel quark and baryon spins) and (with anti-parallel quark and baryon spins) have equal Fock state probability—a feature of “quark chirality invariance”. Thus the proton’s spin is carried by quark orbital angular momentum in the nonperturbative domain. Predictions for the static properties of the nucleons are discussed in Ref. [33]. The predicted spectrum, for mesons and for baryons, is remarkably consistent with observed hadronic spectroscopy. The Regge-slopes in n and L are identical. The predicted meson, baryon and tetraquark masses coincide if one identifies a meson with internal orbital angular momentum with its superpartner baryon or tetraquark with . Superconformal algebra thus predicts that mesons with have the same mass as the baryons in the supermultiplet. An example of the mass degeneracy of the meson Regge trajectory with the -baryon trajectory is shown in Figure 3. The value of can be set by the mass; however, only ratios of masses are predicted.
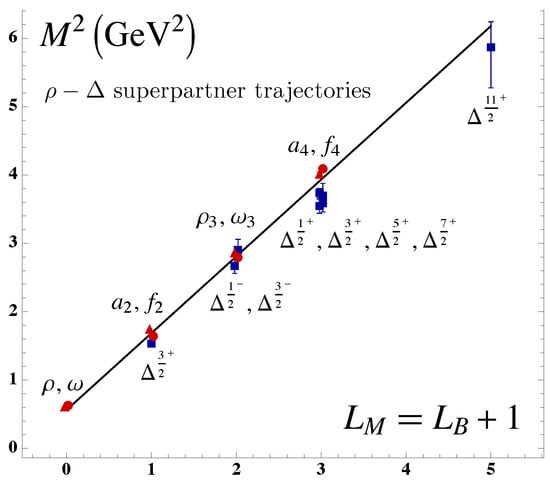
Figure 3.
Comparison of the meson Regge trajectory with the baryon trajectory. Superconformal algebra predicts the degeneracy of the meson and baryon trajectories if one identifies a meson with internal orbital angular momentum with its superpartner baryon with See Refs. [38,39].
The combination of light-front holography with superconformal algebra thus leads to the novel prediction that hadron physics has supersymmetric properties in both spectroscopy and dynamics. The excitation spectra of relativistic light-quark meson, baryon and tetraquark bound states all lie on linear Regge trajectories with identical slopes in the radial and orbital quantum numbers. Detailed predictions for the tetraquark spectroscopy and comparisons with the observed hadron spectrum are presented in ref. [34].
5. Supersymmetric Hadron Spectroscopy for Heavy Quarks
The predictions from light-front holography and superconformal algebra have been extended to mesons, baryons, and tetraquarks with strange, charm and bottom quarks in Refs. [35,36]. Although conformal symmetry is strongly broken by the heavy quark mass, the basic underlying supersymmetric mechanism, which transforms mesons to baryons (and baryons to tetraquarks) into each other, still holds and gives remarkable connections and mass degeneracy across the entire spectrum of light, heavy-light and double-heavy hadrons. The excitation spectra of the heavy quark meson, baryon and tetraquark bound states continue to lie on universal linear Regge trajectories with identical slopes in the radial and orbital quantum numbers, but with an increased value for the slope. For example, the mass of the lightest double-charm baryon , where the is a scalar diquark, is predicted to be identical to the mass of the orbital excitation of the ( the ) and also the mass of the double-charm tetraquark. In fact, the mass of the matches the mass of the double-charm baryon identified by SELEX and a tetraquark candidate the . For more details, see refs. [34,37]. The effective supersymmetric properties of QCD can be used to identify the structure of the heavy quark mesons, baryons and tetraquark states [34].
Thus one predicts supersymmetric hadron spectroscopy – bosons and fermions with the same mass and twist- not only identical masses for the bosonic and fermionic hadron eigenvalues, but also supersymmetric relations between their eigenfunctions– their light-front wavefunctions. The baryonic eigensolutions correspond to bound states of quarks to a spin-0 or spin-1 diquark cluster; the tetraquarks in the 4-plet are bound states of diquarks and anti-diquarks. In the case of a nucleon, the overlap of the and LF wavefunctions in the Drell-Yan-West formula is required to have a non-zero Pauli form factor and anomalous magnetic moment [18]. The existence of both components is also necessary to generate the pseudo-T-odd Sivers single-spin asymmetry in deep inelastic lepton-nucleon scattering [40].
6. Summary
The combination of conformal symmetry, light-front dynamics, its holographic mapping to AdS space, and the dAFF procedure provide new insights, not only into the physics underlying color confinement, but also the nonperturbative QCD coupling and the QCD mass scale. A comprehensive review is given in Ref. [25]. The QCD Lagrangian is not supersymmetrical; however its hadronic eigensolutions conform to a fundamental 4-plet supersymmetric representation of superconformal algebra, reflecting the underlying conformal symmetry of semi-classical QCD for massless quarks. The resulting “Light-Front Schrödinger equations” derived from LF holography incorporates color confinement and other essential spectroscopic and dynamical features of hadron physics, including a massless pion for zero quark mass and linear Regge trajectories with the same slope in the radial quantum number n and internal orbital angular momentum L for mesons, baryons, and tetraquarks. LF holography gives a remarkable first approximation to hadron spectroscopy and the hadronic LFWFs. A new method for solving nonperturbative QCD “Basis Light-Front Quantization” (BLFQ) [41], uses the eigensolutions of a color-confining approximation to QCD (such as LF holography) as the basis functions, rather than the plane-wave basis used in DLCQ, thus incorporating the full dynamics of QCD. This approach predicts novel supersymmetric relations between mesons, baryons, and tetraquarks of the same parity as members of the same 4-plet representation of superconformal algebra. Empirically viable predictions for spacelike and timelike hadronic form factors, structure functions, distribution amplitudes, and transverse momentum distributions have also been obtained [42]. One can also observe features of superconformal symmetry in the spectroscopy and dynamics of heavy-light mesons and baryons. The combination of light-front holography with superconformal algebra thus leads to the novel prediction that hadron physics has supersymmetric properties in both spectroscopy and dynamics. One can test the similarities of their wavefunctions and form factors in exclusive reactions such as where T is a tetraquark [43].
Funding
This research received no external funding.
Acknowledgments
The physics results presented here are based on collaborations and discussions with many collaborators, including Xing-Gang, Wu, Peter Lowdon, Kelly Chiu, Philip Mannheim, Matin Mojaza, Marina Nielsen, Alexandre Deur, Guy de Téramond, and Hans Günter Dosch. This research was supported by the Department of Energy, contract DE–AC02–76SF00515. SLAC-PUB-17341.
Conflicts of Interest
The author declares no conflict of interest.
References
- De Alfaro, V.; Fubini, S.; Furlan, G. Conformal Invariance in Quantum Mechanics. Il Nuovo Cim. A 1976, 34, 569. [Google Scholar] [CrossRef]
- Mojaza, M.; Brodsky, S.J.; Wu, X.G. Systematic All-Orders Method to Eliminate Renormalization-Scale and Scheme Ambiguities in Perturbative QCD. Phys. Rev. Lett. 2013, 110, 192001. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.G.; Brodsky, S.J.; Mojaza, M. The Renormalization Scale-Setting Problem in QCD. Prog. Part. Nucl. Phys. 2013, 72, 44. [Google Scholar] [CrossRef]
- Du, B.L.; Wu, X.G.; Shen, J.M.; Brodsky, S.J. Extending the Predictive Power of Perturbative QCD. arXiv, 2018; arXiv:1807.11144. [Google Scholar]
- Brodsky, S.J.; Lepage, G.P.; Mackenzie, P.B. On the Elimination of Scale Ambiguities in Perturbative Quantum Chromodynamics. Phys. Rev. D 1983, 28, 228. [Google Scholar] [CrossRef]
- Lu, H.J.; Brodsky, S.J. Relating physical observables in QCD without scale - scheme ambiguity. Phys. Rev. D 1993, 48, 3310. [Google Scholar] [CrossRef]
- Shen, J.M.; Wu, X.G.; Ma, Y.; Brodsky, S.J. The Generalized Scheme-Independent Crewther Relation in QCD. Phys. Lett. B 2017, 770, 494. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Gabadadze, G.T.; Kataev, A.L.; Lu, H.J. The Generalized Crewther relation in QCD and its experimental consequences. Phys. Lett. B 1996, 372, 133. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Forms of Relativistic Dynamics. Rev. Mod. Phys. 1949, 21, 392. [Google Scholar] [CrossRef]
- Lowdon, P.; Chiu, K.Y.J.; Brodsky, S.J. Rigorous constraints on the matrix elements of the energy-momentum tensor. Phys. Lett. B 2017, 774, 1–6. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Shrock, R. Condensates in Quantum Chromodynamics and the Cosmological Constant. Proc. Nat. Acad. Sci. USA 2011, 108, 45. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Roberts, C.D.; Shrock, R.; Tandy, P.C. Confinement contains condensates. Phys. Rev. C 2012, 85, 065202. [Google Scholar] [CrossRef]
- Srivastava, P.P.; Brodsky, S.J. A Unitary and renormalizable theory of the standard model in ghost free light cone gauge. Phys. Rev. D 2002, 66, 045019. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Pauli, H.C.; Pinsky, S.S. Quantum chromodynamics and other field theories on the light cone. Phys. Rep. 1998, 301, 299. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Téramond, G.F.; Dosch, H.G. Threefold Complementary Approach to Holographic QCD. Phys. Lett. B 2014, 729, 3. [Google Scholar] [CrossRef]
- De Téramond, G.F.; Brodsky, S.J. Light-Front Holography: A First Approximation to QCD. Phys. Rev. Lett. 2009, 102, 081601. [Google Scholar] [CrossRef] [PubMed]
- Maldacena, J.M. Lectures on AdS/CFT. In From Fields to Strings: Circumnavigating Theoretical Physics; Shifman, M., Vainshtein, A., Wheater, J., Eds.; World Scientific Publishing: Singapore; Volume 2, pp. 1473–1518.
- Brodsky, S.J.; Drell, S.D. The Anomalous Magnetic Moment and Limits on Fermion Substructure. Phys. Rev. D 1980, 22, 2236. [Google Scholar] [CrossRef]
- Polchinski, J.; Strassler, M.J. Hard scattering and gauge/string duality. Phys. Rev. Lett. 2002, 88, 031601. [Google Scholar] [CrossRef] [PubMed]
- Brodsky, S.J.; Farrar, G.R. Scaling Laws at Large Transverse Momentum. Phys. Rev. Lett. 1973, 31, 1153. [Google Scholar] [CrossRef]
- Lepage, G.P.; Brodsky, S.J. Exclusive Processes in Perturbative Quantum Chromodynamics. Phys. Rev. D 1980, 22, 2157. [Google Scholar] [CrossRef]
- De Téramond, G.F.; Brodsky, S.J. Light-Front Holography and Gauge/Gravity Duality: The Light Meson and Baryon Spectra. Nucl. Phys. Proc. Suppl. 2010, 199, 89. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Téramond, G.F. AdS/QCD and Light Front Holography: A New Approximation to QCD. Chin. Phys. C 2010, 34, 1229. [Google Scholar] [CrossRef]
- De Téramond, G.F.; Brodsky, S.J.; Dosch, H.G. Hadron Spectroscopy and Dynamics from Light-Front Holography and Conformal Symmetry. In Proceedings of the EPJ Web Conference, Rome, Italy, 30 September–4 October 2013; Volume 73, p. 01014. [Google Scholar]
- Brodsky, S.J.; de Téramond, G.F.; Dosch, H.G.; Erlich, J. Light-Front Holographic QCD and Emerging Confinement. Phys. Rep. 2015, 584, 1–105. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Deur, A.; de Téramond, G.F.; Dosch, H.G. Light-Front Holography and Superconformal Quantum Mechanics: A New Approach to Hadron Structure and Color Confinement. Int. J. Mod. Phys. Conf. Ser. 2015, 39, 1560081. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Téramond, G.F.; Deur, A. Nonperturbative QCD Coupling and its β-function from Light-Front Holography. Phys. Rev. D 2010, 81, 096010. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; de Téramond, G.F. Connecting the Hadron Mass Scale to the Fundamental Mass Scale of Quantum Chromodynamics. Phys. Lett. B 2015, 750, 528. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Téramond, G.F.; Deur, A.; Dosch, H.G. The Light-Front Schrödinger Equation and the Determination of the Perturbative QCD Scale from Color Confinement: A First Approximation to QCD. Few Body Syst. 2015, 56, 621. [Google Scholar] [CrossRef]
- Trawinski, A.P.; Glazek, S.D.; Brodsky, S.J.; de Téramond, G.F.; Dosch, H.G. Effective confining potentials for QCD. Phys. Rev. D 2014, 90, 074017. [Google Scholar] [CrossRef]
- Haag, R.; Lopuszanski, J.T.; Sohnius, M. All Possible Generators of Supersymmetries of the s Matrix. Nucl. Phys. B 1975, 88, 257. [Google Scholar] [CrossRef]
- Fubini, S.; Rabinovici, E. Superconformal Quantum Mechanics. Nucl. Phys. B 1984, 245, 17. [Google Scholar] [CrossRef]
- Liu, T.; Ma, B.Q. Baryon properties from light-front holographic QCD. Phys. Rev. D 2015, 92, 096003. [Google Scholar] [CrossRef]
- Nielsen, M.; Brodsky, S.J. Hadronic superpartners from a superconformal and supersymmetric algebra. Phys. Rev. D 2018, 97, 114001. [Google Scholar] [CrossRef]
- Dosch, H.G.; de Téramond, G.F.; Brodsky, S.J. Supersymmetry Across the Light and Heavy-Light Hadronic Spectrum II. Phys. Rev. D 2017, 95, 034016. [Google Scholar] [CrossRef]
- Nielsen, M.; Brodsky, S.J.; de Téramond, G.F.; Dosch, H.G.; Navarra, F.S.; Zou, L. Supersymmetry in the Double-Heavy Hadronic Spectrum. Phys. Rev. D 2018, 98, 034002. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Groote, S.; Koshkarev, S. Resolving the SELEX–LHCb double-charm baryon conflict: the impact of intrinsic heavy-quark hadroproduction and supersymmetric light-front holographic QCD. Eur. Phys. J. C 2018, 78, 483. [Google Scholar] [CrossRef]
- De Téramond, G.F.; Dosch, H.G.; Brodsky, S.J. Baryon Spectrum from Superconformal Quantum Mechanics and its Light-Front Holographic Embedding. Phys. Rev. D 2015, 91, 045040. [Google Scholar] [CrossRef]
- Dosch, H.G.; de Téramond, G.F.; Brodsky, S.J. Superconformal Baryon-Meson Symmetry and Light-Front Holographic QCD. Phys. Rev. D 2015, 91, 085016. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Hwang, D.S.; Schmidt, I. Final state interactions and single spin asymmetries in semiinclusive deep inelastic scattering. Phys. Lett. B 2002, 530, 99. [Google Scholar] [CrossRef]
- Vary, J.P.; Zhao, X.; Ilderton, A.; Honkanen, H.; Maris, P.; Brodsky, S.J. Applications of Basis Light-Front Quantization to QED. Nucl. Phys. Proc. Suppl. 2014, 251–252, 10. [Google Scholar] [CrossRef]
- Sufian, R.S.; de Téramond, G.F.; Brodsky, S.J.; Deur, A.; Dosch, H.G. Analysis of nucleon electromagnetic form factors from light-front holographic QCD: The spacelike region. Phys. Rev. D 2017, 95, 014011. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Lebed, R.F. QCD dynamics of tetraquark production. Phys. Rev. D 2015, 91, 114025. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).