Abstract
I present theoretical calculations for Higgs-boson and top-quark production, including high-order soft-gluon corrections. I discuss charged-Higgs production in association with a top quark or a W boson, as well as single-top and top-antitop production. Total cross sections as well as transverse-momentum and rapidity distributions of the top quark or the Higgs boson are presented for various LHC energies.
1. Introduction
The study of the top quark and of Higgs bosons in the Standard Model and beyond are two major active areas of fundamental physics and its exporation at the LHC. To make the most of the physics program at the LHC, we need to be able to predict theoretically the cross sections for processes involving top quarks and Higgs bosons, including processes beyond the Standard Model. Perturbative QCD corrections are typically large for these processes and they are needed to reduce the dependence of the cross sections on factorization and renormalization scales.
Many processes have now been calculated to NLO, and some to NNLO. The complexity of the calculations increases enormously with each order. It is therefore important to identify the sources of specific contributions to the cross sections, and whether they are numerically dominant and can be calculated with alternative techniques. It turns out that soft-gluon corrections, i.e., radiative corrections calculated in the eikonal approximation where the gluons are low-energy, dominate the cross sections for many processes at LHC and Tevatron energies. It is thus important and meaningful to calculate these corrections. See Ref. [1] for a review.
These soft-gluon corrections can be formally resummed in moment space to all orders in the perturbative series by using factorization of the cross section into different functions that describe the behavior of hard, collinear, and soft quanta, and renormalization-group evolution of these functions. However, physical predictions for resummed cross sections need some kind of method or prescription to avoid Landau singularities in the resummed result, and the record of such prescriptions has been rather poor in that they typically grossly underestimate the numerical contribution of the corrections. However, fixed-order expansions of the resummed cross sections bypass such concerns.
Expansions of resummed cross sections have been given at NLO, NNLO, and even NLO for numerous top-quark and Higgs processes [1]. The soft-gluon corrections at NLO typically are excellent approximations to the complete NLO corrections. In cases where the complete NNLO corrections are known, it is also found that the soft-gluon corrections at NNLO are also very good approximations. Even higher-order soft-gluon corrections can provide additional significant contributions.
In this presentation, I discuss the latest results with soft-gluon corrections for various processes involving charged Higgs bosons and top quarks. In particular, I discuss production, production, single-top quark production in the t- and s-channels and production, production via anomalous top-quark couplings, and production. Soft-gluon corrections are very important in all these cases and they approximate exact results very well.
We resum these soft corrections at next-to-next-to-leading logarithm (NNLL) accuracy for the double-differential cross section, and we use the resummed cross section as a generator of finite-order expansions to provide approximate NNLO (aNNLO) and approximate NLO (aNLO) predictions for cross sections and differential distributions. We get the aNNLO prediction by adding the aNNLO soft-gluon corrections to the complete NLO result. The aNLO prediction is found by adding the aNLO soft-gluon corrections to the complete NNLO result if the latter is available (or to the aNNLO result, if it is not).
2. Higher-Order Soft-Gluon Corrections
We consider partonic processes for charged-Higgs production
and for top-quark production
In addition to the usual kinematical variables s, t, u, we define a threshold variable . At partonic threshold , and the soft-gluon corrections are of the form for charged-Higgs production, and for top-quark production, with at order . We resum these soft corrections for the double-differential cross section in t and u, or equivalently in and rapidity.
To derive soft-gluon resummation, we take moments of the partonic cross section with moment variable N, , and write a factorized expression for the cross section in dimensions
where m denotes the charged-Higgs or top-quark masses, depending on the process, and and are the factorization and renormalization scales. is the hard function and is the soft function, both of them matrices in general in the space of color exchanges, and the and collect collinear and soft-gluon corrections from the incoming and outgoing partons. satisfies the renormalization group equation
where is the soft anomalous dimension, thus resulting in the exponentiation of logarithms of N. At NNLL accuracy, we need two-loop soft anomalous dimensions.
Resummed expressions follow from the evolution of the soft function, as determined by the above renormalization group equation, as well as of the J functions in the factorized expression.
3. Charged Higgs Production
We begin with the associated production of a top quark and a charged Higgs boson in the MSSM or other two-Higgs-doublet models [2,3,4]. The lowest-order cross section for the process is proportional to where is the ratio of the vacuum expectation values of the two Higgs doublets. The soft anomalous dimension for the process is , with
and
The analytical expressions for the soft-gluon corrections through NNLO for production have been given in [2,3,4]. The approximate NLO (aNLO) soft-gluon corrections are:
where, for brevity, we do not show explicitly the lower powers of the logarithms.
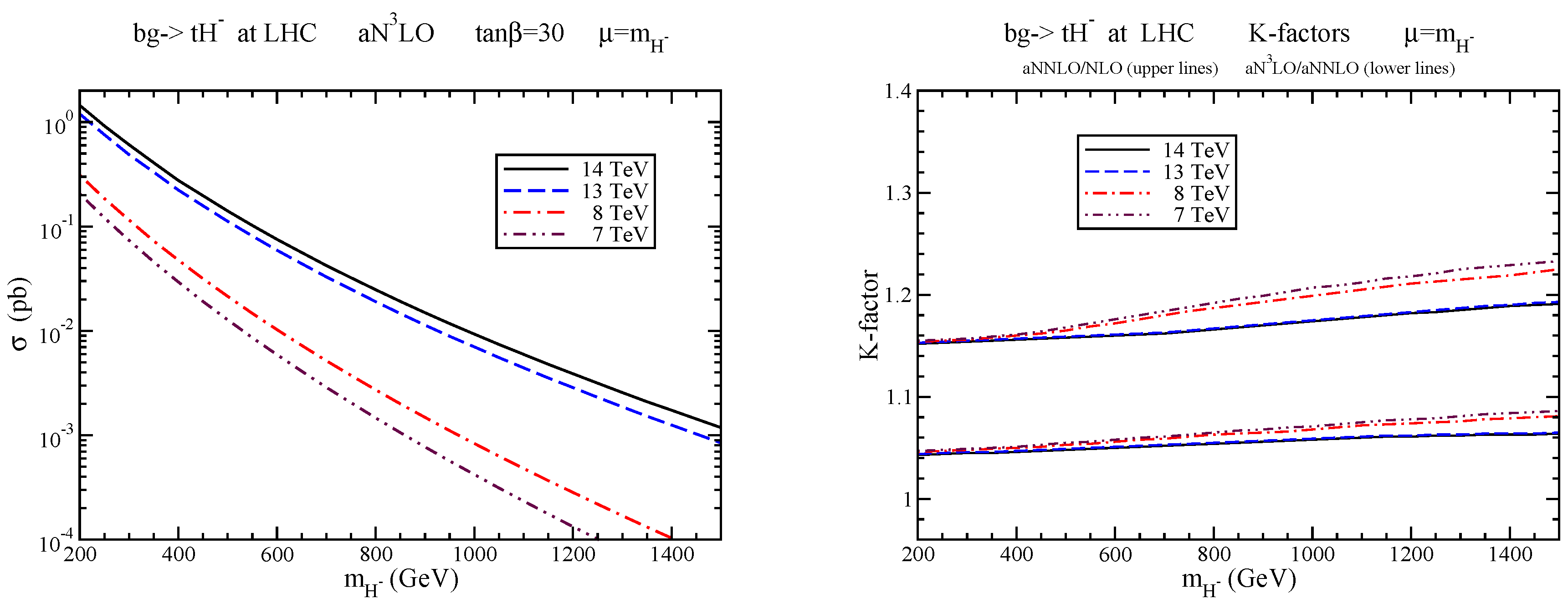
We now present the aNLO total cross sections at LHC energies. We use MMHT2014 NNLO pdf [5] for our numerical results. In the left plot of Figure 1, we show the aNLO total cross section for production, with , as a function of charged-Higgs mass at LHC energies of 7, 8, 13, and 14 TeV. The soft-gluon corrections are large for this process, as shown on the plot on the right. Top-quark and rapidity distributions in this process have also been presented in [3,4].
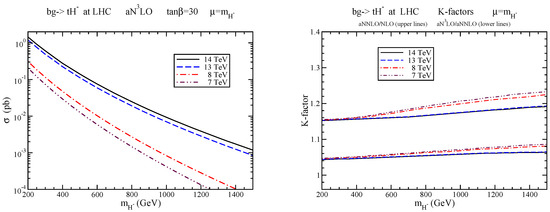
Figure 1.
(Left) aNLO total cross sections for production; (Right) K-factors for production.
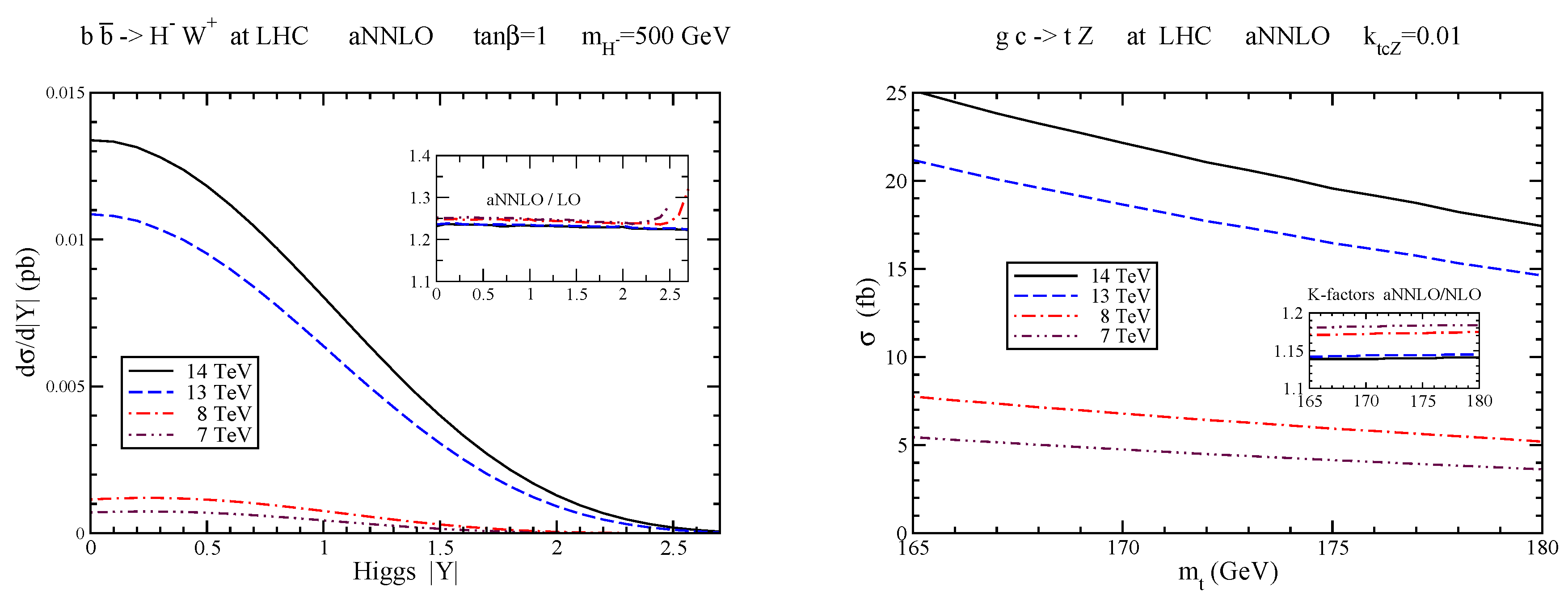
We next discuss production via [6]. In the left plot of Figure 2, we show the aNNLO charged-Higgs rapidity distribution , with and GeV, at 7, 8, 13, and 14 TeV LHC energies with MMHT2014 NNLO pdf. The inset plot shows the aNNLO/LO K-factors. The soft-gluon corrections are clearly very significant.
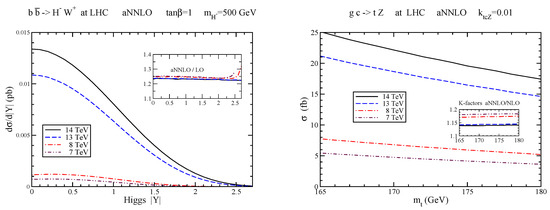
Figure 2.
(Left) the aNNLO rapidity distribution of the charged Higgs boson in production at LHC energies; (Right) the aNNLO total cross section for the process .
4. Production via Anomalous Couplings
In physics beyond the Standard Model, top-quark production may occur via anomalous couplings of the top quark. Here, we discuss soft-gluon corrections in production with anomalous t-q-Z couplings via the processes and [7]. The complete NLO corrections [8] are very well approximated by the soft-gluon corrections at that order.
In the right plot of Figure 2, we show the aNNLO total cross section for as a function of top-quark mass at LHC energies of 7, 8, 13, and 14 TeV with CT14 pdf [9]. The inset plot displays the K-factors, which show that the aNNLO corrections are large. The fact that these corrections significantly enhance the NLO cross section is an important theoretical input to setting experimental limits on the couplings [10,11]. Similar results are found for the process , and top-quark differential distributions for both processes have been presented in Ref. [7].
Related calculations have more recently been done for production via anomalous couplings in Ref. [12], with similar findings on the importance of soft-gluon corrections.
5. Single-Top Production
Next, we discuss single-top production in the t-channel, s-channel, and via production. These processes are now known at NNLO for the t-channel [13,14,15] and the s-channel [16], and at NLO for production [17]. Soft-gluon resummation at NNLL has been performed for all channels [18,19,20,21]. We now present results with soft-gluon corrections at aNNLO [18,20] for the t and s channels, and at aNLO [21] for production.
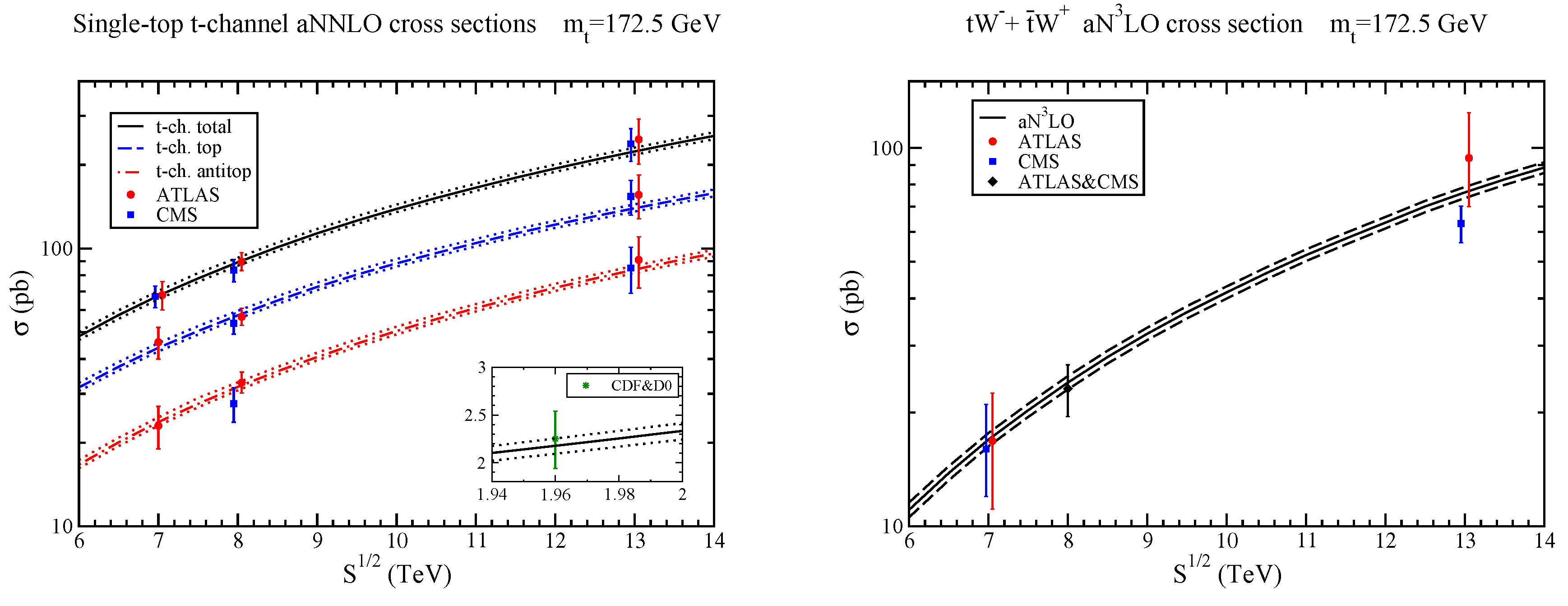
In the left plot of Figure 3, we show aNNLO results for t-channel cross sections, using MMHT2014 NNLO pdf [5], at LHC and (inset) at Tevatron energies. Results are shown separately for the single-top cross section, the single-antitop cross section, and their sum. We find excellent agreement of the aNNLO predictions with all data from the LHC and the Tevatron. The aNNLO normalized top-quark distributions also describe the available data quite well [22].
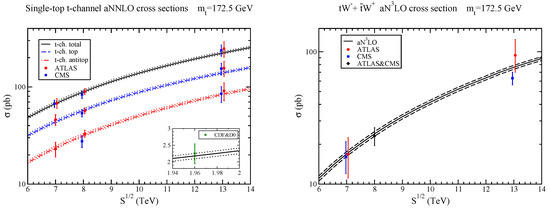
Figure 3.
(Left) single-top t-channel aNNLO cross sections compared with CMS and ATLAS data at 7 TeV [23,24], 8 TeV [25,26], and 13 TeV [27,28], and with CDF and D0 combined data at 1.96 TeV [29]; (Right) aNLO cross sections for production compared to ATLAS and CMS data at 7 TeV [30,31], 8 TeV [32], and 13 TeV [33,34].
We next discuss production at aNLO. In the right plot of Figure 3, we show the total + cross section as a function of energy. We observe very good agreement with LHC data at 7, 8, and 13 TeV energies.
Finally, the theoretical predictions for s-channel production at aNNLO are in good agreement with available LHC and Tevatron data as shown in [22].
6. Top-Antitop Pair Production
Top-antitop pair poduction is the dominant mode at both the Tevatron and the LHC. The theoretical state-of-the-art is currently aNLO [35,36,37]. The soft anomalous dimensions are known at two loops and they are matrices in color space for the channel, and matrices for the channel.
The soft-gluon corrections have been known at NLO and NNLO for total and differential cross sections for some time. These corrections are large and dominant, and they provide excellent approximations to the complete QCD corrections at both NLO and NNLO [1] (see, in particular, Figure 6 in [1]). The further corrections at aNLO are still significant, and they need to be included in theoretical predictions for improved accuracy and smaller theoretical uncertainty. At the LHC, the aNLO corrections increase the NNLO cross section by around 4% at 7 and 8 TeV energies and by around 3% at 13 and 14 TeV energies (see Ref. [35] for details).
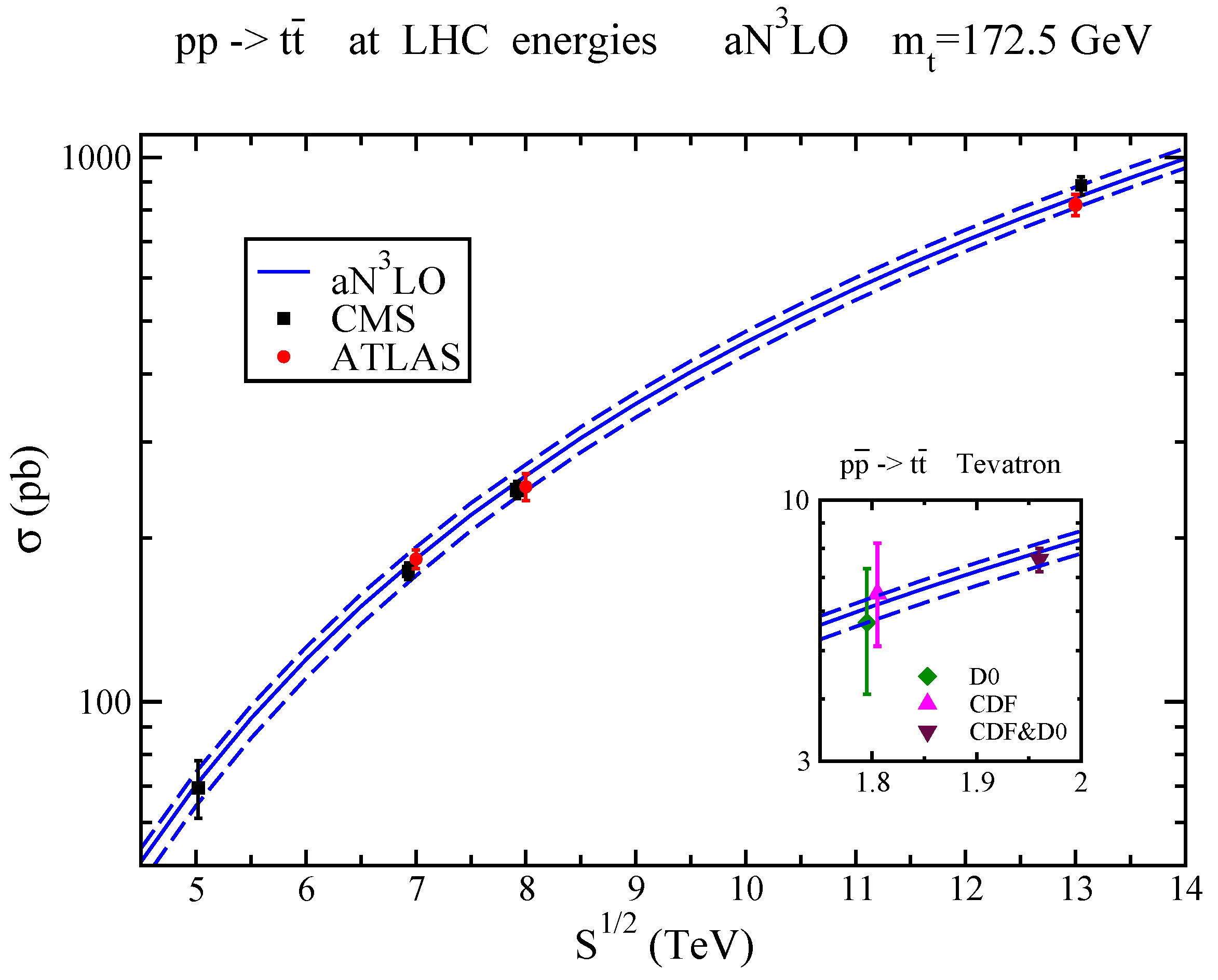
Figure 4 displays the aNLO top-antitop cross sections at LHC and Tevatron energies using MMHT2014 NNLO pdf. There is data from the Tevatron at 1.8 TeV and 1.96 TeV energies, and from the LHC at 5.02, 7, 8, and 13 TeV energies. The theoretical curves describe the data at all energies remarkably well. The fact that aNLO theory has predicted and agrees with the data over such a wide energy range is highly significant. The soft-gluon corrections are important both in enhancing the cross section and in reducing its dependence on renormalization and factorization scales.
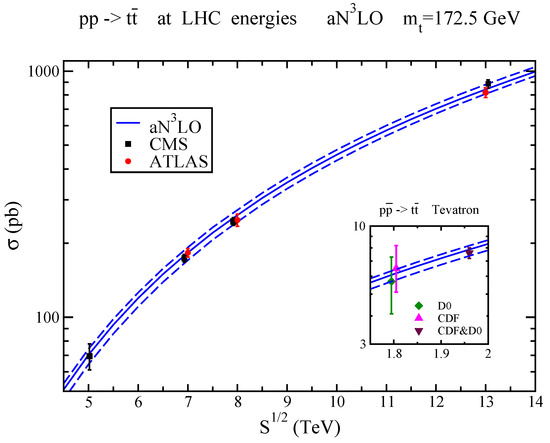
Figure 4.
Top-antitop aNLO cross sections compared with CMS data at 5.02 TeV [38] and with ATLAS and CMS data at 7 TeV [39,40], 8 TeV [40,41], and 13 TeV [42,43] LHC energies. The inset shows the aNLO cross section compared with CDF [44] and D0 [45] data at 1.8 TeV, and CDF&D0 combined data [46] at 1.96 TeV Tevatron energy.
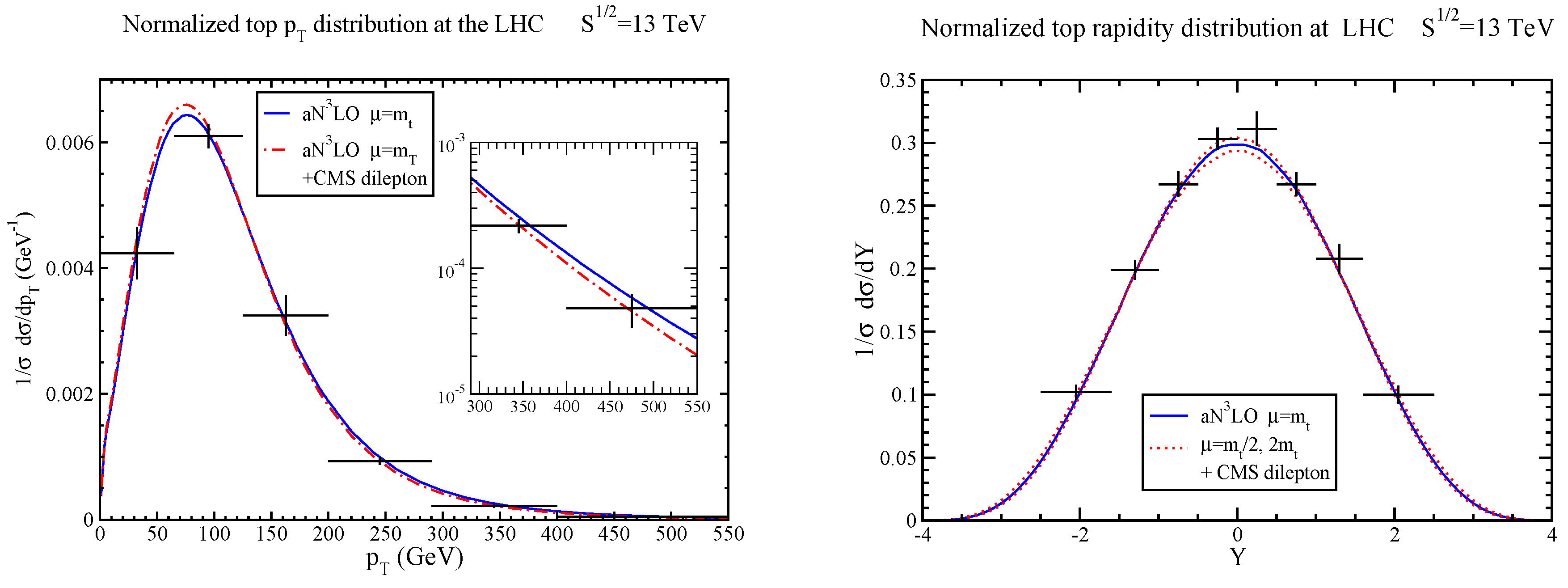
Top-quark differential distributions can provide a lot more information than total cross sections, and they are sensitive to new physics. Top-quark transverse-momentum () and rapidity distributions have been calculated to aNLO, and the soft-gluon contributions are very important [1,22,36].
The aNLO top-quark normalized distributions, , and normalized rapidity distributions, , are shown in Figure 5 at 13 TeV energy and compared with CMS data. Again, we find excellent agreement of the aNLO theoretical predictions for both distributions with the corresponding data.
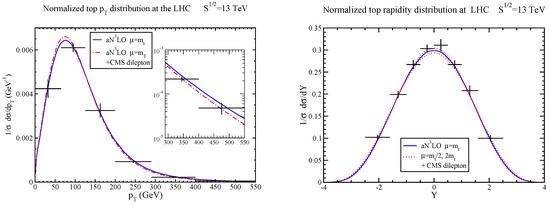
Figure 5.
aNLO top-quark normalized (left) and rapidity (right) distributions at 13 TeV energy compared with CMS [47] data.
7. Conclusions
We have presented results with soft-gluon corrections for total cross sections and differential distributions for various processes involving the production of charged Higgs bosons and top quarks. The soft-gluon corrections are significant and dominant in all the processes that we have discussed.
We have presented aNLO results for production, for production, and for production. We have shown aNNLO results for t-channel and s-channel single-top production, production, and production via anomalous couplings. For the single-top and top-antitop-pair processes, we find excellent agreement with all available collider data. The higher-order soft-gluon corrections are needed for a better description of the data and for setting limits in new physics searches.
Funding
This material is based upon work supported by the National Science Foundation under Grants No. PHY 1519606 and PHY 1820795.
Conflicts of Interest
The author declares no conflict of interest.
References
- Kidonakis, N. Soft-gluon corrections in top-quark production. Int. J. Mod. Phys. A 2018, 33, 1830021. [Google Scholar] [CrossRef]
- Kidonakis, N. Charged Higgs production via bg→tH− at the LHC. JHEP 2005, 0505, 011. [Google Scholar] [CrossRef]
- Kidonakis, N. Charged Higgs production in association with a top quark at approximate NNLO. Phys. Rev. D 2016, 94, 014010. [Google Scholar] [CrossRef]
- Kidonakis, N. Theoretical results for charged-Higgs production. arXiv, 2018; arXiv:1808.02935. [Google Scholar]
- Harland-Lang, L.A.; Martin, A.D.; Molytinski, P.; Thorne, R.S. Parton distributions in the LHC era: MMHT 2014 PDFs. Eur. Phys. J. C 2015, 75, 204. [Google Scholar] [CrossRef] [PubMed]
- Kidonakis, N. Higher-order radiative corrections for b → H−W+. Phys. Rev. D 2018, 97, 034002. [Google Scholar] [CrossRef]
- Kidonakis, N. Higher-order corrections for tZ production via anomalous couplings. Phys. Rev. D 2018, 97, 034028. [Google Scholar] [CrossRef]
- Li, B.H.; Zhang, Y.; Li, C.S.; Gao, J.; Zhu, H.X. Next-to-leading order QCD corrections to tZ associated production via the flavor-changing neutral-current couplings at hadron colliders. Phys. Rev. D 2011, 83, 114049. [Google Scholar] [CrossRef]
- Dulat, S.; Hou, T.-J.; Gao, J.; Guzzi, M.; Huston, J.; Nadolsky, P.; Pumplin, J.; Schmidt, C.; Stump, D.; Yuan, C.-P. New parton distribution functions from a global analysis of quantum chromodynamics. Phys. Rev. D 2016, 93, 033006. [Google Scholar] [CrossRef]
- CMS Collaboration. Search for associated production of a Z boson with a single top quark and for tZ flavour-changing interactions in pp collisions at = 8 TeV. JHEP 2017, 1707, 003. [Google Scholar]
- ATLAS Collaboration. Search for flavour-changing neutral current top quark decays t→qZ in proton-proton collisions at = 13 TeV with the ATLAS Detector. JHEP 2018, 1807, 176. [Google Scholar]
- Forslund, M.; Kidonakis, N. Associated production of a top quark with a photon via anomalous couplings. Phys. Rev. D 2018, 98, 074017. [Google Scholar] [CrossRef]
- Brucherseifer, M.; Caola, F.; Melnikov, K. On the NNLO QCD corrections to single-top production at the LHC. Phys. Lett. B 2014, 736, 58. [Google Scholar] [CrossRef]
- Berger, E.L.; Gao, J.; Yuan, C.-P.; Zhu, H.X. NNLO QCD corrections to t-channel single top-quark production and decay. Phys. Rev. D 2016, 94, 071501. [Google Scholar] [CrossRef]
- Berger, E.L.; Gao, J.; Zhu, H.X. Differential distributions for t-channel single top-quark production and decay at next-to-next-to-leading order in QCD. JHEP 2017, 1711, 158. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, J. s-channel single top quark production and decay at NNLO in QCD. Phys. Rev. D 2018, 98, 071501. [Google Scholar] [CrossRef]
- Zhu, S.H. Next-to-leading order QCD corrections to bg→tW− at the CERN Large Hadron Collider. Phys. Lett. B 2002, 524, 283. [Google Scholar] [CrossRef]
- Kidonakis, N. NNLL resummation for s-channel single top quark production. Phys. Rev. D 2010, 81, 054028. [Google Scholar] [CrossRef]
- Kidonakis, N. Two-loop soft anomalous dimensions for single top quark associated production with a W− or H−. Phys. Rev. D 2010, 82, 054018. [Google Scholar] [CrossRef]
- Kidonakis, N. Next-to-next-to-leading-order collinear and soft gluon corrections for t-channel single top quark production. Phys. Rev. D 2011, 83, 091503. [Google Scholar] [CrossRef]
- Kidonakis, N. Soft-gluon corrections for tW production at N3LO. Phys. Rev. D 2017, 96, 034014. [Google Scholar] [CrossRef]
- Kidonakis, N. Single-top and top-antitop cross sections. arXiv, 2018; arXiv:1809.02524. [Google Scholar]
- CMS Collab. Measurement of the single-top-quark t-channel cross section in pp collisions at = 7 TeV. JHEP 2012, 1212, 035. [Google Scholar]
- ATLAS Collab. Comprehensive measurements of t-channel single top-quark production cross sections at = 7 TeV with the ATLAS detector. Phys. Rev. D 2014, 90, 112006. [Google Scholar] [CrossRef]
- CMS Collab. Measurement of the t-channel single-top-quark production cross section and of the |Vtb| CKM matrix element in pp collisions at = 8 TeV. JHEP 2014, 1406, 090. [Google Scholar]
- ATLAS Collab. Fiducial, total and differential cross-section measurements of t-channel single top-quark production in pp collisions at 8 TeV using data collected by the ATLAS detector. Eur. Phys. J. C 2017, 77, 531. [Google Scholar] [CrossRef] [PubMed]
- ATLAS Collab. Measurement of the inclusive cross-sections of single top-quark and top-antiquark t-channel production in pp collisions at = 13 TeV with the ATLAS detector. JHEP 2017, 1704, 086. [Google Scholar]
- CMS Collab. Cross section measurement of t-channel single top quark production in pp collisions at = 13 TeV. Phys. Lett. B 2017, 772, 752. [Google Scholar] [CrossRef]
- CDF; D0 Collab. Tevatron Combination of Single-Top-Quark Cross Sections and Determination of the Magnitude of the Cabibbo-Kobayashi-Maskawa Matrix Element Vtb. Phys. Rev. Lett. 2015, 115, 152003. [Google Scholar] [CrossRef] [PubMed]
- ATLAS Collab. Evidence for the associated production of a W boson and a top quark in ATLAS at = 7 TeV. Phys. Lett. B 2012, 716, 142. [Google Scholar] [CrossRef]
- CMS Collab. Evidence for associated production of a single top quark and W boson in pp collisions at = 7 TeV. Phys. Rev. Lett. 2013, 110, 022003. [Google Scholar] [CrossRef] [PubMed]
- ATLAS; CMS Collab. Combination of Cross-Section Measurements for Associated Production of a Single Top-Quark and a W Boson at = 8 TeV with the ATLAS and CMS Experiments. 2016. Available online: https://cds.cern.ch/record/2153385 (accessed on 8 November 2018).
- ATLAS Collab. Measurement of the cross-section for producing a W boson in association with a single top quark in pp collisions at = 13 TeV with ATLAS. JHEP 2018, 1801, 063. [Google Scholar]
- CMS Collab. Measurement of the production cross section for single top quarks in association with W bosons in proton-proton collisions at = 13 TeV. JHEP 2018, 1810, 117. [Google Scholar]
- Kidonakis, N. NNNLO soft-gluon corrections for the top-antitop pair production cross section. Phys. Rev. D 2014, 90, 014006. [Google Scholar] [CrossRef]
- Kidonakis, N. NNNLO soft-gluon corrections for the top-quark pT and rapidity distributions. Phys. Rev. D 2015, 91, 031501. [Google Scholar] [CrossRef]
- Kidonakis, N. The top quark forward-backward asymmetry at approximate N3LO. Phys. Rev. D 2015, 91, 071502. [Google Scholar] [CrossRef]
- CMS Collab. Measurement of the inclusive t cross section in pp collisions at = 5.02 TeV using final states with at least one charged lepton. JHEP 2018, 1803, 115. [Google Scholar]
- ATLAS Collab. Measurement of the t production cross-section using eμ events with b-tagged jets in pp collisions at = 7 and 8 TeV with the ATLAS detector. Eur. Phys. J. C 2014, 74, 3109. [Google Scholar] [CrossRef] [PubMed]
- CMS Collab. Measurement of the t production cross section in the eμ channel in proton-proton collisions at = 7 and 8 TeV. JHEP 2016, 1608, 029. [Google Scholar]
- ATLAS Collab. Measurement of the inclusive and fiducial t production cross-sections in the lepton+jets channel in pp collisions at = 8 TeV with the ATLAS detector. Eur. Phys. J. C 2018, 78, 487. [Google Scholar] [CrossRef]
- ATLAS Collab. Measurement of the t production cross-section using eμ events with b-tagged jets in collisions at = 13 TeV with the ATLAS detector. Phys. Lett. B 2016, 761, 136. [Google Scholar] [CrossRef]
- CMS Collab. Measurement of the t production cross section using events with one lepton and at least one jet in pp collisions at = 13 TeV. JHEP 2017, 1709, 051. [Google Scholar]
- CDF Collab. Measurement of the t production cross section in p collisions at = 1.8 TeV. Phys. Rev. D 2001, 64, 032002. [Google Scholar] [CrossRef]
- D0 Collab. t production cross-section in p collisions at = 1.8 TeV. Phys. Rev. D 2003, 67, 012004. [Google Scholar]
- CDF; D0 Collab. Combination of measurements of the top-quark pair production cross section from the Tevatron Collider. Phys. Rev. D 2014, 89, 072001. [Google Scholar] [CrossRef]
- CMS Collab. Measurement of normalized differential t cross sections in the dilepton channel from pp collisions at = 13 TeV. JHEP 2018, 1804, 060. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).