Non-Linear f(Q,T) Gravity and the Late-Time Acceleration of the Universe
Abstract
1. Introduction
2. f(Q,T) Gravity Theory
Spacetime and Modified Field Equations (MFEs)
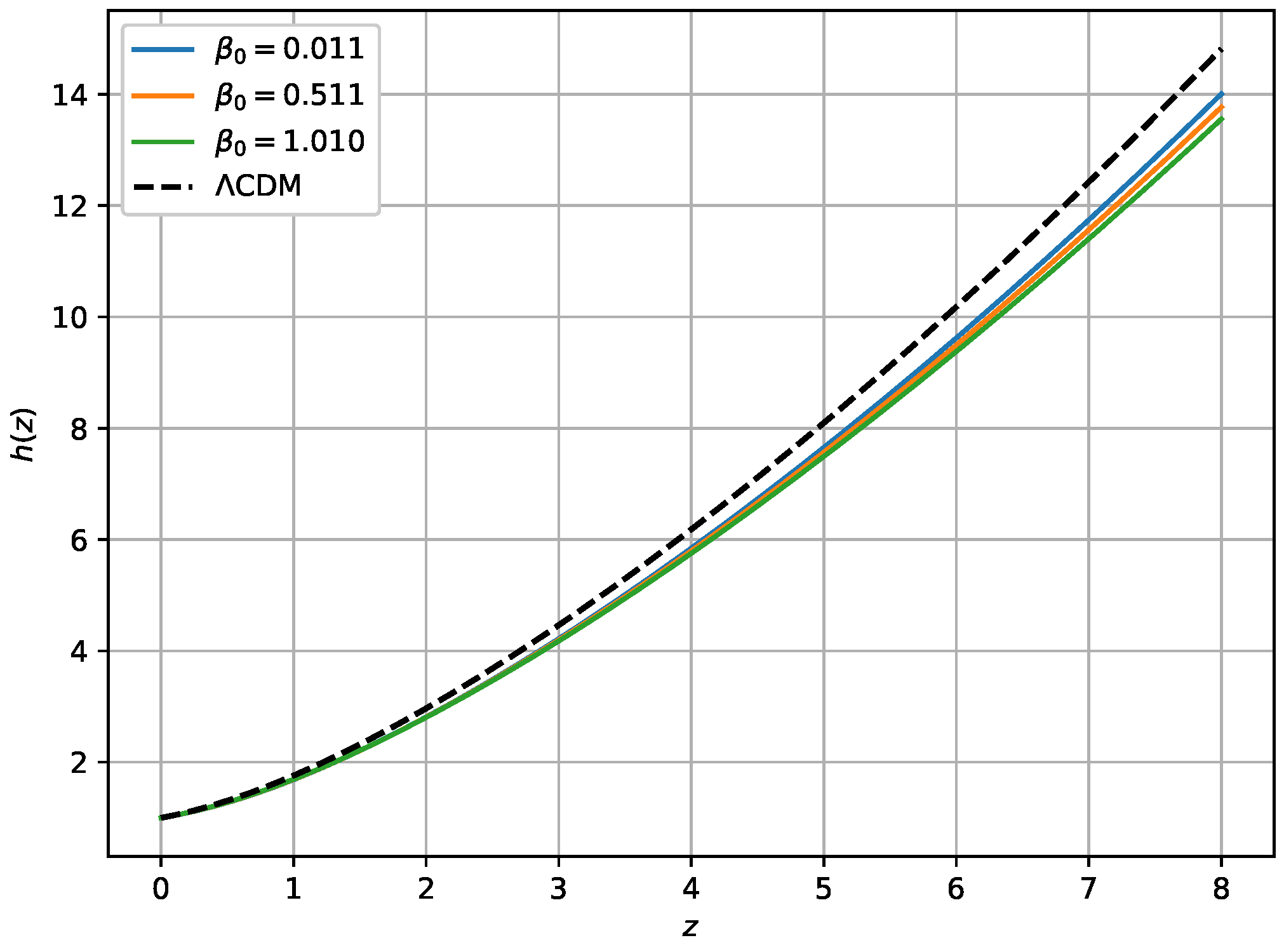
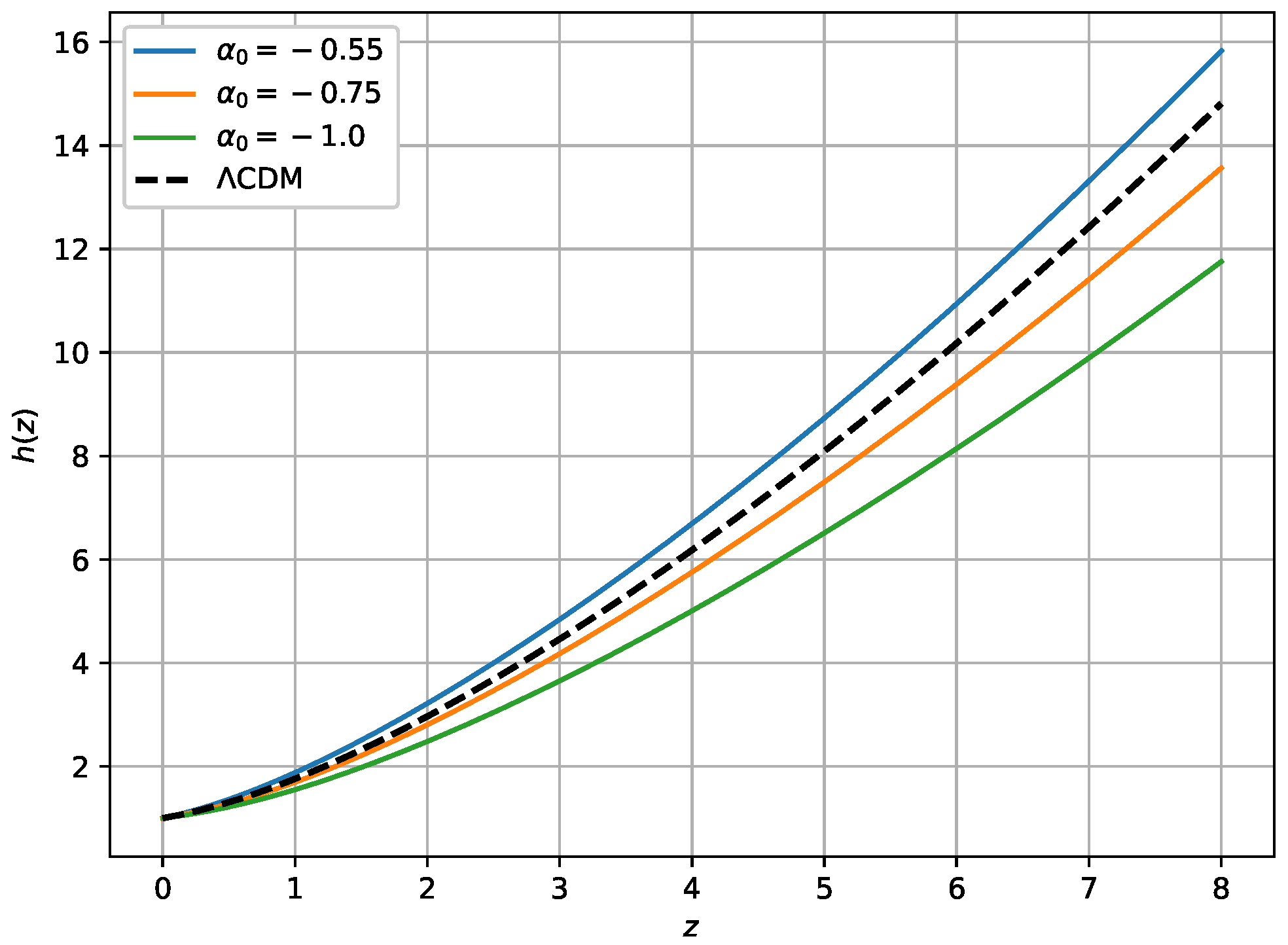
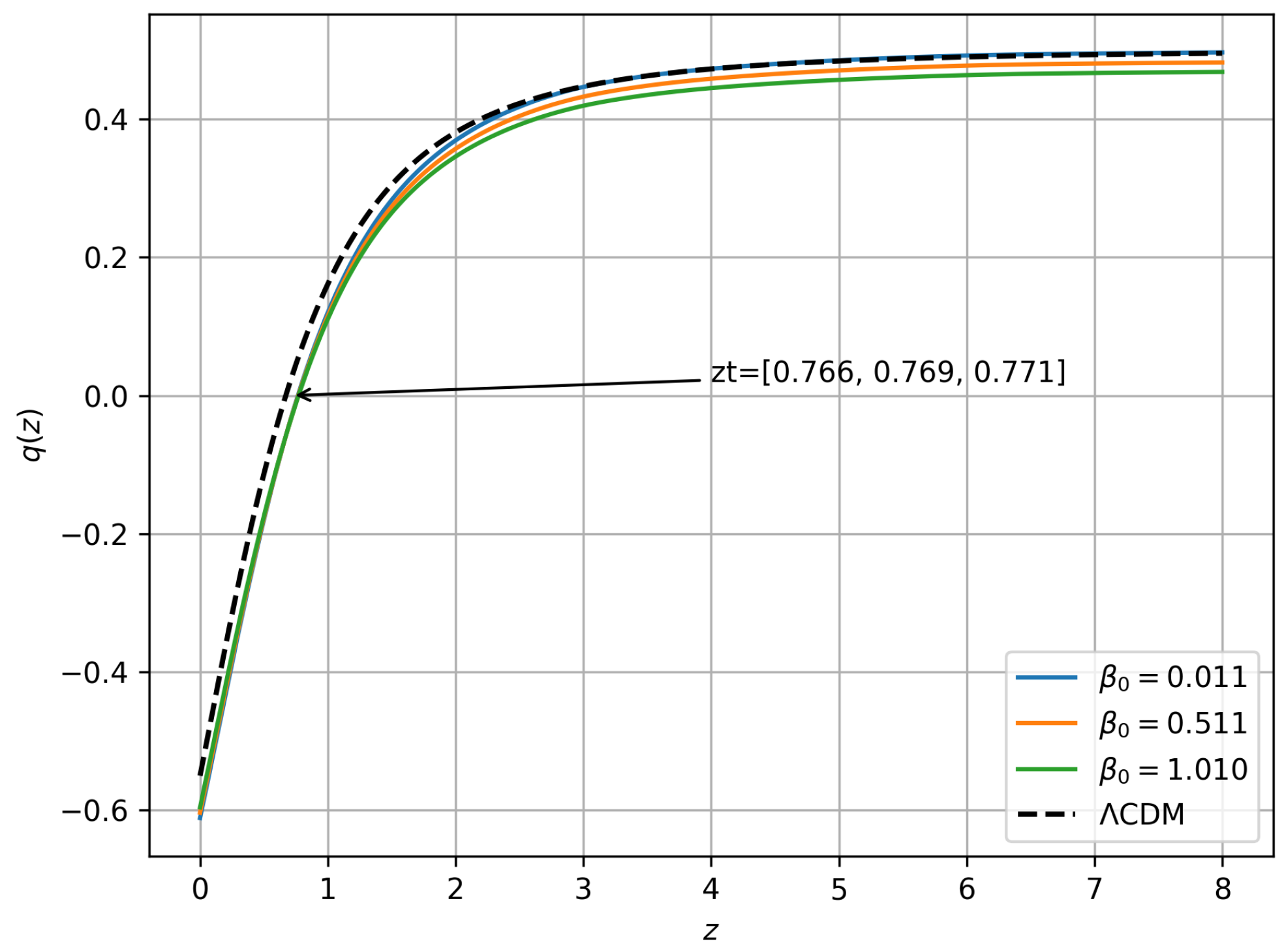
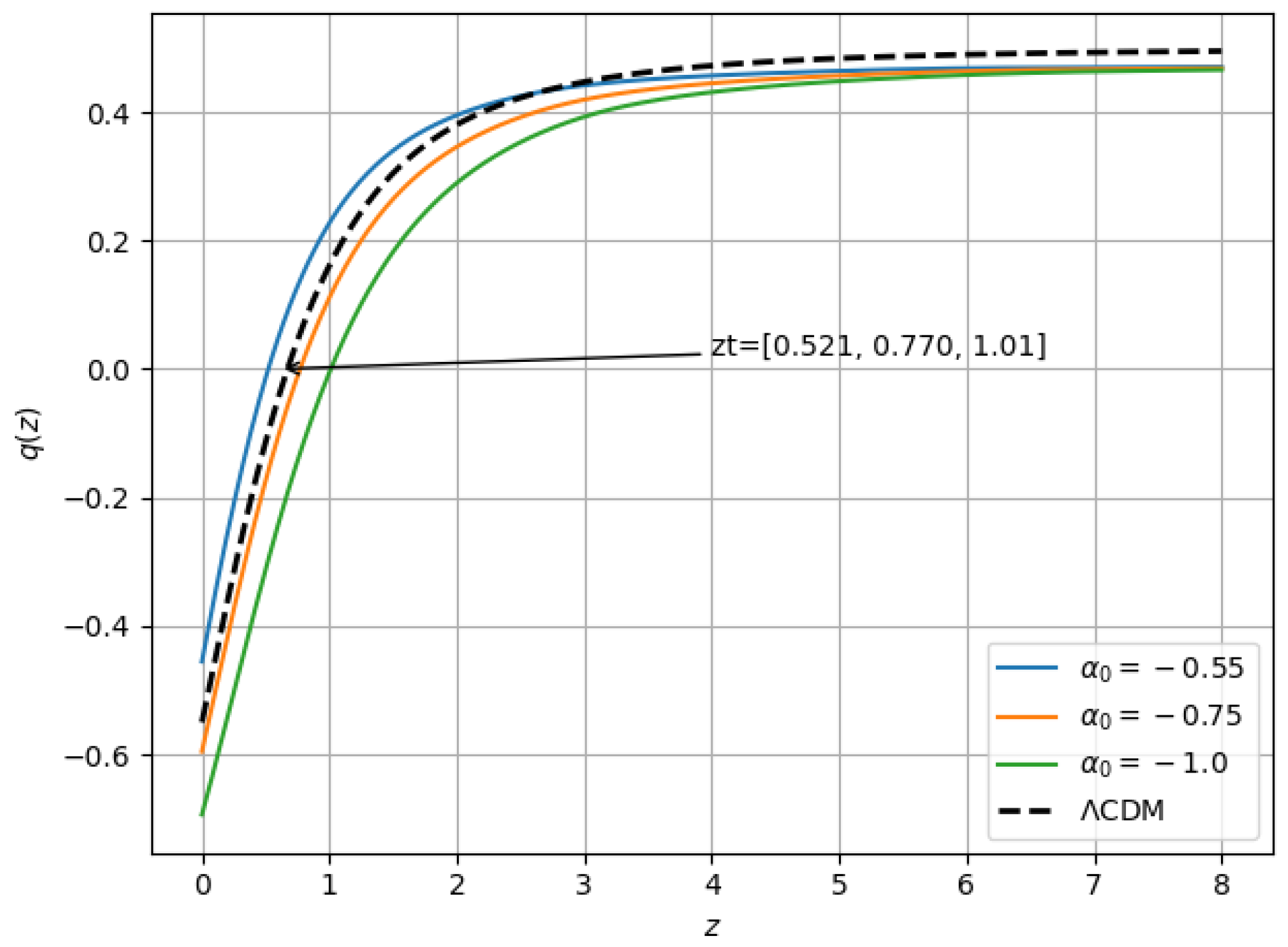
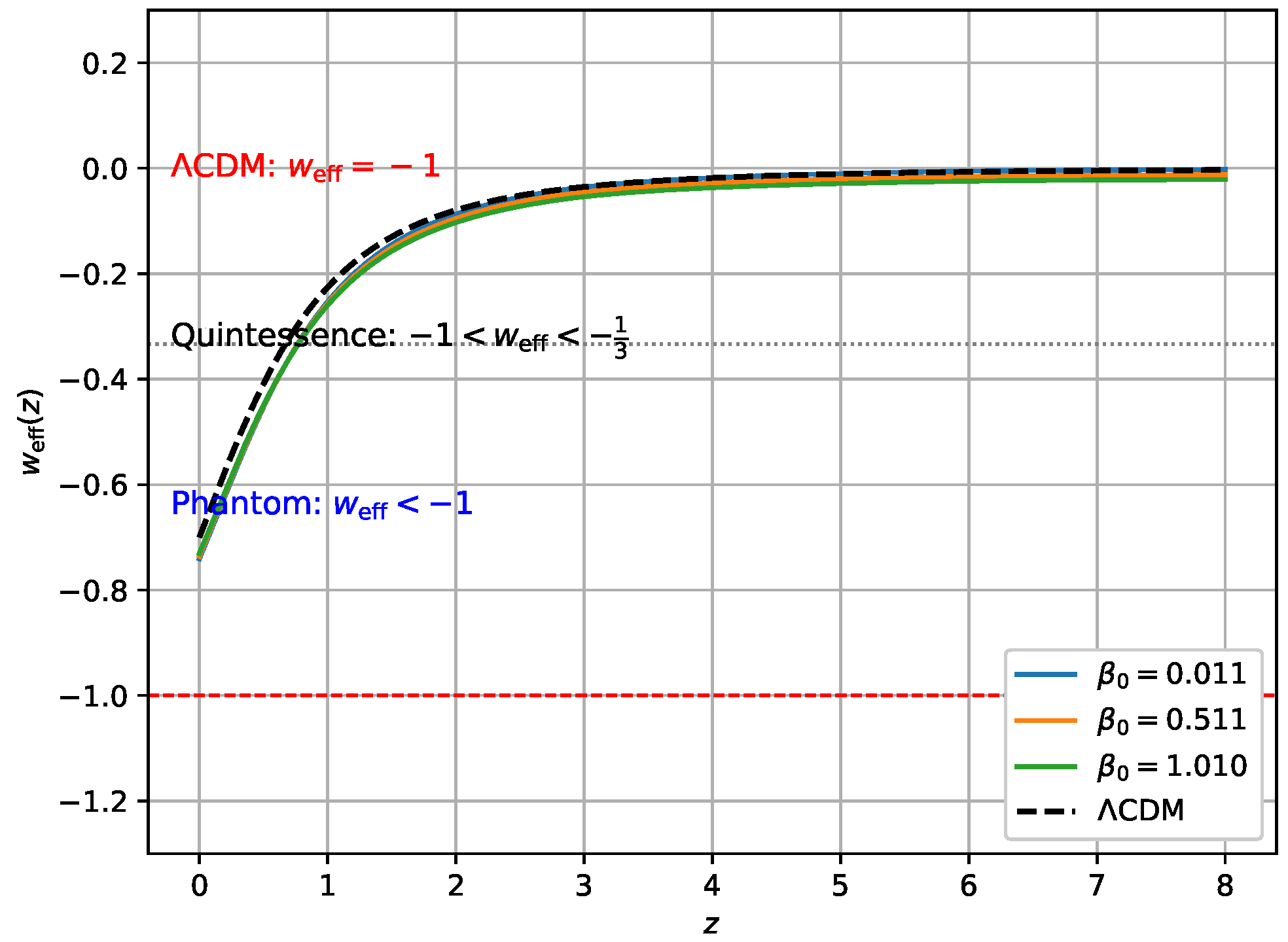
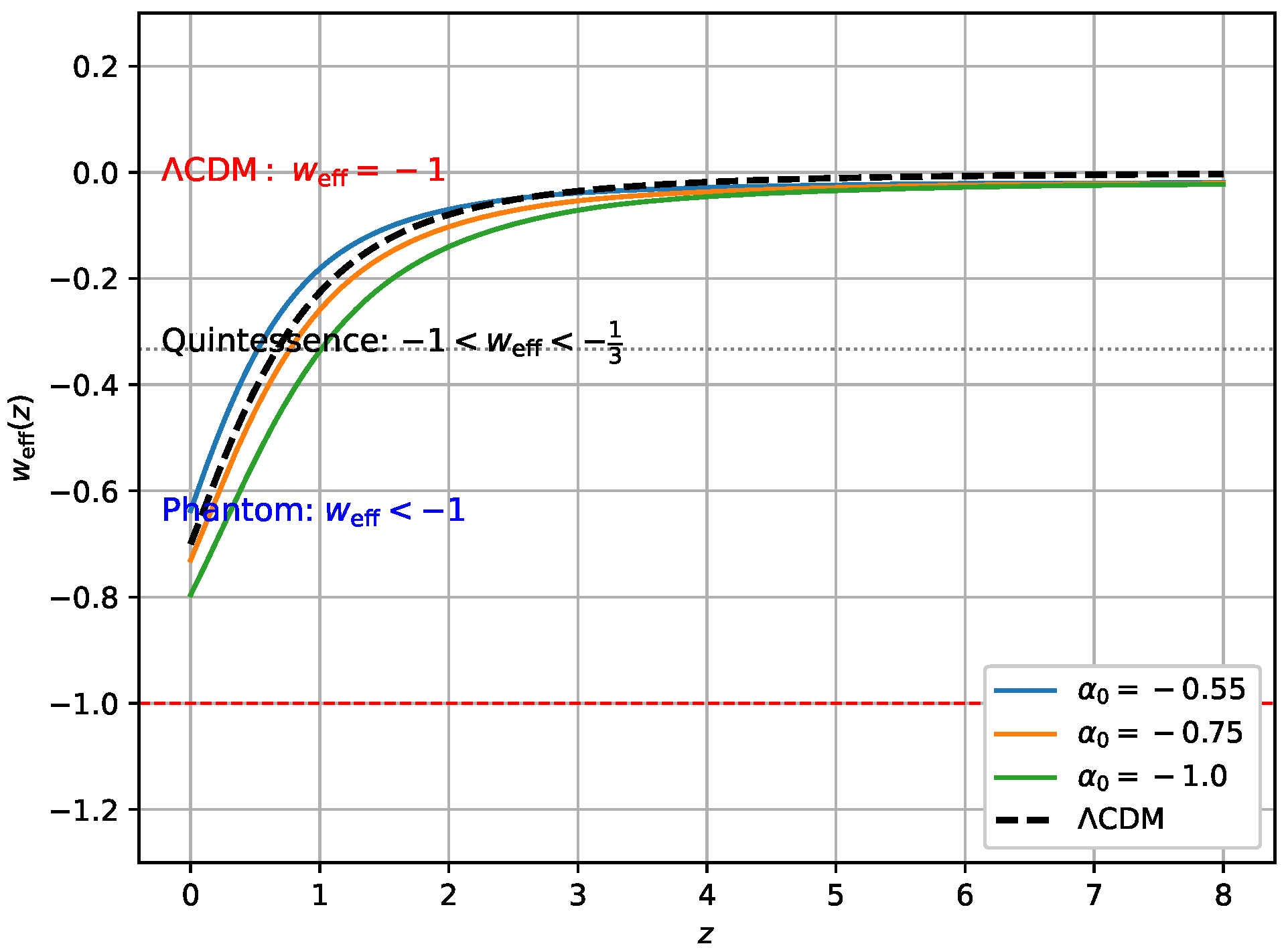
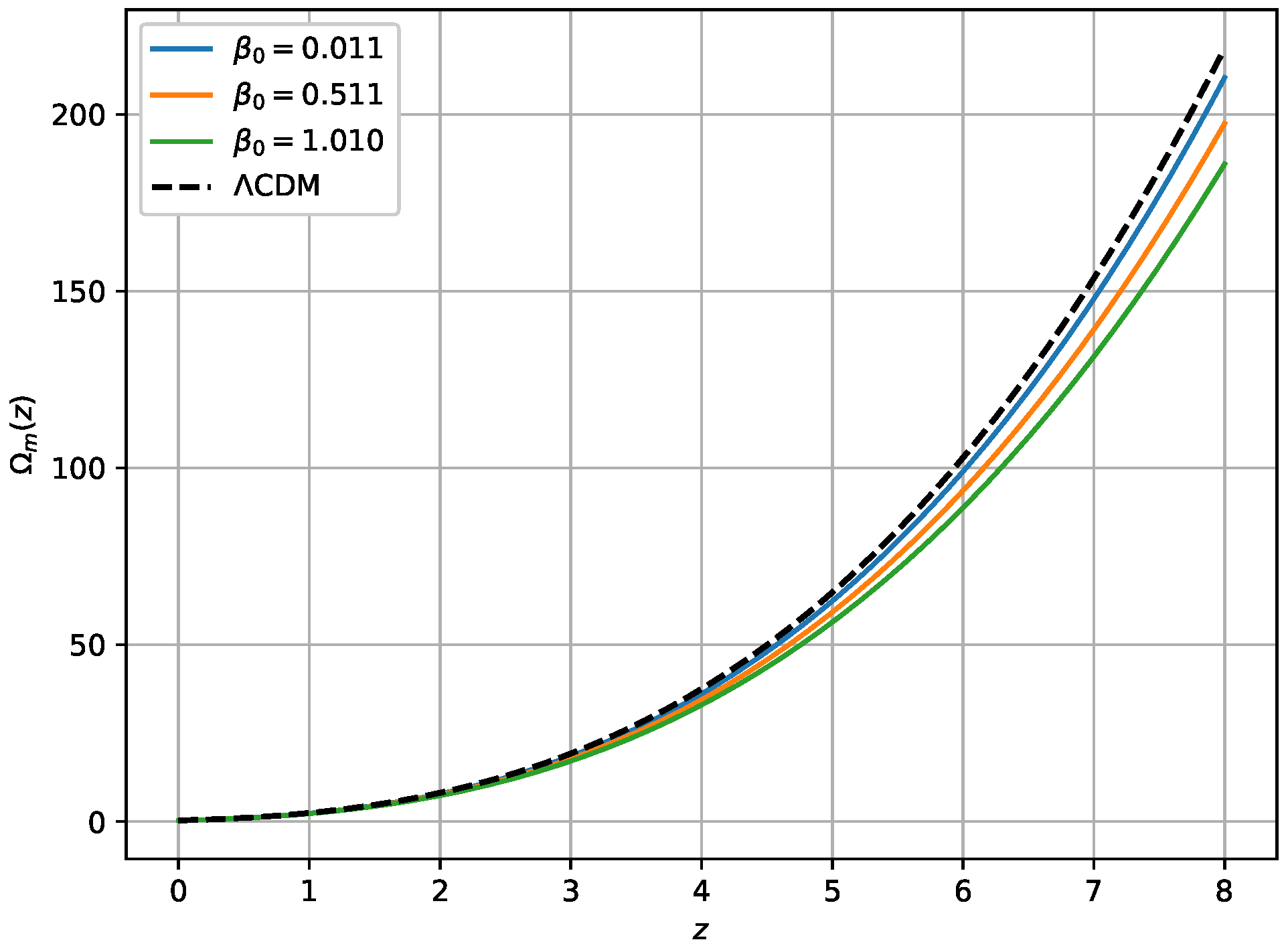
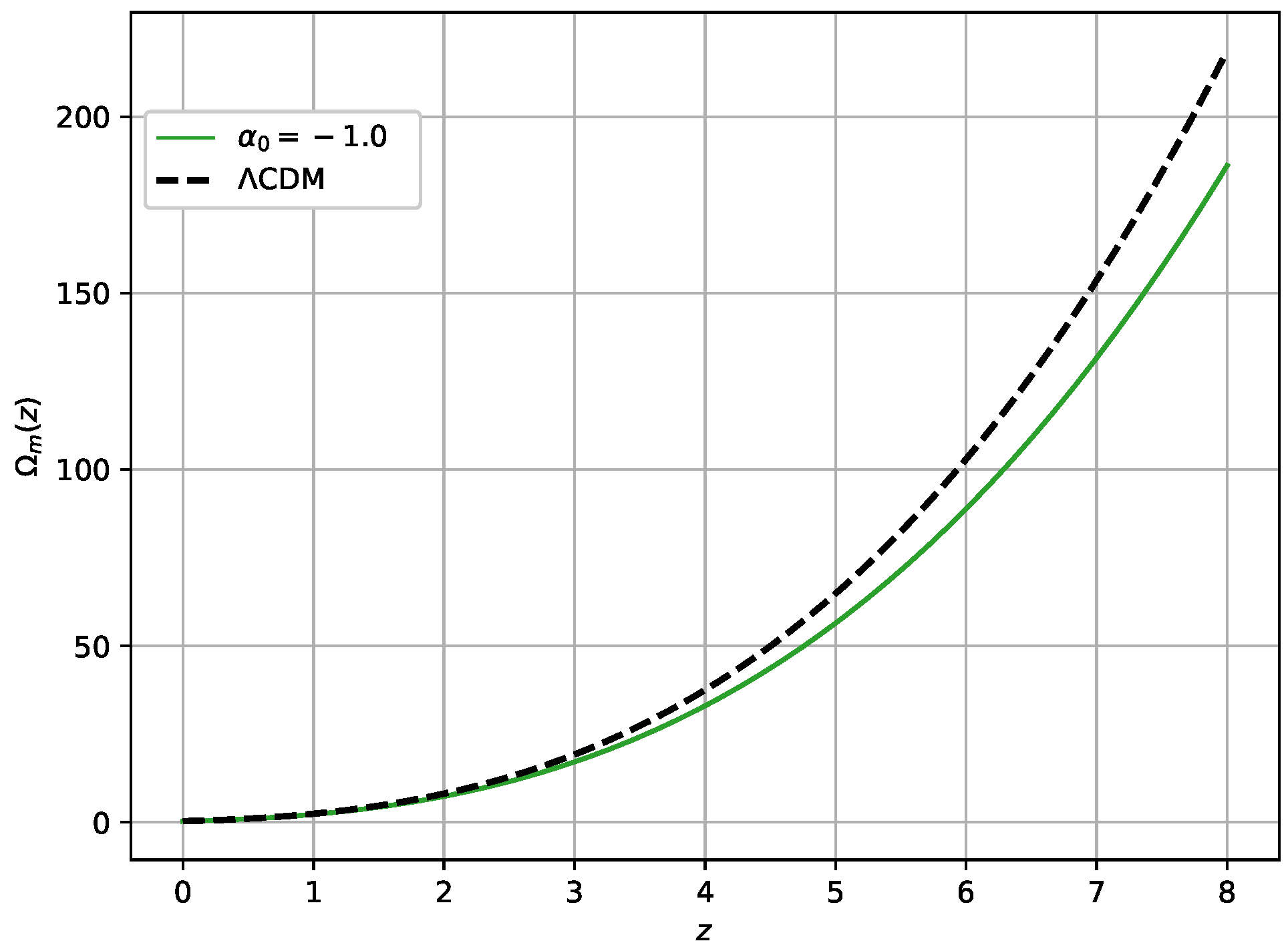
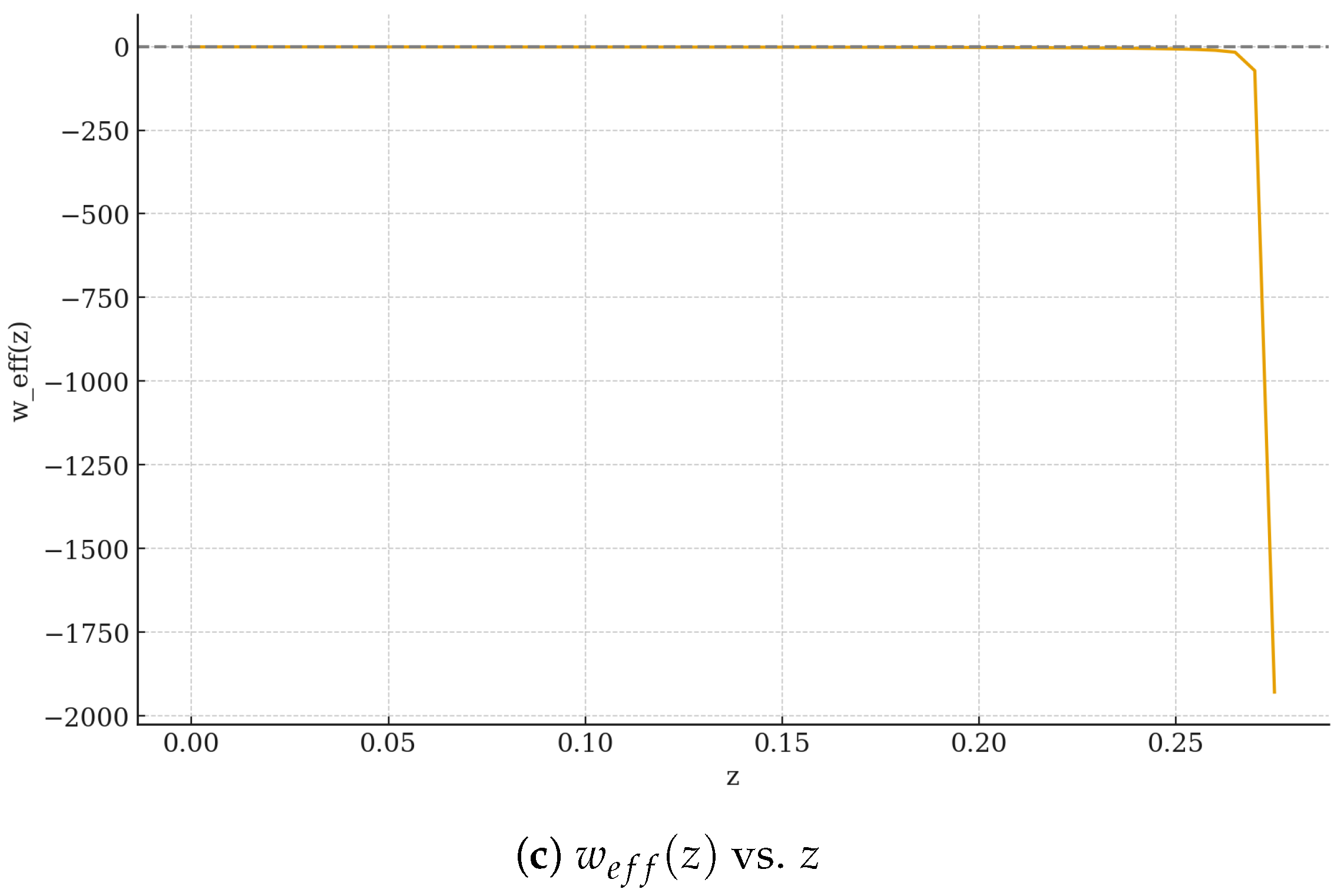
3. Nonlinear Model of f(Q,T)
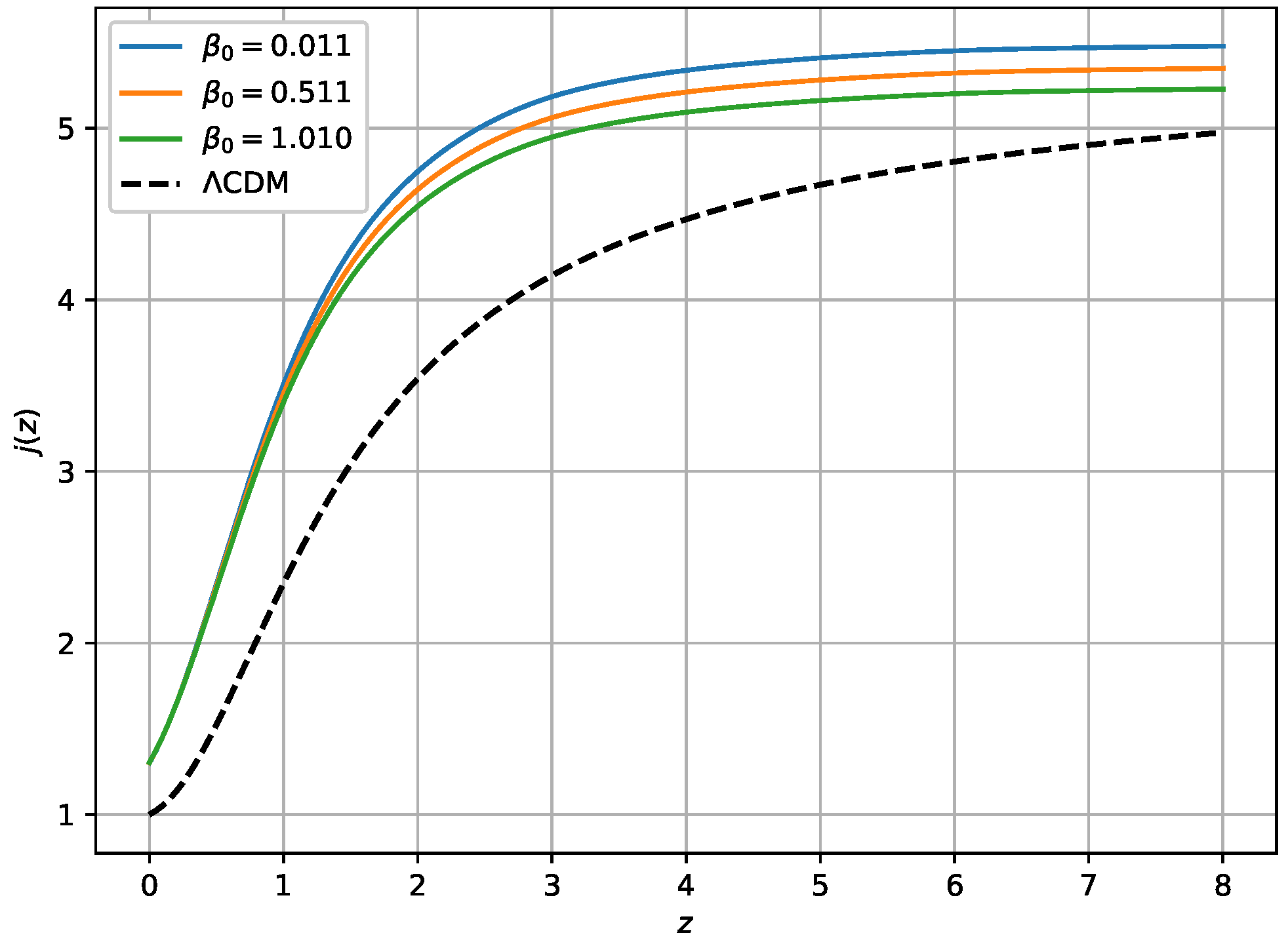
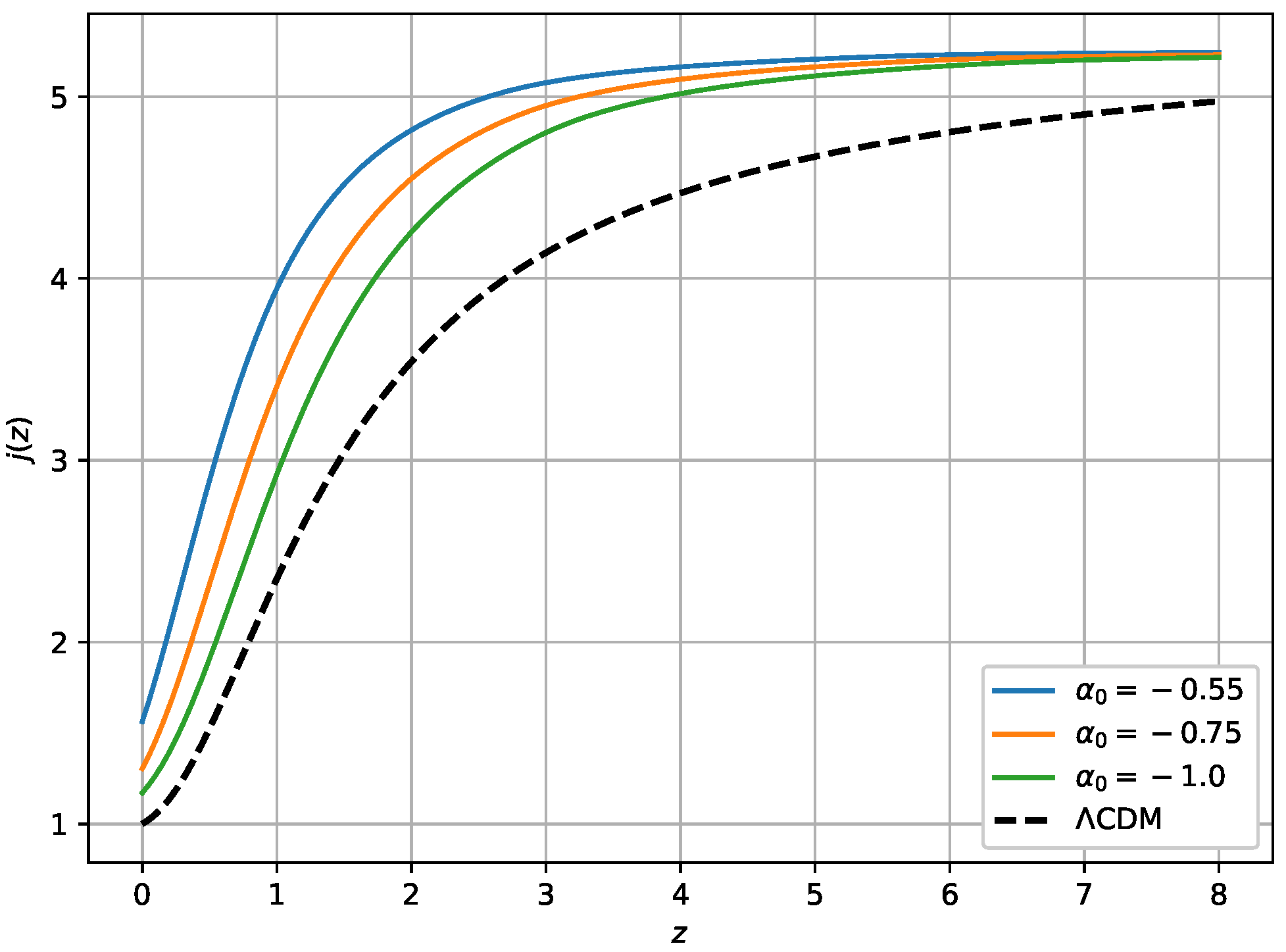
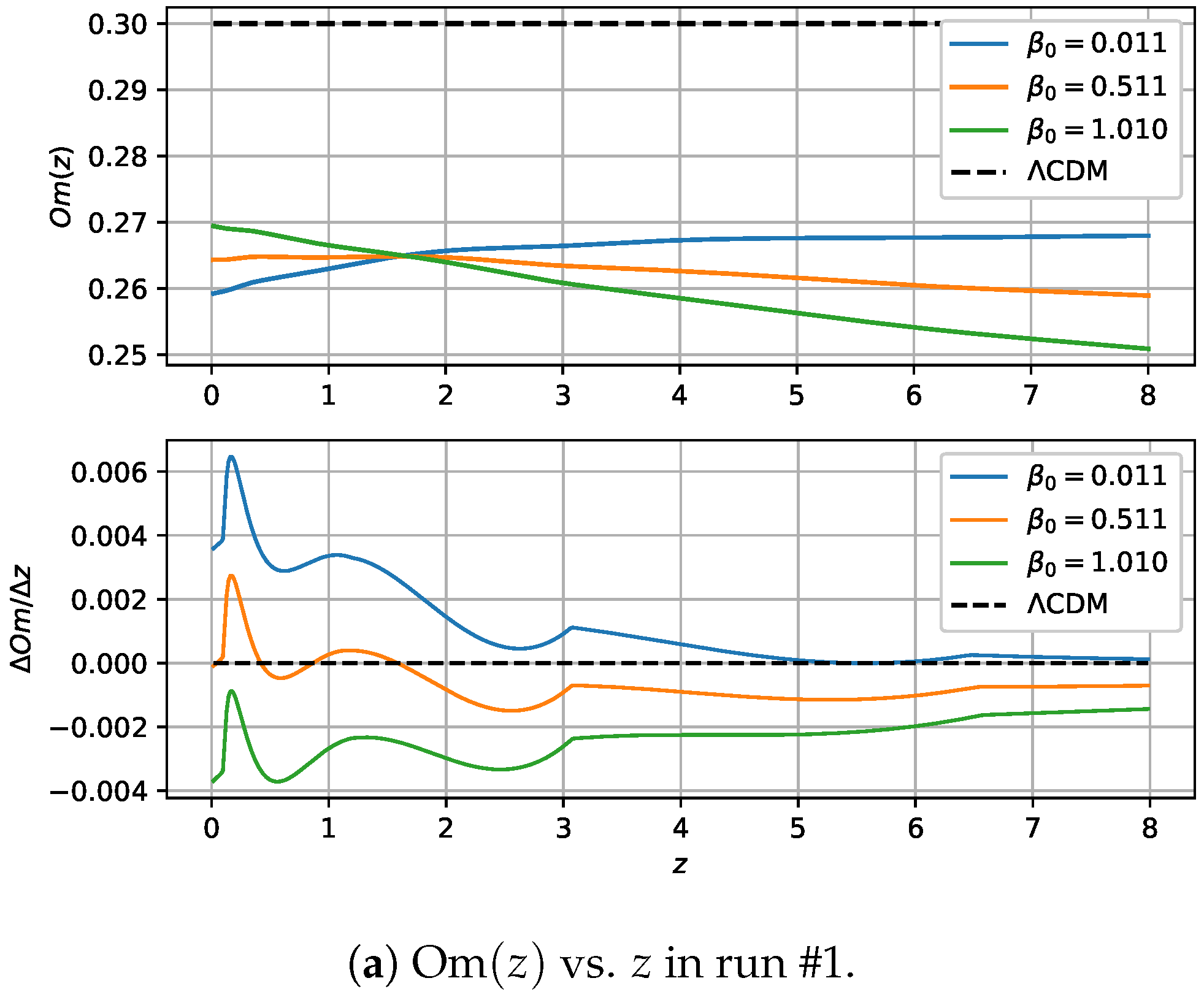
Om Diagnostic Test
4. Comparison with Other Work
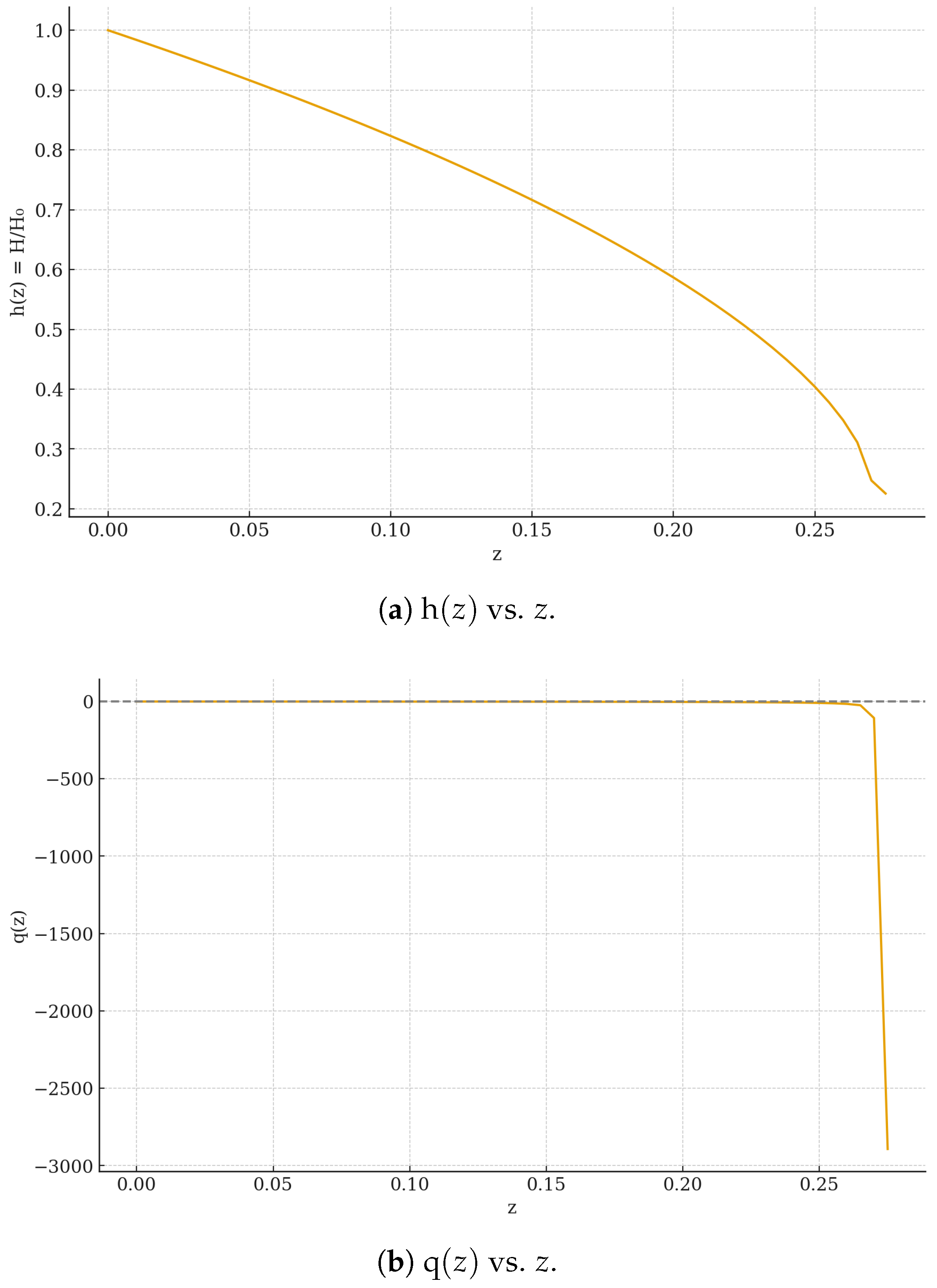
5. Numerical Integration
6. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DE | Dark energy |
| GR | General relativity |
| DP | Deceleration parameter |
| BAO | Baryon acoustic oscillations |
| SNe Ia | Type Ia supernovae |
| EoS | Equation of state |
| RK4 | Fourth-order Runge–Kutta method |
| LTE | Local truncation error |
| DEs | Differential equations |
| MCMC | Markov Chain Monte Carlo |
| CDM | Pronounced lambda-cold dark matter |
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Koivisto, T.; Mota, D.F. Dark energy anisotropic stress and large scale structure formation. Phys. Rev. D—Particles Fields Gravitation Cosmol. 2006, 73, 083502. [Google Scholar] [CrossRef]
- Ivezić, Ž.; Kahn, S.M.; Tyson, J.A.; Abel, B.; Acosta, E.; Allsman, R.; Alonso, D.; AlSayyad, Y.; Anderson, S.F.; Andrew, J.; et al. LSST: From science drivers to reference design and anticipated data products. Astrophys. J. 2019, 873, 111. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the baryon acoustic peak in the large-scale correlation function of SDSS luminous red galaxies. Astrophys. J. 2005, 633, 560. [Google Scholar] [CrossRef]
- Percival, W.J.; Reid, B.A.; Eisenstein, D.J.; Bahcall, N.A.; Budavari, T.; Frieman, J.A.; Fukugita, M.; Gunn, J.E.; Ivezić, Ž.; Knapp, G.R.; et al. Baryon acoustic oscillations in the Sloan Digital Sky Survey data release 7 galaxy sample. Mon. Not. R. Astron. Soc. 2010, 401, 2148–2168. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Doran, M. Cosmic microwave background and supernova constraints on quintessence: Concordance regions and target models. Phys. Rev. D 2004, 69, 103517. [Google Scholar] [CrossRef]
- Chen, H.Y.; Dorey, N.; Okamura, K. On the scattering of magnon boundstates. J. High Energy Phys. 2006, 69, 035. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Kamenshchik, A.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Sahni, V.; Shtanov, Y. Braneworld models of dark energy. J. Cosmol. Astropart. Phys. 2003, 2003, 014. [Google Scholar] [CrossRef]
- Sahni, V.; Shtanov, Y. Did the universe loiter at high redshifts? Phys. Rev. D—Part. Fields Gravit. Cosmol. 2005, 71, 084018. [Google Scholar] [CrossRef]
- Cai, R.G. A dark energy model characterized by the age of the universe. Phys. Lett. B 2007, 657, 228–231. [Google Scholar] [CrossRef]
- Padmanabhan, T. Accelerated expansion of the universe driven by tachyonic matter. Phys. Rev. D 2002, 66, 021301. [Google Scholar] [CrossRef]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Quantum de Sitter cosmology and phantom matter. Phys. Lett. B 2003, 562, 147–152. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef] [PubMed]
- Shukla, B.K.; Sofuoğlu, D.; Khare, S.; Alfedeel, A.H. Accelerating universe in f (T) teleparallel gravity. Int. J. Geom. Methods Mod. Phys. 2025, 22, 2450270. [Google Scholar] [CrossRef]
- dos Santos, F.; Gonzalez, J.; Silva, R. Observational constraints on f (T) gravity from model-independent data. Eur. Phys. J. C 2022, 82, 823. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S.; Saridakis, E.N. New observational constraints on f (T) gravity from cosmic chronometers. J. Cosmol. Astropart. Phys. 2016, 2016, 011. [Google Scholar] [CrossRef]
- Wu, P.; Yu, H. Observational constraints on f (T) theory. Phys. Lett. B 2010, 693, 415–420. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.; Nojiri, S.; Odintsov, S.D. f (R, T) gravity. Phys. Rev. D—Part. Fields Gravit. Cosmol. 2011, 84, 024020. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.; Oikonomou, V. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Bertolami, O.; Lobo, F.S.N.; Páramos, J. Nonminimal coupling of perfect fluids to curvature. Phys. Rev. D 2008, 78, 064036. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. Construction of cosmologically viable f (G) gravity models. Phys. Lett. B 2009, 675, 1–8. [Google Scholar] [CrossRef]
- De Laurentis, M.; Paolella, M.; Capozziello, S. Cosmological inflation in F (R, G) gravity. Phys. Rev. D 2015, 91, 083531. [Google Scholar] [CrossRef]
- de la Cruz-Dombriz, Á.; Sáez-Gómez, D. On the stability of the cosmological solutions in f(R, G) gravity. Class. Quantum Gravity 2012, 29, 245014. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Heisenberg, L.; Koivisto, T. Coincident general relativity. Phys. Rev. D 2018, 98, 044048. [Google Scholar] [CrossRef]
- Xu, Y.; Li, G.; Harko, T.; Liang, S.D. f (Q, T) gravity. Eur. Phys. J. C 2019, 79, 1–19. [Google Scholar] [CrossRef]
- Koussour, M.; Myrzakulov, N.; Alfedeel, A.H.; Awad, F.; Bennai, M. Modeling cosmic acceleration with a generalized varying deceleration parameter. Phys. Dark Universe 2023, 42, 101339. [Google Scholar] [CrossRef]
- Alfedeel, A.H.; Koussour, M.; Myrzakulov, N. Probing Weyl-type f (Q, T) gravity: Cosmological implications and constraints. Astron. Comput. 2024, 47, 100821. [Google Scholar] [CrossRef]
- Myrzakulov, N.; Koussour, M.; Alfedeel, A.H.; Elkhair, H. Cosmological implications of the constant jerk parameter in f (Q, T) gravity theory. Chin. J. Phys. 2023, 86, 300–312. [Google Scholar] [CrossRef]
- Arora, S.; Santos, J.; Sahoo, P. Constraining f (Q, T) gravity from energy conditions. Phys. Dark Universe 2021, 31, 100790. [Google Scholar] [CrossRef]
- Arora, S.; Pacif, S.; Bhattacharjee, S.; Sahoo, P. f(Q,T) gravity models with observational constraints. Phys. Dark Universe 2020, 30, 100664. [Google Scholar] [CrossRef]
- Loo, T.H.; Solanki, R.; De, A.; Sahoo, P. f (Q, T) gravity, its covariant formulation, energy conservation and phase-space analysis. Eur. Phys. J. C 2023, 83, 261. [Google Scholar] [CrossRef]
- Agrawal, A.; Mishra, B.; Tripathy, S. Observationally constrained accelerating cosmological model with higher power of non-metricity and squared trace. J. High Energy Astrophys. 2023, 38, 41–48. [Google Scholar] [CrossRef]
- Pati, L.; Narawade, S.; Tripathy, S.; Mishra, B. Evolutionary behaviour of cosmological parameters with dynamical system analysis in f (Q, T) gravity. Eur. Phys. J. C 2023, 83, 445. [Google Scholar] [CrossRef]
- Narawade, S.; Koussour, M.; Mishra, B. Constrained f(Q,T) gravity accelerating cosmological model and its dynamical system analysis. Nucl. Phys. B 2023, 992, 116233. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Heisenberg, L.; Koivisto, T.; Pekar, S. Cosmology in f (Q) geometry. Phys. Rev. D 2020, 101, 103507. [Google Scholar] [CrossRef]
- Pradhan, A.; Dixit, A. Transit cosmological models with observational constraints in f (Q, T) gravity. arXiv 2020, arXiv:2009.08290. [Google Scholar] [CrossRef]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Two new diagnostics of dark energy. Phys. Rev. D 2008, 78, 103502. [Google Scholar] [CrossRef]

| Ref | Parameterization | N.M. Used | Compare with CDM | |
|---|---|---|---|---|
| [32] | MCMC | Good fit | ||
| [33] | MCMC | |||
| [34] | Exact + MCMC | |||
| Exact + MCMC | ||||
| [35] | Suitable to describe | |||
| [37] | MCMC | Better fit | ||
| [38] | D.S.A | Similar at late times | ||
| [39] | MCMC + D.S.A | Supports |
| z | LTE | |||
|---|---|---|---|---|
| 0.0 | 0.1000 | 1.045256916944 | 1.045256886319 | 2.0 × |
| 0.5 | 0.1000 | 1.094333050753 | 1.094333027138 | 1.6 × |
| 1.0 | 0.1000 | 1.157917980845 | 1.157917901190 | 5.3 × |
| 1.5 | 0.1000 | 1.233634788613 | 1.233632097590 | 1.8 × |
| 2.0 | 0.0860 | 1.277992045787 | 1.277982181618 | 6.6 × |
| 2.5 | 0.0648 | 1.279593520688 | 1.279580900700 | 8.4 × |
| 3.0 | 0.0459 | 1.257626921555 | 1.257617313515 | 6.4 × |
| 3.5 | 0.0364 | 1.255923194858 | 1.255913231958 | 6.6 × |
| 4.0 | 0.0297 | 1.255675705098 | 1.255665353770 | 6.9 × |
| 4.5 | 0.0248 | 1.256293373635 | 1.256282599088 | 7.2 × |
| 5.0 | 0.0210 | 1.257469925505 | 1.257458692019 | 7.5 × |
| 5.5 | 0.0181 | 1.259032651702 | 1.259020922640 | 7.8 × |
| 6.0 | 0.0158 | 1.260877454939 | 1.260865192660 | 8.2 × |
| 6.5 | 0.0140 | 1.262938047331 | 1.262925213082 | 8.6 × |
| 7.0 | 0.0124 | 1.265170187596 | 1.265156741395 | 9.0 × |
| 7.5 | 0.0112 | 1.267543108716 | 1.267529009238 | 9.4 × |
| 8.0 | 0.0101 | 1.270034616902 | 1.270019821378 | 9.9 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfedeel, A.H.A. Non-Linear f(Q,T) Gravity and the Late-Time Acceleration of the Universe. Universe 2025, 11, 382. https://doi.org/10.3390/universe11120382
Alfedeel AHA. Non-Linear f(Q,T) Gravity and the Late-Time Acceleration of the Universe. Universe. 2025; 11(12):382. https://doi.org/10.3390/universe11120382
Chicago/Turabian StyleAlfedeel, Alnadhief H. A. 2025. "Non-Linear f(Q,T) Gravity and the Late-Time Acceleration of the Universe" Universe 11, no. 12: 382. https://doi.org/10.3390/universe11120382
APA StyleAlfedeel, A. H. A. (2025). Non-Linear f(Q,T) Gravity and the Late-Time Acceleration of the Universe. Universe, 11(12), 382. https://doi.org/10.3390/universe11120382







