Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds in Virial Equilibrium
Abstract
1. Introduction
2. Set up of the Model
3. Results
3.1. First Principle and Entropy of Macro-Gas
3.2. Free Energy
3.3. Gibbs Potential
3.4. Stability Analysis
3.4.1. Micro-Canonical Ensemble
3.4.2. Canonical Ensemble
3.4.3. Grand Canonical Ensemble
3.5. The Origin of the Entropy Change
4. Discussion
4.1. Basic Assumptions and Main Results
4.2. Caveats
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MC(s) | Molecular Cloud(s) |
| 3D | three-dimensional space |
| 1 | This range roughly spans between and . According to [16], the injection scale is of the order of the Galactic disk height ∼500 pc. It is commonly accepted, the review states, that the continuous supply of turbulent energy at the injection scale is guaranteed during the cloud’s lifetime. |
| 2 | To avoid the so-called “Jeans swindle”, the assumption for infinite homogeneous medium is actually not really consistent, because the Poisson equation cannot be solved unless the medium density is zero. |
| 3 | According to the classical setting given by Kolmogorov [19], which is supported by Frisch [18], the presence of inertial range, the range of scales in which the turbulent kinetic energy is transferred from the larger to the smaller scales without dissipation (so the dissipation time is not relevant to the inertial range), is guaranteed by the continuous supply of turbulent kinetic energy at the injection scale, several times larger than the upper scale of the inertial range. In other words, the cloud must be submerged in a larger turbulent structure (a point, which is accounted for in our model). Moreover, the existence of the inertial range for supersonic turbulence was shown observationally, numerically, and theoretically during the last twenty years by several works—e.g., Padoan et al. [24], Kritsuk et al. [21], Aluie [22], Galtier & Banerjee [20], Federrath et al. [23], and hence our study can be extended to include the supersonic case, accordingly. |
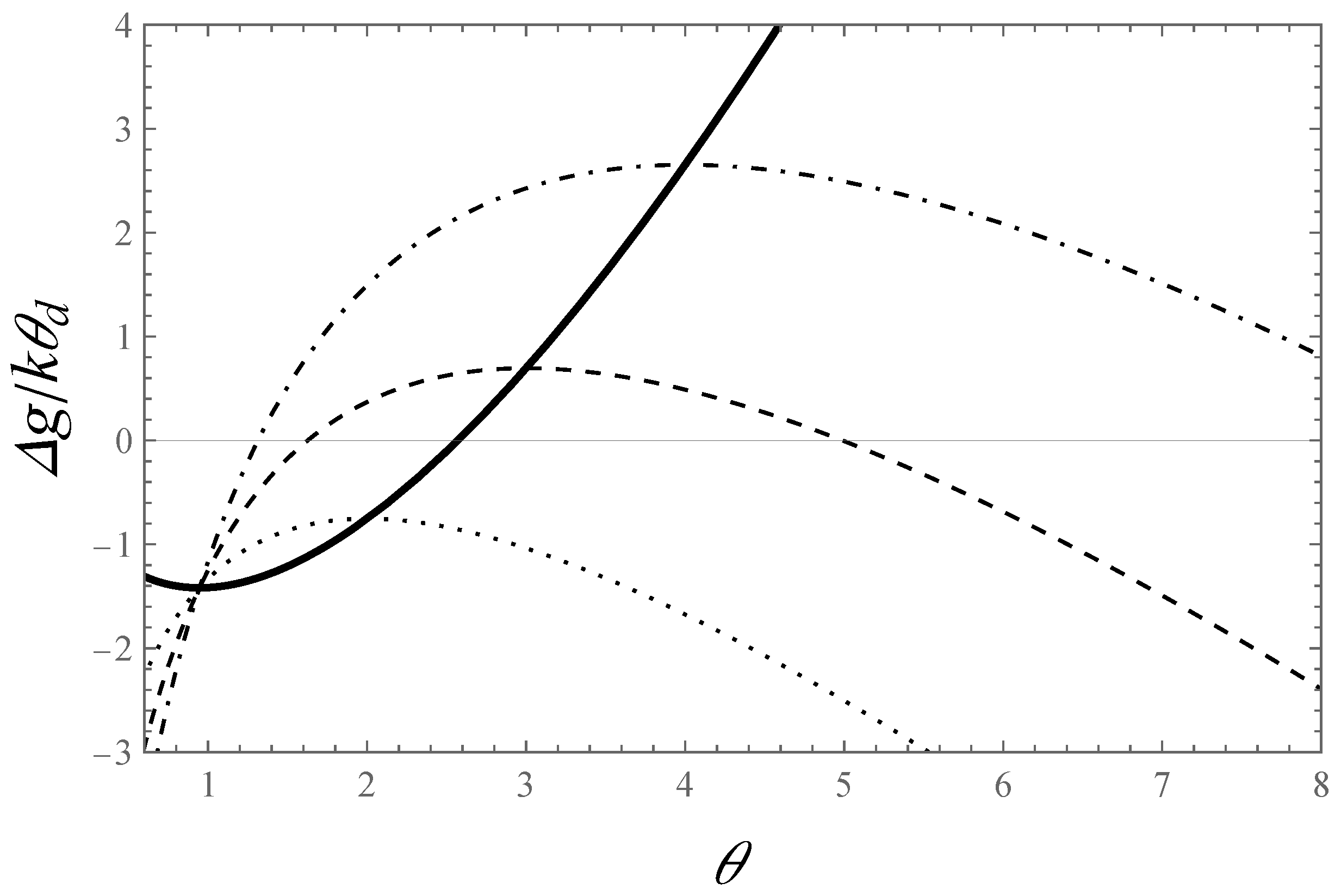
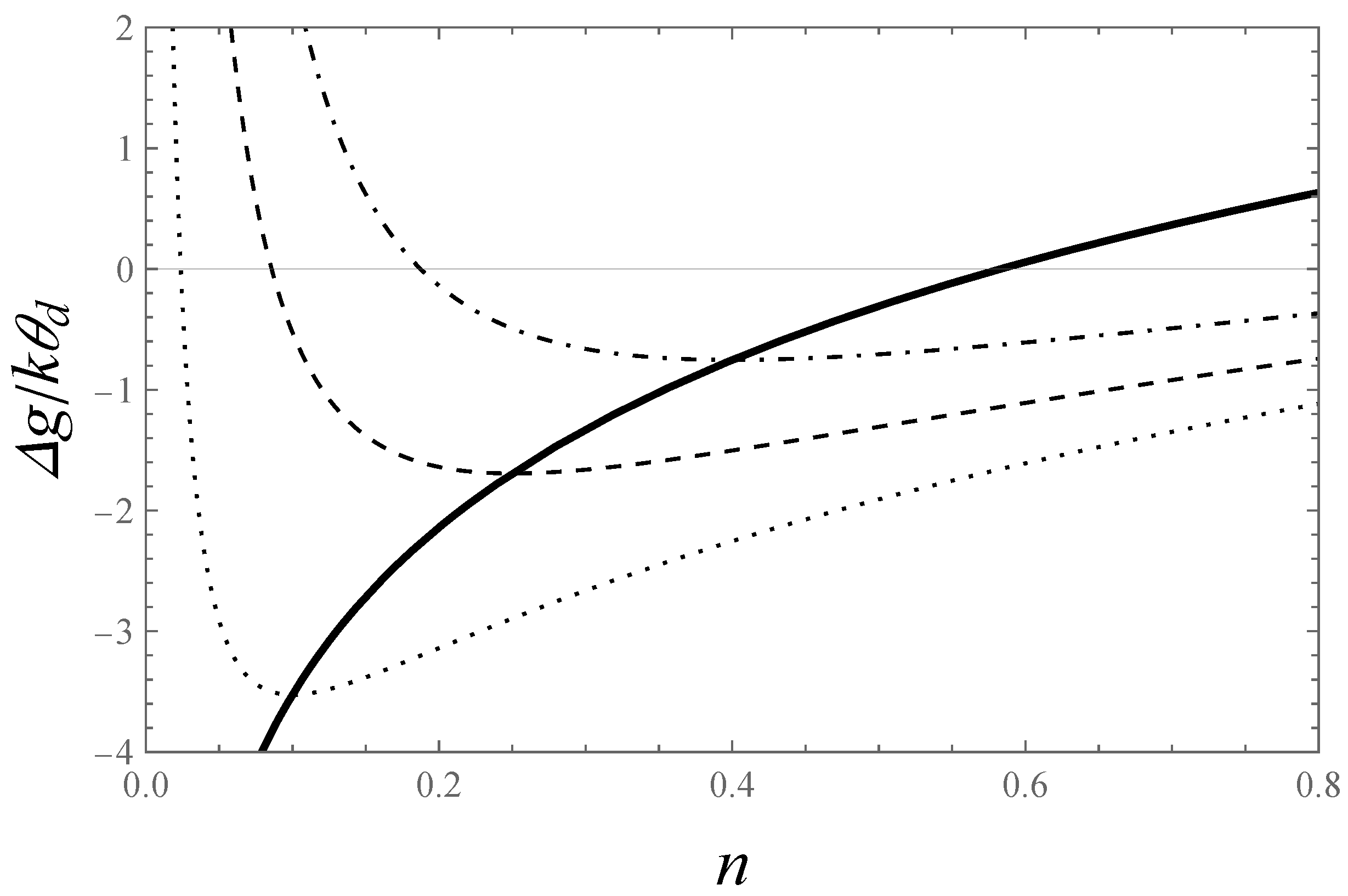
| 4 | We can easily obtain that in canonical variables and v, the conclusion for the stability will be the same. If one accounts for the differential relations and , defining the change of variables in s, obtains: The conditions for stability of the system according to Callen [29] are violated due to the derivative regarding ; the derivative in regard to v is right. Hence, the instability is caused by the energy (temperature). |
| 5 | The detailed derivation of the off-equilibrium form for the Gibbs potential is performed in App.B of the previous paper [26]. The derivation for the free energy is not made, because the calculations in the case of canonical ensemble are (a subcase and) simpler than that for the grand canonical ensemble. |
| 6 | We must note here that a similar consideration of the canonical ensemble, without varying density n, had to be performed in Section 4.4.1 of our previous work [26] too. The right application of the method of off-equilibrium potentials, presented in Reif [30], implies that in the case of the canonical ensemble, the off-equilibrium free energy must be varied only in regard to the temperature, although the equilibrium potential is a function of two variables. Therefore, by the consideration in Section 4.4.1 of [26], we must conclude that the system is in a stable equilibrium state at temperature due to the minimum of the free energy. |
| 7 | See App.B in [26]. |
| 8 | See also the assessment for the macro-temperature performed in our previous paper [26], Section 4.4.2 there. |
| 9 | Here we must note that in [26], Section 4.1, there is a mistake. We consider virialization in the form , which means a strong self-gravitating cloud, like in the present work. The right hypothesis is an equipartition (at all the scales of the inertial range) with a strong domination of the turbulent kinetic energy (i.e., ). The considerations in Section 4.1, there, are in accordance with the latter presumption. |
References
- Antonov, V.A. Most probable phase distribution in spherical star systems and conditions for its existence. Vest. Leningr. Gos. Univ. 1962, 7, 135. [Google Scholar] [CrossRef]
- Katz, J. On the number of unstable modes of an equilibrium. Mon. Not. R. Astron. Soc. 1978, 183, 765–770. [Google Scholar] [CrossRef]
- Lynden-Bell, D.; Wood, R. The gravo-thermal catastrophe in isothermal spheres and the onset of red-giant structure for stellar systems. Mon. Not. R. Astron. Soc. 1968, 138, 495–525. [Google Scholar] [CrossRef]
- Padmanabhan, T. Antonov Instability and Gravothermal Catastrophe–Revisited. Astrophys. J. Suppl. 1989, 71, 651. [Google Scholar] [CrossRef]
- Padmanabhan, T. Statistical mechanics of gravitating systems. Phys. Rep. 1990, 188, 285–362. [Google Scholar] [CrossRef]
- Chavanis, P.-H. Gravitational instability of finite isothermal spheres. Astron. Astrophys. 2002, 381, 340–356. [Google Scholar] [CrossRef]
- Chavanis, P.-H. Gravitational instability of isothermal and polytropic spheres. Astron. Astrophys. 2003, 401, 15–42. [Google Scholar] [CrossRef]
- Chavanis, P.-H. Dynamical stability of collisionless stellar systems and barotropic stars: The nonlinear Antonov first law. Astron. Astrophys. 2006, 451, 109–123. [Google Scholar] [CrossRef]
- de Vega, H.J.; Sanchez, N.; Combes, F. Self-gravity as an explanation of the fractal structure of the interstellar medium. Nature 1996, 383, 56–58. [Google Scholar] [CrossRef]
- de Vega, H.J.; Sanchez, N.; Combes, F. Fractal dimensions and scaling laws in the interstellar medium: A new field theory approach. Phys. Rev. D 1996, 54, 6008–6020. [Google Scholar] [CrossRef]
- de Vega, H.J.; Sanchez, N. The statistical mechanics of the self-gravitating gas: Equation of state and fractal dimension. Phys. Lett. B 2000, 490, 180–186. [Google Scholar] [CrossRef]
- Sormani, M.C.; Bertin, G. Gravothermal catastrophe: The dynamical stability of a fluid model. Astron. Astrophys. 2013, 552, A37. [Google Scholar] [CrossRef]
- Keto, E.; Field, G.B.; Blackman, E.G. A turbulent-entropic instability and the fragmentation of star-forming clouds. Mon. Not. R. Astron. Soc. 2020, 492, 5870–5877. [Google Scholar] [CrossRef]
- Elmegreen, B.; Scalo, J. Interstellar Turbulence I: Observations and Processes. Annu. Rev. Astron. Astrophys. 2004, 42, 211–273. [Google Scholar] [CrossRef]
- Hennebelle, P.; Falgarone, E. Turbulent molecular clouds. Astron. Astrophys. Rev. 2012, 20, 55. [Google Scholar] [CrossRef]
- Klessen, R.S.; Glover, S.C.O. Physical Processes in the Interstellar Medium. In Star Formation in Galaxy Evolution: Connecting Numerical Models to Reality, Saas-Fee Advanced Course; Springer: Berlin/Heidelberg, Germany, 2016; pp. 85–249. ISBN 978-3-662-47889-9. [Google Scholar]
- Ferriere, K.M. The interstellar environment of our galaxy. Rev. Mod. Phys. 2001, 73, 1031–1066. [Google Scholar] [CrossRef]
- Frisch, U.; Donnelly, R.J. Turbulence: The Legacy of A. N. Kolmogorov. Phys. Today 1995, 49, 82. [Google Scholar] [CrossRef]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Dokl. Akad. Nauk SSSR 1941, 30, 301–305. [Google Scholar]
- Galtier, S.; Banerjee, S. Exact Relation for Correlation Functions in Compressible Isothermal Turbulence. Phys. Rev. Lett. 2011, 107, 134501. [Google Scholar] [CrossRef]
- Kritsuk, A.; Norman, M.; Padoan, P.; Wagner, R. The Statistics of Supersonic Isothermal Turbulence. Astrophys. J. 2007, 665, 416–431. [Google Scholar] [CrossRef]
- Aluie, H. Compressible Turbulence: The Cascade and its Locality. Phys. Rev. Lett. 2011, 106, 174502. [Google Scholar] [CrossRef]
- Federrath, C.; Roman-Duval, J.; Klessen, R.; Schmidt, W.; Mac Low, M.-M. Comparing the statistics of interstellar turbulence in simulations and observations. Solenoidal versus compressive turbulence forcing. Astron. Astrophys. 2010, 512, 81. [Google Scholar] [CrossRef]
- Padoan, P.; Juvela, M.; Kritsuk, A.; Norman, M. The Power Spectrum of Supersonic Turbulence in Perseus. Astrophys. J. 2006, 653, L125–L128. [Google Scholar] [CrossRef]
- Keto, E. Scales of Stability and Turbulence in the Molecular ISM. Astron. Nachrichten 2024, 345, e20240044. [Google Scholar] [CrossRef]
- Donkov, S.; Stefanov, I.Z.; Kopchev, V. Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds. Universe 2025, 11, 184. [Google Scholar] [CrossRef]
- Larson, R. Turbulence and star formation in molecular clouds. Mon. Not. R. Astron. Soc. 1981, 194, 809–826. [Google Scholar] [CrossRef]
- Krumholz, M.R.; Lada, C.J.; Forbrich, J. Differential virial analysis: A new technique to determine the dynamical state of molecular clouds. Open J. Astrophys. 2025, 8, 91. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1991; pp. 203–207. ISBN 978-0471862567. [Google Scholar]
- Reif, F. Fundamentals of Statistical and Thermal Physics; Waveland Press, Inc.: Nong Grove, IL, USA, 1965; pp. 288–319. ISBN 978-1-57766-612-7. [Google Scholar]
- Donkov, S.; Stefanov, I.Z.; Veltchev, T.V. Thermodynamics of fluid elements in the context of saturated isothermal turbulence in molecular clouds. Bulg. Astron. J. 2023, 38, 91–97. [Google Scholar]
- Aschwanden, M.J.; Scholkmann, F.; Béthune, W.; Schmutz, W.; Abramenko, V.; Cheung, M.C.; Müller, D.; Benz, A.; Chernov, G.; Kritsuk, A.G.; et al. Order out of Randomness: Self-Organization Processes in Astrophysics. Space Sci. Rev. 2018, 214, 55. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; pp. 13–103. ISBN 978-0-471-24195-9. [Google Scholar]
- Vázquez-Semadeni, E.; Palau, A.; Ballesteros-Paredes, J.; Gómez, G.; Zamora-Aviles, M. Global hierarchical collapse in molecular clouds. Towards a comprehensive scenario. Mon. Not. R. Astron. Soc. 2019, 490, 3061–3097. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic dynamics. In Galactic Dynamics (Princeton Series in Astrophysics); Princeton University Press: Princeton, NJ, USA, 1987; pp. 567–573. [Google Scholar]
- Ganguly, S.; Walch, S.; Clarke, S.D.; Seifried, D. SILCC-Zoom: The dynamic balance in molecular cloud substructures. Mon. Not. R. Astron. Soc. 2024, 528, 3630–3657. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Donkov, S.D.; Stefanov, I.Z.; Kopchev, V. Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds in Virial Equilibrium. Universe 2025, 11, 383. https://doi.org/10.3390/universe11120383
Donkov SD, Stefanov IZ, Kopchev V. Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds in Virial Equilibrium. Universe. 2025; 11(12):383. https://doi.org/10.3390/universe11120383
Chicago/Turabian StyleDonkov, Sava D., Ivan Zhivkov Stefanov, and Valentin Kopchev. 2025. "Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds in Virial Equilibrium" Universe 11, no. 12: 383. https://doi.org/10.3390/universe11120383
APA StyleDonkov, S. D., Stefanov, I. Z., & Kopchev, V. (2025). Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds in Virial Equilibrium. Universe, 11(12), 383. https://doi.org/10.3390/universe11120383





