Gravitational Lensing by Lemaître–Tolman–Bondi Wormholes in a Friedmann Universe
Abstract
1. Introduction
2. The Lemaître–Tolman–Bondi Solution and Wormholes
3. Photon Motion in Wormhole Space-Times
3.1. Null Geodesic Equations
3.2. Geodesics in the Small Approximation
3.3. Photon Paths in Dynamic Wormhole Space-Time
4. A Friedmann Universe with a Dynamic Wormhole
4.1. Null Geodesics in a Friedmann Universe
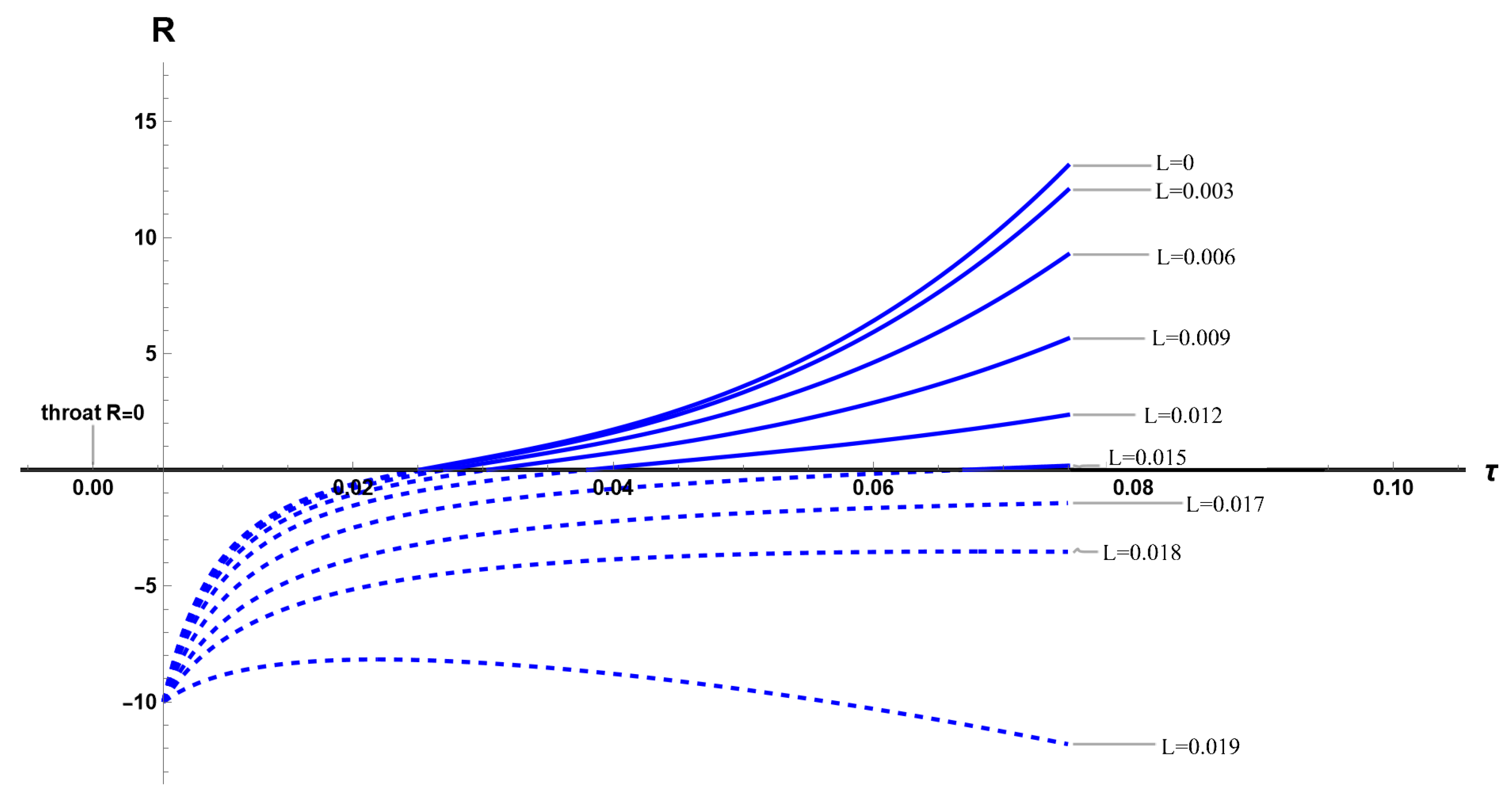
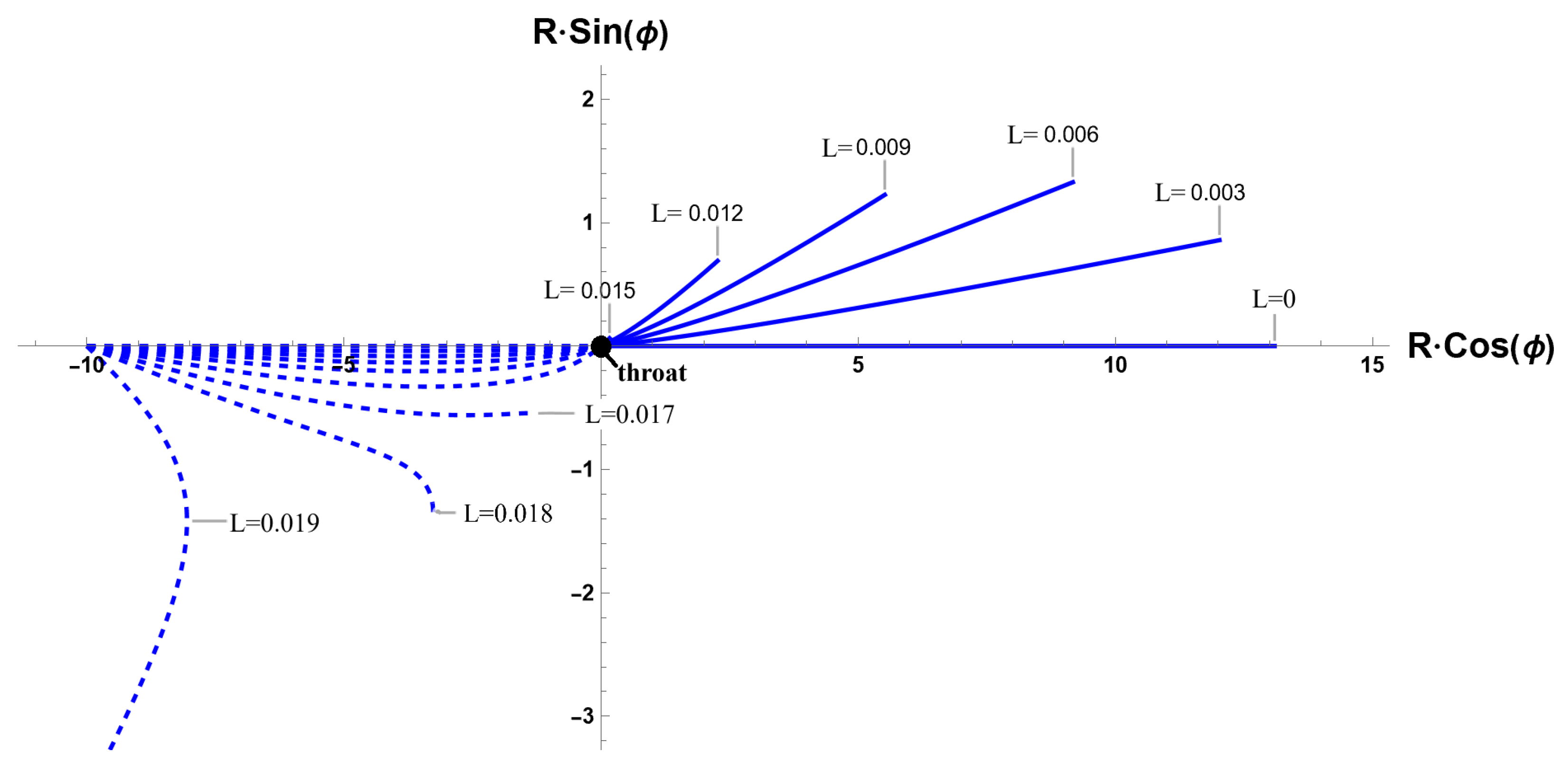
4.2. A Wormhole in a Friedmann Universe
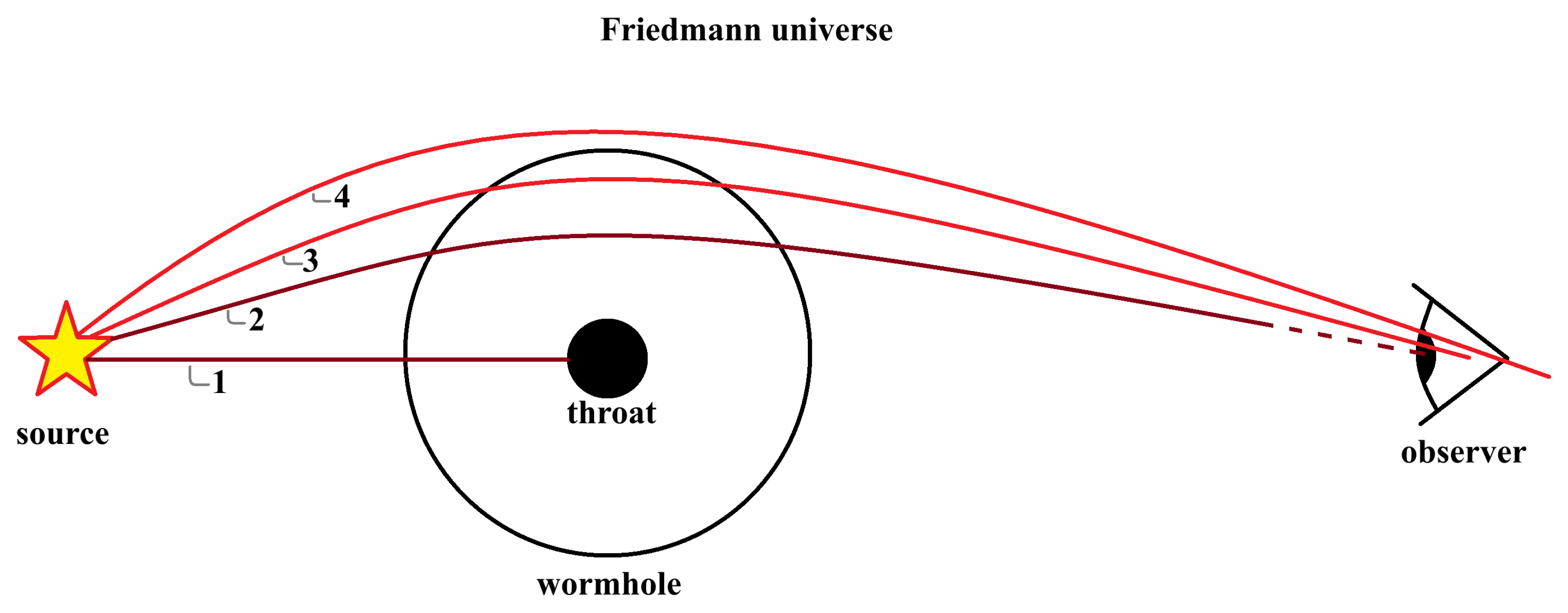
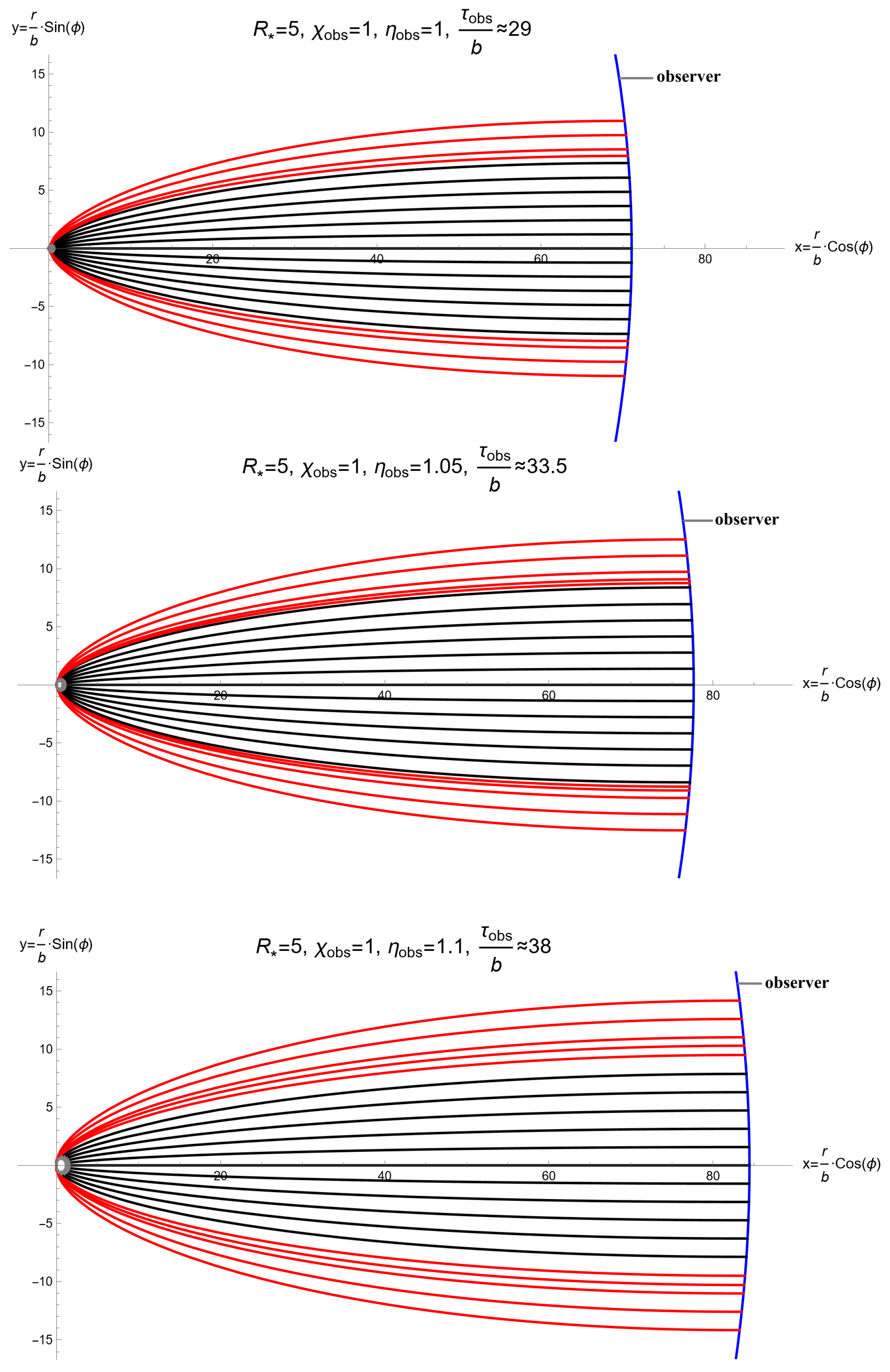
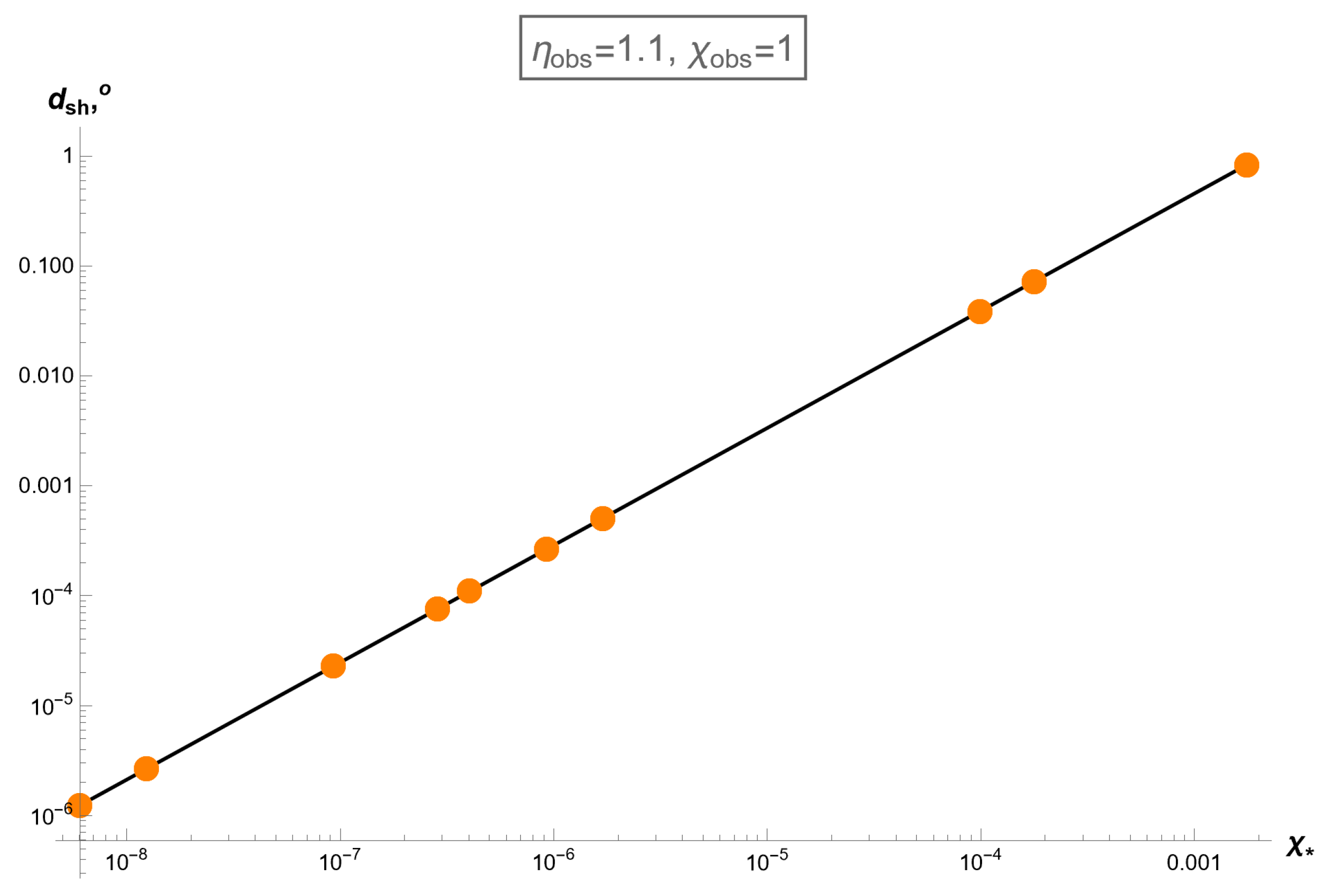
4.3. Shadow of a Dynamic Wormhole
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
- Hochberg, D.; Visser, M. Geometric structure of the generic static traversable wormhole throat. Phys. Rev. D 1997, 56, 4745. [Google Scholar] [CrossRef]
- Will, C.M. The confrontation between General Relativity and experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Knoll, C.; Radu, E. Traversable wormholes in Einstein-Dirac-Maxwell theory. Phys. Rev. Lett. 2021, 126, 101102. [Google Scholar] [CrossRef] [PubMed]
- Konoplya, R.A.; Zhidenko, A. Traversable wormholes in General Relativity without exotic matter. Phys. Rev. Lett. 2022, 128, 091104. [Google Scholar] [CrossRef]
- Bronnikov, K.; Bolokhov, S.; Krasnikov, S.; Skvortsova, M. A note on “Traversable wormholes in Einstein-Dirac-Maxwell theory”. Gravit. Cosmol. 2021, 27, 401–402. [Google Scholar]
- Bronnikov, K.A.; Krechet, V.G. Potentially observable cylindrical wormholes without exotic matter in GR. Phys. Rev. D 2019, 99, 084051. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Krechet, V.G.; Oshurko, V.B. Rotating Melvin-like universes and wormholes in general relativity. Symmetry 2020, 12, 1306. [Google Scholar] [CrossRef]
- Dai, D.-C.; Minic, D.; Stojkovic, D. How to form a wormhole. Eur. Phys. J. C 2020, 80, 1103. [Google Scholar] [CrossRef]
- Dai, D.-C.; Minic, D.; Stojkovic, D. A new wormhole solution in de Sitter space. Phys. Rev. D 2018, 98, 124026. [Google Scholar] [CrossRef]
- Hochberg, D.; Visser, M. Dynamic wormholes, anti-trapped surfaces, and energy conditions. Phys. Rev. D 1998, 58, 044021. [Google Scholar] [CrossRef]
- Arellano, A.V.; Lobo, F.S. Evolving wormhole geometries within nonlinear electrodynamics. Class. Quantum Gravity 2006, 23, 5811. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Nonlinear electrodynamics, regular black holes and wormholes. Int. J. Mod. Phys. D 2018, 27, 1841005. [Google Scholar] [CrossRef]
- Kashargin, P.; Sushkov, S. Collapsing wormholes sustained by dustlike matter. Universe 2020, 6, 186. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Kashargin, P.E.; Sushkov, S.V. Magnetized dusty black holes and wormholes. Universe 2021, 7, 419. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Kashargin, P.E.; Sushkov, S.V. Possible wormholes in a Friedmann universe. Universe 2023, 9, 465. [Google Scholar] [CrossRef]
- Lemaître, A.G. The expanding universe. Gen. Relativ. Gravit. 1997, 29, 641–680. [Google Scholar] [CrossRef]
- Tolman, R.C. Effect of inhomogeneity on cosmological models. Proc. Natl. Acad. Sci. USA 1934, 20, 169–176. [Google Scholar] [CrossRef]
- Bondi, H. Spherically symmetrical models in general relativity. Mon. Not. R. Astron. Soc. 1947, 107, 410–425. [Google Scholar] [CrossRef]
- Chakraborty, S.; Chakraborty, M. A study on existence of wormhole in Lemaitre-Tolman-Bondi model. Eur. Phys. J. C 2024, 84, 915. [Google Scholar] [CrossRef]
- Kopteva, E.; Jalúvková, P.; Bormotova, I.; Stuchlik, Z. Exact solution for a black hole embedded in a nonstatic dust-filled universe. Astroph. J. 2018, 866, 98. [Google Scholar] [CrossRef]
- Sajadi, S.N.; Riazi, N. Gravitational lensing by polytropic wormholes. arXiv 2016, arXiv:1611.04343. [Google Scholar] [CrossRef]
- Bugaev, M.A.; Novikov, I.D.; Repin, S.V.; Samorodskaya, P.S. Uniform sky glow (CMB) observed through the throat of a wormhole. arXiv 2023, arXiv:2305.18041. [Google Scholar]
- Bugaev, M.; Novikov, I.; Repin, S.; Samorodskaya, P.; Novikov, I., Jr. Observing of background electromagnetic radiation of the real sky through the throat of a wormhole. arXiv 2024, arXiv:2412.06872. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Baleevskikh, K.A. On gravitational lensing by symmetric and asymmetric wormholes. Gravit. Cosmol. 2019, 25, 44–49. [Google Scholar] [CrossRef]
- Ishkaeva, V.A.; Sushkov, S.V. Image of an accreting general Ellis-Bronnikov wormhole. Phys. Rev. D 2023, 108, 084054. [Google Scholar] [CrossRef]
- Cramer, J.G.; Forward, R.L.; Morris, M.S.; Visser, M.; Benford, G.; Landis, G.A. Natural wormholes as gravitational lenses. Phys. Rev. D 1995, 51, 3117–3120. [Google Scholar] [CrossRef] [PubMed]
- Nandi, K.; Zhang, Y.Z.; Zakharov, A.V. Gravitational lensing by wormholes. Phys. Rev. D 2006, 74, 024020. [Google Scholar] [CrossRef]
- Perlick, V. On the exact gravitational lens equation in spherically symmetric and static spacetimes. Phys. Rev. D 2004, 69, 064017. [Google Scholar] [CrossRef]
- Toki, Y.; Kitamura, T.; Asada, H.; Abe, F. Astrometric image centroid displacements due to gravitational microlensing by the Ellis wormhole. Astrophys. J. 2011, 740, 121. [Google Scholar] [CrossRef]
- Tsukamoto, N.; Harada, T.; Yajima, K. Can we distinguish between black holes and wormholes by their Einstein-ring systems? Phys. Rev. D 2012, 86, 104062. [Google Scholar] [CrossRef]
- Kuhfittig, P. Gravitational lensing of wormholes in the galactic halo region. Eur. Phys. J. C 2014, 74, 2818. [Google Scholar] [CrossRef]
- Bambi, C. Can the supermassive objects at the centers of galaxies be traversable wormholes? The first test of strong gravity for mm/sub-mm VLBI facilities. Phys. Rev. D 2013, 87, 107501. [Google Scholar] [CrossRef]
- Gjorgjieski, K.; Kunz, J.; Nedkova, P. Circular orbits and photon orbits at wormhole throats. arXiv 2025, arXiv:2505.07507. [Google Scholar] [CrossRef]
- Gyulchev, G.; Nedkova, P.; Tinchev, V.; Yazadjiev, S. On the shadow of rotating traversable wormholes. Eur. Phys. J. C 2018, 78, 544. [Google Scholar] [CrossRef]
- Huang, H.; Kunz, J.; Yang, J.; Zhang, C. Light ring behind wormhole throat: Geodesics, images and shadows. Phys. Rev. D 2023, 107, 104060. [Google Scholar] [CrossRef]
- Övgün, A.; Pantig, R.C. Time-dependent black hole lensing and the unified weak-to-strong deflection framework. arXiv 2025, arXiv:2510.19849. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: Oxford, UK, 1975; Volume 2, 402p. [Google Scholar]
- Vazquez, S.E.; Esteban, E.P. Strong field gravitational lensing by a Kerr black hole. Nuovo C. B 2004, 119, 489–519. [Google Scholar]

| 1 km | cm = 338 pc | |||
| 10 km (neutron star) | 700 pc | |||
| km (Earth) | 5.1 Kpc | |||
| km | 16 Kpc (Milky Way) | |||
| km (Sun) | 23 Kpc | |||
| km (SgrA*) | 56 Kpc | |||
| km (M87*) | 557 Kpc | |||
| 1 pc | 5.7 Mpc | 1165 | ||
| 6.5 pc | 10 Mpc (galaxy cluster) | 0.0015 | 648.8 | |
| 10 Kpc | 100 Mpc (void) | 0.015 | 65.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bronnikov, K.A.; Ishkaeva, V.A.; Sushkov, S.V. Gravitational Lensing by Lemaître–Tolman–Bondi Wormholes in a Friedmann Universe. Universe 2025, 11, 374. https://doi.org/10.3390/universe11110374
Bronnikov KA, Ishkaeva VA, Sushkov SV. Gravitational Lensing by Lemaître–Tolman–Bondi Wormholes in a Friedmann Universe. Universe. 2025; 11(11):374. https://doi.org/10.3390/universe11110374
Chicago/Turabian StyleBronnikov, Kirill A., Valeria A. Ishkaeva, and Sergey V. Sushkov. 2025. "Gravitational Lensing by Lemaître–Tolman–Bondi Wormholes in a Friedmann Universe" Universe 11, no. 11: 374. https://doi.org/10.3390/universe11110374
APA StyleBronnikov, K. A., Ishkaeva, V. A., & Sushkov, S. V. (2025). Gravitational Lensing by Lemaître–Tolman–Bondi Wormholes in a Friedmann Universe. Universe, 11(11), 374. https://doi.org/10.3390/universe11110374








