A Model for the Accretion Disk of Hercules X-1 from 35-Day Cycle Lightcurves

Abstract

The binary Hercules X-1 exhibits a 35-day brightness X-ray cycle, including a Main High state and a Short High state which are separated by two Low states. The cycle is due to blockage of the neutron star by a rotating twisted disk. The best available 35-day average lightcurves are from Swift/BAT observations in the 15–50 keV band and from MAXI observations in the 2–20 keV band. The current work fits both Swift/BAT and MAXI 35-day X-ray lightcurves using a disk plus corona model. The parameters of the disk and its corona from the two data sets are shown to be consistent with each other. The fit of two different data sets with the same model verifies the reliabilty of the disk plus corona model and its parameter values. We derive the scaling of the model disk radius to physical disk radius and use that to find that the physical corona inner radius is very small ∼100 km, and consistent with the estimate from pulse shape analysis. The system inclination of $85.12\pm {0.24}^{°}$ is consistent with the recent value derived from MAXI observations alone, and much improved compared to earlier estimates (∼82 to ${88}^{°}$). This results in significantly improved binary system parameters, including neutron star mass, companion mass and companion radius.

1. Introduction

The X-ray binary system Hercules X-1 (or Her X-1) consists of an accreting neutron star with a ∼2.3 ${\mathrm{M}}_{\odot }$ companion, HZ Her [1,2]. It has a 1.7-day orbit [3] and a 35-day cycle [4,5].

The 35-day cycle is composed of a bright Main High state, an intermediate brightness Short High state (∼20% as bright) and faint Low states (a few % as bright as Main High) separating the two high states. A detailed breakdown of the state changes for the 35-day lightcurve is given by [6] in their Table 2. The variation in X-ray flux is mainly caused by the blockage of the line-of-sight to the neutron star by the disk, e.g., [5,7,8]. However there is a significant contribution to the cycle by X-rays scattered from near the inner part of the accretion disk [7,9,10].

The overall need for a warped accretion disk in Her X-1 was established by [8] which analyzed optical variability, and a satisfactory mechanism for warping was given by [11]. The warped disk’s link with the observed pulse shape systematic variation with 35-day phase was shown by [7]. The measurement of the twist and tilt from models fit to the X-ray lightcurve (in particular, the RXTE/ASM one) was first carried out by [9]. Somewhat later, an ultraviolet light-curve was measured and then modelled with the warped disk model [12]. Thus in multiple aspects (X-ray, UV and optical light-curves, and 35-day evolution of the pulse-shape) a warped accretion disk is required to be present in Her X-11.

Here we are concerned with construction of a 3 dimensional model which can reproduce the 35-day observed X-ray lightcurve. We use ray-tracing simulations to calculate the lightcurve from the model using the Shape software package [15]. The goal is to constrain the properties of the disk by constructing a radiation transfer model which reproduces the 35-day X-ray light-curve of Her X-1. Ref. [9] used analytical models for the optical depth through the disk to the neutron star. Ref. [16] applied the precessing outer disk ring model of [17]. In that, a ring at the outer edge of the disk precesses via tidal forces from the companion star, when there is enough thermal energy in the ring.

Most recently, the ray-tracing software Shape (version X.1.2.1) [15] was applied by Leahy and Mendelsohn [18] to model the average 35-day lightcurve compiled from MAXI [19] observations by [20]. An accretion disk corona was found to be necessary to fit the lightcurve and a tight constraint on the inclination of the Her X-1 binary was obtained. The current work is an extension of the work of [18] by applying the model to Swift/BAT observations [21] (hereafter referred to as BAT) in addition to the MAXI observations. The combination of modelling data from two different instruments and two different energy bands significantly improves the reliability of the modelling. Section 2 describes the data used, Section 3 discusses the analysis applied to the data and Section 4 gives the model description. The results are presented in Section 5, with discussion of implications of the model in Section 6, ending with a summary section.

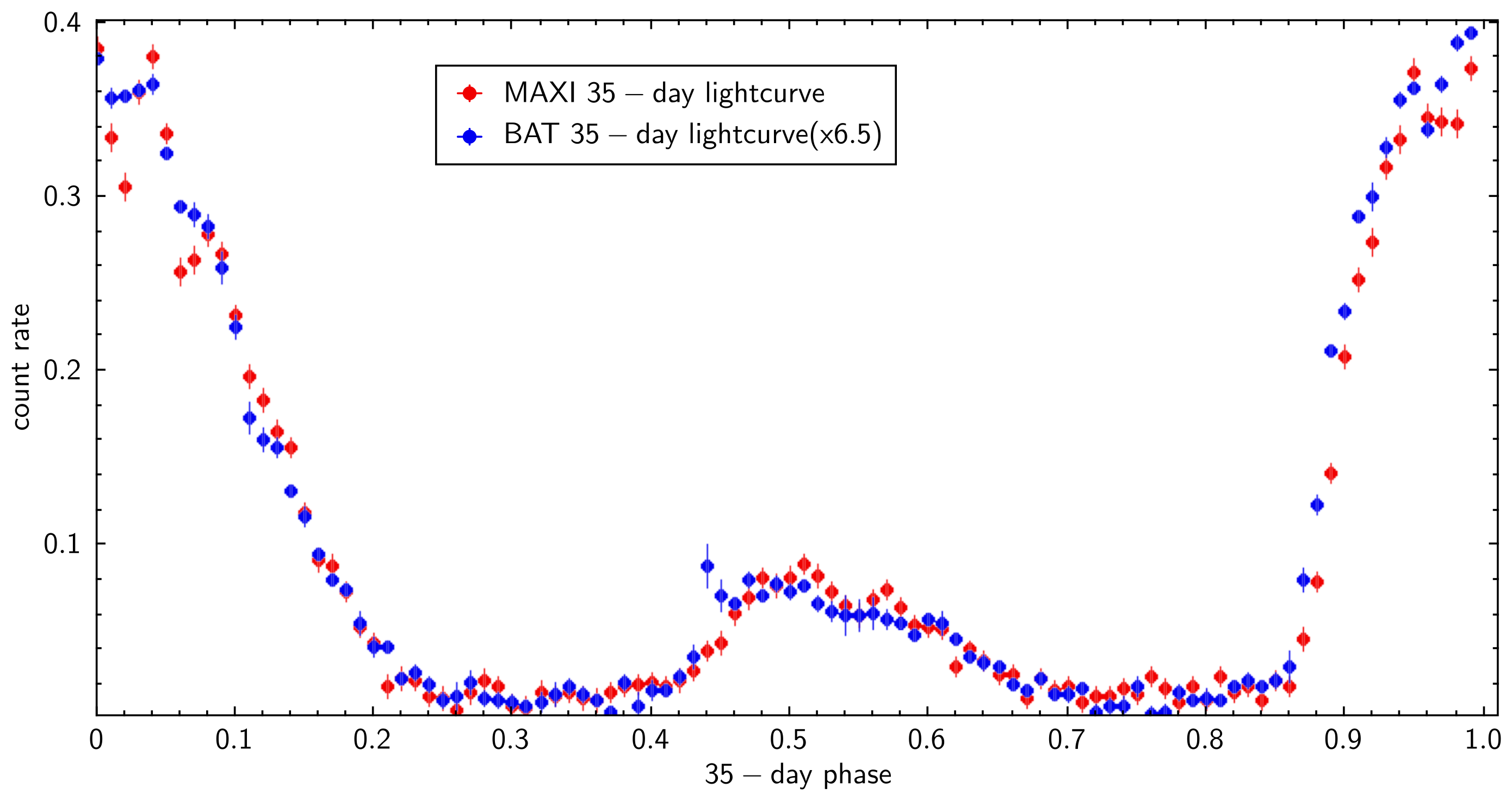
2. 35-Day X-Ray Lightcurves of Her X-1 from BAT and MAXI

For the 35-day light-curve we use the BAT data (energy band 15–50 keV [21]) and the MAXI data (2–20 keV [19]). BAT and MAXI regularly monitor Her X-1 and both have been doing this for more than 10 years, thus they both have complete coverage of the 35-day cycle over a large number of cycles and ideal for constructing an average 35-day lightcurve, unlike higher sensitivity pointed instruments. 35-day average light-curves were constructed from BAT and MAXI data by [6,20], which used a cross-correlation analysis to phase align the 35-day cycles. Those lightcurves had X-ray eclipses removed prior to analysis. That was necessary because the 1.7 day periodic Her X-1 X-ray eclipses of the neutron star do not align with the 35-day cycle. A 2% systematic error was included in addition to the statistical errors on the count rates. The 35-day lightcurves from BAT and MAXI are given in Figure 1.

For the current work, a quantitative method to identify phases where dips significantly affect the lightcurve is followed, which is significantly improved from the method of dip removal in [18]. This change in choice of removed data affected ∼10 phases of the 100, and had a noticable effect on the modelling results carried out below. Here we use significant changes in softness ratio as a reliable indicator of dips, which are caused by cold matter absorption and are accompanied by decreases of softness ratio [22]. The softness ratio is given by the MAXI count rate ($c_{MAXI}$) divided by the BAT count rate ($c_{BAT}$), and its error is given by

$$err(c_{MAXI}/c_{BAT})/(c_{MAXI}/c_{BAT})=\sqrt{err{\left(c_{MAXI}\right)}^2/c_{MAXI}^2+err{\left(c_{BAT}\right)}^2/c_{BAT}^2}$$

(1)

Figure 2 shows the MAXI to BAT count rate ratio and its errors, calculated including error propagation, as given by Equation (1), vs. 35-day phase. The large relative error in the softness ratio is caused by the large relative count rate errors for both BAT and MAXI when Her X-1 is faint, which happens during low states (35-day phases 0.20 to 0.44 and 0.65 to 0.86). For comparison the BAT count rate (scaled to fit the plot) is shown. The points that deviate more than 2$\sigma$ below the softness ratio at peak of Main High (6.7) are flagged and removed from both MAXI and BAT lightcurves. The exception is that no points are removed from Main High Turn-on (35-day phases 0.86 to 0.95) where the outer edge of the disk is known to cause cold matter absorption and low softness ratio. We note that none of the points are more than 2$\sigma$ above the softness ratio at peak of Main High. Some of the points at low count rate are not more than 2$\sigma$ from this value but the error bars are larger than the full scale of 0 to 10, so they are not plotted. The total number of removed points is 10.

3. Analysis Method

The Shape software allows one to specify an emitter as a point source of radiation and a surrounding matter distribution through which the radiation propagates to the observer. The point source emitter is given an emission spectrum specified by the user. The matter distribution is specified by objects with geometrical boundaries (e.g., a sphere or cylindrical ring) and formulae for the density dependence within each object are specified by the user. Absorption or scattering cross-sections for each object are also specified by the user. Ray tracing using the standard radiation transfer equations is carried out to produce a sky-plane image in the direction of the observer from the radiation after transmitting through the matter distribution. Lightcurves are obtained by integrating spatially over the simulated sky plane image. More details are given in the documentation for Shape [15].

For Her X-1, the 35-day lightcurve is caused by radiation from the neutron star propagating through a tilted and twisted accretion disk, with its corona, which rotates with a 35-day period. The disk rotation axis is the binary orbital axis and the observer is located at inclination 85 degrees [18], i.e., 5 degrees from the orbital plane. The measured spectrum of Her X-1 during peak of Main High [23] is used to specify the spectrum of the emitter at the origin of the Shape coordinates, which represents the neutron star. We use Shape to contruct a geometrical model for the accretion disk and its corona around the emitter (the neutron star). The disk is rotated to different angles in steps from 0 to 360 degrees and ray-tracing carried out at each angle to produce a simulated 35-day lightcurve.

A separate calculation is carried out in Shape for the radiation transfer for absorption and that for scattering. The results from these two calculations are called the direct radiation and the scattered radiation, respectively. The first calculation includes absorption cross-sections and scattering cross-sections but only keeps track of rays that are not scattered on their way to the observer. The second (scattered) calculation also includes absorption and scattering cross sections, but tracks only scattered radiation. To fit the result of a Shape model calculation to the observed we apply an overall scale factor and a phase shift. The phase shift is needed to shift the initial rotation angle of the accretion disk to match the start of the observed lightcurve. As noted previously [6] the definition of start phase for the 35-day cycle has been different in different analyses: some use start of Main High (with different definitions of start, e.g., first detection, 20% of peak- some of which depend on the sensitivity of the instrument). Here we use 35-day cycle phase 0 to be peak of Main High.

The scaled and phase shifted model light-curve is:

$$M\left({\varphi }_{35}\right)=A\times M_{dir}({\varphi }_{35}+{\varphi }_0)+B\times M_{scat}({\varphi }_{35}+{\varphi }_0)$$

(2)

where $M_{dir}$ and $M_{scat}$ are the direct and scattered radiation calculations, respectively, and ${\varphi }_0$ is the disk rotation at 35-day phase ${\varphi }_{35}=0$. The fitting is carried out using ${\chi }^2$ minimization. The disk model is then adjusted, by changes to one or more model parameters and Shape is run again to produce new $M_{dir}\left({\varphi }_{35}\right)$ and $M_{scat}\left({\varphi }_{35}\right)$ lightcurves, which are fit to the observed lightcurves to yield a new ${\chi }^2$ value. New parameters are chosen with the goal of improving the model fit to the data. This is repeated hundreds of times as necessary. Typically each Shape run ($M_{dir}\left({\varphi }_{35}\right)$ or $M_{scat}\left({\varphi }_{35}\right)$) takes ∼30 min to run2. The final result is a model where adjustment of the parameters no longer improves the fit to the data.

To obtain model parameter uncertainty estimates we follow the procedure in Chapter 15 of [24]. One parameter is varied around its value for the bestfit model, with three or more values, then a quadratic equation is fit to the ${\chi }^2$ dependence on that parameter. The maximum and minimum values of that parameter are found by the values where the quadratic intercepts ${\chi }_{min}^2+\Delta {\chi }^2$, with ${\chi }_{min}^2$ is the minimum of the quadratic and $\Delta {\chi }^2$ is chosen to yield the ±1-$\sigma$ confidence range.

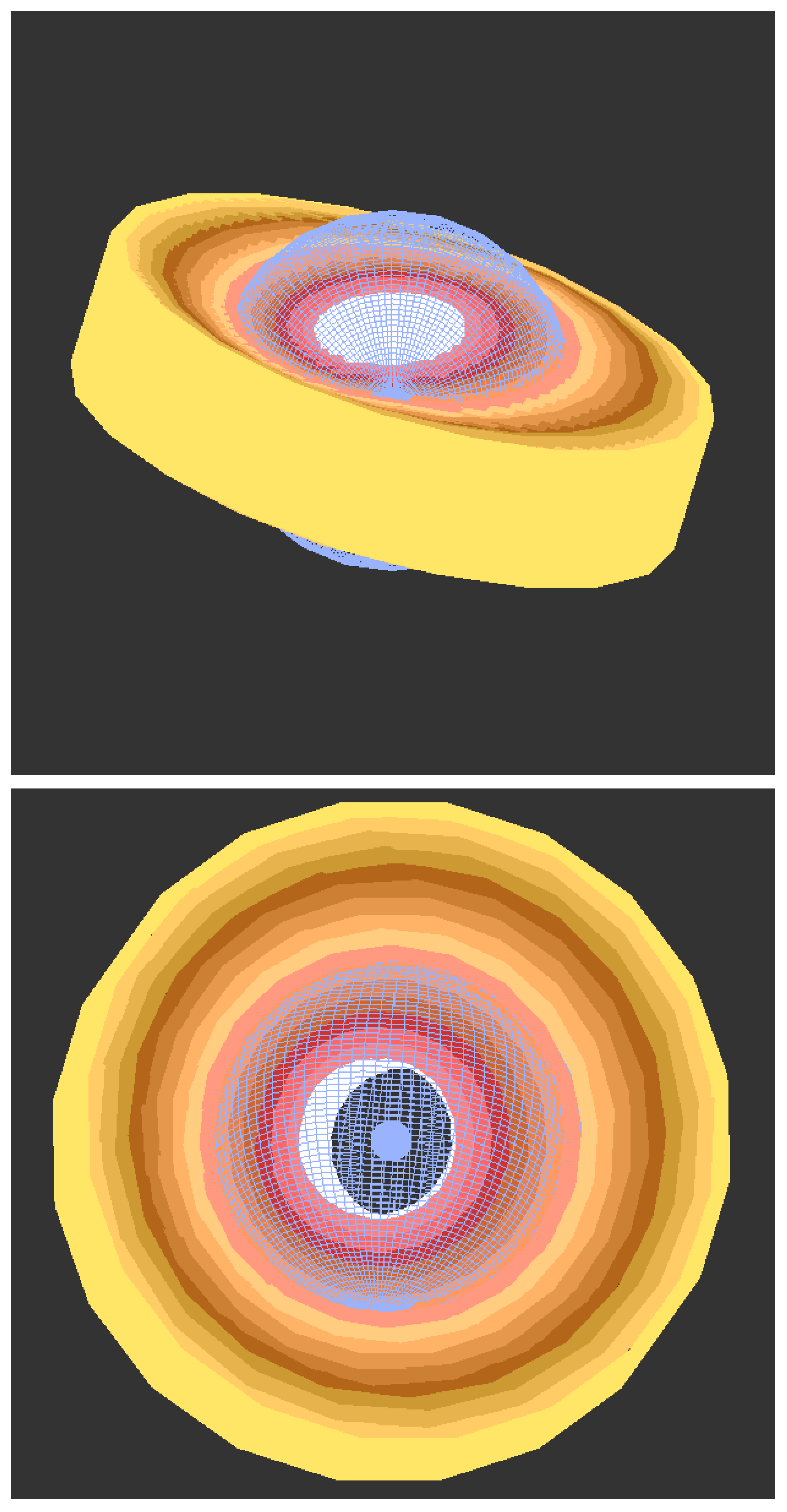
4. Model Description

A model is constructed to reproduce the observed 35-day light curve of Her X-1. The basic parts of the model are an accretion disk and a corona, each with different properties which affect the radiation from the central neutron star. The 35-day light curve is produced by the disk and corona rotating around the neutron star over the 35-day period. In the following subsections we describe the simulation implementation first, because the simulation limitations have an effect on how the disk and corona are represented. Then we describe the disk and corona properties. We finish this section with a description of the radial scaling used in order to use the simulation to calculate down to small distances in the physical disk.

4.1. Simulation Implementation

The Shape software has the matter distribution: (a) bounded by any number of 3-dimensional (3D) basic shapes, such as spheres, cylinders and cones, positioned and oriented inside a 3D rectangular grid which specifies the outer boundaries of the computation; and (b) further given by density functions inside each basic shape. Here, the orbital plane is the $z=0$ plane and the emitter (neutron star) is at $x=y=z=0$ so that the disk rotates around the z-axis as 35-day phase progresses. We approximate the emitter spectrum as a blackbody over the energy range of each of the observations (2–20 keV for MAXI and 15–50 keV for BAT).

The accretion disk has a low ionization state so we take the absorption cross-section to be a sum of the photoelectric and Thompson cross-sections (the latter accounts for X-rays that are scattered once then absorbed). The matter in the corona is highly ionized so the cross-section is that for Thompson scattering. In Shape one can split the spectrum into several energy bands, so that each energy band has a separate ray-tracing calculation, after which the energy bands are summed. We compared using 7 energy bands (each for 15–50 keV for BAT, and 2–20 keV for MAXI) and using 3 energy bands and did not find any difference in the resulting lightcurves. Thereafter 3 energy bands were used. The Shape calculations were repeated for 41 different consecutive rotation phases of the accretion disk to create a model light-curve over the full range of 35-day phase. The model was then interpolated to the observed phases for fitting. Different interpolation methods were compared and cubic spline with linear endpoints was found to be the most accurate, thus was adopted.

The dimension of the Shape grid was ${256}^3$ cells, or $5.12\times {10}^6$ km across per dimension, in order to fit the disk (which has diameter $4.2\times {10}^6$ km). Each grid cell is thus ${10}^4$ km on a side. $R_{in}$ and $R_{out}$ for the disk were fixed at $5\times {10}^5$ km and $2.1\times {10}^6$ km. The inner radius was taken larger than the one for the physical disk so that we could resolve the inner disk in the model disk.

4.2. Disk Properties

The disk has a tilted and twisted shape, as illustrated generally in previous work. E.g., Figures 2 and 3 of [9] show how the disk occultation produces the 35-day flux cycle with High, Low, Short-high and Low states. Arguments for the existence of a twisted and tilted disk in Her X-1 are presented in a series of previous studies on Her X-1, including [5,8], with theoretical disk modelling given by [11]. The disk is composed of a series of circular rings, with twist of each ring specified by giving the angle of line-of-nodes of that ring, and with tilt from the disk plane of each ring also specified. The disk is expected to have finite thickness, e.g., using the standard $\alpha$-disk model of [25]. Currently Shape allows basic functions to be used to specify the density dependence perpendicular to the disk plane.

The disk geometry was specified here using a series of rings, each with height z from $-z_{max}$ to $+z_{max}$ and radius r from $R_{in}$ to $R_{out}$, with r, z and $\varphi$ standard cylindrical coordinates of a ring. The warped disk is formed by an adjacent series of rings, with each ring having its own tilt angle from the orbital plane and twist angle (angle between the grid x-axis and the line of nodes for that ring). These angles for the inner and outer rings are parameters of the model, with those for intermediate rings specified by linear functions. During the 35-day cycle, the blockage of line-of-sight to the X-ray source is done by the outer and inner edges of the disk [7], which is ensured by the linear functions. An disk rotation phase (${\varphi }_0$, Equation (1)) is added as part of fitting process, thus a fixed inner twist involves no loss of generality.

The geometry of the disk is shown in Figure 3. Within the disk the density distribution is taken to be Gaussian with scale-length $H_z$ centred at $z=0$ for each ring: $n_0\times e^{{(-{\displaystyle \frac{z}{H_z}})}^2}$ where $z_{max}$ is taken to be several scaleheights (≃4). The previous work of [18] details the different tests that showed the disk vertical density funtion is best represented by a Gaussian. Thus the density is concentrated toward the (tilted and twisted) center plane of the disk. The disk is required to have an atmosphere (vertical gradient) in order produce the gradual rise and fall from the Main High state which is observed.

4.3. Corona Properties

The corona refers to a region of highly ionized and low density gas, which has the effect of scattering radiation from the central source (neutron star). For Her X-1, the scattering region has been suggested to be quite extended, based on residual flux observations during Main High eclipses [10], or near the inner disk edge in order to provide scattered flux during Short High state [9], or for contributing to the changes in pulse shape profile [7]. Following ref. [18], we found that a spherical corona with inner and outer radius limits and a power-law density profile is adequate to provide a model fit to the 35-day X-ray light curve, so use this model for the corona. The corona is optically thin.

The corona consists of ionised gas (free electrons) above and below the disk which make a contribution to the 35-day lightcurve. A spherical corona with powerlaw density profile is adopted, motivated by the form of the corona used by [10]: $n_{cor}{\left({\displaystyle \frac{r}{R_{cor,in}}}\right)}^{{\alpha }_{cor}},R_{cor,in}<r<R_{cor,out}$ with $R_{cor,in}$ and $R_{cor,out}$ the inner and outer radii, ${\alpha }_{cor}$ the powerlaw index and $n_{cor}$ the density at $R_{cor,in}$. $n_{cor}$ was set to $3\times {10}^{17}$ ${\mathrm{m}}^{-3}$.3 $R_{cor,out}$ was fixed at $1.2\times {10}^6$ km, because the fitting was not sensitive to $R_{cor,out}$.

4.4. Radial Scaling Factor

The Shape model consists of a disk with a z dependence but no r dependence. However the equivalent physical disk it represents does have a $r_{phys}$ dependence, where $r_{phys}$ is the radial coordinate for the physical disk. This is because the inner radius is scaled up by a factor 1250 for the Shape model: from a physical disk inner radius of 400 km to the model disk inner radius of $5\times {10}^5$ km, but the outer radius is not scaled up. Column densities (integral of density along the line of sight) determine the resulting radiation transfer, and the real disk has smaller line-of-sight for the inner rings, proportional to the scaling factor $f_{scale}=r_{phys}/r$ for each ring, which varies from 1/1250 for the inner ring to 1 for the outer ring. Assuming a linear variation, $f_{scale}$ follows the relation:

$$\begin{array}{ccc}\hfill f_{scale}& =& (r-R_{in})/(R_{out}-R_{in})\times (1-R_{in,physical}/R_{in})+R_{in,physical}/R_{in}\hfill \\ & =& (r-R_{in})/(R_{out}-R_{in})\times (1249/1250)+1/1250,R_{in}<r<R_{out}\hfill \end{array}$$

(3)

For $r<R_{in}$, a formula for $f_{scale}$ has to be specified: one suitable choice is $f_{scale}=1/1250$ for $r<R_{in}$. Thus the densities for the physical disk and physical corona increases by a factor of $1/f_{scale}$=1250 for $r<R_{in}$, and by factor $1/f_{scale}\left(r\right)$ for $R_{in}<r<R_{out}$. One can assume more complex forms for the scaling factor. E.g. to get a standard $\alpha$ disk model [25], the Case b disk has a midplane density $\propto r^{-33/20}$ and the Case c disk has a midplane density $\propto r^{-15/8}$. For these two cases one would replace the $(r-R_{in})/(R_{out}-R_{in})$ factor in the formula for $f_{scale}$ by the factors ${[(r-R_{in})/(R_{out}-R_{in})]}^{33/20}$ or ${[(r-R_{in})/(R_{out}-R_{in})]}^{15/8}$, respectively.

As done for the disk model, the corona model inner radius is scaled up by a factor of 1250 to obtain the same disk line-of-sight blockage as the physical case. This implies the density of the physical disk is scaled up by this same factor to obtain the same scattering column density. The outer corona physical radius is scaled down by the factor $f_{scale}$ from the model radius $r=R_{cor,out}$. The inner and outer boundaries of the corona are illustrated in Figure 3.

5. Results

As described above the initial disk plus corona model was adopted from the work of [18]. The two data sets that were modeled were the BAT 35-day lightcurve and the MAXI 35-day lightcurve from [20]. The removal of lightcurve phases where the count rates are affected by dips was carried out as described in Section 2 above.

The inner radius of the corona, $R_{cor,in}$, strongly affects the strength of scattered radiation over the 35-day cycle: due to the blockage of the inner part of the corona by the disk. We specify $R_{cor,in}$ by its ratio to the inner radius of the disk ($R_{in}$). The outer corona is visible for most of disk rotation phase and less modulated.

Figure 4 shows simulated images of the scattered radiation from the corona at 35-day phase 0.0, when the line-of-sight from neutron star to observer gives maximum visibility at peak of Main High; at 35-day phase 0.35, in the middle of the first Low State, when the disk maximally blocks the line-of-sight from neutron star to observer; and 0.52, when the line-of-sight from neutron star to observer gives the maximum visibility at peak of Short High (but less than that for Main High). For phase 0.0 the part of the corona above the disk is visible, whereas for phase 0.52 the corona below the disk is visible and during the two low states both sides of the corona are visible, but the central part of the corona is blocked by the disk.

The disk outer radius was set to $2.1\times {10}^6$ km. The inner radius was set to $5\times {10}^5$ km, to include enough computational cells (${10}^4$ km across) to obtain a resolved ring. The inner twist angle of the disk was set to 75.5 degree, but this is not a restriction for the fits because it is degenerate with the parameter ${\varphi }_0$ in Equation (1). The set of fixed parameters is shown in the top part of

Table 1. Disk with Corona Model: Best Fit Parameters and Uncertainties.

Fixed Parameters	Value
Disk Inner Radius $R_{in}$ (km)	$5\times {10}^5$
Disk Outer Radius $R_{out}$ (km)	$2.1\times {10}^6$
Inner Twist (degrees)	75.5
Corona Outer Radius $R_{cor,out}$(km)	$1.2\times {10}^6$
Variable parameters (geometry)	Value	1$\sigma$-error
BAT Inclination (Degrees)	85.17	0.15
MAXI Inclination (Degrees)	85.07	0.19
BAT Inner Tilt (degrees)	22.5	0.7
MAXI Inner Tilt (degrees)	24.0	1.0
BAT Outer Tilt (degrees)	17	3
MAXI Outer Tilt (degrees)	24	4
BAT Outer Twist (degrees)	22	4
MAXI Outer Twist (degrees)	22	4
BAT $R_{cor,in}/R_{in}$	0.26	0.05
MAXI $R_{cor,in}/R_{in}$	0.23	0.06
Variable parameters (other)
BAT Disk Density (${\mathrm{m}}^{-3}$)	$3.1\times {10}^{20}$	$0.4\times {10}^{20}$
MAXI Disk Density (${\mathrm{m}}^{-3}$)	$3.2\times {10}^{20}$	$0.6\times {10}^{20}$
BAT Inner Scale Height (rad)	$0.22$	0.06
MAXI Inner Scale Height (rad)	$0.30$	0.08
BAT Outer Scale Height (rad)	$0.088$	0.018
MAXI Outer Scale Height (rad)	0.100	0.023
BAT Corona Powerlaw Index ${\alpha }_{cor}$	−0.6	0.5
MAXI Corona Powerlaw Index ${\alpha }_{cor}$	−1.3	0.6
BAT Disk Phase Shift (35-day phase)	0.211	0.006
MAXI Disk Phase Shift (35-day phase)	0.205	0.007
Goodness of fit
BAT ${\chi }^2$	160
MAXI ${\chi }^2$	105

.

We initially fit the BAT lightcurve to obtain best fit parameters for the BAT data, then fit the MAXI lightcurve to obtain best fit parameters for the MAXI data. The best fit model parameters and their errors for BAT and for MAXI are given in Table 1 and the best fit light-curves are shown in Figure 5. The 1$\sigma$ (68.27%) parameter errors were obtained using the standard method for non-linear model fitting [24].

6. Discussion

6.1. Model Fitting Process

The fit residuals for both BAT and MAXI best fit models are shown in Figure 6. There are some 35-day phases of higher residuals: Turn-on to Main High (phase ≃ 0.87) and Decline (≃0.18)4. This indicates some systematic errors in the data or the model at these 35-day phases. A likely explanation is that the effects of dips has not fully removed in our choice of omitted 35-day phases (see Section 2). Dips occur over a wide range of 35-day phase [22] and neither BAT nor MAXI are sensitive to detect most dips: only the strongest dips affect the MAXI to BAT softness ratio. Thus we cannot fully remove dips, which limits the accuracy of the modelling. The effect of systematic effects in the data is partially mitigated by modelling data sets from 2 different instruments (BAT and MAXI).

To estimate errors in the model, we used the standard process for determination of parameter errors for ${\chi }^2$ minimization of a nonlinear model. The model fit to the BAT data agrees with the model fit to the MAXI data within 1$\sigma$ of the combined BAT and MAXI errors for all the variable parameters. This 1$\sigma$ combined error is given by

$$P_{err}=\sqrt{P_{BAT,err}^2+P_{MAXI,err}^2}$$

(4)

where $P_{BAT,err}$ and $P_{MAXI,err}$ are the parameter errors from the BAT fit and from the MAXI fit, respectively. $P_{err}$ is also the error in the mean of the BAT and MAXI parameters. Because the two models give consistent parameters, the best fit disk plus corona model can be taken to have parameters equal to the mean of the BAT and MAXI values, with parameter errors given by the combined error above.

6.2. Interpretation in Terms of a Physical Model

This work uses Shape which carries out a radiation transfer for direct/absorbed X-rays and separately for scattered X-rays. For direct X-rays, the key physical quantity at any 35-day phase (i.e., at a particular observer direction) is the column density for absorption measured on the line-of-sight. For scattered X-rays (the single scattering case considered here), the key physical quantities are the column densities for scattering along all lines of sight from the central X-ray source at the origin. Both of these are invariant to a change in radial scaling of the disk if one conserves the column densities: ${\int }_{\widehat{s}}nds$ where $\widehat{s}$ is the direction of the single line-of-sight from neutron star to observer for the absorbed X-rays calculation and $\widehat{s}$ refers to all lines-of-sight surrounding the neutron star for the scattered X-rays calculation. As discussed in Section 4.4 the physical disk has local densities scaled up by the inverse of the local scaling factor $f_{scale}\left(r\right)$, that is the ratio of physical radius to model radius. We note that angular quantities are not affected by the radius scaling.

6.3. The Disk and Comparison with Previous Work

A precessing and tilted disk is required to explain the 35-day cycle. Ref. [14] demonstrated that the pulse shape cycle and 35-day flux cycle were in phase, and separately suggested that neutron star precession takes place. Some support for this is given by X-ray polarization analyses ([13,26,27]) but those studies did not consider the effect of disk precession or of corona scattering on the polarization changes. The smooth pulse profile changes from precession were argued to be in disagreement with observed sharp pulse shpae changes by [7]. BAT and MAXI observations which were analyzed here have low time resolution (∼1000 s) [20] thus cannot measure nor are affected by pulse profile varations. Thus pulse profile changes should not have a strong effect on the disk modelling carried out here.

Ref. [18] modeled Her X-1’s corona and disk similarly to the work here, using the MAXI lightcurve with 35-day phases removed from the analysis, to compensate for dips, based on manual inspection for decreases in count rate. The current work improves on this by using both MAXI (2–20 keV) and BAT (15–50 keV) lightcurves and removing phases based on changes in softness ratio, which is a direct indication of absorption by dips. The model parameters obtained by [18] are listed in their Table 2. The parameters of [18] that agree with our parameters within 1$\sigma$ are (where we use the average of BAT and MAXI parameters from Table 1 and error given by Equation (3)): inclination, disk density, inner tilt, inner scale height, outer tilt, outer twist, ratio of corona inner radius to disk inner radius and corona powerlaw index. The outer scale height (our value is 0.094 ± 0.029 radians) agrees within 2$\sigma$. We refit the model to the MAXI lightcurve with the same points removed as [18] and verify their results, thus the difference must be caused by the different selection of data points removed. The current work uses a quantitative test to remove dip-affected data thus is more reliable than the results of [18].

The results of the RXTE/ASM 35-day lightcurve analysis were given by [9] with [28] presenting them in a more useful form (their Table 2). The accretion disk parameters of those two studies agree within uncertainties. The outer disk scale height here has a value between the layer 1 and layer 2 scale heights of [28]. However we obtain a better fit to data using a single outer atmospheric scale height, and the newer data has significantly smaller error bars. This is due to our inclusion of the corona, not included in [9] or [28], which better fits the 35-day lightcurve than inclusion of a second layer on the disk.

Ref. [12] constructed a disk model as a model for a far ultraviolet observed light-curve of Her X-1. The observation was short (0.93 days or 0.55 binary orbit) and the model simulated the changing disk shadow on the front surface of the star in its orbits with the neutron star and its disk. The resulting disk model, with ${85}^{°}$ inclination assumed, had inner tilt of ${11}^{°}$ and disk twist of ${110}^{°}$, compared to the current work with inner tilt of ${23}^{°}$ and disk twist (difference between inner and outer twists) of ${52}^{°}$. However that disk was optically thick and had no atmosphere, which explains both the smaller inner tilt and larger twist than the current work. In general, the difference in disk parameters of the current study from previous studies can be explained by the use of simpler (less physical) disk models in the previous studies.

6.4. Disk Corona

A density power law was adopted for the disk corona, as indicated by previous studies of the corona. Ref. [10] found a powerlaw index of −1.25 for the corona by fitting scattered X-rays during neutron star eclipse. Our corona powerlaw index (≃−1) is consistent with this. We find the inner corona extends in to ∼0.26 times the inner disk radius of ∼400 km, i.e., ∼100 km. This is consistent the conclusion of [7] from pulse shape analysis that scattering must occur close (∼100 km) to the neutron star.

6.5. System Inclination

A comprehensive discussion of the effect of the constraint on Her X-1 binary inclination is given by [18]. A general discussion of the system parameters of Her X-1 is given by [1]. A recalculation of the system parameters based on the constraint from the current work (${85.12}^{°}\pm 0.24$) instead of the constraint of (${85.47}^{°}\pm 0.27$) from [18] yields no significant differences, but we summarize updated values here.

The main implication of the inclination constraint is that the binary system parameters are better constrained. The projected distance from neutron star to center of mass of $a_{x}sin\left(i\right)$ [3] yields the neutron star semi-major axis $a_x=13.231\pm 0.008$ light-s. The radius of HZ Her, $R_{tan}$ [1], is better determined: 2.64 to $2.84\times {10}^{11}$ cm. $R_{tan}$ is measured by eclipse duration corrected by orbital inclination with correction assuming a spherical star. The Roche Lobe calculator [29], which implements an accurate calculation of Roche lobe properties, allows one to find companion star radii in units of a. Assuming HZ Her is Roche lobe filling one finds: front or L1 radius- $R_{L1}/a=0.54$; side or y radius- $R_y/a=0.41$; top or z radius- $R_z/a=0.39$; and backside radius $R_{bk}/a=0.44$. The Roche Lobe calculator is used to determine that the uncertainties in the different radii (in units of a) are ∼0.6%.

$R_{tan}$ is from the surface element causing the eclipse to the companion’s mass center. The element has polar angles $\theta =85.1^{°}$ and $tan\left(\varphi \right)={90}^{°}-R_{tan}/a$, where $\varphi$ is in the orbital plane and the z-axis normal to the orbit. The Roche Lobe calculator [29] gives the mass ratio q. Using $q=0.67\pm 0.02$ (see below) and the updated $a_x$ already given, an updated semi-major axis is found: $a=6.61(\pm 0.20)\times {10}^{11}$ cm. The uncertainty in q of ±3% is the main contributor to the uncertainty in a.

A smaller radius error yields a smaller error in luminosity of 11% and reduces the size of the allowed band in Figure 4 of [1] to about 55% as wide. The new allowed mass of HZ Her from the evolutionary tracks is 2.34–2.45 ${\mathrm{M}}_{\odot }$ for the case of increasing radius, which is required for mass accretion. Table 3 of [1] is recalculated with the new inclination and mass range to give new limits on the companion velocity amplitude, $K_c$ and neutron star mass, $M_x$. The new limits are: 110 km/s $\le K_c\le$ 116 km/s and 1.52 ${\mathrm{M}}_{\odot }\le M_x\le$ 1.69 ${\mathrm{M}}_{\odot }$. This results in a limit on the mass ratio of $0.65\le q=M_x/M_c\le 0.69$.

The cross-sectional area of the Roche lobe fillling star during eclipse is 0.9455 $\pi R_{tan}^2$ [1]. With the measured continuum flux during eclipse [30] a new distance D is determined: 6.1 $\le D\le$ 6.4 kpc.

7. Summary

In this study we constructed a 3D disk plus corona model and applied ray tracing software to create model 35-day X-ray lightcurves which were fit to both BAT and MAXI observations of Her X-1. The disk and corona properties and system inclination and their uncertainties were determined. The general disk plus corona model of [18] is confirmed with improved analysis: this includes: (i) use of two independent data sets, and (ii) removal of dip-affected data. The latter was not correctly done in the previous analysis: comparison of the parameters from the fit to the MAXI data by [18] and the current parameters from the fit to the MAXI data (in Table 1) shows that a number of parameter values have changed by small amounts due to the improved data selection. The disk and corona parameters from the current fits to the BAT data and to the MAXI data agree to within uncertainties. We derive the scaling of model radius to physical radius, to find that the inner radius of the scattering corona extends down to ≃100 km from the neutron star, which is consistent with the previous estimate from [7], based on pulse shape studies.

The inclination $i=85.12\pm 0.{24}^{°}$ is the best determination to date, and improves constraints on the radius (2.64 $\times {10}^{11}$ cm $\le R_{tan}\le$ 2.84 $\times {10}^{11}$ cm) and mass (2.34 ${\mathrm{M}}_{\odot }\le M_{HZHer}\le$ 2.45 ${\mathrm{M}}_{\odot }$) of the companion HZ Her. The new allowed ranges for $K_c$ are 110 km/s $\le K_c\le$ 116 km/s; for neutron star mass are 1.52 ${\mathrm{M}}_{\odot }\le M_x\le$ 1.69 ${\mathrm{M}}_{\odot }$ and for mass ratio q are $0.65\le q=M_x/M_c\le 0.69$. The neutron star mass is within the range of masses for neutron stars (see the review by [31]5) but more accurate than most other determinations.

Studies to be carried out in future that would improve knowledge on the disk plus corona include the following. More observations should be carried out in ultraviolet and optical wavelengths which are sensitive to the heated surface of the companion, followed by modelling of the observations. The disk shadow on the companion changes with both orbital phase (due to change in observer viewpoint) and 35-day phase (due to changes in disk rotation). Thus the modeling is more complex than that for the 35-day X-ray cycle (with no significant companion emission) but it would provide an independent test of the disk plus corona model. There are X-ray spectral observations of Her X-1, e.g., with RXTE/PCA, that have not been analyzed yet and cover a good part of 35-day phase and which would be valuable to analyze, followed by modelling using a future version of the Shape software which could output model X-ray spectra.