Abstract
We propose a non-exotic electromagnetic solution (within the standard model of particle physics) to the cosmological 7Li problem based upon a narrow 2 MeV photo-emission line from the decay of light glueballs (LGBs). These LGBs form within color superconducting quark clusters (SQCs), which are tens of Fermi in size, in the radiation-dominated post-BBN epoch. The mono-chromatic line from the decay reduces Big Bang nucleosynthesis (BBN) 7Be by without affecting other abundances or the cosmic microwave background (CMB) physics, provided the combined mass of the SQCs is greater than the total baryonic mass in the universe. Following the LGB emission, the in-SQC Quantum ChromoDynamics (QCD) vacuum becomes unstable and “leaks” (via quantum tunneling) into the external space-time (trivial) vacuum, inducing a decoupling of SQCs from hadrons. In seeking a solution to the 7Li problem, we uncovered a solution that also addresses the Dark Energy (DE) and dark matter (DM) problem, making these critical problems intertwined in our model. Being colorless, charge-neutral, optically thin, and transparent to hadrons, SQCs interact only gravitationally, making them a viable cold DM (CDM) candidate. The leakage (i.e., quantum tunneling) of the in-SQC QCD vacuum to the trivial vacuum offers an explanation of DE in our model and allows for a cosmology that evolves into a CDM universe at a low redshift with a possible resolution of the Hubble tension. Our model distinguishes itself by proposing that the QCD vacuum within SQCs possesses the ability to tunnel into the exterior trivial vacuum, resulting in the generation of DE. This implies the possibility that DM and hadrons might represent distinct phases of quark matter within the framework of QCD, characterized by different vacuum properties. We discuss SQC formation in heavy-ion collision experiments at moderate temperatures and the possibility of detection of MeV photons from the decay.
1. Introduction
The primordial abundances of the light elements produced in the first few minutes of the universe predicted by standard hot Big Bang cosmology [1,2,3] are in excellent agreement with the abundances inferred from data (e.g., [4]). Big Bang nucleosynthesis (BBN) starts when the deuteron (D) bottleneck is overcome at keV and terminates at keV (redshift ) due to electrostatic repulsion between nuclei (e.g., [5]); is the Boltzmann constant. Significant amounts of D, 3H, and 4He build up followed by the production of much less abundant elements such as 7Be. With a half-life of ∼53 days, 7Be decays into 7Li via bound electron capture, with the emission of a neutrino (e.g., [6]). This cannot occur, however, until recombination at 1100 when 7Be becomes singly ionized. The measured 7Li abundance is ∼1/3 of what is expected from this process [7] defining the cosmological 7Li problem (see [8] for a review). Dimensionless quantities are defined as with quantities in cgs units unless specified otherwise.
The standard theory of electromagnetic cascades onto a photon background predicts a quasi-universal shape for the resulting non-thermal photon spectrum (e.g., [9]). In the case of non-thermal BBN, cosmological constraints using this quasi-universal shape make purely electromagnetic solutions to the 7Li problem impossible (e.g., [10]) unless the injected photon energy falls below the pair-production threshold, in which case the spectral shape is very different (see [11] and references therein). The effective pair production threshold is , below which the double photon pair-creation process receives a Boltzmann suppression ([10]; see also [12]); is the electron mass. If injected when BBN is over, the sub-threshold photons act to post-process the abundances computed in the standard scenario. Photons injected with MeV can destroy 7Be (suppressing 7Li production) without affecting other BBN abundances, distorting the CMB background, or injecting excess entropy [11,13].
In this paper, we sketch a model for the injection of sub-threshold photons () in the radiation-dominated post-BBN epoch, characterized by a universe temperature in the keV range. The condition implies keV, which corresponds to the post-BBN era when the universe is a few hours old and has a redshift below , where keV. This model focuses on the nearly instantaneous emission (with a timescale of ∼ s) of a mono-chromatic 2 MeV line by quark clusters (QCs). These QCs are formed during the early universe’s Quantum ChromoDynamics (QCD) cross-over phase transition at a redshift of , when the universe was a few microseconds old and had a temperature of MeV.
Our model is grounded in the fundamental principles of QCD and relies on the properties of quark matter in a regime where quarks are deconfined and form Cooper pairs. Prior to delving into the details of our model, we provide a didactic introduction to the QCD phase diagram, the quark–gluon plasma (QGP), and other pertinent phases of quark matter in Appendix A (titled “Pedagogical Framework”). Additionally, we offer a general overview of our model and the resulting interconnectedness of the 7Li problem, Dark Energy (DE), and dark matter (DM) enigmas.
In our study, QCs consist of collections of up and down quarks. To ensure charge neutrality, the number density of down quarks (with a charge of −1/3) is twice that of up quarks (with a charge of ). These QCs, which are assemblies of the quark–gluon plasma (QGP), have a radius of approximately 100 Fermi, rendering them transparent to photons.
Being composed of quarks, QCs are classified as baryons and are thus encompassed within the standard model of particle physics. They can be envisioned as macroscopic nucleons (not nuclei) carrying baryon numbers entirely through the quarks. Here and throughout the paper, baryonic matter includes all quarks, which is more general than just protons and neutrons. The density of QCs is on the order of ∼ cm−3, which is approximately ten times the nuclear saturation density. Consequently, an approximately 100 Fermi QC possesses a baryon number . QCs are distinct entities from the significantly larger () cosmic strange-quark nuggets [14] and Axion quark nuggets [15], requiring different formation mechanisms (see bullet point #7 in Section 5).
In the post-BBN era, QCs transition into a color superconducting (CSC) phase, where their constituent quarks form Cooper pairs (see Appendix A) and give rise to what we refer to as Superconducting Quark Clusters (SQCs). For the purposes of this paper, we select the two-flavor color superconducting (2SC) phase as the reference phase, allowing us to convey the essence of our idea. Within the 2SC phase, a significant fraction of gluons (3/8 of them) do not interact with the paired quarks. Instead, they form their own condensate in the form of light glueballs (LGBs). Unlike the confined quark matter, where GeV-scale glueballs are anticipated, LGBs within the 2SC phase exhibit a mass () in the MeV range.
Crucially, in the 2SC phase, it can be demonstrated that LGBs are electromagnetically unstable and decay into photons via the process (by coupling with virtual quark loops, which carry the electric charge). With a reasonable choice of QCD parameters, the 2SC phase accommodates LGBs with a mass of approximately MeV.
During the post-BBN epoch, where , the decay of these MeV-scale LGBs generates a narrow, mono-chromatic ∼2 MeV line. This line emission presents a promising avenue for potentially resolving the enduring 7Li problem.
The total mass of SQCs required to address the 7Li problem is comparable to the observed value of dark matter (DM) in the universe. Furthermore, the distinctive properties of SQCs—being colorless, cold, charge-neutral, optically thin, and decoupled from hadrons—position them as a plausible candidate for Cold Dark Matter (CDM).
We propose that the decay of LGBs within SQCs may lead to the destabilization of the in-SQC Quantum QCD vacuum. This destabilization, in turn, causes the in-SQC vacuum to undergo quantum tunneling into the external (trivial) vacuum of space-time, a phenomenon we refer to as “leakage”. Notably, this leakage process involves the transition to a vacuum state characterized by vanishing QCD (quark and gluon) condensates.
The tunneling of the in-SQC QCD vacuum, behaving as Dark Energy (DE), occurs in the exterior space-time within our model. At low redshifts, the cosmological behavior aligns with the CDM model. Therefore, in our model, the loss of gluonic content from SQCs due to LGB decay not only provides a potential solution to the 7Li problem but also triggers the leakage process, leading to a cosmological scenario encompassing both Cold Dark Matter (CDM) in the form of SQCs and Dark Energy (DE) arising from the tunneling of the in-SQC QCD vacuum.
The paper is structured as follows: In Section 2, we provide the derivation of the equations concerning the destruction of 7Be through interaction with a 2 MeV monochromatic line. We explore the possibility of generating such a line through a lukewarm twi-flavor superconducting (2SC-like) quark phase, where a fraction () of the gluonic energy is converted into 2 MeV photons. The leakage phenomenon of the in-SQC QCD vacuum, involving a fraction () of the SQC mass, is examined in Section 3. Here, we present the resulting cosmology and discuss how it may offer a plausible resolution to the Hubble tension, a discrepancy in the measurement of the expansion rate of the universe. In Section 4, we delve into the discussion of SQCs as a candidate for Cold Dark Matter (CDM). We analyze their properties and explore their viability as a constituent of the cosmic dark matter content. The limitations and predictions of our model are outlined in Section 5, offering insights into the boundaries and potential implications of our proposed framework. Finally, we conclude the paper in Section 6, summarizing the key findings and discussing the broader implications of our model.
2. Post-BBN 7Be Destruction
In our model, the CSC phase produces gluon condensation (i.e., MeV mass LGBs), which decays to 2 MeV mono-energetic photons. To ensure that the energy of the 2 MeV line remains below the pair-creation threshold, we impose the condition 2 MeV < 12 MeV/, which translates to keV. In other words, the QCs enter the color superconducting (CSC) phase and transform into SQCs during the radiation-dominated post-BBN era. Henceforth, quantities labeled with the letter “G” pertain to values associated with the LGB-decay/photon-burst event. This event occurs when the age of the universe exceeds approximately 10 h, corresponding to a redshift .
The formation of LGBs takes place on a timescale comparable to that of hadronic processes when QCs enter the CSC phase. Subsequently, LGBs decay into photons almost instantaneously, with a timescale of s, significantly shorter than the Hubble expansion timescale (as discussed in Section 2.1).
Subscripts “sG” and “eG” refer to the start and end, respectively, of this LGB-decay phase, denoted by and . The duration of this phase is approximately equal to the LGB decay timescale, i.e., . Consequently, we have , where is much smaller than . Effectively, this implies that , indicating that the redshifts at the start of, during, and at the end of the LGB-decay phase are approximately equal.
The photon production is a delta function, , which in our model is at time . As shown in Appendix B, the destruction rates for 7Be nuclei due to such a sudden release of mono-energetic photons is
where Y is the abundance. Here, is the universe’s co-moving baryon number density at , while is the co-moving number density of photons from the LGB decay. The 7Be photo-dissociation cross-section is and is the Compton scattering cross-section. A reduction in 7Be by 2/3 imposes that the RHS in Equation (1) is unity (i.e., ∼−1.1).
Let us define as the initial total amount in mass of SQCs (the DM in our model) compared to baryons, i.e., before LGB decay. The corresponding SQC co-moving number density is
with the cluster’s baryon number. The emitted photons co-moving number density is then
with as the total number of photons emitted per SQC. Here, is the fraction of the gluonic energy per equivalent proton rest mass converted to the mono-chromatic line at energy ; is the proton mass.
Equation (1) becomes
where, in order to obtain the last expression, we made use of the fact that the SQC total mass after conversion of gluonic energy to photons is or .
The 7Be photo-dissociation cross-section, , is given by Equation (III.8) in Ishida et al. [16]. The ratio of to Compton scattering cross-section, , varies widely, as shown in Figure 1. We see that for MeV, we have . If the SQC total mass after the conversion of gluonic energy to photons is the observed CDM amount, , then . In this case, the 7Li problem is solved if , meaning
which requires that on average ∼50% (i.e., ) of the SQCs gluonic energy is converted to MeV photons.
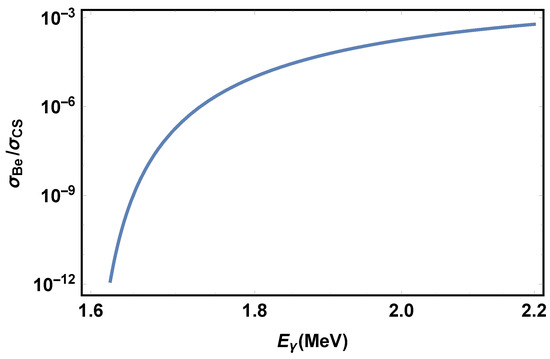
Figure 1.
The ratio versus photon energy. The 7Be photo-dissociation cross-section is from Equation III.8 in [16]. The Compton scattering cross-section is given in Appendix (IV) in [10].
As explained later in Section 5, the value of can be lower (less gluonic energy shed by SQCs) while still solving the 7Li puzzle. This is because, in addition to losing gluonic energy via LGB decay, SQCs will lose more during the leakage of its QCD vacuum so that if in today’s universe (the subscript “0” refers to values at redshift ), then must have been higher due to leakage (see first bullet point in Section 5).
It is crucial to emphasize the requirement for a narrow band emission, preferably a mono-energetic photon source, in order to maximize the number of photo-dissociated 7Be nuclei (as described by Equation (1)). Without such a narrow emission, there would not be sufficient gluonic energy available from the SQCs—which serve as the dark matter (DM) in our model—to achieve the desired 2/3 reduction. In this context, the decay channel of LGBs presents an appealing mechanism for generating such a narrow emission (see Appendix C). The feasibility of this mechanism can be tested in ongoing experiments (as indicated in bullet point #5 in Section 5).
2.1. The Mono-Chromatic ∼2 MeV Line
The QCD phase diagram is complex (e.g., [17,18,19]), and in principle, one cannot exclude the existence of a CSC phase where gluon condensation would yield electromagnetically unstable X “particles” (here LGBs), as required in our model. Figure 2 shows a hypothetical phase diagram with the dashed line depicting a possible trajectory leading a quark cluster from its state at birth (in an unpaired phase) to the CSC phase. We require an unpaired phase at chemical potential , which bridges the hadronic phase and the CSC phase. That is, the CSC phase is accessed, at low T, from a low-density unpaired phase with a first-order line separating the two phases. Once in the CSC phase, a cluster becomes a SQC and produces LGBs in the radiation-dominated post-BBN epoch at keV temperatures.
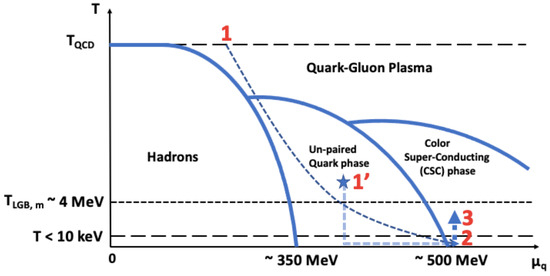
Figure 2.
A possible QCD phase diagram; temperature versus quark chemical potential. The dashed curve (“1 to 2”) depicts the cooling path of the quark cluster (formed at “1” with 150 MeV) traversing the unpaired phase and entering the CSC phase, at a keV temperature, from the low density phase (“2”). A first-order line separates the unpaired phase from the CSC phase releasing heat (the vertical “2 to 3” arrow). A SQC is heated to a temperature not exceeding the LGB melting temperature (see Section 2.1). The ∼4 MeV LGBs decay to the 2 MeV narrow photon line via . “” shows the initial state of a NS core making its way to “2” via cooling and compression (see Section 5 and Appendix C).
In this paper, we will use the neutral 2SC phase as a reference CSC phase. It has the interesting property of converting a percentage () of its gluonic energy to LGBs (i.e., gluonic condensation) at low temperature with a subsequent decay to a mono-chromatic line via the channel (see Appendix C for details). In the 2SC phase, an LGB with mass MeV would decay to two MeV photons on timescales of s. We set the CSC quark chemical potential at MeV with a corresponding number density cm−3. Thus, the density inside an SQC is , which is about ten times nuclear saturation density when it enters the CSC phase at time ; should not to be confused with the SQC co-moving density given in Equation (2).
Once the cluster crosses into the CSC phase, the first-order transition proceeds on hadronic timescales. During the transition, and because of latent heat released, an SQC is heated to a temperature , where is the CSC superconducting gap; here, and are in units of MeV (see Equation (A7)). LGBs cannot form at temperatures exceeding the melting temperature, which is on the order of the LGB’s rest-mass energy; . Thus we must ensure that in addition to MeV, where the 2.2 MeV upper limit keeps the line below the deuteron photo-ionization threshold (see Section 1). In general, for MeV, or , these conditions are satisfied. MeV is achieved for a reasonable range in , as shown in Figure 3. The width of the ∼2 MeV line is given in Equation (A8) in Appendix C, and for typical values, it is expected to be <0.1 MeV.
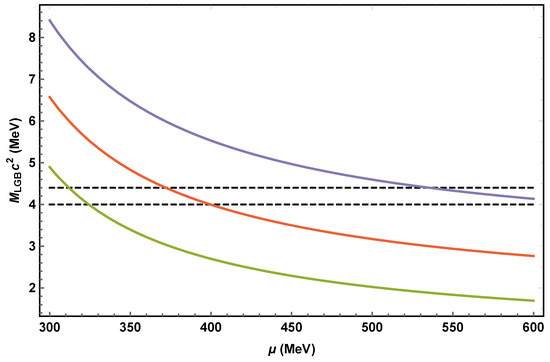
Figure 3.
LGB mass versus quark chemical potential () for MeV (the scalar parameter of QCD; see Section 2.1 and Appendix C for details). The curves from top to bottom are for , respectively. The two dashed lines show the range yielding a mono-chromatic photon line in the range. Using MeV, expected using the usual renormalization scheme with 3 quark flavors, we obtain MeV for (see Equation (A6)).
2.2. The SQC Size and Baryon Number
To the first order, the SQC’s photon mean-free-path is fm with as the Thomson cross-section for photon scattering off up and down quarks. By setting a typical SQC radius to be , the SQC is optically thin to all photons, including the 2 MeV photons. Being transparent to electromagnetic radiation of all energies, the SQC makes a good DM candidate (which is still within the standard model of particle physics) with a corresponding baryon number .
3. SQCs and Dark Energy (DE)
Both hadrons and SQCs exist as states within QCD, but they exhibit different symmetries associated with their respective vacuum states. Hadrons, as discussed in [20], are characterized by confinement in their vacuum state, while SQCs are influenced by the formation and decay of LGBs to photons, leading to distinct symmetries. In Appendix C.1, we discuss the confinement of the phase within SQCs, where the vacuum state is speculated to undergo a tunneling process, referred to as “leakage”, into the external trivial vacuum. This tunneling phenomenon is triggered by instabilities resulting from various mechanisms, including electromagnetic gluonic decay, such as the formation and subsequent decay of light gluonic bound states into photons in the CSC phase.
Although we chose to focus on the 2SC phase due to its simplicity, it is important to note that any CSC quark phase capable of converting gluonic energy into approximately 2 MeV photons and initiating a transition to the trivial vacuum could be equally effective in our proposed framework. This innovative concept offers an intriguing explanation for DE and establishes a cosmological framework that has the potential to address the Hubble tension while still yielding a universe consistent with the CDM model at low redshifts.
The total amount of confined QCD vacuum energy stored in the SQCs is with as the density of the QCD condensates and as the total volume occupied by the SQCs, which is constant in time (and assumed to not change on LGB decay). “Leakage” means that the density inside the SQC decreases from
at (at the end of the LGB phase denoted by “eG”) to
at redshift with the assumption that the leakage timescale is a fraction of the age of the universe Gyrs (see below). The parameter is a measure of the contribution of the QCD condensates to the SQC rest-mass energy; naturally, . At the start of the LGB phase (denoted by “sG”), we have .
We can obtain a rough estimate of the time (the e-folding time) it would take the in-SQC QCD vacuum to leak into the exterior space-time trivial QCD vacuum. A rigorous calculation would follow, for example Coleman [21], and is beyond the scope of this paper. We consider instead a simple tunnelling problem across a square barrier with height given by the expectation value of the QCD vacuum and width . The corresponding tunneling probability is then , where is the penetration depth (e.g., [22]). The tunneling timescale is giving us
where ; the tunneling timescale is highly sensitive to x. With on of the order of a Fermi (which is not unrealistic), solutions with tunneling timescales on the order of a billion years ( Gyr) require to be approximately 88 fm. If exceeds 90 fm, the tunneling timescale becomes longer than the age of the universe, . Furthermore, the size of the SQC cannot be too small for leakage to occur on astrophysical timescales, ensuring that . Therefore, an optimal range for the SQC radius is found to be , which is consistent with our model. It is worth noting that, in our model, optically thin SQCs with fm are required to address the cosmological 7Li problem.
We can then write the time evolution of the density inside the SQC as
The equation above incorporates the key parameters in our cosmology, namely, , and which are all fundamentally related to QCD.
The DM density in our model is the SQC density averaged over the volume of the universe. Its time evolution, with being the Hubble volume at time t, is
with the resulting cosmology analyzed in Appendix D.
Our model offers a resolution to the Hubble tension (see [23] for a recent review and references therein) and can be understood as a consequence of a CDM universe converting into a CDM universe at . Figure 4 shows that km s−1 Mpc−1 can be obtained for a range in and values with a leakage characteristic redshift (i.e., ). It is both noteworthy and encouraging that the timescale , which is tightly constrained by the size of the SQC at approximately 100 Fermi, coincides with the timescale required to address the Hubble tension. This convergence underscores the interconnection of these two phenomena.
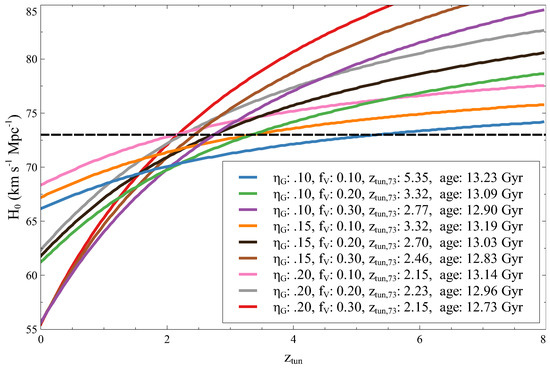
Figure 4.
The Hubble constant as a function of (the leakage characteristic redshift) in our model for different values of and . The km s−1 Mpc−1 value is shown as the horizontal line. The resulting age of the universe is shown for each case and is younger than the CDM universe.
Our cosmology yields a universe that is younger than the CDM universe with an age of ∼13 Gyrs with and with percentages each on the order of tens. It remains to be shown whether our cosmology is in agreement with other cosmological data and measurements, which the flat CDM model explains extremely well (see e.g., metrics and tests suggested in [24]). Furthermore, we caution that the details of how the QCD vacuum mixes with the space-time vacuum and how it evolves while preserving flatness remain to be understood. Nevertheless, being a vacuum, the “DE” component in our model should obey an equation-of-state with parameter .
4. SQCs as Cold Dark Matter (CDM)
Evidence for CDM is abundant, but its nature remains unknown despite many theoretical investigations and dedicated experiments, which have yet to detect any associated particle (e.g., [25,26,27,28,29,30]). In our model, the 7Li problem is solvable if the total mass in SQCs is on the order of the measured CDM value. In addition, SQCs are colorless, cold, optically thin, and electrically neutral and would make an ideal CDM candidate if they decouple from the strong force (or interact minimally with baryons) following leakage.
We have put forward the argument that SQCs that have undergone tunneling would decouple from hadrons, resulting in their interaction being solely gravitational in nature. Consequently, these tunneled SQCs would elude detection in current dark matter (DM) experiments. In the pre-LGB era, QCs should possess a sufficiently extended lifespan, allowing them to persist into the post-BBN era at without experiencing any growth in size due to interactions with hadrons. The rate at which non-tunnelled SQCs interact with hadrons depends on the fraction of SQCs that have survived until the present time. For instance, for a tunneling timescale of Gyr, this survival fraction is , and it drops significantly to for Gyr. Below, we employ the term “baryon” specifically to refer to non-QC baryons (e.g., protons), allowing us to examine the interactions of QCs and SQCs with hadrons during these two distinct epochs.
4.1. The Pre-LGB Era
In the pre-LGB (i.e., pre-SQC at ) epoch, QCs should interact with baryons. The QC-baryon reaction rate is , with as the baryon’s number density and ; is the baryon-to-photon ratio. The QC-baryon interaction cross-section is , while the QC-baryon relative velocity is dominated by that of baryons; c is the speed of light, and the proton mass. For the QC not to grow in size in the pre-LGB era (i.e., up to ), we impose . With , we have so that gives
i.e., with .
The above ensures that the QC will neither grow in size in the pre-LGB era nor interact with baryons in the subsequent periods where baryons are more diffuse. We can express the effective cross-section in terms of the geometric one as . Here, is the baryon QC crossing time, and is the conversion timescale of a baryon to the CSC phase (i.e., for a baryon to be absorbed by the QC). The ratio accounts for the fraction of time the baryon spends inside the QC. With , the condition in Equation (11) translates to ; here cm−3 is the QC’s density.
The fact that the conversion timescale exceeds the timescales associated with strong interactions provides support for the notion that the QC state is distinct from the hadronic phase. Alternatively, it suggests that the conversion process may involve two steps, where the baryon first undergoes deconfinement, possibly requiring an injection of energy, before transitioning into the unpaired quark phase characteristic of QCs. Another interpretation is that quarks within a hadron, where chiral symmetry is broken, perceive the QC as a distinct and separate phase of quark matter even before it becomes an SQC. This intriguing aspect highlights the complexity and richness of the underlying physics involved in the conversion process and the distinct properties of QC and SQC phases.
4.2. The Post-LGB Era
From this point forward, when we refer to SQCs, we are referring to the clusters that did not undergo tunneling. The SQCs that have undergone tunneling, on the other hand, constitute the dark matter (DM) component within our proposed model. To impose a constraint on the SQC–baryon interaction cross-section , we will utilize the measured lower limit on the proton lifetime ( years; [31]). This lower limit on the proton lifetime provides valuable information about the strength of the SQC–baryon interaction and allows us to further refine our model.
The SQC reaction rate per baryon is , and is the SQC–baryon relative velocity. The SQC co-moving number density (not to be confused with the SQC density cm−3) is
where GeV cm−3 is the local DM density [32], which is that of the tunnelled SQCs in our model. Imposing and using km s−1, we arrive at
i.e., with .
Consistent with expectations, the aforementioned analysis reveals that the efficiency of tunneling, indicated by the presence of fewer remaining SQCs today, directly correlates with the permissible range for the SQC–baryon interaction cross-section . Specifically, a more efficient tunnelling process allows for a higher allowable value of . This relationship underscores the significance of the tunneling mechanism in influencing the interaction dynamics between SQCs and baryons within our model. In terms of the baryon-to-SQC conversion timescale (to be differentiated from the conversion of a baryon to a QC above), and with , we obtain .
In Section 3, we have established that a cosmological model capable of resolving the Hubble tension and simultaneously yielding the observed age of the universe necessitates a tunneling timescale of approximately one gigayear (Gyr), corresponding to an exponential suppression factor of . Consequently, this implies that , or equivalently, that the conversion timescale exceeds s.
Intuitively, assume would imply or Gyr, which is also consistent with our cosmology. We caution, though, that making direct comparisons between the QC and SQC states may not be justified. We should add that if SQC vacuum leakage is not a simple tunneling process, then it can deviate from a pure exponential process (e.g., [33]), which could affect our findings here. This is left as an avenue for future research.
Furthermore, we can employ neutron stars (NSs) to impose even more stringent constraints on the SQC–baryon cross-section by studying the interactions between SQCs and baryonic matter within an NS. If , the SQC slows down inside the neutron star and is captured. For typical neutron star parameters, such as cm−3 and cm, the condition for no capture implies that . Referring to Equation (13), this condition is always satisfied if , indicating that neutron stars will not be converted through SQC capture. For an NS formed at time , the mass of SQCs that accumulate over the Hubble time can be estimated as . Here, we assume a SQC–neutron star relative velocity of cm s−1 and a representative local DM density of GeV cm−3. Thus, even if a certain amount of SQC is captured, it is not evident whether it would be sufficient to convert a neutron star.
Due to the likelihood that the leakage timescale exceeds the typical timescale for the formation and subsequent collapse of structures during the early universe, we anticipate that primordial halos will be predominantly composed of non-leaked SQCs that formed after the light glueball (LGB) era. Baryonic matter will gravitationally accrete onto these halos, but as demonstrated earlier, the diffuse baryons will not interact with either leaked or non-leaked SQCs. However, we anticipate a critical change or “phase transition” in the growth of structures after the time This is because (i) a significant fraction of the SQCs’ mass is converted into Dark Energy (DE), and (ii) the SQCs would have decoupled from hadrons. Understanding the precise impact of these effects on subsequent structure growth requires more advanced investigations beyond the scope of this paper. Only state-of-the-art Cold Dark Matter (CDM) simulations, which incorporate the leakage of SQC mass as detailed in Appendix D, can provide insights into this aspect of our model.
To summarize, SQCs present a viable candidate for Cold Dark Matter (CDM) and may play a role in the formation of both mini-halos and larger structures in the universe, as indicated in previous studies [34,35]. Once halos form and reach a state of virialization, SQCs are expected to interact most strongly with stars, particularly with matter at high densities, such as neutron stars (NSs). However, if the tunneling timescale is a small fraction of the age of the universe, as suggested earlier, then SQCs would have decoupled from hadrons by the time compact stars begin to form (as discussed in Section 3). In other words, even the densest stars, such as neutron stars, are unlikely to undergo conversion through the capture of SQCs. However, if the cores of neutron stars can access the Color Superconducting Quark matter (CSC) phase through phenomena like cooling and mass accretion, it could have intriguing implications for astrophysics (as shown in Equation (18)). This possibility opens up new avenues for research in understanding the behavior and properties of neutron stars within the framework of our model.
5. Discussion
Here, we briefly discuss some limitations and distinctive features of our model and leave these as avenues for future investigations.
- 1.
- The evolution of the SQC and of the DM densities: We first recall, from Equation (9), that the density inside an SQC evolves from to after the LGB phase. Leakage further decreases the SQC density to an asymptotic value of at (which we associate with ). The minimum possible value of an SQC would be given by the bare quarks masses, or % of their original mass. However, we find and to be on the order of tens of percent each (see Section 3), and an SQC would lose a fraction of its mass to DE over the age of the universe. Meaning that the DM content in today’s universe is a fraction of that in the pre-BBN era according to our model.Averaging the total SQC mass over the Hubble volume gives us the DM density in our model. The ratio of the total amount of DM to that of the baryonic matter evolves from a maximum value of before LGB decay to after the LGB decay to photons just before leakage starts. At full leakage, which we associate with , the ratio isAssuming as measured today and extrapolating back to the LGB era, it means that the amount of DM content is larger than what we used in Section 2, where we set (i.e., when taking ).
- 2.
- The 7Li problem revisited: The solution to the cosmological 7Li problem presented in Section 2 did not take into account the further loss of gluonic energy due to in-SQC vacuum leakage following LGB decay as discussed above. From Equation (14), and when plugged into Equation (4), we obtainEquation (5) becomesThat is, a smaller percentage of the gluonic energy of the SQCs converted to LGBs could resolve the 7Li problem. For , we recover the values we arrived at in Section 2, while for , we obtain , which is less than the maximum expected from the 2SC-phase.The ratio between the DE density and the DM energy density at is (from Equation (7)),To have as measured in today’s universe requires , in which case Equation (14) gives and . On the other hand, the resolution of the Hubble tension suggests that a favored parameter combination lies around , as illustrated in Figure 4. This discrepancy could potentially be mitigated by relaxing some of the approximations made in our cosmological model or by adopting a more realistic approach to the tunneling process, moving beyond the simple assumption of exponential decay.
- 3.
- The CSC phase and neutron stars: Figure 2 shows a suggested pathway, starting at point “”, an NS core could take to enter the CSC phase since conversion following SQC capture is suppressed (see Section 4). An NS born with (or which acquiring through evolution) a core in the unpaired phase could transition to the CSC phase by a sequence of cooling (to keV temperature via the URCA process, e.g., [36]) and compression (to MeV via mass accretion). Take an NS with a core making up a fraction of the total mass. The energy released from the conversion of gluonic condensation (e.g., LGBs) to photons is . Comparing this to the NS binding energy , we conclude that NSs with compactness parametermay be completely obliterated in the process; the NS mass and radius are in units of solar mass, , and cm, respectively. NSs with higher compactness parameters would lose mass, leaving behind a pure CSC core. In this latter case, the conversion to a CSC star puts a constraint on due to the black hole limit 2 with as the radius of the CSC star. With , this gives which is consistent with the MeV (i.e., a 2SC-like phase) adopted in our model. Thus, if some NSs follow a path as suggested in Figure 2, the resulting photon fireball may have interesting implications for explosive astrophysics.
- 4.
- SQC–hadron decoupling: Following the leakage and loss of more gluonic energy, it is not unreasonable to assume that the quarks within the SQC become undressed and should in principle decouple (or at least experience some level of decoupling) from the strong interaction. They would still rely on gluons to remain bound while exhibiting minimal interaction with hadrons. We speculate that DM and hadrons may represent separate phases of quark matter within the framework of QCD, characterized by distinct vacuum properties. If our model is correct, it allows a unique connection between cosmology and the properties of the QCD vacuum in the CSC quark phase. An estimate of the parameter from cosmological observations may be an indication of the contribution of the QCD condensates in CSC to the SQC mass, which may have implications, albeit indirect, to the mass of hadrons. The exact details of the SQC–hadron decoupling remain to be worked out.
- 5.
- SQCs and LGBs in today’s detectors: SQCs (the DM in our model; see Section 4) would interact only gravitationally and would thus evade detection in current DM experiments. Instead, we propose that our model can be tested by experiments that can access the 2SC phase at temperatures below the LGB melting temperature; i.e., at MeV (see Appendix C). The Compressed Baryonic Matter experiment (CBM) at FAIR explores the QCD phase diagram in the region of high baryon densities (representative of neutron star densities) and moderate temperatures using high-energy nucleus–nucleus collisions (e.g., [37,38]). We note that the 2SC phase carries MeV LGBs (i.e., can solve the cosmological 7Li problem) at a baryonic density as low as a few times that of nuclear matter (see Figure 3) and that LGBs form on strong interaction timescales and decay to MeV photons on timescales of ∼ s. Thus, experiments such as the CBM at FAIR could potentially be used to detect the photons from the LGB decay.The width of the line can be found in Equation (A8) in Appendix C, and for typical values, it is expected to be <0.1 MeV. If this width were to be measured, it would provide a direct estimation of the 2SC dielectric constant, which could then be used to infer the ratio and consequently determine (as per Equation (A8)). However, it remains unclear whether and how the CBM experiment could explore the temperature regime relevant to our study. More significantly, the 2 MeV line may be overshadowed by the anticipated high low-energy electromagnetic background in high-energy ion–ion collisions. Even if the background were to diminish as the QGP transitions into the 2SC phase and subsequently cools down to the LGB phase ( MeV), detecting the 2 MeV line would likely prove challenging. Calculating the strength of the LGB 2 MeV line is beyond the scope of this paper.
- 6.
- The stability of the CSC phase: Our findings seem to hint at the standard neutral 2SC phase (adopted in our theoretical framework) as the unspecified CSC phase. However, the 2SC phase may be unstable at small superconducting gap () values due to the mismatch in the up and down quarks chemical potential [39]. It suggests that either the 2SC phase is stable in the regime of chemical potential () and values we used or that another stable 2SC-like phase exists in nature and remains to be identified. A 2SCus phase, which has u-s pairs instead of u-d pairs, is also a candidate. This phase, however, faces a similar challenge in that the u and s Fermi momenta are split apart by the strange-quark mass (combined with electrical neutrality; e.g., [40]). The color-flavor-locked phase may be one candidate if the strange-quark effective mass is small or alternatively a crystalline quark phase if strange-quark mass is heavier (e.g., [41]). However, these phases do not possess properties that allow for the conversion of gluonic energy to photons. Despite its limitations, the u-d 2SC phase remains one of the candidate phases for dense quark matter (adopted in our model), pending the determination of its exact phase structure.Another possibility is collective excitations (i.e., phonons) of SQCs, which would decay directly to photons via phonon-to-photon conversion channels. Mono-chromatic photons of energy MeV would result if the SQC radius were fm. Physically, the decaying particle is not an LGB but is instead a long-wavelength mode that is resonant with the quark cluster containing it. In this scenario, higher resonant modes should also be excited, and these could affect the very sensitive D abundance, which is not desired. Superconducting strings [42] are an interesting avenue to explore in this context. If such domain walls could form during the cosmic QCD phase, one could imagine a scenario where they would evolve into 2SC-dominated strings in the post-BBN era. It remains to be shown that LGBs as described in our model could form in this case.
- 7.
- Matter–antimatter annihilation and SQC size: We hypothesize that each quark cluster is born with an anti-matter deficit of , meaning that there is one extra baryon per quark–antiquark pair; is the baryon-to-photon ratio. After annihilation (on timescales of s with mbarn), a cluster has only baryons left in it; this assumes that annihilation does not destroy the cluster, and instead it reduces it into a pure baryon cluster of radius where “f” stands for final. Here, fm is the typical size of an SQC set by the photon mean-free-path in the 2SC phase. In other words, we claim that the maximum size of the “shrapnel” of the annihilated much bigger parent cluster is on the order of (see Section 2.2). In this case, a cluster’s birth radius can be obtained from , which gives fm. Some constraints and implications to consider in the future include the following. (i) Annihilation should also yield pions. These would decay on weak-interaction timescales, and if their mean-free-path turns out to be much smaller than that of photons, they may affect the ∼ fm SQCs. (ii) While cluster formation (when the universe has aged such that its temperature is in the tens of MeV) is followed rapidly by annihilation, we must avoid the re-creation of matter–antimatter pairs, i.e., ensure that pair-creation timescales exceed the Hubble expansion timescale. (iii) In the framework we outline here, SQCs would require a formation mechanism that is different from that of the much larger cosmic strange-quark nuggets [14] (which require a first-order QCD phase transition) and Axion quark nuggets [15] (which require their co-existence with Axions). Additionally, the mechanism by which these nuggets can convert their stored gluonic energy into MeV photons is a serious limitation.
6. Conclusions
We have proposed that a color superconducting (CSC) phase of lukewarm QCD matter could offer a non-exotic solution to the cosmological 7Li, the CDM, and the Dark Energy enigmas. We attribute the narrow 2 MeV photon line that destroys 7Be in the radiation-dominated post-BBN epoch to gluonic condensation (i.e., light glueballs or LGBs) in the CSC phase and its electro-magnetic decay modes (Section 2). The detailed properties of the CSC phase remain to be scrutinized, although a neutral 2SC-like phase with a superconducting gap is hinted at.
CDM, according to our model, consists of colorless, charge-neutral, optically thin cosmic quark clusters in the CSC phase (SQCs) with fm in size and baryon number . They decouple from hadrons and interact only gravitationally, thus evading detection in current DM experiments. If SQCs could be produced in experiments such as the Compressed Baryon Experiment at FAIR (see bullet point #5 in Section 5), they could be detected via the MeV photons from decay, giving support to our model.
The decoupling of SQCs from hadrons is due to the leakage of the in-SQCs vacuum into the trivial vacuum of the exterior space-time, which yields DE. As leakage proceeds, our cosmology gradually transitions from a non-DE to a DE (CDM-like) universe at a moderate redshift while allowing for a possible resolution of the Hubble tension (Section 3). It is crucial to recognize the significance of having optically thin SQCs with a size on the order of 100 Fermi in resolving the 7Li problem. This requirement directly sets the timescale for the tunneling process to be on the order of a Giga-year. The connection between the Fermi scales, which govern particle interactions, and the astrophysical scales suggests a fundamental connection between the 7Li problem and Dark Energy (DE) unique to our model.
Our model does not introduce new physics to solve the 7Li, DM, and DE problems but instead makes use of still uncertain properties of QCD phases and their vacuum properties. We are not the first to discuss a connection between QCD vacuum and cosmology. It has been argued based on the empirical properties of hadrons that confinement is a prerequisite for retaining condensates inside hadrons, which then largely eliminates the problem of the smallness of the cosmological constant. On the other hand, our model introduces the concept of the tunneling of the in-SQC vacuum into the exterior trivial vacuum and the decoupling of SQCs from hadrons (see Section 3). This distinctive proposition raises the intriguing possibility that DM and hadrons could represent separate phases of quark matter within the framework of QCD, characterized by distinct vacuum properties that may turn out to have other useful physical applications.
Author Contributions
Conceptualization, R.O. and P.J.; Methodology, R.O. and D.L.; Formal analysis, R.O. and N.K.; Investigation, R.O.; Writing—original draft, R.O.; Writing—review & editing, R.O., D.L., N.K. and P.J. All authors have read and agreed to the published version of the manuscript.
Funding
R.O., D.L. and N.K. acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC). P.J. is supported by a grant from the Natural Science Foundation PHY-2310003.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We thank R. Rapp for interesting discussions on various aspects of the paper. R.O. thanks P. Serpico for their brief comments on Appendix A. We thank the referees for their insightful comments and suggestions, which improved the quality and rigor of our paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Pedagogical Framework
Appendix A.1. A Quantum Chromodynamics (QCD) Phase Diagram
QCD is the theory governing the strong nuclear force. Figure A1 shows a simplified QCD phase diagram in the T- (temperature vs. quark chemical potential) plane featuring three distinct phases. The chemical potential is related to the number density by . At low temperatures and densities is the confined phase, where quarks and gluons are bound within color-neutral hadrons, such as protons and neutrons. In this phase, quarks are unable to exist freely as individual particles. As the temperature and/or density increases, the QCD phase diagram exhibits a transition to a deconfined phase called the quark–gluon plasma (QGP). In the QGP phase, quarks and gluons move more freely and are not confined within hadrons. Lattice simulations have shown that there is a smooth transition (a cross-over) between the confined hadronic phase and the deconfined quark–gluon plasma phase (see [43] for a recent review). Unlike a first-order phase transition, where there is a distinct jump in thermodynamic quantities at a critical point, a cross-over is characterized by a gradual change in the system’s behavior. This means that there is no precise temperature at which the transition occurs, but rather a temperature range over which the transition takes place.
At higher densities (or chemical potential) and lower temperatures is the color superconductivity (CSC) phase. This phase is characterized by the condensation of Cooper pairs of quarks, similar to how electrons form pairs in traditional superconductors. A CSC is characterized by its superconducting gap ( in the tens of MeV range), which is the energy required to break a Cooper pair. The vacuum ground state energies in the CSC and hadronic phases are drastically different. The formation of Cooper pairs alters the QGP, leading to changes in the gluon spectrum and dispersion relations. It has been demonstrated that the CSC is the ground state of quark matter at asymptotically large densities (e.g., [18]).
The simplest form of CSC is known as two-flavor color superconductivity (2SC), which arises in QCD when quarks of two different flavors (usually up and down quarks) form Cooper pairs due to the attractive interaction mediated by the strong force. The Cooper pairs in the 2SC phase are made of the red and green quarks only, and the blue quarks do not participate in pairing. Only five out of a total of eight gluons become massive, while the other three gluons remain massless and do not interact with the paired red and green quarks nor with the gapless blue quarks. These three gluons obey their own gluon dynamics and form their own condensate made of bound states of pure gluons, similar to how mesons are bound states of quarks and antiquarks. This gluon condensate is unstable electromagnetically and emits photons. The decay process of the electrically neutral condensate into photons occurs through its interaction with virtual quark loops, which carry the electric charge (see Appendix C). This electromagnetic decay plays a crucial role in resolving the cosmological Lithium-7 problem within our model, as explained in the following description.
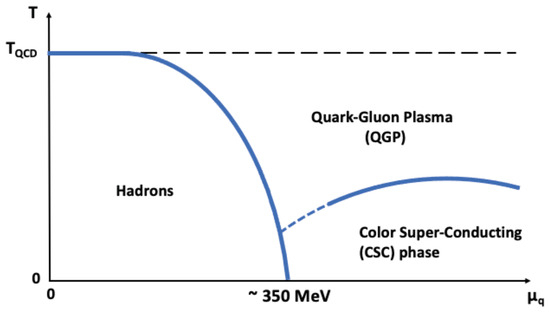
Figure A1.
A simplified QCD phase diagram in the density–temperature plane; the density is represented by the quark chemical potential . The hadronic phase exists at a temperature of MeV and chemical potential MeV. The dashed line in the diagram represents unexplored phases that could potentially exist within the QGP phase before reaching the CSC phase.
Appendix A.2. Our Model in a Nutshell
The cosmological lithium-7 (7Li) problem relates to a significant discrepancy on a factor of 3 between the predicted abundance of cosmological beryllium-7 (7Be) and the lower measured abundance of 7Li in the universe. In this context, we present a proposal for a non-exotic electromagnetic solution within the standard model of particle physics to address the cosmological 7Li problem, a crucial element in the theory of Big Bang nucleosynthesis (BBN). Our model utilizes properties of deconfined quark matter to offer a potential solution to the enigma of 7Li. Additionally, we explore the interconnectedness of this solution with the problems of Dark Energy (DE) and dark matter (DM), all of which highlight our limited understanding of the quark–gluon plasma (QGP) and the phases of quark matter as described in QCD.
At the core of our model lies the conversion of the gluonic energy (i.e., of the gluons) of superconducting deconfined quark matter into a narrow 2 MeV line, capable of selectively destroying primordial 7Be without impacting other products or the physics of the cosmic microwave background (CMB). One key assumption in our model posits that, in addition to the known hadrons (protons, neutrons, and mesons) formed during the QCD phase transition in the early universe, assemblies of deconfined quark matter, referred to as quark clusters (QCs), can also form. These QGP clusters have a size of approximately 100 Fermi (and are thus optically thin to photons) and are composed of up and down quarks and gluons in proportions that make them charge-neutral. Inside a QC, the density reaches approximately ten times the nuclear saturation density, which is on the order of cm−3 (equivalently, MeV). This high-density environment corresponds to a baryon number, with .
The second key assumption in our model is that these QCs transition into a color superconducting state (CSC) in the post-BBN era, when the universe is a few hours old, at a redshift of . The two-flavor color superconductivity (2SC) phase specifically involves two flavors of quarks, typically up and down quarks, as seen in QCs. When QCs reach this phase and become superconducting (referred to as SQCs), a percentage of their gluons form light glueballs (LGBs). Glueballs are bound states of gluons, analogous to how mesons are bound states of quarks and antiquarks. LGBs are considered to be relatively light, with a mass in the MeV range, compared to other possible glueball states with masses in the GeV range. LGBs are electromagnetically unstable, and by appropriately selecting 2SC parameters, they can decay into a monochromatic ∼2 MeV line, capable of selectively destroying primordial 7Be while leaving other BBN products and CMB physics unaffected.
To resolve the 7Li problem, approximately 20–30% of the gluonic energy in SQCs needs to be converted into a monochromatic 2 MeV line. Interestingly, the total mass of SQCs required for this solution corresponds to the observed DM in the universe. SQCs, being cold, colorless, charge-neutral, and optically thin to all photon energies, present an attractive DM candidate that is deeply intertwined with the enigma of 7Li. We would like to emphasize the necessity of a narrow band emission (preferably a mono-energetic photon source) to optimize the number of photo-dissociated 7Be nuclei (see Equation (1)). Otherwise, there will not be enough gluonic energy from the SQCs (the DM in our model) for the 2/3 reduction. The LGB decay channel is an attractive mechanism for such a line (see Appendix C) and may be tested in current heavy-ion collision experiments (see bullet point #5 in Section 5).
The nature of the QCD ground state continues to be a topic of active research and debate. There are many possible forms of the ground state wavefunction (in a many-body variational approach). Even when comparing the many ground states using free energies, one can never be certain that the true ground state is found (see discussion in [44]). In principle, the vacuum state within SQCs after the formation and decay of LGBs can potentially exhibit different symmetries compared to the vacuum state of confined quark matter in hadrons; see Appendix C.1. This brings us to the third assumption in our model, which has implications for DE. By assuming that the in-SQC QCD vacuum becomes unstable following LGB decay, we allow it to “leak” into the trivial vacuum of the surrounding space-time via quantum tunneling (Appendix C.1). This “leakage” process behaves as a cosmological constant and occurs late in the evolution of the universe (at a redshift of a few units), leading to a transition to a CDM-dominated era (see Figure 4). This “leakage” effectively separates the pre-CDM and CDM phases and offers a potential resolution to the Hubble tension (see Section 3).
Through our efforts to resolve the 7Li problem, we have uncovered a solution that effectively tackles the challenges of DE and DM, thus revealing the intrinsic connection of these critical cosmological issues within our proposed model. For example, the in-SQC vacuum would be stable to decay if its gluonic sector were stable (as in hadrons). The cosmological 7Be nuclei act as absorbers of LGB decay products (with the 2 MeV photons ideal in this scenario) and avoid affecting BBN and CMB properties. Without addressing the 7Li, DM, and DE problems simultaneously, our model would not hold together. Despite its assumptions and limitations, it is important to reiterate that our framework operates within the standard model of particle physics but in an unexplored regime of QCD, emphasizing the need for further investigation and empirical validation.
Appendix B. Post-BBN 7Be Destruction
In Poulin & Serpico [11] (and references therein), the photon-generating particle X decays exponentially on timescale and forms at an early time in the universe at t. In our model, the X particle (i.e., the LGB) forms and decays to a narrow 2 MeV photons nearly instantaneously in the radiation-dominated post-BBN era at time when the quark cluster enters the CSC phase; here, “G” stands for gluons as a reference to the LGB era (see Section 2). Thus, we have a delta function production at time ; . The source injection term (e.g., Equation (2) in Poulin & Serpico [11] and Section IV in Kawasaki & Moroi [10]) becomes
with as the co-moving photon density at time t; is the spectral shape factor for a monochromatic line at .
Making use of Equations (4) and (5) in Poulin & Serpico [11] with the destruction of element A only (i.e., ) gives the abundance
where and are the photon interaction rate and the photo-dissociation cross-section, respectively. The interaction rate is for all processes, including the Bethe–Heitler pair-creation on nuclei, double photon pair-creation, scattering off thermal background photons, and Compton scattering. Red-shifting is negligible because the rates of electromagnetic interactions are faster than the cosmic expansion rate.
This assumes a single scattering (, as in our model) is enough to make the photon no longer dissociate a 7Be nucleus. Otherwise, should be divided by .
Dissociation starts at redshift and ends abruptly at redshift with ; subscripts “eG” and “sG” stand for end and start, respectively, of the photon burst from LGB decay in the post-BBN era. After integration over a very small time t with and but , one obtains
where is the co-moving number density of photons from LGB decay. Here, while and are the corresponding 7Be abundances.
With MeV, the Bethe–Heitler pair-creation on nuclei (see Equations (4)–(356) in [5]) is negligible, and so is pair creation off the CMB background photons when is a few keV or less; the interaction rate is dominated by Compton scattering (CS). Thus, with the CS cross-section given in Appendix (IV) in Kawasaki & Moroi [10]. Furthermore, because at keV, positrons are negligible (e.g., Appendix C in [45]), the total electron density is on the order of the baryon number density, . The destruction rates for 7Be nuclei due to a sudden release of mono-energetic photons at becomes
Appendix C. Light Glueballs (LGBs) in the 2SC Phase
The spectrum in the 2SC state is made of five massive gluons with a mass of the order of the gap , three massless gluons, and gapless up and down quarks in the direction 3 (blue) of color; in this appendix, we use QCD natural units with ħ . The three massless gluons in the 2SC phase do not interact with the gapless blue quasi-particles and the quasiparticles from the green and red paired quarks decouple from the low-energy confined phase. The three massless gluons in the 2SC phase bind, or are confined, into LGBs when the temperature is below the melting temperature ([46] and references therein). That is, LGBs melt when the temperature exceeds the confinement value [47].
The LGB mass at is with the intrinsic scale associated with the theory. It is the confining scale of the gluon-dynamics in 2SC, and when , the one loop relation gives [48]
with and the coupling constant evaluated at ; is the scalar parameter of QCD and the number of relevant quark flavors. For and for MeV (expected from a pure gluonic theory), we obtain MeV for a range in quark chemical potential as shown in Figure 3. Using MeV expected using the usual renormalization scheme with three quark flavors, we obtain MeV when .
Once created, LGBs are stable against strong interactions but not with respect to electromagnetic processes. The two-photon decay mechanism of the electrically neutral LGB was estimated in [46] based on the saturation of the electromagnetic trace anomaly at the effective Lagrangian level. In other words, the coupling between the LGBs, which dominate the energy-momentum tensor at low energies, and two photons occurs through virtual quark loops which carry the electric charge. The decay occurs on timescale of [46].
The pairing energy density released during the unpaired-to-2SC phase transition is (e.g., [49,50]). Thus, during the transition, to a first approximation, an SQC is heated to a temperature
LGBs would not melt during the unpaired-to-CSC heating phase if , allowing for the to occur (see Section 2.1).
The LGBs within an SQC move with the same velocity, denoted as v, as the underlying gluons. The broadening of the line can then be expressed as
The last equality in the equation above means that the velocity is determined by the dielectric constant of the 2SC medium given as [48]. We see that yields (or ), which ensures a narrow line. The regime is also the reason that the LGBs are not dynamically important in the 2SC phase because their mass scale is relative to the in-vacuum case.
When , and . For instance, for MeV, where is required to obtain MeV, we have or MeV. It also implies that the range of falls between 2.0 MeV and 2.2 MeV, which aligns remarkably well with the range necessary to address the 7Li problem (see Section 2).
Appendix C.1. The Confined SUc(2) Phase and Its Vacuum
At temperatures below is the phase, which effectively constitutes partial confinement within the 2SC phase. The deconfined-to-confined phase transition, as the temperature decreases within the 2SC phase is of the second order (i.e., symmetry breaking has occurred; see [46] and references therein). The 2SC without LGB decay belongs to a different global symmetry, while after LGB decay, one is left with the confined , which breaks the -symmetry (see e.g., [51] for phase transitions in QCD). While the flavor symmetries and other (e.g., Poincaré) symmetries remain the same during the transition from deconfined-to-confined , the vacuum loses the -symmetry associated with the center of the group and “chooses” a specific direction or configuration. The vacuum of the confined is in principle different from that of the unconfined , and it is not unreasonable to assume that it may be metastable.
-symmetry breaking and false vacuum metastability and tunneling into the true vacuum with consequences for cosmology have been discussed in the literature (e.g., [52] and references therein). In our case, the phenomenon of tunneling or leaking could be attributed to two potential factors: (i) the zero-momentum loop at the origin of zero-point energy at zero temperature; (ii) the gluon condensate if we allow for a small temperature that is insignificant compared to any other scale in the problem. Which mechanism is exactly at play is currently uncertain within the scope of our model, and what is presented here serves as preliminary outlines for potential future research directions. The main point is that the leakage suggests a mechanism to explain -CDM cosmology in our model.
Appendix D. Our Cosmology
Let us write again the time evolution of the density inside an SQC as given in Equation (9):
with , the SQC density at the end of the LGB/photon-burst phase. As noted earlier, the equation above incorporates the key parameters in our cosmology, namely, , and which are all fundamentally related to QCD.
The time evolution of the DM density given in Equation (10) can be expanded as
where the subscript “0” refers to the current age of the universe at (i.e., at ); recall that is a fraction of , which simplifies our equations. is the total volume occupied by SQCs, which is constant in time, and is the Hubble volume at time t.
Putting Equation (A9) into Equation (A10), we obtain
with , , and ; see Section 3. Also, is the DM density at . The jump in the value of at in the equation above is due to the fact that a fraction of the DM is lost to the 2 MeV radiation before the start of the leakage era at (see Section 2).
Equation (A11) can be expressed in terms of redshift as
where we emphasize the dependency of on the leakage characteristic redshift to help differentiate our model from the CDM cosmology. Because (or ) and most of the time between and is in the matter-dominated era, we approximate and . Our model does not depend critically on , and by setting , where is the redshift at matter–radiation equality, we can simplify the equations without changing the final results.
The redshift of matter-radiation equality in our model is estimated by writing , with (i.e., ) so that . This yields
with , and as measured by Planck [53]; km s−1 Mpc−1 is the dimensionless Hubble constant in today’s universe. As expected, in our model is larger (i.e., requires an increase in the radiation to compensate for larger DM in the past) than in the case of the pure CDM cosmology, which does not capture the converted (by LGB decay and vacuum leakage) component of the DM.
Finally, our cosmology can be described by
with and where is today’s critical density; .
The co-moving sound horizon and the co-moving angular-diameter distance to the surface of the last scatter are [54]
The sound speed of the photon-baryon fluid at is with and .
The Hubble constant is found by solving with the angle subtended by the sound horizon [53]. For the CDM, one finds km s−1 Mpc−1 (; by solving using standard CDM cosmology). In our case, km s−1 Mpc−1 () can be obtained for a range in and values (see examples in Figure 4) with a leakage characteristic redshift (i.e., ); see Section 3.
References
- Hoyle, F.; Tayler, R.J. The Mystery of the Cosmic Helium Abundance. Nature 1964, 203, 1108. [Google Scholar] [CrossRef]
- Peebles, J.P.E. Primordial Helium Abundance and the Primordial Fireball. II. Astrophys. J. 1966, 146, 542. [Google Scholar] [CrossRef]
- Wagoner, R.V.; Fowler, W.A.; Hoyle, F. On the Synthesis of Elements at Very High Temperatures. Astrophys. J. 1967, 148, 3. [Google Scholar] [CrossRef]
- Tytler, D.; O’Meara, J.M.; Suzuki, N.; Lubin, D. Review of Big Bang Nucleosynthesis and Primordial Abundances. Phys. Scripta 2000, T85, 12. [Google Scholar] [CrossRef]
- Lang, K.R. Astrophysical Formulae, Volume II: Space, Time, Matter and Cosmology; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Khatri, R.; Sunyaev, R.A. Time of primordial 7Be conversion into 7Li, energy release and doublet of narrow cosmological neutrino lines. Astron. Lett. 2011, 37, 367. [Google Scholar] [CrossRef]
- Spite, F.; Spite, M. Abundance of lithium in un-evolved stars and old disk stars: Interpretation and consequences. Astron. Astrophys. 1982, 115, 357. [Google Scholar]
- Fields, B.D. The Primordial Lithium Problem. Annu. Rev. Nucl. Part. Sci. 2011, 61, 47. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Bulanov, S.V.; Dogiel, V.A.; Ginzburg, V.L.; Ptuskin, V.S. Astrophysics of Cosmic Rays; North-Holland: Amsterdam, The Netherlands, 1990; 534p. [Google Scholar]
- Kawasaki, M.; Moroi, T. Electromagnetic Cascade in the Early Universe and Its Application to the Big Bang Nucleosynthesis. Astrophys. J. 1995, 452, 506. [Google Scholar] [CrossRef][Green Version]
- Poulin, V.; Serpico, P.D. Loophole to the universal photon spectrum in electromagnetic cascades: Application to the “cosmological lithium problem”. Phys. Rev. Lett. 2015, 114, 091101. [Google Scholar] [CrossRef]
- Protheroe, R.J.; Stanev, T.; Berezinsky, V.S. Electromagnetic cascades and cascade nucleosynthesis in the early Universe. Phys. Rev. D 1995, 51, 4134. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kohri, K.; Moroi, T.; Murai, K.; Murayama, H. Big Bang nucleosynthesis with sub-GeV massive decaying particles. J. Cosmol. Astropart. Phys. 2020, 2020, 048. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272. [Google Scholar] [CrossRef]
- Zhitnitsky, A.R. ‘Nonbaryonic’ dark matter as baryonic colour superconductor. J. Cosmol. Astropart. Phys. 2003, 2003, 010. [Google Scholar] [CrossRef]
- Ishida, H.; Kusakabe, M.; Okada, H. Effects of long-lived 10 MeV-scale sterile neutrinos on primordial elemental abundances and the effective neutrino number. Phys. Rev. D 2014, 90, 083519. [Google Scholar] [CrossRef]
- Rüster, S.B.; Shovkovy, I.A.; Rischke, D.H. Phase diagram of dense neutral three-flavor quark matter. Nucl. Phys. A 2004, 743, 127. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Roberts, C.D.; Shrock, R.; Tandy, P.C. Confinement contains condensates. Phys. Rev. C 2012, 85, 065202. [Google Scholar] [CrossRef]
- Coleman, S.R. Fate of the false vacuum: Semiclassical theory. Phys. Rev. D 1977, 15, 2929, Erratum in Phys. Rev. D 1977, 16, 1248. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Diu, B.; Laloe, F. Quantum Mechanics; Hermann and John Wiley & Sons: Paris, France, 2006. [Google Scholar]
- Kamionkowski, M.; Riess, A.G. The Hubble Tension and Early Dark Energy. Ann. Rev. Nucl. Part. Sci. 2023, 73, 153–180. [Google Scholar] [CrossRef]
- Schöneberg, N.; Abellán, G.F.; Sánchez, A.P.; Witte, S.J.; Poulin, V.; Lesgourgues, J. The H0 Olympics: A fair ranking of proposed models. Phys. Rep. 2022, 984, 1–55. [Google Scholar] [CrossRef]
- Garrett, K.; Gintaras, D. Dark Matter: A Primer. Adv. Astron. 2011, 2011, 968283. [Google Scholar] [CrossRef]
- Schumann, M. Dark Matter 2014. Eur. Phys. J. Web Conf. 2015, 96, 01027. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Kisslinger, L.S.; Das, D. A brief review of dark matter. Int. J. Mod. Phys. A 2019, 34, 1930013. [Google Scholar] [CrossRef]
- Oks, E. Brief Review of Recent Advances in Understanding Dark Matter and Dark Energy. New Astron. Rev. 2021, 93, 101632. [Google Scholar] [CrossRef]
- Arbey, A.; Mahmoudi, F. Dark matter and the early Universe: A review. Prog. Part. Nucl. Phys. 2021, 119, 103865. [Google Scholar] [CrossRef]
- Matsumoto, R. et al. [Super-Kamiokande Collaboration] Search for proton decay via p→μ+K0 in 0.37 megaton-years exposure of Super-Kamiokande. arXiv 2002, arXiv:2208.13188. [Google Scholar]
- Sofue, Y. Rotation Curve of the Milky Way and the Dark Matter Density. Galaxies 2020, 8, 37. [Google Scholar] [CrossRef]
- Kanno, S.; Soda, J. Exact Coleman-De Luccia instantons. Int. J. Mod. Phys. 2012, 21, 1250040. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Abel, T.; Bryan, G.L.; Norman, M.L. The Formation of the First Star in the Universe. Science 2002, 295, 93. [Google Scholar] [CrossRef]
- Paczyński, B. Carbon Ignition in Degenerate Stellar Cores. Astrophys. J. 1972, 11, 53. [Google Scholar]
- Ablyazimov, T.; Abuhoza, A.; Adak, R.P.; Adamczyk, M.; Agarwal, K.; Aggarwal, M.M.; Ahammed, Z.; Ahmad, F.; Ahmad, N.; Ahmad, S.; et al. Challenges in QCD matter physics—The scientific programme of the Compressed Baryonic Matter experiment at FAIR. Eur. Phys. J. 2017, 53, 60. [Google Scholar] [CrossRef]
- Senger, P. Status of the Compressed Baryonic Matter experiment at FAIR. Int. J. Mod. Phys. E 2020, 29, 2030001. [Google Scholar] [CrossRef]
- Huang, M.; Shovkovy, I.A. Chromomagnetic instability in dense quark matter. Phys. Rev. D 2004, 70, 051501. [Google Scholar] [CrossRef]
- Alford, M.; Kouvaris, C.; Rajagopal, K. Evaluating the gapless color-flavor locked phase. Phys. Rev. D 2005, 71, 054009. [Google Scholar] [CrossRef]
- Cao, G.; He, L.; Zhuang, P. Solid-state calculation of crystalline color superconductivity. Phys. Rev. 2015, 91, 114021. [Google Scholar] [CrossRef]
- Haber, A.; Schmitt, A. New color-magnetic defects in dense quark matter. J. Phys. Nucl. Phys. 2018, 45, 065001. [Google Scholar] [CrossRef]
- Guenther, J.N. Overview of the QCD phase diagram—Recent progress from the lattice. Eur. Phys. J. A 2021, 57, 136. [Google Scholar] [CrossRef] [PubMed]
- Alford, M. Color superconducting quark matter. Annu. Rev. Nucl. Part. Sci. 2001, 51, 131. [Google Scholar] [CrossRef]
- Svensson, R.; Zdziarski, A.A. Photon-Photon Scattering of Gamma Rays at Cosmological Distances. Astrophys. J. 1990, 349, 415. [Google Scholar] [CrossRef]
- Ouyed, R.; Sannino, F. The Glueball sector of two-flavor Color Superconductivity. Phys. Lett. B 2001, 511, 66. [Google Scholar] [CrossRef][Green Version]
- Sannino, F.; Marchal, N.; Schäfer, W. Partial Deconfinement in Color Superconductivity. Phys. Rev. D 2002, 66, 016007. [Google Scholar] [CrossRef]
- Rischke, D.H.; Son, D.T.; Stephanov, M.A. Asymptotic Deconfinement in High-Density QCD. Phys. Rev. Lett. 2001, 87, 062001. [Google Scholar] [CrossRef]
- Alford, M.; GRajagopal, K.; Reddy, S.; FWilczek, F. Minimal color-flavor-locked–nuclear interface. Phys. Rev. D 2001, 64, 074017. [Google Scholar] [CrossRef]
- Shovkovy, I.A. Lectures delivered at the IARD 2004 conference, Saas Fee, Switzerland, June 12–19, and at the Helmholtz International Summer School and Workshop on Hot points in Astrophysics and Cosmology, JINR, Dubna, Russia, Aug. 2–13. arXiv 2004, arXiv:nucl-th/0410091. [Google Scholar]
- Satz, H. Phase transitions in QCD. Nucl. Phys. A 2001, 681, 3. [Google Scholar] [CrossRef][Green Version]
- Addazi, A.; Marcianò, A.; Pasechnik, R.; Prokhorov, G. Mirror symmetry of quantum Yang-Mills vacua and cosmological implications. Eur. Phys. J. 2019, 79, 251. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2018, 641, A6. [Google Scholar]
- Ryden, B. Introduction to Cosmology, 2nd ed.; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).