Unveiling the Emission and Variation Mechanism of Mrk 501: Using the Multi-Wavelength Data at Different Time Scale
Abstract
1. Introduction
2. Data Collection
3. Location of Emitting Regions
3.1. Correlation Analysis
3.2. Time Lag Analysis
3.3. Location of Emitting Regions
4. Study of Variations
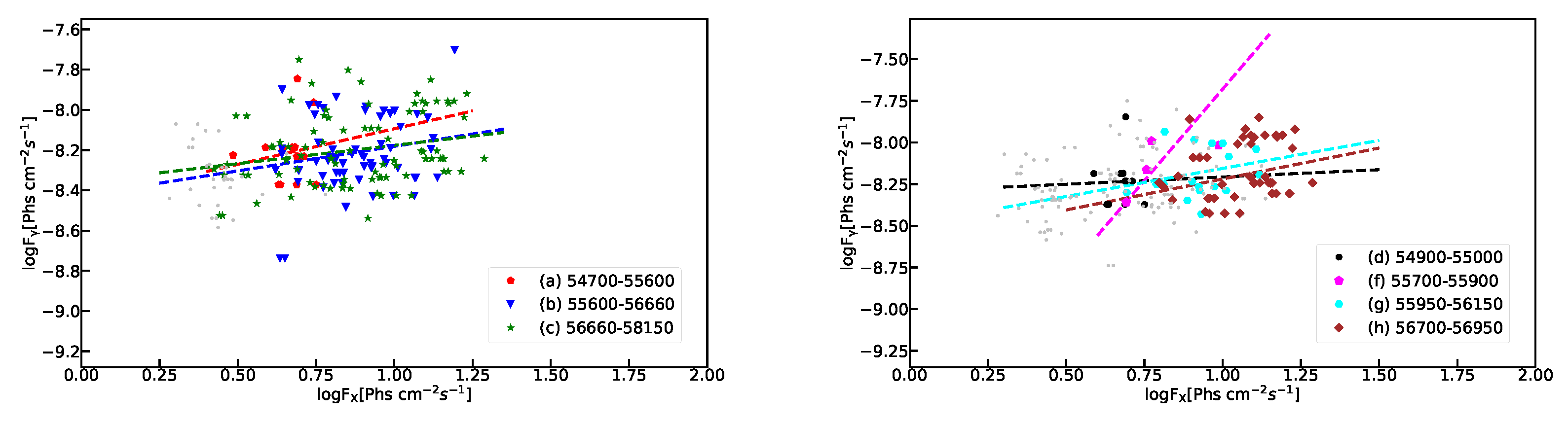
4.1. Correlation between X-ray and -ray
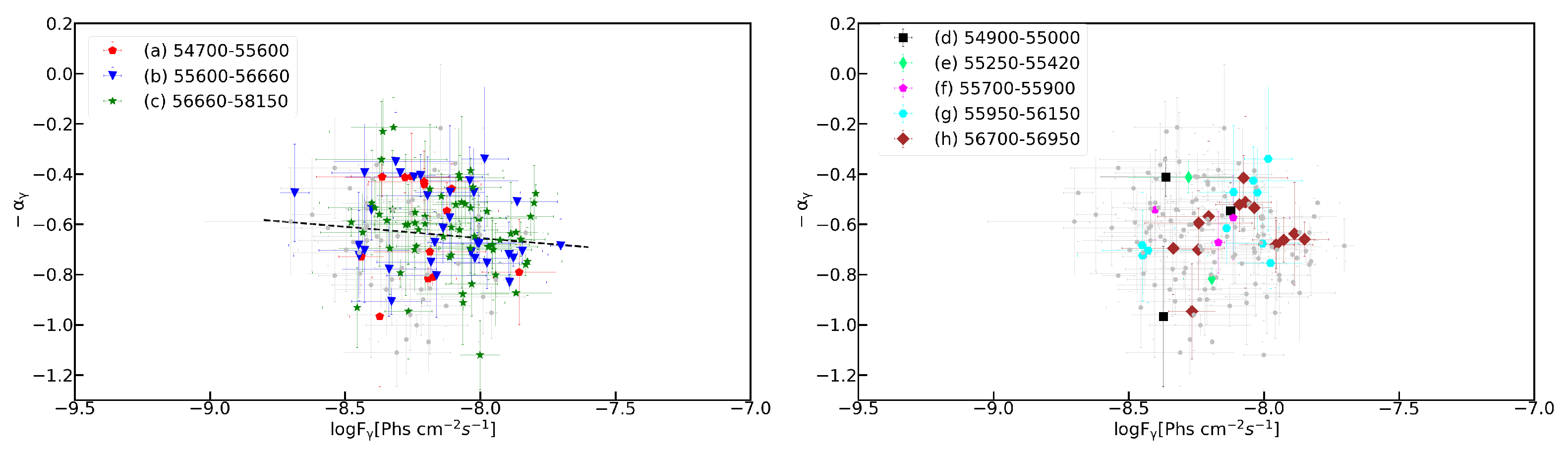
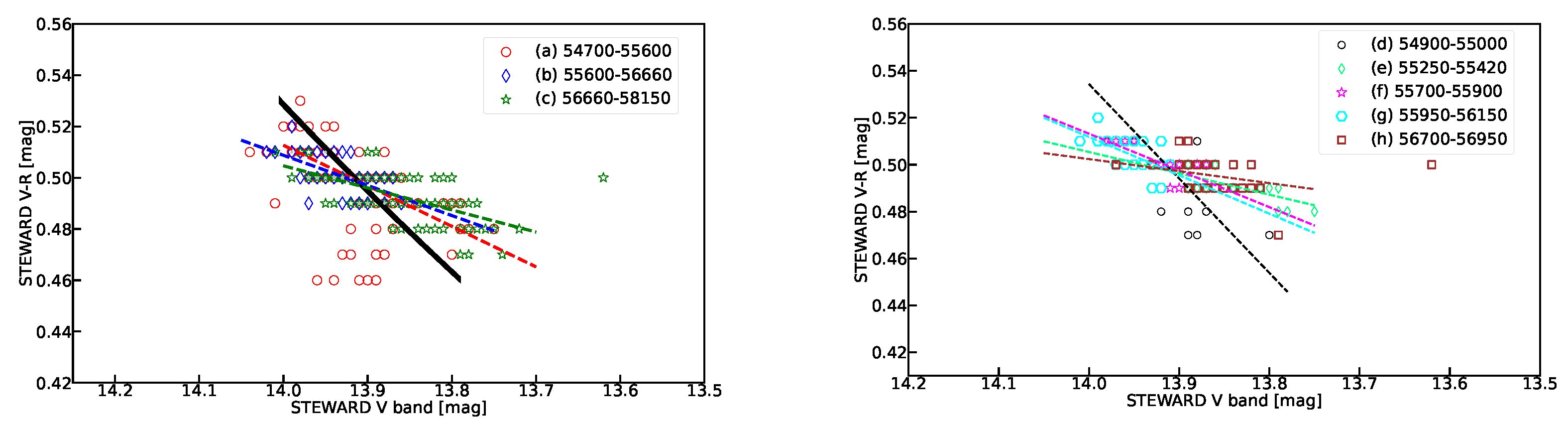
4.2. Color Index and -ray Spectral Index
| Periods | -ray Flux vs. X-ray Flux | () vs. V | Optical PD vs. Optical Flux | |||
|---|---|---|---|---|---|---|
| Slope | Pearson’s r | Slope | Pearson’s r | Slope | Pearson’s r | |
| a | 0.16 | −0.57 | 0.57 | |||
| b | 0.19 | −0.56 | 0.31 | |||
| c | 0.23 | −0.67 | 0.19 | |||
| d | 0.02 | −0.77 | 0.76 | |||
| e | – | – | −0.69 | 0.51 | ||
| f | 0.46 | −0.74 | 0.8 | |||
| g | 0.24 | −0.60 | 0.49 | |||
| h | 0.22 | −0.38 | 0.17 | |||
4.3. Optical Polarization and Optical Flux
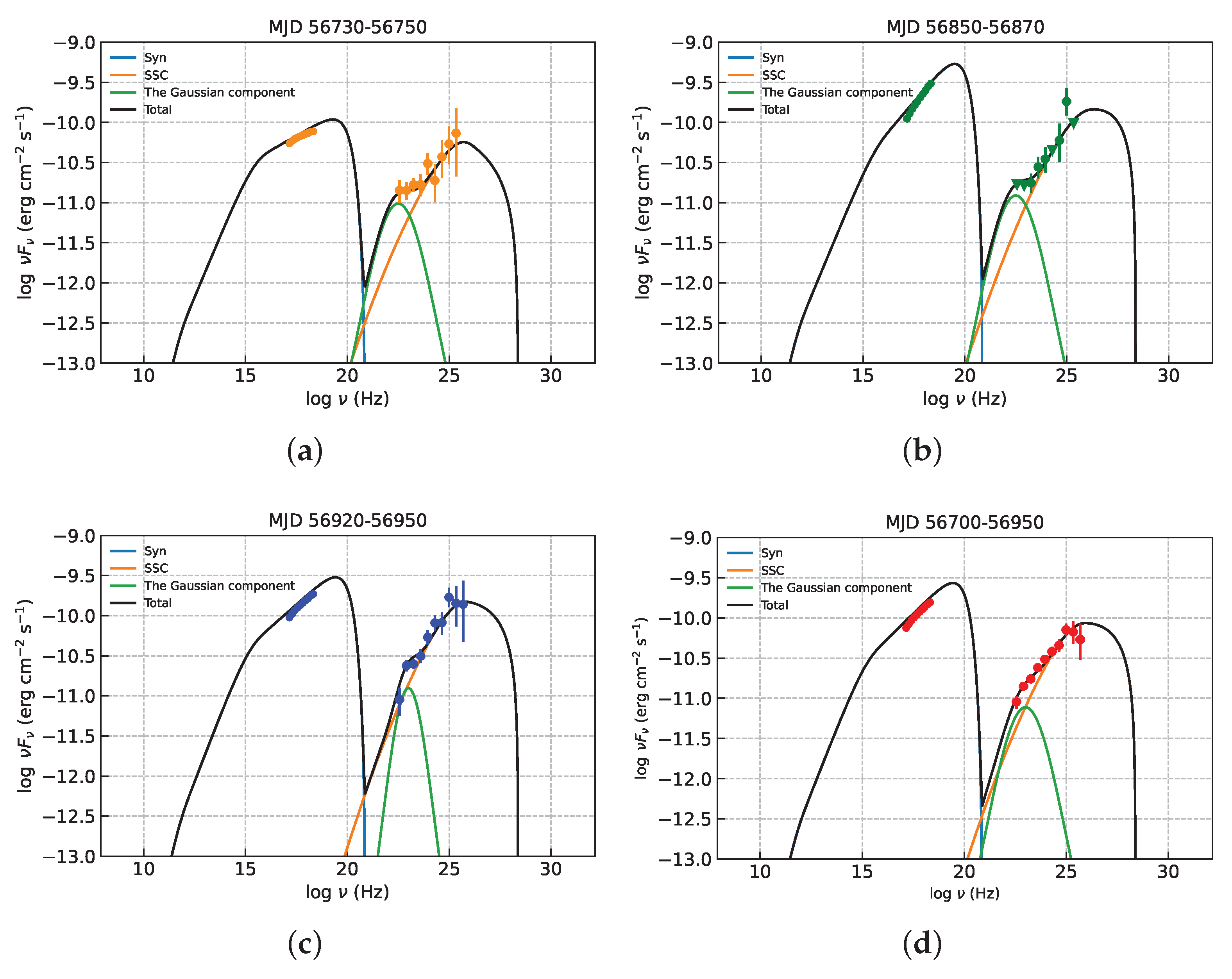
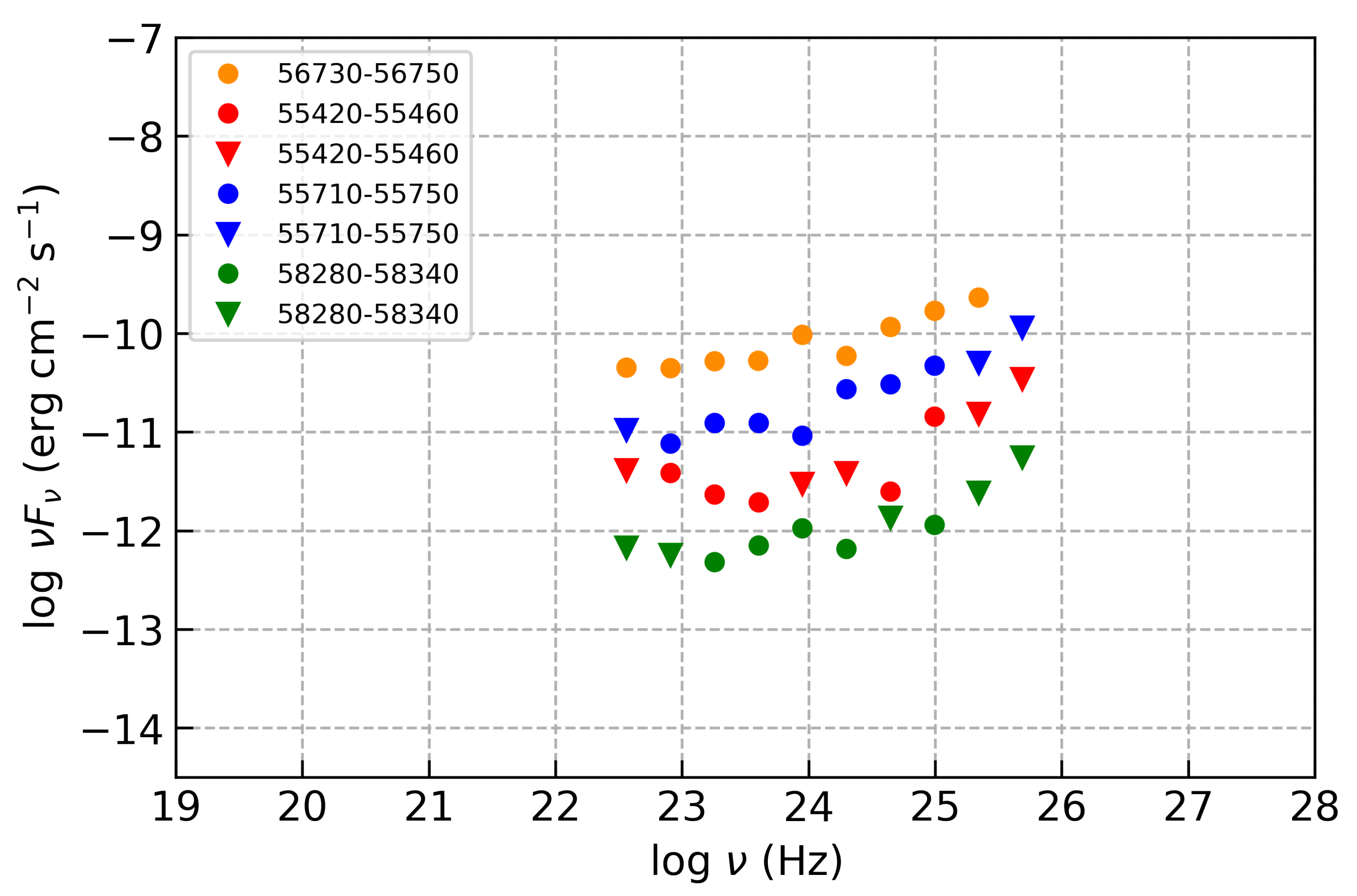
5. SED Analysis
6. Conclusions
- Based on the LCCF results, we observed that the distance between the jet base and the optical emitting region is pc, while for the X-ray emitting region, it is pc. We also get that the -ray emitting region is most likely the same as the X-ray emitting region and X-rays and -ray emitting are produced by the same particle population. The X-ray, -ray, and optical emitting regions along the jet are situated upstream of the radio core region. Similar research has also been conducted by Bhatta [43], Acharyya and Sadun [44];
- We analyzed the correlation between X-ray and -ray. We get the slope of vs. in different periods. The results show that the SSC process modulated by Doppler factor can be ruled out as the variation mechanism for the -ray radiation in the one-zone SSC scenario. For the variation of color index and the optical PD, we found the BWB trend and the positive correlation between the optical PD and flux, which could be explained by the two-component model. Based on this model, We obtain that the magnitude of the host galaxy component in the R band is 14.23 magnitude. This is consistent with the values measured by Nilsson et al. [45] with an aperture diameter of 5 arcsec;
- We detected the presence of a soft component in the low-activity state of -ray radiation. The broadband SED for the period from MJD 56,700 to MJD 56,950 is fitted by using the one-zone SSC plus the Gaussian component model. The Gaussian component may originate from the layer of the jet.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | https://fermi.gsfc.nasa.gov/cgi-bin/ssc/LAT/LATDataQuery.cgi (accessed on 1 January 2024). |
| 2 | https://pypi.org/project/easyFermi/ (accessed on 1 January 2024). |
| 3 | http://www.swift.psu.edu/monitoring/ (accessed on 1 January 2024). |
| 4 | http://james.as.arizona.edu/~psmith/Fermi/ (accessed on 1 January 2024). |
| 5 | http://www.astro.caltech.edu/ovroblazars/ (accessed on 1 January 2024). |
References
- Urry, C.M.; Padovani, P. Unified Schemes for Radio-Loud Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1995, 107, 803. [Google Scholar] [CrossRef]
- Ulrich, M.H.; Maraschi, L.; Urry, C.M. Variability of Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 1997, 35, 445–502. [Google Scholar] [CrossRef]
- Scarpa, R.; Falomo, R. Are high polarization quasars and BL Lacertae objects really different? A study of the optical spectral properties. Astron. Astrophys. 1997, 325, 109–123. [Google Scholar]
- Abdo, A.A.; Ackermann, M.; Agudo, I.; Ajello, M.; Aller, H.D.; Aller, M.F.; Angelakis, E.; Arkharov, A.A.; Axelsson, M.; Bach, U.; et al. The Spectral Energy Distribution of Fermi Bright Blazars. Astrophys. J. 2010, 716, 30–70. [Google Scholar] [CrossRef]
- Markarian, B.E.; Lipovetskij, V.A. Galaxies with ultraviolet continuum: V. Astrofizika 1972, 8, 155–164. [Google Scholar]
- Pushkarev, A.B.; Hovatta, T.; Kovalev, Y.Y.; Lister, M.L.; Lobanov, A.P.; Savolainen, T.; Zensus, J.A. MOJAVE: Monitoring of Jets in Active galactic nuclei with VLBA Experiments. IX. Nuclear opacity. Astron. Astrophys. 2012, 545, A113. [Google Scholar] [CrossRef]
- Quinn, J.; Akerlof, C.W.; Biller, S.; Buckley, J.; Carter-Lewis, D.A.; Cawley, M.F.; Catanese, M.; Connaughton, V.; Fegan, D.J.; Finley, J.P.; et al. Detection of Gamma Rays with E > 300 GeV from Markarian 501. Astrophys. J. 1996, 456, L83. [Google Scholar] [CrossRef]
- Xiong, D.; Zhang, H.; Zhang, X.; Yi, T.; Bai, J.; Wang, F.; Liu, H.; Zheng, Y. Multi-color Optical Monitoring of MRK 501 from 2010 to 2015. Astrophys. J. Suppl. Ser. 2016, 222, 24. [Google Scholar] [CrossRef]
- Abe, H. et al. [MAGIC Collaboration] Multi-messenger characterization of Mrk 501 during historically low X-ray and γ-ray activity. arXiv 2022, arXiv:2210.02547. [Google Scholar] [CrossRef]
- Liodakis, I.; Marscher, A.P.; Agudo, I.; Berdyugin, A.V.; Bernardos, M.I.; Bonnoli, G.; Borman, G.A.; Casadio, C.; Casanova, V.; Cavazzuti, E.; et al. Polarized blazar X-rays imply particle acceleration in shocks. Nature 2022, 611, 677–681. [Google Scholar] [CrossRef]
- MAGIC Collaboration; Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. Study of the variable broadband emission of Markarian 501 during the most extreme Swift X-ray activity. Astron. Astrophys. 2020, 637, A86. [Google Scholar] [CrossRef]
- Hu, W.; Yan, D. On the narrow spectral feature at 3 TeV in the MAGIC spectrum of Mrk 501. Mon. Not. R. Astron. Soc. 2021, 508, 4038–4046. [Google Scholar] [CrossRef]
- Abdollahi, S.; Acero, F.; Baldini, L.; Ballet, J.; Bastieri, D.; Bellazzini, R.; Berenji, B.; Berretta, A.; Bissaldi, E.; Blandford, R.D.; et al. VizieR Online Data Catalog: Incremental Fermi LAT 4th source cat. (4FGL-DR3) (Fermi-LAT col., 2022). VizieR Online Data Catalog 2022, IX/67. [Google Scholar]
- Stroh, M.C.; Falcone, A.D. Swift X-ray Telescope Monitoring of Fermi-LAT Gamma-Ray Sources of Interest. Astrophys. J. Suppl. Ser. 2013, 207, 28. [Google Scholar] [CrossRef]
- Richards, J.L.; Max-Moerbeck, W.; Pavlidou, V.; King, O.G.; Pearson, T.J.; Readhead, A.C.S.; Reeves, R.; Shepherd, M.C.; Stevenson, M.A.; Weintraub, L.C.; et al. VizieR Online Data Catalog: Observations of blazars at 15GHz (Richards+, 2011). VizieR Online Data Catalog 2011, J/ApJS/194/29. [Google Scholar]
- Kudryavtseva, N.A.; Gabuzda, D.C.; Aller, M.F.; Aller, H.D. A new method for estimating frequency-dependent core shifts in active galactic nucleus jets. Mon. Not. R. Astron. Soc. 2011, 415, 1631–1637. [Google Scholar] [CrossRef]
- Max-Moerbeck, W.; Richards, J.L.; Hovatta, T.; Pavlidou, V.; Pearson, T.J.; Readhead, A.C.S. A method for the estimation of the significance of cross-correlations in unevenly sampled red-noise time series. Mon. Not. R. Astron. Soc. 2014, 445, 437–459. [Google Scholar] [CrossRef]
- Edelson, R.A.; Krolik, J.H. The Discrete Correlation Function: A New Method for Analyzing Unevenly Sampled Variability Data. Astrophys. J. 1988, 333, 646. [Google Scholar] [CrossRef]
- Max-Moerbeck, W.; Hovatta, T.; Richards, J.L.; King, O.G.; Pearson, T.J.; Readhead, A.C.S.; Reeves, R.; Shepherd, M.C.; Stevenson, M.A.; Angelakis, E.; et al. Time correlation between the radio and gamma-ray activity in blazars and the production site of the gamma-ray emission. Mon. Not. R. Astron. Soc. 2014, 445, 428–436. [Google Scholar] [CrossRef]
- White, R.J.; Peterson, B.M. Comments on Cross-Correlation Methodology in Variability Studies of Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1994, 106, 879. [Google Scholar] [CrossRef]
- Welsh, W.F. On the Reliability of Cross-Correlation Function Lag Determinations in Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1999, 111, 1347–1366. [Google Scholar] [CrossRef]
- Max-Moerbeck, W. Scheduling and calibration strategy for continuous radio monitoring of 1700 sources every three days. In Observatory Operations: Strategies, Processes, and Systems V; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; Peck, A.B., Benn, C.R., Seaman, R.L., Eds.; SPIE: Bellingham, WC, USA, 2014; Volume 9149, p. 914925. [Google Scholar] [CrossRef]
- Timmer, J.; Koenig, M. On generating power law noise. Astron. Astrophys. 1995, 300, 707. [Google Scholar]
- Shao, X.; Jiang, Y.; Chen, X. Curvature-induced Polarization and Spectral Index Behavior for PKS 1502+106. Astrophys. J. 2019, 884, 15. [Google Scholar] [CrossRef]
- Peterson, B.M.; Wanders, I.; Horne, K.; Collier, S.; Alexander, T.; Kaspi, S.; Maoz, D. On Uncertainties in Cross-Correlation Lags and the Reality of Wavelength-dependent Continuum Lags in Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1998, 110, 660–670. [Google Scholar] [CrossRef]
- Larsson, S. Statistical Analysis of Multiwavelength Light curves. arXiv 2012, arXiv:1207.1459. [Google Scholar] [CrossRef]
- Konigl, A. Relativistic jets as X-ray and gamma-ray sources. Astrophys. J. 1981, 243, 700–709. [Google Scholar] [CrossRef]
- Lobanov, A.P. Ultracompact jets in active galactic nuclei. Astron. Astrophys. 1998, 330, 79–89. [Google Scholar]
- Hirotani, K. Kinetic Luminosity and Composition of Active Galactic Nuclei Jets. Astrophys. J. 2005, 619, 73–85. [Google Scholar] [CrossRef]
- O’Sullivan, S.P.; Gabuzda, D.C. Magnetic field strength and spectral distribution of six parsec-scale active galactic nuclei jets. Mon. Not. R. Astron. Soc. 2009, 400, 26–42. [Google Scholar] [CrossRef]
- Chatterjee, R.; Bailyn, C.D.; Bonning, E.W.; Buxton, M.; Coppi, P.; Fossati, G.; Isler, J.; Maraschi, L.; Urry, C.M. Similarity of the Optical-Infrared and γ-Ray Time Variability of Fermi Blazars. Astrophys. J. 2012, 749, 191. [Google Scholar] [CrossRef]
- Mohorian, M.; Bhatta, G.; Adhikari, T.P.; Dhital, N.; Pánis, R.; Dinesh, A.; Chaudhary, S.C.; Bachchan, R.K.; Stuchlík, Z. X-ray timing and spectral variability properties of blazars S5 0716 + 714, OJ 287, Mrk 501, and RBS 2070. Mon. Not. R. Astron. Soc. 2022, 510, 5280–5301. [Google Scholar] [CrossRef]
- Gupta, A.C.; Agarwal, A.; Bhagwan, J.; Strigachev, A.; Bachev, R.; Semkov, E.; Gaur, H.; Damljanovic, G.; Vince, O.; Wiita, P.J. Multiband optical variability of three TeV blazars on diverse time-scales. Mon. Not. R. Astron. Soc. 2016, 458, 1127–1137. [Google Scholar] [CrossRef]
- Nilsson, K.; Pasanen, M.; Takalo, L.O.; Lindfors, E.; Berdyugin, A.; Ciprini, S.; Pforr, J. Host galaxy subtraction of TeV candidate BL Lacertae objects. Astron. Astrophys. 2007, 475, 199–207. [Google Scholar] [CrossRef]
- Wang, Y.F.; Jiang, Y.G. A Comprehensive Study on the Variation Phenomena of AO 0235+164. Astrophys. J. 2020, 902, 41. [Google Scholar] [CrossRef]
- Shukla, A.; Chitnis, V.R.; Singh, B.B.; Acharya, B.S.; Anupama, G.C.; Bhattacharjee, P.; Britto, R.J.; Mannheim, K.; Prabhu, T.P.; Saha, L.; et al. Multi-frequency, Multi-epoch Study of Mrk 501: Hints for a Two-component Nature of the Emission. Astrophys. J. 2015, 798, 2. [Google Scholar] [CrossRef]
- Chen, L. On the Origin of the Hard X-Ray Excess of High-Synchrotron-Peaked BL Lac Object Mrk 421. Astrophys. J. 2017, 842, 129. [Google Scholar] [CrossRef]
- MacDonald, N.R.; Marscher, A.P.; Jorstad, S.G.; Joshi, M. Through the Ring of Fire: Gamma-Ray Variability in Blazars by a Moving Plasmoid Passing a Local Source of Seed Photons. Astrophys. J. 2015, 804, 111. [Google Scholar] [CrossRef]
- Britzen, S.; Krishna, G.; Kun, E.; Olivares, H.; Pashchenko, I.; Jaron, F.; González, J.B.; Paneque, D. Detection of a Peculiar Drift in the Nuclear Radio Jet of the TeV Blazar Markarian 501. Universe 2023, 9, 115. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bechtol, K.; et al. Insights into the High-energy γ-ray Emission of Markarian 501 from Extensive Multifrequency Observations in the Fermi Era. Astrophys. J. 2011, 727, 129. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Kang, S.J.; Yang, C.Y.; Bai, J.M. Particle Acceleration and Synchrotron Self-Compton Emission in Blazar Jets. I. An Application to Quiescent Emission. Astrophys. J. 2019, 873, 7. [Google Scholar] [CrossRef]
- Tavecchio, F.; Maraschi, L.; Ghisellini, G. Constraints on the Physical Parameters of TeV Blazars. Astrophys. J. 1998, 509, 608–619. [Google Scholar] [CrossRef]
- Bhatta, G. Characterizing Long-term Optical Variability Properties of γ-Ray-bright Blazars. Astrophys. J. 2021, 923, 7. [Google Scholar] [CrossRef]
- Acharyya, A.; Sadun, A.C. Investigating Possible Correlations between Gamma-Ray and Optical Lightcurves for TeV-Detected Northern Blazars over 8 Years of Observations. Galaxies 2023, 11, 81. [Google Scholar] [CrossRef]
- Nilsson, K.; Pursimo, T.; Takalo, L.O.; Sillanpää, A.; Pietilä, H.; Heidt, J. Two-dimensional Photometric Decomposition of the TeV BL Lacertae Objects Markarian 421, Markarian 501, and 1ES 2344+514. Publ. Astron. Soc. Pac. 1999, 111, 1223–1232. [Google Scholar] [CrossRef]
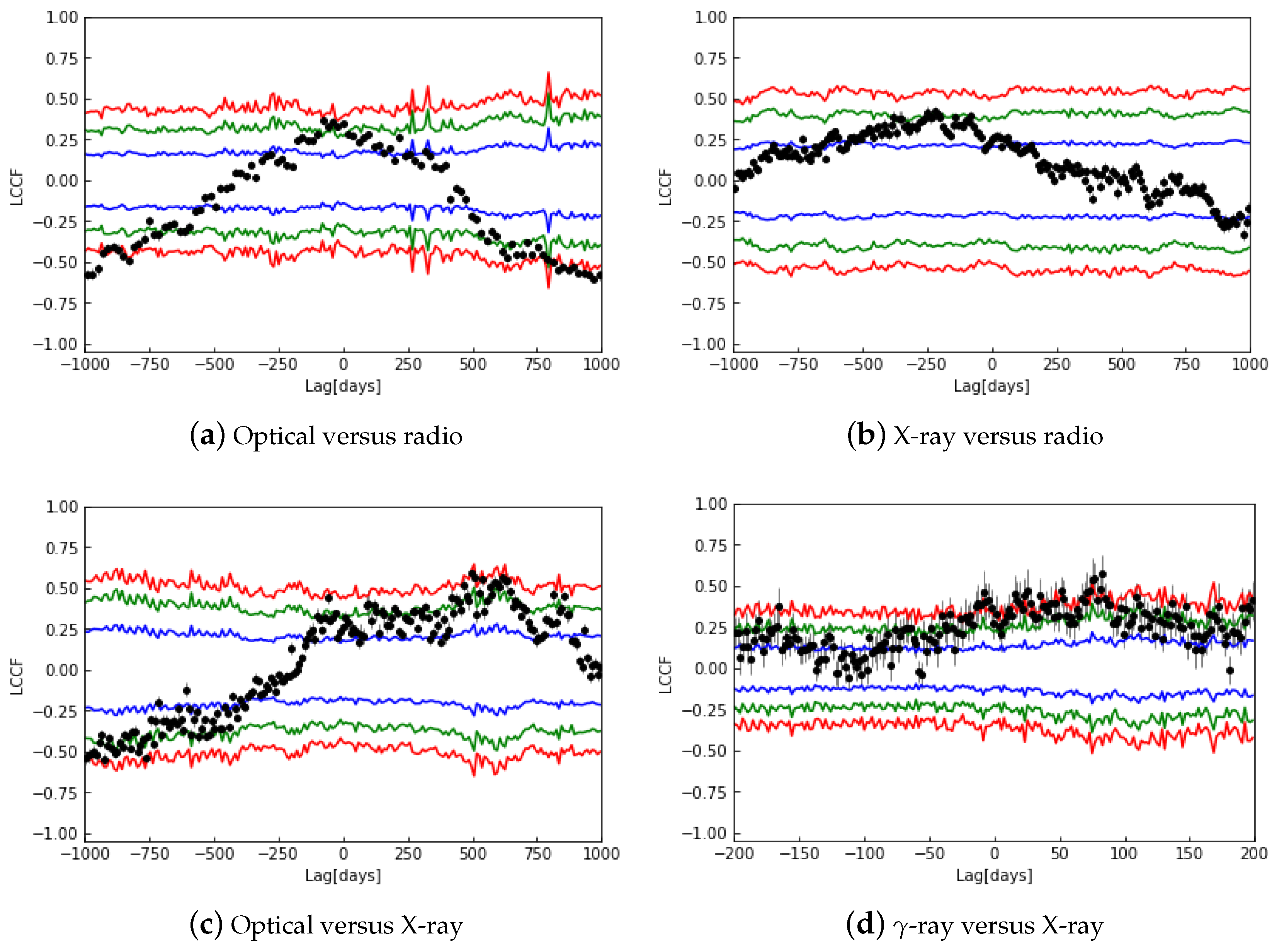


| Correlations | Time Lag | Relative Distances | ||||
|---|---|---|---|---|---|---|
| Optical vs. radio | ||||||
| X-ray vs. radio | ||||||
| Optical vs. X-ray | ||||||
| -ray vs. X-ray | ||||||
| Periods | MJD 56,730–56,750 | MJD 56,850–56,870 | MJD 56,920–56,950 | MJD 56,700–56,950 |
|---|---|---|---|---|
| Flux State | Low Flux State | High Flux State | Low State | Mean |
| 20 | 20 | 10 | 10 | |
| 1.2 × | 7.5 × | 7.5 × | ||
| 2 × | 2 × | 2 × | 2 × | |
| 1.78 | 1.77 | 1.67 | 1.7 | |
| 2.71 | 2.4 | 2.55 | 2.5 | |
| B(G) | 0.01 | 0.01 | 0.01 | 0.01 |
| R(cm) | ||||
| 12 | 12 | 12 | 12 | |
| 22.5 | 22.5 | 23 | 23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Jiang, Y.; Deng, J.; Chen, Z.; Ma, C. Unveiling the Emission and Variation Mechanism of Mrk 501: Using the Multi-Wavelength Data at Different Time Scale. Universe 2024, 10, 114. https://doi.org/10.3390/universe10030114
Liu L, Jiang Y, Deng J, Chen Z, Ma C. Unveiling the Emission and Variation Mechanism of Mrk 501: Using the Multi-Wavelength Data at Different Time Scale. Universe. 2024; 10(3):114. https://doi.org/10.3390/universe10030114
Chicago/Turabian StyleLiu, Lizhi, Yunguo Jiang, Junhao Deng, Zhaohao Chen, and Chenli Ma. 2024. "Unveiling the Emission and Variation Mechanism of Mrk 501: Using the Multi-Wavelength Data at Different Time Scale" Universe 10, no. 3: 114. https://doi.org/10.3390/universe10030114
APA StyleLiu, L., Jiang, Y., Deng, J., Chen, Z., & Ma, C. (2024). Unveiling the Emission and Variation Mechanism of Mrk 501: Using the Multi-Wavelength Data at Different Time Scale. Universe, 10(3), 114. https://doi.org/10.3390/universe10030114







