Abstract
We develop a cosmological model based on a quadratic equation of state , where is the Planck density and the cosmological density, “unifying” vacuum energy and dark energy in the spirit of a generalized Chaplygin gas model. For , it reduces to leading to a phase of early accelerating expansion (early inflation) with a constant density equal to the Planck density (vacuum energy). For , we recover the standard linear equation of state describing radiation () or pressureless matter () and leading to an intermediate phase of decelerating expansion. For , we get leading to a phase of late accelerating expansion (late inflation) with a constant density equal to the cosmological density (dark energy). The pressure is successively negative (vacuum energy), positive (radiation and matter), and negative again (dark energy). We show a nice “symmetry” between the early universe (vacuum energy + α-fluid) and the late universe (α-fluid + dark energy). In our model, they are described by two polytropic equations of state with index and respectively. Furthermore, the Planck density in the early universe plays a role similar to the cosmological density in the late universe. They represent fundamental upper and lower density bounds differing by 122 orders of magnitude. The cosmological constant “problem” may be a false problem. We study the evolution of the scale factor, density, and pressure. Interestingly, our quadratic equation of state leads to a fully analytical model describing the evolution of the universe from the early inflation (Planck era) to the late accelerating expansion (de Sitter era). These two phases are bridged by a decelerating algebraic expansion (α-era). Our model does not present any singularity at and exists eternally in the past (although it may be incorrect to extrapolate the solution to the infinite past). On the other hand, it admits a scalar field interpretation based on an inflaton, quintessence, or tachyonic field. Our model generalizes the standard ΛCDM model by incorporating naturally a phase of early inflation that avoids the primordial singularity. Furthermore, it describes the early inflation, the intermediate decelerating expansion, and the late accelerating expansion of the universe simultaneously in terms of a single equation of state. We determine the corresponding scalar field potential that unifies the inflaton and quintessence potentials.
1. Introduction
The evolution of the universe may be divided into four main periods [1]. In the vacuum energy era (Planck era), the universe undergoes a phase of early inflation that brings it from the Planck size to an almost “macroscopic” size in a tiniest fraction of a second [2,3,4,5]. The universe then enters in the radiation era and, when the temperature cools down below approximately , in the matter era [6]. Finally, in the dark energy era (de Sitter era), the universe undergoes a phase of late inflation [7]. The early inflation is necessary to solve notorious difficulties such as the singularity problem, the flatness problem, and the horizon problem [2,3,4,5]. The late inflation is necessary to account for the observed accelerating expansion of the universe [8,9,10,11]. At present, the universe is composed of approximately baryonic matter, dark matter, and dark energy [1]. Despite the success of the standard ΛCDM model, the nature of vacuum energy, dark matter, and dark energy remains very mysterious and leads to many speculations.
The phase of inflation in the early universe is usually described by some hypothetical scalar field ϕ, called inflaton, with its origin in the quantum fluctuations of the vacuum [2,3,4,5]. This leads to an equation of state , implying a constant energy density, called the vacuum energy. This energy density is usually identified with the Planck density . As a result of the vacuum energy, the universe expands exponentially rapidly on a timescale of the order of the Planck time .
The phase of acceleration in the late universe is usually ascribed to the cosmological constant Λ which is equivalent to a constant energy density called the dark energy [7]. This acceleration can be modeled by an equation of state implying a constant energy density identified with the cosmological density . As a result of the dark energy, the universe expands exponentially rapidly on a timescale of the order of the cosmological time (de Sitter solution). This leads to a phase of late inflation. Instead of introducing a cosmological constant, some authors have proposed to explain the acceleration of the universe in terms of a dark energy with a time-varying density associated with a canonical scalar field called quintessence [12,13,14,15,16,17,18,19,20,21,22,23,24], or in terms of a tachyonic field [25,26,27,28].
Between the phase of early inflation and the phase of late accelerating expansion, the universe is in the radiation era, then in the matter era [6]. These phases are described by a linear equation of state with for the radiation and for the pressureless matter (including baryonic matter and dark matter). The scale factor increases algebraically as and the density decreases algebraically as . For , the universe is decelerating.
In recent works [29,30,31,32], we have proposed to describe the transition between a phase of algebraic expansion () and a phase of exponential expansion () by a generalized polytropic equation of state of the form
This is the sum of a standard linear equation of state and a polytropic equation of state with . Polytropic equations of state play an important role in astrophysics [33,34], statistical physics [35] and mathematical biology [36], and they may also be relevant in cosmology. We have studied the equation of state (1) for any values of α, k and n and found the following structure. Positive indices describe the early universe where the polytropic component dominates the linear component because the density is high. Negative indices describe the late universe where the polytropic component dominates the linear component because the density is low. On the other hand, a positive polytropic pressure () leads to past or future singularities (or peculiarities) while a negative polytropic pressure () leads to a phase of exponential expansion (inflation) in the past or in the future [Note 1: the polytropic equation of state (1) with and is equivalent to the generalized Chaplygin gas model with that has been proposed to describe the late accelerating expansion of the universe (the original Chaplygin gas model corresponds to and ) [37,38,39,40,41,42,43,44,45]. Therefore, the polytropic equation of state (1) with and introduced in [29] can be seen as an extension of the generalized Chaplygin gas model to describe the early accelerating expansion of the universe (inflation).]. In the early universe (, ), the generalized polytropic equation of state (1) leads to a maximum bound for the density that it is natural to identify with the Planck density (vacuum energy). In the late universe (, ), it leads to a minimum bound for the density that it is natural to identify with the cosmological density (dark energy). These bounds differ by 122 orders of magnitude. Taking , and we obtain an equation of state that describes the transition between the vacuum energy era () and the radiation era. On the other hand, taking , and we obtain an equation of state that describes the transition between the matter era and the dark energy era (). More generally, the equation of state describes the transition between the vacuum energy era and an α-era in the early universe, and the equation of state describes the transition between an α-era and the dark energy era in the late universe.
In this paper, we propose to describe the vacuum energy, the α-fluid, and the dark energy in a “unified” manner by a single, quadratic, equation of state of the form [Note 2: This idea was sketched in [30,32] and is here systematically developed.]:
involving the Planck density and the cosmological density [Note 3: It is oftentimes argued that the dark energy (cosmological constant) corresponds to the vacuum energy. This leads to the so-called cosmological constant problem [46,47] because the cosmological density and the Planck density differ by about 122 orders of magnitude. We think it is a mistake to identify the dark energy with the vacuum energy. In this paper, we regard the vacuum energy and the dark energy as two distinct entities. We call vacuum energy the energy associated with the Planck density and dark energy the energy associated with the cosmological density. The vacuum energy is responsible for the inflation of the early universe and the dark energy for the inflation (acceleration) of the late universe. In this viewpoint, the vacuum energy is due to quantum mechanics and the dark energy is an effect of general relativity. The cosmological constant Λ is interpreted as a fundamental constant of nature applying to the cosmophysics in the same way the Planck constant ℏ applies to the microphysics.]. In the early universe (), we recover the equation of state unifying the vacuum energy () and the α-fluid. In the late universe (), we recover the equation of state unifying the α-fluid and the dark energy (). The α-fluid may represent radiation () or pressureless dark matter (). Actually, some works [48] indicate that dark matter may be described by an isothermal equation of state with a small value of . It is therefore useful to leave α unspecified and treat the general case of arbitrary α. However, to simplify the discussion, we shall assume . Moreover, for illustrations, we will select the values (radiation) and (pressureless matter) considered in our previous studies [29,30,31,32].
The quadratic equation of state (2) leads to a fully analytical cosmological model describing the evolution of the universe from the initial inflation (Planck era) to the late accelerating expansion (de Sitter era). These two phases are bridged by an algebraic decelerating expansion (α-era). The pressure is successively negative (vacuum energy), positive (α-era), and negative again (dark energy). Our model does not present any singularity at —the phase of early inflation avoids the primordial Big Bang singularity—and exists eternally in the past (although it may be incorrect to extrapolate the solution to the infinite past). On the other hand, our model admits a scalar field interpretation based on an inflaton, quintessence, or tachyonic field. This correspondence is interesting because the early inflation and the late acceleration of the universe are usually described in terms of a scalar field. There exist general techniques [7,49] to represent a fluid model in terms of a (canonical or tachyonic) scalar field. Although the hydrodynamic and field representations are equivalent at the background level, they may totally differ at the level of the perturbations when the fluid has a negative pressure. As a result, it is important to give the two representations and study the evolution of the perturbations in each case. It is known that the scalar field representation is more complete than the hydrodynamic representation, and provides a more realistic model [Note 4: The perfect fluid approach is more rough than the scalar field approach because for given perfect fluid variables ρ and P one cannot restore the scalar field variables ϕ, and in the inhomogeneous case (while the converse is always possible).]. In this paper, we only consider the evolution of the background where the hydrodynamic and field representations are equivalent. The study of the perturbations will be considered in future works.
The paper is organized as follows. In Section 2, we recall the basic equations of cosmology that are needed in our study. In Section 3, we describe the transition between the vacuum energy era () and the α-era in the early universe. In Section 4, we describe the transition between the α-era and the dark energy era () in the late universe. In Section 5, we introduce the general model where vacuum energy +α-era + dark energy are described by the quadratic equation of state (2). This model reveals a nice “symmetry” between the early universe (vacuum energy +α-era) and the late universe (α-era + dark energy). These two phases are described by two polytropic equations of state with index and respectively. The mathematical formulae in the early and in the late universe are strikingly symmetric. Furthermore, the cosmological density in the late universe plays a role similar to the Planck density in the early universe. They represent fundamental lower and upper density bounds differing by 122 orders of magnitude. Interestingly, these densities and (together with α) appear as the coefficients of the equation of state (2). Therefore, this equation of state provides a “unification” of vacuum energy and dark energy. We propose to interpret vacuum energy, radiation and dark energy as a “generalized radiation” described by the equation of state (2) with and treat baryonic matter and dark matter as independent species. This leads to Equation (110) that generalizes Equation (107) of the standard ΛCDM model. This equation avoids the primordial singularity and describes the whole evolution of the universe from the early inflation to the late accelerating expansion. In Appendix A, we develop a scalar field theory and derive the potential associated with the quadratic equation of state (2). This potential (see Equations (119)–(121)) unifies the inflaton potential in the early universe (see Equation (35)) and the quintessence potential in the late universe (see Equation (62)).
2. Basic Equations of Cosmology
In a space with uniform curvature, the line element of the expanding universe is given by the Friedmann-Lemaître-Roberston-Walker (FLRW) metric
where represents the radius of curvature of the 3-dimensional space, or the scale factor. By an abuse of language, we shall sometimes call it the “radius of the universe”. On the other hand, k determines the curvature of space. The universe may be closed (), flat (), or open ().
If the universe is isotropic and homogeneous at all points in conformity with the line element of Equation (3), and contains a uniform perfect fluid of energy density and isotropic pressure , the energy-momentum tensor is
The Einstein equations
relate the geometrical structure of the spacetime () to the content of the universe (). For the sake of generality, we have accounted for a possibly non-zero cosmological constant Λ. Given Equations (3) and (4), these equations reduce to
where dots denote differentiation with respect to time. These are the well-known cosmological equations describing a non-static universe first derived by Friedmann [6].
The Friedmann equations are usually written in the form
where we have introduced the Hubble parameter . Among these three equations, only two are independent. The first equation, which can be viewed as an “equation of continuity”, can be directly derived from the conservation of the energy momentum tensor which results from the Bianchi identities. For a given barotropic equation of state , it determines the relation between the density and the scale factor. Then, the temporal evolution of the scale factor is given by Equation (9).
In this paper, we consider a flat universe () in agreement with the observations of the cosmic microwave background (CMB) [50,51]. On the other hand, we set because the contribution of the dark energy will be taken into account in the equation of state. The Friedmann equations then reduce to
The deceleration parameter is defined by
The universe is decelerating when and accelerating when . Introducing the equation of state parameter , and using the Friedmann equations (11) and (12), we obtain for a flat universe
We see from Equations (11) and (14) that the universe is decelerating if (strong energy condition) and accelerating if [Note 5: According to general relativity, the source for the gravitational potential is . Indeed, the spatial part of the geodesic acceleration satisfies the exact equation showing that the source of geodesic acceleration is not ρ [47]. Therefore, in general relativity, gravitation becomes “repulsive” when .]. On the other hand, according to Equation (10), the density decreases with the scale factor if (null dominant energy condition) and increases with the scale factor if . The latter case corresponds to a “phantom” universe [52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69].
3. The Early Universe
In Reference [29], we have proposed to describe the transition between the vacuum energy era and the α-era in the early universe by a single equation of state of the form of Equation (1) with and . It can be written as
Assuming , the equation of continuity (10) can be integrated into
where and is a constant of integration. We see that corresponds to an upper bound (maximum value) for the density reached for . Since this solution describes the early universe, it is natural to identify with the Planck density . As a result, the equation of state (15) can be rewritten as
For the sake of simplicity, and for definiteness, we shall select the index . The general case has been treated in [29] and leads to qualitatively similar results. Therefore, we propose to describe the transition between the vacuum energy era and the α-era in the early universe by a single equation of state of the form
where is the Planck density. This equation of state corresponds to a generalized polytropic equation of state (1) with and . For , we recover the linear equation of state . For , we get corresponding to the vacuum energy. The relation of Equation (16) between the density and the scale factor becomes
The characteristic scale marks the transition between the vacuum energy era and the α-era. The equation of state (18) interpolates smoothly between the vacuum energy era (, ) and the α-era (, ). It provides therefore a “unified” description of the vacuum energy (Planck) era and α-era in the early universe. This amounts to summing the inverse of the densities of these two phases. Indeed, Equation (19) can be rewritten as
At we have so that . Writing , where is the present value of the scale factor and is the present density of the α-fluid, and using the asymptotic expression , we find that the transition scale factor is determined by the relation .
The equation of state parameter and the deceleration parameter q are given by
The velocity of sound is given by
As the universe expands from to , the density decreases from to 0, the equation of state parameter w increases from to α, the deceleration parameter q increases from to , and the ratio increases from to α (see Figures 2 and 6 of [29]).
3.1. The Vacuum Energy Era: Early Inflation
When , the density tends to a maximum value
and the pressure tends to . The Planck density (vacuum energy) represents a fundamental upper bound for the density. A constant value of the density gives rise to a phase of early inflation. From the Friedmann equation (12), we find that the Hubble parameter is constant, , where we have introduced the Planck time . Numerically, . Therefore, for , the scale factor increases exponentially rapidly with time as
The timescale of the exponential growth is the Planck time . We have defined the “original” time such that is equal to the Planck length . Mathematically speaking, the universe exists at any time in the past ( and for ), so there is no primordial singularity (Big Bang). However, when , we cannot ignore the quantum fluctuations associated with the spacetime. In that case, we cannot use the classical Einstein equations anymore and a theory of quantum gravity is required. It is not known whether quantum gravity will remove, or not, the primordial singularity. Therefore, we cannot extrapolate the solution in Equation (24) to the infinite past. However, this solution may provide a semi-classical description of the phase of early inflation when .
3.2. The α-Era
When , we recover the equation
corresponding to the pure linear equation of state . When , the Friedmann equation (12) yields
We then have
During the α-era, the scale factor increases algebraically as and the density decreases algebraically as .
3.3. The General Solution
For the equation of state (18), the density is related to the scale factor by Equation (19). It is possible to solve the Friedmann equation (12) with the density-radius relation of Equation (19) analytically. Introducing , we obtain
which can be integrated into [29]:
where C is a constant of integration determined such that at . Setting , we get
For , Equation (29) reduces to Equation (26). For , we have the exact asymptotic result
with . In general (for the radiation , we find [29]), so that C and D can be approximated by and . With this approximation, Equation (31) returns Equation (24). The time marking the end of the inflation is obtained by substituting in Equation (29). According to Equation (21), the universe is accelerating when (i.e., ) and decelerating when (i.e., ) where and . The time at which the universe starts decelerating is obtained by substituting in Equation (29). This corresponds to the time at which the curve presents an inflexion point. For (radiation) this inflexion point coincides with so it also marks the end of the inflation (). For the two points differ.
3.4. The Pressure
The pressure is given by Equation (18). Using Equation (19), we get
The pressure starts from at , remains approximately constant during the inflation, increases at the end of the inflation, becomes positive, reaches a maximum value , and decreases algebraically during the α-era. At , . The point at which the pressure vanishes () corresponds to and . On the other hand, the pressure reaches its maximum () when and [Note 6: The velocity of sound is imaginary () when and real () when . It is always less than the speed of light.]. The maximum pressure is . At the transition point , we have . At the deceleration point , we have .
3.5. The Evolution of the Early Universe
In our model, the universe “starts” at with a vanishing radius , a finite density , and a finite pressure . The universe exists at any time in the past and does not present any singularity. For , the radius of the universe is less than the Planck length . In the Planck era, quantum gravity should be taken into account so our semi-classical approach is probably not valid in the infinite past. At , the radius of the universe is equal to the Planck length . The corresponding density and pressure are and . We note that quantum mechanics regularizes the finite time singularity present in the standard Big Bang theory. This is similar to finite size effects in second order phase transitions (see Section 3.6). The Big Bang theory is recovered for . The universe first undergoes a phase of inflation during which its radius increases exponentially rapidly with time while its density and pressure remain approximately constant. The inflation “starts” at and ends at . The timescale of the inflation corresponds to the Planck time (for the radiation , we find [29]). During this very short lapse of time, the scale factor grows from to (for , we find ). By contrast, the density and the pressure do not change significatively: they go from and to and (for , we find and ). The pressure passes from negative values to positive values at (for , we find , , ). After the inflation, the universe enters in the α-era. The radius increases algebraically as while the density decreases algebraically as . The pressure achieves its maximum value at (for , we find , , , ). During the inflation, the universe is accelerating and during the α-era it is decelerating (if ). The transition (marked by an inflexion point) takes place at a time (for it coincides with the end of the inflation ). The evolution of the scale factor and density as a function of time are represented in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 in logarithmic and linear scales (the figures correspond to the radiation ).
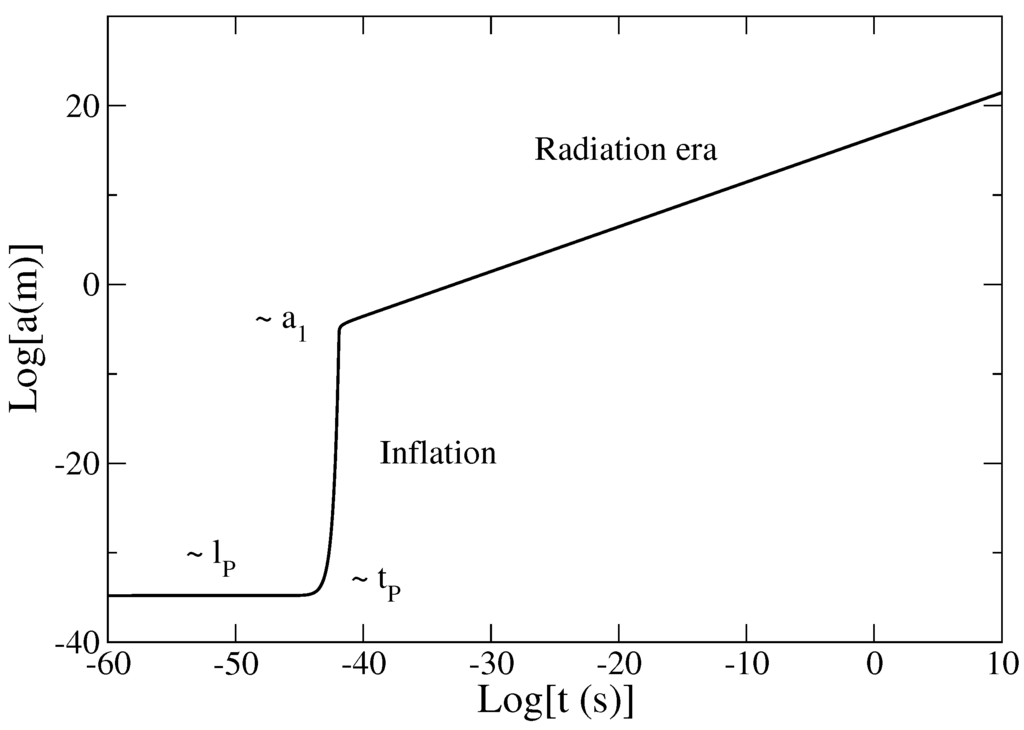
Figure 1.
Evolution of the scale factor a with the time t in logarithmic scales. This figure clearly shows the phase of inflation connecting the vacuum energy era to the α-era (representing here the radiation era). During the inflation, the scale factor increases exponentially rapidly on a timescale of the order of the Planck time (for it increases by 29 orders of magnitude in less than s). In the α-era, the scale factor increases algebraically as .
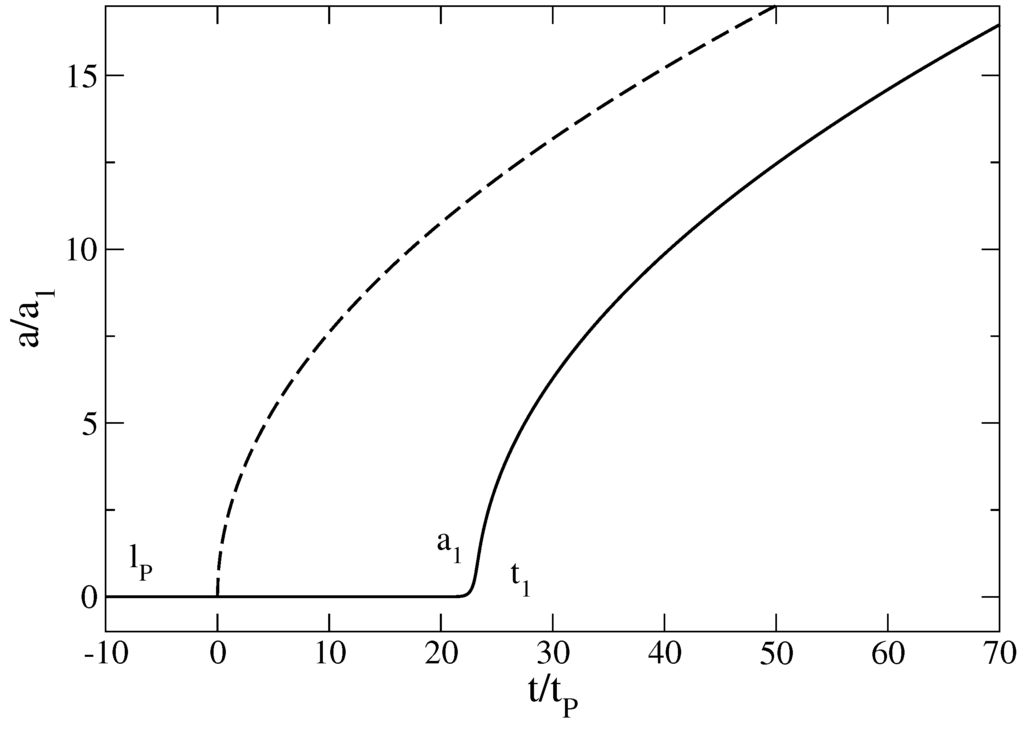
Figure 2.
Evolution of the scale factor a with the time t in linear scales. The dashed line corresponds to a pure linear equation of state leading to a finite time singularity at where (Big Bang). When quantum mechanics is taken into account (as in our semi-classical model), the initial singularity is smoothed-out and the scale factor at is equal to the Planck length . This is similar to a second order phase transition where the Planck constant plays the role of finite size effects (see Section 3.6 for a development of this analogy).
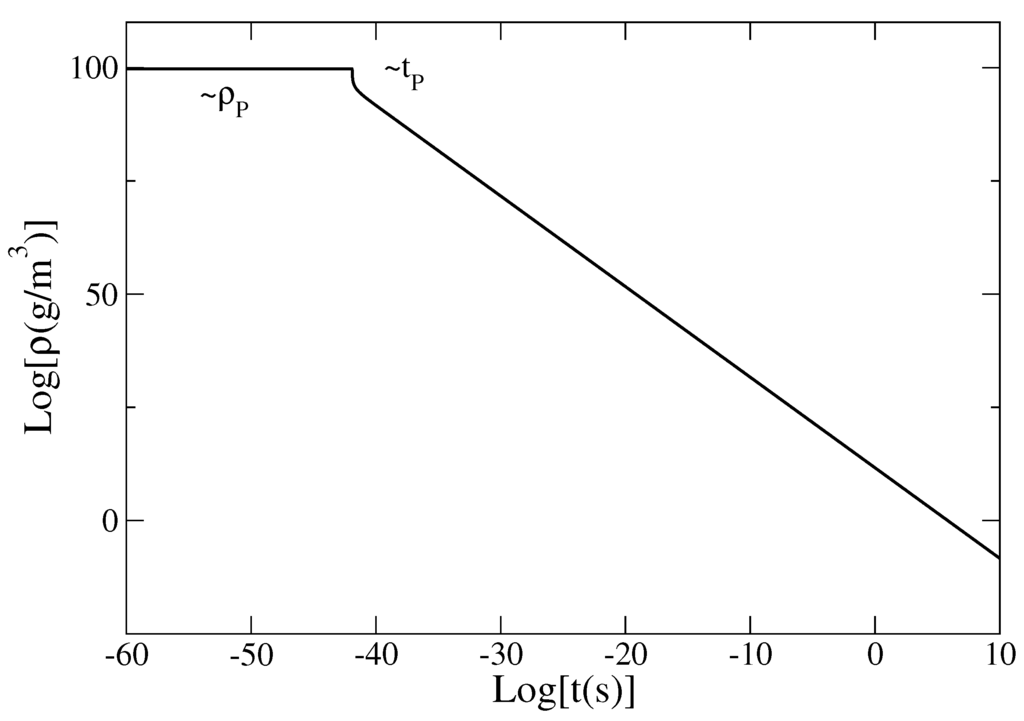
Figure 3.
Evolution of the density ρ with the time t in logarithmic scales. During the inflation, the density remains approximately constant with the Planck value which represents an upper bound. In the α-era, ρ decreases algebraically as .

Figure 4.
Evolution of the density ρ with the time t in linear scales. The dashed line corresponds to a pure linear equation of state leading to a finite time singularity at . Quantum mechanics limits the rise of the density to the Planck value .
Remark: If we consider the transition between the inflation era and the radiation era (), we find that the temperature is given by a generalized Stefan-Boltzmann law (see Equation (84a) in [29]). The evolution of the temperature is discussed in detail in References [29,32,70]. In our model, the temperature is initially very low, increases exponentially rapidly during the inflation up to a fraction () of the Planck temperature which is of the order of the Grand Unified Theories (GUT) scale, then decreases algebraically during the radiation era. On the other hand, our model generates a value of the entropy as large as [29]. This is very different from the standard inflationary scenario [2,3,4,5]. In that scenario, the universe is radiation dominated up to and expands exponentially rapidly by a factor in the interval with . For , the evolution is again radiation dominated. At , the temperature is about (this corresponds to the epoch at which most GUTs have a significant influence on the evolution of the universe). During the exponential inflation, the temperature drops drastically and one must advocate a phase of re-heating by various high energy processes (not very well understood) to restore the initial temperature.
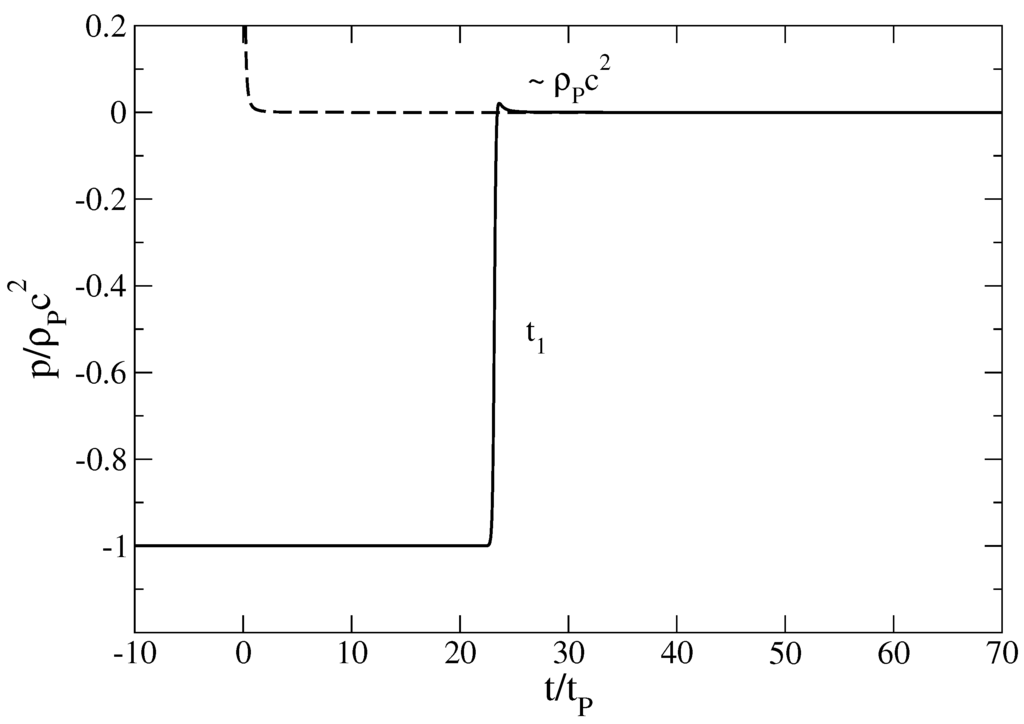
Figure 5.
Evolution of the pressure p with the time t in linear scales. The dashed line corresponds to a pure linear equation of state leading to a finite time singularity at . Quantum mechanics limits the rise of the pressure to a maximum value . In the vacuum energy era, the pressure decreases exponentially rapidly as we go backward in time, becomes negative, and tends to for .
3.6. Analogy with Phase Transitions
The standard Big Bang theory is a classical theory in which quantum effects are neglected. In that case, it exhibits a finite time singularity: the radius of the universe is equal to zero at while its density is infinite. For , the solution is not defined and we may take . For the radius of the universe increases as . This is similar to a second order phase transition if we view the time t as the control parameter (e.g., the temperature T) and the scale factor a as the order parameter (e.g., the magnetization M). For (radiation), it is amusing to note that the exponent in is the same as in mean field theories of second order phase transitions (i.e., ) but this is essentially a coincidence.
When quantum mechanics is taken into account, as in our semi-classical model, the singularity at disappears and the curves and are regularized. In particular, we find that at , instead of , due to the finite value of ℏ. This is similar to the regularization due to finite size effects (e.g., the system size L or the number of particles N) in ordinary phase transitions. In this sense, the classical limit is similar to the thermodynamic limit ( or ) in ordinary phase transitions. The convergence of our semi-classical solution towards the classical Big Bang solution when is shown in Figure 6 for (radiation).
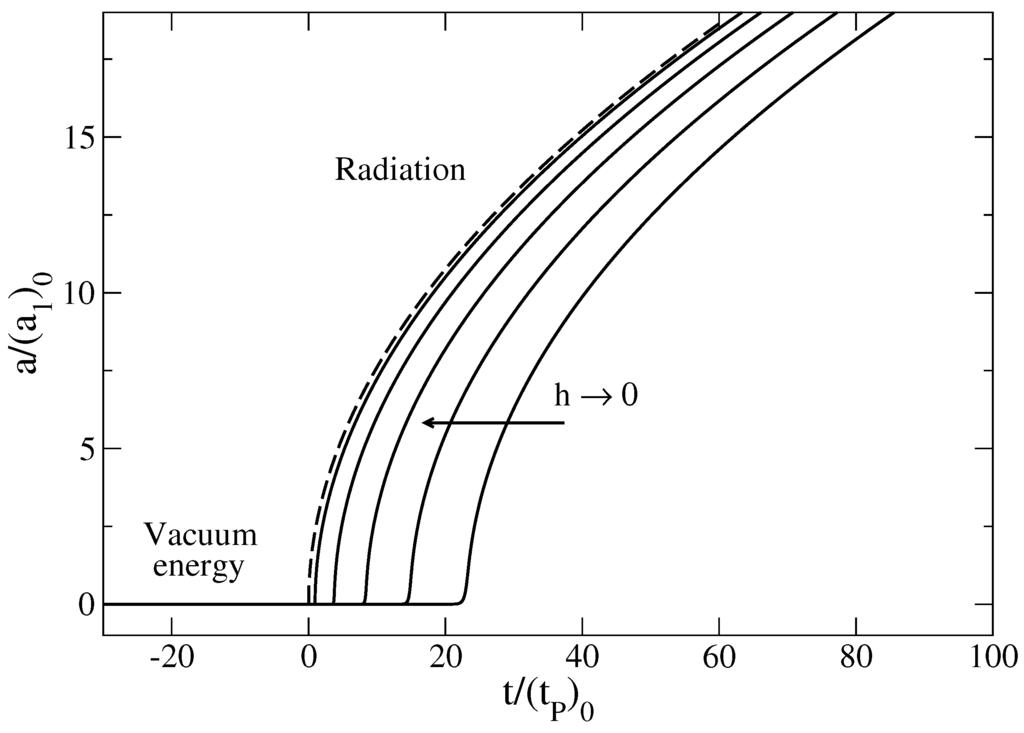
Figure 6.
Effect of quantum mechanics (finite value of the Planck constant) on the regularization of the singular Big Bang solution (, dashed line) in our semi-classical model (see [29] for details about the construction of this curve). The singularity at is replaced by an inflationary expansion from the vacuum energy era to the α-era. We can draw an analogy with second order phase transitions where the Planck constant plays the role of finite size effects.
3.7. Scalar field theory
The phase of inflation in the very early universe is usually described by a scalar field called inflaton [5]. A canonical scalar field minimally coupled to gravity evolves according to the Klein-Gordon equation
where is the potential of the scalar field. The scalar field tends to run down the potential towards lower energies. The density and the pressure of the universe are related to the scalar field by
Using standard techniques [7,49], we find that the inflaton potential corresponding to the equation of state (18) is (see Section 8.1 of [30]):
where we have defined
For ,
which is consistent with the symmetry breaking scalar field potential used to describe inflation. For ,
We can also show [30] that the relation between the scalar field and the scale factor is
The end of the inflation, and the beginning of the α-era, corresponds to , hence to . Combining Equations (18), (19) and (40), we find that the energy density and the pressure of the universe are related to the scalar field by
Using Equation (40), and the results of the previous sections, we can obtain the temporal evolution of the scalar field. In the vacuum energy era (), using Equation (24), we get
In the α-era (), using Equation (26), we get
More generally, using Equation (29), the evolution of the scalar field in the early universe is given by
These results are illustrated in Figure 7 and Figure 8 for (radiation).
Remark: The canonical scalar field potential of Equation (35) describing the transition between the inflation (vacuum energy) era and the α-era involves hyperbolic functions. The inflation due to another scalar field with a hyperbolic potential was investigated recently in [71] and confronted to the Planck 2015 data set, giving promising results. We are carrying out a similar study with the scalar field potential of Equation (35) to test its performance against Planck inflationary parameters.
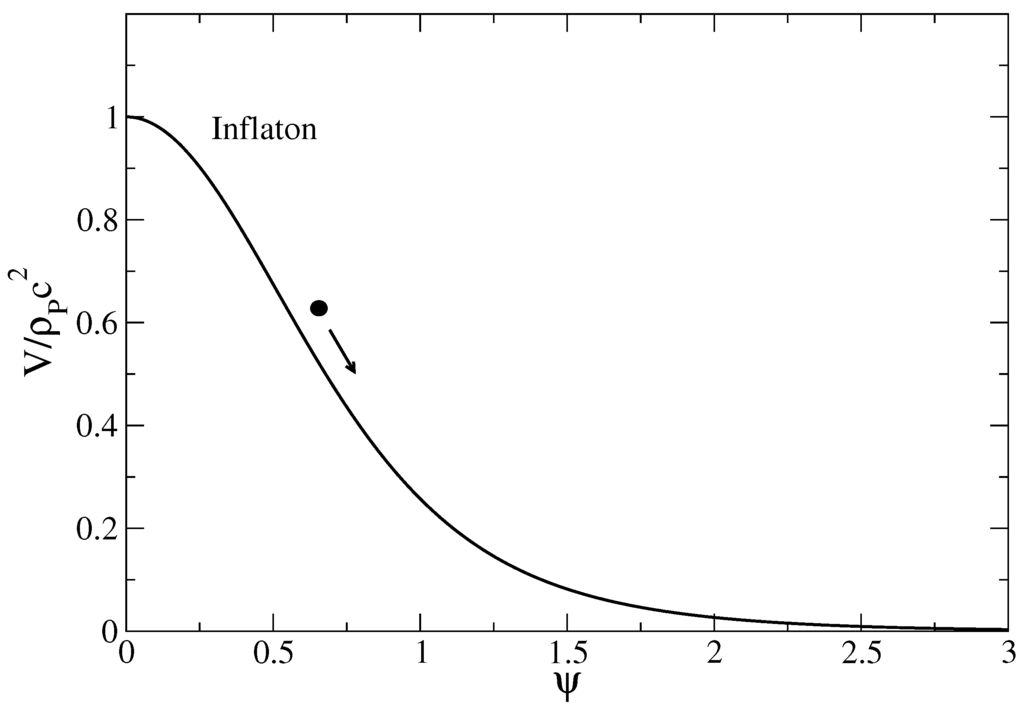
Figure 7.
Potential of the scalar field (inflaton) in the early universe. The field tends to run down the potential.
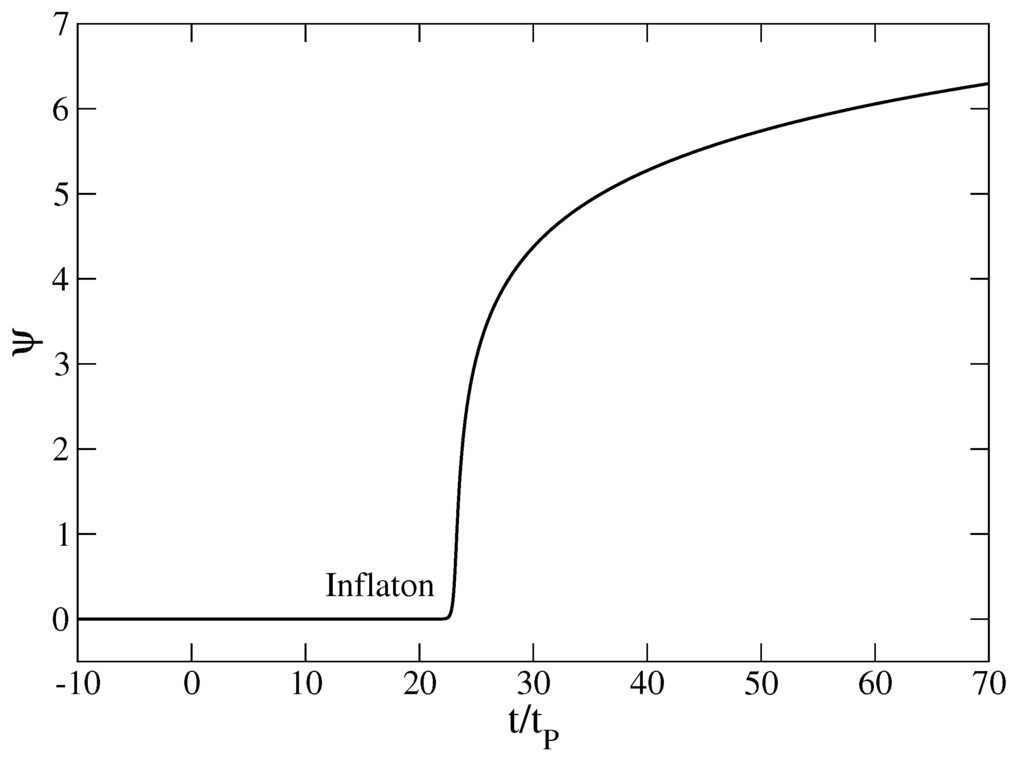
Figure 8.
Evolution of the scalar field (inflaton) as a function of time in the early universe. It displays a phase of early inflation before entering in the α-era.
4. The Late Universe
In Reference [30], we have proposed to describe the transition between the α-era and the dark energy era in the late universe by a single equation of state of the form of Equation (1) with and . It can be written as
Assuming , the equation of continuity (10) can be integrated into
where and is a constant of integration. We see that corresponds to a lower bound (minimum value) for the density reached for . Since this solution describes the late universe, it is natural to identify with the cosmological density . As a result, the equation of state (45) can be rewritten as
For the sake of simplicity, and for definiteness, we shall select the index . The general case has been treated in [30] and leads to qualitatively similar results. Therefore, we propose to describe the transition between the α-era and the dark energy era in the late universe by a single equation of state of the form
where is the cosmological density. This equation of state corresponds to a generalized polytropic equation of state (1) with and . It can be viewed as the “symmetric” version of the equation of state (18) in the early universe. For , we recover the linear equation of state . For , we get corresponding to the dark energy. The relation in Equation (46) between the density and the scale factor becomes
The characteristic scale marks the transition between the α-era and the dark energy era. The equation of state (48) interpolates smoothly between the α-era ( and ) and the dark energy era ( and ). It provides therefore a “unified” description of the α-era and dark energy era (de Sitter) in the late universe. This amounts to summing the density of these two phases. Indeed, Equation (49) can be rewritten as
At we have so that . Writing , where is the present value of the scale factor and is the present density of the α-fluid, and using the asymptotic expression , we find that the transition scale factor is determined by the relation . On the other hand, comparing Equations (19) and (49) in the α-era (i.e., ) where the two equations of state overlap, we get .
The equation of state parameter and the deceleration parameter q are given by
The velocity of sound is given by
As the universe expands from to , the density decreases from to , the equation of state parameter w decreases from α to , the deceleration parameter q decreases from to , and the ratio remains constant with the value α (see Figures 1 and 5 of [30]).
4.1. The Dark Energy Era: Late Inflation
When , the density tends to a minimum value
and the pressure tends to . The cosmological density (dark energy) represents a fundamental lower bound for the density. A constant value of the density gives rise to a phase of late inflation (accelerating expansion). It is convenient to define a cosmological time and a cosmological length . These are the counterparts of the Planck scales for the late universe (see Appendix B of [30]). From the Friedmann equation (12), we find that the Hubble parameter is constant . Numerically, . Therefore, the scale factor increases exponentially rapidly with time as
This exponential growth corresponds to the de Sitter solution [1]. The timescale of the exponential growth is the cosmological time . This solution exists at any time in the future ( and for ), so there is no future singularity [Note 7: This is not the case of all cosmological models. In a “phantom universe” [52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69], violating the null dominant energy condition (), the density increases as the universe expands. The models based on phantom dark energy usually predict a future singularity in which the scale factor, the energy density, and the pressure of the universe become infinite in a finite time. This would lead to the death of the universe in a singularity called Big Smash [54], Big Rip, or Cosmic Doomsday [53]. Contrary to the Big Crunch, the universe is destroyed not by excessive contraction but rather by excessive expansion. Every gravitationally bound system (e.g., the solar system, the Milky Way, the local group, galaxy clusters) is dissociated before the singularity [53,59], and the black holes gradually lose their mass and finally vanish at the Big Rip time [60,61,62]. This scenario allows the explicit calculation of the rest of the lifetime of the universe. Actually, as we approach the singularity, the energy scale may grow up to the Planck scale, giving rise to a second quantum gravity era. Eventually, quantum effects may moderate or even prevent the singularity [63]. It has also been proposed that, before reaching the Big Rip singularity, the universe could be swallowed by a wormhole [72]. This is due to the accretion of the ever-increasing phantom energy by the wormhole. This accretion induces an increase of the wormhole throat so rapid that the size of the wormhole throat becomes infinite in a finite time preceding the Big Rip. As a result, the wormhole can engulf the entire universe before it reaches the Big Rip singularity. The wormhole would then act as a spacetime tunnel (Einstein-Rosen bridge) allowing the universe to pass to another, more gentle, universe without future singularity. This could be a way to escape the programmed death of the universe. This has been called the Big Trip. The possibility that we live in a phantom universe is not excluded by the observations. Indeed, observational data indicate that the equation of state parameter w lies in a narrow strip around , possibly being below this value. It is important to stress, however, that the phantom models with do not necessarily lead to finite-time future singularities, as discussed in [73]. For example, the scale factor and the density may increase indefinitely and become infinite in infinite time. This has been called Little Rip [69]. In these models, the black holes disappear in infinite time while the wormhole’s throat still becomes infinite in a finite time. The phantom models without future singularity are attractive from the physical viewpoint because the occurrence of a finite time singularity may lead to some inconsistencies.].
4.2. The α-era
When , we recover the equation
corresponding to the pure linear equation of state . When , the Friedmann equation (12) yields
We then have
During the α-era, the scale factor increases algebraically as and the density decreases algebraically as .
4.3. The General Solution
For the equation of state (48), the density is related to the scale factor by Equation (49). It is possible to solve the Friedmann equation (12) with the density-radius relation of Equation (49) analytically. Introducing , we obtain
which can be integrated into [30]:
The density is then given by
For , Equation (59) reduces to Equation (56) and for we obtain Equation (54) with a prefactor .
The time corresponding to the transition between the α-era and the dark energy era is obtained by substituting in Equation (59). On the other hand, according to Equation (51), we find that the universe is decelerating when (i.e., ) and accelerating when (i.e., ) where and . The time at which the universe starts accelerating is obtained by substituting in Equation (59). This corresponds to the time at which the curve presents an inflexion point. For (radiation), this inflexion point coincides with (). For the two points differ.
4.4. The Pressure
The pressure is given by Equation (48). Using Equation (49), we get
For , the pressure decreases algebraically during the α-era and tends to a negative constant value for . The point at which the pressure vanishes () corresponds to and . For , the pressure is a constant . At the transition point , we have . At the acceleration point , we have .
4.5. The Evolution of the Late Universe
When , the universe is in the α-era. Its radius increases algebraically as while its density decreases algebraically as . For , the expansion of the universe is decelerating. When , the universe is in the dark energy era. It undergoes a phase of accelerating expansion (late inflation) during which its radius increases exponentially rapidly with time while its density remains constant and equal to the cosmological density . The Hubble constant, the Hubble time, the Hubble radius, and the density of the present universe are , , , and . For (pressureless matter), the transition between the matter era and the dark energy era takes place at , , and [30]. The moment at which the universe starts accelerating corresponds to , , and . The age of the universe is ( if we use a more precise value of [30]). The present values of the deceleration parameter and of the equation of state parameter are and . The evolution of the scale factor and density as a function of time are represented in Figure 9, Figure 10, Figure 11 and Figure 12 in logarithmic and linear scales (the figures correspond to pressureless matter ).
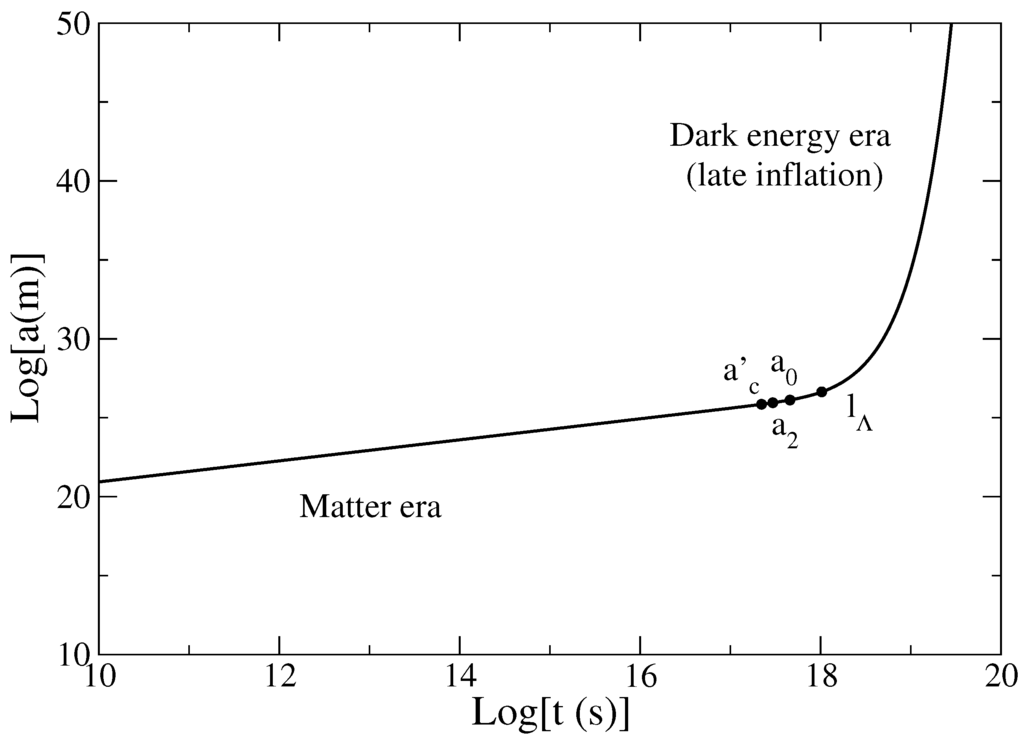
Figure 9.
Evolution of the scale factor a with the time t in logarithmic scales. This figure clearly shows the transition between the α-era and the dark energy era (de Sitter). In the α-era, the radius increases as . In the dark energy era, the radius increases exponentially rapidly on a timescale of the order of the cosmological time . This corresponds to a phase of late inflation. The universe is decelerating for and accelerating for . The transition between the α-era and the dark energy era takes place at .
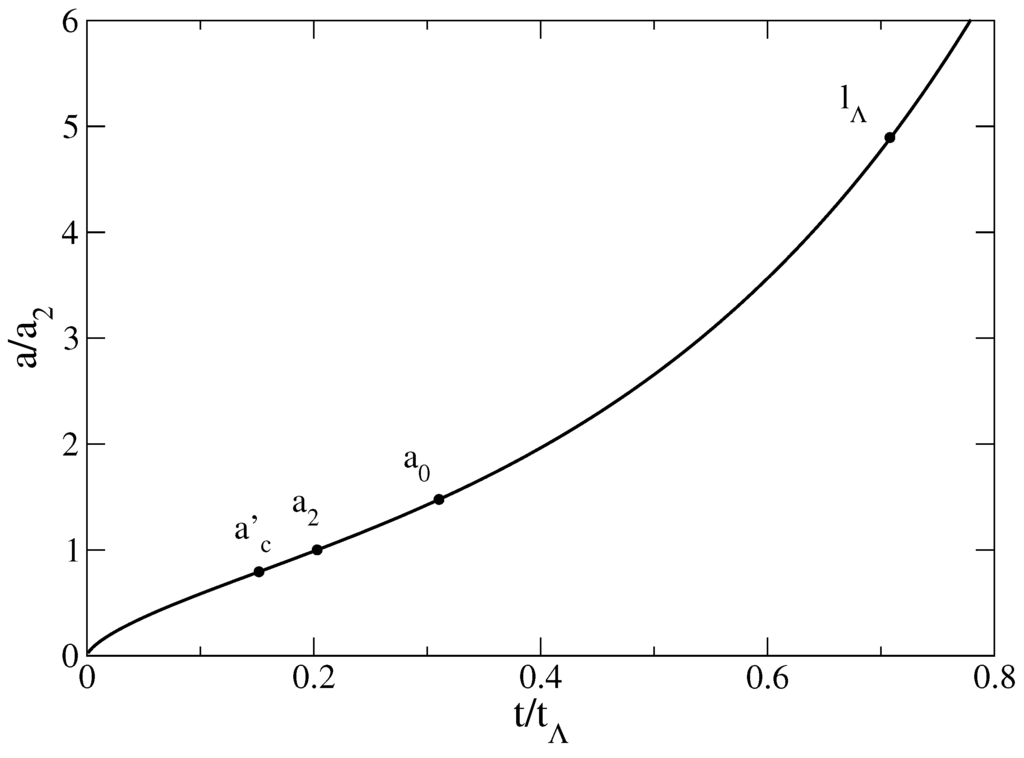
Figure 10.
Evolution of the scale factor a with the time t in linear scales.

Figure 11.
Evolution of the density ρ with the time t in logarithmic scales. In the α-era, the density decreases as . During the late inflation (accelerating expansion), the density remains approximately constant with the cosmological value representing a lower bound.
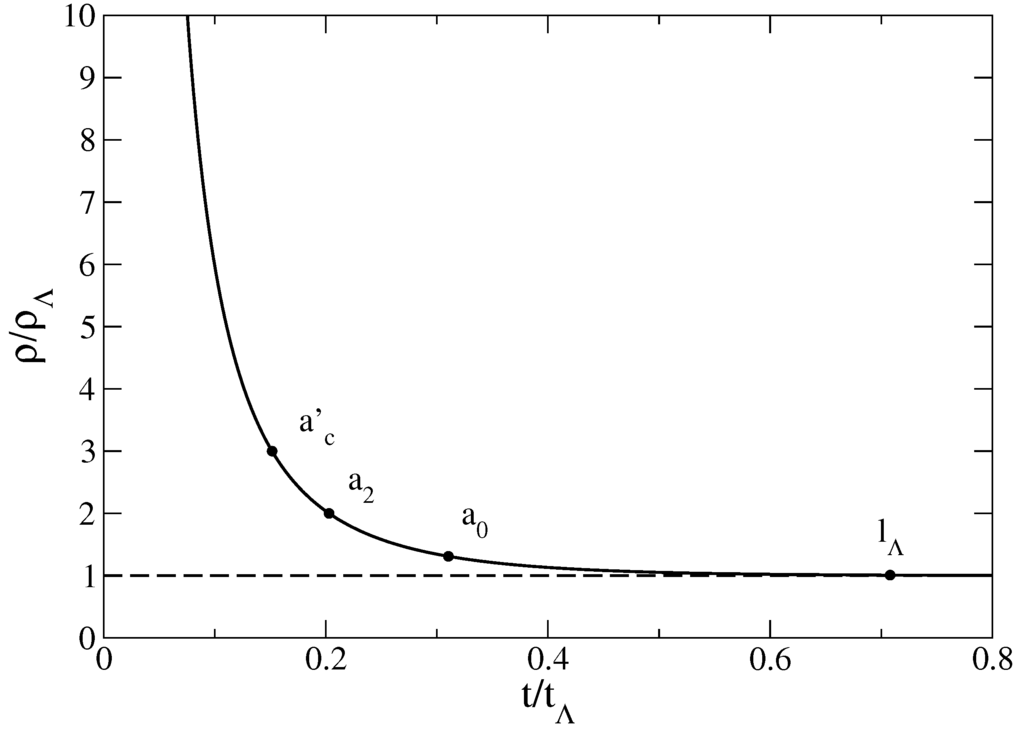
Figure 12.
Evolution of the density ρ with the time t in linear scales. General relativity (cosmological constant) limits the decay of the density to the cosmological value .
4.6. Scalar Field Theory
In alternative theories to the cosmological constant, the dark energy is usually described by a scalar field, defined by Equations (33) and (34), called quintessence [12,13,14,15,16,17,18,19,20,21,22,23,24]. Using standard techniques [7,49], we find that the quintessence potential corresponding to the equation of state (48) is (see Section 8.1 of [30]):
where we have defined
For ,
For ,
For , the scalar field potential is constant. We can also show [30] that the relation between the scalar field and the scale factor is
The end of the α-era, and the beginning of the dark energy era, corresponds to , hence to . Combining Equations (48), (49) and (66), we find that the energy density and the pressure of the universe are related to the scalar field by
Using Equation (66), and the results of the previous sections, we can obtain the temporal evolution of the scalar field. For , using Equation (56), we get
For , using Equation (54) with the prefactor , we get
More generally, using Equation (59), the evolution of the scalar field in the late universe is given by
These results are illustrated in Figure 13 and Figure 14 for (pressureless matter).
Some authors have proposed to represent the dark energy by a rolling tachyon condensate appearing in a class of string theories [25]. A tachyonic scalar field [26,27,28] has an equation of state with . This scalar field evolves according to the equation
The tachyonic field tends to run down the potential towards lower energies. The density and the pressure of the universe are related to the tachyonic field by
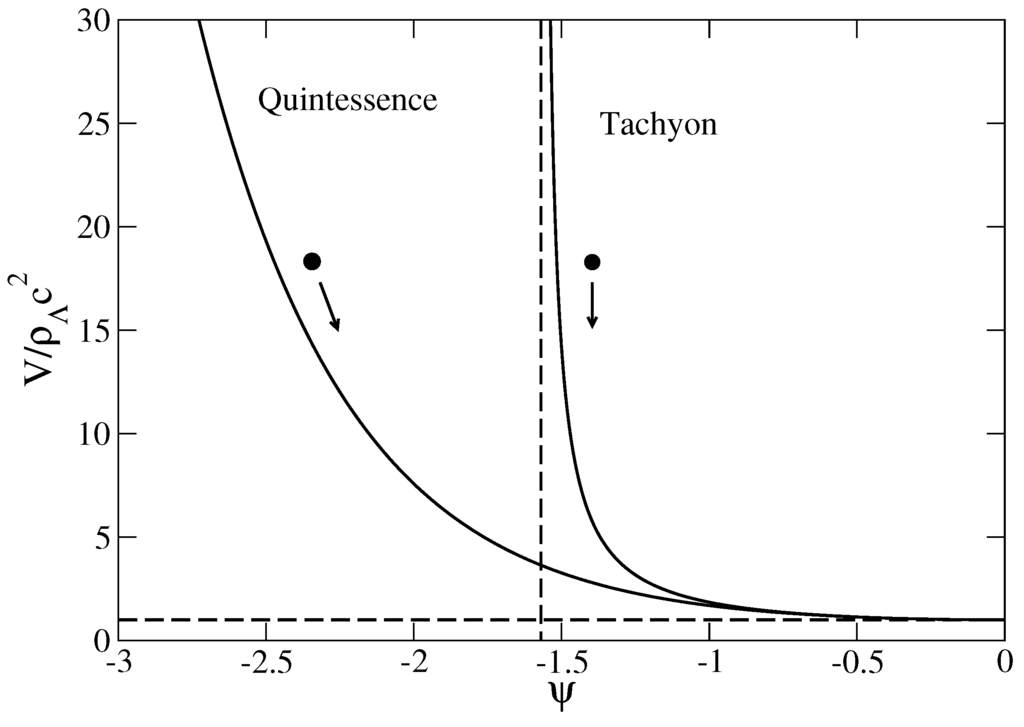
Figure 13.
Potential of the quintessence field and tachyonic field in the late universe. The field tends to run down the potential.
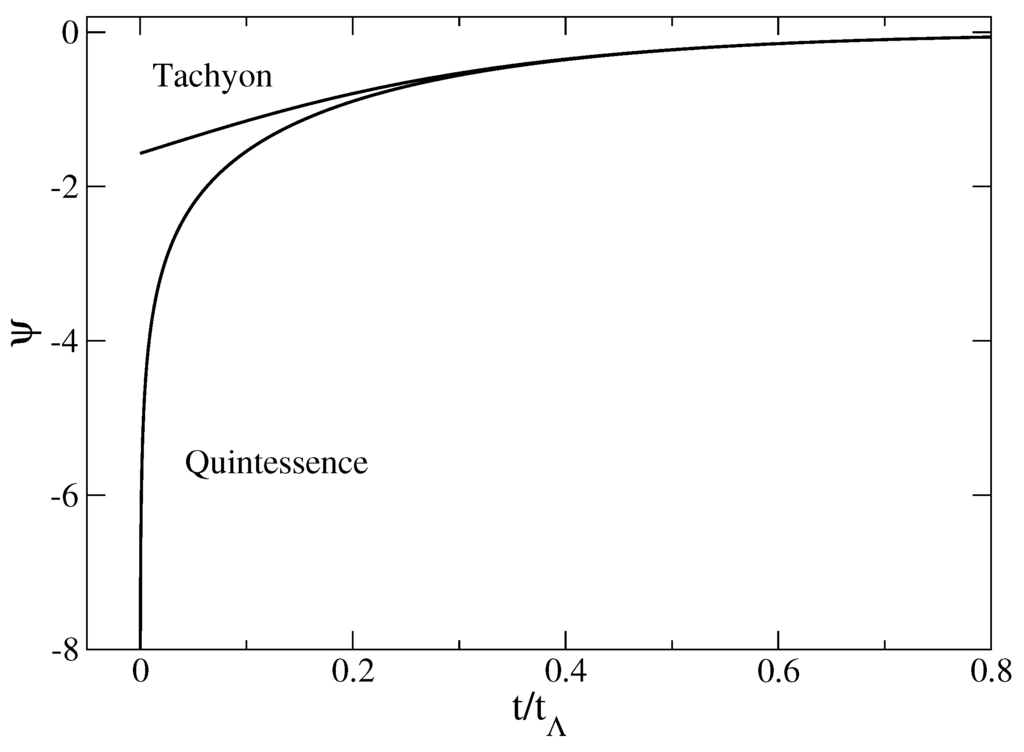
Figure 14.
Evolution of the quintessence field and tachyonic field as a function of time in the late universe.
Let us consider the equation of state (48) with the specific index (pressureless matter). Since is between and 0, the equation of state (48) can be associated with a tachyonic field. Using standard techniques [7,49], we find that its potential is (see Section 8.2 [30]):
where we have defined
For ,
For ,
We can also show [30] that the relation between the scalar field and the scale factor is
The end of the matter-era (), and the beginning of the dark energy era, corresponds to , hence to . Combining Equations (48), (49) and (77), we find that the energy density and the pressure of the universe are related to the scalar field by
Using Equation (77), and the results of the previous sections, we can obtain the temporal evolution of the scalar field. In the matter era (), using Equation (56), we get
In the dark energy era (), using Equation (54) with a prefactor , we get
More generally, using Equation (59), the evolution of the tachyonic field in the late universe is given by
These results are illustrated in Figure 13 and Figure 14 for (pressureless matter).
Remark: The canonical scalar field potential of Equation (62) describing the transition between the α-era and the dark energy era involves hyperbolic functions. It corresponds to the scalar field potential associated with the generalized Chaplygin gas (see Note 1) [37,38,39,40,41,42,43,44,45]. Other types of hyperbolic scalar field potentials have been introduced in the past. The first potential with hyperbolic functions driving the observed acceleration of the universe was proposed by Sahni and Wang [74] and has been confronted to the observations in [75]. Related potentials were considered in [76,77,78]. Models with hyperbolic potentials exploiting dynamical Noether symmetries of the field equations and admiting analytical solutions were constructed and compared with cosmological data in [79], finding a good agreement. On the other hand, the tachyonic scalar field potential of Equation (73) describing the transition between the α-era and the dark energy era involves trigonometric functions. A tachyonic field with a trigonometric potential was proposed in [80] to describe the transition between dark matter and dark energy. Interestingly, this model admits different solutions depending on the initial condition. It can either describe an eternally expanding universe or lead to a future finite time singularity, called Big Brake, which is characterized by an infinite deceleration. This model has been recently subjected to several cosmological tests in [81].
5. The General Model
5.1. The Quadratic Equation of State
We propose to describe the vacuum energy, the α-fluid, and the dark energy by a unique equation of state
where and are the polytropic indices of the early and late universe, respectively. For the sake of simplicity, and for definiteness, we shall select the indices and . Therefore, we consider the quadratic equation of state
For , (vacuum energy). For , (α-fluid). For , (dark energy). The pressure vanishes at and at . It has a maximum at . The pressure is negative for , positive for and negative for (to obtain these results, we have used the fact that ). The quadratic equation of state (83) combines the properties of the equation of state (18) valid in the early universe, and of the equation of state (48) valid in the late universe. A nice feature of this equation of state is that both the Planck density (vacuum energy) and the cosmological density (dark energy) explicitly appear. Therefore, this equation of state reproduces both the early inflation and the late inflation, described by an equation of state , in which the scale factor increases exponentially rapidly. They are connected by the α-era, with a linear equation of state , in which the scale factor increases algebraically. For , the universe is decelerating during this period.
The equation of state parameter and the deceleration parameter q are given by
The velocity of sound is given by
Using the equation of continuity (10), we get
To obtain this expression, we have used the fact that so that (see Appendix C). When , (vacuum energy). When , (α-era). When , (dark energy). In the early universe, the contribution of dark energy is negligible and we recover Equation (19). In the late universe, the contribution of vacuum energy is negligible and we recover Equation (49) with .
Using , where is the present density of the α-fluid and is the present distance of cosmological horizon determined by the Hubble constant (the Hubble time is ), we can rewrite Equation (86) in the form
Substituting this relation in the Friedmann equation (12), and writing and , where is the present density of the universe, we obtain
Using Equations (83) and (86), the pressure can be written in very good approximation as
Finally, if we assume that the α-fluid represents the radiation (), we find that the temperature associated with the quadratic equation of state (83) is given by a generalized Stefan-Boltzmann law (see Equation (C.4) in [30]).
5.2. The Early Universe
In the early universe, we can neglect the contribution of the dark energy in the density. We only consider the contribution of the vacuum energy and of the α-fluid. Equation (87) then reduces to
The Friedmann equation (88) becomes
It has the analytical solution given by Equation (29).
In the vacuum energy era (), the density is constant:
Therefore, the Hubble parameter is also a constant . In that case, the scale factor increases exponentially rapidly with time according to Equation (24).
In the α-era (), we have
The Friedmann equation (91) reduces to
The scale factor increases algebraically rapidly as
and the density decreases as
The transition between the vacuum energy era and the α-era corresponds to . This yields and . The inflation ends at the time . The universe starts decelerating when and . This corresponds to the first inflexion point of the curve . The universe is accelerating for and decelerating for . For , .
5.3. The Late Universe
In the late universe, we can neglect the contribution of the vacuum energy in the density. We only consider the contribution of the α-fluid and of the dark energy. Equation (87) then reduces to
The Friedmann equation (88) becomes
It has the analytical solution
This corresponds to the ΛCDM model. The density evolves as
Setting in Equation (99), we find the age of the universe [Note 8: Of course, for the determination of the age of the universe, we can neglect the contribution of the vacuum energy in the early universe and take (strictly speaking, the age of the universe is infinite since it has no origin; however, we define the age of the universe from the time at which ).]:
The present values of the equation of state parameter and deceleration parameter are
In the dark energy era (), the density is constant:
Therefore, the Hubble parameter is also a constant . Using Equation (99), we find that the scale factor increases exponentially rapidly as
This corresponds to de Sitter’s solution.
The transition between the α-era and the dark energy era corresponds to . This yields and . The universe starts accelerating when and . This corresponds to the second inflexion point of the curve . The universe is decelerating for and accelerating for . For , .
5.4. The General Solution
For the quadratic equation of state (83), the density is related to the scale factor by Equation (86). It is possible to solve the Friedmann equation (12) with the density-radius relation of Equation (86) analytically. Introducing and , we obtain
which can be integrated into
where and C is a constant determined such that at . This solution is interesting because it describes analytically a phase of early inflation and a phase of late inflation (or late accelerating expansion) connected by a power-law expansion (α-era). The corresponding scalar field theory is developed in Appendix A. We obtain a scalar field potential (see Equations (119)—(121)) that unifies the inflaton potential of Section 3.7 and the quintessence potential of Section 4.6.
5.5. The Whole Evolution of the Universe
In our model, the evolution of the scale factor is given by Equation (88). For , we obtain the same equation as in the ΛCDM model (slightly generalized to account for a possibly non-zero value of α) where the contributions of matter and dark energy are added individually [1]. However, the ΛCDM model does not describe the phase of early inflation and presents a singularity at (Big Bang). For , we obtain a generalized model which does not present a primordial singularity and which displays a phase of early inflation. In this model, the universe always existed in the past but, for , it has a very small radius, smaller than the Planck length [Note 9: Our semi-classical model certainly breaks down in this period since it does not take quantum fluctuations into account. The Planck era may not be described in terms of an equation of state , or even in terms of the Einstein equations, as we have assumed. It probably requires the development of a theory of quantum gravity that does not exist for the moment. An interesting description of the early inflation has been given by Monerat et al. [82] in terms of a quantized model based on a simplified Wheeler-DeWitt (WdW) equation. In that model, a quantum tunneling process explains the birth of the universe with a well defined size after tunneling.]. At , it undergoes an inflationary expansion in a very short lapse of time of the order of the Planck time. For , this model gives the same results as the ΛCDM model (see Equation (98)): the universe first undergoes an algebraic expansion in the α-era, then an exponential expansion (late inflation) in the dark energy era. A nice feature of this model is its simplicity since it incorporates a phase of early inflation in a very simple manner. We just have to add a term in the standard Equation (98) of the ΛCDM model. This term has the effect of a small scale cut-off. Therefore, the modification implied by Equation (88) to describe the early inflation is very natural. On the other hand, this model gives the same results in the late universe as the standard ΛCDM model, so this does not bring any modification to the usual Equation (98). Therefore, our model completes the standard ΛCDM model by incorporating the phase of early inflation in a natural manner. This is an interest of this description since the standard ΛCDM model gives results that agree with the observations after the Planck era.
In Figure 15 and Figure 16, we have represented the evolution of the scale factor and density of the universe as a function of time. The universe exhibits two types of inflations: an early inflation due to the Planck density (vacuum energy) and a late inflation due to the cosmological density (dark energy). They are connected by an α-era during which the scale factor and the density evolve algebraically. In this period, the universe is decelerating (for ). There exists a striking “symmetry” between the early and the late evolution of the universe. The early universe is described by a polytropic equation of state of index and the late universe is described by a polytropic equation of state of index . On the other hand, the cosmological constant Λ in the late universe plays the same role as the Planck constant ℏ in the early universe. In particular, Figure 16 shows that the density varies between two bounds and that are fixed by fundamental constants [Note 10: these bounds come from the properties of the polytropic equation of state (1). This is a bit similar to the bound on the mass of white dwarf stars (Chandrasekhar’s mass) which also comes from the properties of a polytropic equation of state with index describing an ultra-relativistic degenerate fermionic gas [83].]. These values differ by a factor of the order of . The early universe is governed by quantum mechanics (ℏ) and the late universe by general relativity (Λ).
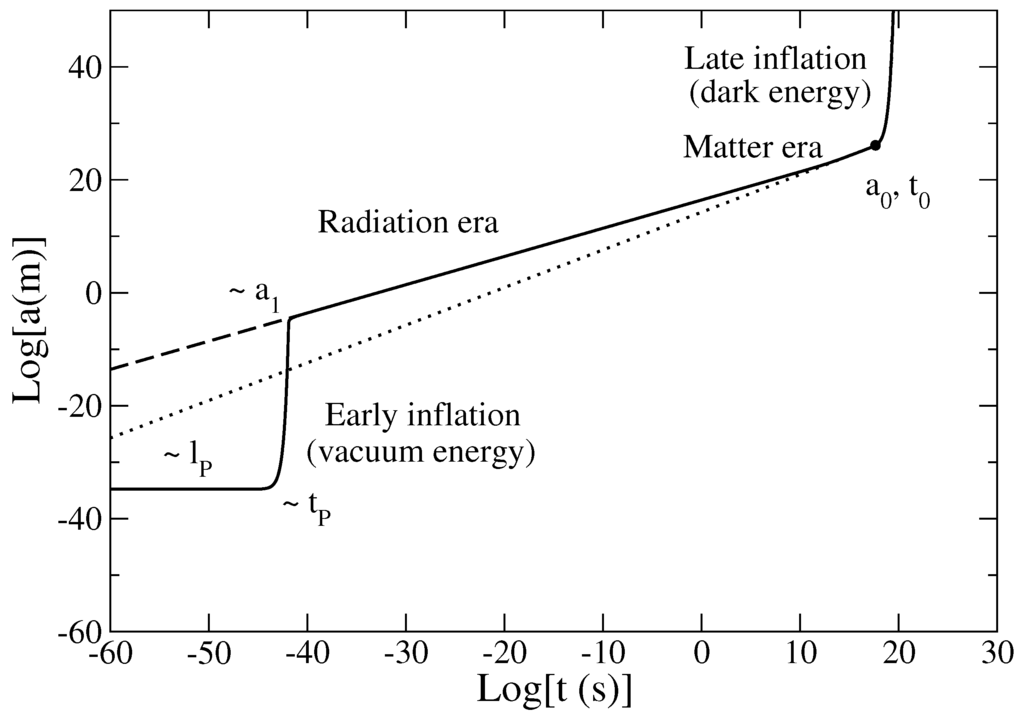
Figure 15.
Evolution of the scale factor a as a function of time in logarithmic scales. The universe exists at all times in the past and in the future and there is no singularity (aioniotic universe). The universe first undergoes a phase of early inflation (Planck era) due to the vacuum energy during which the scale factor increases exponentially rapidly on a timescale of the order of the Planck time (for it increases by 29 orders of magnitude in less than s). This is followed by the α-era during which the scale factor increases algebraically (). The dashed line corresponds to (radiation) and the dotted line corresponds to (matter). Without the early inflation, the universe would exhibit a primordial singularity (Big Bang). Finally, the universe undergoes a phase of late inflation (de Sitter era) due to the dark energy during which the scale factor increases exponentially rapidly on a timescale of the order of the cosmological time . The universe exhibits two types of inflation: an early inflation corresponding to the Planck density (vacuum energy) due to quantum mechanics (Planck constant) and a late inflation corresponding to the cosmological density (dark energy) due to general relativity (cosmological constant). The evolution of the early and late universe is remarkably symmetric. In our model, it is described by two polytropic equations of state with index and that can be combined into a single quadratic equation of state (83). The expansion of the universe is accelerating during the phases of inflation and decelerating during the α-era (if ). We have also represented the location of the present universe (bullet). It happens to be just at the transition between the matter era and the dark energy era (see Section 5.6).
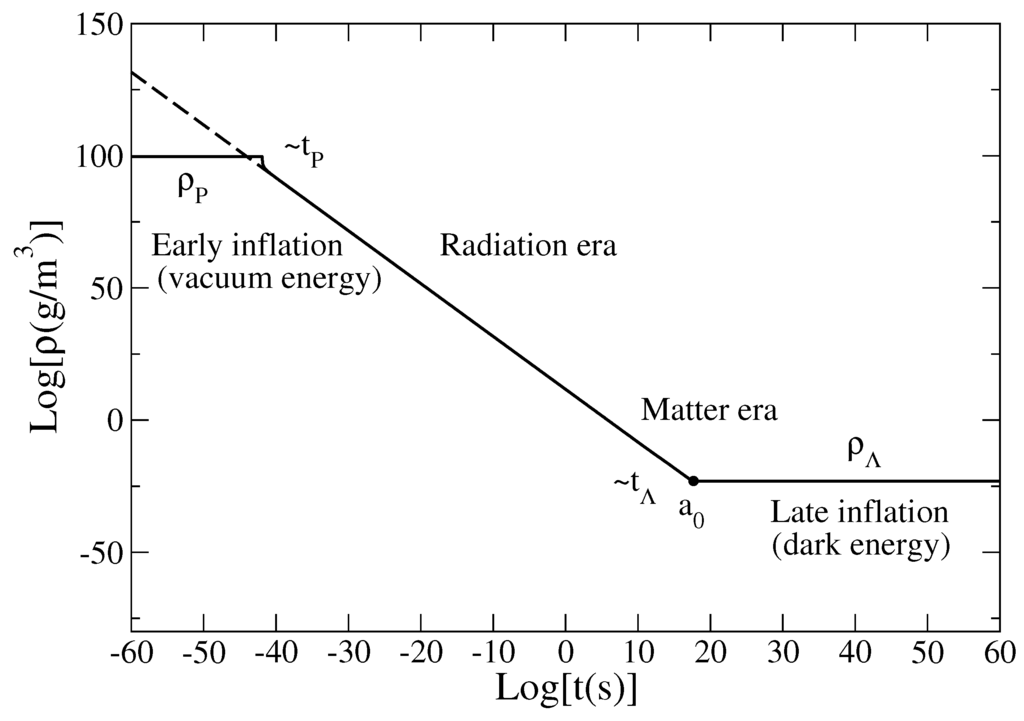
Figure 16.
Evolution of the density ρ as a function of time in logarithmic scales. The density goes from a maximum value determined by the Planck constant (quantum mechanics) to a minimum value determined by the cosmological constant (general relativity). These two bounds, which are fixed by fundamental constants of physics, are responsible for the early and late inflation of the universe. In between, the density decreases as .
5.6. The Cosmic Coincidence Problem
Let us consider the transition between the matter era () and the dark energy era described by Equation (98). It is striking to note that the present size of the universe is precisely of the order of the transition scale (). We have and . Therefore, we live just at the transition between the matter era and the dark energy era (see the bullets in Figure 9, Figure 10, Figure 11 and Figure 12, Figure 15 and Figure 16). In the context of the standard ΛCDM model, the way to state this observation is to say that the present ratio between dark energy and matter is of order unity. Since the matter density changes as the ratio between matter and dark energy is of order unity only during a “brief” period of time in the evolution of the universe. It turns out that we live precisely in this period. This coincidence [Note 11: We should be careful about this statement. It is true that the order of magnitude of and is the same. As a result, these two times appear very close to each other on a logarithmic scale (see Figure 9 and Figure 11). However, on a linear scale, these two times differ by (see Figure 10 and Figure 12). In this sense, there is no real coincidence.] is intriguing and often referred to as the “cosmic coincidence problem” [84]. Several theories have been proposed to explain why [85,86,87,88]. However, this may be just a pure coincidence without deeper reason. Life (and researchers inquiring about cosmology) may have emerged at this special moment of the history of the universe, Gyrs after the Big Bang, precisely at the epoch where . Life cannot have emerged much earlier because galaxies, stars and planets are not created, and it may not persist much later because planets, stars, and galaxies will die. Therefore, this coincidence is not really a “problem”. Furthermore, we note that, in our model, matter and dark energy are two manifestations of the same fluid described by a single equation of state (48). Since we are considering a single “dark” fluid, the cosmic coincidence problem discussed above may be alleviated.
5.7. The Cosmological Constant Problem
The cosmological constant Λ is equivalent to a constant density called dark energy. Its value resulting from observations is . It is oftentimes argued that the cosmological density should correspond to the vacuum energy density due to quantum fluctuations [89,90,91]. However, according to particle physics and quantum field theory, the vacuum energy density is of the order of the Planck density which is times larger than the cosmological density. This leads to the so-called cosmological constant problem [46,47].
Actually, as illustrated in Figure 16, the Planck density and the cosmological density represent fundamental upper and lower density bounds acting in the early and late universe, respectively. It is not surprising therefore that they are so different: . Because of these bounds, the universe undergoes two phases of inflation. The inflation in the early universe is due to quantum mechanics (Planck constant) and is related to the Planck density (vacuum energy). The inflation in the late universe is due to general relativity (cosmological constant) and is related to the cosmological density (dark energy). Quantum mechanics is negligible in the late universe. Therefore, we should not identify the dark energy (or the cosmological constant) with the vacuum energy. The cosmological constant should be interpreted as a fundamental constant of physics. It applies to the very large universe (cosmophysics) exactly like the Planck constant applies to the very small universe (microphysics). Actually, there is a complete symmetry between the small and large universe where ℏ and Λ play symmetric roles. Therefore, we propose to interpret the cosmological constant as a fundamental constant of physics describing the cosmophysics (late universe) in the same sense that the Planck constant describes the microphysics (early universe).
If this interpretation is correct, the origin of the dark energy density should not be sought in quantum mechanics, but in pure general relativity. In this sense, the cosmological constant “problem” may be a false problem. If Λ is a fundamental constant of physics, independent from the others, its value should not cause problem. It is fixed by nature, just like the values of G, c, and ℏ. In other words, it has the value that it has! One can just expect that is “very large” and is “very small”. Of course, the origin of the cosmological constant still needs to be understood by developing a theory of cosmophysics. In addition, it would be important to understand why and represent upper and lower bounds, and if these bounds are as fundamental as, for example, the bound on the velocity fixed by the speed of light.
5.8. A Generalization of the ΛCDM Model Incorporating a Phase of Early Inflation
In the standard ΛCDM model, radiation, baryonic matter, dark matter and dark energy are treated as four independent species characterized by different equations of state [1]. The equation of state is for radiation, for baryonic matter and dark matter, and for dark energy. We then solve the equation of continuity (10) for these four species in order to obtain the relation between their density and the scale factor, i.e., , , , and . Finally, we add their individual densities and substitute in the Friedmann equation (12). This leads to the standard equation [1]:
with . From observations , , , , and [1]. The ΛCDM model provides a good description of the universe after the Planck era. It describes the radiation era, the matter era, and the dark energy era (late accelerating expansion). However, it exhibits a primordial singularity at (Big Bang). Furthermore, it does not describe the phase of early inflation. This phase is usually described by another theory, e.g., a scalar field theory [2,3,4,5], that is then connected to the ΛCDM model.
Our approach is physically different from the ΛCDM model and generalizes it. In our model, based on the quadratic equation of state (83), the evolution of the scale factor is given by Equation (88). For , Equation (88) takes a form similar to Equation (107) of the ΛCDM model. For , it describes the transition between the radiation era and the dark energy era. For , it describes the transition between the matter era (having possibly a small temperature) and the dark energy era. However, this approach is incomplete. Indeed, the equation of state (83) is not able to describe the transition between the radiation era and the matter era. It can only describe one of these two phases depending on the chosen value of α. This is not a drawback of the model. Indeed, there is no reason to “unify” radiation and matter in a single equation of state. Radiation and matter are different entities that should be treated as two different species as in the standard ΛCDM model. By contrast, our approach suggests that vacuum energy, radiation, and dark energy may be the manifestation of a unique form of “generalized radiation”. Therefore, by selecting in Equation (83) we obtain an equation of state
that unifies vacuum energy, radiation, and dark energy. This leads to the density (see Equation (87)):
This “generalized radiation” is one component of the Friedmann equation (12). Then, the contribution of baryonic matter and dark matter is introduced in the Friedmann equation (12) as other species described by the equation of state leading to a density (or by the equation of state with leading to a density if we take into account the effect of a small temperature). As a result, we obtain the complete equation [Note 12: By selecting in Equation (83) we could unify vacuum energy, matter and dark energy, then introduce radiation as an independent species with an equation of state leading to a density . However, we believe that it is more relevant to unify vacuum energy, radiation and dark energy, and treat baryonic matter and dark matter as independent species. We note that baryonic matter and dark matter must be introduced at sufficiently late time in Equation (110) in order to avoid a spurious divergence when due to the fact that in our model. For exemple, we can replace and by and , where H is the Heaviside function.]:
with . For , our model gives the same result as the ΛCDM model of Equation (107), although the justification is different. This is a good thing because it ensures that our model produces results that agree with the observations after the Planck era (i.e., for ). For , our model generalizes the ΛCDM model of Equation (107) by naturally incorporating a phase of early inflation and avoiding the primordial singularity, as discussed in Section 5.5. Equation (110) is interesting because it describes the early inflation (Planck era), the radiation era, the matter era, and the dark energy era (de Sitter era) in a self-consistent manner. The evolution of the scale factor with time is obtained by solving the first order differential Equation (110). This yields
where in the standard ΛCDM model and in our model. This is how we have obtained the solid curves of Figure 15 and Figure 16. They provide the complete evolution of the universe from the early inflation to the late acceleration. The age of the universe is
Of course, for the determination of the age of the universe we can neglect the vacuum energy era and take . We obtain the standard result [Note 13: The Hubble constant is usually written as where the dimensionless parameter is about of unity [1]. For simplicity, we have taken in the numerical applications. The current value is . If we take , the age of the universe is .]. Actually, we find the same result if we neglect radiation and use the analytical expression of Equation (101) with instead of Equation (112).
5.9. Discussion
The main novelty of our paper is the quadratic equation of state (2). To the best of our knowledge, this equation of state has never been introduced before. A nice feature of this equation of state is that it incorporates both the Planck density (vacuum energy) and the cosmological density (dark energy). We are not aware of any equation of state of that kind. For example, the usual equation of state used to model the primordial inflation or the late acceleration of the universe leads to a constant density but the value of this density cannot be read from the equation of state itself and it has to be adapted, rather arbitrarily, to the situation (e.g., one takes to describe the early inflation and to describe the late acceleration). In Equation (2) there is no arbitrariness since this equation of state explicitly contains and as parameters. This equation of state naturally imposes in the early universe and in the late universe. These two densities appear as fundamental upper and lower bounds in the model. In this sense, the equation of state (2) with suggests a sort of “unification” of vacuum energy, radiation, and dark energy. This may be the same entity, a “generalized radiation”, described by a unique equation of state (2), but its density is very different in the early and in the late universe causing an early inflation and a late acceleration.
Our aim was to show that this equation of state is “viable” and that it can reproduce the basic features of the universe. To that purpose, we considered its limiting behavior in the early and in the late universe:
(i) In the late universe, the equation of state (2) reduces to Equation (48) which can be viewed as a generalized Chaplygin/polytropic gas model with . This model is physically different from the usual ΛCDM model but it gives the same results. Therefore, it is able to reproduce the observations. This shows that the equation of state (2) is viable in the late universe.
(ii) In the early universe, the equation of state (2) reduces to Equation (18) which can be viewed as a generalized Chaplygin/polytropic gas model with . This model is different from the usual models of inflation [2,3,4,5] but it gives similar results. In particular, it can account for an increase of the scale factor by about 29 orders of magnitude in less than . It would be important to determine whether this equation of state can reproduce the observed primordial fluctuations and power spectrum. This problem has been considered recently in [92,93,94]. The conclusion of these works is that the polytropic equation of state represents a robust and interesting scenario to study the evolution of the universe. Therefore, the equation of state (2) may be viable in the early universe.
(iii) In between, the equation of state (2) reduces to a linear equation of state describing a phase of decelerating expansion (when ).
As a whole, the equation of state (2) describes an early and late acceleration connected by a deceleration phase. Therefore, it accounts for the basic features of the universe and it may be viable. The drawback of the ΛCDM model is that it does not describe a phase of early inflation and displays instead a primordial singularity (Big Bang). The equation of state (2) returns the result of the ΛCDM model for sufficiently late times but it also naturally incorporates a phase of early inflation. As a result, it describes the early inflation and the late acceleration simultaneously. This is the main interest of this model.
Interestingly, the phase of early inflation and the phase of late acceleration are described by two symmetric (or dual) Chaplygin/polytropic gas models with index and , respectively. The quadratic equation of state (2) combines these two symmetric models into a single equation of state. As a result, this equation of state displays both a phase of early inflation driven by the Planck density and a phase of late acceleration driven by the cosmological density . These two phases are bridged by a phase of deceleration. The pressure is successively negative (vacuum energy), positive (α-era), and negative again (dark energy).
There has been many works attempting to unify two phases (deceleration + acceleration) in the evolution of the universe with a unique equation of state of the Chaplygin form [37,38,39,40,41,42,43,44,45]. We have proposed in this paper to unify three phases (inflation + deceleration + acceleration) with the quadratic equation of state (2), or more generally with Equation (82), which can be viewed as a generalized Chaplygin gas model.
6. Conclusions
We have constructed a cosmological model based on the quadratic equation of state (2). This equation of state describes the evolution of a universe presenting a phase of early inflation (Planck era), a phase of decelerating expansion (α-era), and a phase of late accelerating expansion (de Sitter era). An interest of this model is its simplicity (while being already quite rich) and the fact that it admits a fully analytical solution (see Equation (106)). It provides a particular solution of the Friedmann equations. In addition, it is in qualitative agreement with the evolution of our own universe. Finally, it admits a scalar field interpretation based on an inflaton, quintessence, or tachyonic field.
This model does not present any singularity and exists “eternally” in the past and in the future, so that it has no origin nor end (we call it aioniotic universe). In particular, the phase of early inflation avoids the Big Bang singularity and replaces it by a sort of second order phase transition where the non-zero value of the Planck constant ℏ plays the same role as finite size effects in statistical mechanics. Of course, it is probably incorrect to extrapolate the results in the infinite past since our model is purely classical, or semi-classical, and does not take quantum gravity into account. In our model, the universe starts from but, for , its size is less than the Planck length . In the Planck era, the classical Einstein equations may be incorrect and should be replaced by a theory of quantum gravity that still has to be constructed.
Another interest of this model is that it describes the early universe and the late universe in a symmetric manner. The early universe is described by a polytrope and the late universe by a polytrope . The mathematical formulae are then strikingly symmetric (we sum the inverse of the densities in the early universe and we sum the densities in the late universe). Furthermore, the Planck density in the early universe plays the same role as the cosmological density in the late universe. They represent fundamental upper and lower density bounds differing by 122 orders of magnitude. They lead to phases of early and late inflation with very different timescales and . The densities and (together with α) appear as the coefficients of the equation of state (2). Therefore, this equation of state provides a “unification” of vacuum energy and dark energy.
A limitation of this equation of state is that it cannot describe the transition between the radiation era and the matter era because they are both described by a linear equation of state with and respectively. Therefore, the equation of state (2) with describes a universe without matter while the equation of state (2) with describes a universe without radiation. A better model can be achieved by letting vary with time and decrease smoothly from to 0. Alternatively, we can “unify” vacuum energy + radiation + dark energy into a “generalized radiation” described by the equation of state (2) with and treat baryonic matter and dark matter as independent species described by the equations of state and . This general approach (see Section 5.8) allows us to describe the complete evolution of the universe (inflation + radiation + matter + acceleration). It leads to an interesting generalization of the ΛCDM model where Equation (107) is replaced by Equation (110). As a result, our model generalizes the standard ΛCDM model by incorporating naturally a phase of early inflation that avoids the primordial singularity. Furthermore, it describes the early inflation and the late acceleration simultaneously with a single equation of state that unifies vacuum energy and dark energy, and a single scalar field potential that unifies the inflaton potential and the quintessence potential (see Appendix A).
Dark matter is usually described by a pressureless equation of state . This leads to the famous Einstein-de Sitter (EdS) model. However, there are indications that dark matter may be described by an isothermal equation of state with [48]. Therefore, it is useful to provide general results valid for arbitrary values of α as we have done here. This allows us to describe either radiation (), pressureless matter (), or isothermal matter ().
In this paper, for definiteness, we have selected the indices and in Equation (82) to describe the early and the late universe respectively. As we have seen, the equation of state (82) with leads to results that coincide with the ΛCDM model in the late universe. This equivalence is not trivial since our approach is fundamentally different from the ΛCDM model (in particular this coincidence is not true anymore for ). Since the ΛCDM model provides a good description of the universe after the Planck era, this implies that observations tend to favor the value of the polytropic index. This is a reason why we have selected this index. However, we can obtain more general models by taking different from . In particular, a value of close to may be consistent with the observations and may improve upon the ΛCDM model. In this respect, Asadzadeli et al. [95] have shown that the observations constrain the index to be in the range or at and confidence levels, respectively. On the other hand, we have selected the index in Equation (82) to describe the inflation in the early universe. More general models of inflation can be obtained by selecting other values of . The value of could be determined from the measurements of the cosmic microwave background (CMB) radiation. Therefore, possible extensions of our study would be to consider the generalized equation of state (82) with arbitrary values of and . General results valid for the asymptotic expressions (Equations (17) and (47)) of the equation of state (82) in the early and late universe are given in [29,30,31].
A weakness of our work is that we have not given a justification of the quadratic equation of state (2) [Note 14: It would be of considerable interest to justify this equation of state from a microscopic model of radiation since we argued that this equation of state provides an effective model of “generalized radiation”. The quadratic equation of state (18) and the analytical solution of Equation (29) describing the phase of inflation were first given in [96] in relation to Bose-Einstein condensates (BECs) with an attractive self-interaction (negative scattering length ). Although this BEC model may be too simplistic (see the discussion in Appendix B of [29]), it shows how a quadratic equation of state with a negative pressure may arise in practice. We may also draw an analogy between the BEC model and the primeval atom of Lemaître [97].]. However, since this equation of state is connected to the Chaplygin gas model, there is some hope that this equation of state could arise from fundamental theories since the original Chaplygin gas model [37,38,39,40,41,42,43,44,45] is motivated by some works on string theory. It can be obtained from the Nambu-Goto (or Born-Infeld) action for d-branes moving in a -dimensional spacetime in the light-cone parametrization [Note 15: We also note that a theoretical justification of a polytropic equation of state of the form with for a perfect relativistic fluid in cosmology has been given recently by Kazinski [98] in relation to the quantum gravitational anomaly.]. We may also argue that the quadratic equation of state (2) (and its generalization in Equation (82)) is the “simplest” equation of state that we can imagine in order to obtain a non singular model of universe (see the discussion in Section 7.4 of [30]). This “simplest” model is in agreement with the known properties of our universe. It is interesting that these properties can be reproduced by an equation of state of the form where the three coefficients are related to ℏ, α, and Λ.
In this paper, the quadratic equation of state (2) has been introduced heuristically in order to obtain a cosmological model that describes simultaneously a phase of inflation, a phase of decelerating expansion, and a phase of acceleration. The Planck constant ℏ and the cosmological constant Λ are interpreted as two fundamental constants fixed by nature that appear in the coefficients of this equation of state. In a sense, this equation of state can be viewed as a simple interpolation formula between different, well-motivated, equations of state. Interpolation formulae are often useful in physics and the equation of state (2) is also interesting in this respect.
The next step would be to study the growth of perturbations in our model. In particular, it would be important to confront the model of inflation based on the polytropic equation of state (15) to the Planck 2015 data set. In this respect, it may be necessary to use the scalar field interpretation instead of the hydrodynamic interpretation because it is known that, although the hydrodynamic and scalar field equations coincide at the background level, they may show differences at the level of the perturbations. A first study has been made in this direction by Freitas and Gonçalves [94] using our model of inflation. They studied the primordial quantum fluctuations in the slow-roll approximation and calculated the scalar perturbations, the scalar power spectrum, and the spectral index. They obtained encouraging results, but some of their results need to be further developed. This will be considered in future works.
Remark: In this paper, we have proposed to describe the complete evolution of the universe (early and late inflation) by the quadratic equation of state (2). A quadratic equation of state aiming at describing the late acceleration of the universe has been considered in [63,64,99,100] and compared to the observations by Sharov [101]. Sharov mentions that a quadratic equation of state with a positive coefficient in front of can lead to past singularities. In the present paper, we have considered a quadratic equation of state with a small negative coefficient in front of (of the order of ), so that the quadratic term accounts for the early inflation, not for the late acceleration. This is why we do not have past singularities in our model (the universe exits at any time in the past). The possibility of past singularities when the coefficient in front of is positive is discussed in [29].
Conflicts of Interest
The author declares no conflict of interest.
Appendix
A. Scalar Field Theory
In this Appendix, we determine the canonical scalar field potential and the tachyonic potential corresponding to the quadratic equation of state (83). Interestingly, this scalar field theory describes, with a single potential, the whole evolution of the universe, from the early inflation to the late acceleration, passing through a phase of algebraically decelerating expansion.
A.1. Canonical Scalar Field
We consider a canonical scalar field defined by Equations (33) and (34). From Equation (34), we get
where we recall that . Using and the Friedmann equation (12) valid for a flat universe, we find that the relation between the scalar field and the scale factor is given by
On the other hand, according to Equation (34), the potential of the scalar field is given by
For the quadratic equation of state (83), we have
and
where and . With the change of variables
we obtain after simple calculations (using the fact that to simplify some terms):
where is the Jacobian Elliptic function. We have where is the Elliptic integral of the first kind. We have taken when . Equations (119) and (120) define the potential in parametric form with parameter x going from 0 to . The scalar field goes from to where K is the complete Elliptic integral of the first kind [Note 16: For , we have as will be found below by a different method.]. Eliminating x between Equations (119) and (120), we get
In the early universe, we can neglect the dark energy () so that Equations (119) and (120) reduce to
Equations (122) and (123) are equivalent to Equations (35) and (40) defining the inflaton potential
In the late universe, we can neglect the vacuum energy (which amounts to taking ) so that Equations (119) and (120) reduce to
where is a constant of integration. Equations (125) and (126) are equivalent to Equations (62) and (66) defining the quintessence potential
where we have arbitrarily taken in Equations (62) and (66). Therefore, the scalar field potential defined by Equation (121) provides a unification of the inflaton and quintessence potentials defined by Equations (124) and (127) respectively.
The constant can be obtained by matching the solutions from Equations (122), (123), (125) and (126) in the intermediate region of algebraic expansion (α-era). First, we note that for () and for (). For , Equations (122) and (123) reduce to and yielding
On the other hand, for , Equations (125) and (126) reduce to and yielding
This exponential potential corresponds to the potential of a scalar field with a linear equation of state (see, e.g., Section 8.1 of [30]). Comparing Equations (128) and (129), we find that
We note that is of the order of the famous number appearing in relation to the cosmological constant problem [46,47]. Using Equations (106) and (119), we can obtain the evolution of the scalar field with time. Using the asymptotic results of Section 3 and Section 4, we find that the scalar field evolves as in the vacuum energy era, as in the α-era, and as in the dark energy era. Some representative curves are shown in Figure A1, Figure A2, Figure A3 and Figure A4 for .

Figure A1.
Potential in logarithmic coordinates.
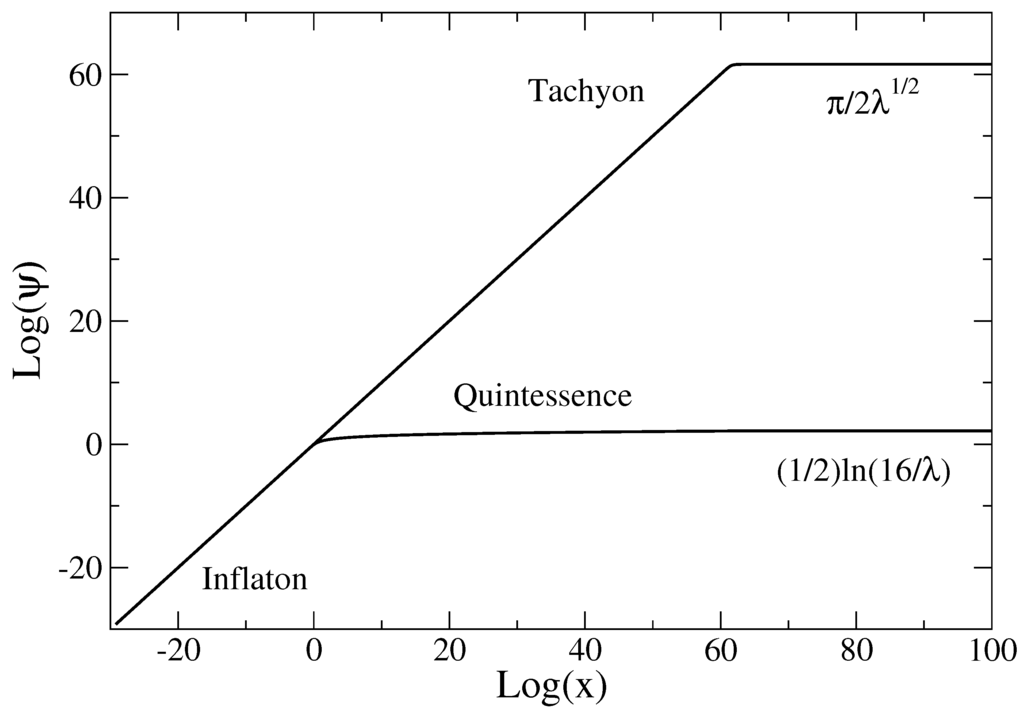
Figure A2.
Evolution of the scalar field ψ with the normalized scale factor x in logarithmic coordinates.
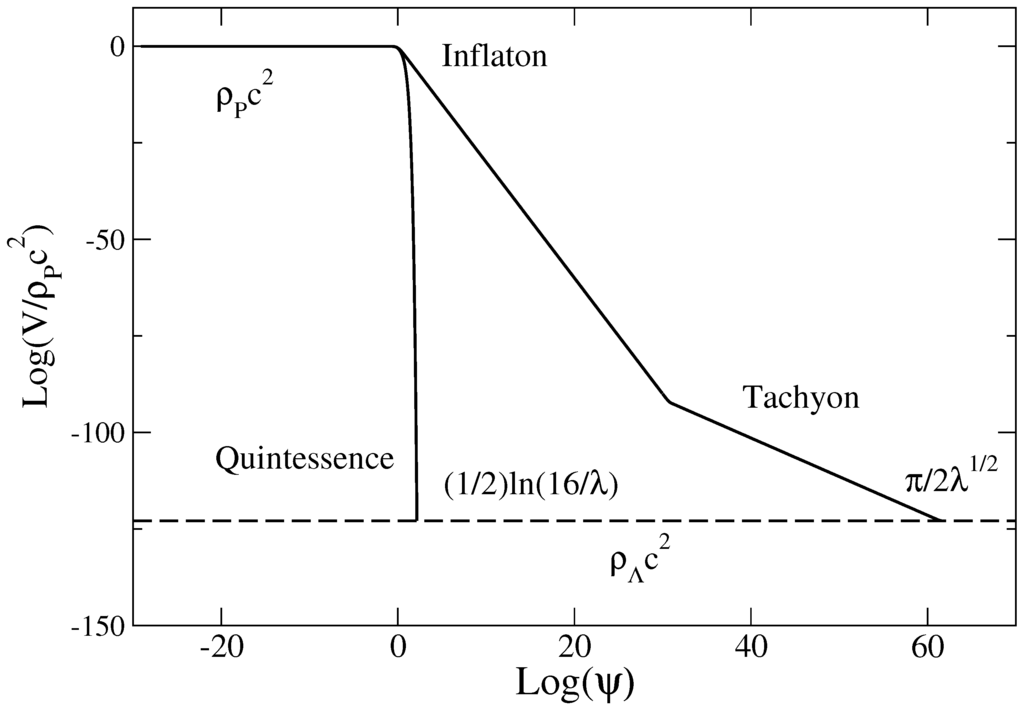
Figure A3.
Potential in logarithmic coordinates.

Figure A4.
Evolution of the scalar field ψ with the normalized time in logarithmic coordinates.
Remark: Using matched asymptotics, we can propose a simple analytical expression of the scalar field potential that unifies the inflaton and quintessence potentials. Indeed, the following potential
provides a good approximation of the exact potential given by Equation (121).
A.2. Tachyonic field
We consider a tachyonic field defined by Equations (71) and (72). From Equation (72), we get
Using and the Friedmann equation (12) valid for a flat universe, we find that the relation between the tachyonic field and the scale factor is given by
On the other hand, according to Equation (72), the potential of the scalar field is given by
The tachyonic field is defined provided that . This is the case for all times with the quadratic equation of state (83) when . Using Equations (116) and (117) and making the change of variables
we obtain after simple calculations (using the fact that to simplify some terms):
We have taken when . Equations (136) and (137) define the potential in parametric form with parameter x going from 0 to . The scalar field goes from to . Eliminating x between Equations (136) and (137), we obtain
For , we get
In the early universe, we can neglect the dark energy () so that Equations (136) and (137) reduce to
giving
For , we get
For , we have . For we obtain if and if . In the late universe, we can neglect the vacuum energy (which amounts to taking ) so that Equations (136) and (137) reduce to
giving
For , we get
Equations (143) and (145) are equivalent to Equations (73) and (77) where we have arbitrarily shifted by . For (), we have . For (), we have and we obtain if and if . The algebraic potential corresponds to the potential of a tachyonic field with a linear equation of state (see, e.g., Section 8.2 of [30]) [Note 17: For , the tachyonic scalar field potential behaves as at the end of the early universe and as at the beginning of the late universe (this is because the potential of a tachyonic field with an equation of state degenerates to when ; see, e.g., Section 8.2 of [30]). This implies a discontinuity of during the matter era as is apparent on Figure A1 and Figure A3.]. Using Equations (106) and (136), we can obtain the evolution of the scalar field with time. Using the asymptotic results of Section 3 and Section 4, we find that the tachyonic field evolves as in the vacuum energy era, as in the α-era, and as in the dark energy era. Some representative curves are shown in Figure A1, Figure A2, Figure A3 and Figure A4 for .
B. Further Generalizations of the Cosmological Model
In the standard model of cosmology, the universe undergoes a radiation era, a (baryonic + dark) matter era, and a dark energy era. These different phases are described by a linear equation of state with for the radiation, for the pressureless matter (including baryonic matter and dark matter), and for the dark energy. The corresponding evolution of the universe is described by Equation (107). It has been proposed in certain cosmological models [102,103,104,105,106] that the universe also experiences a primordial stiff matter era during which the speed of sound is equal to the speed of light (). This phase is described by a linear equation of state with . If we take into account a stiff matter era, Equation (107) is generalized into
For convenience, we have written . Even more generally, we can introduce an α-era with an equation of state so that Equation (146) becomes
The α-fluid may describe a new hypothetical fluid that dominates in the very early universe (if ). Alternatively, the exponent α may be a convenient notation standing for stiff matter (), radiation () or pressureless matter () depending on the situation contemplated.
The cosmological model defined by Equation (147) generates a primordial Big Bang singularity in which the energy density diverges as the scale factor goes to zero. Using the procedure introduced in this paper, it is easy to modify Equation (147) so as to incorporate an inflation era that replaces the initial Big Bang singularity. Indeed, we can describe the transition between an inflation era and a generic α-era by an equation of the form
with . This corresponds to the model of Section 3 based on the quadratic equation of state (18). We can generalize this model further by considering a polytropic equation of state of the form of Equation (17) with an arbitrary index . In that case, we obtain
The cosmological model defined by Equation (149) exhibits a phase of early inflation followed by an α-era (which may represent a new exotic era, a stiff matter era, or a radiation era), a radiation era (if different from the α era), a matter era, and a dark energy era.
Remark: An additional generalization may be introduced if dark matter is made of Bose-Einstein condensates (BECs) instead of being pressureless. In that case, the term should be replaced by as proposed in References [96,107]. It is shown in these papers that the presence of BECs can substantially accelerate the formation of large-scale structures in the universe.
C. Exact Solution of the Quadratic Equation of State
In this Appendix, we present the exact solution of the quadratic equation of state (83) and show the extreme relevance of the approximations made in the core of the paper.
Substituting the equation of state (83) in the equation of continuity (10) and solving the resulting differential equation by retaining all the terms, we obtain after elementary calculations
where we recall that . Since by 123 orders of magnitude (!), we see that the approximations leading to Equation (86) are excellent.
Substituting Equation (150) into the Friedmann equation (12) and introducing the notation , we obtain
with
Since , we have , , , and in excellent approximation. We note that Equation (151) has the same form as Equation (105) with the star variables. Therefore, its solution is given by Equation (106) where κ, λ and are replaced by , and . For (early inflation), we get
For (late inflation), we get
Again, since , we commit almost no mistake by replacing the star variables by the naked ones.
D. Scalar Field Theory Taking into Account the Presence of Radiation and Matter
We assume that the universe contains radiation
and (baryonic + dark) matter
The relations on the right between the density and the scale factor have been obtained from the equation of continuity (10) applied to each species considered as a perfect fluid.
In order to unify vacuum energy () and dark energy (), we assume that the universe contains a scalar field with a quadratic equation of state
The α-component may represent radiation () or dark matter (), or be a new species. The scalar field evolves according to the Equations (33) or (71) that describe a canonical or a tachyonic scalar field, respectively. We can check that they imply the equation of continuity for the scalar field
Therefore, the energy density of the scalar field is given by (see Section 5.1):
The Friedmann equation taking into account the contribution of all the species writes
If radiation or dark matter is included in the scalar field, it should not be counted as a new species, i.e., one should set or in Equation (161). Following the suggestion of Section 5.8, we should include radiation in the scalar field so that [and in Equation (161)] but, for the sake of generality, we leave α unspecified.
Generalizing the procedure of Appendix A by taking into account the presence of radiation and matter, we find that the potential of the canonical scalar field is determined by the equations
We have defined , , and . We have assumed that at the present epoch (). If we take , considering a single scalar field, we recover the results of Appendix A. Therefore, the present Appendix generalizes the results of Appendix A by taking into account the presence of radiation and matter. Although it does not seem possible to obtain the scalar field potential analytically, it can be obtained numerically and it provides a unification of vacuum energy (inflaton) and dark energy (quintessence) in the presence of radiation and matter. In very good approximation (using the fact that ), we obtain
In the early universe (), we can make the approximation
In the late universe (), we can make the approximation
Generalizing the procedure of Appendix A by taking into account the presence of radiation and matter, we find that the potential of the tachyonic scalar field is determined by the equations
If we take , considering a single scalar field, we recover the results of Appendix A. In very good approximation (using the fact that ), we obtain
In the early universe (), we can make the approximation
In the late universe (), we can make the approximation
In conclusion, we have given the general equations that allow us to construct the scalar field potential that unifies the inflaton and quintessence potentials in the presence of radiation and matter. The physical consequences of this model will be developed elsewhere.
References
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J.; Turner, M.S.; Wilczek, F. Reheating an inflationary universe. Phys. Rev. Lett. 1982, 48, 1437–1440. [Google Scholar] [CrossRef]
- Linde, A. Particle Physics and Inflationary Cosmology; Harwood: Chur, Switzerland, 1990. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology; John Wiley & Sons: Hoboken, NJ, USA, 1972. [Google Scholar]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of Dark Energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- De Bernardis, P.; Ade, P.A.R.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B.P.; de Gasperis, G.; Farese, P.C.; et al. A flat Universe from high-resolution maps of the cosmic microwave background radiation. Nature 2000, 404, 955–959. [Google Scholar] [CrossRef] [PubMed]
- Hanany, S.; Ade, P.; Balbi, A.; Bock, J.; Borrill, J.; Boscaleri, A.; de Bernardis, P.; Ferreira, P.G.; Hristov, V.V.; Jaffe, A.H.; et al. MAXIMA-1: A Measurement of the Cosmic Microwave Background Anisotropy on Angular Scales of 10′-5o. Astrophys. J. 2000, 545, L5–L9. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, J. Cosmological consequences of a rolling homogeneous scalar field. Phys. Rev. D 1988, 37, 3406–3427. [Google Scholar] [CrossRef]
- Starobinski, A.A. How to determine an effective potential for a variable cosmological term. JETP Lett. 1998, 68, 757–763. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological Imprint of an Energy Component with General Equation of State. Phys. Rev. Lett. 1998, 80, 1582–1585. [Google Scholar] [CrossRef]
- Brax, P.; Martin, J. Quintessence and supergravity. Phys. Lett. B 1999, 468, 40–45. [Google Scholar] [CrossRef]
- Albrecht, A.; Skordis, C. Phenomenology of a Realistic Accelerating Universe Using Only Planck-Scale Physics. Phys. Rev. Lett. 2000, 84, 2076–2079. [Google Scholar] [CrossRef] [PubMed]
- Barreiro, T.; Copeland, E.J.; Nunes, N.J. Quintessence arising from exponential potentials. Phys. Rev. D 2000, 61, 127301. [Google Scholar] [CrossRef]
- Ureña-López, L.A.; Matos, T. New cosmological tracker solution for quintessence. Phys. Rev. D 2000, 62, 081302. [Google Scholar] [CrossRef]
- Brax, P.; Martin, J. Robustness of quintessence. Phys. Rev. D 2000, 61, 103502. [Google Scholar] [CrossRef]
- Saini, T.D.; Raychaudhury, S.; Sahni, V.; Starobinsky, A.A. Reconstructing the Cosmic Equation of State from Supernova Distances. Phys. Rev. Lett. 2000, 85, 1162–1165. [Google Scholar] [CrossRef] [PubMed]
- Sahni, V.; Starobinsky, A.A. The Case for a Positive Cosmological Λ-Term. Int. J. Mod. Phys. D 2000, 9, 373–443. [Google Scholar] [CrossRef]
- Sahni, V. The cosmological constant problem and quintessence. Class. Quantum Grav. 2002, 19, 3435–3448. [Google Scholar] [CrossRef]
- Pavlov, M.; Rubano, C.; Sazhin, M.; Scudellaro, P. Analysis of Two Quintessence Models with Type Ia Supernova Data. Astrophys. J. 2002, 566, 619–622. [Google Scholar] [CrossRef]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder–A new geometrical diagnostic of dark energy. JETP Lett. 2003, 77, 201–206. [Google Scholar] [CrossRef]
- Sen, A. Rolling Tachyon. J. High Energy Phys. 2002, 4, 048. [Google Scholar] [CrossRef]
- Gibbons, G.W. Cosmological evolution of the rolling tachyon. Phys. Lett. B 2002, 537, 1–4. [Google Scholar] [CrossRef]
- Padmanabhan, T. Accelerated expansion of the universe driven by tachyonic matter. Phys. Rev. D 2002, 66, 021301. [Google Scholar] [CrossRef]
- Frolov, A.; Kofman, L.; Starobinsky, A. Prospects and problems of tachyon matter cosmology. Phys. Lett. B 2002, 545, 8–16. [Google Scholar] [CrossRef]
- Chavanis, P.H. Models of universe with a polytropic equation of state: I. The early universe. Eur. Phys. J. Plus 2014, 129, 38. [Google Scholar] [CrossRef]
- Chavanis, P.H. Models of universe with a polytropic equation of state: II. The late universe. Eur. Phys. J. Plus 2014, 129, 222. [Google Scholar] [CrossRef]
- Chavanis, P.H. Models of universe with a polytropic equation of state: III. The phantom universe. 2012; arXiv:1208.1185. [Google Scholar]
- Chavanis, P.H. A simple model of universe describing the early inflation and the late accelerated expansion in a symmetric manner. AIP Conf. Proc. 2013, 1548, 75–115. [Google Scholar]
- Chandrasekhar, S. An Introduction to the Study of Stellar Structure; Dover: New York, NY, USA, 1958. [Google Scholar]
- Shapiro, S.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Murray, J.D. Mathematical Biology; Springer: Berlin, Germany, 1991. [Google Scholar]
- Kamenshchik, A.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Bilic, N.; Tuper, G.B.; Viollier, R. Unification of dark matter and dark energy: the inhomogeneous Chaplygin gas. Phys. Lett. B 2002, 535, 17–21. [Google Scholar] [CrossRef]
- Fabris, J.S.; Gonçalves, S.V.; de Souza, P.E. Density Perturbations in a Universe Dominated by the Chaplygin Gas. Gen. Relativ. Gravit. 2002, 34, 53–63. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Benaoum, H.B. Accelerated Universe from Modified Chaplygin Gas and Tachyonic Fluid. 2002; arXiv:hep-th/0205140. [Google Scholar]
- Gorini, V.; Kamenshchik, A.; Moschella, U. Can the Chaplygin gas be a plausible model for dark energy? Phys. Rev. D 2003, 67, 063509. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Revival of the unified dark energy—dark matter model? Phys. Rev. D 2004, 70, 083519. [Google Scholar] [CrossRef]
- Debnath, U.; Banerjee, A.; Chakraborty, S. Role of modified Chaplygin gas in accelerated universe. Class. Quantum Grav. 2004, 21, 5609–5617. [Google Scholar] [CrossRef]
- Karami, K.; Ghaffari, S.; Fehri, J. Interacting polytropic gas model of phantom dark energy in non-flat universe. Eur. Phys. J. C 2009, 64, 85–88. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant—the weight of the vacuum. Phys. Rep. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Müller, C.M. Cosmological bounds on the equation of state of dark matter. Phys. Rev. D 2005, 71, 047302. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: the equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, 66. [Google Scholar]
- Planck Collaboration. Planck 2015 results. XIII. Cosmological parameters. 2015; arXiv:1502.01589. [Google Scholar]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom Energy: Dark Energy with w < −1 Causes a Cosmic Doomsday. Phys. Rev. Lett. 2003, 91, 071301. [Google Scholar] [PubMed]
- McInnes, B. The dS/CFT Correspondence and the Big Smash. J. High Energy Phys. 2002, 8, 029. [Google Scholar] [CrossRef]
- Carroll, S.M.; Hoffman, M.; Trodden, M. Can the dark energy equation-of-state parameter w be less than −1? Phys. Rev. D 2003, 68, 023509. [Google Scholar] [CrossRef]
- Singh, P.; Sami, M.; Dadhich, N. Cosmological dynamics of a phantom field. Phys. Rev. D 2003, 68, 023522. [Google Scholar] [CrossRef]
- Cline, J.M.; Jeon, S.; Moore, G.D. The phantom menaced: Constraints on low-energy effective ghosts. Phys. Rev. D 2004, 70, 043543. [Google Scholar] [CrossRef]
- Sami, M.; Toporensky, A. Phantom Field and the Fate of the Universe. Mod. Phys. Lett. A 2004, 19, 1509–1517. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. Fate of bound systems in phantom and quintessence cosmologies. Phys. Rev. D 2004, 70, 123529. [Google Scholar] [CrossRef]
- Babichev, E.; Dokuchaev, V.; Eroshenko, Y. Black Hole Mass Decreasing due to Phantom Energy Accretion. Phys. Rev. Lett. 2004, 93, 021102. [Google Scholar] [CrossRef] [PubMed]
- González-Días, P.F.; Sigüenza, C.L. The fate of black holes in an accelerating universe. Phys. Lett. B 2004, 589, 78–82. [Google Scholar] [CrossRef]
- González-Días, P.F.; Sigüenza, C.L. Phantom thermodynamics. Nucl. Phys. B 2004, 697, 363–386. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Final state and thermodynamics of a dark energy universe. Phys. Rev. D 2004, 70, 103522. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Tsujikawa, S. Properties of singularities in the (phantom) dark energy universe. Phys. Rev. D 2005, 71, 063004. [Google Scholar] [CrossRef]
- Stefancić, H. Expansion around the vacuum equation of state: Sudden future singularities and asymptotic behavior. Phys. Rev. D 2005, 71, 084024. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Gonzalez-Díaz, P.F.; Martín-Moruno, P. Worse than a big rip? Phys. Lett. B 2008, 659, 1–5. [Google Scholar] [CrossRef]
- García-Compeán, H.; García-Jiménez, G.; Obregón, O.; Ramírez, C. Crossing the phantom divide in an interacting generalized Chaplygin gas. J. Cosmo. Astropart. Phys. 2008, 7, 016. [Google Scholar] [CrossRef]
- Fernández-Jambrina, L. ω-cosmological singularities. Phys. Rev. D 2010, 82, 124004. [Google Scholar] [CrossRef]
- Frampton, P.H.; Ludwick, K.J.; Scherrer, R.J. The little rip. Phys. Rev. D 2011, 84, 063003. [Google Scholar] [CrossRef]
- Chavanis, P.H. A Cosmological Model Based on a Quadratic Equation of State Unifying Vacuum Energy, Radiation, and Dark Energy. J. Grav. 2013, 2013, 682451. [Google Scholar] [CrossRef]
- Basilakos, S.; Barrow, J.D. Hyperbolic inflation in the light of Planck 2015 data. Phys. Rev. D 2015, 91, 103517. [Google Scholar] [CrossRef]
- González-Días, P.F.; Jiménez-Madrid, J.A. Phantom inflation and the “Big Trip”. Phys. Lett. B 2004, 596, 16–25. [Google Scholar] [CrossRef]
- Astashenok, A.; Nojiri, S.; Odintsov, S.D.; Yurov, A.V. Phantom cosmology without Big Rip singularity. Phys. Lett. B 2012, 709, 396–403. [Google Scholar] [CrossRef]
- Sahni, V.; Wang, L. New cosmological model of quintessence and dark matter. Phys. Rev. D 2000, 62, 103517. [Google Scholar] [CrossRef]
- Shahalam, M.; Sami, S.; Agarwal, A. Om diagnostic applied to scalar field models and slowing down of cosmic acceleration. Mon. Not. R. Astron. Soc. 2015, 448, 2948–2959. [Google Scholar] [CrossRef]
- Chimento, L.P.; Jakubi, A.S. Scalar Field Cosmologies with Perfect Fluid in Robertson-Walker Metric. Int. J. Mod. Phys. D 1996, 5, 71–84. [Google Scholar] [CrossRef]
- Ureña-López, L.A.; Matos, T. New cosmological tracker solution for quintessence. Phys. Rev. D 2000, 62, 081302. [Google Scholar] [CrossRef]
- Rubano, C.; Barrow, J.D. Scaling solutions and reconstruction of scalar field potentials. Phys. Rev. D 2001, 64, 127301. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Tsamparlis, M.; Basilakos, S. Dynamical symmetries and observational constraints in scalar field cosmology. Phys. Rev. D 2014, 90, 103524. [Google Scholar] [CrossRef]
- Gorini, V.; Kamenshchik, A.; Moschella, U.; Pasquier, V. Tachyons, scalar fields, and cosmology. Phys. Rev. D 2004, 69, 123512. [Google Scholar] [CrossRef]
- Keresztes, Z.; Gergely, L.A. Combined cosmological tests of a bivalent tachyonic dark energy scalar field model. J. Cosmo. Astropart. Phys. 2014, 11, 026. [Google Scholar] [CrossRef]
- Monerat, G.A.; Oliveira-Neto, G.; Corrêa Silva, E.V.; Ferreira Filho, L.G.; Romildo, P., Jr.; Fabris, J.C.; Fracalossi, R.; Gonçalves, S.V.B.; Alvarenga, F.G. Dynamics of the early universe and the initial conditions for inflation in a model with radiation and a Chaplygin gas. Phys. Rev. D 2007, 76, 024017. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Maximum Mass of Ideal White Dwarfs. Astrophys. J. 1931, 74, 81. [Google Scholar] [CrossRef]
- Steinhardt, P. Critical Problems in Physics; Fitch, V.L., Marlow, D.R., Eds.; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Zlatev, I.; Wang, L.; Steinhardt, P.J. Quintessence, Cosmic Coincidence, and the Cosmological Constant. Phys. Rev. Lett. 1999, 82, 896–899. [Google Scholar] [CrossRef]
- Amendola, L.; Tocchini-Valentini, D. Stationary dark energy: The present universe as a global attractor. Phys. Rev. D 2001, 64, 043509. [Google Scholar] [CrossRef]
- Chimento, L.P.; Jakubi, A.S.; Pavón, D. Dark energy, dissipation, and the coincidence problem. Phys. Rev. D 2003, 67, 087302. [Google Scholar] [CrossRef]
- García-Compeán, H.; García-Jiménez, G.; Obregón, O.; Ramírez, C. Crossing the phantom divide in an interacting generalized Chaplygin gas. J. Cosmo. Astropart. Phys. 2008, 7, 016. [Google Scholar] [CrossRef]
- Lemaître, G. Evolution of the Expanding Universe. Proc. Nat. Acad. Sci. 1934, 20, 12–17. [Google Scholar] [CrossRef] [PubMed]
- Sakharov, A.D. Vacuum quantum fluctuations in curved space and the theory of gravitation. Dokl. Akad. Nauk SSSR 1967, 177, 70. [Google Scholar]
- Zel’dovich, Y.B. Special Issue: the Cosmological Constant and the Theory of Elementary Particles. Sov. Phys. Uspek. 1968, 11, 381–393. [Google Scholar] [CrossRef]
- Setare, M.R.; Kamali, V. Tachyon-polytropic inflation on the brane. Cent. Eur. J. Phys. 2013, 11, 545–552. [Google Scholar] [CrossRef]
- Setare, M.R.; Houndjo, M.J.S.; Kamali, V. Warm-Polytropic Inflationary Universe Model. Int. J. Mod. Phys. D 2013, 22, 1350041. [Google Scholar] [CrossRef]
- Freitas, R.C.; Gonçalves, S.V.B. Polytropic equation of state and primordial quantum fluctuations. Eur. Phys. J. C 2014, 74, 3217. [Google Scholar] [CrossRef]
- Asadzadeli, S.; Safari, Z.; Karami, K.; Abdolmaleki, A. Cosmological Constraints on Polytropic Gas Model. Int. J. Theor. Phys. 2014, 53, 1248–1262. [Google Scholar] [CrossRef]
- Chavanis, P.H. Growth of perturbations in an expanding universe with Bose-Einstein condensate dark matter. Astron. Astrophys. 2012, 537, A127. [Google Scholar] [CrossRef]
- Lemaître, G. The Primeval Atom; Munitz, M.K., Ed.; The Free Press: New York, NY, USA, 1957. [Google Scholar]
- Kazinski, P.O. Quantum gravitational anomaly as a dark matter. 2015; arXiv:1501.05777. [Google Scholar]
- Ananda, K.N.; Bruni, M. Cosmological dynamics and dark energy with a nonlinear equation of state: A quadratic model. Phys. Rev. D 2006, 74, 023523. [Google Scholar] [CrossRef]
- Linder, E.V.; Scherrer, R.J. Aetherizing Lambda: Barotropic fluids as dark energy. Phys. Rev. D 2009, 80, 023008. [Google Scholar] [CrossRef]
- Sharov, G.S. Observational constraints on cosmological models with Chaplygin gas and quadratic equation of state. 2015; arXiv:1506.05246. [Google Scholar]
- Zel’dovich, Y.B. The equation of state at ultrahigh densities and its relativistic limitations. Soviet Phys. JETP 1962, 14, 1143. [Google Scholar]
- Zel’dovich, Y.B. A hypothesis, unifying the structure and the entropy of the Universe. Mon. Not. R. Astron. Soc. 1972, 160, 1. [Google Scholar] [CrossRef]
- Li, B.; Rindler-Daller, T.; Shapiro, P.R. Cosmological constraints on Bose-Einstein-condensed scalar field dark matter. Phys. Rev. D 2014, 89, 083536. [Google Scholar] [CrossRef]
- Chavanis, P.H. Partially relativistic self-gravitating Bose-Einstein condensates with a stiff equation of state. Eur. Phys. J. Plus 2015, 130, 181. [Google Scholar] [CrossRef]
- Chavanis, P.H. Cosmology with a stiff matter era. 2014; arXiv:1412.0743. [Google Scholar]
- Harko, T. Evolution of cosmological perturbations in Bose-Einstein condensate dark matter. Mon. Not. R. Astron. Soc. 2011, 413, 3095–3104. [Google Scholar] [CrossRef]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).