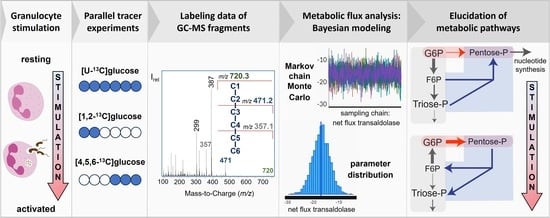
Bayesian 13C-Metabolic Flux Analysis of Parallel Tracer Experiments in Granulocytes: A Directional Shift within the Non-Oxidative Pentose Phosphate Pathway Supports Phagocytosis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of RPMI Tracer Medium
2.3. Isolation of Granulocytes from Whole Blood
2.4. Phagocytosis Assay
2.5. Isotopic Tracer Experiments
2.6. Extraction of Intracellular Metabolites
2.7. Derivatization and GC−MS Analysis of Intracellular Metabolites
2.8. Metabolic Network Model and Metabolic Flux Analysis
2.8.1. Glossary
- C1, C2, …, C6: Designation of the position for the carbons of a metabolite.
- : Isolated labeling on the carbons of a fragment metabolite.
- CMD: Normalized carbon mass distribution of a fragment with the elements , where denotes the mass offset or number of simultaneously labeled carbons.
- MID: Normalized mass isotopomer distribution of a fragment without correction for naturally occurring isotopes of its elements (e.g., H, C, N, O, and Si). Values are expressed as mol%.
- : Number of carbon labeling positions of a fragment metabolite.
2.8.2. 13C-Positional Labeling Approach
2.8.3. Accurate Assessment of the Selected Fragments for 13C-MFA
- : number of carbons
- : fractional abundance of each isotopomer of a fragment (M+0 to M+(n+1))
- peak area of an individual mass isotopomer
- : sum of all signal areas
2.8.4. Bayesian Modeling for 13C-MFA
2.8.5. Stoichiometric Flux Restraint Analysis of the Metabolic Network
2.8.6. Evaluation of the Bayesian 13C-MFA
2.8.7. Evaluation of Flux Precision for Monitored Fragments
2.9. Principal Component Analysis
3. Results and Discussion
3.1. GC-MS Analysis of Intracellular Metabolites as Their Ethyloxime-Trimethylsilyl Derivatives
3.2. Evaluation of 13C-Isotopomer Mass Distribution Based on Established Models and Concepts
3.2.1. Characterization of Glucose Pathway Utilization Based on Interpretation of 13C Labeling Patterns
3.2.2. Estimation of Fractional Contribution Using the [U-13C]glucose Tracer
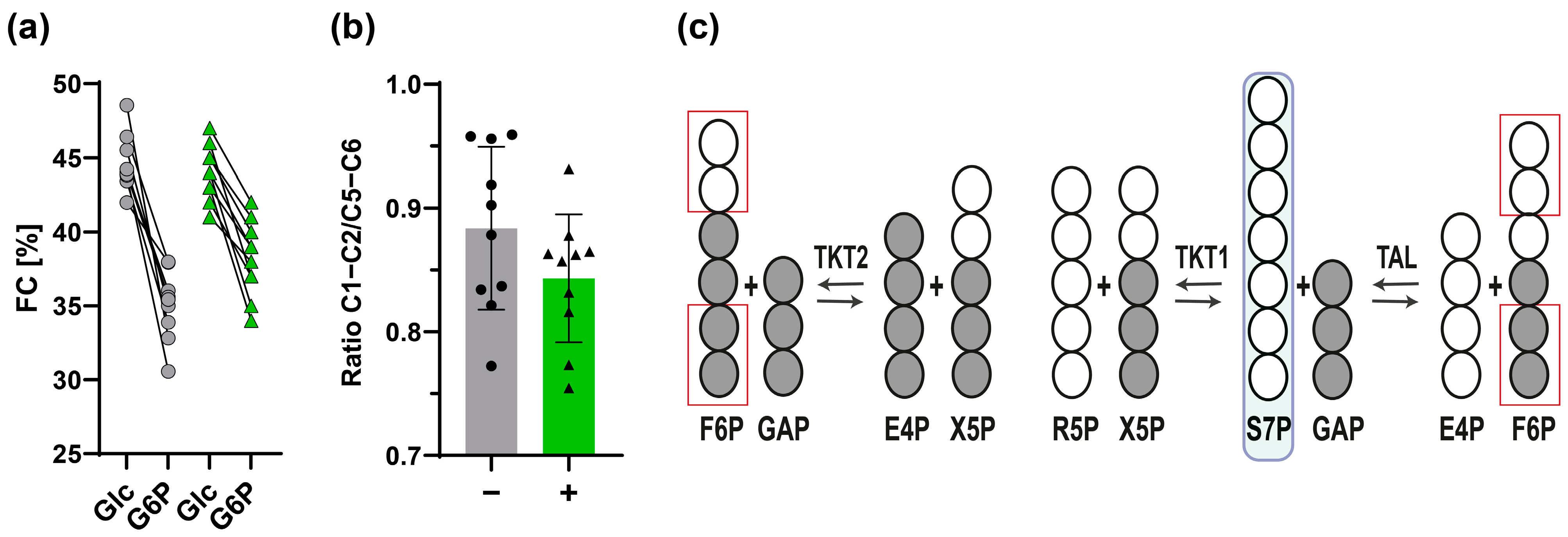
3.2.3. 13C-Positional Labeling Analysis of G6P Indicates an Input of Unlabeled S7P into the Non-Oxidative PPP
3.3. Validation and Evaluation of our Bayesian 13C-MFA Performance
3.3.1. Validation of the Proposed 13C-MFA Approach: Accuracy and Precision Were Comparable with State-of-the-Art Software Packages
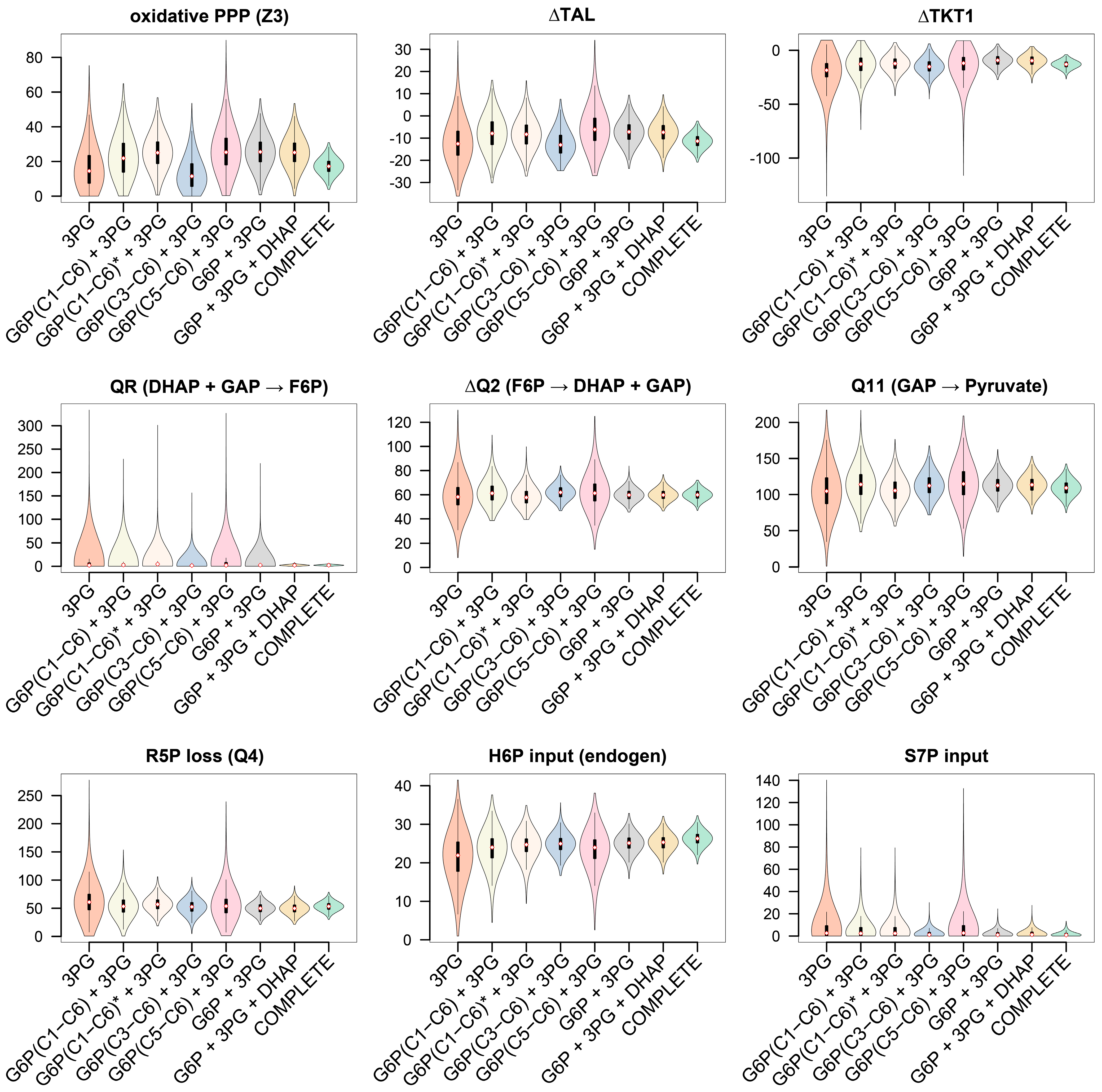
3.3.2. Selection of 13C-Labeled Glucose Tracers for 13C-MFA of Glycolysis and PPP
3.3.3. GC−MS Fragments of G6P Improve Flux Precision of the Glucose Metabolism
3.4. Glucose Metabolism of Granulocytes: Identification of Metabolic Patterns and Their Regulation
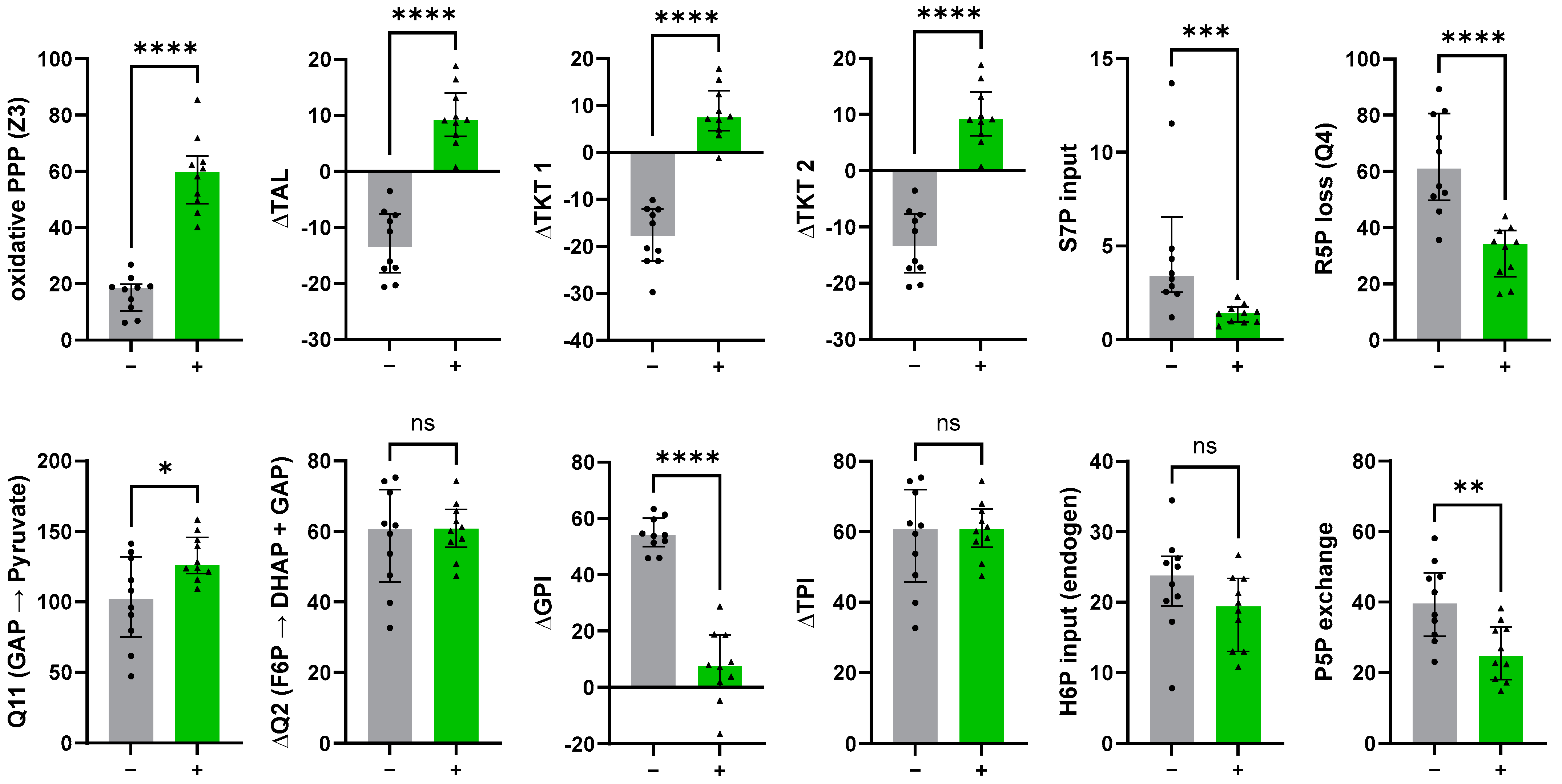
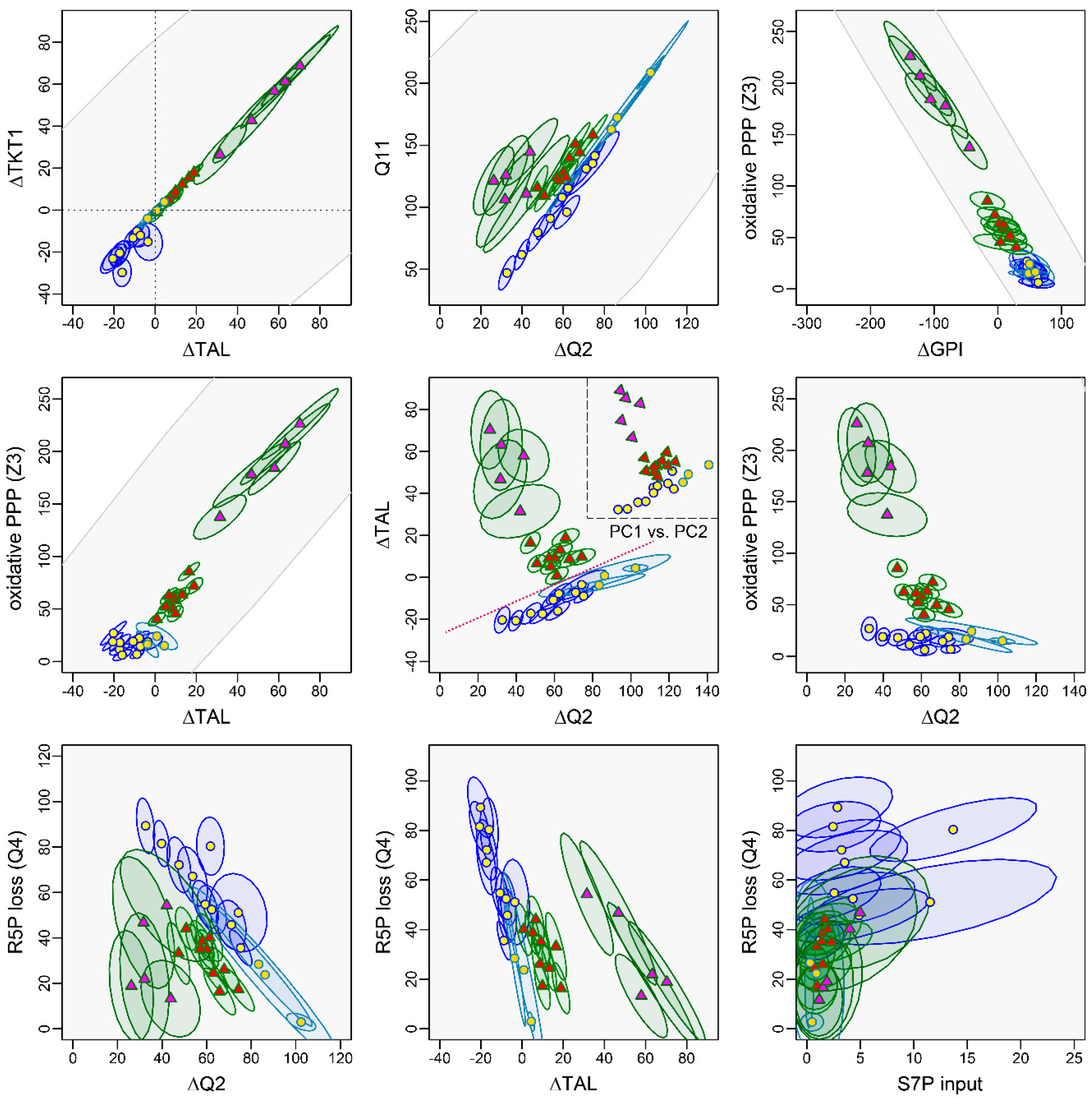
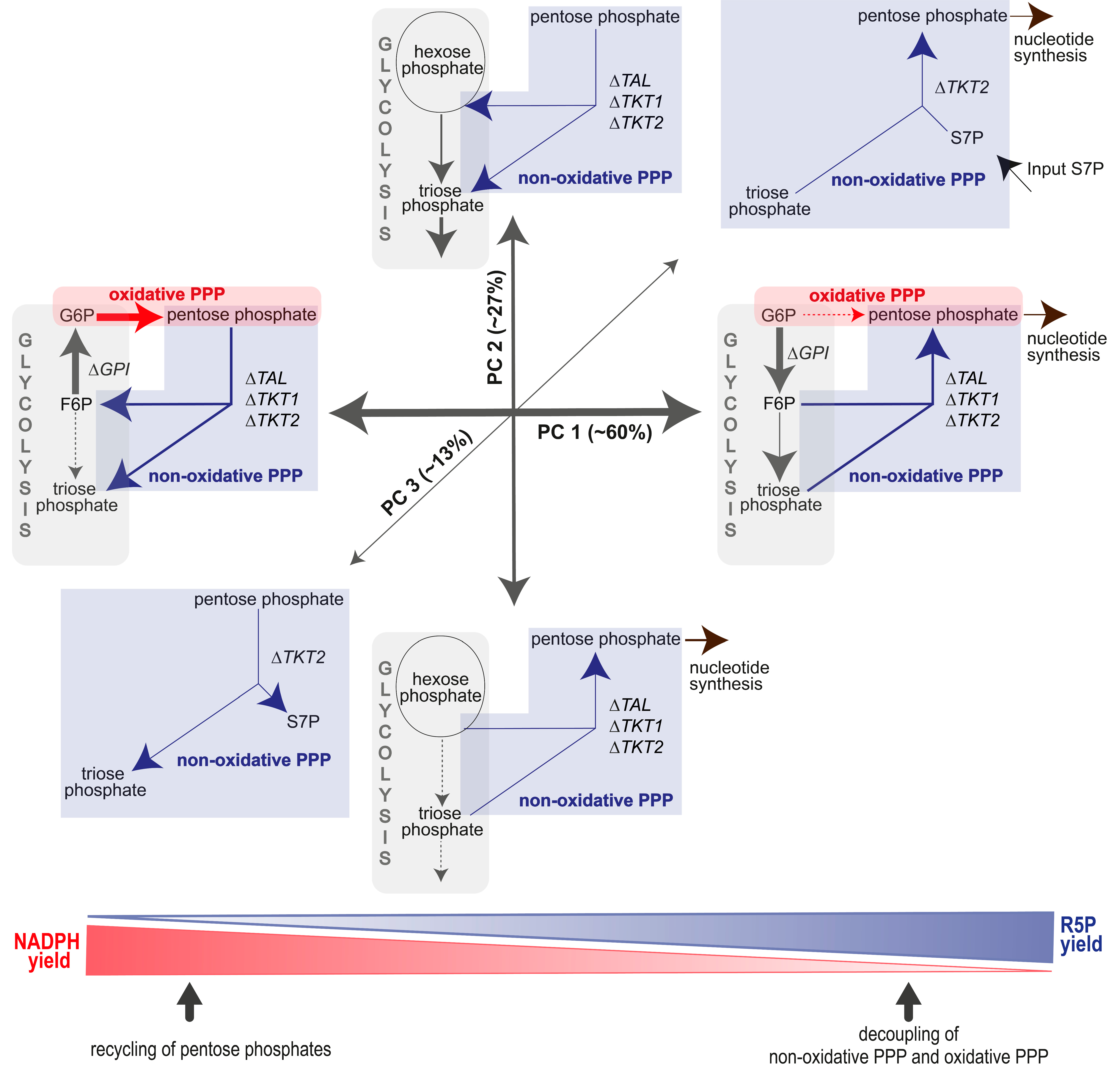
3.4.1. The Non-Oxidative PPP Promotes Ribose-5-Phosphate Biosynthesis in Granulocytes
3.4.2. A “Hard-Wired” PPP Network Gives Insight into Cellular Mechanisms
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, S.; Dikshit, M. Metabolic Insight of Neutrophils in Health and Disease. Front. Immunol. 2019, 10, 2099. [Google Scholar] [CrossRef] [PubMed]
- Toller-Kawahisa, J.E.; O’Neill, L.A.J. How neutrophil metabolism affects bacterial killing. Open Biol. 2022, 12, 220248. [Google Scholar] [CrossRef] [PubMed]
- Britt, E.C.; Lika, J.; Giese, M.A.; Schoen, T.J.; Seim, G.L.; Huang, Z.; Lee, P.Y.; Huttenlocher, A.; Fan, J. Switching to the cyclic pentose phosphate pathway powers the oxidative burst in activated neutrophils. Nat. Metab. 2022, 4, 389–403. [Google Scholar] [CrossRef] [PubMed]
- Paclet, M.-H.; Laurans, S.; Dupré-Crochet, S. Regulation of Neutrophil NADPH Oxidase, NOX2: A Crucial Effector in Neu-trophil Phenotype and Function. Front. Cell Dev. Biol. 2022, 10, 945749. [Google Scholar] [CrossRef] [PubMed]
- TeSlaa, T.; Ralser, M.; Fan, J.; Rabinowitz, J.D. The pentose phosphate pathway in health and disease. Nat. Metab. 2023, 5, 1275–1289. [Google Scholar] [CrossRef] [PubMed]
- Simon-Molas, H.; Vallvé-Martínez, X.; Caldera-Quevedo, I.; Fontova, P.; Arnedo-Pac, C.; Vidal-Alabró, A.; Castaño, E.; Na-varro-Sabaté, À.; Lloberas, N.; Bartrons, R.; et al. TP53-Induced Glycolysis and Apoptosis Regulator (TIGAR) Is Upregulated in Lymphocytes Stimulated with Concanavalin A. Int. J. Mol. Sci. 2021, 22, 7436. [Google Scholar] [CrossRef] [PubMed]
- Stanton, R.C. Glucose-6-phosphate dehydrogenase, NADPH, and cell survival. IUBMB Life 2012, 64, 362–369. [Google Scholar] [CrossRef]
- Li, Y.; Yao, C.-F.; Xu, F.-J.; Qu, Y.-Y.; Li, J.-T.; Lin, Y.; Cao, Z.-L.; Lin, P.-C.; Xu, W.; Zhao, S.-M.; et al. APC/CCDH1 synchronizes ribose-5-phosphate levels and DNA synthesis to cell cycle progression. Nat. Commun. 2019, 10, 2502. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, F.; Liu, X.; Lu, Y.; Yao, K.; Tian, N.; Tong, L.; Figge, D.A.; Wang, X.; Han, Y.; et al. Non-oxidative pentose phosphate pathway controls regulatory T cell function by integrating metabolism and epigenetics. Nat. Metab. 2022, 4, 559–574. [Google Scholar] [CrossRef]
- Jeon, J.-H.; Hong, C.-W.; Kim, E.Y.; Lee, J.M. Current Understanding on the Metabolism of Neutrophils. Immune Netw. 2020, 20, e46. [Google Scholar] [CrossRef]
- Sadiku, P.; Willson, J.A.; Ryan, E.M.; Sammut, D.; Coelho, P.; Watts, E.R.; Grecian, R.; Young, J.M.; Bewley, M.; Arienti, S.; et al. Neutrophils Fuel Effective Immune Responses through Gluconeogenesis and Glycogenesis. Cell Metab. 2021, 33, 411–423.e4. [Google Scholar] [CrossRef] [PubMed]
- Zamboni, N.; Fendt, S.-M.; Rühl, M.; Sauer, U. 13C-based metabolic flux analysis. Nat. Protoc. 2009, 4, 878–892. [Google Scholar] [CrossRef] [PubMed]
- Hanke, T.; Nöh, K.; Noack, S.; Polen, T.; Bringer, S.; Sahm, H.; Wiechert, W.; Bott, M. Combined fluxomics and transcriptomics analysis of glucose catabolism via a partially cyclic pentose phosphate pathway in Gluconobacter oxydans 621H. Appl. Environ. Microbiol. 2013, 79, 2336–2348. [Google Scholar] [CrossRef] [PubMed]
- Haschemi, A.; Kosma, P.; Gille, L.; Evans, C.R.; Burant, C.F.; Starkl, P.; Knapp, B.; Haas, R.; Schmid, J.A.; Jandl, C.; et al. The sedoheptulose kinase CARKL directs macrophage polarization through control of glucose metabolism. Cell Metab. 2012, 15, 813–826. [Google Scholar] [CrossRef] [PubMed]
- Rühl, M.; Rupp, B.; Nöh, K.; Wiechert, W.; Sauer, U.; Zamboni, N. Collisional fragmentation of central carbon metabolites in LC-MS/MS increases precision of 13C metabolic flux analysis. Biotechnol. Bioeng. 2012, 109, 763–771. [Google Scholar] [CrossRef] [PubMed]
- Okahashi, N.; Maeda, K.; Kawana, S.; Iida, J.; Shimizu, H.; Matsuda, F. Sugar phosphate analysis with baseline separation and soft ionization by gas chromatography-negative chemical ionization-mass spectrometry improves flux estimation of bidirectional reactions in cancer cells. Metab. Eng. 2019, 51, 43–49. [Google Scholar] [CrossRef] [PubMed]
- Wiechert, W. 13C metabolic flux analysis. Metab. Eng. 2001, 3, 195–206. [Google Scholar] [CrossRef] [PubMed]
- Crown, S.B.; Long, C.P.; Antoniewicz, M.R. Integrated 13C-metabolic flux analysis of 14 parallel labeling experiments in Escherichia coli. Metab. Eng. 2015, 28, 151–158. [Google Scholar] [CrossRef]
- Antoniewicz, M.R. 13C metabolic flux analysis: Optimal design of isotopic labeling experiments. Curr. Opin. Chem. Biotechnol. 2013, 24, 1116–1121. [Google Scholar] [CrossRef]
- Antoniewicz, M.R. Parallel labeling experiments for pathway elucidation and 13C metabolic flux analysis. Curr. Opin. Chem. Biotechnol. 2015, 36, 91–97. [Google Scholar] [CrossRef]
- Nagy, C.; Haschemi, A. Sedoheptulose kinase regulates cellular carbohydrate metabolism by sedoheptulose 7-phosphate supply. Biochem. Soc. Trans. 2013, 41, 674–680. [Google Scholar] [CrossRef] [PubMed]
- Münz, F.; Wolfschmitt, E.-M.; Zink, F.; Abele, N.; Hogg, M.; Hoffmann, A.; Gröger, M.; Calzia, E.; Waller, C.; Radermacher, P.; et al. Porcine blood cell and brain tissue energy metabolism: Effects of “early life stress”. Front. Mol. Biosci. 2023, 10, 1113570. [Google Scholar] [CrossRef] [PubMed]
- Kuehne, A.; Emmert, H.; Soehle, J.; Winnefeld, M.; Fischer, F.; Wenck, H.; Gallinat, S.; Terstegen, L.; Lucius, R.; Hildebrand, J.; et al. Acute Activation of Oxidative Pentose Phosphate Pathway as First-Line Response to Oxidative Stress in Human Skin Cells. Mol. Cell 2015, 59, 359–371. [Google Scholar] [CrossRef] [PubMed]
- van Winden, W.A.; Wittmann, C.; Heinzle, E.; Heijnen, J.J. Correcting mass isotopomer distributions for naturally occurring isotopes. Biotechnol. Bioeng. 2002, 80, 477–479. [Google Scholar] [CrossRef]
- Wolfschmitt, E.-M.; Hogg, M.; Vogt, J.A.; Zink, F.; Wachter, U.; Hezel, F.; Zhang, X.; Hoffmann, A.; Gröger, M.; Hartmann, C.; et al. The effect of sodium thiosulfate on immune cell metabolism during porcine hemorrhage and resuscitation. Front. Immunol. 2023, 14, 1125594. [Google Scholar] [CrossRef]
- Lima, V.F.; Erban, A.; Daubermann, A.G.; Freire, F.B.S.; Porto, N.P.; Cândido-Sobrinho, S.A.; Medeiros, D.B.; Schwarzländer, M.; Fernie, A.R.; Dos Anjos, L.; et al. Establishment of a GC-MS-based 13C-positional isotopomer approach suitable for investigating metabolic fluxes in plant primary metabolism. Plant J. 2021, 108, 1213–1233. [Google Scholar] [CrossRef]
- Stan Development Team. RStan: The R interface to Stan. Available online: http://mc-stan.org/ (accessed on 9 November 2023).
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.A.; Guo, J.; Li, P.; Riddell, A. Stan: A Probabilistic Programming Language. J. Stat. Softw. 2017, 76, 1. [Google Scholar] [CrossRef]
- Antoniewicz, M.R.; Kelleher, J.K.; Stephanopoulos, G. Elementary metabolite units (EMU): A novel framework for modeling isotopic distributions. Metab. Eng. 2007, 9, 68–86. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Backman, T.W.H.; Schenk, C.; Radivojevic, T.; Ando, D.; Singh, J.; Czajka, J.J.; Costello, Z.; Keasling, J.D.; Tang, Y.; Akhmatskaya, E.; et al. BayFlux: A Bayesian method to quantify metabolic Fluxes and their uncertainty at the genome scale. PLoS Comput. Biol. 2023, 19, e1011111. [Google Scholar] [CrossRef]
- Theorell, A.; Leweke, S.; Wiechert, W.; Nöh, K. To be certain about the uncertainty: Bayesian statistics for 13C metabolic flux analysis. Biotechnol. Bioeng. 2017, 114, 2668–2684. [Google Scholar] [CrossRef] [PubMed]
- Borah Slater, K.; Beyß, M.; Xu, Y.; Barber, J.; Costa, C.; Newcombe, J.; Theorell, A.; Bailey, M.J.; Beste, D.J.V.; McFadden, J.; et al. One-shot 13C 15N-metabolic flux analysis for simultaneous quantification of carbon and nitrogen flux. Mol. Syst. Biol. 2023, 19, e11099. [Google Scholar] [CrossRef]
- Crown, S.B.; Long, C.P.; Antoniewicz, M.R. Optimal tracers for parallel labeling experiments and 13C metabolic flux analysis: A new precision and synergy scoring system. Metab. Eng. 2016, 38, 10–18. [Google Scholar] [CrossRef]
- Forina, M.; Armanino, C.; Lanteri, S.; Leardi, R. Methods of varimax rotation in factor analysis with applications in clinical and food chemistry. J. Chemom. 1989, 3, 115–125. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 9 November 2023).
- Abdi, H.; Williams, L.J. Principal component analysis. WIREs Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Babamoradi, H.; van den Berg, F.; Rinnan, Å. Bootstrap based confidence limits in principal component analysis—A case study. Chemom. Intell. Lab. Syst. 2013, 120, 97–105. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Bootstrap Methods for Standard Errors, Confidence Intervals, and Other Measures of Statistical Accuracy. Stat. Sci. 1986, 1, 54–77. [Google Scholar] [CrossRef]
- Antoniewicz, M.R. A guide to 13C metabolic flux analysis for the cancer biologist. Exp. Mol. Med. 2018, 50, 1–13. [Google Scholar] [CrossRef]
- Buescher, J.M.; Antoniewicz, M.R.; Boros, L.G.; Burgess, S.C.; Brunengraber, H.; Clish, C.B.; DeBerardinis, R.J.; Feron, O.; Frezza, C.; Ghesquiere, B.; et al. A roadmap for interpreting 13C metabolite labeling patterns from cells. Curr. Opin. Chem. Biotechnol. 2015, 34, 189–201. [Google Scholar] [CrossRef]
- Ma, J.; Wei, K.; Liu, J.; Tang, K.; Zhang, H.; Zhu, L.; Chen, J.; Li, F.; Xu, P.; Liu, J.; et al. Glycogen metabolism regulates macrophage-mediated acute inflammatory responses. Nat. Commun. 2020, 11, 1769. [Google Scholar] [CrossRef]
- Clasquin, M.F.; Melamud, E.; Singer, A.; Gooding, J.R.; Xu, X.; Dong, A.; Cui, H.; Campagna, S.R.; Savchenko, A.; Yakunin, A.F.; et al. Riboneogenesis in yeast. Cell 2011, 145, 969–980. [Google Scholar] [CrossRef] [PubMed]
- Katz, J.; Rognstad, R. The labeling of pentose phosphate from glucose-14C and estimation of the rates of transaldolase, transketolase, the contribution of the pentose cycle, and ribose phosphate synthesis. Biochemistry 1967, 6, 2227–2247. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R.; Kelleher, J.K.; Stephanopoulos, G. Determination of confidence intervals of metabolic fluxes estimated from stable isotope measurements. Metab. Eng. 2006, 8, 324–337. [Google Scholar] [CrossRef] [PubMed]
- Young, J.D. INCA: A computational platform for isotopically non-stationary metabolic flux analysis. Bioinformatics 2014, 30, 1333–1335. [Google Scholar] [CrossRef]
- Long, C.P.; Au, J.; Gonzalez, J.E.; Antoniewicz, M.R. 13C metabolic flux analysis of microbial and mammalian systems is enhanced with GC-MS measurements of glycogen and RNA labeling. Metab. Eng. 2016, 38, 65–72. [Google Scholar] [CrossRef]
- Nagy, C.; Haschemi, A. Time and Demand are Two Critical Dimensions of Immunometabolism: The Process of Macrophage Activation and the Pentose Phosphate Pathway. Front. Immunol. 2015, 6, 164. [Google Scholar] [CrossRef]
- Ying, H.; Kimmelman, A.C.; Lyssiotis, C.A.; Hua, S.; Chu, G.C.; Fletcher-Sananikone, E.; Locasale, J.W.; Son, J.; Zhang, H.; Coloff, J.L.; et al. Oncogenic Kras maintains pancreatic tumors through regulation of anabolic glucose metabolism. Cell 2012, 149, 656–670. [Google Scholar] [CrossRef]
- Theorell, A.; Jadebeck, J.F.; Nöh, K.; Stelling, J. PolyRound: Polytope rounding for random sampling in metabolic networks. Bioinformatics 2022, 38, 566–567. [Google Scholar] [CrossRef]

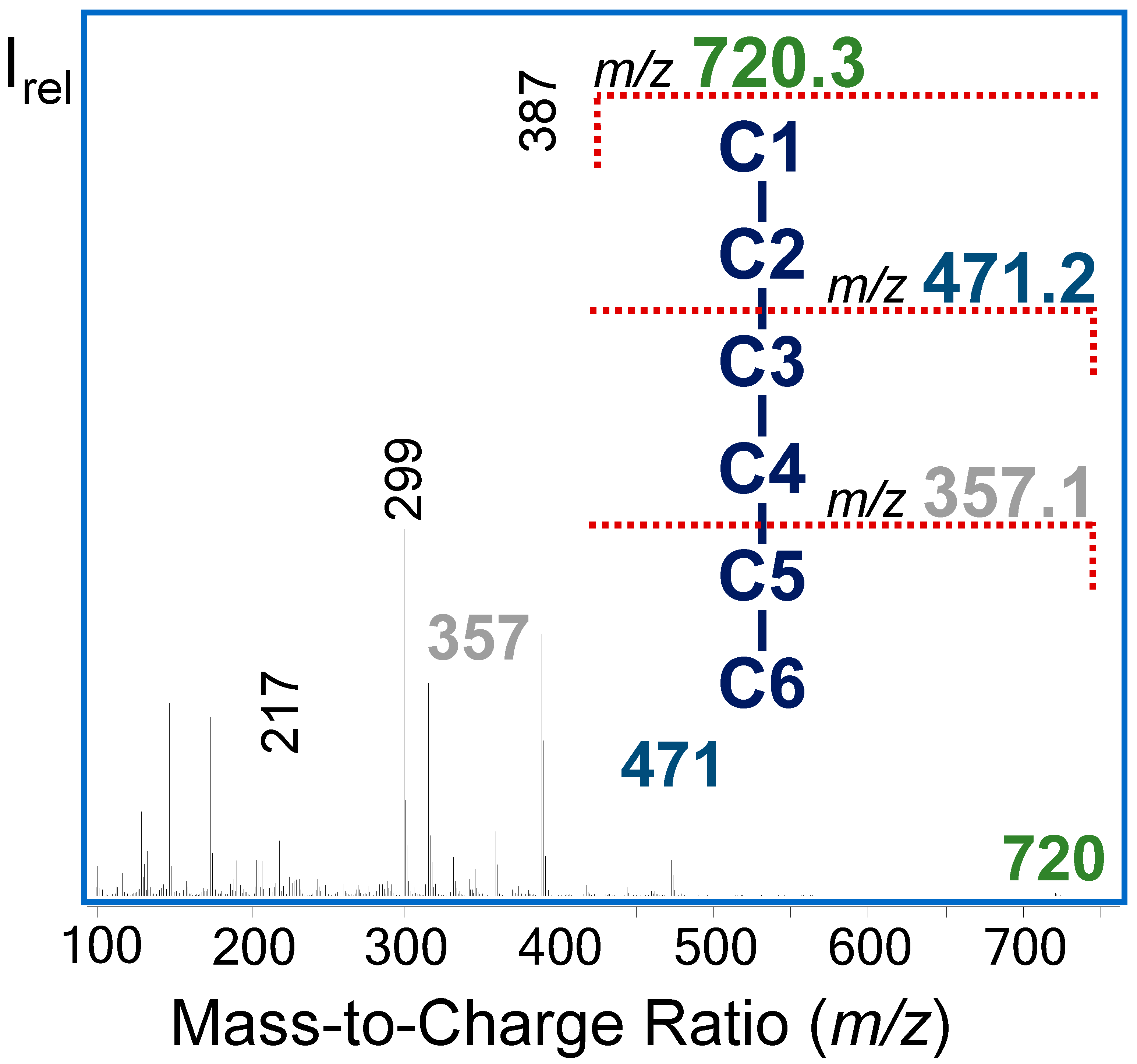





| Metabolite | m/z | Carbon Atoms | Molecular Formula |
|---|---|---|---|
| Glucose | 568 | C1−C6 | C22H54O6NSi5 |
| 319 | C3−C6 | C13H31O3Si3 | |
| G6P | 720 | C1−C6 | C25H63O9NSi6P |
| 471 | C3−C6 | C16H40O6Si4P | |
| 357 | C5−C6 | C11H30O5Si3P | |
| X5P, Ru5P, R5P | 618 | C1−C5 | C21H53O8NSi5P |
| R5P | 459 | C3−C5 | C15H40O6Si4P |
| DHAP | 414 | C1−C3 | C13H33O6NSi3P |
| 3PG | 459 | C1−C3 | C14H36O7Si4P |
| Metabolic Flux | PC1 (60%) | PC2 (27%) | PC3 (13%) | |
|---|---|---|---|---|
| glycolysis | ∆GPI | −57.2 | -6.6 | |
| ∆Q2 | −10.0 | −15.0 | ||
| Q11 | −32.7 | |||
| oxidative PPP | Z3 | 63.1 | ||
| non-oxidative PPP | ∆TAL | 24.4 | −3.2 | |
| ∆TKT1 | 24.8 | −3.8 | 5.2 | |
| ∆TKT2 | 24.4 | −3.2 | ||
| Input S7P | −3.0 | |||
| R5P loss (Q4) | −10.1 | 17.7 | −8.0 | |
| Novel GC−MS-Based Bayesian 13C-MFA | Alternative Methods | Advantage of Our Proposed Method | |
|---|---|---|---|
| Extraction and Derivatization for GC−MS analysis | water/methanol/acetonitrile extraction one derivatization: glucose/sugar phosphates, incl. triose-phosphates (EtOX-TMS) | methanol/chloroform/water extraction [47] acid hydrolysis of glycogen and RNA [47] two derivatizations: sugar (aldonitrile propionate), triose phosphates (TBDMS) [47] |
|
| Chromatography | baseline separation H6P with a total run time of 15 min | baseline separation H6P with a total run time of 31 min (GC−NCI−MS) [16] coelution of H6P without derivatization (LC−MS) [3] |
|
| MS | detection of multiple fragments of sugar phosphates and glucose (GC−MS) | detection of the entire carbon skeleton of sugar phosphates (LC−MS/GC−NCI−MS) [3,11,16] |
|
| Tracer experiments | parallel tracer experiments | single-tracer experiment [3] |
|
| Formal analysis | flux constraint analysis as a central element analysis of the feasible flux space | “black box” or integrated into software algorithms (INCA software, Bayesian MFA) [31,46,50] |
|
| Bayesian 13C-MFA vs. optimization approach | detection of multiple optima that could be caused by measurement errors | single set of flux values that best fit the measurement data |
|
| full uncertainty distribution of fluxes | only upper and lower confidence interval |
| |
| pairwise correlation of fluxes with their joint confidence regions | may not be integrated into well-established MFA software (i.e., INCA) |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hogg, M.; Wolfschmitt, E.-M.; Wachter, U.; Zink, F.; Radermacher, P.; Vogt, J.A. Bayesian 13C-Metabolic Flux Analysis of Parallel Tracer Experiments in Granulocytes: A Directional Shift within the Non-Oxidative Pentose Phosphate Pathway Supports Phagocytosis. Metabolites 2024, 14, 24. https://doi.org/10.3390/metabo14010024
Hogg M, Wolfschmitt E-M, Wachter U, Zink F, Radermacher P, Vogt JA. Bayesian 13C-Metabolic Flux Analysis of Parallel Tracer Experiments in Granulocytes: A Directional Shift within the Non-Oxidative Pentose Phosphate Pathway Supports Phagocytosis. Metabolites. 2024; 14(1):24. https://doi.org/10.3390/metabo14010024
Chicago/Turabian StyleHogg, Melanie, Eva-Maria Wolfschmitt, Ulrich Wachter, Fabian Zink, Peter Radermacher, and Josef Albert Vogt. 2024. "Bayesian 13C-Metabolic Flux Analysis of Parallel Tracer Experiments in Granulocytes: A Directional Shift within the Non-Oxidative Pentose Phosphate Pathway Supports Phagocytosis" Metabolites 14, no. 1: 24. https://doi.org/10.3390/metabo14010024
APA StyleHogg, M., Wolfschmitt, E.-M., Wachter, U., Zink, F., Radermacher, P., & Vogt, J. A. (2024). Bayesian 13C-Metabolic Flux Analysis of Parallel Tracer Experiments in Granulocytes: A Directional Shift within the Non-Oxidative Pentose Phosphate Pathway Supports Phagocytosis. Metabolites, 14(1), 24. https://doi.org/10.3390/metabo14010024