Modeling Between-Subject Variability in Subcutaneous Absorption of a Fast-Acting Insulin Analogue by a Nonlinear Mixed Effects Approach
Abstract
1. Introduction
2. Materials and Methods
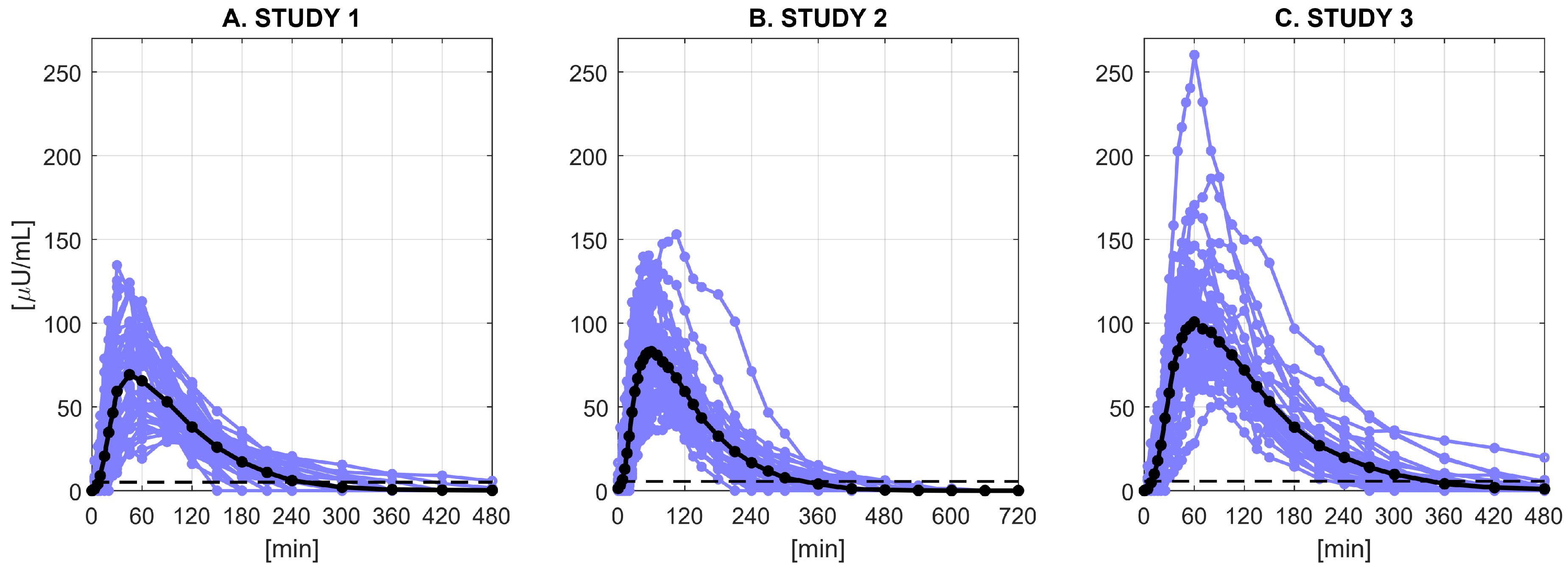
2.1. Database and Protocols
2.1.1. Study 1
2.1.2. Study 2
2.1.3. Study 3
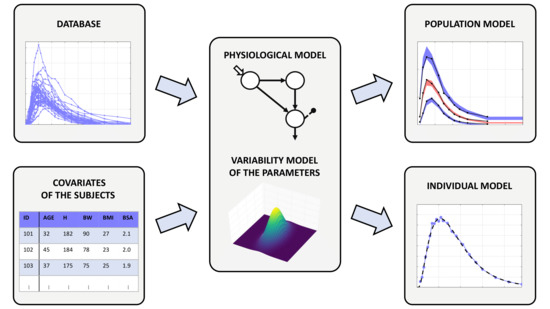
2.2. The Nonlinear Mixed Effects Model
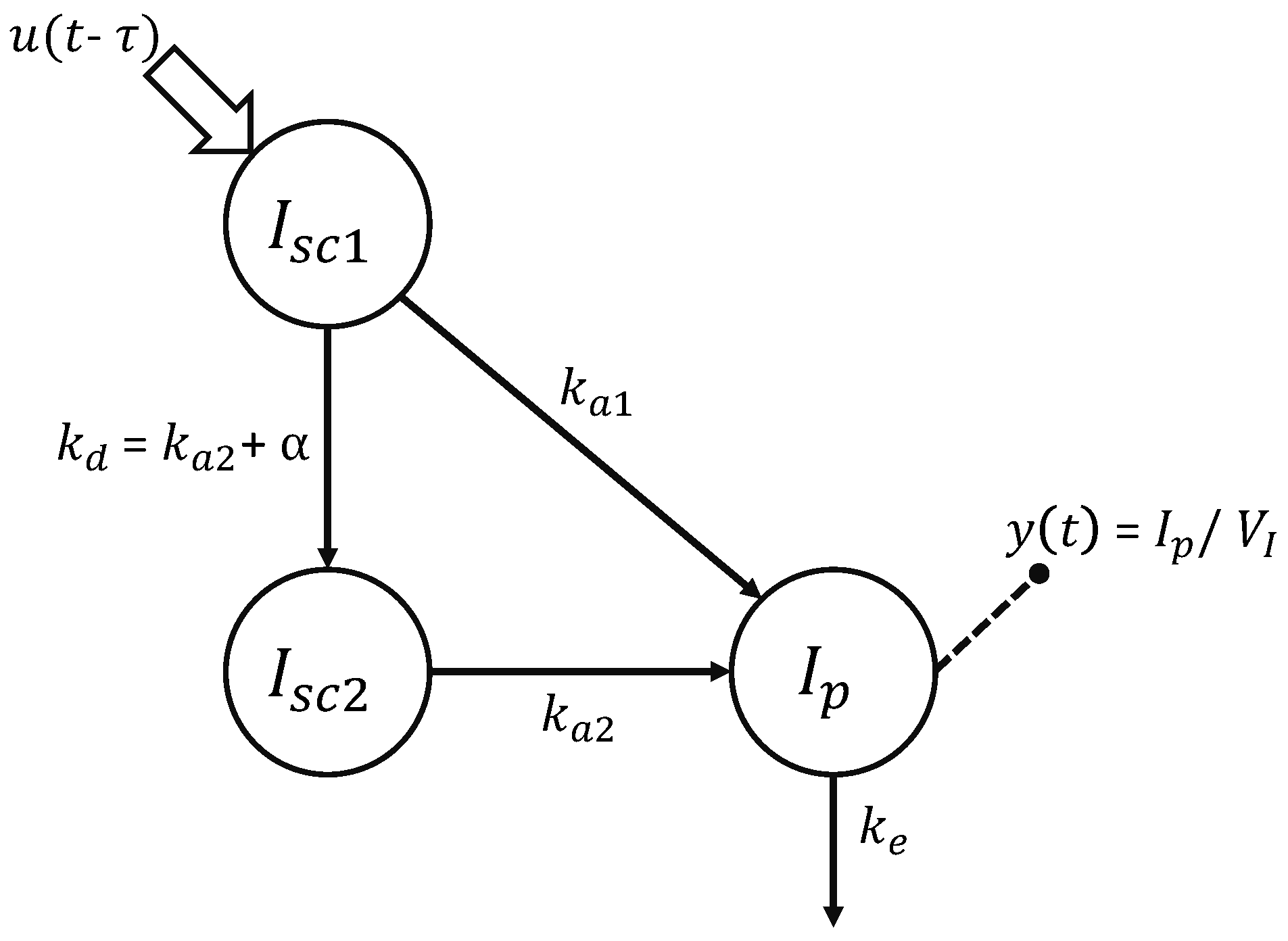
2.2.1. Physiological Model of Insulin Kinetics
2.2.2. Model of the Parameter Variability
2.2.3. Measurement Error Model
2.3. Parameter Estimation
2.4. Model Assessment and Comparison
3. Results
3.1. Comparison of the Variability Models
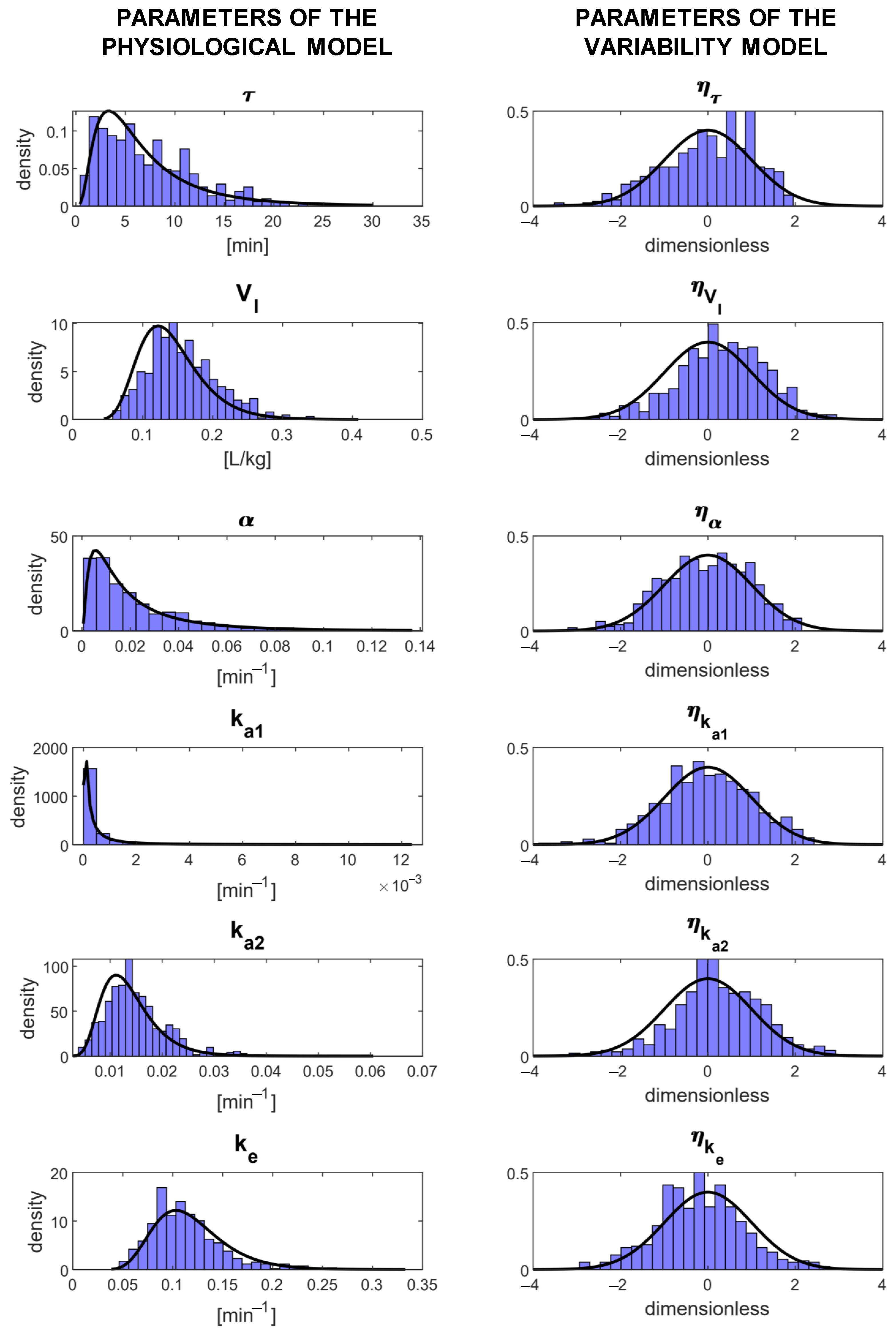
3.2. Selected Model of the Parameter Variability
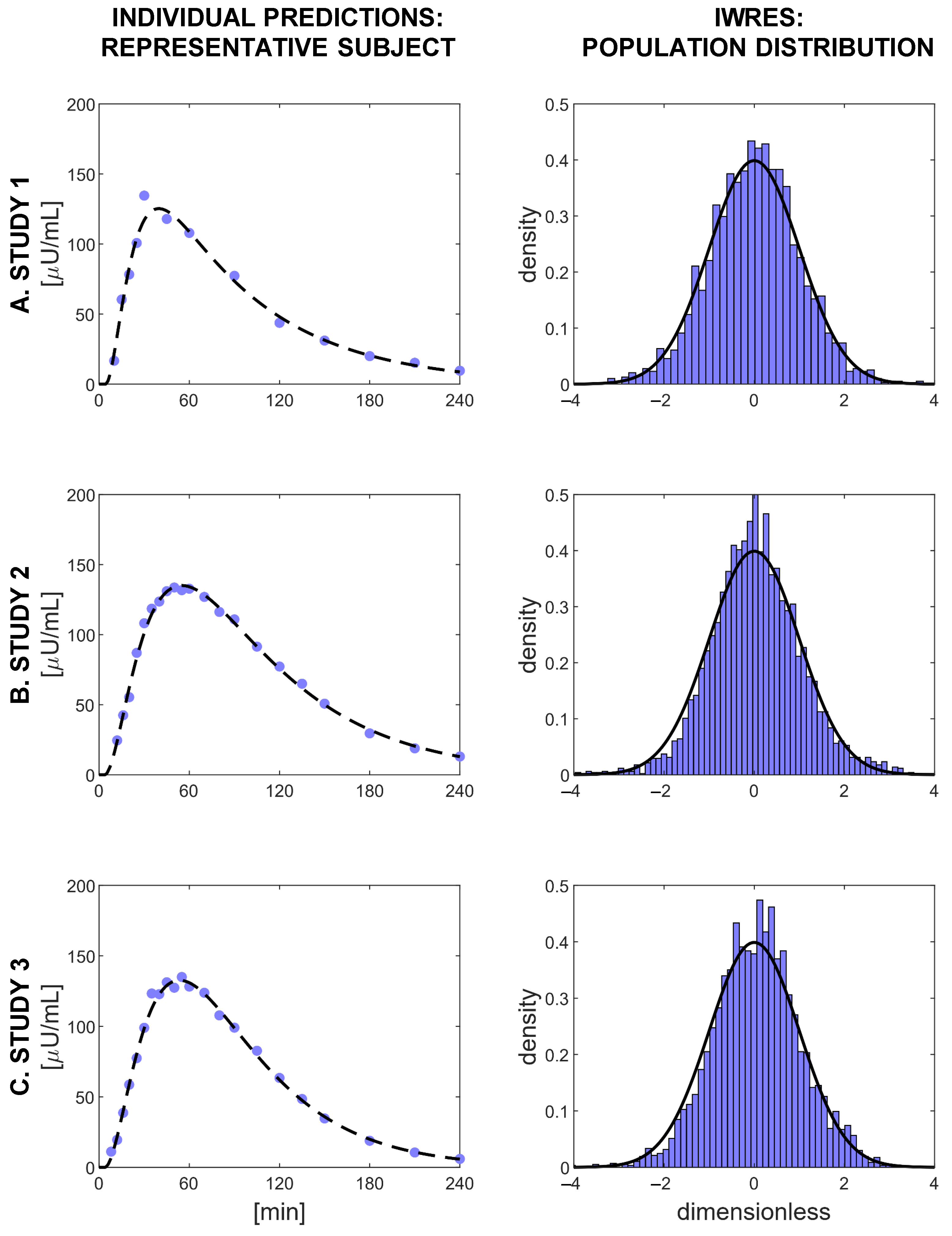
3.3. Validation of the Selected Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BH | Body height |
| BICc | Bayesian information criterion corrected for NLME models |
| BMI | Body mass index |
| BQL | Below the quantification limit |
| BSA | Body surface area |
| BSV | Between subject variability |
| BW | Body weight |
| FDA | Food and Drug Administration |
| IWRES | Individual weighted residuals |
| MCMC | Markov chain Monte Carlo |
| NLME | Nonlinear mixed effects |
| RSE | Relative standard error |
| SAEM | Stochastic approximation of expectation maximization |
| T1D | Type 1 diabetes |
| T2D | Type 2 diabetes |
| UVa | University of Virginia |
| VPC | Visual predictive check |
| WSV | Within-subject variability |
References
- Heinemann, L. Variability of Insulin Absorption and Insulin Action. Diabetes Technol. Ther. 2002, 4, 673–682. [Google Scholar] [CrossRef]
- Binder, C. Absorption of Injected Insulin. Acta Pharmacol. Toxicol. 1969, 27, 1–83. [Google Scholar] [CrossRef]
- Berger, M.; Cüppers, H.J.; Hegner, H.; Jörgens, V.; Berchtold, P. Absorption Kinetics and Biologic Effects of Subcutaneously Injected Insulin Preparations. Diabetes Care 1982, 5, 77–91. [Google Scholar] [CrossRef]
- Hildebrandt, P.; Sejrsen, P.; Nielsen, S.L.; Birch, K.; Sestoft, L. Diffusion and polymerization determines the insulin absorption from subcutaneous tissue in diabetic patients. Scand. J. Clin. Lab. Investig. 1985, 45, 685–690. [Google Scholar] [CrossRef] [PubMed]
- Fernqvist, E.; Linde, B.; Östman, J.; Gunnarsson, R. Effects of physical exercise on insulin absorption in insulin-dependent diabetics. A comparison between human and porcine insulin. Clin. Physiol. 1986, 6, 489–497. [Google Scholar] [CrossRef] [PubMed]
- Brange, J.; Owens, D.R.; Kang, S.; Vølund, A. Monomeric Insulins and Their Experimental and Clinical Implications. Diabetes Care 1990, 13, 923–954. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.; Brange, J.; Burch, A.; Vølund, A.; Owens, D.R. Subcutaneous Insulin Absorption Explained by Insulin’s Physicochemical Properties: Evidence From Absorption Studies of Soluble Human Insulin and Insulin Analogues in Humans. Diabetes Care 1991, 14, 942–948. [Google Scholar] [CrossRef]
- Chen, J.W.; Frystyk, J.; Lauritzen, T.; Christiansen, J.S. Impact of insulin antibodies on insulin aspart pharmacokinetics and pharmacodynamics after 12-week treatment with multiple daily injections of biphasic insulin aspart 30 in patients with type 1 diabetes. Eur. J. Endocrinol. 2005, 153, 907–913. [Google Scholar] [CrossRef]
- Ette, E.I.; Williams, P.J. Population Pharmacokinetics II: Estimation Methods. Ann. Pharmacother. 2004, 38, 1907–1915. [Google Scholar] [CrossRef] [PubMed]
- Vicini, P.; Cobelli, C. The iterative two-stage population approach to IVGTT minimal modeling: Improved precision with reduced sampling. Am. J. Physiol. Endocrinol. Metab. 2001, 280, E179–E186. [Google Scholar] [CrossRef]
- Denti, P.; Bertoldo, A.; Vicini, P.; Cobelli, C. IVGTT glucose minimal model covariate selection by nonlinear mixed-effects approach. Am. J. Physiol. Endocrinol. Metab. 2010, 298, E950–E960. [Google Scholar] [CrossRef] [PubMed]
- Schiavon, M.; Dalla Man, C.; Cobelli, C. Modeling Subcutaneous Absorption of Fast-Acting Insulin in Type 1 Diabetes. IEEE Trans. Biomed. Eng. 2018, 65, 2079–2086. [Google Scholar] [CrossRef] [PubMed]
- Schiavon, M.; Visentin, R.; Giegerich, C.; Klabunde, T.; Cobelli, C.; Dalla Man, C. Modeling Subcutaneous Absorption of Long-Acting Insulin Glargine in Type 1 Diabetes. IEEE Trans. Biomed. Eng. 2020, 67, 624–631. [Google Scholar] [CrossRef] [PubMed]
- Dalla Man, C.; Micheletto, F.; Lv, D.; Breton, M.; Kovatchev, B.; Cobelli, C. The UVa/Padova Type 1 Diabetes Simulator: New Features. J. Diabetes Sci. Technol. 2014, 8, 26–34. [Google Scholar]
- Kovatchev, B.; Breton, M.; Dalla Man, C.; Cobelli, C. In Silico Preclinical Trials: A Proof of Concept in Closed-Loop Control of Type 1 Diabetes. J. Diabetes Sci. Technol. 2009, 3, 44–55. [Google Scholar] [CrossRef]
- Edelman, S.V. Regulation Catches Up to Reality: Nonadjunctive Use of Continuous Glucose Monitoring Data. J. Diabetes Sci. Technol. 2017, 11, 160–164. [Google Scholar] [CrossRef] [PubMed]
- Visentin, R.; Giegerich, C.; Jäger, R.; Dahmen, R.; Boss, A.; Grant, M.; Dalla Man, C.; Cobelli, C.; Klabunde, T. Improving Efficacy of Inhaled Technosphere Insulin (Afrezza) by Postmeal Dosing: In-silico Clinical Trial with the UVa/Padova Type 1 Diabetes Simulator. Diabetes Technol. Ther. 2016, 18, 574–585. [Google Scholar] [CrossRef] [PubMed]
- Schiavon, M.; Visentin, R.; Giegerich, C.; Sieber, J.; Dalla Man, C.; Cobelli, C.; Klabunde, T. In Silico Head-to-Head Comparison of Insulin Glargine 300 U/mL and Insulin Degludec 100 U/mL in Type 1 Diabetes. Diabetes Technol. Ther. 2020, 22, 553–561. [Google Scholar] [CrossRef] [PubMed]
- Visentin, R.; Cobelli, C.; Dalla Man, C. The Padova Type 2 Diabetes Simulator from Triple-Tracer Single-Meal Studies: In Silico Trials Also Possible in Rare but Not-So-Rare Individuals. Diabetes Technol. Ther. 2020, 22, 892–903. [Google Scholar] [CrossRef]
- Hovorka, R.; Allen, J.M.; Elleri, D.; Chassin, L.J.; Harris, J.; Xing, D.; Kollman, C.; Hovorka, T.; Larsen, A.M.F.; Nodale, M.; et al. Manual closed-loop insulin delivery in children and adolescents with type 1 diabetes: A phase 2 randomised crossover trial. Lancet 2010, 375, 743–751. [Google Scholar] [CrossRef]
- Kovatchev, B.; Cobelli, C.; Renard, E.; Anderson, S.; Breton, M.; Patek, S.; Clarke, W.; Bruttomesso, D.; Maran, A.; Costa, S.; et al. Multinational Study of Subcutaneous Model-Predictive Closed-Loop Control in Type 1 Diabetes Mellitus: Summary of the Results. J. Diabetes Sci. Technol. 2010, 4, 1374–1381. [Google Scholar] [CrossRef] [PubMed]
- Heinemann, L.; Nosek, L.; Flacke, F.; Albus, K.; Krasner, A.; Pichotta, P.; Heise, T.; Steiner, S. U-100, pH-Neutral formulation of VIAject®: Faster onset of action than insulin lispro in patients with type 1 diabetes. Diabetes Obes. Metab. 2012, 14, 222–227. [Google Scholar] [CrossRef]
- Documentation of Monolix, Version 2020R1. Available online: http://monolix.lixoft.com/ (accessed on 9 April 2021).
- Kuhn, E.; Lavielle, M. Maximum Likelihood Estimation in Nonlinear Mixed Effects Models. Comput. Stat. Data Anal. 2005, 49, 1020–1038. [Google Scholar] [CrossRef]
- Campioni, M.; Toffolo, G.; Basu, R.; Rizza, R.A.; Cobelli, C. Minimal model assessment of hepatic insulin extraction during an oral test from standard insulin kinetic parameters. Am. J. Physiol. Endocrinol. Metab. 2009, 297, E941–E948. [Google Scholar] [CrossRef] [PubMed]
- Documentation of R, Version 4.0.3. Available online: https://www.r-project.org/other-docs.html (accessed on 15 January 2021).
- Delattre, M.; Lavielle, M.; Poursat, M.A. A note on BIC in mixed-effects models. Electron. J. Stat. 2014, 8, 456–475. [Google Scholar] [CrossRef]
- Derraik, J.; Rademaker, M.; Cutfield, W.; Pinto, T.; Tregurtha, S.; Faherty, A.; Peart, J.; Drury, P.; Hofman, P. Effects of Age, Gender, BMI, and Anatomical Site on Skin Thickness in Children and Adults with Diabetes. PLoS ONE 2014, 9, e86637. [Google Scholar] [CrossRef]
- Wilinska, M.E.; Chassin, L.J.; Schaller, H.C.; Schaupp, L.; Pieber, T.R.; Hovorka, R. Insulin kinetics in type-1 diabetes: Continuous and bolus delivery of rapid acting insulin. IEEE Trans. Biomed. Eng. 2005, 52, 3–12. [Google Scholar] [CrossRef]
- Toffolo, G.M.; Campioni, M.; Basu, R.; Rizza, R.; Cobelli, C. A minimal model of insulin secretion and kinetics to assess hepatic insulin extraction. Am. J. Physiol. Endocrinol. Metab. 2006, 290, E169–E176. [Google Scholar] [CrossRef]
- Website of NONMEM. Available online: https://www.iconplc.com/innovation/nonmem/ (accessed on 9 April 2021).

| Model | Covariate | Correlation | Number of | Precision of the Estimates | % of Subjects that Passed: | BICc | ||
|---|---|---|---|---|---|---|---|---|
| Number | Coefficients | Parameters | Parameters | Mean RSE | RSE >50% | SW Test | Runs Test | |
| 1 | - | - | 18 | 8.29 | 0 | 89.7 | 89.7 | 14,535.48 |
| 2 | - | 19 | 9.57 | 0 | 92.2 | 88.8 | 14,523.40 | |
| 3 | - | 21 | 9.35 | 0 | 90.5 | 88.8 | 14,494.36 | |
| 4 | 22 | 11.11 | 1 | 90.5 | 88.8 | 14,510.54 | ||
| 5 | 22 | 32.24 | 1 | 91.4 | 88.8 | 14,506.42 | ||
| 6 | 22 | 10.95 | 0 | 90.5 | 88.8 | 14,505.33 | ||
| 7 | 22 | 10.48 | 0 | 90.5 | 89.7 | 14,495.18 | ||
| 8 | 22 | 11.61 | 1 | 90.5 | 88.8 | 14,487.14 | ||
| 9 | 22 | 9.58 | 0 | 91.4 | 89.7 | 14,484.42 | ||
| 10 | 22 | 8.59 | 0 | 91.4 | 88.8 | 14,477.76 | ||
| 11 | 22 | 9.11 | 0 | 91.4 | 88.8 | 14,476.86 | ||
| 12 | ; | 23 | 11.01 | 1 | 91.4 | 87.9 | 14,481.72 | |
| 13 | ; | 23 | 10.03 | 0 | 91.4 | 88.8 | 14,478.24 | |
| 14 | ; | 23 | 10.67 | 1 | 91.4 | 87.9 | 14,475.43 | |
| Estimates of the population parameters | ||||
|---|---|---|---|---|
| Parameter | Estimated Value | Unit of Measurement | RSE | |
| Fixed effects | 5.62 | min | 7.5 | |
| 0.135 | L/kg | 3.58 | ||
| 0.0155 | min | 10.5 | ||
| 0.000134 | min | 36.9 | ||
| 0.0128 | min | 3.43 | ||
| 0.113 | min | 3.33 | ||
| −0.0865 | m/kg | 13.6 | ||
| Standard deviations of the random effects | 0.731 | dimensionless | 8.81 | |
| 0.319 | dimensionless | 7.17 | ||
| 1.02 | dimensionless | 7.98 | ||
| 1.86 | dimensionless | 11.8 | ||
| 0.322 | dimensionless | 7.23 | ||
| 0.303 | dimensionless | 6.51 | ||
| Correlations between random effects | 0.681 | dimensionless | 8.19 | |
| −0.579 | dimensionless | 11.1 | ||
| −0.506 | dimensionless | 14 | ||
| Error model parameters | 1.96 | U/mL | 8.85 | |
| 0.0773 | dimensionless | 7.66 | ||
| 2.33 | U/mL | 5.47 | ||
| 0.0516 | dimensionless | 5.79 | ||
| 2.77 | U/mL | 5.17 | ||
| 0.0559 | dimensionless | 5.76 | ||
| Estimates of the individual parameters | ||||||
|---|---|---|---|---|---|---|
| Parameter | Min | Q1 | Median | Q2 | Max | Unit of Measurement |
| 0.748 | 4.03 | 5.98 | 10.5 | 21.9 | min | |
| 0.0741 | 0.121 | 0.146 | 0.17 | 0.29 | L/kg | |
| 0.00364 | 0.00968 | 0.0192 | 0.0334 | 0.116 | min | |
| 0.000079 | 0.000118 | 0.000132 | 0.000166 | 0.00824 | min | |
| 0.00418 | 0.0107 | 0.0136 | 0.0169 | 0.0313 | min | |
| 0.046 | 0.0974 | 0.112 | 0.13 | 0.195 | min | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faggionato, E.; Schiavon, M.; Dalla Man, C. Modeling Between-Subject Variability in Subcutaneous Absorption of a Fast-Acting Insulin Analogue by a Nonlinear Mixed Effects Approach. Metabolites 2021, 11, 235. https://doi.org/10.3390/metabo11040235
Faggionato E, Schiavon M, Dalla Man C. Modeling Between-Subject Variability in Subcutaneous Absorption of a Fast-Acting Insulin Analogue by a Nonlinear Mixed Effects Approach. Metabolites. 2021; 11(4):235. https://doi.org/10.3390/metabo11040235
Chicago/Turabian StyleFaggionato, Edoardo, Michele Schiavon, and Chiara Dalla Man. 2021. "Modeling Between-Subject Variability in Subcutaneous Absorption of a Fast-Acting Insulin Analogue by a Nonlinear Mixed Effects Approach" Metabolites 11, no. 4: 235. https://doi.org/10.3390/metabo11040235
APA StyleFaggionato, E., Schiavon, M., & Dalla Man, C. (2021). Modeling Between-Subject Variability in Subcutaneous Absorption of a Fast-Acting Insulin Analogue by a Nonlinear Mixed Effects Approach. Metabolites, 11(4), 235. https://doi.org/10.3390/metabo11040235