Pathway-Activity Likelihood Analysis and Metabolite Annotation for Untargeted Metabolomics Using Probabilistic Modeling
Abstract
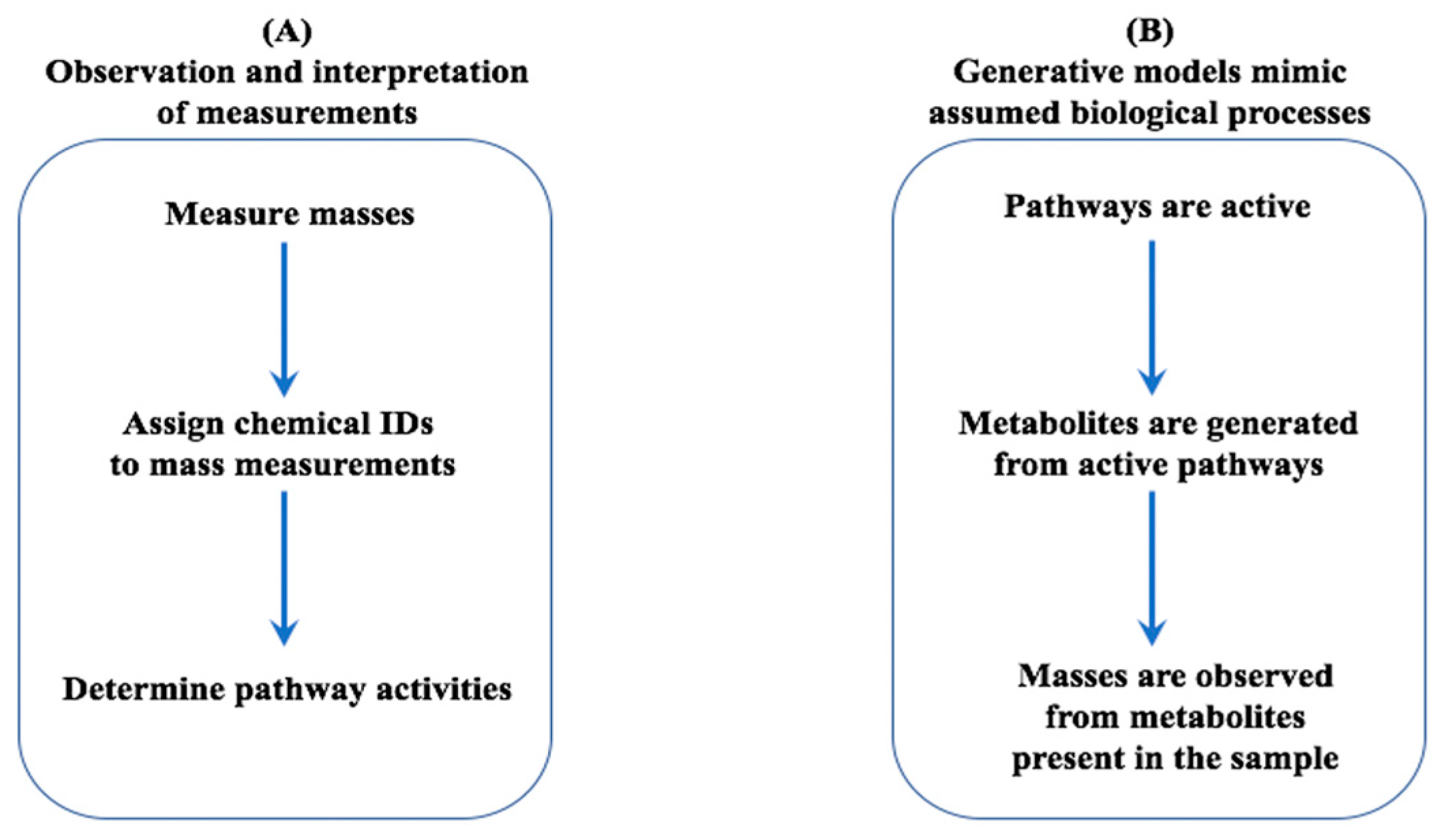
1. Introduction
2. Methods
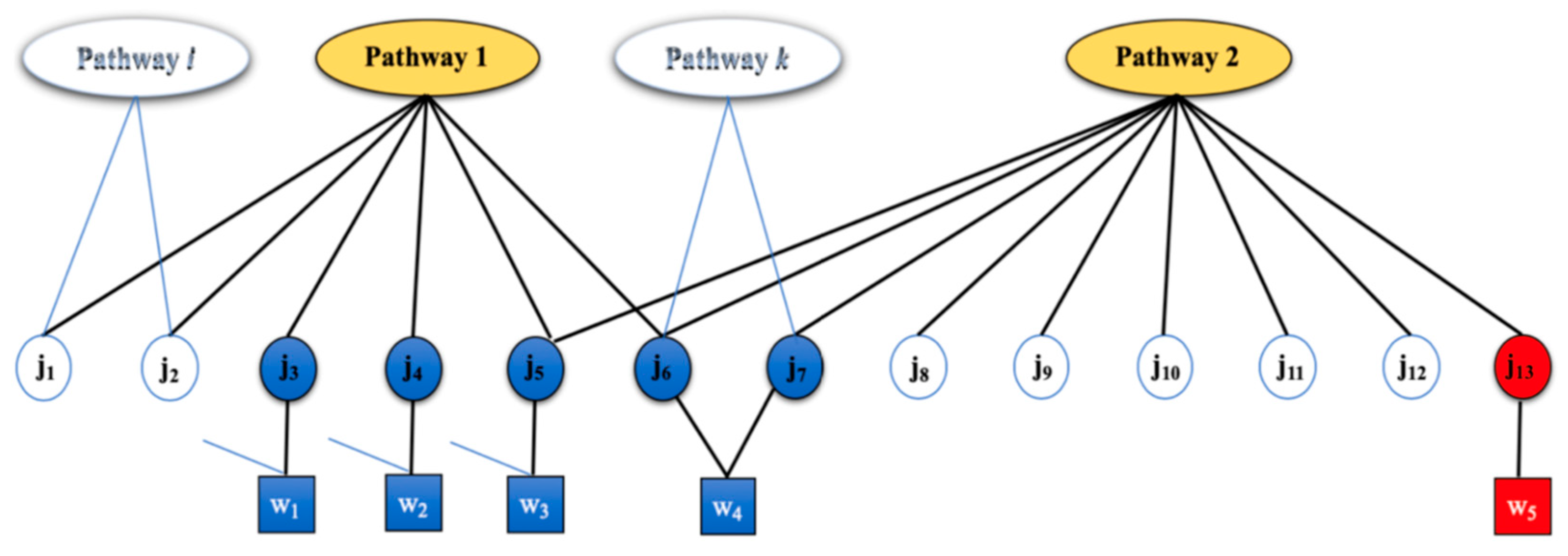
2.1. Motivating Example
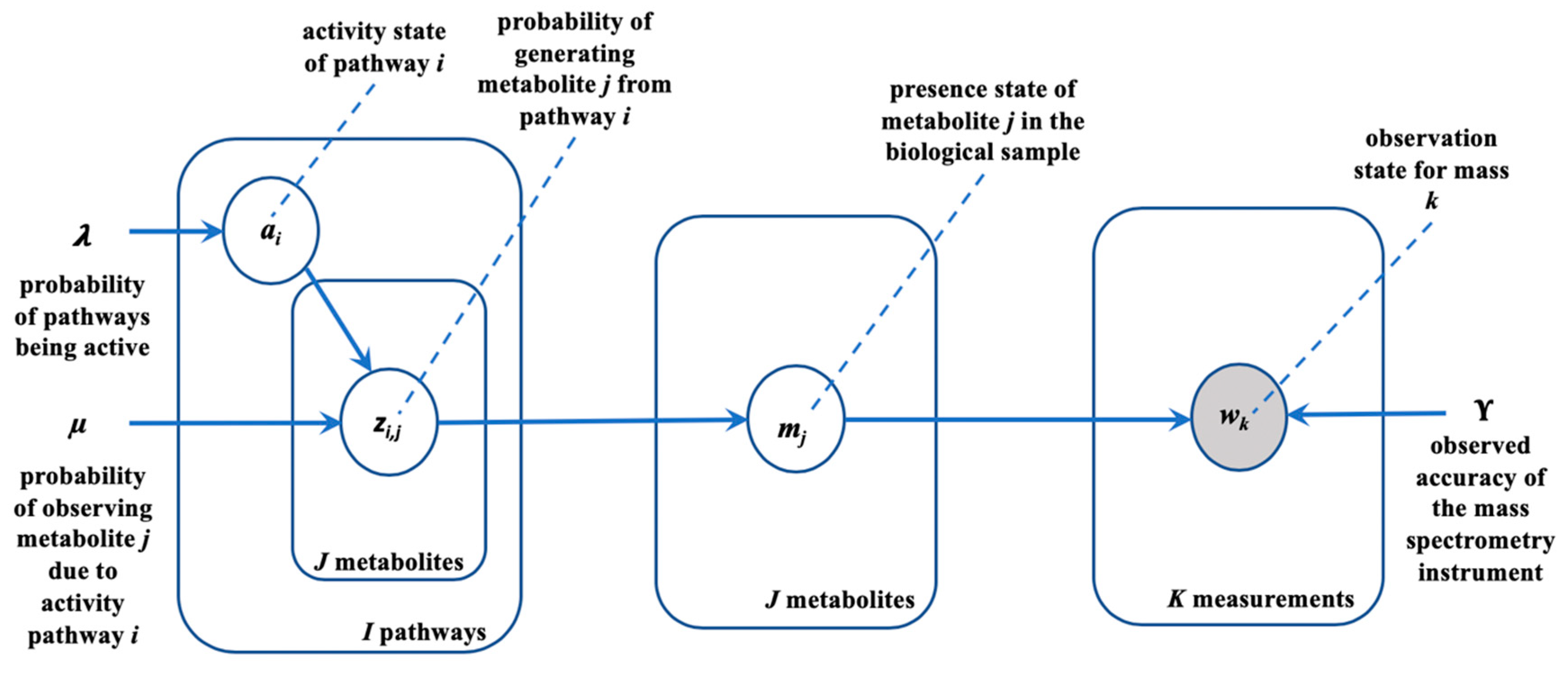
2.2. Generative Model
2.3. Inference
2.3.1. Inferring Pathway Activities
2.3.2. Inferring Metabolite Annotations
2.4. Implementation and Parameter Initialization
3. Results
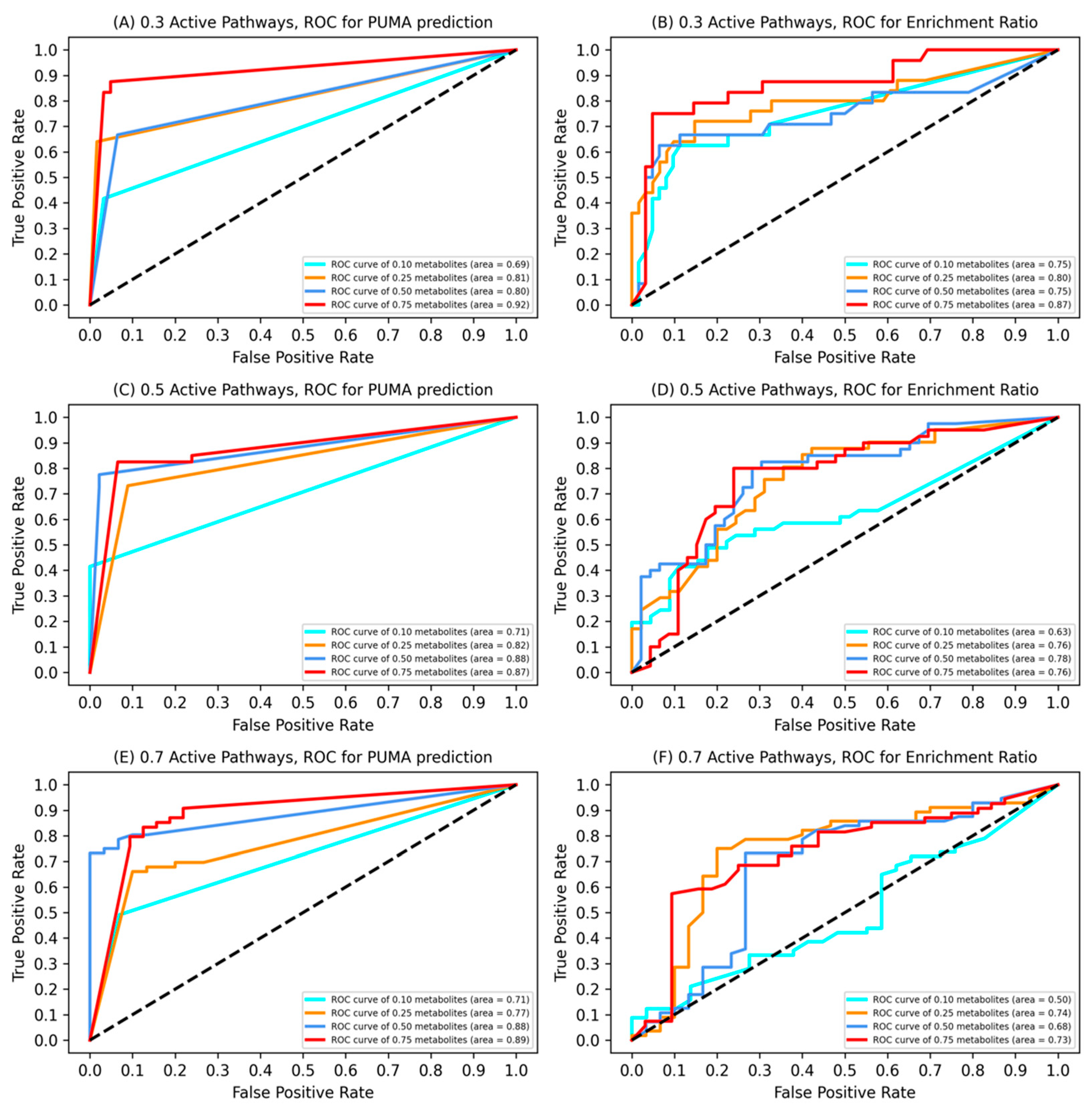
3.1. Model Validation
3.2. Case Study: Chinese Hamster Ovary (CHO) Cell
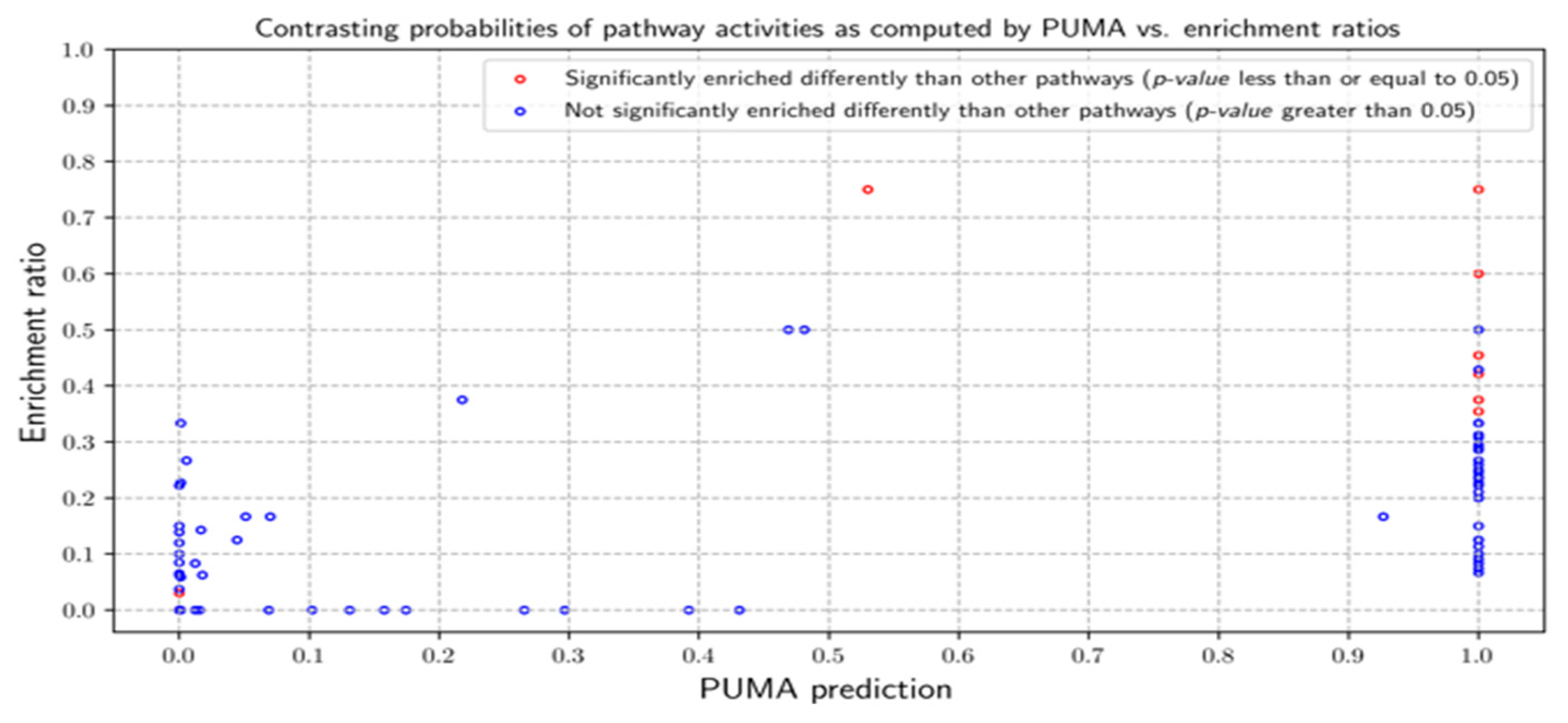
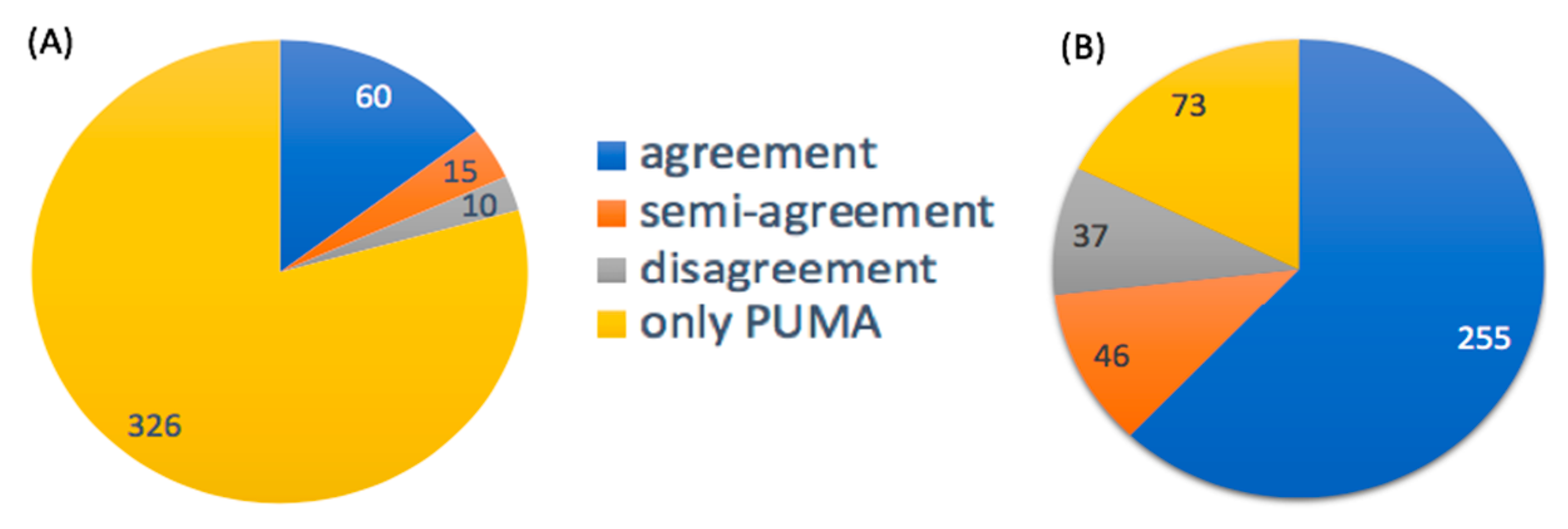
3.2.1. Probabilities of Pathway Activities
3.2.2. Probabilities of Metabolite Annotations
3.2.3. Evaluation of PUMA in Overcoming Uncertainty in Annotation
3.3. Case Study: Human Urinary Sample
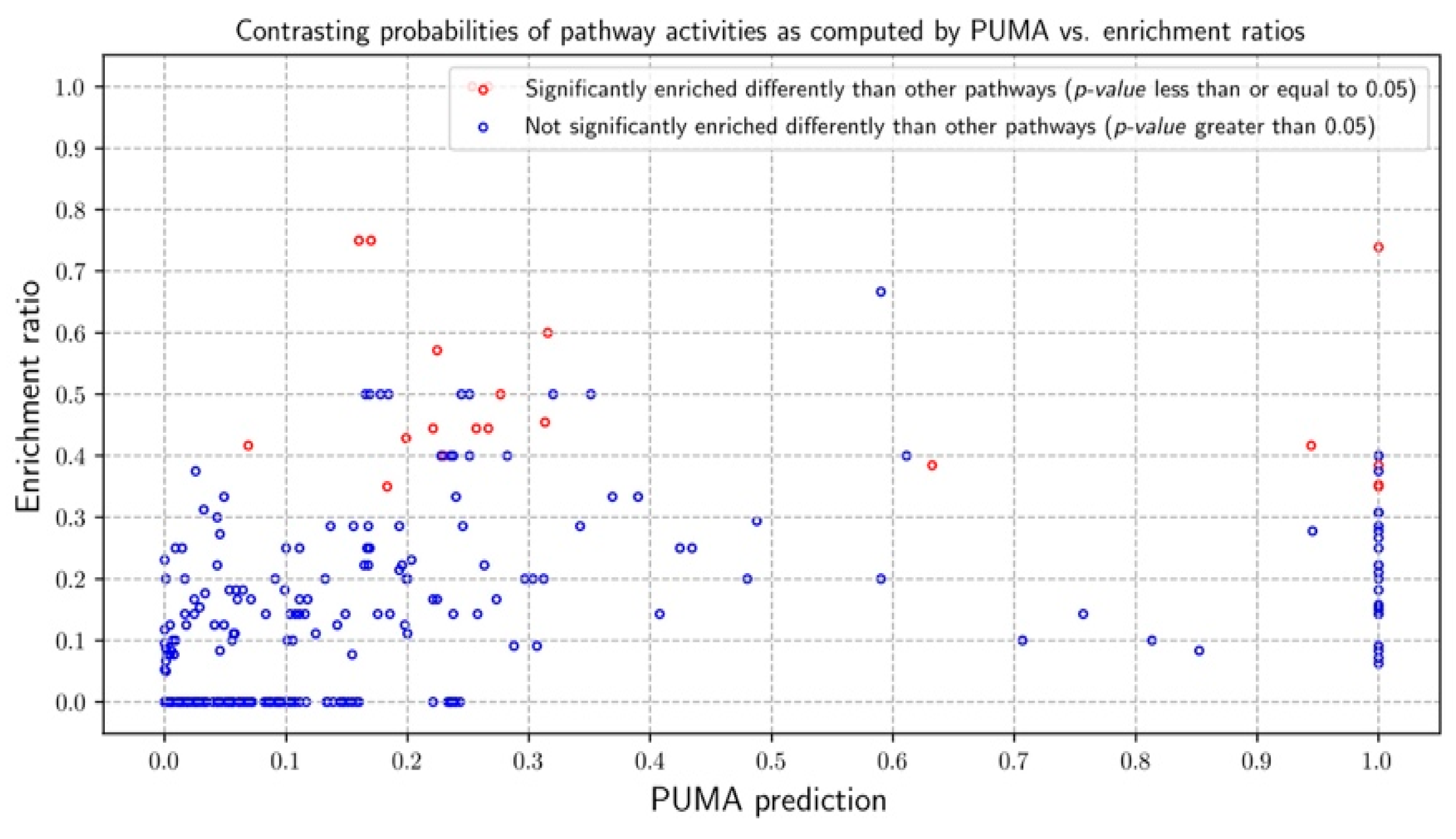
3.3.1. Probabilities of Pathway Activities
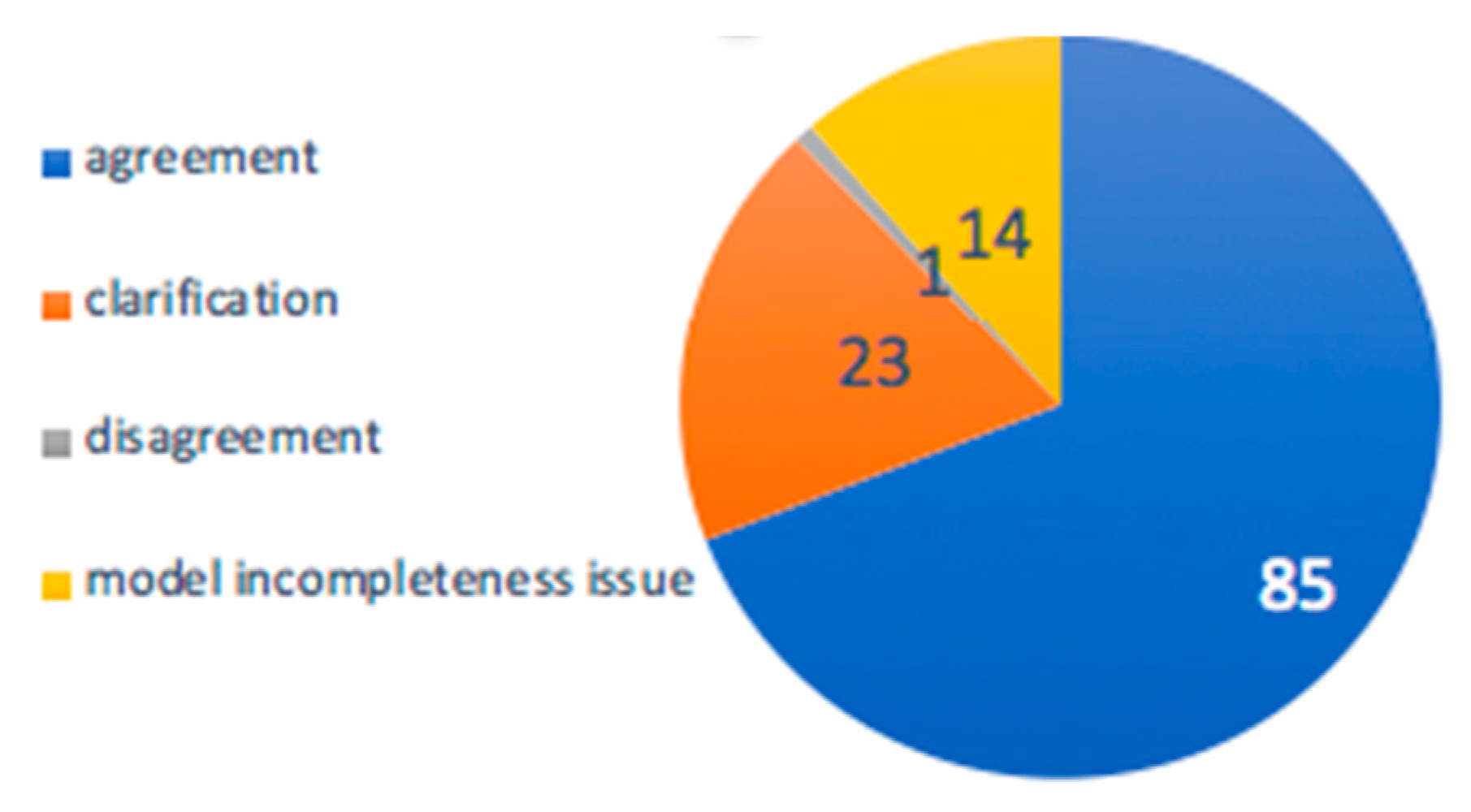
3.3.2. Probabilities of Metabolite Annotations
3.4. Model Convergence, Complexity, and Runtimes
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Availability
References
- Xia, J.; Broadhurst, D.; Wilson, M.; Wishart, D.S. Translational biomarker discovery in clinical metabolomics: An introductory tutorial. Metabolomics 2012, 9, 280–299. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, G.W.; Leo, G.C. Can Untargeted Metabolomics Be Utilized in Drug Discovery/Development? Curr. Top Med. Chem. 2017, 17, 2716–2739. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Alonso, M.-M.; Carrasco-Loba, V.; Medina, J.; Vicente-Carbajosa, J.; Pollmann, S. When Transcriptomics and Metabolomics Work Hand in Hand: A Case Study Characterizing Plant CDF Transcription Factors. High Throughput 2018, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.P.; Park, Y.H.; Ziegler, T. Nutritional metabolomics: Progress in addressing complexity in diet and health. Annu. Rev. Nutr. 2012, 32, 183–202. [Google Scholar] [CrossRef]
- Betts, K.; Sawyer, K. Use of Metabolomics to Advance Research on Environmental Exposures and the Human Exposome; National Academy of Sciences: Washington, DC, USA, 2016. [Google Scholar]
- Guijas, C.; Montenegro-Burke, R.; Domingo-Almenara, X.; Palermo, A.; Warth, B.; Hermann, G.; Koellensperger, G.; Huan, T.; Uritboonthai, W.; Aisporna, A.E.; et al. METLIN: A Technology Platform for Identifying Knowns and Unknowns. Anal. Chem. 2018, 90, 3156–3164. [Google Scholar] [CrossRef]
- Wishart, D.S.; Jewison, T.; Guo, A.C.; Wilson, M.; Knox, C.; Liu, Y.; Djoumbou, Y.; Mandal, R.; Aziat, F.; Dong, E.; et al. HMDB 3.0—The Human Metabolome Database in 2013. Nucleic Acids Res. 2012, 41, D801–D807. [Google Scholar] [CrossRef]
- Horai, H.; Arita, M.; Kanaya, S.; Nihei, Y.; Ikeda, T.; Suwa, K.; Ojima, Y.; Tanaka, K.; Tanaka, S.; Aoshima, K.; et al. MassBank: A public repository for sharing mass spectral data for life sciences. J. Mass Spectrom. 2010, 45, 703–714. [Google Scholar] [CrossRef]
- Lam, H.; Deutsch, E.W.; Eddes, J.; Eng, J.K.; King, N.; Stein, S.E.; Aebersold, R. Development and validation of a spectral library searching method for peptide identification from MS/MS. Proteomics 2007, 7, 655–667. [Google Scholar] [CrossRef]
- Wolf, S.; Schmidt, S.; Müller-Hannemann, M.; Neumann, S. In silico fragmentation for computer assisted identification of metabolite mass spectra. BMC Bioinform. 2010, 11, 148. [Google Scholar] [CrossRef]
- Heinonen, M.; Rantanen, A.; Mielikäinen, T.; Kokkonen, J.; Kiuru, J.; Ketola, R.A.; Rousu, J. FiD: A software forab initiostructural identification of product ions from tandem mass spectrometric data. Rapid Commun. Mass Spectrom. 2008, 22, 3043–3052. [Google Scholar] [CrossRef]
- Allen, F.; Pon, A.; Wilson, M.; Greiner, R.; Wishart, D.S. CFM-ID: A web server for annotation, spectrum prediction and metabolite identification from tandem mass spectra. Nucleic Acids Res. 2014, 42, W94–W99. [Google Scholar] [CrossRef] [PubMed]
- Dührkop, K.; Shen, H.; Meusel, M.; Rousu, J.; Böcker, S. Searching molecular structure databases with tandem mass spectra using CSI: FingerID. Proc. Natl. Acad. Sci. USA 2015, 112, 12580–12585. [Google Scholar] [CrossRef] [PubMed]
- Aguilar-Mogas, A.; Sales-Pardo, M.; Navarro, M.; Tautenhahn, R.; Guimerà, R.; Yanes, O. iMet: A computational tool for structural annotation of unknown metabolites from tandem mass spectra. arXiv 2016, arXiv:1607.04122. [Google Scholar]
- Alden, N.; Krishnan, S.; Porokhin, V.; Raju, R.; Mcelearney, K.; Gilbert, A.; Lee, K. Biologically Consistent Annotation of Metabolomics Data. Anal. Chem. 2017, 89, 13097–13104. [Google Scholar] [CrossRef] [PubMed]
- Hassanpour, N.; Alden, N.; Menon, R.; Jayaraman, A.; Lee, K.; Hassoun, S. Biological Filtering and Substrate Promiscuity Prediction for Annotating Untargeted Metabolomics. Metabolites 2020, 10, 160. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Wishart, D.S. MSEA: A web-based tool to identify biologically meaningful patterns in quantitative metabolomic data. Nucleic Acids Res. 2010, 38, W71–W77. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Sinelnikov, I.V.; Han, B.; Wishart, D.S. Metabo Analyst 3.0—Making metabolomics more meaningful. Nucleic Acids Res. 2015, 43, W251–W257. [Google Scholar] [CrossRef]
- Kankainen, M.; Peddinti, G.; Holm, L.; Orešič, M. MPEA—Metabolite pathway enrichment analysis. Bioinform. 2011, 27, 1878–1879. [Google Scholar] [CrossRef]
- Marco-Ramell, A.; Palau-Rodriguez, M.; Alay, A.; Tulipani, S.; Urpi, M.; Sánchez-Pla, A.; Andres-Lacueva, C. Evaluation and comparison of bioinformatic tools for the enrichment analysis of metabolomics data. BMC Bioinform. 2018, 19, 1. [Google Scholar] [CrossRef]
- Kamburov, A.; Cavill, R.; Ebbels, T.M.D.; Herwig, R.; Keun, H.C. Integrated pathway-level analysis of transcriptomics and metabolomics data with IMPaLA. Bioinformatics 2011, 27, 2917–2918. [Google Scholar] [CrossRef]
- Li, S.; Park, Y.H.; Duraisingham, S.; Strobel, F.H.; Khan, N.; Soltow, Q.A.; Jones, D.P.; Pulendran, B. Predicting Network Activity from High Throughput Metabolomics. PLoS Comput. Biol. 2013, 9, e1003123. [Google Scholar] [CrossRef] [PubMed]
- Pluskal, T.; Castillo, S.; Villar-Briones, A.; Orešič, M. MZmine 2: Modular framework for processing, visualizing, and analyzing mass spectrometry-based molecular profile data. BMC Bioinform. 2010, 11, 395. [Google Scholar] [CrossRef] [PubMed]
- Forsberg, E.M.; Huan, T.; Rinehart, D.; Benton, H.P.; Warth, B.; Hilmers, B.; Siuzdak, G. Data processing, multi-omic pathway mapping, and metabolite activity analysis using XCMS Online. Nat. Protoc. 2018, 13, 633–651. [Google Scholar] [CrossRef] [PubMed]
- Kuhl, C.; Tautenhahn, R.; Böttcher, C.; Larson, T.R.; Neumann, S. CAMERA: An Integrated Strategy for Compound Spectra Extraction and Annotation of Liquid Chromatography/Mass Spectrometry Data Sets. Anal. Chem. 2011, 84, 283–289. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Basics of Markov Chain Simulation, in Bayesian Data Analysis; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Roux, A.; Xu, Y.; Heilier, J.-F.; Olivier, M.-F.; Ezan, E.; Tabet, J.-C.; Junot, C. Annotation of the Human Adult Urinary Metabolome and Metabolite Identification Using Ultra High Performance Liquid Chromatography Coupled to a Linear Quadrupole Ion Trap-Orbitrap Mass Spectrometer. Anal. Chem. 2012, 84, 6429–6437. [Google Scholar] [CrossRef]
- Jordan, M.I. Learning in Graphical Models; Springer Science & Business Media: New York, NY, USA, 1998; Volume 89. [Google Scholar]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC. Peer J. Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef]
- Yildirim, I. Bayesian Inference: Gibbs Sampling; Technical Note; University of Rochester: Rochester, NY, USA, 2012. [Google Scholar]
- Haug, O.K.; Salek, R.M.; Conesa, P.; Hastings, J.; De Matos, P.; Rijnbeek, M.; Mahendraker, T.; Williams, M.; Neumann, S.; Rocca-Serra, P.; et al. MetaboLights—An open-access general-purpose repository for metabolomics studies and associated meta-data. Nucleic Acids Res. 2012, 41, D781–D786. [Google Scholar] [CrossRef]
- Sud, M.; Fahy, E.; Cotter, D.; Azam, K.; Vadivelu, I.; Burant, C.; Edison, A.S.; Fiehn, O.; Higashi, R.; Nair, K.S.; et al. Metabolomics Workbench: An international repository for metabolomics data and metadata, metabolite standards, protocols, tutorials and training, and analysis tools. Nucleic Acids Res. 2015, 44, D463–D470. [Google Scholar] [CrossRef]
- Cary, M.P.; Bader, G.; Sander, C. Pathway information for systems biology. FEBS Lett. 2005, 579, 1815–1820. [Google Scholar] [CrossRef]
- Peregrin-Alvarez, J.M.; Sanford, C.; Parkinson, J. The conservation and evolutionary modularity of metabolism. Genome Biol. 2009, 10, R63. [Google Scholar] [CrossRef]
- Kanehisa, M. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef]
- Caspi, R.; Billington, R.; Ferrer, L.; Foerster, H.; Fulcher, C.A.; Keseler, I.M.; Kothari, A.; Krummenacker, M.; Latendresse, M.; Mueller, L.A.; et al. The MetaCyc Database of metabolic pathways and enzymes and the BioCyc collection of Pathway/Genome Databases. Nucleic Acids Res. 2008, 3, D623–D631. [Google Scholar]
- Da Silva, R.R.; Jourdan, F.; Salvanha, D.M.; Letisse, F.; Jamin, E.L.; Guidetti-Gonzalez, S.; Labate, C.A.; Vêncio, R. ProbMetab: An R package for Bayesian probabilistic annotation of LC-MS-based metabolomics. Bioinformatics 2014, 30, 1336–1337. [Google Scholar] [CrossRef]
- Rogers, S.; Scheltema, R.A.; Girolami, M.; Breitling, R. Probabilistic assignment of formulas to mass peaks in metabolomics experiments. Bioinformatics 2008, 25, 512–518. [Google Scholar] [CrossRef]
- Jeong, J.; Shi, X.; Zhang, X.; Kim, S.; Shen, C. An empirical Bayes model using a competition score for metabolite identification in gas chromatography mass spectrometry. BMC Bioinform. 2011, 12, 392. [Google Scholar] [CrossRef]
- Del Carratore, F.; Schmidt, K.; Vinaixa, M.; Hollywood, K.A.; Greenland-Bews, C.; Takano, E.; Rogers, S.; Breitling, R. Integrated Probabilistic Annotation: A Bayesian-Based Annotation Method for Metabolomic Profiles Integrating Biochemical Connections, Isotope Patterns, and Adduct Relationships. Anal. Chem. 2019, 91, 12799–12807. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, M.; Nothias, L.-F.; Dührkop, K.; Koester, I.; Fleischauer, M.; Hoffmann, M.A.; Petras, D.; Vargas, F.; Morsy, M.; Aluwihare, L.I.; et al. ZODIAC: Database-independent molecular formula annotation using Gibbs sampling reveals unknown small molecules. BioRxiv 2019, 842740. [Google Scholar] [CrossRef]
- Dührkop, K.; Fleischauer, M.; Ludwig, M.; Aksenov, A.A.; Melnik, A.V.; Meusel, M.; Dorrestein, P.C.; Rousu, J.; Böcker, S. SIRIUS 4: A rapid tool for turning tandem mass spectra into metabolite structure information. Nat. Methods 2019, 16, 299–302. [Google Scholar] [CrossRef] [PubMed]
- Amin, S.A.; Chavez, E.; Porokhin, V.; Nair, N.U.; Hassoun, S. Towards creating an extended metabolic model (EMM) for E. coli using enzyme promiscuity prediction and metabolomics data. Microb. Cell Factories 2019, 18, 109. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini, R.; Hassanpour, N.; Liu, L.-P.; Hassoun, S. Pathway-Activity Likelihood Analysis and Metabolite Annotation for Untargeted Metabolomics Using Probabilistic Modeling. Metabolites 2020, 10, 183. https://doi.org/10.3390/metabo10050183
Hosseini R, Hassanpour N, Liu L-P, Hassoun S. Pathway-Activity Likelihood Analysis and Metabolite Annotation for Untargeted Metabolomics Using Probabilistic Modeling. Metabolites. 2020; 10(5):183. https://doi.org/10.3390/metabo10050183
Chicago/Turabian StyleHosseini, Ramtin, Neda Hassanpour, Li-Ping Liu, and Soha Hassoun. 2020. "Pathway-Activity Likelihood Analysis and Metabolite Annotation for Untargeted Metabolomics Using Probabilistic Modeling" Metabolites 10, no. 5: 183. https://doi.org/10.3390/metabo10050183
APA StyleHosseini, R., Hassanpour, N., Liu, L.-P., & Hassoun, S. (2020). Pathway-Activity Likelihood Analysis and Metabolite Annotation for Untargeted Metabolomics Using Probabilistic Modeling. Metabolites, 10(5), 183. https://doi.org/10.3390/metabo10050183





