Computer-Aided Design of Peptidomimetic Inhibitors of Falcipain-3: QSAR and Pharmacophore Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Biological Activities of Compounds Included in the Training and Validation Sets
2.2. Molecular Modeling
2.3. Molecular Mechanics
2.4. Conformational Search
2.5. Solvation Gibbs Free Energy
2.6. Calculation of the Entropic Term
2.7. Binding Affinity Calculations
2.8. Interaction Energy Calculations
2.9. Pharmacophore (PH4) Modeling
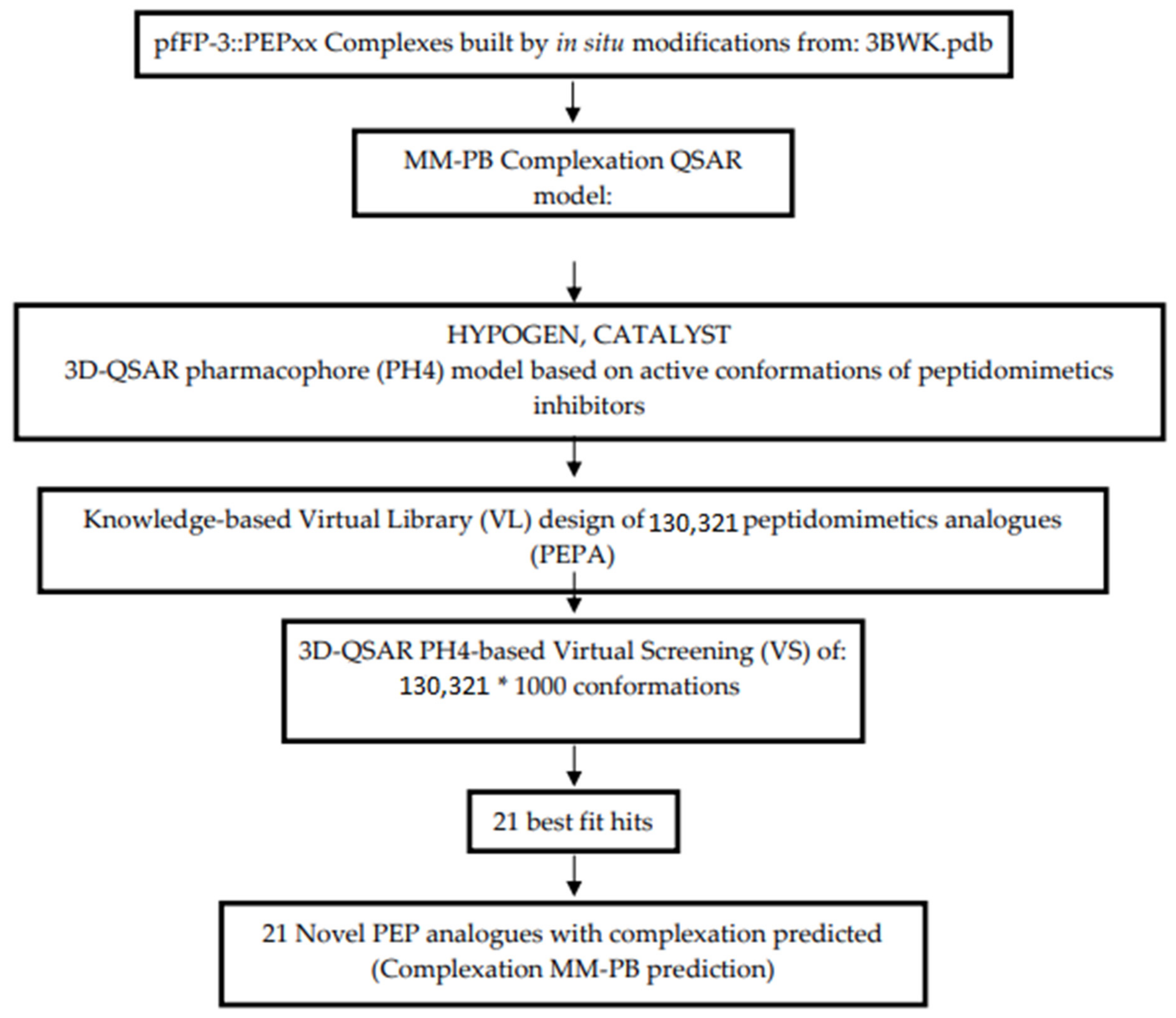
2.10. Generation of the Virtual Library
2.11. In Silico Screening
3. Results and Discussion
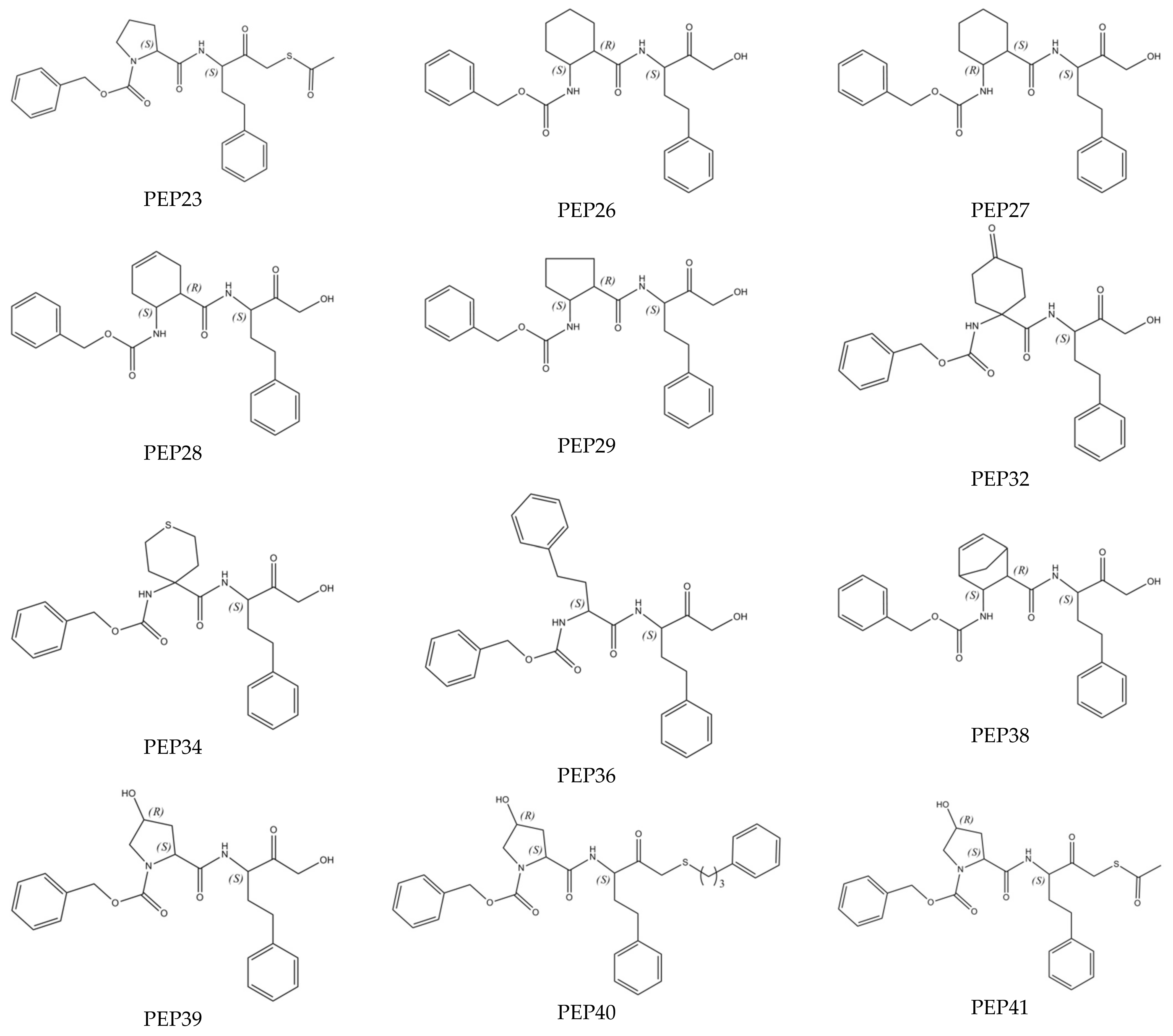
3.1. Selection of Training and Validation (or Test) Data Sets
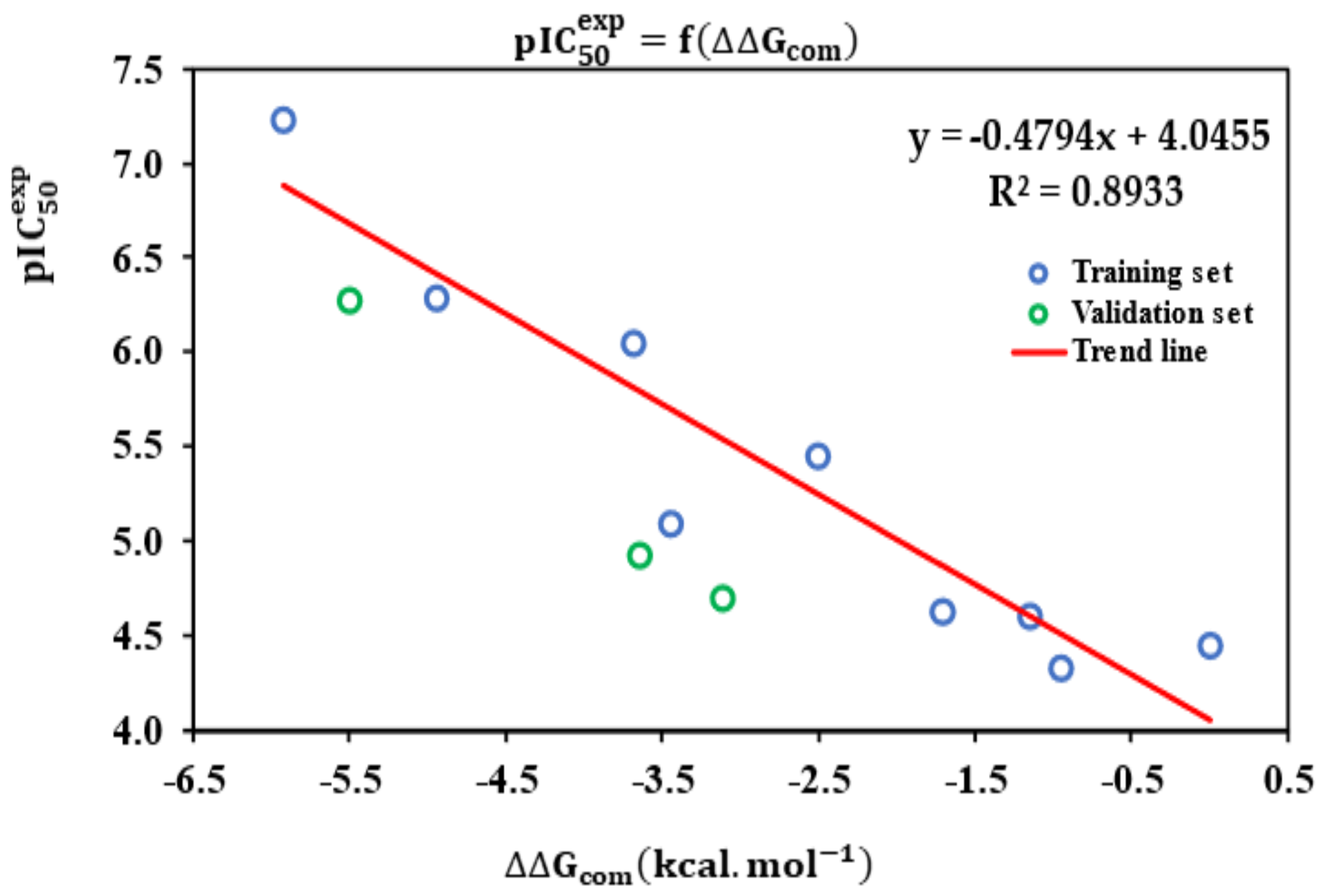
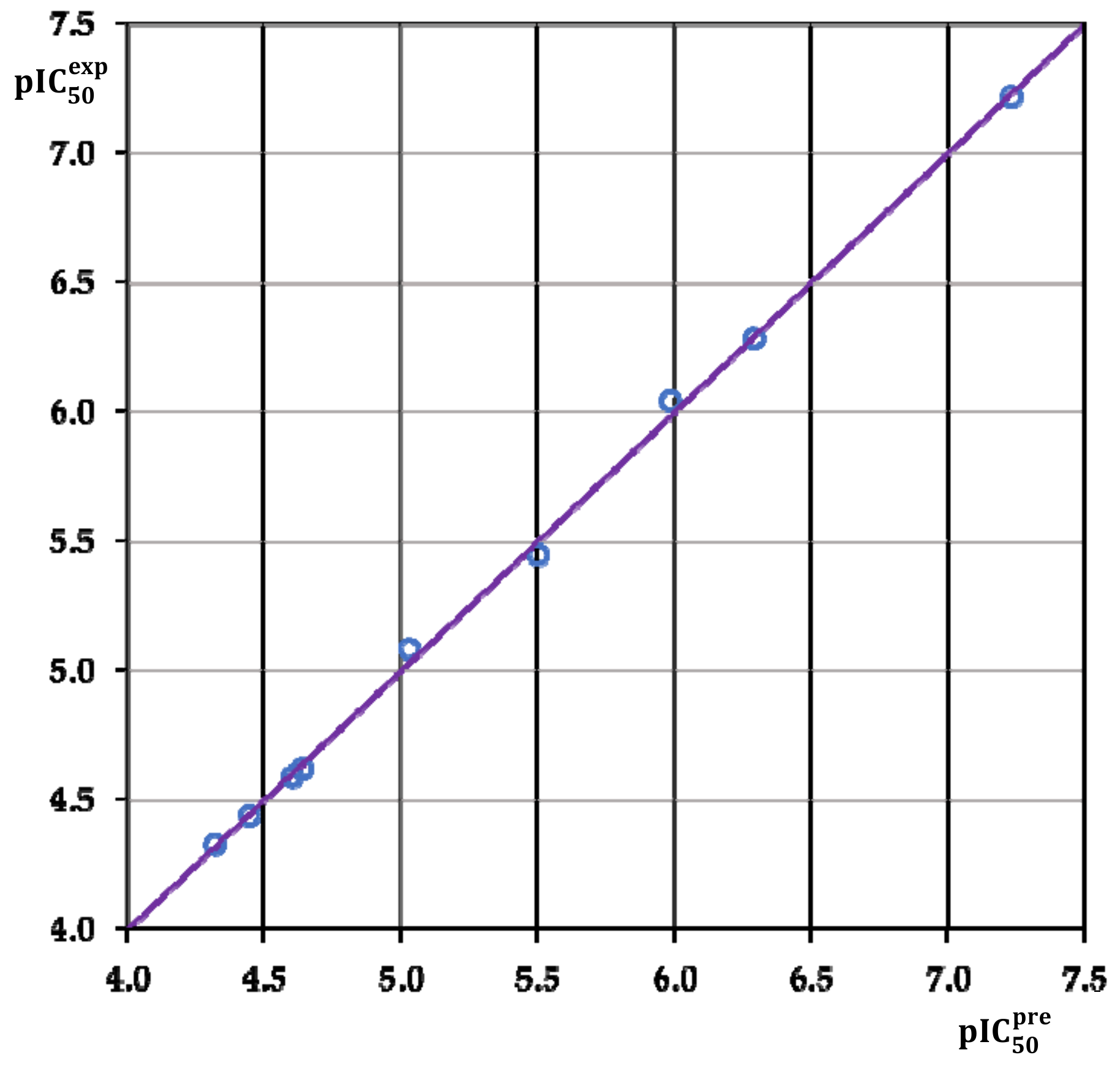
3.2. Obtained QSAR Model
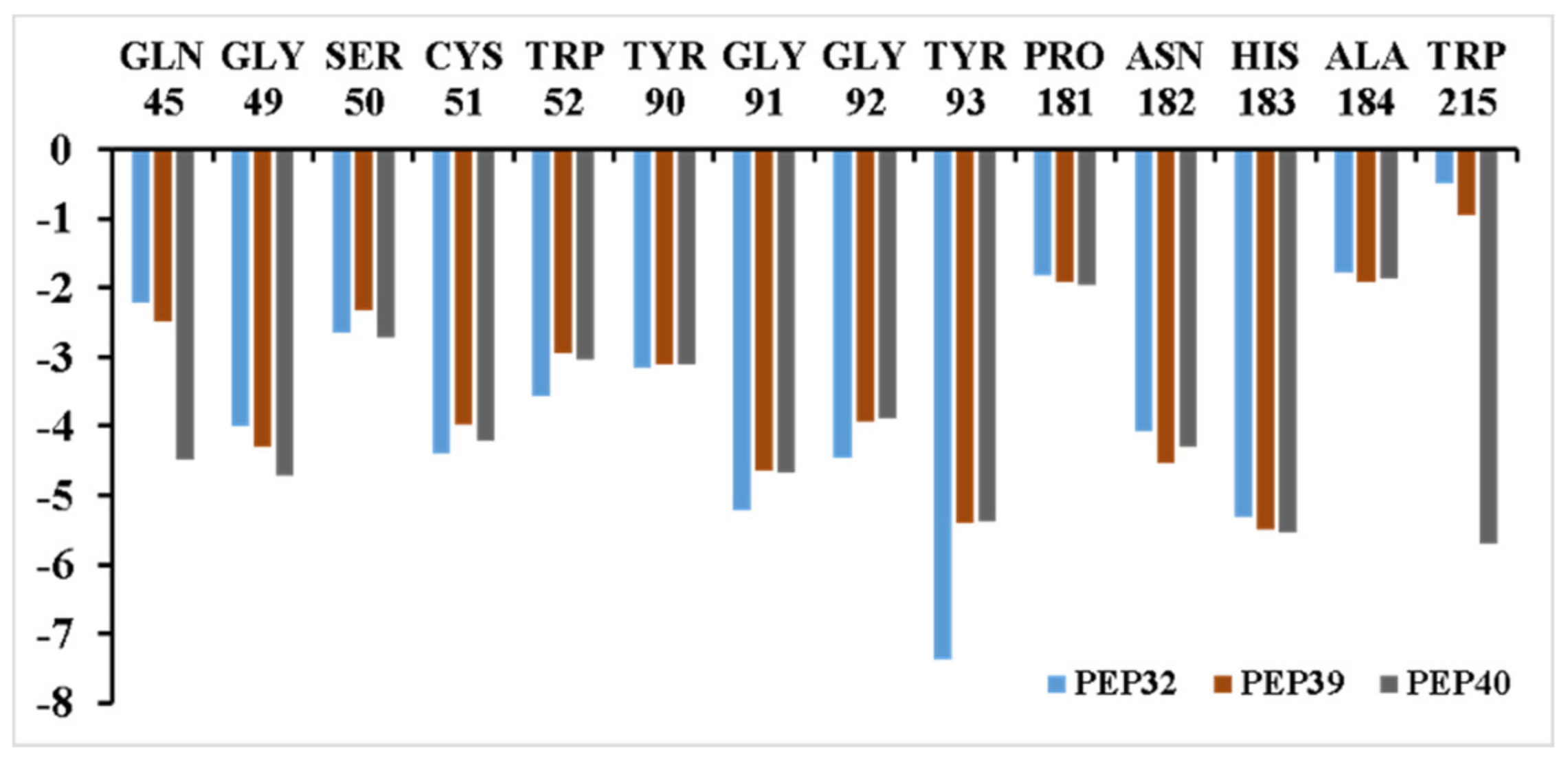
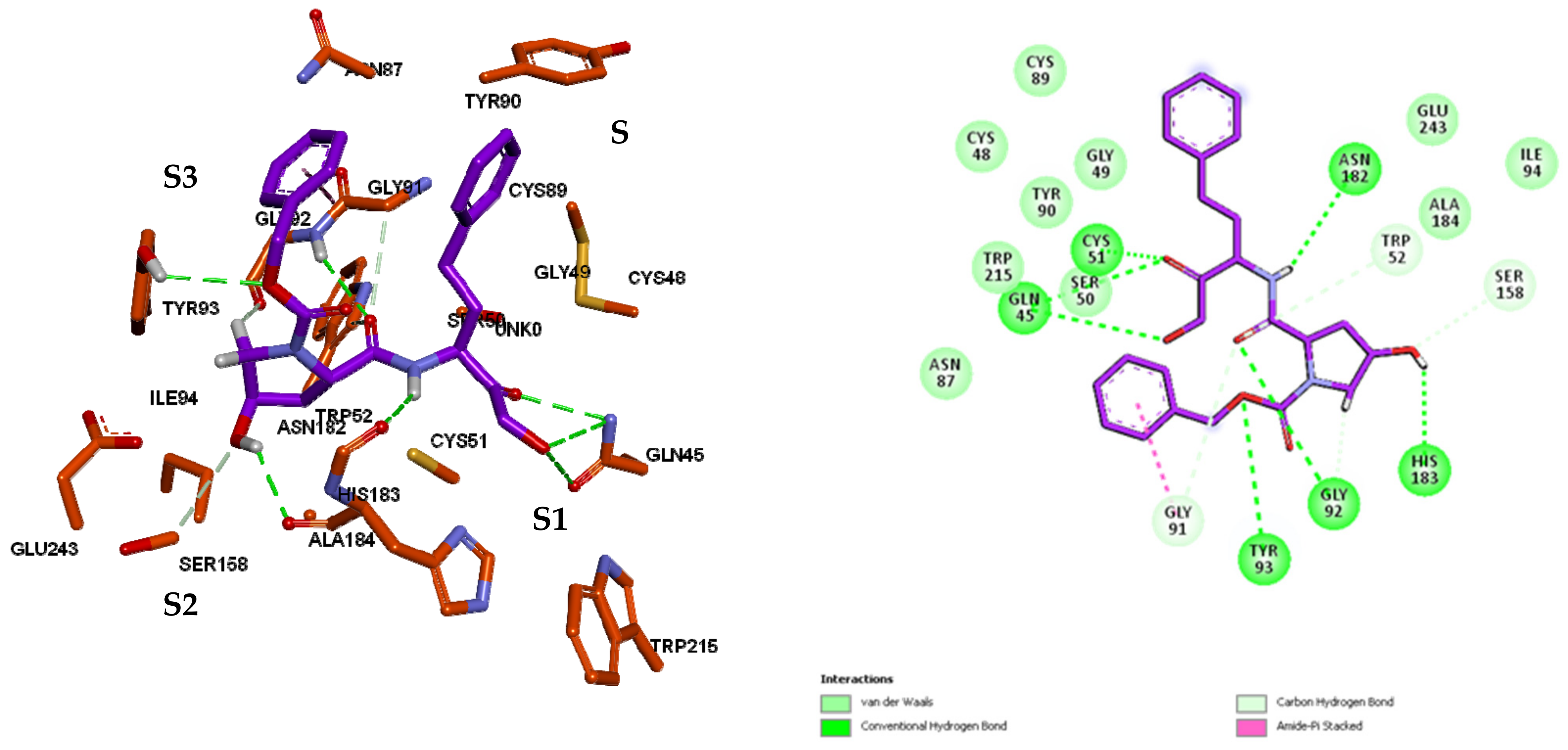
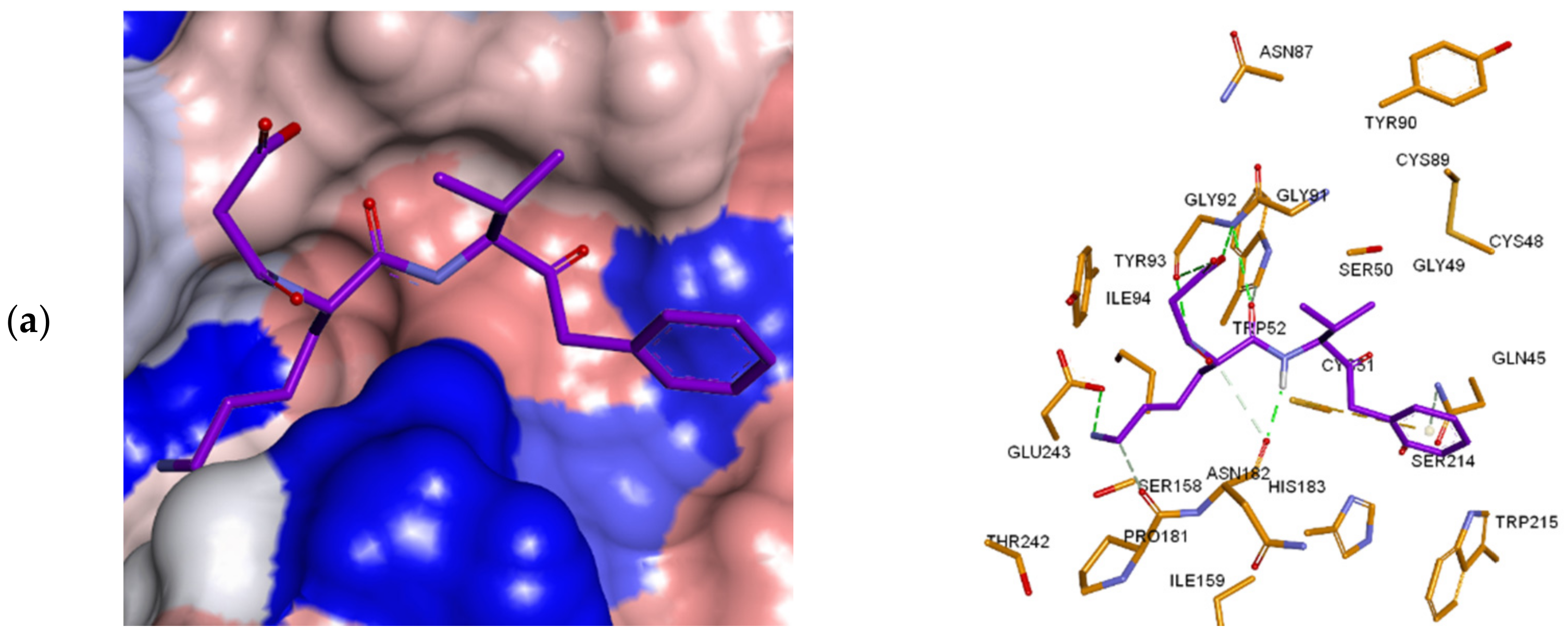
3.3. Inhibitor Binding Modes
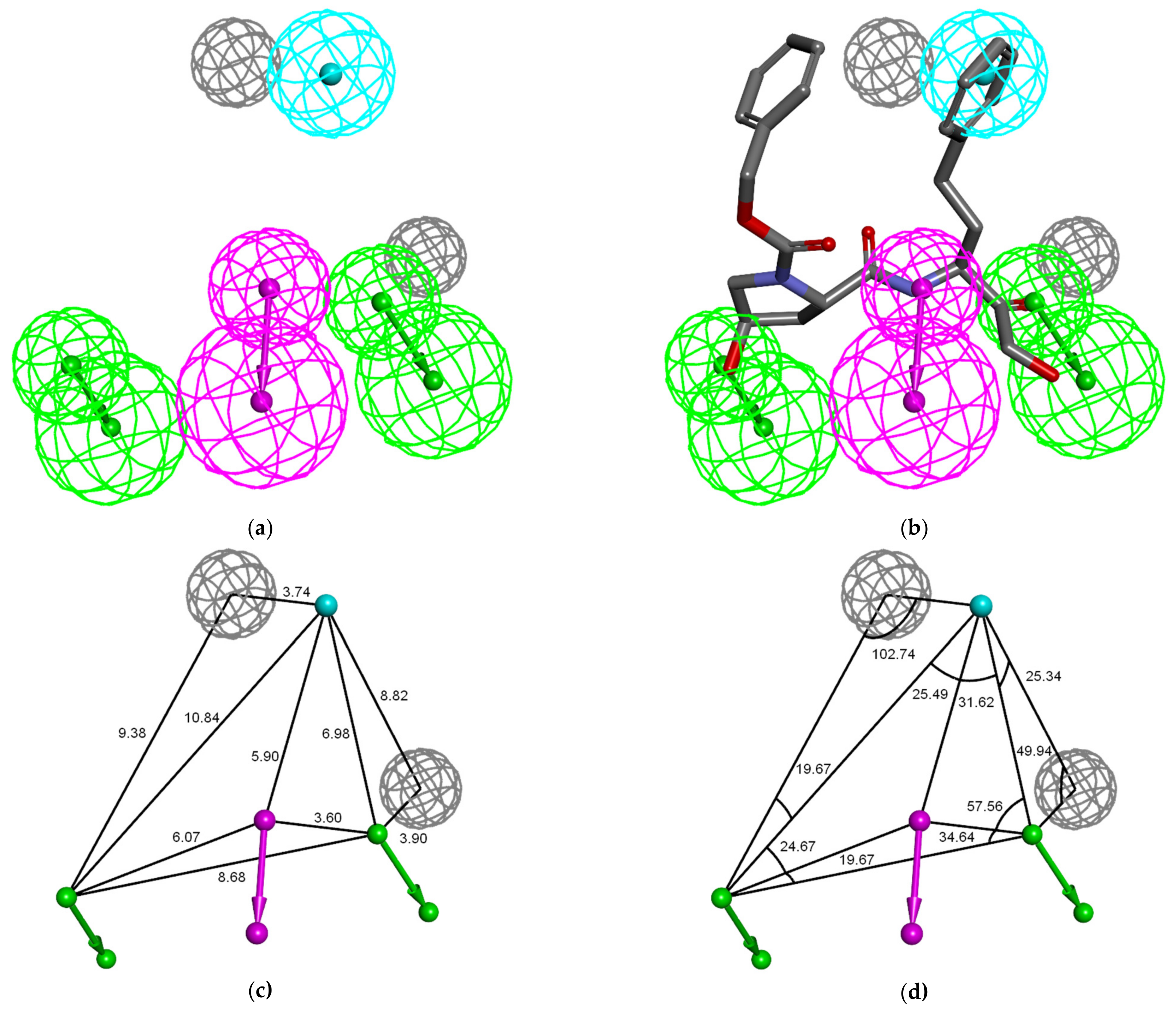
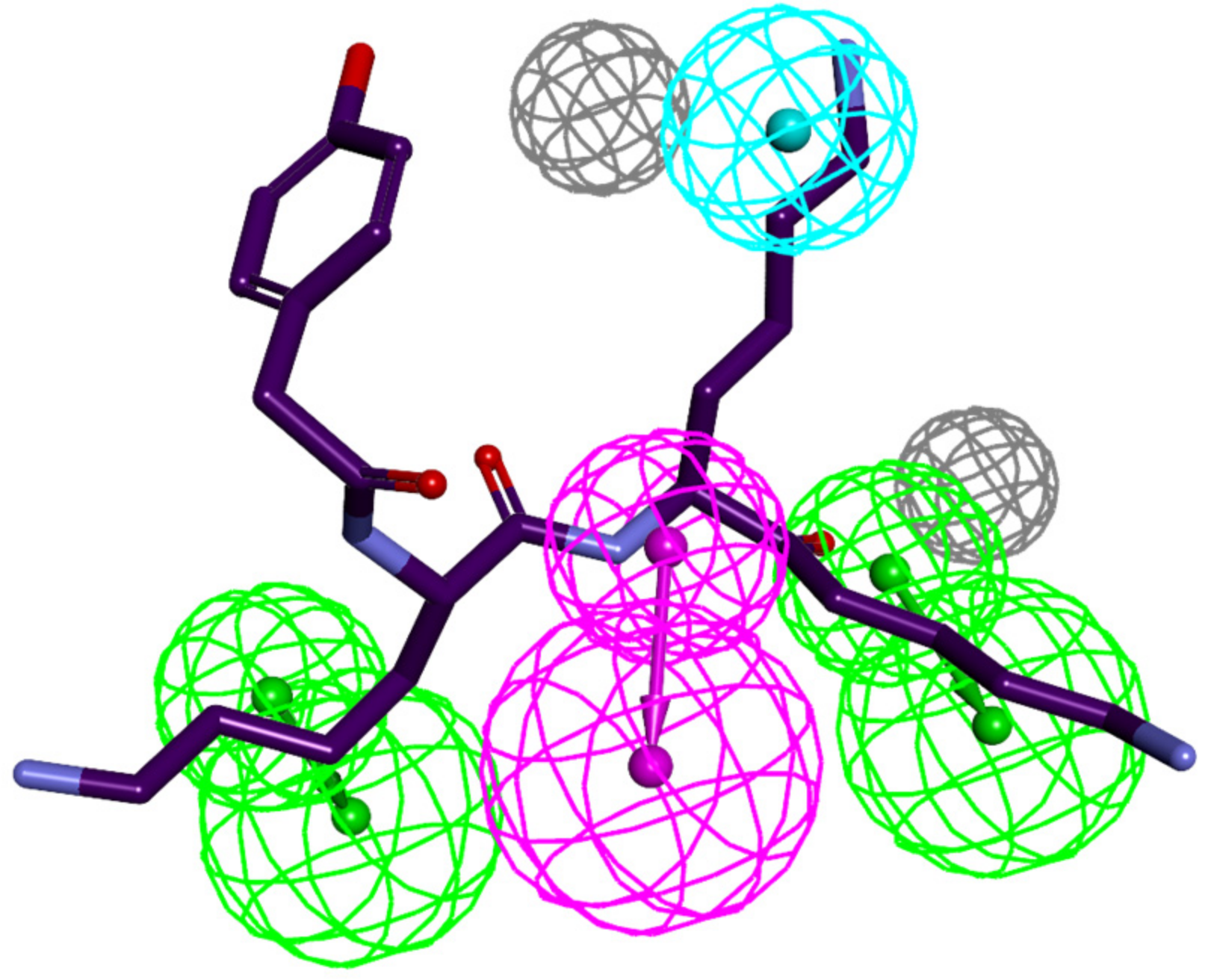
3.4. Ligand-Based 3D-QSAR PH4 Model of FP3 Inhibition
3.5. Library Design and ADME Focusing
3.6. Screening PEPs Virtual Library Using the Obtained in Silico Model
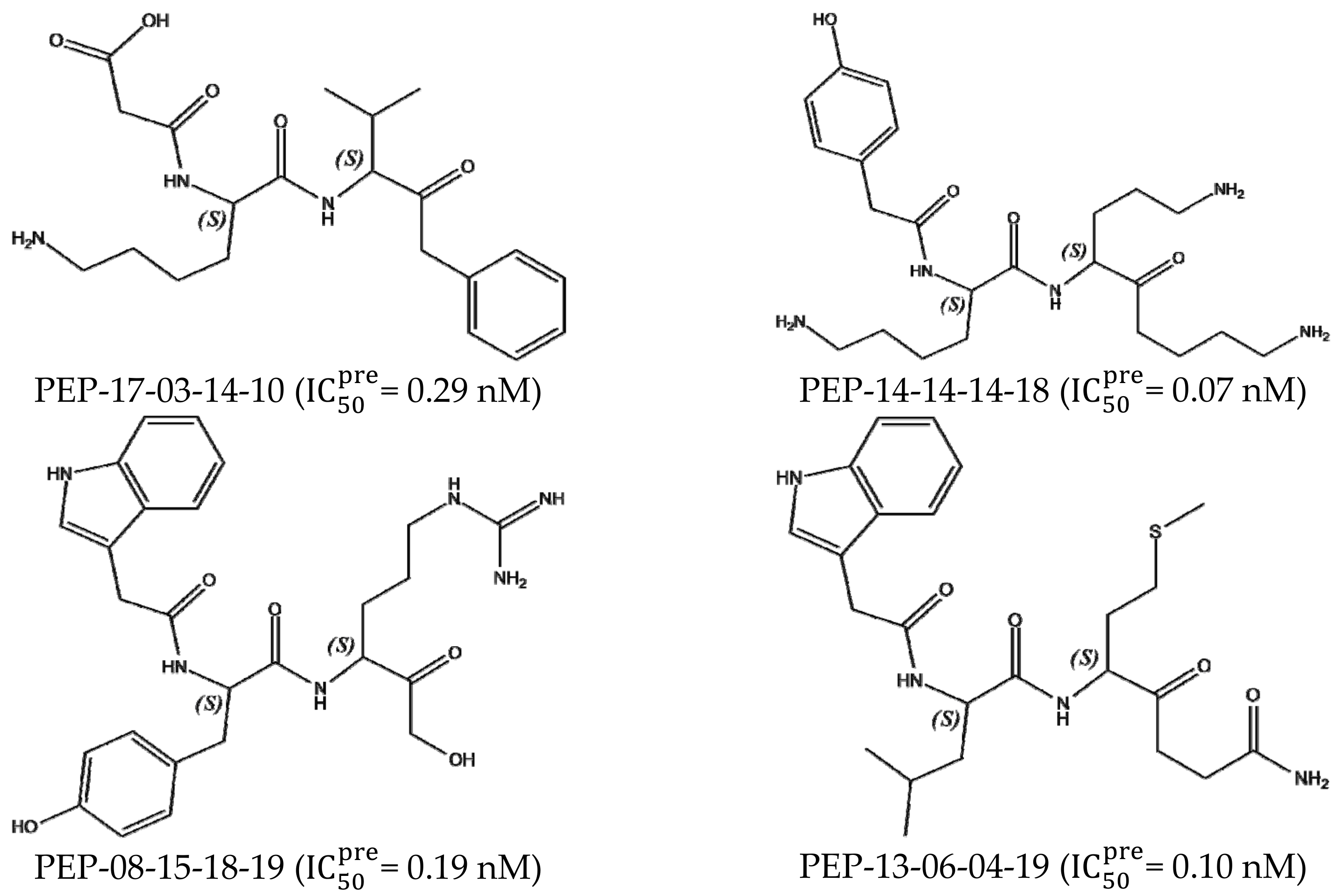
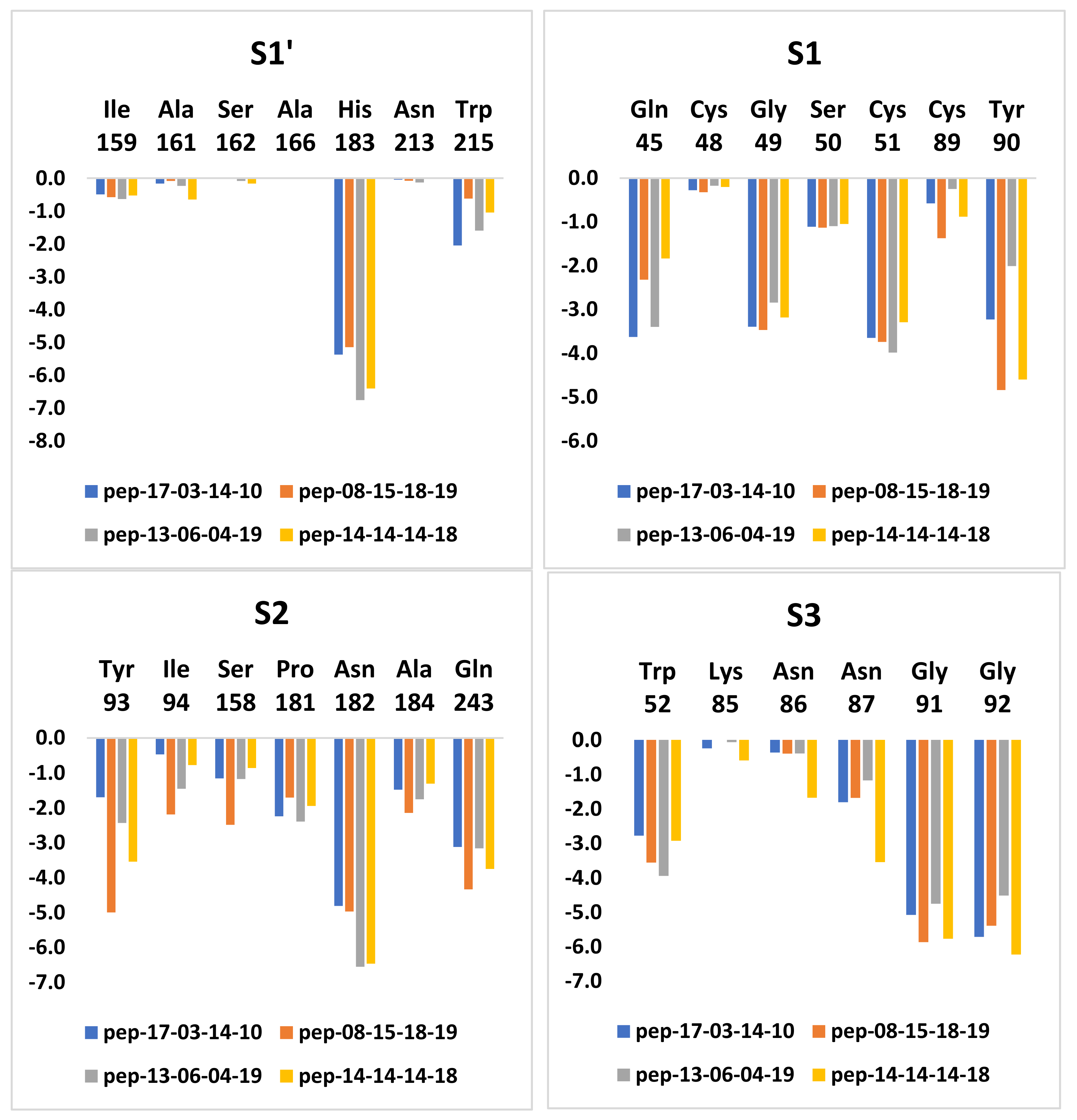
3.7. Analysis of New Inhibitors
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bekono, B.D.; Ntie-Kang, F.; Owono Owono, L.C.; Megnassan, E. Targeting cysteine proteases from plasmodium falciparum: A general overview, rational drug design and computational approaches for drug discovery. Curr. Drug Targets 2018, 19, 501–526. [Google Scholar] [CrossRef] [PubMed]
- Dye, C. Global epidemiology of tuberculosis. Lancet 2006, 367, 938–940. [Google Scholar] [CrossRef]
- WHO. World Malaria Report; WHO: Geneva, Switzerland, 2015. [Google Scholar]
- Rosenthal, P.; Sijwali, P.; Singh, A.; Shenai, B. Cysteine proteases of malaria parasites: Targets for chemotherapy. Curr. Pharm. Des. 2002, 8, 1659–1672. [Google Scholar] [CrossRef] [PubMed]
- Yeh, I.; Altman, R. Drug targets for plasmodium falciparum: A Post-Genomic Review/Survey. Mini-Rev. Med. Chem. 2006, 6, 177–202. [Google Scholar] [CrossRef] [PubMed]
- White, S.W.; Zheng, J.; Zhang, Y.-M.; Rock, C.O. The structural biology of type ii fatty acid biosynthesis. Annu. Rev. Biochem. 2005, 74, 791–831. [Google Scholar] [CrossRef]
- Zhang, Y.-M.; Lu, Y.-J.; Rock, C.O. The reductase steps of the type II fatty acid synthase as antimicrobial targets. Lipids 2004, 39, 1055–1060. [Google Scholar] [CrossRef] [PubMed]
- Elliott, D.A.; McIntosh, M.T.; Hosgood, H.D.; Chen, S.; Zhang, G.; Baevova, P.; Joiner, K.A. Four distinct pathways of hemoglobin uptake in the malaria parasite plasmodium falciparum. Proc. Natl. Acad. Sci. USA 2008, 105, 2463–2468. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Gluzman, I.Y.; Drew, M.E.; Goldberg, D.E. The role of plasmodium falciparum food vacuole plasmepsins. J. Biol. Chem. 2004, 280, 1432–1437. [Google Scholar] [CrossRef]
- Blackman, M. Proteases involved in erythrocyte invasion by the malaria parasite function and potential as chemotherapeutic targets. Curr. Drug Targets 2000, 1, 59–83. [Google Scholar] [CrossRef]
- Eggleson, K.K.; Duffin, K.L.; Goldberg, D.E. Identification and characterization of falcilysin, a metallopeptidase involved in hemoglobin catabolism within the malaria parasite Plasmodium falciparum. J. Biol. Chem. 1999, 274, 32411–32417. [Google Scholar] [CrossRef]
- Klemba, M.; Gluzman, I.; Goldberg, D.E. A Plasmodium falciparum dipeptidyl aminopeptidase I participates in vacuolar hemoglobin degradation. J. Biol. Chem. 2004, 279, 43000–43007. [Google Scholar] [CrossRef] [PubMed]
- Coterón, J.M.; Catterick, D.; Castro, J.; Chaparro, M.J.; Díaz, B.; Fernández, E.; Ferrer, S.; Gamo, F.J.; Gordo, M.; Gut, J.; et al. Falcipain inhibitors: Optimization studies of the 2-pyrimidinebcarbonitrile lead series†. J. Med. Chem. 2010, 53, 6129–6152. [Google Scholar] [CrossRef]
- Sijwali, P.S.; Koo, J.; Singh, N.; Rosenthal, P.J. Gene disruptions demonstrate independent roles for the four falcipain cysteine proteases of plasmodium falciparum. Mol. Biochem. Parasitol. 2006, 150, 96–106. [Google Scholar] [CrossRef] [PubMed]
- Ramjee, M.K.; Flinn, N.S.; Pemberton, T.P.; Quibell, M.; Wang, Y.; Watts, J.P. Substrate mapping and inhibitor profiling of falcipain-2, falcipain-3 and berghepain-2: Implications for peptidase anti-malarial drug discovery. Biochem. J. 2006, 399, 47–57. [Google Scholar] [CrossRef] [PubMed]
- Ang, K.K.H.; Ratnam, J.; Gut, J.; Legac, J.; Hansell, E.; Mackey, Z.B.; Skrzypczynska, K.M.; Debnath, A.; Engel, J.C.; Rosenthal, P.J.; et al. Mining a cathepsin inhibitor library for new antiparasitic drug leads. PLoS Negl. Trop. Dis. 2011, 5, e1023. [Google Scholar] [CrossRef] [PubMed]
- Chibale, K.; Musonda, C. The synthesis of parasitic cysteine protease and trypanothione reductase inhibitors. Curr. Med. Chem. 2003, 10, 1863–1889. [Google Scholar] [CrossRef] [PubMed]
- Desai, P.V.; Patny, A.; Gut, J.; Rosenthal, P.J.; Tekwani, B.; Srivastava, A.; Avery, M. Identification of novel parasitic cysteine protease inhibitors by use of virtual screening. 2. The available chemical directory. J. Med. Chem. 2006, 49, 1576–1584. [Google Scholar] [CrossRef]
- Rosenthal, P.J.; Wollish, W.S.; Palmer, J.T.; Rasnick, D. Antimalarial effects of peptide inhibitors of a plasmodium falciparum cysteine proteinase. J. Clin. Investig. 1991, 88, 1467–1472. [Google Scholar] [CrossRef] [PubMed]
- Rosenthal, P.J.; Lee, G.K.; Smith, R.E. Inhibition of a plasmodium vinckei cysteine proteinase cures murine malaria. J. Clin. Investig. 1993, 91, 1052–1056. [Google Scholar] [CrossRef] [PubMed]
- Rosenthal, P.J.; Olson, J.E.; Lee, G.K.; Palmer, J.T.; Klaus, J.L.; Rasnick, D. Antimalarial effects of vinyl sulfone cysteine proteinase inhibitors. Antimicrob. Agents Chemother. 1996, 40, 1600–1603. [Google Scholar] [CrossRef] [PubMed]
- Olson, J. Antimalarial effects in mice of orally administered peptidyl cysteine protease inhibitors. Bioorg. Med. Chem. 1999, 7, 633–638. [Google Scholar] [CrossRef]
- Verissimo, E.; Berry, N.; Gibbons, P.; Cristiano, M.L.S.; Rosenthal, P.J.; Gut, J.; Ward, S.A.; O’Neill, P.M. Design and synthesis of novel 2-pyridone peptidomimetic falcipain 2/3 inhibitors. Bioorg. Med. Chem. Lett. 2008, 18, 4210–4214. [Google Scholar] [CrossRef] [PubMed]
- Weldon, D.J.; Shah, F.; Chittiboyina, A.G.; Sheri, A.; Chada, R.R.; Gut, J.; Rosenthal, P.J.; Shivakumar, D.; Sherman, W.; Desai, P.; et al. Synthesis, biological evaluation, hydration site thermodynamics, and chemical reactivity analysis of α-keto substituted peptidomimetics for the inhibition of plasmodium falciparum. Bioorg. Med. Chem. Lett. 2014, 24, 1274–1279. [Google Scholar] [CrossRef] [PubMed]
- Potshangbam, A.M.; Tanneeru, K.; Reddy, B.M.; Guruprasad, L. 3D-QSAR and molecular docking studies of 2-pyrimidinecarbonitrile derivatives as inhibitors against falcipain-3. Bioorg. Med. Chem. Lett. 2011, 21, 7219–7223. [Google Scholar] [CrossRef]
- Desai, P.V.; Patny, A.; Sabnis, Y.; Tekwani, B.; Gut, J.; Rosenthal, P.; Srivastava, A.; Avery, M. Identification of novel parasitic cysteine protease inhibitors using virtual screening. 1. The ChemBridge Database. J. Med. Chem. 2004, 47, 6609–6615. [Google Scholar] [CrossRef] [PubMed]
- Shah, F.; Mukherjee, P.; Desai, P.; Avery, M. Computational approaches for the discovery of cysteine protease inhibitors against malaria and SARS. Curr. Comput. Aided-Drug Des. 2010, 6, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Shah, F.; Mukherjee, P.; Gut, J.; Legac, J.; Rosenthal, P.J.; Tekwani, B.L.; Avery, M.A. Identification of novel malarial cysteine protease inhibitors using structure-based virtual screening of a focused cysteine protease inhibitor library. J. Chem. Inf. Modeling 2011, 51, 852–864. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, J.; Shiri, F.; Pirhadi, S.; Heidari, Z. Discovery of New potential antimalarial compounds using virtual screening of ZINC database. Comb. Chem. High Throughput Screen. 2015, 18, 227–234. [Google Scholar] [CrossRef]
- Kerr, I.D.; Lee, J.H.; Farady, C.J.; Marion, R.; Rickert, M.; Sajid, M.; Pandey, K.C.; Caffrey, C.R.; Legac, J.; Hansell, E.; et al. Vinyl sulfones as antiparasitic agents and a structural basis for drug design. J. Biol. Chem. 2009, 284, 25697–25703. [Google Scholar] [CrossRef]
- Kerr, I.D.; Lee, J.H.; Pandey, K.C.; Harrison, A.; Sajid, M.; Rosenthal, P.J.; Brinen, L.S. Structures of falcipain-2 and falcipain-3 bound to small molecule inhibitors: Implications for substrate specificity‡. J. Med. Chem. 2009, 52, 852–857. [Google Scholar] [CrossRef]
- Berman, H.M.; Bhat, T.N.; Bourne, P.E.; Feng, Z.; Gilliland, G.; Weissig, H.; Westbrook, J. The Protein Data Bank and the challenge of structural genomics. Nat. Struct. Biol. 2000, 7, 957–959. [Google Scholar] [CrossRef]
- Accelrys, version 2.5; Discovery Studio: San Diego, CA, USA, 2009.
- Frecer, V.; Kabeláč, M.; De Nardi, P.; Pricl, S.; Miertuš, S. Structure-based design of inhibitors of NS3 serine protease of hepatitis C virus. J. Mol. Graph. Model. 2004, 22, 209–220. [Google Scholar] [CrossRef]
- Frecer, V.; Jedinak, A.; Tossi, A.; Berti, F.; Benedetti, F.; Romeo, D.; Miertus, S. Structure based design of inhibitors of aspartic protease of HIV-1. Lett. Drug Des. Discov. 2005, 2, 638–646. [Google Scholar] [CrossRef]
- Frecer, V.; Berti, F.; Benedetti, F.; Miertus, S. Design of peptidomimetic inhibitors of aspartic protease of HIV-1 containing –PheΨPro– core and displaying favourable ADME-related properties. J. Mol. Graph. Model. 2008, 27, 376–387. [Google Scholar] [CrossRef]
- Frecer, V.; Seneci, P.; Miertus, S. Computer-assisted combinatorial design of bicyclic thymidine analogs as inhibitors of mycobacterium tuberculosis thymidine monophosphate kinase. J. Comput.-Aided Mol. Des. 2010, 25, 31–49. [Google Scholar] [CrossRef] [PubMed]
- Dali, B.; Keita, M.; Megnassan, E.; Frecer, V.; Miertus, S. Insight into selectivity of peptidomimetic inhibitors with modified statine core for Plasmepsin II of Plasmodium falciparum over human cathepsin D. Chem. Biol. Drug Des. 2012, 79, 411–430. [Google Scholar] [CrossRef]
- Megnassan, E.; Keita, M.; Bieri, C.; Esmel, A.; Frecer, V.; Miertus, S. Design of novel dihydroxynaphthoic acid inhibitors of Plasmodium falciparum lactate dehydrogenase. Med. Chem. 2012, 8, 970–984. [Google Scholar] [CrossRef] [PubMed]
- Owono Owono, L.C.; Keita, M.; Megnassan, E.; Frecer, V.; Miertus, S. Design of thymidine analogues targeting thymidilate kinase of mycobacterium tuberculosis. Tuberc. Res. Treat. 2013, 2013, 1–13. [Google Scholar] [CrossRef]
- Keita, M.; Kumar, A.; Dali, B.; Megnassan, E.; Siddiqi, M.I.; Frecer, V.; Miertus, S. Quantitative structure–activity relationships and design of thymine-like inhibitors of thymidine monophosphate kinase of mycobacterium tuberculosis with favourable pharmacokinetic profiles. RSC Adv. 2014, 4, 55853–55866. [Google Scholar] [CrossRef]
- Kouassi, A.; Kone, M.; Keita, M.; Esmel, A.; Megnassan, E.; N’Guessan, Y.; Frecer, V.; Miertus, S. Computer-aided design of orally bioavailable pyrrolidine carboxamide inhibitors of enoyl-acyl carrier protein reductase of mycobacterium tuberculosis with favorable pharmacokinetic profiles. Int. J. Mol. Sci. 2015, 16, 29744–29771. [Google Scholar] [CrossRef]
- Owono Owono, L.C.; Ntie-Kang, F.; Keita, M.; Megnassan, E.; Frecer, V.; Miertus, S. Virtually designed triclosan-based inhibitors of enoyl-acyl carrier protein reductase of mycobacterium tuberculosisand of Plasmodium falciparum. Mol. Inform. 2015, 34, 292–307. [Google Scholar] [CrossRef] [PubMed]
- Esmel, A.; Keita, M.; Eugene, M.; Toï, B.; Frecer, V.; Miertus, S. Insight into binding mode of nitrile inhibitors of Plasmodium falciparum falcipain-3, QSAR and pharmacophore models, virtual design of new analogues with favorable pharmacokinetic profiles. J. Comput. Chem. Mol. Model. 2017, 2, 103–124. [Google Scholar] [CrossRef]
- N’Guessan, A.; Megnassan, E.; Ziao, N.; Frecer, V.; N’Guessan, Y.T.; Miertus, S. Artemisinin-dipeptidyl vinyl sulfone hybrid inhibitors of plasmodium falciparum falcipain 2 with favorable pharmacokinetic profile. J. Drug Des. Dev. 2017, 1, 11–28. [Google Scholar] [CrossRef]
- N’Guessan, H.; Megnassan, E. In silico design of phosphonic arginine and hydroxamic acid inhibitors of Plasmodium falciparum M17 Leucyl Aminopeptidase with favorable pharmacokinetic profile. J. Drug Des. Med. Chem. 2017, 3, 98. [Google Scholar] [CrossRef][Green Version]
- Kily Herve Fagnidi, Y.; Toi, B.; Megnassan, E.; Frecer, V.; Miertus, S. In silico design of plasmodium falciparum cysteine protease falcipain 2 inhibitors with favorable pharmacokinetic profile. J. Anal. Pharm. Res. 2018, 7, 298–309. [Google Scholar] [CrossRef][Green Version]
- Kouman, K.C.; Keita, M.; Kre N’Guessan, R.; Owono Owono, L.C.; Megnassan, E.; Frecer, V.; Miertus, S. Structure-based design and in silico screening of virtual combinatorial library of benzamides inhibiting 2-trans enoyl-acyl carrier protein reductase of Mycobacterium tuberculosis with favorable predicted pharmacokinetic profiles. Int. J. Mol. Sci. 2019, 20, 4730. [Google Scholar] [CrossRef]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Accelrys, version 4.4; Materials Studio: San Diego, CA, USA, 2009.
- Gilson, M.; Honig, B. The inclusion of electrostatic hydration energies in molecular mechanics calculations. J. Comput.-Aided Mol. Des. 1991, 5, 5–20. [Google Scholar] [CrossRef]
- Rocchia, W.; Sridharan, S.; Nicholls, A.; Alexov, E.; Chiabrera, A.; Honig, B. Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: Applications to the molecular systems and geometric objects. J. Comput. Chem. 2001, 23, 128–137. [Google Scholar] [CrossRef]
- BÖTtcher, C.J.F. NON-LINEAR EFFECTS. In Theory of Electric Polarization; Elsevier: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Frecer, V.; Miertuš, S. Polarizable continuum model of solvation for biopolymers. Int. J. Quantum Chem. 1992, 42, 1449–1468. [Google Scholar] [CrossRef]
- Fischer, S.; Smith, J.C.; Verma, C.S. Dissecting the vibrational entropy change on protein/ligand binding: Burial of a water molecule in bovine pancreatic trypsin inhibitor. J. Phys. Chem. B 2001, 105, 8050–8055. [Google Scholar] [CrossRef]
- Schwarzl, S.M.; Tschopp, T.B.; Smith, J.C.; Fischer, S. Can the calculation of ligand binding free energies be improved with continuum solvent electrostatics and an ideal-gas entropy correction? J. Comput. Chem. 2002, 23, 1143–1149. [Google Scholar] [CrossRef]
- Freire, E. Do enthalpy and entropy distinguish first in class from best in class? Drug Discov. Today 2008, 13, 869–874. [Google Scholar] [CrossRef] [PubMed]
- Copeland, R.A.; Lombardo, D.; Giannaras, J.; Decicco, C.P. Estimating KI values for tight binding inhibitors from dose-response plots. Bioorg. Med. Chem. Lett. 1995, 5, 1947–1952. [Google Scholar] [CrossRef]
- Frecer, V.; Miertus, S.; Tossi, A.; Romeo, D. Rational design of inhibitors for drug-resistant HIV-1 aspartic protease mutants. Drug Des. Discov. 1998, 15, 211–231. [Google Scholar]
- Frecer, V.; Miertus, S. Interactions of ligands with macromolecules: Rational design of specific inhibitors of aspartic protease of HIV-1. Macromol. Chem. Phys. 2002, 203, 1650–1657. [Google Scholar] [CrossRef]
- MOE. Molecular Operating Environment (MOE); Chemical Computing Group Inc.: Montreal, QC, Canada, 2014. [Google Scholar]
- Available Chemicals Directory. Available online: https://www.psds.ac.uk/acd (accessed on 12 July 2021).
- Lipinski, C.A.; Lombardo, F.; Dominy, B.W.; Feeney, P.J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 1997, 23, 3–25. [Google Scholar] [CrossRef]
| Training Set [a] | ||
|---|---|---|
| PEP23 (Ref) | 482.61 | 36,360 |
| PEP27 | 452.56 | 910 |
| PEP29 | 438.53 | 23,900 |
| PEP32 | 466.54 | 47,230 |
| PEP34 | 470.60 | 8220 |
| PEP38 | 462.55 | 25,440 |
| PEP39 | 440.50 | 60 |
| PEP40 | 574.75 | 520 |
| PEP41 | 498.61 | 3560 |
| Validation Set [a] | [b](g · mol−1) | [c](nM) |
| PEP26 | 452.56 | 540 |
| PEP28 | 450.54 | 20,180 |
| PEP36 | 488.59 | 11,910 |
| PEP23 (Ref) | 0.00 | 0.00 | 0.00 | 0.00 | 4.44 |
| PEP27 | −3.81 | −0.04 | -0.16 | −3.69 | 6.04 |
| PEP29 | −0.39 | 0.13 | 1.45 | −1.71 | 4.62 |
| PEP32 | 6.21 | −7.77 | -0.60 | −0.95 | 4.33 |
| PEP34 | 5.97 | −9.92 | -0.51 | −3.44 | 5.09 |
| PEP38 | 0.21 | 0.77 | 2.13 | −1.15 | 4.59 |
| PEP39 | −2.07 | 0.12 | 3.98 | −5.92 | 7.22 |
| PEP40 | −6.33 | 1.64 | 0.26 | −4.95 | 6.28 |
| PEP41 | −3.24 | 1.16 | 0.42 | −2.50 | 5.45 |
[a] | [b] | [c] | [d] | [e] | [g] |
| PEP26 | −7.67 | 1.39 | −0.78 | −5.50 | 1.07 |
| PEP28 | −4.13 | 0.61 | −0.41 | −3.12 | 1.18 |
| PEP36 | 6.51 | −10.30 | −0.15 | −3.64 | 1.18 |
| Statistical Data of Linear Regression | |
|---|---|
| Number of compounds n | 9 |
| Statistical significance of regression, Fisher F-test | 58.58 |
| Level of statistical significance α | |
| (nM) | 60–47,230 |
| Hypothesis | RMSD [a] | R2 [b] | Total Costs [c] | Costs Difference [d] | Closest Random [e] |
|---|---|---|---|---|---|
| Hypo 1 | 0.795 | 0.999 | 24.13 | 2293.1 | 31.20 |
| Hypo 2 | 2.958 | 0.991 | 60.64 | 2256.6 | 31.90 |
| Hypo 3 | 3.623 | 0.987 | 80.35 | 2236.9 | 39.75 |
| Hypo 4 | 4.907 | 0.976 | 130.37 | 2186.9 | 42.21 |
| Hypo 5 | 5.128 | 0.974 | 139.89 | 2177.4 | 44.21 |
| Hypo 6 | 5.203 | 0.973 | 143.71 | 2173.5 | 45.02 |
| Hypo 7 | 5.880 | 0.966 | 177.49 | 2139.8 | 45.02 |
| Hypo 8 | 7.910 | 0.937 | 304.23 | 2013.0 | 45.03 |
| Hypo 9 | 9.767 | 0.902 | 451.68 | 1865.6 | 46.00 |
| Hypo 10 | 9.830 | 0.901 | 456.44 | 1860.8 | 47.18 |
| Statistical Data of Linear Regression | |
|---|---|
| Number of compounds n | 9 |
| 99 | |
| 0.04 | |
| Statistical significance of regression, Fisher F-test | 5675.56 |
| Level of statistical significance α | |
| (nM) | 60–47,230 |
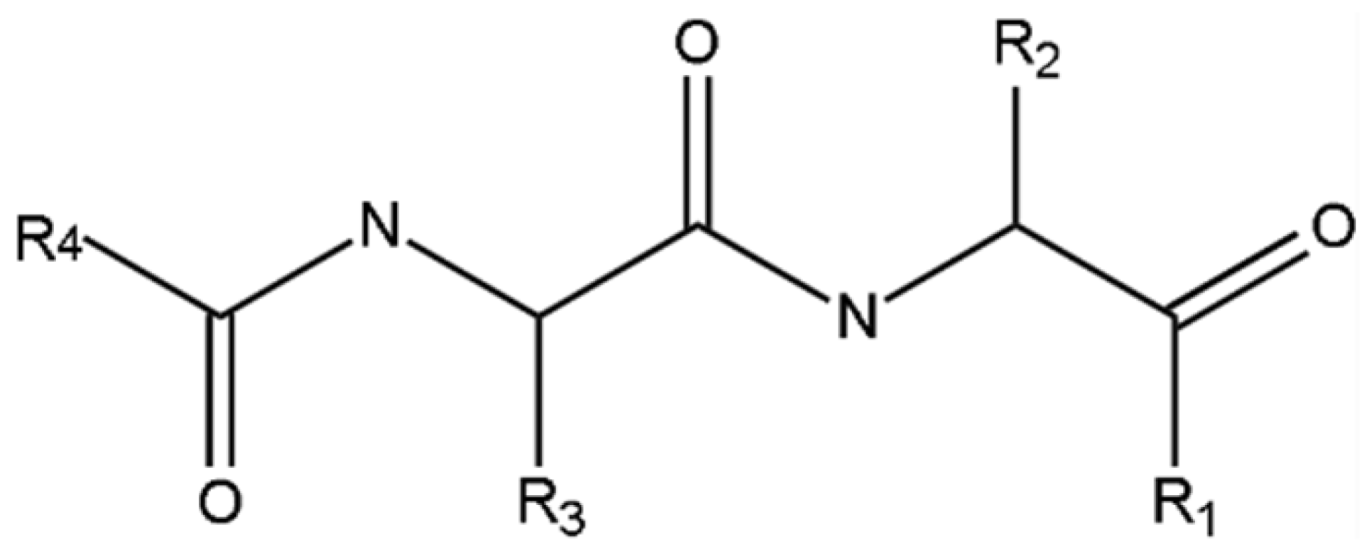 | |||||||
|---|---|---|---|---|---|---|---|
| 1 [Gly] | –H | 2 [Ala] | –CH3 | 3 [Val] | –CH(CH3)2 | 4 [Leu] | –CH2-CH(CH3)2 |
| 5 [Ile] | –C(CH3)–C2H5 | 6 [Met] | –-(CH2)2–S–CH3 | 7 [Cys] | –CH2–SH | 8 [Ser] | –CH2–OH |
| 9 [Thr] | –CH(OH)-CH3 | 10 [Asp] | –CH2–COOH | 11 [Glu] | –(CH2)2–COOH | 12 [Asn] | –CH2–CONH2 |
| 13 [Gln] | –(CH2)2–CONH2 | 14 [Lys] | –(CH2)4–NH2 | 15 [Arg] | –(CH2)3–NH–C(NH)-NH2 | 16 [His] | 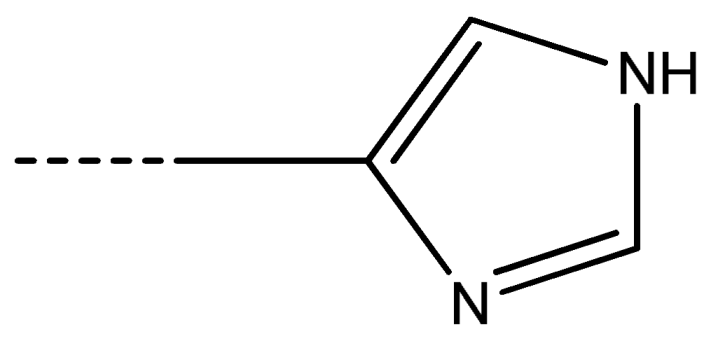 |
| 17 [Phe] |  | 18 [Tyr] | 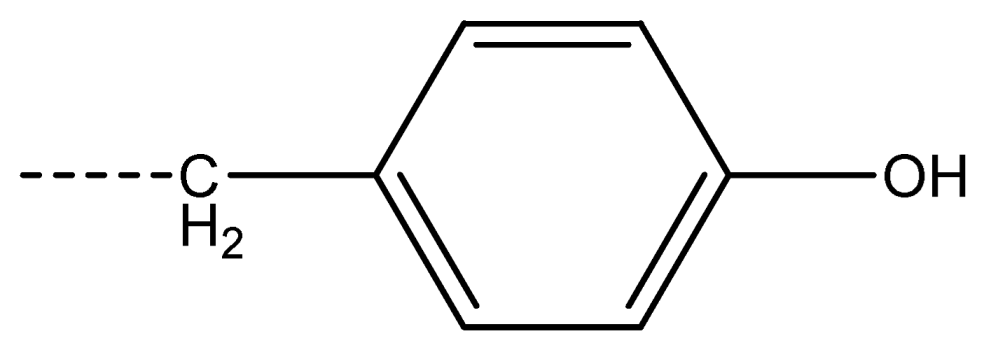 | 19 [Trp] | 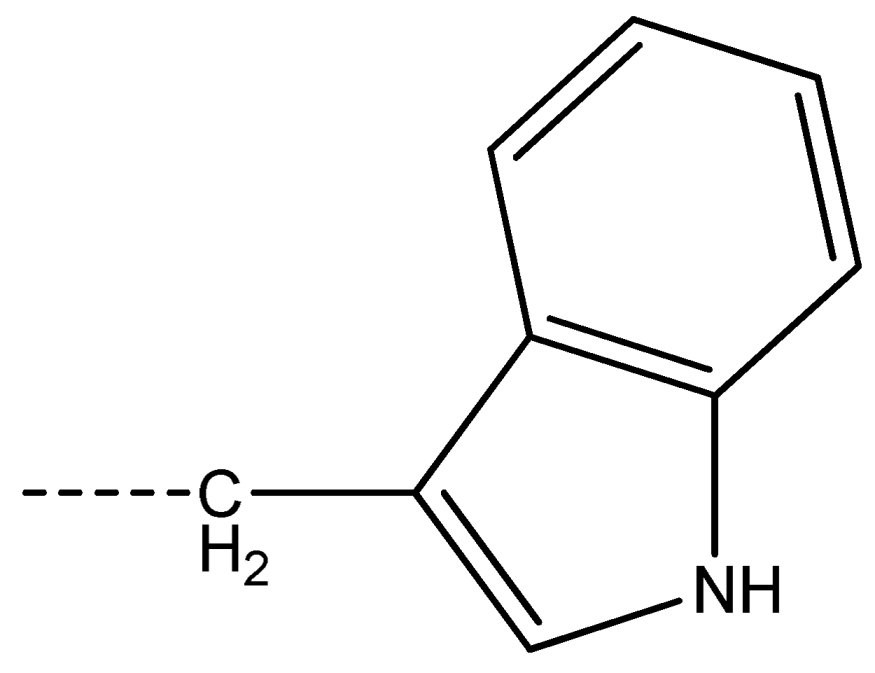 | ||
| Analogues [a] | ||||||
|---|---|---|---|---|---|---|
| PEP23 | 482.61 | 0.00 | 0.00 | 0.00 | 0.00 | 36,360 |
| PEP-14-19-04-01 | 400.53 | 5.54 | −6.82 | 0.75 | −2.03 | 9580.30 |
| PEP-15-04-17-01 | 389.50 | −1.05 | −6.59 | 0.72 | −8.36 | 8.76 |
| PEP-15-04-18-01 | 405.50 | −4.11 | −1.27 | 1.32 | −6.69 | 55.75 |
| PEP-05-12-19-03 | 428.54 | −5.96 | 1.25 | 1.43 | −6.14 | 102.41 |
| PEP-15-04-17-03 | 431.58 | −6.25 | −2.27 | 2.78 | −11.30 | 0.34 |
| PEP-18-05-14-03 | 419.57 | −6.60 | −1.08 | 2.02 | −9.70 | 2.00 |
| PEP-01-19-18-04 | 435.53 | −5.83 | -2.45 | −1.49 | −6.79 | 49.62 |
| PEP-18-19-15-04 | 534.66 | −5.78 | −6.88 | −2.56 | −10.10 | 1.29 |
| PEP-17-03-14-10 | 405.50 | −7.71 | −1.01 | 2.73 | −11.45 | 0.29 |
| PEP-04-07-19-14 | 446.62 | −7.68 | 4.89 | 1.27 | −4.07 | 1009.94 |
| PEP-17-09-19-15 | 506.61 | −12.07 | 11.41 | 2.83 | −3.49 | 1906.57 |
| PEP-04-06-05-17 | 420.62 | −5.31 | −2.99 | 0.55 | −8.85 | 5.13 |
| PEP-05-03-18-18 | 454.57 | −1.58 | −0.74 | 0.57 | −2.90 | 3676.95 |
| PEP-14-14-14-18 | 463.63 | −9.46 | −2.40 | 0.91 | −12.76 | 0.07 |
| PEP-02-15-03-19 | 428.54 | −3.28 | −2.99 | 1.78 | −8.05 | 12.35 |
| PEP-03-08-15-19 | 444.54 | −2.26 | −5.00 | −0.81 | −6.45 | 72.74 |
| PEP-08-15-17-19 | 492.58 | −9.89 | −0.26 | 0.54 | −10.69 | 0.67 |
| PEP-08-15-18-19 | 508.58 | −12.30 | 0.84 | 0.38 | −11.83 | 0.19 |
| PEP-09-18-18-19 | 529.60 | −7.61 | −0.28 | −0.19 | −7.70 | 18.29 |
| PEP-10-18-18-19 | 543.58 | −10.16 | −0.81 | 0.19 | −11.15 | 0.40 |
| PEP-13-06-04-19 | 474.63 | −10.05 | −1.60 | 0.76 | −12.42 | 0.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekono, B.D.; Esmel, A.E.; Dali, B.; Ntie-Kang, F.; Keita, M.; Owono, L.C.O.; Megnassan, E. Computer-Aided Design of Peptidomimetic Inhibitors of Falcipain-3: QSAR and Pharmacophore Models. Sci. Pharm. 2021, 89, 44. https://doi.org/10.3390/scipharm89040044
Bekono BD, Esmel AE, Dali B, Ntie-Kang F, Keita M, Owono LCO, Megnassan E. Computer-Aided Design of Peptidomimetic Inhibitors of Falcipain-3: QSAR and Pharmacophore Models. Scientia Pharmaceutica. 2021; 89(4):44. https://doi.org/10.3390/scipharm89040044
Chicago/Turabian StyleBekono, Boris D., Akori E. Esmel, Brice Dali, Fidele Ntie-Kang, Melalie Keita, Luc C. O. Owono, and Eugene Megnassan. 2021. "Computer-Aided Design of Peptidomimetic Inhibitors of Falcipain-3: QSAR and Pharmacophore Models" Scientia Pharmaceutica 89, no. 4: 44. https://doi.org/10.3390/scipharm89040044
APA StyleBekono, B. D., Esmel, A. E., Dali, B., Ntie-Kang, F., Keita, M., Owono, L. C. O., & Megnassan, E. (2021). Computer-Aided Design of Peptidomimetic Inhibitors of Falcipain-3: QSAR and Pharmacophore Models. Scientia Pharmaceutica, 89(4), 44. https://doi.org/10.3390/scipharm89040044







