Open-Circuit Fault-Tolerant Design of the Cascaded H-Bridge Rectifier Incorporating Reactive Power Compensation

Abstract

This paper proposes an open-circuit fault-tolerant design for the cascaded H-Bridge rectifier incorporating reactive power compensation. If one or two switching devices of the H-bridge modules are fault, the drive signals of the faulty H-bridge modules will be artificially redistributed into the bridgeless mode (including the boost bridgeless mode, the symmetric boost bridgeless mode, the totem-pole bridgeless mode and the symmetry totem-pole bridgeless mode) and cooperate with the normally operated H-bridge modules. In this case, the faulty cascaded H-bridge rectifier is not only able to achieve active power transmission, but also can still provide part of reactive power compensation when injecting reactive power from the power grid. Nonetheless, the reactive power that it can supply will be limited, due to the unidirectional characteristics of the bridgeless mode for the faulty modules. Therefore, a method for calculating its adjustable power factor angle range is also presented, which provides the basis for the faulty modules switching to the bridgeless mode. Then, a control strategy of the cascaded H-bridge rectifier incorporating reactive power compensation under the faulty condition and normal operation is presented. Finally, an experimental platform with a single-phase cascaded H-bridge rectifier containing three cells is given to verify the proposed theories.

1. Introduction

In recent years, due to the access of nonlinear loads in the power system, the power quality control technology with power electronic converters as the core has attracted increasing attention. Increasing scholars and research teams believe that integrating reactive power compensation functionality with bidirectional rectifiers that exist in practice to construct multifunctional power electronic rectifiers in the distributed generation system is a more reasonable and cost-effective solution [1,2,3]. These multifunctional power rectifiers can not only realize their functions, but also complete the reactive power compensation for the grid. [4] has pointed out that the multifunctional power rectifiers are essential to employed in the smart grid and modular multicell converter to feature a two-way flow of electricity between production and consumption. [5,6] has pointed out that the Vienna rectifier and bridgeless rectifier and can be a multifunctional power rectifier with a power-quality added function. The advantage of the multifunctional power rectifier is that reactive power can be processed locally and distributed, thereby the loss of reactive power on power transmission line is reduced. In addition, realizing reactive power compensation requires almost no additional hardware costs [4,5,6].

The cascaded H-bridge rectifier is a bidirectional rectifier used in many practical applications, such as the static synchronous compensators [7], grid-connected photovoltaic inverters [8], solid-state transformers [9], high-frequency isolated cascaded medium/high voltage converters [10], energy storage systems [11] and has the advantages of low switching loss, low stress, simple structure, easy modularization and redundant operation. However, the insulated gate bipolar transistor (IGBT) of the cascaded H-bridge rectifier is very fragile and has a high failure rate, which can be roughly classified as short-circuit faults and open-circuit faults [12]. Short-circuit faults can be eliminated by adding hardware [13]. Although open-circuit faults will not immediately shut down the system [14], they can distort the input current and even cause serious economic losses to the power grid—especially when reactive power needs to be injected into the power grid to maintain bus-voltage stability [15]. When open-switch faults happen, the first step is to do fault detection and localization [16,17]. The second step is to take measures to make the faulty converter run normally. As the number of cascaded H-bridge modules increases, the fault tolerance of the high component count of the multilevel rectifier can enable the overall availability increase. Fault-tolerant control of the cascaded H-bridge rectifiers has been studied by many researchers [18,19,20]. One technique of fault-tolerant control is to bypass the fault power-switching devices or modules so that the cascaded H-bridge rectifier can continue to operate at reduced capacity. Generally speaking, it is best to reduce the capacity rather than completely shut down. Another technique of fault-tolerant control is to provide redundant fault power-switching devices or modules beyond the minimum number required. In this case, this rectifier can withstand at the minimum of one fault without capacity loss. This method is usually applied to critical applications. However, it has the disadvantages of increasing costs and reducing efficiency [21].

However, the above-mentioned fault-tolerant methods are only aimed at a single-function cascaded H-bridge rectifier—for example, only for active power transmission or only performing reactive power compensation. Until now, there has been no paper studying fault-tolerant methods for multifunctional cascaded H-bridge rectifiers. Therefore, adopting the fault-tolerant control to keep the multifunctional power rectifier in its original state is a key issue. Inspired by [22], this paper presents a new fault-tolerant operating mode for multifunctional cascaded H-bridge rectifiers. In practical circuits, one or two switches in the H-bridge module have a much higher probability of failure than three or more switches [16], so this paper only analyzes the fault-tolerant method for open-circuit switch faults of one or two. In this case, the faulty H-bridge module can be switched to bridgeless operation modes (including the boost bridgeless mode, the symmetric boost bridgeless mode, the totem-pole bridgeless mode and the symmetry totem-pole bridgeless mode) and cooperate with the normally operated H-bridge modules. Below, this mode is defined as the hybrid cascaded rectifier mode, which is not only able to achieve active power transmission, but also still provide continuous leading to lagging reactive power. However, due to the unidirectional characteristics of the bridgeless mode in the faulty modules, the input current will become distorted [23,24], resulting in the limited reactive power [25]. Therefore, in the case where the reactive power is required, it is imperative to calculate the adjustable power factor angle to provide a basis for switching to the proposed hybrid rectifier operating mode. The fault-tolerant design approach posed in this paper fully utilizes normally operating switching devices in the fault modules, ensuring this multifunctional cascaded rectifier will still have the same reactive power-compensation capability within a certain range in case of the fault. Thus, it not only reduces the influence of the faulty switch tube on the circuit, but also further improves the reliability of the multifunctional cascaded H-bridge rectifier.

The rest of this paper is shown as follows: Section 2 presents the proposed hybrid cascaded rectifier mode for the multifunctional cascaded H-bridge rectifier under open-circuit fault. The reason the proposed hybrid cascaded rectifier mode has the limited reactive power-compensation capability is presented in Section 3. The adjustable power factor angle range of the hybrid cascaded rectifier mode is given in Section 4. Based on the above analysis, Section 5 presents the control strategy of the multifunctional rectifier under the faulty condition and normal operation. Experimental results are given in Section 6. Finally, the conclusions are recapitulated in Section 7.

2. Fault-Tolerant Design

Figure 1 shows the multifunctional cascaded H-bridge rectifier and its hybrid cascaded rectifier mode under open-circuit fault, wherein the power-switching devices are numbered as S_k1, S_k2, S_k3 and S_k4 (k = 1, …, m + n). u_s is the input voltage. i_s is the input current. L is the boost inductance. C is the capacitance in each module’s DC-side. In the following paper, the value of DC capacitance in each module is equal. The output DC-side equivalent resistance for each module is R_k (k = 1, …, m + n). u_con is the AC-side voltage. There are eight states when one or two switches of the basic H-bridge module have an open-circuit fault. The basic H-bridge module can be artificially switched to the four bridgeless operation modes to overcome it, which includes the boost bridgeless, symmetric boost bridgeless, the totem-pole bridgeless and the symmetric totem- pole bridgeless operation modes.

Table 1. Drive signal allocation and operation mode of different faulty switches.

Faulty Switch	Drive Signal				Operation Mode
	Sk1	Sk2	Sk3	Sk4
None	p	−p	−p	p	H-bridge
Sk1	/	0	−p	p	Symmetry totem-pole bridgeless
	/	p	0	p	Boost bridgeless
	/	−p	0	p
Sk2	p	/	p	0	Symmetry boost bridgeless
	p	/	−p	0
	0	/	−p	p	Symmetry totem-pole bridgeless
Sk3	0	p	/	p	Boost bridgeless
	0	−p	/	p
	p	−p	/	0	Totem-pole bridgeless
Sk4	p	0	p	/	Symmetry boost bridgeless
	p	0	−p	/
	p	−p	0	/	Totem-pole bridgeless
Sk1& Sk2	/	/	−p	p	Symmetry totem-pole bridgeless
Sk1& Sk3	/	p	/	p	Boost bridgeless
	/	−p	/	p
Sk2& Sk4	p	/	p	/	Symmetry boost bridgeless
	p	/	−p	/
Sk3& Sk4	p	−p	-	/	Totem-pole bridgeless
Sk1& Sk4	/	-	-	/	Bypass
Sk2& Sk3	-	/	/	-	Bypass

“0”—low level; “p”—PWM signal; “/”—open circuit fault.

shows the four-fault operation modes and the corresponding drive signals under these eight open-circuit fault states. The boost bridgeless operation mode and the symmetric boost bridgeless operation mode can adopt synchronous drive signals or complementary drive signals, while the totem-pole bridgeless operation mode and the symmetrical totem-pole bridgeless operation mode can only use the complementary drive signals to avoid the short-circuit fault caused by the direct connection of the upper and lower switching devices. Then the above faulty H-bridge module operated in the bridgeless operation mode can cooperate with the normally operated H-bridge module to achieve active power transmission and provide reactive power compensation. This faulty operation mode is defined as the hybrid cascaded rectifier mode. It should be noted that when S_k1 and S_k4 fail at the same time or S_k2 and S_k3 fail at the same time, the output level of each faulty module will be reduced. In this regard, cascaded H-bridge rectifier can operate normally through bypassing faulty modules.

3. Analysis of Input Current Distortion for Hybrid Cascaded Rectifier Operation Mode

When the faulty cascaded H-bridge rectifier switches to the hybrid cascaded rectifier operation mode composed of m boost bridgeless modules and n H-bridge modules, which is shown in Figure 2, the input current distortion mechanism should be analyzed first. The output DC-side equivalent resistance for bridgeless modules is R_i (i = 1, … m) and the output DC-side equivalent resistance for H-bridge modules is R_j (j = m + 1, … m + n). u_dci (i = 1, … m) and u_dcj (j = m + 1, … m + n) are the DC-side voltages for bridgeless modules and H-bridge modules, respectively. u_{con_BR} and u_{con_H} are the AC-side voltage of bridgeless modules and AC-side voltage of H-bridge modules, respectively. It should be noted that the following analysis are also suitable for the m symmetry boost bridgeless modules, totem pole bridgeless modules or symmetry totem pole bridgeless modules and n H-bridge modules.

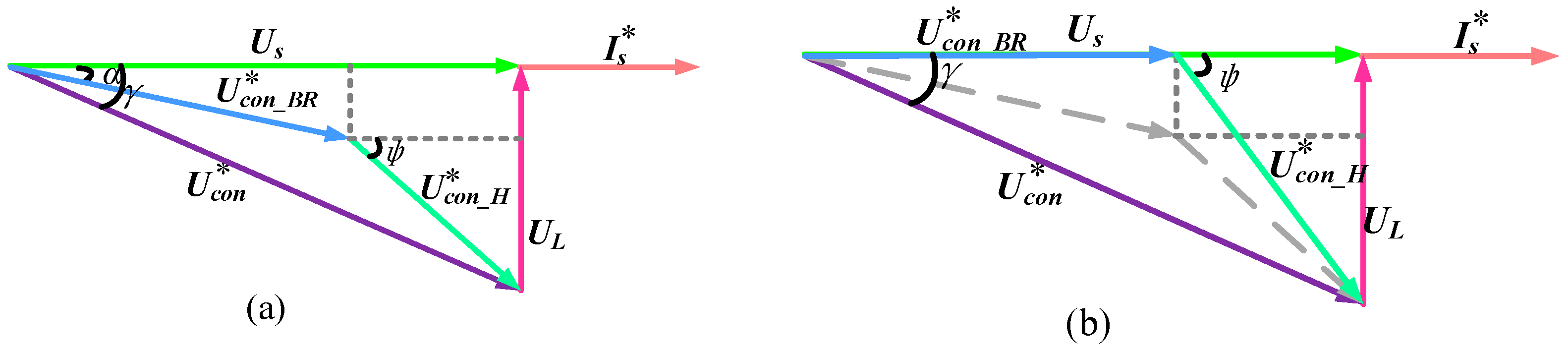
Based on the assumption that the hybrid cascaded rectifier operates under the unity power factor, the steady-state AC-side phasor diagram is shown in Figure 3a. It is apparent that the power supply voltage U_s is in phase with the command input current I_s* and inductor voltage U_L is orthogonal to I_s*. According to the triangle law of vector addition, the AC-side reference voltage of the hybrid cascaded rectifier $U_{con}^{*}$ is lagging I_s* than γ. 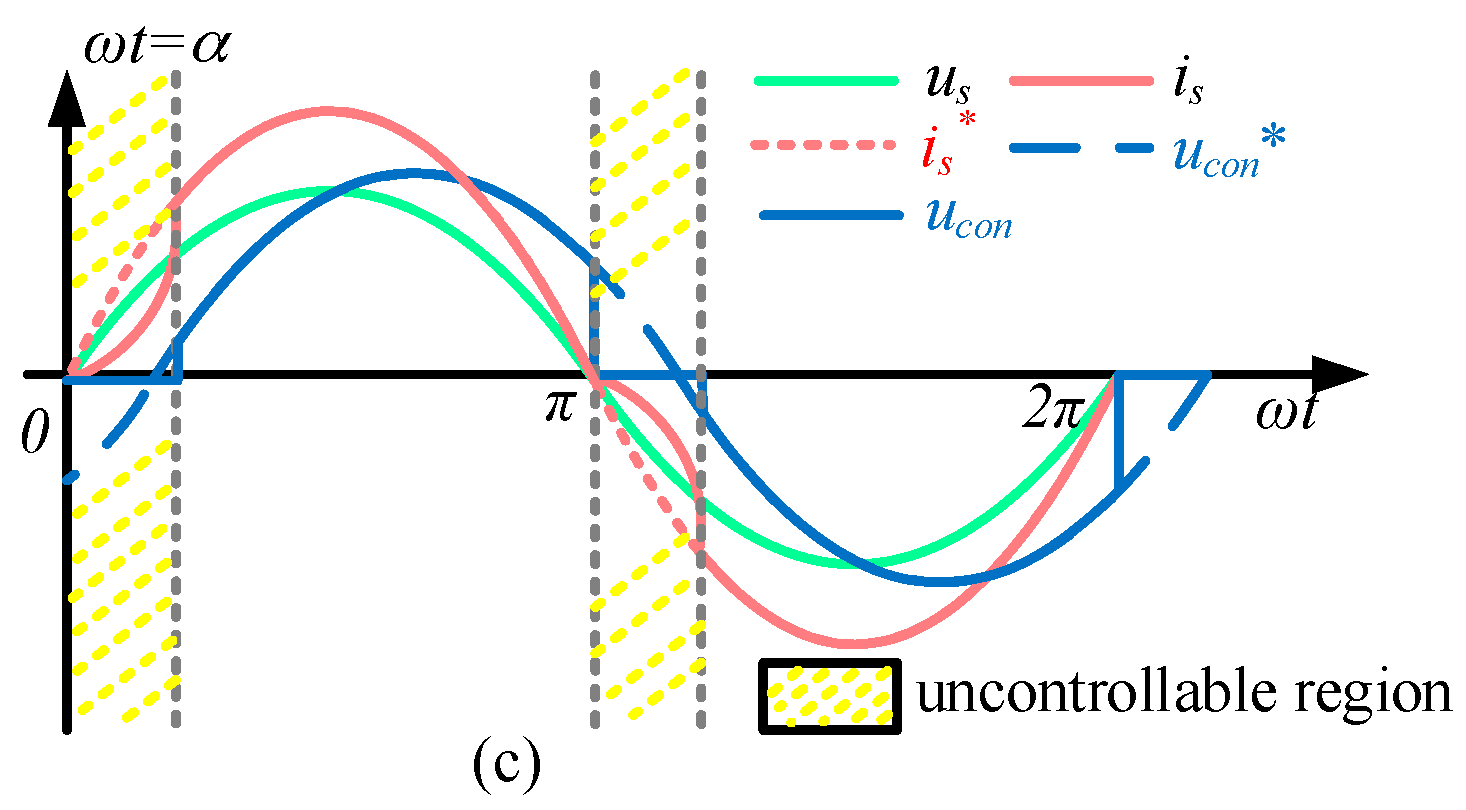The AC-side reference voltage of bridgeless modules $U_{con\_BR}^{*}$ is lagging I_s* than α and the AC-side reference voltage of H-bridge modules U_{con_H}* is lagging I_s* than ψ. The unidirectional power transmission characteristics of the bridgeless modules will cause serious distortion in the period between the zero-crossing point of the input current i_s and the zero-crossing point of the u_con [23]. To make the bridgeless modules input current not distorted, the best way is to make $U_{con\_BR}^{*}$ in phase with I_s*as shown in Figure 3b [21,23]. In this case, bridgeless modules cannot provide the required reactive power of inductor L [22]. Moreover, it will be fully undertaken by the H-bridge modules. In the case of the AC-side reference voltage of the H-bridge module reaches its maximum value. However, the desired reactive power consumed by L that the H-bridge module should provide is not reached, the remaining reactive power consumed by L must be provided by the bridgeless module. In this case, the steady-state AC-side phasor diagram changes to Figure 3a. From the aforementioned analysis, input current will be distorted as shown in Figure 3c. Especially when injecting reactive power from the power grid, this distortion will greatly increase. Moreover, the adjustable power factor angle range that hybrid cascaded rectifier operation mode can provide will be limited. It is therefore important to calculate the adjustable power factor angle range to provide a basis for switching to the hybrid cascaded rectifier operation mode when the open-circuit fault happens.

4. Analysis of Adjustable Power Factor Angle in the Hybrid Cascaded Rectifier Operation Mode

In the hybrid cascaded rectifier operation mode, $U_{con\_BR}^{*}$ is always kept in phase with I_s* to provide the active power required by DC-side loads, and the H-bridge modules provide the reactive power required by the AC-side and the active power required by the DC-side loads simultaneously. The AC-side phasor diagrams under lagging power factor and leading power factor are shown in Figure 4. The voltage across the input inductor U_L is orthogonal to I_s and the AC-side reference voltage $U_{con}^{*}$ is lagging U_s than φ. In the case of lagging power factor, φ < θ and φ ≥ θ may occur according to the different power, voltage level and power factor. The input current I_s^* is lagging grid voltage U_s than θ. On the condition of leading power factor, the input current I_s^* is leading grid voltage U_s than θ. The following relationships exist:

$$\{\begin{array}{l}{U}_{con\_BR}^{*}={\displaystyle \sum _{i=1}^m{U}_{coni}^{*}}\\ U_{con\_H}^{*}={\displaystyle \sum _{j=m+1}^{m+n}{U}_{conj}^{*}}\end{array}$$

(1)

where $U_{coni}^{*}$ (i = 1, ..., m) and $U_{conj}^{*}$ (j = m + 1, ... m + n) are the AC-side reference voltage for each bridgeless module and H-bridge module, respectively.

Each module’s DC-side output voltage is U_dc. The maximum output voltages U_conmax in rms of each cascaded module can be expressed as [24,26]:

$$U_{con\max }=\frac{2\sqrt{2}}{\pi }{U}_{dc}$$

(2)

Assuming the bridgeless modules can provide rms of the maximum AC-side reference voltage. the step-up ratio k is defined as:

$$k=\frac{(m+n)U_{dc}}{U_s}$$

(3)

Considering that the DC-side voltages can be balanced in steady-state, the input current is derived by:

$$I_{\mathrm{s}}=\frac{U_{dc}^2}{U_s\cos \theta }\cdot ({\displaystyle \sum _{i=1}^m\frac{1}{R_i}}+{\displaystyle \sum _{j=m+1}^{m+n}\frac{1}{R_j})}$$

(4)

Base on the analysis of Section 3. The AC-side voltage of the n H-bridge modules $U_{con\_H}^{*}$ should not exceed the maximum total AC-side reference voltage, which can be expressed as:

$$U_{\mathrm{con}\_H}^{*}\le n{U}_{con\max }$$

(5)

In the case of φ < θ of lagging power factor operation, applying geometric relationship in ∆HPC yields:

$$\{\begin{array}{l}{U}_{PC}=U_s-m\frac{2\sqrt{2}}{\pi }{U}_{dc}\cos \theta -\omega L{I}_{\mathrm{s}}\sin \theta \\ U_{PH}=m\frac{2\sqrt{2}}{\pi }{U}_{dc}\sin \theta -\omega L{I}_{\mathrm{s}}\cos \theta \\ U_{\mathrm{con}\_H}^{*}=\sqrt{U_{PH}^2+U_{PC}^2}\end{array}$$

(6)

Substituting Equation (2), (3), (4), and (6) into (5) yields:

$$\begin{array}{l}[\frac{2\sqrt{2}mk}{\pi }\sin \theta -\frac{\omega L{k}^2}{(m+n)}\cdot {({\displaystyle \sum _{i=1}^m\frac{1}{R_i}}+{\displaystyle \sum _{j=m+1}^{m+n}\frac{1}{R_j})}]}^2+[m+n-\frac{2\sqrt{2}mk}{\pi }\cos \theta -\frac{\omega L{k}^2}{(m+n)}\tan \theta \cdot ({\displaystyle \sum _{i=1}^m\frac{1}{R_i}}+{\displaystyle \sum _{j=m+1}^{m+n}\frac{1}{R_j}){]}^2}\\ \le {(\frac{2\sqrt{2}nk}{\pi })}^2\end{array}$$

(7)

On the condition of φ ≥ θ of lagging power factor operation, applying the geometric relationship in ∆HDC yields:

$$\{\begin{array}{l}{U}_{HD}=(U_s-m\frac{2\sqrt{2}}{\pi }{U}_{dc}\cos \theta -m\frac{2\sqrt{2}}{\pi }{U}_{dc}\tan \theta \sin \theta )\cos \theta \\ U_{DC}=\omega L{I}_s-U_s\sin \theta \\ U_{con\_H}^{*}=\sqrt{U_{HD}^2+U_{DC}^2}\end{array}$$

(8)

Due to the AC-side voltage of n H-bridge modules $U_{con\_H}^{*}$ satisfies (5), Substituting (3), (4), and (8) into (5) yields:

$${[(U_s-m\frac{2\sqrt{2}}{\pi }{U}_{dc}\cos \theta -m\frac{2\sqrt{2}}{\pi }{U}_{dc}\tan \theta \sin \theta )\cos \theta ]}^2+{[\omega L{I}_s-U_s\sin \theta ]}^2\le {(\frac{2\sqrt{2}nk}{\pi })}^2$$

(9)

In the case of leading power factor operation, hybrid cascaded rectifier’s AC-side reference voltage $u_{con}^{*}$ can be expressed as:

$$u_{con}^{*}=U_{con}^{*}\sin (\omega t-\phi )$$

(10)

where the rms value of $U_{con}^{*}$ and the corresponding lagging angle φ are derived by:

$$\{\begin{array}{l}{U}_{con}^{*}=\sqrt{U_{\mathrm{s}}^2+{(\omega L{I}_s)}^2-2U_s{I}_s\omega L\sin \theta }\\ \phi =\arccos (\frac{U_s-\omega L{I}_s\sin \theta }{\sqrt{U_s^2+{\omega }^2{L}^2{I}_s^2-2\omega L{I}_s{U}_s\sin \theta }})\end{array}$$

(11)

Applying the law of cosines in ΔOHC, the AC-side reference voltage of the n H-bridge modules $U_{con\_H}^{*}$ can be expressed as:

$$U_{\mathrm{con}\_H}^{*}=\sqrt{U_{con\_BR}^{{*}^2}+U_{con}^{{*}^2}-2U_{con\_BR}^{*}{U}_{con}^{*}\cos (\theta +\phi )}$$

(12)

Substituting (3), (4), (11) and (12) into (5) yield:

$$\begin{array}{l}{(\frac{2\sqrt{2}mk}{\pi })}^2+{(m+n)}^2+[\frac{\omega L{k}^2}{(m+n)\cos \theta }\cdot {({\displaystyle \sum _{i=1}^m\frac{1}{R_i}}+{\displaystyle \sum _{j=m+1}^{m+n}\frac{1}{R_j})}]}^2-2k^2\omega L\tan \theta ({\displaystyle \sum _{i=1}^m\frac{1}{R_i}}+{\displaystyle \sum _{j=m+1}^{m+n}\frac{1}{R_j})}\\ -\frac{4\sqrt{2}mk}{\pi }\cdot \cos (\theta +\phi )\cdot \{{(m+n)}^2+[\frac{\omega L{k}^2}{(m+n)\cos \theta }\cdot {({\displaystyle \sum _{i=1}^m\frac{1}{R_i}}+{\displaystyle \sum _{j=m+1}^{m+n}\frac{1}{R_j})}]}^2\\ -2k^2\omega L\tan \theta {({\displaystyle \sum _{i=1}^m\frac{1}{R_i}}+{\displaystyle \sum _{j=m+1}^{m+n}\frac{1}{R_j})}\}}^{\frac{1}{2}}\le {(\frac{2\sqrt{2}nk}{\pi })}^2\end{array}$$

(13)

Equation (7), (9) and (13) shows that the adjustable lagging power factor angle and leading power factor angle θ is related to the step-up ratio k, inductance L and load resistance R_i and R_j. In most cases, the voltage drop on the boost inductor is usually small, so φ < θ is the common lagging power factor operation mode. By drawing the curve of the left Equation of (7) and (13) versus power factor angle θ and the curve of the right Equation of (7) and (13), respectively, the intersection point is the maximum lagging power factor angle θ_{lag_acmax} and the maximum leading power factor angle θ_{lead_acmax} that this hybrid cascaded rectifier operation mode can operate. In this case, the adjustable lagging power factor angle range and the adjustable leading power factor angle range are (0, θ_{lag_acmax}) and (θ_{lead_acmax}, 0), respectively.

The adjustable power factor angle of the hybrid cascaded rectifier operation mode is not only affected by whether the AC-side voltage of the H-bridge modules can reach the maximum value which has been analyzed above, but also by the limit of the rated power S of the cascaded H-bridge rectifier. Then the maximum adjustable power factor angle can be expressed as:

$${\theta }_{ra\_\max }=\arctan \frac{\sqrt{S^2-P^2}}{P}$$

(14)

where P is the active power of the cascaded H-bridge rectifier. The adjustable lagging power factor angle range and the adjustable leading power factor angle range are (0, θ_{ra_max}) and (−θ_{ra_max}, 0), respectively. Based on the above-mentioned two qualifications, the adjustable lagging power factor angle range is the interaction between the set of (0, θ_{ra_max}) and (0, θ_{lag_acmax}). Moreover, the adjustable leading power factor angle range is the interaction between the set of (−θ_{ra_max}, 0) and (−θ_{lead_acmax}, 0).

For example, based on the parameters presented in

Table 2. Parameters for the system.

Parameters	Quantity
Grid voltage/frequency	Us/f = 50 V(rms)/50 Hz
Boost inductance	L = 0.005H
Output load resistance	R1 = 100 Ω, R2 = 100 Ω,R3 = 90 Ω
Rated power	120 VA

, Figure 5 depicts the curves of AC-side voltage of the H-bridge modules $U_{con\_H}^{*}$ at different power factor angle θ with the various number of bridgeless modules m and H-bridge modules n under the same step-up ratio k or with various step-up ratio k under the same number of bridgeless modules m and H-bridge modules n in the lagging power factor operation and leading power factor operation. The solid line shows the left Equation of (7) and (13) versus θ. The dotted line depicts the right Equation of (7) and (13) versus θ. The intersection points (K, S, T, U, W, X, Y, Z) between the solid line and the dotted line is the maximum power factor angle that this hybrid cascaded rectifier operation mode can operate. Considering the limit of the rated power, the adjustable lagging power factor angle range and the adjustable leading power factor angle range are (0, 58°) and (−58°, 0°), respectively. The calculation results corresponding to Figure 5 and the final adjustable lagging power factor angle range and the final adjustable leading power factor angle range when considering the rated power restriction are shown in

Table 3. Main parameters and calculated results.

Number of Bridgeless Modules m	Number of H-Bridge Module n	Step-Ratio k	Adjustable Lagging Power Factor Angle θ			Adjustable Leading Power Factor Angle θ
			Intersection Point	Calculation Result	Final Results Considering Rated Power	Intersection Point	Calculation Result	Final Result Considering Rated Power
1	2	2.7	none	0°–90°	0°–58°	none	−90°–0°	−58°–0°
2	1	2.7	K	0°–25°	0°–25°	W	−27°–0°	−27°–0°
2	1	2.1	S	0°–31°	0°–31°	X	−32°–0°	−32°–0°
2	1	2.7	T	0°–25°	0°–25°	Y	−27°–0°	−27°–0°
2	1	3	U	0°–19°	0°–19°	Z	−22°–0°	−22°–0°

. Based on the above analysis, when the total number of cascaded modules is determined, the adjustable lagging power factor angle range and the adjustable leading power factor angle range that the hybrid cascaded rectifier operation mode can operate will increase with the increase of the number of H-bridge modules n or with the decrease of the step-up ratio k.

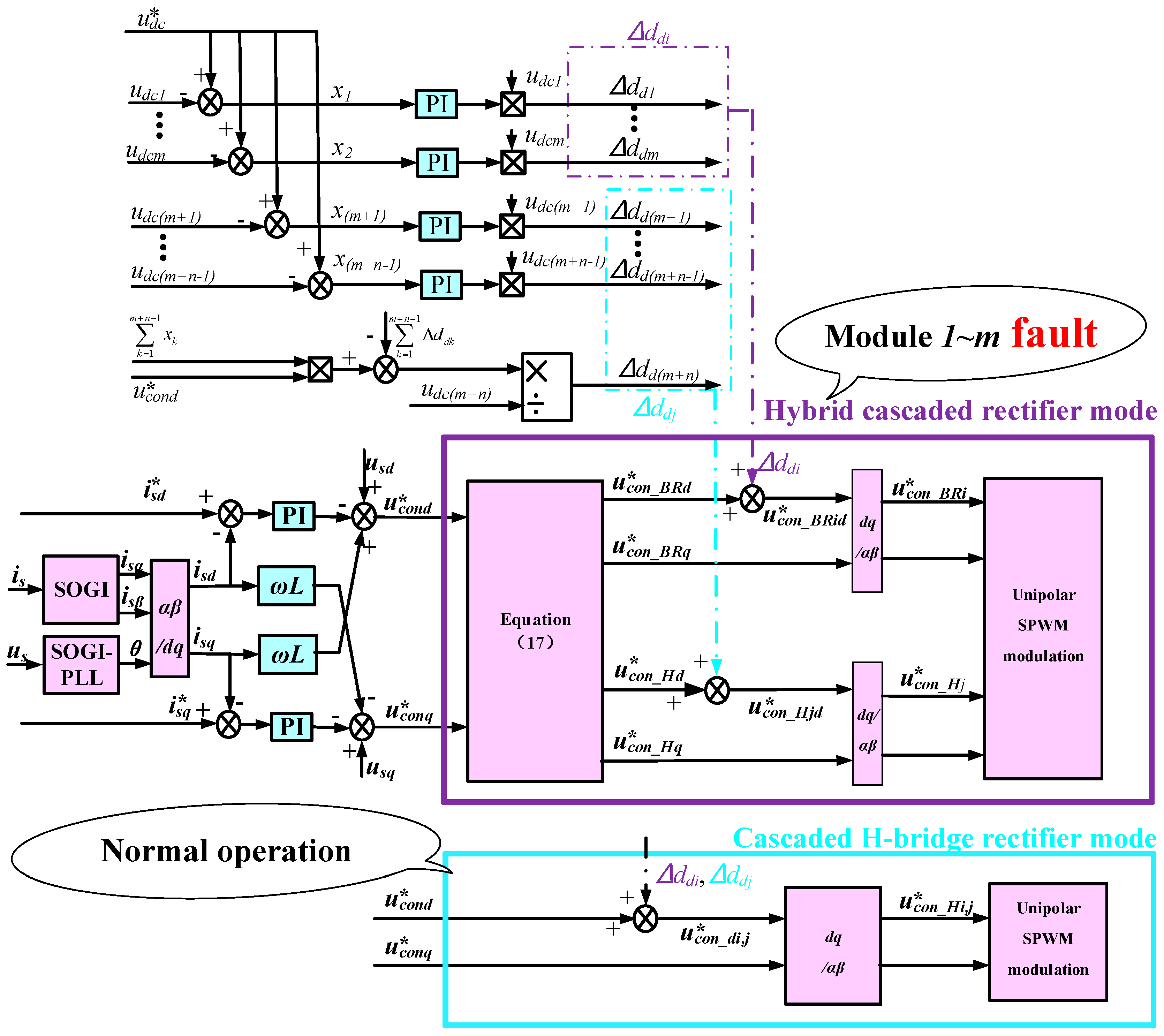
5. Control Strategy

The multifunctional rectifier operates in the hybrid cascaded rectifier mode when one or two switches are faulty while it operates normally when there is no fault. The voltage and current double closed-loop control strategy can be used to achieve the control strategy. The active current reference $i_{sd}^{*}$ in the current loop is derived by (15).

$$i_{sd}^{*}=-(K_{iP}+\frac{K_{iI}}{s})(u_{dc}{}^{*}-\frac{{\displaystyle \sum _{i=1}^m{u}_{dci}}+{\displaystyle \sum _{j=m+1}^{m+n}{u}_{dcj}}}{m+n})$$

(15)

where K_iP and K_iI are the proportional coefficient and Integral coefficient, respectively. The reactive current reference $i_{sq}^{*}$ depends on the desired reactive power. In this case, the power factor angle θ can also be defined as:

$$\theta =\arctan \frac{i_{sq}^{*}}{i_{sd}^{*}}$$

(16)

By adopting the dq decoupling control, the active component and reactive component of the total AC-side reference voltage of the multifunctional cascaded rectifier, i.e., $u_{cond}^{*}$ and $u_{conq}^{*}$, are obtained. In the case of the hybrid cascaded rectifier mode, $u_{con\_BRd}^{*}$ needs to be always in phase with i_s to avoid input current zero-crossing distortion. The AC-side reference voltage of bridgeless modules $u_{con\_BRd}^{*}$ and $u_{con\_BRq}^{*}$, as well as the AC-side reference voltage of the H-bridge modules $u_{con\_Hd}^{*}$ and $u_{con\_Hq}^{*}$ can be expressed as:

$$\{\begin{array}{l}{u}_{con\_BRd}^{*}=\frac{m}{m+n}\frac{i_{sd}^{*}\left(i_{sd}^{*}{u}_{cond}^{*}+i_{sq}^{*}{u}_{conq}^{*}\right)}{i_{sd}^{{*}^2}+i_{s\mathrm{q}}^{{*}^2}}\\ u_{con\_BRq}^{*}=\frac{m}{m+n}\frac{i_{sq}^{*}\left(i_{sd}^{*}{u}_{cond}^{*}+i_{sq}^{*}{u}_{conq}^{*}\right)}{i_{sd}^{{*}^2}+i_{s\mathrm{q}}^{{*}^2}}\\ u_{con\_Hd}^{*}=\frac{1}{n}(u_{cond}^{*}-u_{con\_BRd}^{*})\\ u_{con\_Hq}^{*}=\frac{1}{n}(u_{conq}^{*}-u_{con\_BRq}^{*})\end{array}$$

(17)

If the system is unbalanced, the total input active power should be redistributed according to the different active power required by each bridgeless module and H-bridge module. The active-duty cycle should be modified by adding the voltage balance controller [26]. Then the new AC-side reference voltage of bridgeless module $u_{con\_BRid}^{*}$, as well as the new AC-side reference voltage of H-bridge module $u_{con\_Hjd}^{*}$ can be expressed as:

$$\{\begin{array}{l}{u}_{con\_BRid}^{*}=u_{con\_BRd}^{*}+\Delta d_{di}\\ u_{con\_Hjd}^{*}=u_{con\_Hd}^{*}+\Delta d_{dj}\end{array}$$

(18)

where ∆d_di (i = 1,...,m) and ∆d_dj (j = m + 1,...,m + n) are the active regulation component and the reactive regulation component of duty cycles for the bridgeless modules and the H-bridge modules, respectively. By employing m + n inverse dq transformations, the final AC-side reference voltages, $u_{con\_BRi}^{*}$ and $u_{con\_Hj}^{*}$, can be obtained. In the case of normal operation and when the system is unbalanced, the AC-side reference voltage $u_{con\_dk}^{*}$ (k = 1, ..., m + n) for the cascaded H-bridge rectifier module is the sum of $u_{cond}^{*}$ and ∆d_di and the sum of $u_{cond}^{*}$ and ∆d_dj. By employing m + n single-phase inverse dq transformations, the final AC-side reference voltages $u_{con\_Hk}^{*}$ can be obtained. Then the unipolar modulation is adopted for the multifunctional cascaded H-bridge rectifier. This is because it possesses the merit of smaller switching loss and lower DC voltage ripple compared with bipolar modulation [27]. The control diagram of the multifunctional cascaded H-bridge rectifier under normal operation and the faulty condition is shown in Figure 6.

6. Experiment Results

An experimental platform as shown in Figure 7 was established; its specifications are shown in

Table 4. Specifications of the system.

Parameters	Quantity
Grid voltage/frequency	Us/f = 50 V(rms)/50 Hz
Boost inductance	L = 0.005 H
Output DC voltage	Udc1 = 45 V, Udc2 = 45 V, Udc3 = 45 V
Output load resistance	R1 = 100 Ω, R2 = 100 Ω, R3 = 90 Ω
DC capacitance	C = 2200 μF
Switching frequency	fs = 10 kHz
Rated power	120 VA

. In the experimental tests, Modules 1 and 2 worked in bridgeless mode, while Module 3 works in H-bridge mode. REN-DSP28335 is selected as the core controller. First, considering the limit of rated power, the adjustable lagging and leading power factor angle range were 0°–58° and −58°–0°, respectively. Then it was essential to verify the calculated maximum power factor angle range when the cascaded H-bridge rectifier operated in the hybrid cascaded rectifier mode. 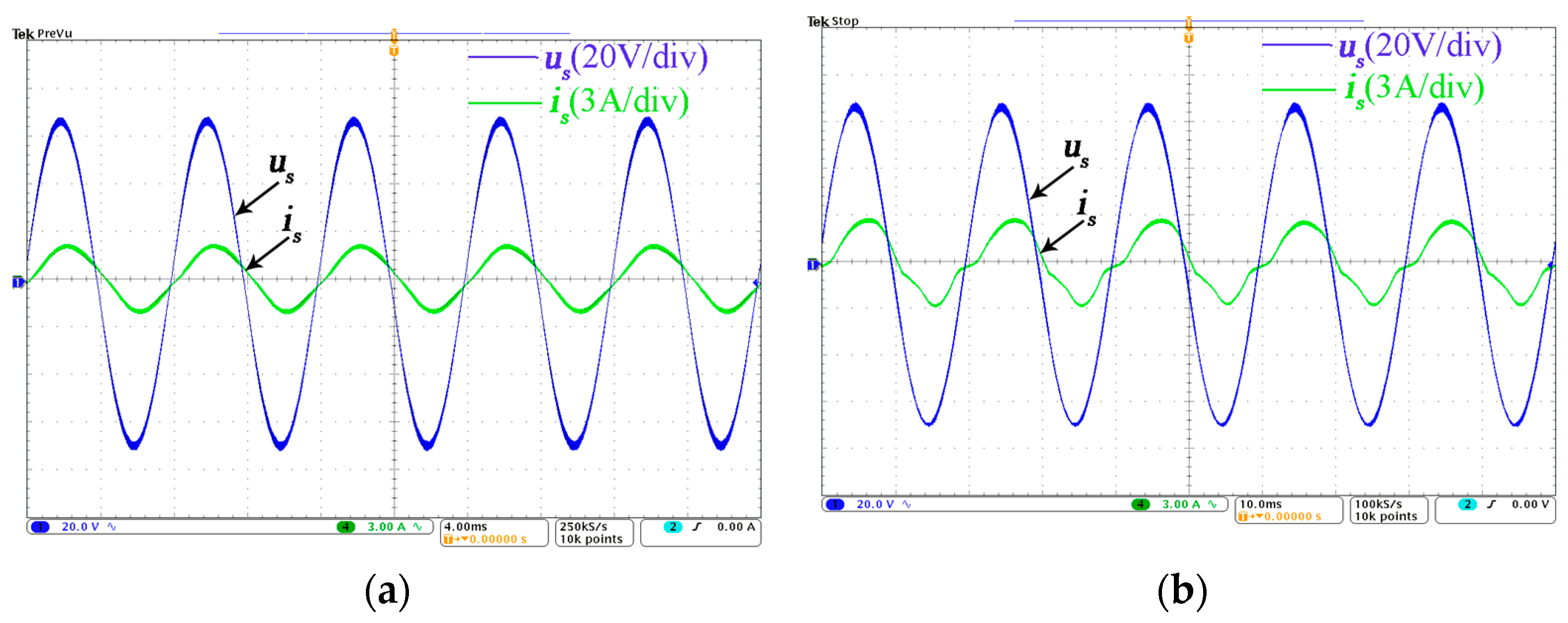Based on the analysis in Section 4, the adjustable lagging and leading power factor angle at which the hybrid cascaded rectifier operation mode could theoretically operate was 0°–25° and −27°–0°, respectively, which were in the range of the adjustable power factor angle ranges when considering the rated power. On the condition of the lagging power factor angle of the hybrid cascaded rectifier operation mode was 18°, Figure 8a shows that the input current was sinusoidal and showing a satisfactory current quality. However, when the lagging power factor angle of the hybrid cascaded rectifier operation mode beyond the range of the adjustable power factor angle and was set as 35°, Figure 8b shows that the input current becomes seriously distorted, which means this hybrid cascaded rectifier operation mode cannot provide such a large reactive power. In the case of the leading power factor angle of the hybrid cascaded rectifier operation mode was −24°, Figure 9a shows that the input current was sinusoidal and showing a satisfactory current quality. However, when the leading power factor angle of the hybrid cascaded rectifier operation mode beyond the range of the adjustable power factor angle that the hybrid cascaded rectifier operation mode could operate and was set as -36°, Figure 9b shows that the input current becomes distorted seriously, which means this rectifier cannot provide such a large reactive power. It is evident in Figure 8; Figure 9 that the input current was approximately sinusoidal within the range of the calculated adjustable power factor angle while the input current was seriously distorted beyond the calculated adjustable power factor angle in the hybrid cascaded rectifier operation mode. 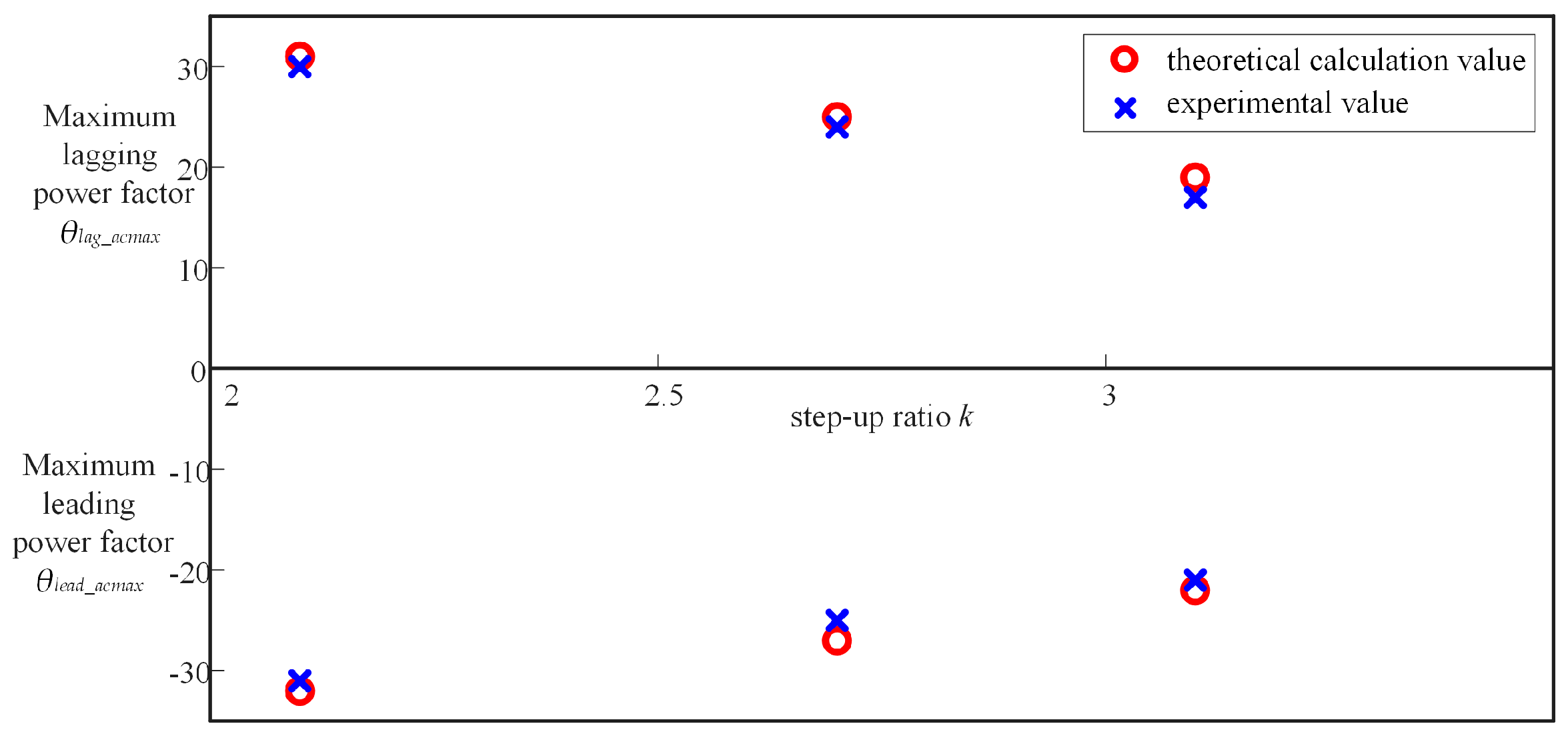Figure 10 shows the maximum adjustable power factor comparison between the theoretical calculation values and experimental values under different step-up ratio k. 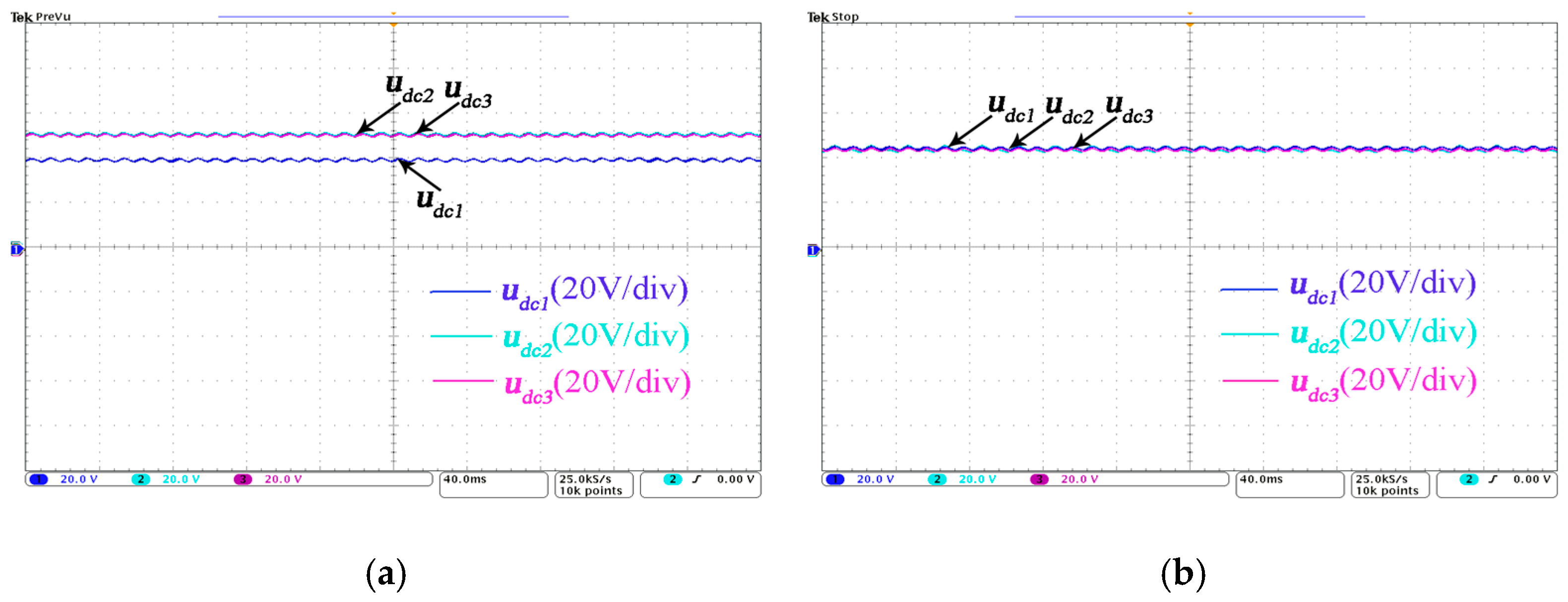It can be seen in Figure 10 that the experimental values were close to the theoretical calculation values. The waveforms of the DC-side voltage are shown in Figure 11. It is clear that under the voltage balance control presented in this paper, all the DC voltages were balanced, which proves the feasibility of the presented method.

7. Conclusions

A new hybrid cascaded rectifier operation mode is proposed in this paper when the open-circuit fault happens in the cascaded H-bridge rectifier incorporating reactive power compensation. Then the adjustable power factor angle range for the hybrid cascaded rectifier operation mode can operate is calculated. It provides the basics about whether the cascaded H-bridge rectifier can switch to the hybrid cascaded rectifier mode when injecting reactive power from the power grid. Moreover, the control strategy for the cascaded H-bridge rectifier under the faulty operation and normal operation is presented. Finally, experiments verify the correctness of the calculated adjustable power factor angle range of the hybrid cascaded rectifier operation mode containing two bridgeless mode modules and one H-bridge mode module. Compared with the traditional faulty cascaded H-bridge rectifier without an adjustable power factor angle, the adjustable power factor angle range of the method presented in this paper is −27°–25°.