Fractional-Order Fuzzy Control Approach for Photovoltaic/Battery Systems under Unknown Dynamics, Variable Irradiation and Temperature

Abstract

For this paper, the problem of energy/voltage management in photovoltaic (PV)/battery systems was studied, and a new fractional-order control system on basis of type-3 (T3) fuzzy logic systems (FLSs) was developed. New fractional-order learning rules are derived for tuning of T3-FLSs such that the stability is ensured. In addition, using fractional-order calculus, the robustness was studied versus dynamic uncertainties, perturbation of irradiation, and temperature and abruptly faults in output loads, and, subsequently, new compensators were proposed. In several examinations under difficult operation conditions, such as random temperature, variable irradiation, and abrupt changes in output load, the capability of the schemed controller was verified. In addition, in comparison with other methods, such as proportional-derivative-integral (PID), sliding mode controller (SMC), passivity-based control systems (PBC), and linear quadratic regulator (LQR), the superiority of the suggested method was demonstrated.

1. Introduction

Today, photovoltaic (PV) panels are extensively used for energy production, due to their renewability, availability, and clarity [1,2]. However, the main problem in the use of PV panels, is their natural dependance to the weather conditions. Then, to get a stable output voltage, it is necessary that PV panels to be combined with some energy storage systems, such as batteries. A powerful management system is required to make a balance between energy generation, saving, and consumption. The accurate management of this class of hybrid systems is so challenging because of high dependence of renewable energy generators to the level of irradiation and temperature and the existence of high level of uncertainties, such as time-varying output load.

When it comes to system control, the main factors that should be fully considered are: the influence of the irradiation, temperature, measurement errors of currents of PV/battery and output voltage, mathematical dynamics uncertainties, and dynamic perturbation, such as variable output load. The presented studies in this field can be classified in two general categories: classic control systems and intelligent control systems. In the following, some of recent studies are investigated.

Up to now, many classic control systems have been developed for voltage/energy regulation in PV/battery systems. For example, in Reference [3], the impact of cloudy day and energy demand is considered, and the problem of voltage regulation is studied by supercapacitors and batteries. In Reference [4], the lifetime of energy storage units and converters is taken to account, and the reliability of PV/battrey systems is investigated. In Reference [5], considering the mathematical model of units, a cost function is developed to effective use of battery and PV panel. In Reference [6], a comprehensive control scheme is presented for voltage, frequency, and power management, and the stability versus variable irradiation is studied. In Reference [7], by demand forecasting, a predictive control system is designed for energy control and peak shaving. In Reference [8], a charging plan is suggested to decrease the consumption cost of electricity energy, and the maximum power extraction in PV panels is studied. In Reference [9], the switching frequency of converters is controlled by the theory of synchronous reference frame to achieve optimal energy form PV panel, and the suggested method is examined on IEEE-519 standard system. In Reference [10], a predictive controller by applying on distributed inverters is designed to voltage control and power sharing problem. In Reference [11], an adaptive controller optimized by the backpropagation algorithm is developed to carry out a voltage balance, and the output power quality is investigated. In Reference [12], a coordinated control system is proposed for voltage management, and the impact of fluctuation of energy generators is studied.

Recently, it was shown that fractional-order controllers result in effectively better control proficiency in comparison with the integer-order counterpart [13,14,15]. However, this control approach has rarely applied on PV/battery systems, and only some simple fractional-order controllers with no stability guarantee have been developed. For example, in Reference [16], a simple proportional-derivative-integral (PID) controller using fractional-order calculus is reformulated for a PV/battery system, and it is optimized by grey wolf method. In Reference [17], similar to Reference [16], the proportional-integral (PI) controller is developed based on fractional-order calculus, and its superiority is shown in contrast to conventional PI controller. In Reference [18], a simple fractional-order controller is optimized using root locus approach, and it is shown that fractional-order controller results in better power extraction in various climate conditions, in contrast to the integer-order one. In Reference [19], the fractional-order PID controller is designed for power flow control between battery, PV panel, and output load, and its superiority versus a conventional PID is studied. In Reference [20], a fractional-order sliding mode controller (SMC) is examined versus an integer-order one. In Reference [21], a fractional-order PID control system is optimized using Yin-Yang-Pair method, and it is compared with other conventional controllers.

In most of the above studies, the management techniques are designed on basis of mathematical model of converters, PV, and battery storage systems. To deal with unknown mathematical models, some controllers using fuzzy logic systems (FLSs) have been developed for this problem. In Reference [22], the energy flow between battery and PV panel is controlled by an FLS such that the maintenance cost of battery in versus of weather condition fluctuation to be decreased. In Reference [23], an FLS-based controller is designed to improve lifespan of battery and it is shown that the FLS-based controller attenuates the battery peak current about 0.22%. In Reference [24], an FLS-based controller is suggested for frequency control and also the power fluctuations in large scale systems is studied. In Reference [24], it is shown that the use of an FLS-based controller results in fast response and better power control performance in noisy condition. In Reference [25], the superiority of fuzzy controllers is shown in the improvement of life cycle of battery systems. In Reference [26], it is shown that, by the use of an FLS-based energy management system, cost savings of more than 13% can be achieved. In Reference [27], a fuzzy controller is applied on a PV/battery/diesel system, and its proficiency is studied. In Reference [28], the effectiveness of a fuzzy controller is examined under partial shading conditions and variable temperature. In Reference [29], a fuzzy controller is designed for power management, and it is shown that the power quality is improved by the use of FLS-based control system.

In the most of the above studies, a simple type-1 FLS was used to cope with unknown mathematical models. However, high-order FLSs have more capability in practical nonlinear systems [30,31,32,33,34]. In addition, the tuning process in the most of above mentioned controllers is done as a non-adaptive and off-line approach. Furthermore, the robustness against fluctuation of irradiation and abrupt variation of load demand are not investigated. By the above motivations, in the current study, a new fractional-order control scenario was introduced on the basis of type-3 (T3)-FLSs such that T3-FLSs are online-optimized through the robustness investigation against perturbations. The main advantages are:

• A new type-3 fuzzy fractional-order control scenario is proposed.
• The dynamics of PV, converters, and battery are assumed to be unknown and are perturbed by variable irradiation, random temperature, and sudden changes in output load.
• The new fractional-order adaptation rules are derived for T3-FLS such that the stability to be ensured.
• New combustors are proposed such that the robustness to be guaranteed.

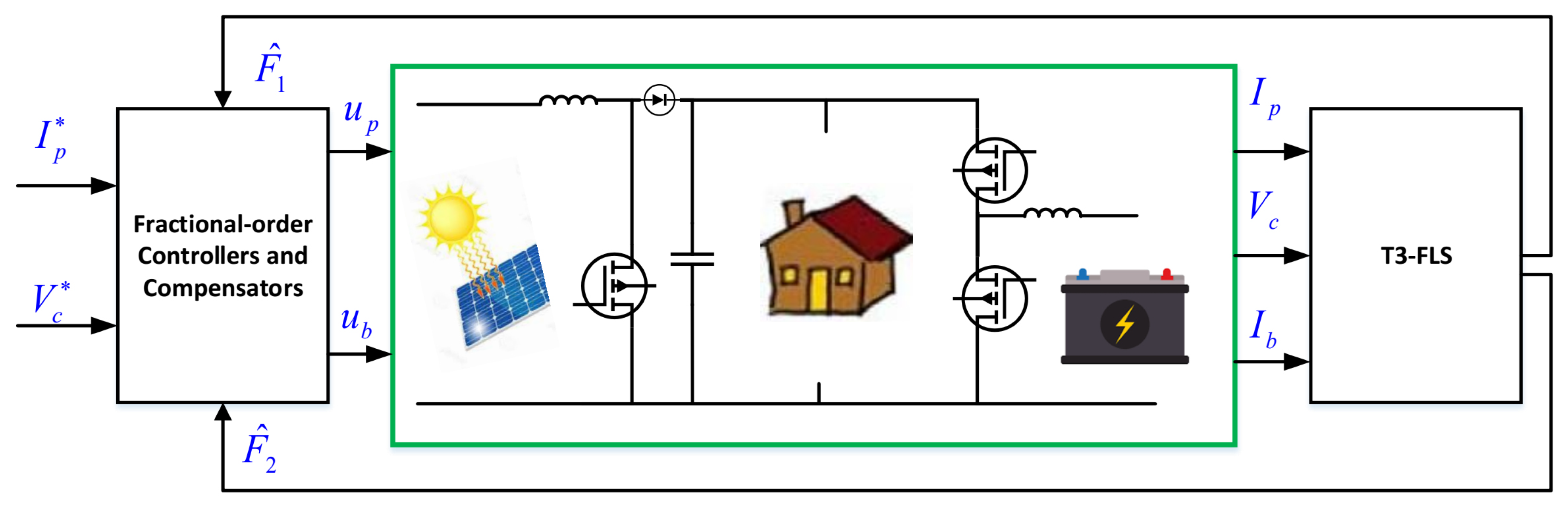
2. Problem Formulation

2.1. General View

The general block diagram is shown in Figure 1, and the detailed control block diagram is given in Figure 2. It is seen that the currents of the PV/battery $I_p/I_b$ and output voltage $V_c$ are measured by current and voltage sensors. In Figure 1, T3-FLSs (${\widehat{F}}_1$, ${\widehat{F}}_2$) are used for online dynamic estimation, and the controllers (${\mu }_p$, ${\mu }_b$) are designed on the basis of the online T3-FLS model. The parameters of T3-FLSs (${\theta }_1$, ${\theta }_1$) and control gains (${\widehat{g}}_1$, ${\widehat{g}}_1$) are online-tuned. The compensators (${\mu }_{cp}$, ${\mu }_{cb}$) are carried out through the robustness study on basis of fractional-order calculus, tracking errors ($e_1$, $e_2$), and upper bounds of approximation errors (${\overline{E}}_1$ and ${\overline{E}}_1$ ) such that a good robustness to be achieved against dynamic perturbation and common irradiation and temperature disturbances. The detailed descriptions are given in Theorem 1.

The output load energy is supplied by PV or battery at each sample time. If the required energy cannot be supplied by the PV panel, then the battery systems get to work. In addition, whenever the generated energy by PV panel is more than needed, the extra energy is stored in battery. The converters are used to construct a switching mechanism between PV and battery. The schematic of the converter is depicted in Figure 3. By considering the states of switchers $\mathrm{S}{\mathrm{W}}_1$, $\mathrm{S}{\mathrm{W}}_2$, and $\mathrm{S}{\mathrm{W}}_3$, four modes, as shown in Figure 4, can be derived [35]. If $\mathrm{S}{\mathrm{W}}_1$ and $\mathrm{S}{\mathrm{W}}_3$ are open and $\mathrm{S}{\mathrm{W}}_2$ is closed, then the switching mode is obtained as shown in Figure 4a. If $\mathrm{S}{\mathrm{W}}_1$ and $\mathrm{S}{\mathrm{W}}_2$ are closed and $\mathrm{S}{\mathrm{W}}_3$ is open, the switching mode is obtained as shown in Figure 4b. If $\mathrm{S}{\mathrm{W}}_1$ and $\mathrm{S}{\mathrm{W}}_2$ are open and $\mathrm{S}{\mathrm{W}}_3$ is closed, the switching mode is obtained as shown in Figure 4c. Finally, if $\mathrm{S}{\mathrm{W}}_1$ and $\mathrm{S}{\mathrm{W}}_3$ are closed and $\mathrm{S}{\mathrm{W}}_2$ is open, then the switching mode is obtained as shown in Figure 4d. For each switching mode, one state space formulation can be written. Then, by taking the average of four state space representation, the dynamics of plant are given as:

$$\begin{array}{c}{\dot{\varsigma }}_1=\left(-{\varsigma }_2+{\nu }_p+{\varsigma }_2{\mu }_p\right)/{\iota }_p\hfill \\ {\dot{\varsigma }}_2=\frac{1}{C}\left({\varsigma }_1-{\varsigma }_2/R+{\varsigma }_3{\mu }_b-{\varsigma }_1{\mu }_p\right)\hfill \\ {\dot{\varsigma }}_3=\left(-{\varsigma }_2{\mu }_b+{\nu }_b\right)/{\iota }_b\hfill \end{array},$$

(1)

where ${\varsigma }_1$, ${\varsigma }_2$, and ${\varsigma }_3$ are the current of PV, current of battery, and load voltage, respectively. ${\iota }_p$/${\iota }_b$, R, and C are values of inductances, resistor, and capacitor in the converter. ${\nu }_p$ and ${\nu }_v$ are the voltages of PV and battery, respectively, and ${\mu }_p$ and ${\mu }_b$ are control signals.

2.2. PV Modeling

By the single-diode modeling technique of PV panels, dynamics of PV are described as [36]:

$${\ell }_{ph}=\left({\ell }_{sc}+\left(T-T_r\right){\kappa }_i\right)s,$$

(2)

$$\begin{array}{c}{I}_p=I_{phg}G-exp\left(\left(V_p+I_p{R}_{sg}\right)q/nT{\kappa }_b-1\right){\ell }_o\hfill \\ -\frac{1}{R_{shg}}\left(I_p{R}_{sg}+V_p\right),\hfill \end{array}$$

(3)

$${\ell }_0=exp\left[q{E}_g\left(\frac{1}{T_r+273}-\frac{1}{T+273}\right)/{\kappa }_{b}A\right]{\left(T+273/T_r+273\right)}^3{\ell }_r,$$

(4)

where all parameter definitions are given in

Table 1. Parameter definition of photovoltaic (PV); see Equation (2).

Parameter	Description
n	Cell Number
G (w/m${}^2$)	Solar irradiation
${\kappa }_b$ (J/K)	Boltzmann’s constant
$E_g$ (ev)	Band-Gap energy
$R_{sh}$ /$R_s\left(\Omega \right)$	Equivalent resistances
T (${}^{\circ }$C)	Temperature of PV
q	Electron charge
A	Constant of the diode ideality
${\ell }_r$ (A)	Saturation current
$T_r$ (${}^{\circ }$C)	Reference temperature
${\ell }_{ph}$ (A)	Photo generated currents

. As depicted in Figure 5, the power of PV panel is not constant but is changed by its current. As it can be observed, at an optimal current, the maximum energy can be achieved.

2.3. Battery Modeling

The battery dynamics can be given as Equations (5)–(8) [36]:

$$\mathrm{E}\left(t\right)=-\int \eta {\nu }_{boc}{I}_b+{\mathrm{E}}_{Loss}dt$$

(5)

$$\eta =\left\{\begin{array}{c}{\eta }_1{I}_b\ge 0\\ {\eta }_2{I}_b<0\end{array}\right.$$

(6)

$${\nu }_b=-R_b{I}_b+{\nu }_{boc}$$

(7)

$$SoC\left(t\right)=\mathrm{E}\left(t\right)/{\mathrm{E}}_{\mathrm{Max}}$$

(8)

where all parameter definitions in Equations (5)–(8) are given in

Table 2. Parameter description of battery system, see Equation (5).

Parameter	Unit	Description
$R_b$	$\left(\Omega \right)$	Battery internal resistance
${\mathrm{E}}_{Loss}$	(w)	Power losses
${\nu }_{boc}$	(v)	Voltage of battery open circuit
${\eta }_1$ and ${\eta }_2$	-	Rates of charge and discharge
${\mathrm{E}}_{\mathrm{Max}}$	(J)	Maximum storable energy

.

3. Uncertainty Estimation by Type-3 FLS

T3-FLSs are the generalization of T2-FLSs. The main idea for T3-FLS is presented in Reference [37], which was developed in this study for dynamic identification of a practical system. The basic superiority of T3-FLSs with respect to T2-FLSs is that, in type-3 membership functions (MFs), the upper and lower of uncertainties are considered to be fuzzy set, while, in the type-2 MFs, the upper and lower of uncertainties are considered to be crisp values. In this section, the proposed T3-FLS is explained. The structure is given in Figure 6. T3-FLSs are used to deal with dynamic perturbation of PV, battery, and other units. The details are given below.

(1) The inputs of T3-FLSs are ${\varsigma }_1=I_p$, ${\varsigma }_2=\nu$, ${\varsigma }_3=I_b$. (2) For each input ${\varsigma }_j,j=1,2,3$, two MFs are considered with centers ${\underline{c}}_{{\tilde{\psi }}_{{\varsigma }_j}^1}$ and ${\underline{c}}_{{\tilde{\psi }}_{{\varsigma }_j}^2}$ (see Reference [37]), upper standard division ${\overline{\sigma }}_{{\tilde{\psi }}_{{\varsigma }_j}^k}^{}$, and lower standard division ${\underline{\sigma }}_{{\tilde{\psi }}_{{\varsigma }_j}^k}^{}$. The type-3 MFs have one more degree of freedom, in contrast to the type-2 counterparts. It is seen that the secondary membership is also type-2 MF. For example, consider a type-2 MF for input x in which its primary domain is between $\underset{\overline{}}{u}$ and $\overline{u}$. In a type-3 MF for input x, the upper and lower bounds of primary domain are not constant, but they are the fuzzy sets. For input $I_p$, one has:

$$\begin{array}{c}{\overline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\overline{\chi }}\left({\varsigma }_1=I_p\right)=exp\left(-{\left({\varsigma }_1-{\underline{c}}_{{\tilde{\psi }}_{I_p}^1}\right)}^2/{\overline{\sigma }}_{{\tilde{\psi }}_{I_p}^1|\overline{\chi }}^2\right)\hfill \\ {\overline{\pi }}_{{\tilde{\psi }}_{I_p}^2|\underline{\chi }}\left({\varsigma }_1=I_p\right)=exp\left(-{\left({\varsigma }_1-{\overline{c}}_{{\tilde{\psi }}_{I_p}^2}\right)}^2/{\overline{\sigma }}_{{\tilde{\psi }}_{I_p}^2|\underline{\chi }}^2\right)\hfill \end{array},$$

(9)

$$\begin{array}{c}{\underline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\overline{\chi }}\left({\varsigma }_1=I_p\right)=exp\left(-{\left({\varsigma }_1-{\underline{c}}_{{\tilde{\psi }}_{I_p}^1}\right)}^2/{\underline{\sigma }}_{{\tilde{\psi }}_{I_p}^1|\overline{\chi }}^2\right)\hfill \\ {\underline{\pi }}_{{\tilde{\psi }}_{I_p}^2|\underline{\chi }}\left({\varsigma }_1=I_p\right)=exp\left(-{\left({\varsigma }_1-{\overline{c}}_{{\tilde{\psi }}_{I_p}^2}\right)}^2/{\underline{\sigma }}_{{\tilde{\psi }}_{I_p}^2|\underline{\chi }}^2\right)\hfill \end{array},$$

(10)

where $\chi$ is the value of secondary membership. ${\overline{\pi }}_{{\tilde{\psi }}_{{\varsigma }_j}^k|\chi }$ and ${\underline{\pi }}_{{\tilde{\psi }}_{{\varsigma }_j}^k|\chi }$ are the upper and lower memberships for ${\tilde{\psi }}_{{\varsigma }_j}^k$. Similarly to (9) and (10), for other inputs $I_b$ and $V_c$, one has:

$$\begin{array}{c}{\overline{\pi }}_{{\tilde{\psi }}_{I_b}^1|\overline{\chi }}\left({\varsigma }_2=I_b\right)=exp\left(-{\left({\varsigma }_2-{\underline{c}}_{{\tilde{\psi }}_{I_p}^1}\right)}^2/{\overline{\sigma }}_{{\tilde{\psi }}_{I_b}^1|\overline{\chi }}^2\right)\hfill \\ {\overline{\pi }}_{{\tilde{\psi }}_{I_b}^2|\underline{\chi }}\left({\varsigma }_2=I_b\right)=exp\left(-{\left({\varsigma }_2-{\overline{c}}_{{\tilde{\psi }}_{I_b}^2}\right)}^2/{\overline{\sigma }}_{{\tilde{\psi }}_{I_b}^2|\underline{\chi }}^2\right)\hfill \end{array},$$

(11)

$$\begin{array}{c}{\underline{\pi }}_{{\tilde{\psi }}_{I_b}^1|\overline{\chi }}\left({\varsigma }_2=I_b\right)=exp\left(-{\left({\varsigma }_2-{\underline{c}}_{{\tilde{\psi }}_{I_b}^1}\right)}^2/{\underline{\sigma }}_{{\tilde{\psi }}_{I_b}^1|\overline{\chi }}^2\right)\hfill \\ {\underline{\overline{\pi }}}_{{\tilde{\psi }}_{I_b}^2|\underline{\chi }}\left({\varsigma }_2=I_b\right)=exp\left(-{\left({\varsigma }_2-{\overline{c}}_{{\tilde{\psi }}_{I_b}^2}\right)}^2/{\underline{\sigma }}_{{\tilde{\psi }}_{I_b}^2|\underline{\chi }}^2\right)\hfill \end{array},$$

(12)

$$\begin{array}{c}{\overline{\pi }}_{{\tilde{\psi }}_{V_c}^1|\overline{\chi }}\left({\varsigma }_3=V_c\right)=exp\left(-{\left({\varsigma }_3-{\underline{c}}_{{\tilde{\psi }}_{V_c}^1}\right)}^2/{\overline{\sigma }}_{{\tilde{\psi }}_{V_c}^1|\overline{\chi }}^2\right)\hfill \\ {\overline{\pi }}_{{\tilde{\psi }}_{V_c}^2|\underline{\chi }}\left({\varsigma }_3=V_c\right)=exp\left(-{\left({\varsigma }_3-{\overline{c}}_{{\tilde{\psi }}_{V_c}^2}\right)}^2/{\overline{\sigma }}_{{\tilde{\psi }}_{V_c}^2|\underline{\chi }}^2\right)\hfill \end{array},$$

(13)

$$\begin{array}{c}{\underline{\pi }}_{{\tilde{\psi }}_{V_c}^1|\overline{\chi }}\left({\varsigma }_3=V_c\right)=exp\left(-{\left({\varsigma }_3-{\underline{c}}_{{\tilde{\psi }}_{V_c}^1}\right)}^2/{\underline{\sigma }}_{{\tilde{\psi }}_{V_c}^1|\overline{\chi }}^2\right)\hfill \\ {\underline{\overline{\pi }}}_{{\tilde{\psi }}_{V_c}^2|\underline{\chi }}\left({\varsigma }_3=V_c\right)=exp\left(-{\left({\varsigma }_3-{\overline{c}}_{{\tilde{\psi }}_{V_c}^2}\right)}^2/{\underline{\sigma }}_{{\tilde{\psi }}_{V_c}^2|\underline{\chi }}^2\right)\hfill \end{array}.$$

(14)

(3) The lower rule firing is obtained as Equations (15) and (16):

$$\begin{array}{c}{\underline{\xi }}_{\underline{\chi }}^2={\underline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\underline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{I_b}^1|\underline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{V_c}^2|\underline{\chi }}\hfill \\ {\underline{\xi }}_{\underline{\chi }}^3={\underline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\underline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{I_b}^2|\underline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{V_c}^1|\underline{\chi }}\hfill \\ ⋮\hfill \\ {\underline{\xi }}_{\underline{\chi }}^8={\underline{\pi }}_{{\tilde{\psi }}_{I_p}^2|\underline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{I_b}^2|\underline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{V_c}^2|\underline{\chi }}\hfill \end{array},$$

(15)

$$\begin{array}{c}{\underline{\xi }}_{\overline{\chi }}^2={\underline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\overline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{I_b}^1|\overline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{V_c}^2|\overline{\chi }}\hfill \\ {\underline{\xi }}_{\overline{\chi }}^3={\underline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\overline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{I_b}^2|\overline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{V_c}^1|\overline{\chi }}\hfill \\ ⋮\hfill \\ {\underline{\xi }}_{\overline{\chi }}^8={\underline{\pi }}_{{\tilde{\psi }}_{I_p}^2|\overline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{I_b}^2|\overline{\chi }}{\underline{\pi }}_{{\tilde{\psi }}_{V_c}^2|\overline{\chi }}\hfill \end{array}.$$

(16)

Similarly, for the upper rule firing, one has:

$$\begin{array}{c}{\overline{\xi }}_{\underline{\chi }}^1={\overline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\underline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{I_b}^1|\underline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{V_c}^1|\underline{\chi }}\hfill \\ {\overline{\xi }}_{\underline{\chi }}^2={\overline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\underline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{I_b}^1|\underline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{V_c}^2|\underline{\chi }}\hfill \\ {\overline{\xi }}_{\underline{\chi }}^3={\overline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\underline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{I_b}^2|\underline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{V_c}^1|\underline{\chi }}\hfill \\ ⋮\hfill \\ {\overline{\xi }}_{\underline{\chi }}^8={\overline{\pi }}_{{\tilde{\psi }}_{I_p}^2|\underline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{I_b}^2|\underline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{V_c}^2|\underline{\chi }}\hfill \end{array},$$

(17)

$$\begin{array}{c}{\overline{\xi }}_{\overline{\chi }}^1={\overline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\overline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{I_b}^1|\overline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{V_c}^1|\overline{\chi }}\hfill \\ {\overline{\xi }}_{\overline{\chi }}^2={\overline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\overline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{I_b}^1|\overline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{V_c}^2|\overline{\chi }}\hfill \\ {\overline{\xi }}_{\overline{\chi }}^3={\overline{\pi }}_{{\tilde{\psi }}_{I_p}^1|\overline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{I_b}^2|\overline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{V_c}^1|\overline{\chi }}\hfill \\ ⋮\hfill \\ {\overline{\xi }}_{\overline{\chi }}^8={\overline{\pi }}_{{\tilde{\psi }}_{I_p}^2|\overline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{I_b}^2|\overline{\chi }}{\overline{\pi }}_{{\tilde{\psi }}_{V_c}^2|\overline{\chi }}\hfill \end{array}.$$

(18)

(4) The output of ${\widehat{F}}_1$ and ${\widehat{F}}_2$ are:

$$\begin{array}{c}{\widehat{F}}_1={\theta }_1^T{\varphi }_1\hfill \\ {\widehat{F}}_2={\theta }_2^T{\varphi }_2\hfill \end{array},$$

(19)

where ${\theta }_i$ and ${\varphi }_i$ are:

$$\begin{array}{c}{\theta }_i={\left[{\underline{\theta }}_{i1},...,{\underline{\theta }}_{iM},{\overline{\theta }}_{i1},...,{\overline{\theta }}_{iM}\right]}^T\hfill \\ {\varphi }_i={\left[{\underline{\varphi }}_{i1},...,{\underline{\varphi }}_{iM},{\overline{\varphi }}_{i1},...,{\overline{\varphi }}_{iM}\right]}^T\hfill \end{array},$$

(20)

where M represents number of rules. ${\underline{\varphi }}_r$ and ${\overline{\varphi }}_R$ are:

$$\begin{array}{c}{\overline{\varphi }}_r=\frac{{\displaystyle \sum _{j=1}^{n_{\chi }}}{\overline{\chi }}_j\frac{{\overline{\xi }}_{{\overline{\chi }}_j}^r}{{\displaystyle \sum _{r=1}^R}\left({\overline{\xi }}_{{\overline{\chi }}_j}^r+{\underline{\xi }}_{{\overline{\chi }}_j}^r\right)}}{{\displaystyle \sum _{j=1}^{n_{\chi }}}\left({\overline{\chi }}_j+{\underline{\chi }}_j\right)}\hfill \\ +\frac{{\displaystyle \sum _{j=1}^{n_{\chi }}}{\underline{\chi }}_j\frac{{\overline{\xi }}_{{\underline{\chi }}_j}^r}{{\displaystyle \sum _{r=1}^R}\left({\overline{\xi }}_{{\underline{\chi }}_j}^r+{\underline{\xi }}_{{\underline{\chi }}_j}^r\right)}}{{\displaystyle \sum _{j=1}^{n_{\chi }}}\left({\overline{\chi }}_j+{\underline{\chi }}_j\right)},r=1,...,8\hfill \end{array},$$

(21)

$$\begin{array}{c}{\underline{\varphi }}_r=\frac{{\displaystyle \sum _{j=1}^{n_{\chi }}}{\overline{\chi }}_j\frac{{\underline{\xi }}_{{\overline{\chi }}_j}^r}{{\displaystyle \sum _{r=1}^R}\left({\overline{\xi }}_{{\overline{\chi }}_j}^r+{\underline{\xi }}_{{\overline{\chi }}_j}^r\right)}}{{\displaystyle \sum _{j=1}^{n_{\chi }}}\left({\overline{\chi }}_j+{\underline{\chi }}_j\right)}\hfill \\ +\frac{{\displaystyle \sum _{j=1}^{n_{\chi }}}{\underline{\chi }}_j\frac{{\underline{\xi }}_{{\underline{\chi }}_j}^r}{{\displaystyle \sum _{r=1}^R}\left({\overline{\xi }}_{{\underline{\chi }}_j}^r+{\underline{\xi }}_{{\underline{\chi }}_j}^r\right)}}{{\displaystyle \sum _{j=1}^{n_{\chi }}}\left({\overline{\chi }}_j+{\underline{\chi }}_j\right)},r=1,...,8\hfill \end{array},$$

(22)

where $n_{\chi }$ is number of slices.

4. Main Results

The control signals and tuning rules are summarized in the following theorem:

Theorem 1.

For the given controllers as Equations (23) and (24), tuning rules as Equations (25)–(28), and compensators as Equations (29) and (30), the asymptotic stability is guaranteed.

$${\mu }_p=\frac{1}{{\varsigma }_2{\widehat{g}}_1}\left(D_t^{\alpha }{\varsigma }_{1r}-{\widehat{F}}_1\left(\varsigma ,{\theta }_1\right)-k_p{e}_1+{\mu }_{cp}\right),$$

(23)

$${\mu }_b=\frac{1}{{\varsigma }_3{\widehat{g}}_2}\left(D_t^{\alpha }{\varsigma }_{2r}-{\widehat{F}}_2\left(\varsigma ,{\theta }_2\right)-k_b{e}_2+{\mu }_{cb}\right),$$

(24)

$$D_t^{\alpha }{\widehat{\theta }}_1=\upsilon {\tilde{\varsigma }}_1{\varphi }_1,$$

(25)

$$D_t^{\alpha }{\widehat{\theta }}_2=\upsilon {\tilde{\varsigma }}_2{\varphi }_2,$$

(26)

$$D_t^{\alpha }{\widehat{g}}_1=\upsilon {\tilde{\varsigma }}_1{\varsigma }_2{\mu }_p,$$

(27)

$$D_t^{\alpha }{\widehat{g}}_2=\upsilon {\tilde{\varsigma }}_2{\varsigma }_3{\mu }_b,$$

(28)

$${\mu }_{cp}=-{\overline{\mathrm{E}}}_2\frac{e_1\left|{\tilde{\varsigma }}_1\right|}{e_1^2+\delta },$$

(29)

$${\mu }_{cb}=-{\overline{\mathrm{E}}}_1\frac{e_2\left|{\tilde{\varsigma }}_2\right|}{e_2^2+\delta },$$

(30)

where $\upsilon$, $\delta$, $k_b$, $k_p$, ${\overline{\mathrm{E}}}_{i}i=1,2$ are constant. ${\mu }_{cp}$ and ${\mu }_{cb}$ represent compensators. ${\varsigma }_{1r}$ and ${\varsigma }_{2r}$ are reference signals for ${\varsigma }_1$ and ${\varsigma }_2$, respectively. $e_1$ and $e_2$ are errors that are defined as $e_i={\varsigma }_i-{\varsigma }_{ir}$. ${\tilde{\varsigma }}_i$ is defined as ${\tilde{\varsigma }}_i={\varsigma }_i-{\widehat{\varsigma }}_i$.

Proof. 

The output dynamics (1) are:

$$\begin{array}{c}{\dot{\varsigma }}_1=\left(-{\varsigma }_2+V_p\left({\varsigma }_1\right)\right)/L_p+\frac{{\varsigma }_2}{L_p}{\mu }_p\hfill \\ {\dot{\varsigma }}_2=\left({\varsigma }_1/C-{\varsigma }_1{\mu }_p/C-{\varsigma }_2/CR\right)+\frac{{\varsigma }_3}{C}{\mu }_b\hfill \end{array}.$$

(31)

To design ${\mu }_p$ and ${\mu }_b$, the dynamics of ${\varsigma }_1$ and ${\varsigma }_2$ are estimated as suggested fractional-order T3-FLS model:

$$\begin{array}{c}{D}_t^{\alpha }{\widehat{\varsigma }}_1={\widehat{F}}_1\left(\varsigma ,{\theta }_1\right)+{\widehat{g}}_1{\varsigma }_2{\mu }_p\hfill \\ D_t^{\alpha }{\widehat{\varsigma }}_2={\widehat{F}}_2\left(\varsigma ,{\theta }_2\right)+{\widehat{g}}_2{\varsigma }_3{\mu }_b\hfill \end{array},$$

(32)

where $D_t^{\alpha }{\varsigma }_i,i=1,2$ are the fractional derivatives, and ${\widehat{\varsigma }}_1$ and ${\widehat{\varsigma }}_2$ are the estimation of ${\varsigma }_1$ and ${\varsigma }_2$. ${\widehat{g}}_1$ and ${\widehat{g}}_2$ are the estimations of $1/L_p$ and $1/C$, respectively. ${\widehat{F}}_1$ and ${\widehat{F}}_2$ are the T3-FLSs. From the universal estimation feature of FLSs, the dynamics of ${\varsigma }_1$ and ${\varsigma }_2$ in (32) can be written as:

$$\begin{array}{c}{D}_t^{\alpha }{\varsigma }_1={\widehat{F}}_1^{*}\left(\varsigma ,{\theta }_1\right)+{\widehat{g}}_1^{*}{\varsigma }_2{\mu }_p+{\mathrm{E}}_1\hfill \\ D_t^{\alpha }{\varsigma }_2={\widehat{F}}_2^{*}\left(\varsigma ,{\theta }_2\right)+{\widehat{g}}_2^{*}{\varsigma }_3{\mu }_b+{\mathrm{E}}_2\hfill \end{array},$$

(33)

where ${\widehat{F}}_1^{*}$ and ${\widehat{F}}_2^{*}$ are optimal T3-FLS, and ${\widehat{g}}_1^{*}$ and ${\widehat{g}}_2^{*}$ are the optimal values of ${\widehat{g}}_1$ and ${\widehat{g}}_2$, respectively. ${\mathrm{E}}_i,i=1,2$ are the approximation errors. From (32) and (33), the estimation error dynamics (${\tilde{\varsigma }}_i={\varsigma }_i-{\widehat{\varsigma }}_i$) can be obtained as:

$$\begin{array}{c}{D}_t^{\alpha }{\tilde{\varsigma }}_1={\widehat{F}}_1^{*}\left(\varsigma ,{\theta }_1\right)-{\widehat{F}}_1\left(\varsigma ,{\theta }_1\right)+\left({\widehat{g}}_1^{*}-{\widehat{g}}_1\right){\varsigma }_2{\mu }_p+{\mathrm{E}}_1\hfill \\ D_t^{\alpha }{\tilde{\varsigma }}_2={\widehat{F}}_2^{*}\left(\varsigma ,{\theta }_2\right)-{\widehat{F}}_2\left(\varsigma ,{\theta }_2\right)+\left({\widehat{g}}_2^{*}-{\widehat{g}}_2\right){\varsigma }_3{\mu }_b+{\mathrm{E}}_2\hfill \end{array}.$$

(34)

Considering definitions:

$$\begin{array}{c}{\tilde{\theta }}_i={\theta }_i^{*}-{\theta }_i\hfill \\ {\tilde{g}}_i=g_i^{*}-g_i\hfill \end{array}.$$

(35)

From (34), one has:

$$\begin{array}{c}{D}_t^{\alpha }{\tilde{\varsigma }}_1={\mathrm{E}}_1+{\tilde{\theta }}_1^T{\varphi }_1+{\tilde{g}}_1{\varsigma }_2{\mu }_p\hfill \\ D_t^{\alpha }{\tilde{\varsigma }}_2={\mathrm{E}}_2+{\tilde{\theta }}_2^T{\varphi }_2+{\tilde{g}}_2{\varsigma }_3{\mu }_b\hfill \end{array}.$$

(36)

Applying the control signals (23), (24), and (32) on the estimated model (32), one has:

$$D_t^{\alpha }{e}_1=-k_p{e}_1+{\mu }_{cp},$$

(37)

$$D_t^{\alpha }{e}_2=-k_b{e}_2+{\mu }_{cb}.$$

(38)

To examine the robustness and stability, Lyapunov function is considered as:

$$\begin{array}{c}V=\frac{1}{2}{\tilde{\varsigma }}_1^2+\frac{1}{2}{\tilde{\varsigma }}_2^2+\frac{1}{2}{e}_1^2+\frac{1}{2}{e}_2^2\hfill \\ \frac{1}{2\upsilon }{\tilde{g}}_1^2+\frac{1}{2\upsilon }{\tilde{g}}_2^2+\frac{1}{2\upsilon }{\tilde{\theta }}_1^T{\tilde{\theta }}_1^{}+\frac{1}{2\upsilon }{\tilde{\theta }}_2^T{\tilde{\theta }}_2^{}\hfill \end{array}.$$

(39)

By taking fractional time-derivative, $D_t^{\alpha }V$ is written as:

$$\begin{array}{c}{D}_t^{\alpha }V\le D_t^{\alpha }{\tilde{\varsigma }}_1{\tilde{\varsigma }}_1+D_t^{\alpha }{\tilde{\varsigma }}_2{\tilde{\varsigma }}_2+D_t^{\alpha }{e}_1{e}_1+D_t^{\alpha }{e}_2{e}_2\hfill \\ -\frac{1}{\upsilon }{\tilde{g}}_1{D}_t^{\alpha }{\widehat{g}}_1-\frac{1}{\upsilon }{\tilde{g}}_2{D}_t^{\alpha }{\widehat{g}}_2-\frac{1}{\upsilon }{\tilde{\theta }}_1^T{D}_t^{\alpha }{\widehat{\theta }}_1-\frac{1}{\upsilon }{\tilde{\theta }}_2^T{D}_t^{\alpha }{\widehat{\theta }}_2\hfill \end{array}.$$

(40)

From (40), $D_t^{\alpha }V$ becomes:

$$\begin{array}{c}{D}_t^{\alpha }V\le {\tilde{\varsigma }}_1\left({\tilde{\theta }}_1^T{\varphi }_1+{\varsigma }_2{\tilde{g}}_1{\mu }_p+{\mathrm{E}}_2\right)+{\tilde{\varsigma }}_2\left({\tilde{\theta }}_2^T{\varphi }_2+{\varsigma }_3{\tilde{g}}_2{\mu }_b+{\mathrm{E}}_1\right)\hfill \\ +e_1\left(-k_p{e}_1+{\mu }_{cp}\right)+e_2\left(-k_b{e}_2+{\mu }_{cb}\right)\hfill \\ -\frac{1}{\upsilon }{\tilde{g}}_1{D}_t^{\alpha }{\widehat{g}}_1-\frac{1}{\upsilon }{\tilde{g}}_2{D}_t^{\alpha }{\widehat{g}}_2-\frac{1}{\upsilon }{\tilde{\theta }}_1^T{D}_t^{\alpha }{\widehat{\theta }}_1-\frac{1}{\upsilon }{\tilde{\theta }}_2^T{D}_t^{\alpha }{\widehat{\theta }}_2\hfill \end{array}.$$

(41)

From (41), one has:

$$\begin{array}{c}{D}_t^{\alpha }V\le -k_p{e}_1^2+{\mu }_{cp}{e}_1-k_b{e}_2^2+{\mu }_{cb}{e}_2\hfill \\ +{\tilde{\theta }}_1^T\left({\tilde{\varsigma }}_1{\varphi }_1-\frac{1}{\upsilon }{D}_t^{\alpha }{\widehat{\theta }}_1\right)+{\tilde{\theta }}_2^T\left({\tilde{\varsigma }}_2{\varphi }_2-\frac{1}{\upsilon }{D}_t^{\alpha }{\widehat{\theta }}_2\right)\hfill \\ +{\tilde{\delta }}_p\left({\tilde{\varsigma }}_1{\varsigma }_2{\mu }_p-\frac{1}{\upsilon }{D}_t^{\alpha }{\widehat{g}}_1\right)+{\tilde{\delta }}_b\left({\tilde{\varsigma }}_2{\varsigma }_3{\mu }_b-\frac{1}{\upsilon }{D}_t^{\alpha }{\widehat{g}}_2\right)\hfill \\ +{\mathrm{E}}_2{\tilde{\varsigma }}_1+{\mathrm{E}}_1{\tilde{\varsigma }}_2\hfill \end{array}.$$

(42)

Considering tuning rules $D_t^{\alpha }{\widehat{\theta }}_i=\upsilon {\tilde{\varsigma }}_i{\varphi }_i,i=1,2$, $D_t^{\alpha }{\widehat{g}}_1=\upsilon {\tilde{\varsigma }}_1{\varsigma }_2{\mu }_p$, and $D_t^{\alpha }{\widehat{g}}_2=\upsilon {\tilde{\varsigma }}_2{\varsigma }_3{\mu }_b$, $D_t^{\alpha }V$ becomes:

$$D_t^{\alpha }V\le -k_b{e}_2^2-k_p{e}_1^2+{\mu }_{cp}{e}_1+{\mu }_{cb}{e}_2+E_2{\tilde{\varsigma }}_1+E_1{\tilde{\varsigma }}_2.$$

(43)

Then, one has:

$$D_t^{\alpha }V\le -k_b{e}_2^2-k_p{e}_1^2+\left|{\mathrm{E}}_2\right|\left|{\tilde{\varsigma }}_1\right|+{\mu }_{cp}{e}_1+{\mu }_b{e}_2+\left|{\mathrm{E}}_1\right|\left|{\tilde{\varsigma }}_2\right|.$$

(44)

Now, applying the compensators results in:

$$\begin{array}{c}{D}_t^{\alpha }V\le -k_b{e}_2^2-k_p{e}_1^2+\left[\left|{\mathrm{E}}_2\right|\left|{\tilde{\varsigma }}_1\right|-{\overline{\mathrm{E}}}_2\left|{\tilde{\varsigma }}_1\right|\frac{e_1^2}{e_1^2+\delta }\right]+\hfill \\ \left[\left|{\mathrm{E}}_1\right|\left|{\tilde{\varsigma }}_2\right|-{\overline{\mathrm{E}}}_1\left|{\tilde{\varsigma }}_2\right|\frac{e_2^2}{e_2^2+\delta }\right]\hfill \end{array}.$$

(45)

Then, it is proved that $D_t^{\alpha }V\le 0$. Considering Barbalat’s Lemma and from the fact that $\ddot{V}$ is bounded, the proof is completed. ☐

5. Simulation Studies

The efficiency and good output voltage and power regulation performance of suggested technique is shown in this section. Simulation and control parameters are given in

Table 3. Simulation parameters.

Parameter	Value	Parameter	Value
$L_p$	10 (mH)	$L_b$	12 ($mH$)
q	1.60 $\times {10}^{-19}$	n	45
$P_b$	56 (w)	$i_{sc}$	3.56 (A)
C	521 ($\mu$f)	$r_p$	36 ($m\Omega$)
$r_b$	70 (m$\Omega$)	$k_b$	1.481 $\times {10}^{-23}$
$T_r$	(${}^{\circ }$C)	$k_i$	1.2 ($A/k$)
A	1.1	$V_{boc}$	9 (v)
$i_r$	5.97 $\times {10}^{-8}$ (A)	$E_g$	1.42 ($ev$)
${\beta }_1$	0.95	${\beta }_2$	1.4
$P_b$	25 (w)	$W_{Loss}$	25 (w)

and

Table 4. Control parameters.

Parameters	Value	Equation
${\overline{\mathrm{E}}}_i,i=1,2$	10	(29) and (30)
$\alpha$	0.9	(23) and (24)
$k_p$, $k_b$	100	(23) and (24)
$\delta$	0.01	(29) and (30)
$\upsilon$	0.1	(25)–(28)
${\underline{c}}_{{\tilde{\psi }}_{V_c}^1}$, ${\underline{c}}_{{\tilde{\psi }}_{I_p}^1}$ and ${\underline{c}}_{{\tilde{\psi }}_{I_b}^1}$	–10	(12)–(14)
${\overline{c}}_{{\tilde{\psi }}_{V_c}^2}$, ${\overline{c}}_{{\tilde{\psi }}_{I_p}^2}$ and ${\overline{c}}_{{\tilde{\psi }}_{I_b}^2}$	10	(11)–(13)
${\underline{\sigma }}_{{\tilde{\psi }}_{V_c}^j}$, ${\underline{\sigma }}_{{\tilde{\psi }}_{I_p}^j}$ and ${\underline{\sigma }}_{{\tilde{\psi }}_{I_b}^j}$, $j=1,2$	5	(12)–(14)
${\overline{\sigma }}_{{\tilde{\psi }}_{V_c}^j}$, ${\overline{\sigma }}_{{\tilde{\psi }}_{I_p}^j}$ and ${\overline{\sigma }}_{{\tilde{\psi }}_{I_b}^j}$, $j=1,2$	10	(11)–(13)
$\overline{\chi }$	[0.6 0.8 1]	(12) and (13)
$\underline{\chi }$	[0 0.2 0.4]	(12) and (13)

.

Example 1.

In this example, the normal condition is taken to account such that the irradiation is assumed to be fixed at level 300 w/m${}^2$. The trajectories of ${\varsigma }_i,i=1,2$ and power of PV P and controllers ${\mu }_p$ and ${\mu }_b$ are shown in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. From Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, one can realize that the suggested scenario results in desired regulation performance, and the control signals have smooth shape. It is seen that the trajectories of the current of PV $I_p$ and the output voltage $V_c$ are converged to the desired level less than 10 s.

Example 2.

In this example, the irradiation is changed from 200 w/m${}^2$ into 600 w/m${}^2$ at time t = 55 s and also the temperature is changed as $T=50-10sin\left(t\right)$. The trajectories of ${\varsigma }_i,i=1,2$ and power of PV P and controllers ${\mu }_p$ and ${\mu }_b$ are shown in Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16. It is observed that a well power regulation is achieved in spite of time-varying temperature and irradiation. It is seen that the effect of variation of irradiation is well handled, and output voltage is well regulated on its desired level. In addition, the current of PV track its optimal level in less than 10 s.

Example 3.

In this example, a Gaussian noise with variance 0.05 is added to temperature and the temperature is randomly changed between 30 and 50, irradiation is changed as same Example 2, and output load is suddenly changed from 70 (Ω) into 40 (Ω) at time $t=55s$. The trajectories of ${\varsigma }_i,i=1,2$ and power of PV P and controllers ${\mu }_p$ and ${\mu }_b$ are shown in Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. It can be realized that a well tracking performance is achieved versus abrupt changes in load, time-varying temperature, and variable irradiation. In addition, it should be remembered that the dynamics of all units are unknown for the controller unit. It is seen that the effect of noise is also well eliminated, and the output voltage well tracks the reference signal. It should be noted that the T3-FLSs have better performance is noisy conditions, in contrast to the type-2 counterparts.

Example 4.

For the last example, a numerical and graphical comparison is provided with conventional PID [38], PBC [39], SMC [40], LQR [41], and our method on the basis of integer-order calculus (IOC). The simulation conditions are the same as Example 3 with the difference being that temperature and irradiation are changed at times $t=40s$ and $t=80s$, respectively. The values of mean square errors (MSEs) in

Table 5. Example 4: Mean square error (MSE) Comparison.

Method	Signal
	$\mathbf{\varsigma }\mathbf{1}$	$\mathbf{\varsigma }\mathbf{2}$
LQR [41]	0.8259	148.9198
PBC [39]	0.9579	11.2450
PID [38]	1.1029	15.2295
SMC [40]	0.5161	9.3327
Our method by IOC	0.3101	0.9114
Our method by FOC	0.2021	0.8102

and the trajectories of $I_p$ and $V_c$ in Figure 22 clearly show the superiority of the suggested control scenario. It is observed that the suggested method on the basis of fractional-order calculus (FOC) results in more accurate power/voltage regulation proficiency. It is seen that, when the dynamic perturbation occurrs at times 40 s and 80 s, the classic controllers LQR and PID failed to track reference signals. Furthermore, the settling time for the suggested controller is less than the others we compared.

Remark 1.

It should be noted that the perturbations, such as changes of irradiation, output load, and temperature, are not predicted. But, these perturbations are considered as a part of dynamic uncertainties. The dynamic uncertainties are handled by the online optimization of T3-FLSs and compensators.

Remark 2.

From the trajectories of $I_p$ and $V_c$ in all Examples, a small initial over shout can be seen. This problem is the cost of unknown dynamics assumption. In other words, the dynamics of all units are assumed to be unknown and are estimated by the suggested T3-FLSs. Furthermore, the effects of dynamic perturbations, such as changes of irradiation, temperature, and output load, are considered as a part of approximation error. The effect of approximation errors are eliminated by the online optimization of T3-FLSs and compensators. Because of stability considerations, the adaptation rate of T3-FLSs are chosen to be small. On the other hand, the upper bound of approximation errors in compensators are concentratively considered to be large. Then, it takes few times for regulation error to be reached on the zero level, and a small over shout begins to be seen. However, if the upper bounds of approximation errors are decreased, the initial peaks are diminished, but settling time is increased, and the subsidence of regulation error takes more time.

Remark 3.

The regulation accuracy and speed of the suggested controller depend on the modeling accuracy and speed. In other words, if the estimation error reaches zero level in less time, accordingly, the subsidence of the regulation error is increased. On the other hand, it has been shown in literature that, by the use of fractional-order calculus, the nonlinear dynamics can be modeled with more accuracy. Because of this motivation, the suggested controller was designed on basis of fractional-order calculus, and its effectiveness is shown in Example 4.

6. Conclusions

In this study, a new control approach considering T3-FLSs and fractional-order calculus was developed for voltage/power management in PV/battery systems. The uncertain time-varying dynamics are online-modeled by the suggested fractional-order T3-FLS. Because of one more degree of freedom in type-3 MFs, the capability of type-3 MFs to represent the high level of uncertainties is more than the type-2 and type-1 counterparts. It should be noted that the secondary membership in type-3 MFs is a type-2 MF. The new factional-order tuning rules are derived to optimize T3-FLS such that the stability to be guaranteed. In addition, the robustness is ensured by the adaptive compensators. In four simulation examples, the superiority and well performance of the suggested control scenario was demonstrated. In the first example, a normal condition was taken to account. In the second example, the impacts of variable irradiation and temperature were examined. In the third example, in addition to the variable irradiation and temperature, an abrupt change in output load was also applied on the system as dynamic perturbation. Finally, in the last example, a comparison with other popular techniques was completed. For future studies, the optimization of the value of fractional-order and the rule database of the suggested fuzzy controller can be considered. Also the uncertainties can be estimated with other intelligent systems such as group method for data handling neural networks (GMDH-NNs) and the fuel cells can be added to PV/Battery system to ensure the maximum charging of battery. Furthermore, the upper bound of approximation error (AE) is assumed to be known and fixed in this paper, for the our future studies, the upper bound of AE is online estimated and then a new compensator in integer-order calculus is designed to deal with the effects of AEs and by the Lyapunov and LaSalle’s invariant set theorems the asymptotic stability is investigated.