A Fast-Converging Scheme for the Electromagnetic Scattering from a Thin Dielectric Disk
Abstract
:1. Introduction
2. Formulation and Solution of the Problem
2.1. Integral Equations in the Spectral Domain
2.2. Helmholtz Decomposition
2.3. Discretization of the Integral Equations
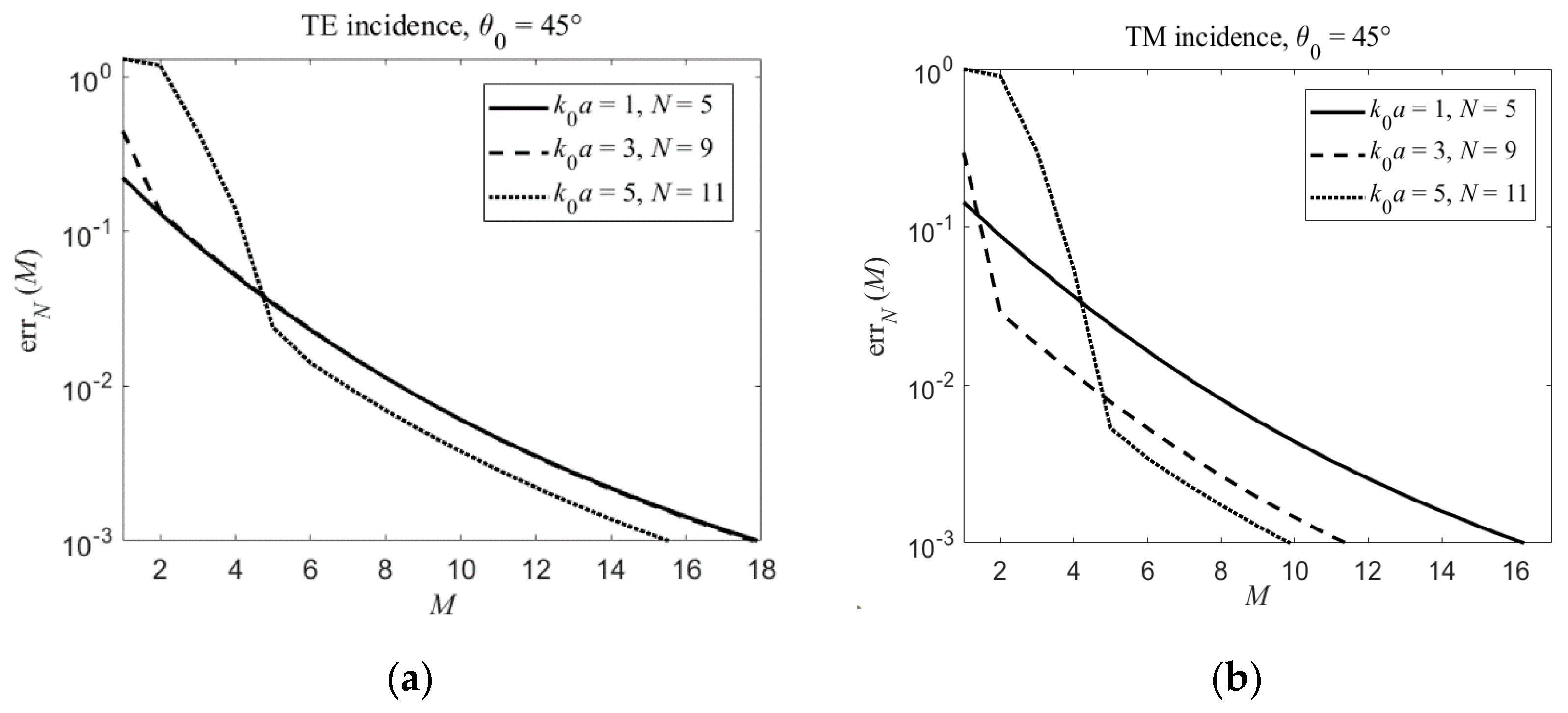
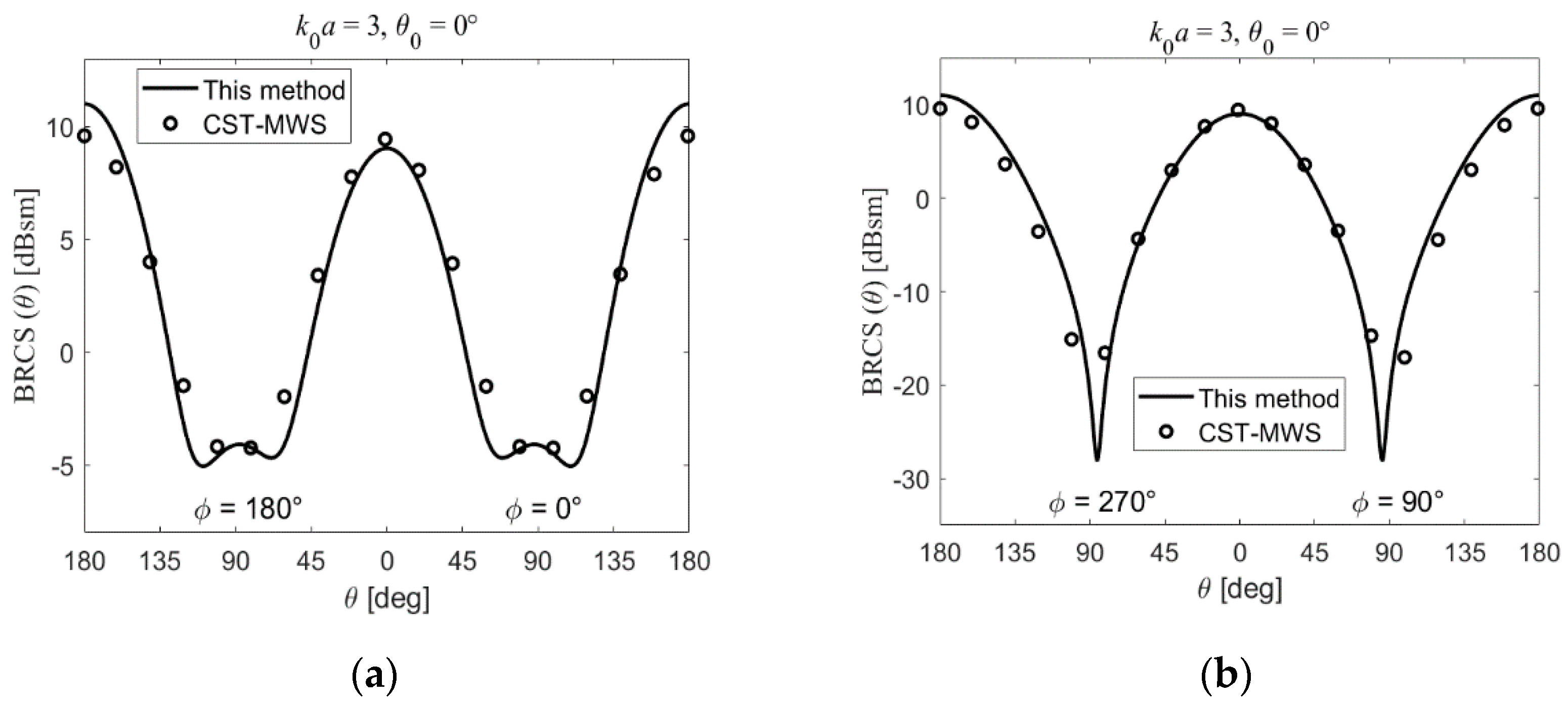
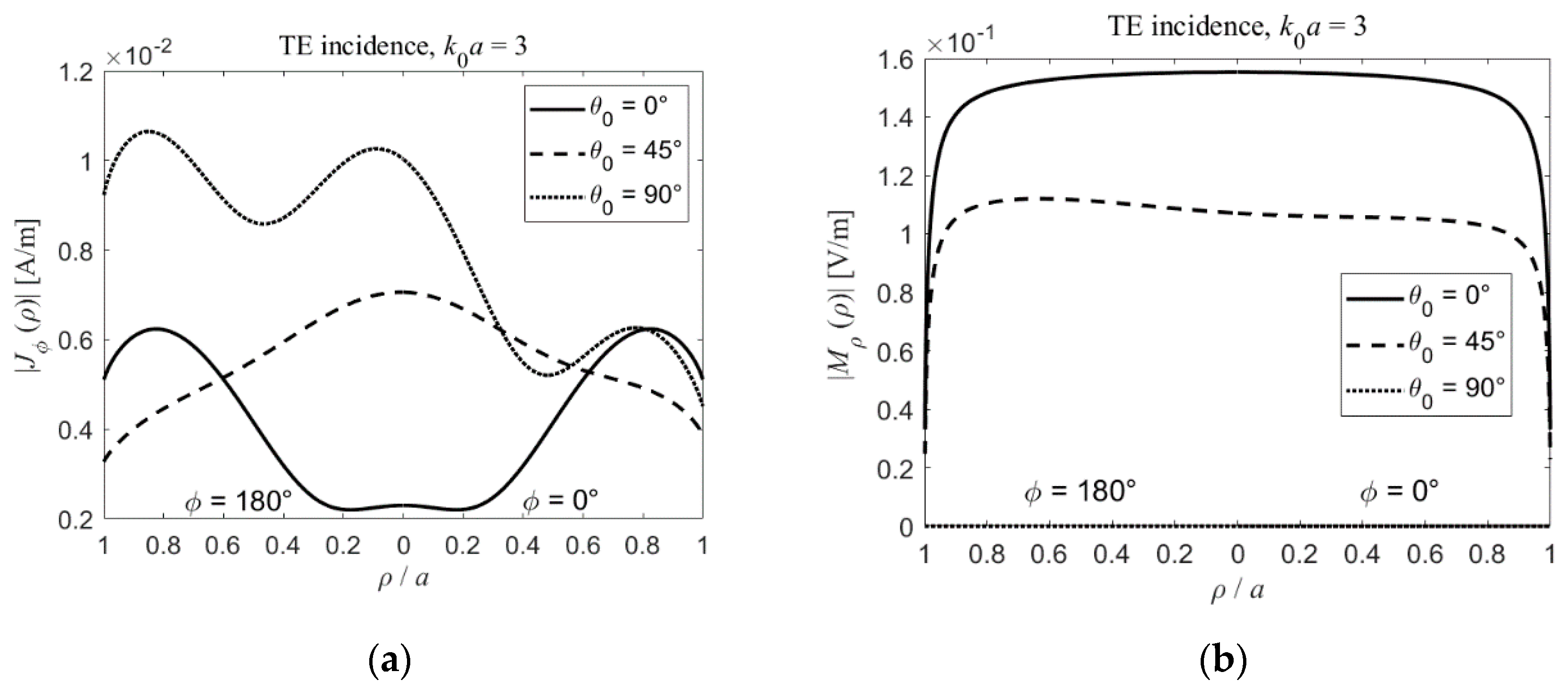
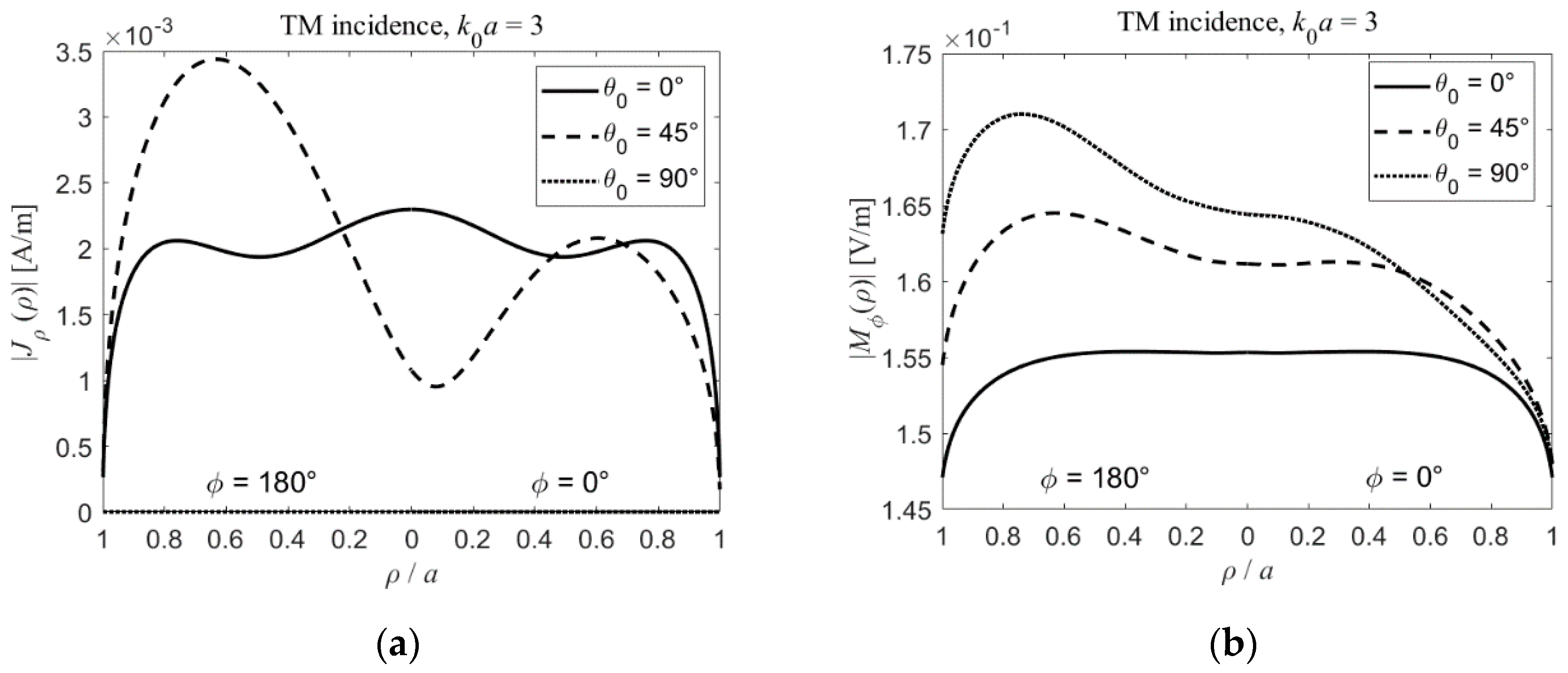
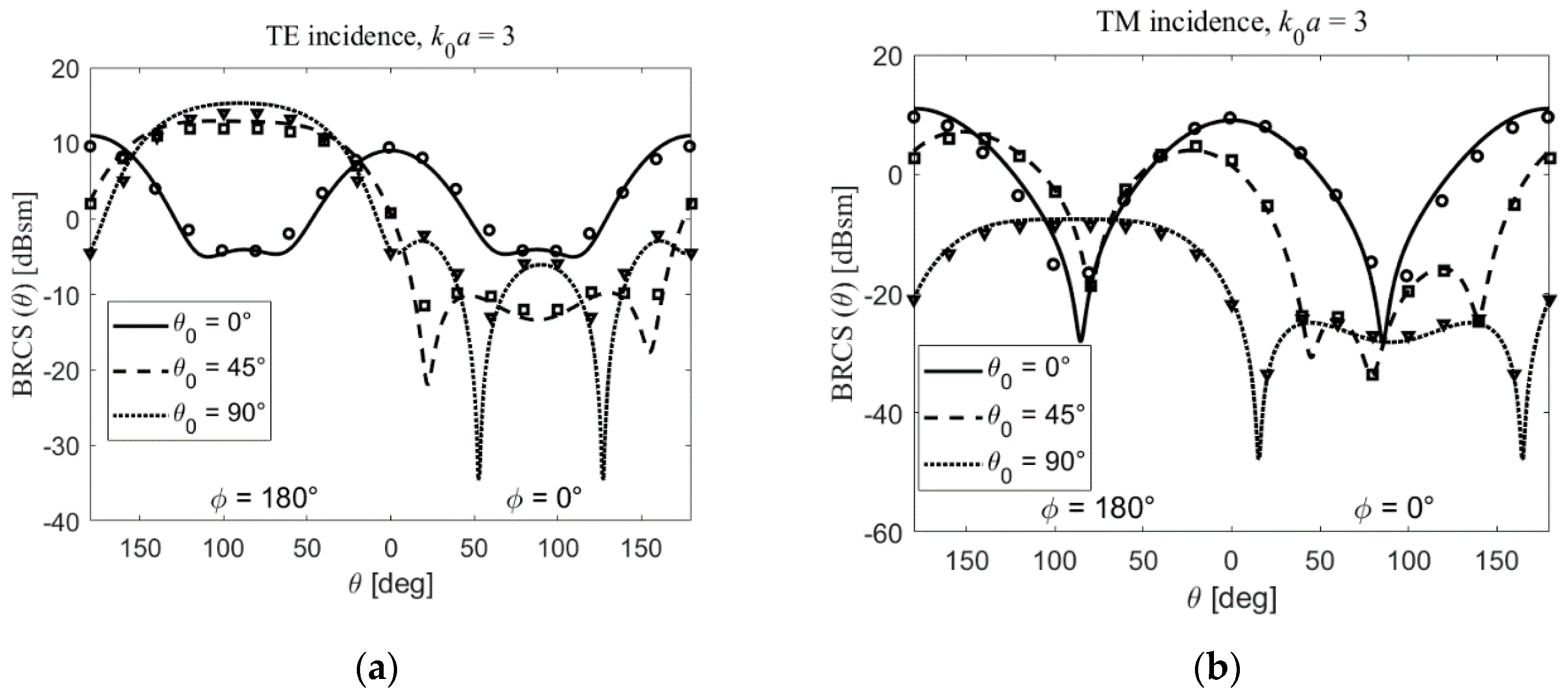
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- LeVine, D.M.; Schneider, A.; Lang, R.H.; Carter, H.G. Scattering from thin dielectric disks. IEEE Trans. Antennas Propag. 1985, 33, 1410–1413. [Google Scholar] [CrossRef] [Green Version]
- Karam, M.A.; Fung, A.K.; Antar, Y.M. Electromagnetic wave scattering from some vegetation samples. IEEE Trans. Geosci. Remote Sens. 1988, 26, 799–808. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Rahmat-Samii, Y. Microstrip antennas integrated with electromagnetic band-gap (EBG) structures: A low mutual coupling design for array applications. IEEE Trans. Antennas Propag. 2003, 51, 2936–2946. [Google Scholar] [CrossRef] [Green Version]
- Pan, G.; Narayanan, R.M. Electromagnetic scattering from dielectric sheet using the method of moments with approximate boundary condition. Electromagnetics 2004, 24, 369–384. [Google Scholar] [CrossRef]
- Koh, I.S.; Sarabandi, K. A new approximate solution for scattering by thin dielectric disks of arbitrary size and shape. IEEE Trans. Antennas Propag. 2005, 53, 1920–1926. [Google Scholar] [CrossRef] [Green Version]
- Raffaelli, S.; Sipus, Z.; Kildal, P.-S. Analysis and measurements of conformal patch array antennas on multilayer circular cylinder. IEEE Trans. Antennas Propag. 2005, 53, 1105–1113. [Google Scholar] [CrossRef]
- Schild, S.; Chavannes, N.; Kuster, N. A robust method to accurately treat arbitrarily curved 3-D thin conductive sheets in FDTD. IEEE Trans. Antennas Propag. 2007, 55, 3587–3594. [Google Scholar] [CrossRef]
- Balaban, M.V.; Sauleau, R.; Benson, T.M.; Nosich, A.I. Accurate quantification of the Purcell effect in the presence of a microdisk of nanoscale thickness. IET Micro Nano Lett. 2011, 6, 393–396. [Google Scholar] [CrossRef]
- Lee, J.; Yoo, M.; Lim, S. A study of ultra-thin single layer frequency selective surface microwave absorbers with three different bandwidths using double resonance. IEEE Trans. Antennas Propag. 2015, 63, 221–230. [Google Scholar] [CrossRef]
- Omar, A.A.; Shen, Z. Thin 3-D bandpass frequency-selective structure based on folded substrate for conformal radome applications. IEEE Trans. Antennas Propag. 2019, 67, 282–290. [Google Scholar] [CrossRef]
- Bleszynski, E.; Bleszynski, M.; Jaroszewicz, T. Surface-integral equations for electrmagnetic scattering from impenetrable and penetrable sheets. IEEE Antennas Propagat. Magaz. 1993, 35, 14–24. [Google Scholar] [CrossRef]
- Balaban, M.V.; Sauleau, R.; Benson, T.M.; Nosich, A.I. Dual integral equations technique in electromagnetic scattering by a thin disk. Prog. Electromagn. Res. B 2009, 16, 107–126. [Google Scholar] [CrossRef] [Green Version]
- Nazarchuk, Z.; Kobayashi, K. Mathematical modelling of electromagnetic scattering from a thin penetrable target. Prog. Electromagn. Res. 2005, 55, 95–116. [Google Scholar] [CrossRef] [Green Version]
- Dudley, D.G. Error minimization and convergence in numerical methods. Electromagnetics 1985, 5, 89–97. [Google Scholar] [CrossRef]
- Migliore, M.D.; Pinchera, D.; Lucido, M.; Schettino, F.; Panariello, G. A sparse recovery approach for pattern correction of active arrays in presence of element failures. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1027–1030. [Google Scholar] [CrossRef]
- Pinchera, D.; Migliore, M.D.; Lucido, M.; Schettino, F.; Panariello, G. A compressive-sensing inspired alternate projection algorithm for sparse array synthesis. Electronics 2017, 6, 3. [Google Scholar] [CrossRef] [Green Version]
- Bulygin, V.S.; Gandel, Y.V.; Nosich, A.I. Nystrom-type method in three-dimensional electromagnetic diffraction by a finite PEC rotationally symmetric surface. IEEE Trans. Antennas Propag. 2012, 60, 4710–4718. [Google Scholar] [CrossRef]
- Sukharevsky, I.O.; Shapoval, O.V.; Nosich, A.I.; Altintas, A. Validity and limitations of the median-line integral equation technique in the scattering by material strips of sub-wavelength thickness. IEEE Trans. Antennas Propag. 2014, 62, 3623–3631. [Google Scholar] [CrossRef]
- Tsalamengas, J.L. Quadrature rules for weakly singular, strongly singular, and hypersingular integrals in boundary integral equation methods. J. Computat. Phys. 2015, 303, 498–513. [Google Scholar] [CrossRef]
- Nosich, A.I. Method of analytical regularization in computational photonics. Radio Sci. 2016, 51, 1421–1430. [Google Scholar] [CrossRef]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis, 2nd ed.; Pergamon Press: Oxford, UK, 2014. [Google Scholar]
- Veliev, E.I.; Veremey, V.V. Numerical-analytical approach for the solution to the wave scattering by polygonal cylinders and flat strip structures. In Analytical and Numerical Methods in Electromagnetic Wave Theory; Hashimoto, M., Idemen, M., Tretyakov, O.A., Eds.; Science House: Tokyo, Japan, 1993. [Google Scholar]
- Bliznyuk, N.Y.; Nosich, A.I.; Khizhnyak, A.N. Accurate computation of a circular-disk printed antenna axisymmetrically excited by an electric dipole. Microw. Opt. Technol. Lett. 2000, 25, 211–216. [Google Scholar] [CrossRef]
- Losada, V.; Boix, R.R.; Medina, F. Fast and accurate algorithm for the short-pulse electromagnetic scattering from conducting circular plates buried inside a lossy dispersive halfspace. IEEE Trans. Geosci. Remote Sens. 2003, 41, 988–997. [Google Scholar] [CrossRef]
- Hongo, K.; Naqvi, Q.A. Diffraction of electromagnetic wave by disk and circular hole in a perfectly conducting plane. Prog. Electromagn. Res. 2007, 68, 113–150. [Google Scholar] [CrossRef] [Green Version]
- Lucido, M.; Panariello, G.; Schettino, F. TE scattering by arbitrarily connected conducting strips. IEEE Trans. Antennas Propag. 2009, 57, 2212–2216. [Google Scholar] [CrossRef]
- Coluccini, G.; Lucido, M.; Panariello, G. TM scattering by perfectly conducting polygonal cross-section cylinders: A new surface current density expansion retaining up to the second-order edge behavior. IEEE Trans. Antennas Propag. 2012, 60, 407–412. [Google Scholar] [CrossRef]
- Coluccini, G.; Lucido, M.; Panariello, G. Spectral domain analysis of open single and coupled microstrip lines with polygonal cross-section in bound and leaky regimes. IEEE Trans. Microw. Theory Technol. 2013, 61, 736–745. [Google Scholar] [CrossRef]
- Coluccini, G.; Lucido, M. A new high efficient analysis of the scattering by a perfectly conducting rectangular plate. IEEE Trans. Antennas Propag. 2013, 61, 2615–2622. [Google Scholar] [CrossRef]
- Lucido, M. Electromagnetic scattering by a perfectly conducting rectangular plate buried in a lossy half-space. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6368–6378. [Google Scholar] [CrossRef]
- Lucido, M.; Migliore, M.D.; Pinchera, D. A new analytically regularizing method for the analysis of the scattering by a hollow finite-length PEC circular cylinder. Prog. Electromagn. Res. B 2016, 70, 55–71. [Google Scholar] [CrossRef] [Green Version]
- Lucido, M.; Panariello, G.; Schettino, F. Scattering by a zero-thickness PEC disk: A new analytically regularizing procedure based on Helmholtz decomposition and Galerkin method. Radio Sci. 2017, 52, 2–14. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Verlag Harri Deutsch: Frankfurt, Germany, 1984. [Google Scholar]
- Chew, W.C.; Kong, J.A. Resonance of nonaxial symmetric modes in circular microstrip disk antenna. J. Math. Phys. 1980, 21, 2590–2598. [Google Scholar] [CrossRef]
- Van Bladel, J. A discussion of Helmholtz’ theorem on a surface. AEÜ 1993, 47, 131–136. [Google Scholar]
- Wilkins, J.E. Neumann series of Bessel functions. Trans. Am. Math. Soc. 1948, 64, 359–385. [Google Scholar] [CrossRef]
- Gradstein, S.; Ryzhik, I.M. Tables of Integrals, Series and Products; Academic Press: New York, NY, USA, 2000. [Google Scholar]
- Lucido, M.; Di Murro, F.; Panariello, G. Electromagnetic scattering from a zero-thickness PEC disk: A note on the Helmholtz-Galerkin analytically regularizing procedure. Prog. Electromagn. Res. Lett. 2017, 71, 7–13. [Google Scholar]
- Geng, N.; Carin, L. Wide-band electromagnetic scattering from a dielectric BOR buried in a layered lossy dispersive medium. IEEE Trans. Antennas Propag. 1999, 47, 610–619. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucido, M.; Balaban, M.V.; Dukhopelnykov, S.; Nosich, A.I. A Fast-Converging Scheme for the Electromagnetic Scattering from a Thin Dielectric Disk. Electronics 2020, 9, 1451. https://doi.org/10.3390/electronics9091451
Lucido M, Balaban MV, Dukhopelnykov S, Nosich AI. A Fast-Converging Scheme for the Electromagnetic Scattering from a Thin Dielectric Disk. Electronics. 2020; 9(9):1451. https://doi.org/10.3390/electronics9091451
Chicago/Turabian StyleLucido, Mario, Mykhaylo V. Balaban, Sergii Dukhopelnykov, and Alexander I. Nosich. 2020. "A Fast-Converging Scheme for the Electromagnetic Scattering from a Thin Dielectric Disk" Electronics 9, no. 9: 1451. https://doi.org/10.3390/electronics9091451
APA StyleLucido, M., Balaban, M. V., Dukhopelnykov, S., & Nosich, A. I. (2020). A Fast-Converging Scheme for the Electromagnetic Scattering from a Thin Dielectric Disk. Electronics, 9(9), 1451. https://doi.org/10.3390/electronics9091451







