Abstract
The multilevel fast multipole algorithm (MLFMA) using K-means clustering to accelerate electromagnetic scattering analysis for large complex targets is presented. By replacing the regular cube grouping with the K-means clustering, the addition theorem is more accurately approximated. The convergence rate of an iterative solver is thus improved significantly. However, irregular centroid locations as a result of the K-means clustering increase the amount of explicit transfer function calculations, compared with the regular cubes. In the MLFMA, a multilevel hierarchical structure is applied to the finite multipole method (FMM) to reduce transfer function calculations. Therefore, the MLFMA is suitable for applying K-means clustering. Simulation results with both canonical and realistic targets show an improvement in the computation time of the proposed algorithm.
1. Introduction
Radar cross-section (RCS) characteristics represent electromagnetic scattering phenomena of targets [1]. Radar systems recognize an unknown target based on the RCS or additional data refined from the RCS [2,3]. With the rapid progress of computational electromagnetics (CEM), diverse electromagnetic scattering problems, which could not be solved analytically previously, are solved numerically [4]. Nonetheless, the computational cost of the numerical analysis increases significantly due to a large number of unknowns regarding electrically large targets. Therefore, an acceleration of the CEM algorithm is essential to calculate the electromagnetic scattering of electrically large targets, e.g., stealth aircraft.
In the conventional numerical analysis for electromagnetic scattering problems, the method of moment (MoM) has been widely used to discretize the surface integral equations into a linear problem [5,6,7]. The linear equation is then solved by iterative solvers. In the iterative solvers, the matrix-vector product (MVP) is the most time-consuming calculation. The fast multipole method (FMM) mitigates the computational complexity of MVP from O(N2) to O(N1.5), where N is the number of basis functions [7]. The multi-level fast multipole algorithm (MLFMA) applies recursive clustering based on octree levels to the FMM to alleviate the computational complexity to O(NlogN) [8,9]. Specifically, the FMM and MLFMA classify basis functions into clusters by distance. The algorithms invoke the addition theorem to calculate mutual couplings between basis functions in far groups rapidly. Note that the MLFMA can also be used for volumetric problems including highly inhomogeneous media with O(N) complexity [10]. Another application is to solve inverse problems. Parallel versions are applied for CPU [11] and GPU [12] architectures.
Various reports have been published on the acceleration of the MLFMA for electrically large scattering problems. The preconditioner is primarily used to mitigate the condition number of the impedance matrix to improve the convergence rate in the iterative solver [4,8,13,14,15,16,17]. The diagonal preconditioner and MN preconditioner enhance the convergence rate of the electric field integral equation (EFIE) case [13,14]. In practice, some of the basis functions are expected to persist over some angular range. Thus, the current solution from the previous angle can be used as the initial guess for the next angle, and the number of iterations decreases considerably [8]. The hierarchical structure consists of the octree is customized and improved to analyze the rectangular components inside the building in the two-dimensional MLFMA [15]. The K-means clustering is applied to partition parallel hierarchical N-body interactions in the N-body simulation that can approximate the direct summation [16]. Recently, we proposed applying K-means clustering to the FMM to improve the computation time of scattering analysis [17]. By replacing the conventional cube grouping with K-means clustering [18], the addition theorem is more accurately approximated. The convergence rate of an iterative solver, which solves MVP operations in the linear equation, is thus improved significantly. Nonetheless, the K-means clustering increases the computational cost of the pre-processing of CEM due to the randomly distributed cluster centroids.
In this paper, we propose the MLFMA using K-means clustering to accelerate the scattering analysis of large complex targets. In particular, compared to the method presented by the authors in the past [17], the effectiveness of the proposed method is further increased. As a result of the K-means clustering, the locations of the cluster centroids are not regular. Entire transfer functions thus must be calculated explicitly, and the computation time is increased. Regarding the pre-processing, the MLFMA alleviates the transfer function calculations compared with the FMM using the multilevel structure. Therefore, in terms of the calculation efficiency, K-means clustering is more suitable to be applied to the MLFMA rather than the FMM. From a numerical implementation point of view, the proposed method also facilitates the convergence of the iterative solver compared with the conventional MLFMA, which uses the regular cube grouping.
This paper is organized as follows: In Section 2, the conventional MLFMA is described. Next, the proposed acceleration method is presented in Section 3. In Section 4, numerical simulations for canonical and realistic aircraft CAD models are provided to demonstrate the performance of the proposed method. Finally, Section 5 describes the conclusions.
2. Multi-Level Fast Multipole Algorithm
Electromagnetic scattering problems are solved through the two stages described below. First, unknown local currents are calculated by considering the known incident field. The EFIE for the perfect electric conductor (PEC) is defined as follows:
where r’ and n denote source points and normal vector on the PEC surface, respectively. Ei and J are defined as known incident electric field and unknown induced current, respectively. G is the Green’s function, and k is the wavenumber. Second, unknown scattered fields are then calculated based on the definition of the Green’s function. By using the MoM, the continuous calculation Equation (1) is discretized. When the Rao, Wilton, and Glisson (RWG) basis functions and Galerkin’s method are used, the EFIE is refined as a well-known linear equation [4].
Iterative methods are widely used to solve the linear equation for electrically large targets. Because the massive MVP operation is calculated per iterations, it is a dominant factor of the computational cost. The computational complexity of the MVP is O(N2) in the MoM, which uses direct calculations. In the MLFMA, the MVP operations between near clusters are computed explicitly. On the other hand, the operations between far clusters of basis functions are calculated rapidly using the multilevel and the addition theorem, as shown in Figure 1. First, basis functions distributed on the target are grouped into octree cubes. The length of the edge of the cubes at the lowest level is determined as a quarter of the wavelength [4]. Based on the location of the basis functions, the basis functions are grouped into the cube of the lowest level so that all basis functions can be included. The groups are then grouped into higher level cubes iteratively. For example, the blue cubes (lower level) are regrouped into a red cube (higher level), as shown in Figure 1.

Figure 1.
Outline of the MVP calculations in the conventional MLFMA.
Second, the MVP operation is calculated. Mutual couplings of the basis functions are aggregated into the cluster centroids at each level. The aggregated fields are then transferred and dis-aggregated to the test basis function [8]. The mutual coupling between testing functions and well-separated groups of basis functions is thus calculated as follows:
where the unit sphere integration is approximated as summation in terms of sample direction ks. The center locations of the group to which r and r’ belong are defined as a and b, respectively. TL is the transfer function, which presents interactions between groups a and b. Here, L is the number of multipole and it decides the number of sample directions S. Tbr’ and Rra are defined as the radiation and receive function, which are functions of ks, respectively. The radiation function represents the interaction from the basis function to the group it belongs to, and the receive function represents vice versa. The transfer function is approximated as follows:
where k is the unit radial vector, k is the wavenumber, Pl is a Legendre polynomial of order l, jl is the spherical Bessel function of the first kind, and is the spherical Hankel function of the second kind. The underlying addition theorem is defined as follows:
The distance between well-separated group centers is denoted as |D|. d denotes the sum of a vector from source basis function r’ to a and the vector from testing basis function r to b. The addition theorem remains valid provided that |d| < |D|. Regarding numerical implementations, the infinite number of modes is truncated into finite mode L. Where, L is determined based on the single precision criteria as follows [4,8]:
here, d denotes the length of diagonal across the bounding box cube. Note that the value of L cannot be much larger than the argument of the Hankel function in Equation (3) due to the divergence problem [4]. The accuracy of the approximation is thus dependent on the distance condition. In other words, the higher the ratio of |D| to |d|, the more accurate the approximation is.
The preconditioner concept is widely used to alleviate the condition number and facilitate the iterative solver for the linear equation [4,8]:
Although additional calculations are required to consider preconditioner M−1, the number of iterations is decreased. Therefore, the total computational cost is mitigated significantly. Regarding the EFIE case, the diagonal preconditioner is widely used [13]. It is a simple and memory-efficient method. The diagonal elements of M−1 are the reciprocal of the diagonal elements of Z.
3. Proposed Acceleration Method
3.1. Principle of the Proposed Method
In this paper, we propose to classify basis functions using K-means clustering in the pre-processing of the MLFMA. The K-means clustering process only requires location information of the elements to be grouped and the number of groups (that is K value). Other parameters including distance calculation criteria or the maximum number of iterations are optional [18]. In the proposed method, we simply set the K value to the same number as the existing octree method. In other words, the depth of the tree structure is the same as the existing method, and the number of groups is also identical to the existing method. The reason for this setting is that the previous method has been proven to be valid for the fixed length of the lowest level cube [4]. It is also for a fair comparison with the existing method. Discrete basis functions are then initially labeled to the closest cluster, which is randomly determined. The clusters are updated based on the average of the included basis functions iteratively [18]. At a higher level, the finer clusters are classified to the coarser cluster using the standard Euclidean distance between centroids, as in the lower levels [19]. Near and far clusters are then classified for all basis functions based on the distance between cluster centroids. At the finest level, when the distance is less than half the wavelength, groups are classified into near. As the level increases, the distance threshold doubles.
The ratio of |D| to |d| is increased by using the K-means clustering compared with the regular cube grouping [17]. Figure 2 compares the clustering methods of basis functions in a canonical sphere computer-aided design (CAD) model.

Figure 2.
Sliced top view of basis functions and clusters in the canonical sphere CAD model: (a) conventional cube grouping; (b) proposed K-means clustering.
In the conventional cube grouping, basis functions are subdivided into regular grid structures. The group itself and directly adjacent 26 groups (3 × 3 × 3 cubes) are then decided as the near groups. In this case, the core condition, |d| < |D|, is always satisfied. However, the ratio of |D| to |d| could be less than 2. Specifically, when each basis function belonging to each of the two cubes attached across space (closest within far groups) is located at the vertex of the cube, the ratio of |D| to |d| could be 2 over square root of 3, as shown in Figure 3. In this case, the accuracy of the addition based on the finite multipole is significantly decreased.
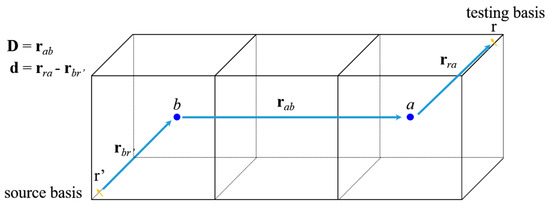
Figure 3.
The worst case when the ratio |D| to |d| is minimal in the conventional cube grouping.
On the other hand, in the K-means clustering, basis functions are evenly assigned to the clusters, which are determined randomly and iteratively based on the standard Euclidean distance criteria [18]. The ratio of |D| to |d| is thus increased, as shown in Figure 4, which compares the histograms of the ratio of |D| to |d| for 3 m radius sphere CAD model with 50,000 basis functions. The accuracy of MLFMA approximation is also increased for the numerical implementation of the truncated value of L. Although, the accurate MLFMA approximation does not always improve the condition number and the convergence rate. However, in this particular case of the numerical integration, the small error generated in the approximation is significantly magnified and the matrix can be poorly conditioned [4]. Therefore, in most cases, the convergence rate of the iterative solver is improved. The principle of the MVP calculation is the same as the existing octree method. The radiation functions between the lowest cluster centroids and the basis functions are calculated. The radiation functions are aggregated to higher levels and transferred to a group where the testing function belongs at each level using Equation (3). The received fields are dis-aggregated toward the lower level, and the received field at the lowest level is calculated by using the receive function.

Figure 4.
Histogram of the ratio |D| to |d| for each basis to basis interaction in canonical 3 m sphere CAD model.
3.2. Research on the Drawbacks of Applying K-Means Clustering
Although the iterative solver for each observation angle is accelerated using the K-means, the computational cost of the pre-processing is increased. First, the K-means requires an iterative cluster update in the clustering process. The computation time of clustering is thus increased compared with the regular cube grouping, which simply compares the location of basis functions with the centroid of clusters. The increase in the calculation time is inevitable but tolerable. For example, the clustering takes hundreds of seconds for 0.3 million basis problems on a personal computer (Intel Core i7-8700 CPU at 3.2 GHz, 64-GB RAM).
Second, the K-means requires detailed discrimination of near and far groups. In the regular cube grouping, the cube itself and its 26 adjacent cubes are assigned to the near group, and the rest are assigned to the far group. On the other hand, because of the randomness in the cluster locations, the K-means requires that the distance between all clusters are calculated and compared with the distance threshold. Nonetheless, the separation time difference is negligible.
Third, the computational cost of the transfer functions is increased in the K-means clustering. In the cube grouping, the centroid of the cube is located in a regular grid as shown in Figure 5a. Most transfer functions are duplicated because the rab vectors are the same regardless of the variable location of the cube. The transfer functions thus only require to calculate a small number of unique elements. However, the K-means requires an explicit calculation of transfer functions because clusters are randomly determined, as shown in Figure 5b. Furthermore, the transfer functions should be calculated for L multipoles and L ∙ (L + 1) samples to implement the unit sphere integral [4].

Figure 5.
Comparisons of transfer calculation scheme: (a) transfer function calculations in the regular cube grouping; (b) transfer function calculations in the K-means clustering.
In this work, we expand the previous concept, which applies K-means clustering to the FMM, to the MLFMA. Specifically, additional clustering is applied to the finest level of clusters. The coarser clusters are then determined using the locations of finer clusters. This recursive clustering is conducted until there are no far relations. The transfer functions between two groups at a distance are replaced by a coarser level of the aggregated transfer function as shown in Figure 6. The transfer function calculations are efficiently alleviated by the MLFMA. Therefore, the pre-processing, as well as the MVP operation are accelerated significantly by using the proposed method.
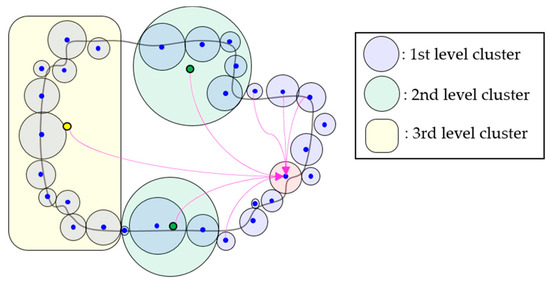
Figure 6.
Hierarchical transfer function calculations in the MLFMA.
4. Numerical Results
4.1. Comparisons between the Previous FMM with K-Means Clustering and the Proposed MLFMA with K-Means Clustering
In the context of scattering analysis, our goal is to assess how the proposed method accelerates the MLFMA. We calculate monostatic radar cross-section (RCS) and demonstrate the performance of the proposed method. In the canonical target simulation, the center frequency is 300 MHz, and the 3 m radius sphere model is composed of 0.3 million basis functions, as shown in Figure 2. We use the mesh-neighbor (MN) preconditioner [13]. In the FMM, the basis functions are classified into 2594 clusters. It thus requires six million transfer operations close to 2594 squares. However, in the MLFMA, the basis functions are classified into 2594, 572, 133, and 29 clusters in terms of multilevel. The value of L is determined based on the single-precision criteria. The MLFMA thus requires a total of 0.13 million transfer operations. Figure 7 shows that the previous and proposed methods have the same number of iterations, but the computation time is highly reduced for the MLFMA.

Figure 7.
Comparisons between the previous and proposed method for a 3 m radius sphere CAD model: (a) the number of iterations as a function of the incidence angle; (b) the computation time per iteration as a function of the incidence angle.
The key advantage that can be obtained when the K-means clustering is applied to the MLFMA is the reduction in the transfer function pre-calculation time. As shown in Figure 5, we pointed out the limitation of the rapid increase in pre-processing time in the FMM [17]. However, the MLFMA efficiently reduces the transfer function calculations by using a tree hierarchy, as shown in Figure 6. Therefore, it is a more appropriate approach to apply the K-means clustering to the MLFMA. To demonstrate efficiency, we compare the computation time of transfer function pre-calculation as a function of basis functions, as shown in Figure 8. In the canonical sphere simulation, the radius of the sphere increases from 1.0 m to 3.5 m. The number of basis functions increases from 50,000 to 400,000 in proportion to the radius. The number of multipoles (L) and groups (K) are determined using the single precision criteria. When using the existing octree clustering technique, both FMM and MLFMA require negligible pre-processing time. On the other hand, in the previously proposed method (FMM using K-means clustering), the pre-processing time increases extremely due to the transfer function pre-calculation. However, when the K-means clustering is applied to the MLFMA, which is proposed in this paper, the pre-processing time is drastically reduced.

Figure 8.
Comparisons the transfer function pre-computation time between the existing method and the proposed method as a function of the number of basis functions.
4.2. Canonical Sphere Target Simulations
We also compare the MLFMA using the existing octree grouping and K-means clustering to verify the effectiveness of the proposed method. In the canonical sphere simulation, target specifications are identical to the above canonical simulations. The number of multipoles (L) and groups (K) are determined using the single precision criteria. The number of iterations and the computation time per iterations are shown in Figure 9. Because the principle of the MVP calculation is identical, the computation time per iteration is similar. However, the number of iterations is decreased using the proposed method. Therefore, the total computation time is decreased by using the proposed MLFMA.
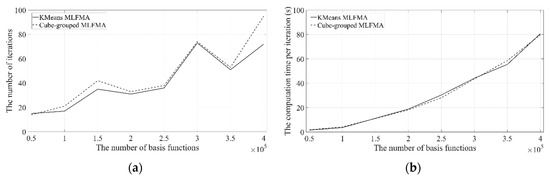
Figure 9.
Canonical sphere CAD model simulation results: (a) the number of iterations as a function of the number of basis functions; (b) the computation time per iteration as a function of the number of basis functions.
One should not ignore the comparison of the computational time required for pre-processing. We compare the computation time required for the three main pre-processing: clustering, near and far group separation, and transfer function calculation, as shown in Figure 10. Based on the results, the increase in computation time accompanying the proposed method is analyzed. Because the clustering is performed in a regular grid, overall pre-processing time is generally small in the conventional MLFMA. On the other hand, in the case of the proposed method requiring iterative clustering, the pre-processing time is rather high. Particularly, the K-means clustering time increases in proportion to the square of degree of freedom [20].

Figure 10.
The pre-processing time as a function of the number of basis functions by using the proposed K-Means MLFMA and the conventional octree MLFMA.
4.3. Realistic Stealth Target Simulations
In the realistic target simulation, the same center frequency is used and the stealth model is composed of 14,040 basis functions, as shown in Figure 11. It has dimensions of 8 m × 4 m × 1 m and is oriented at 20° azimuth and in 30° elevation. We used a bi-conjugate stabilized (BiCG-Stab) iterative solver with 3 × 10−3 residual error and 500 maximum iterations. Figure 12 shows that the conventional and proposed MLFMA present accurate RCS results. Figure 13 shows the number of iterations in the iterative solver is alleviated significantly using the proposed MLFMA with K-means clustering. Specifically, the average computation time in one direction in the conventional method and the proposed method are 229.92 s and 105.75 s, respectively. Note that, the computation time per iteration is barely changed because MVP operations in the MLFMA are equivalently calculated from the precomputed data (radiation, transfer, receive functions).
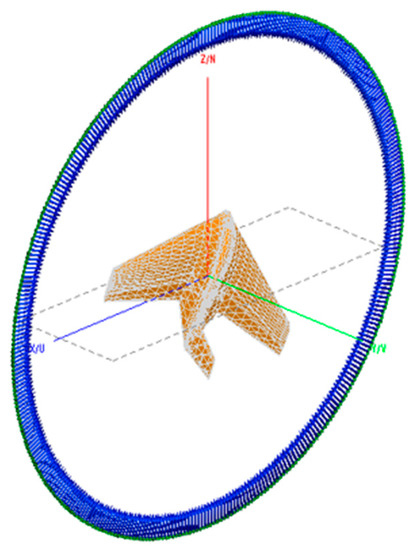
Figure 11.
Target geometry of the B-2 stealth CAD model.
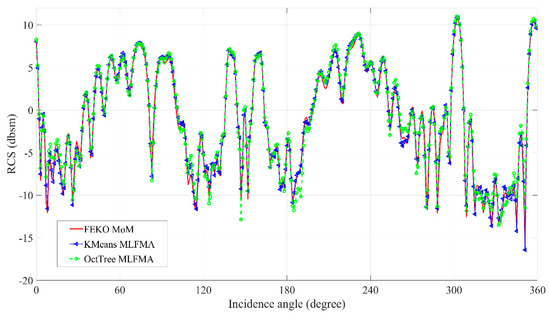
Figure 12.
Monostatic RCS results of the realistic stealth CAD model.

Figure 13.
Realistic stealth CAD model simulation results: (a) the number of iterations as a function of the number of basis functions; (b) the computation time per iteration as a function of the number of basis functions.
We also analyze the case where K-means clustering is appropriate to be applied to the MLFMA. Compared to the conventional octree clustering, the proposed method causes an increase in pre-processing time. Therefore, if multiple-angle scattering analysis is not performed, K-means clustering is not suitable for the MLFMA. In the realistic stealth case, due to the complexity of the shape, it is necessary to analyze all 360 degrees at 1 degree intervals, so the proposed method is efficient, as shown in Table 1. On the other hand, in the canonical sphere case, due to extreme symmetry, only scattering analysis at single direction is required. Table 2 shows a decrease in efficiency in the proposed method. Note that, the elapsed time to calculate the part of the impedance matrix (for near terms) is excluded from the pro-processing time.

Table 1.
Comparisons of the computation time of the conventional and proposed MLFMA for the realistic stealth CAD model.

Table 2.
Comparisons of the computation time of the conventional and proposed MLFMA for the canonical sphere CAD model with 100,000 basis functions (1-degree case).
In addition, we demonstrate another realistic target (F16 aircraft) simulation, the same center frequency is used and the aircraft model is composed of 17,859 basis functions, as shown in Figure 14. It has dimensions of 5 m × 8 m × 4 m and is oriented at 50° azimuth and in 20° elevation. We used the same iterative solver. Figure 15 shows that the proposed method agrees well with the conventional method. Figure 16a shows that the proposed method does not seem to improve the convergence rate. The reason for this result is the difference in the MVP calculation process resulting from the difference in clustering techniques. In the case of the stealth CAD, the number of near (Accurately calculated in the same way as MoM) and far terms (approximated by the MLFMA) according to the results of each clustering were similar. Due to the same number of far terms, the convergence rates of the proposed method and the conventional method could be compared equally, as shown in Figure 13. However, in this aircraft CAD, the number of near terms obtained from the K-means clustering result was only 40% of the value obtained from the octree clustering result. Therefore, the existing method with many near terms provides more accurate MVP results, resulting in a similar convergence rate. However, since the proposed method has fewer near terms, the amount of explicit calculation is less than that of the existing method, and the calculation time per iteration is reduced as shown in Figure 16b. In summary, the proposed method accelerates the MLFMA when targeting the same level of accuracy.
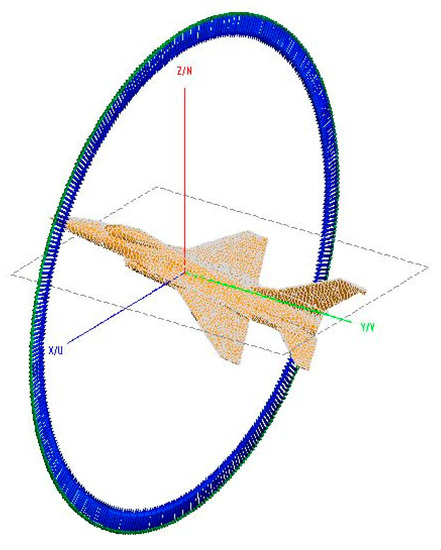
Figure 14.
Target geometry of the F16 aircraft CAD model.

Figure 15.
Monostatic RCS results of the F16 aircraft CAD model.
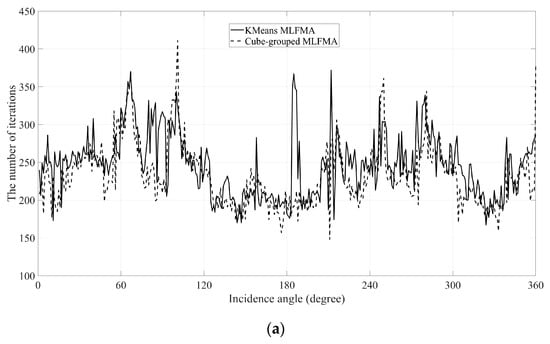

Figure 16.
F16 aircraft CAD model simulation results: (a) the number of iterations as a function of the number of basis functions; (b) the computation time per iteration as a function of the number of basis functions.
5. Conclusions
The MLFMA using K-means clustering was proposed to accelerate the scattering analysis of large complex targets. The simulation results with the realistic target presented that faster convergence of numerical results is achieved compared with the conventional cube-grouped MLFMA. Furthermore, the simulation results with the canonical target showed that the pre-processing computation time is also mitigated compared with the FMM using K-means clustering, which we previously proposed. Therefore, we demonstrate that the proposed method accelerates both pre-processing and numerical solver of the MLFMA. One should note, however, that there are cases that are not suitable for K-means clustering in MLFMA. The main drawback of the proposed method is an increase in pre-processing time. Therefore, as the number of multi-angle scattering analyzes decreases, the pre-processing time compared to the iterative scattering analysis increases, and the calculation efficiency decreases.
Author Contributions
D.-j.Y. proposed the idea and designed the demonstration process. D.-j.Y., H.J. and H.K. performed the simulations. D.-j.Y. and W.-Y.Y. wrote the manuscript. D.-W.S. revised and finalized the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Korea Research Institute of Standards and Science, grant number 2020GP2020-0009. This research was also funded by the Ministry of Science and ICT(MSIT), grant number 2020-Performance Advancement & Foundation Construction-01.
Acknowledgments
This research was supported by Development of core technologies for advanced measuring instruments funded by Korea Research Institute of Standards and Science (KRISS–2020–GP2020-0009). This research was also supported by the Commercialization Promotion Agency for R&D Outcomes(COMPA). (2020-Performance Advancement & Foundation Construction-01).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ha, J.; Shin, W.; Lee, J.H.; Kim, Y.; Kim, D.; Lee, Y.; Yook, J.G. Effect of plasma area on frequency of monostatic radar cross section reduction. J. Electromagn. Eng. Sci. 2017, 17, 153–158. [Google Scholar] [CrossRef]
- Yun, D.J.; Lee, J.I.; Bae, K.U.; Yoo, J.H.; Kwon, K.I.; Myung, N.H. Improvement in computation time of 3-D scattering center extraction using the shooting and bouncing ray technique. IEEE Trans. Antennas Propagat. 2017, 65, 4191–4199. [Google Scholar] [CrossRef]
- Wu, X.; Jin, Y. Scattering model for electrical-large target employing MLFMA and radar imaging formation. J. Electromagn. Eng. Sci. 2010, 10, 166–170. [Google Scholar] [CrossRef]
- Gibson, W.C. The Method of Moments in Electromagnetics, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007; pp. 209–253. [Google Scholar]
- Rao, S.M.; Wilton, D.R.; Glisson, A.W. Electromagnetic scattering by surfaces of arbitrary shape. IEEE Trans. Antennas Propagat. 1982, 30, 409–418. [Google Scholar] [CrossRef]
- Eibert, T.F.; Hansen, V. On the calculation of potential integrals for linear source distributions on triangular domains. IEEE Trans. Antennas Propagat. 1995, 43, 1499–1502. [Google Scholar] [CrossRef]
- Coifman, R.; Rokhlin, V.; Wandzura, S. The fast multipole method for the wave equation: A pedestrian prescription. IEEE Antennas Propagat. Mag. 1993, 35, 7–12. [Google Scholar] [CrossRef]
- Song, J.M.; Lu, C.C.; Chew, W.C. Multilevel fast multipole algorithm for electromagnetic scattering by large complex objects. IEEE Trans. Antennas Propagat. 1997, 45, 1488–1493. [Google Scholar] [CrossRef]
- Song, J.M.; Chew, W.C. Multilevel fast-multipole algorithm for solving combined field integral equations of electromagnetic scattering. Microw. Optic. Technol. Lett. 1995, 10, 14–19. [Google Scholar] [CrossRef]
- Hidayetoglu, M.; Chew, W.C. On computational complexity of the multilevel fast multipole algorithm in various dimensions. In Proceedings of the IEEE International Symposium on Antennas and Propagation (AP-S), Fajardo, Puerto Rico, 26 June–1 July 2016; pp. 1559–1560. [Google Scholar]
- Hesford, A.J.; Chew, W.C. A frequency-domain formulation of the Fréchet derivative to exploit the inherent parallelism of the distorted Born iterative method. Waves Random Complex Media 2006, 16, 495–508. [Google Scholar] [CrossRef]
- Hidayetoglu, M.; Pearson, C.; El Hajj, I.; Gurel, L.; Chew, W.C.; Hwu, W.-M. A fast and massively-parallel inverse solver for multiple-scattering tomographic image reconstruction. In Proceedings of the IEEE International Parallel and Distributed Processing Symposium (IPDPS), Vancouver, CA, USA, 21–25 May 2018; pp. 64–74. [Google Scholar]
- Xie, Y.; He, J.; Sullivan, A.; Carin, L. A simple preconditioner for electric-field integral equations. Microw. Opt. Technol. Lett. 2001, 30, 51–54. [Google Scholar] [CrossRef]
- Yun, D.J.; Kim, H.J.; Yang, S.J.; Lee, J.I.; Yang, W.Y.; Myung, N.H. Method of moment using matrix equilibration for stealth aircraft scattering analysis in VHF band. In Proceedings of the 2017 IEEE Asia Pacific Microwave Conference (APMC), Kuala Lumpur, Malaysia, 13–16 November 2017; pp. 1–3. [Google Scholar]
- Barakat, K.; Webb, J. A Clustering Algorithm for Multilevel Fast Multipole Methods. IEEE Trans. Magn. 2004, 40, 1072–1075. [Google Scholar] [CrossRef]
- Marzouk, Y.M.; Ghoniem, A.F. K-means clustering for optimal partitioning and dynamic load balancing of parallel hierarchical N-body simulations. J. Comput. Phys. 2005, 207, 493–528. [Google Scholar] [CrossRef]
- Yun, D.-J.; Jung, I.I.; Jung, H.; Kang, H.; Yang, W.-Y.; Park, I.Y. Improvement in Computation Time of the Finite Multipole Method by Using K-Means Clustering. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1814–1817. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.; Netanyahu, N.; Piatko, C.; Silverman, R.; Wu, A. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Czink, N.; Cera, P.; Salo, J.; Bonek, E.; Nuutinen, J.-P.; Ylitalo, J. Improving clustering performance using multipath component distance. Electron. Lett. 2006, 42, 33. [Google Scholar] [CrossRef]
- Pakhira, M.K. A linear time-complexity k-means algorithm using cluster shifting. In Proceedings of the IEEE International Conference on Computational Intelligence and Communication Networks (CICN), Bhopal, India, 14–16 November 2014; pp. 1047–1051. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).