Backhaul-Aware Dimensioning and Planning of Millimeter-Wave Small Cell Networks
Abstract
1. Introduction
2. System Model and Problem Description
2.1. System Model
2.2. Problem Description
3. Proposed Dimensioning and Planning Algorithm
| Algorithm 1 CEBA dimensioning and planning algorithm | |
| Input: initial solution: q0 = [x, zSC], BS,0; zMC, BM,0, Du, NS, α, β | |
| 1: | initialize q ← q0, BS ← BS,0 |
| 2: | while constraints in (11) or (12) are not met |
| 3: | add a new SC, |BS| ← |BS| + 1 |
| 4: | use k-means to partition ω = (cx, cy, F(dx,y)) in |BS| clusters and obtain centroids sb, b ∈ BS |
| 5: | optimize sb by applying the steepest-ascent method n times to the function F(dx,y) |
| 6: | select |BS,0| elements b ∈ BS having the smallest dE (sb, sb0) and replace them by b0 ∈ BS,0, BS,0 ⊂ BS; update sb, zSC |
| 7: | assign BH node to each b ∈ BS: hb = argc max pcRX with c ∈ BM and sb ∈ ScLOS; if not possible, try with c ∈ BS only if c has LOS BH with 1-hop link; update x |
| 8: | if ∃ b ∈ BS | b has NLOS BH or b does not satisfy (14) then |
| 9: | execute Algorithm 2, backhaul-aware optimization |
| 10: | end if |
| 11: | end while |
| Output: optimized q and BS | |
| Algorithm 2 Backhaul-aware optimization algorithm | |
| Input: q = [x, zSC], B, {sb}, NS | |
| 1: | forb ∈ BS |
| 2: | if b has NLOS BH then |
| 3: | create a set C of candidate BH nodes: C ← B\{b, nodes with NLOS BH or 2-hop BH link} |
| 4: | for c ∈ C |
| 5: | given the locations scLOS ∈ ScLOS having LOS with c, calculate: = argmin dE (sb,) |
| 6: | end for |
| 7: | set BH node for b: hb = argc min dE (sb,), update x |
| 8: | set location: sb =, update zSC |
| 9: | end if |
| 10: | end for |
| 11: | forb ∈ BS |
| 12: | if constraint in (14) is not met for b then |
| 13: | create a set G of SCs backhauled by b |
| 14: | for g ∈ G |
| 15: | create a set C of candidate BH nodes: C ← B\{b,g, nodes with NLOS BH or 2-hop BH link} |
| 16: | for c ∈ C |
| 17: | given the locations scLOS ∈ ScLOS having LOS with c, calculate: = argmin dE (sg,) |
| 18: | end for |
| 19: | calculate: hg = argc min dE (sg,), rg = dE (sg,) |
| 20: | end for |
| 21: | sort g ∈ G by rg in descending order with new index g’ |
| 22: | for g’ ∈ G |
| 23: | if constraint in Equation (14) is met for hg’ then |
| 24: | set sg’ =, update zSC |
| 25: | set hg’ as BH node for g’, update x |
| 26: | end if |
| 27: | if constraint in (14) is met for b then |
| 28: | break |
| 29: | end if |
| 30: | end for |
| 31: | end if |
| 32: | end for |
4. Performance Evaluation
4.1. Simulation Scenario and Setup
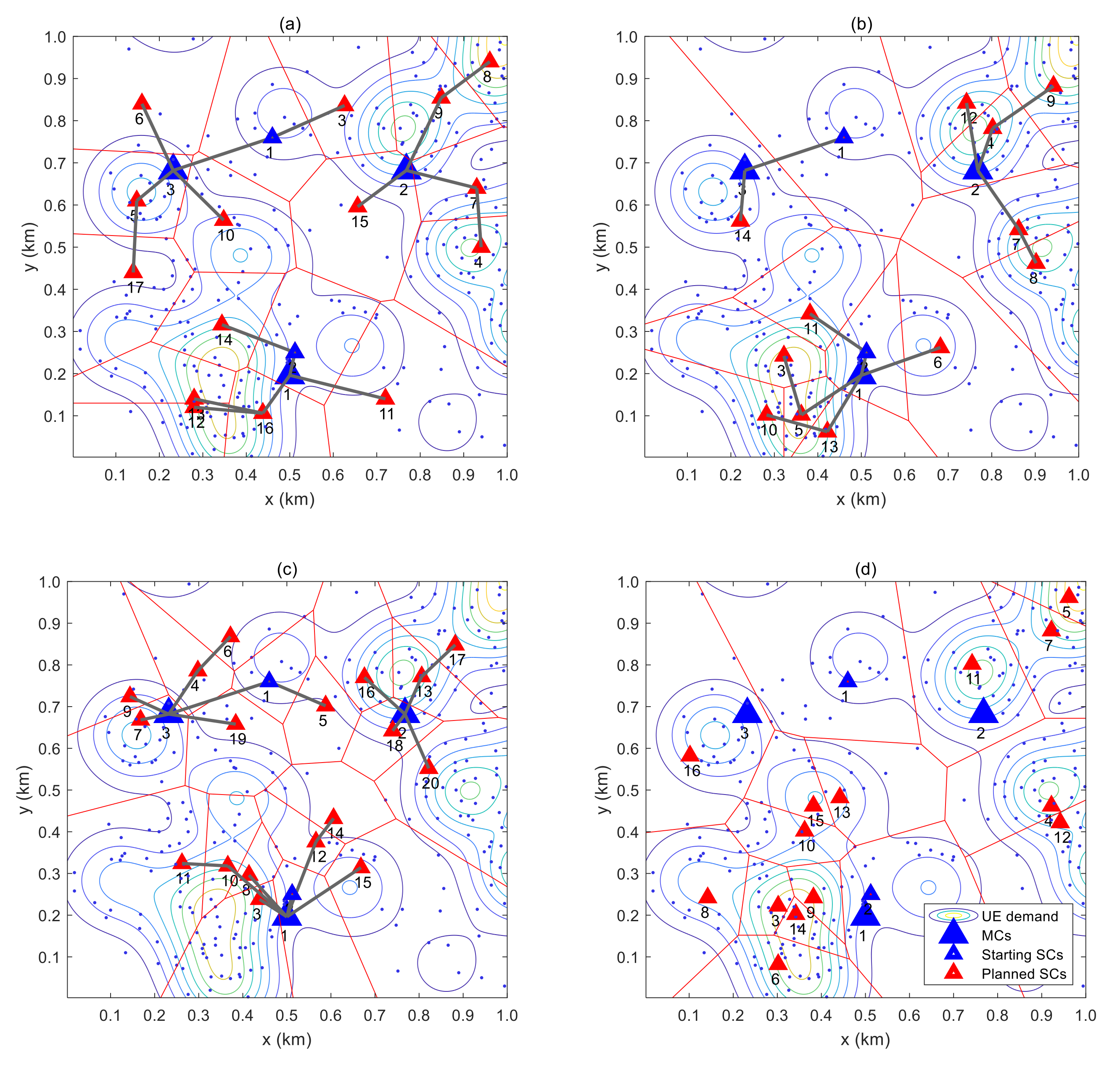
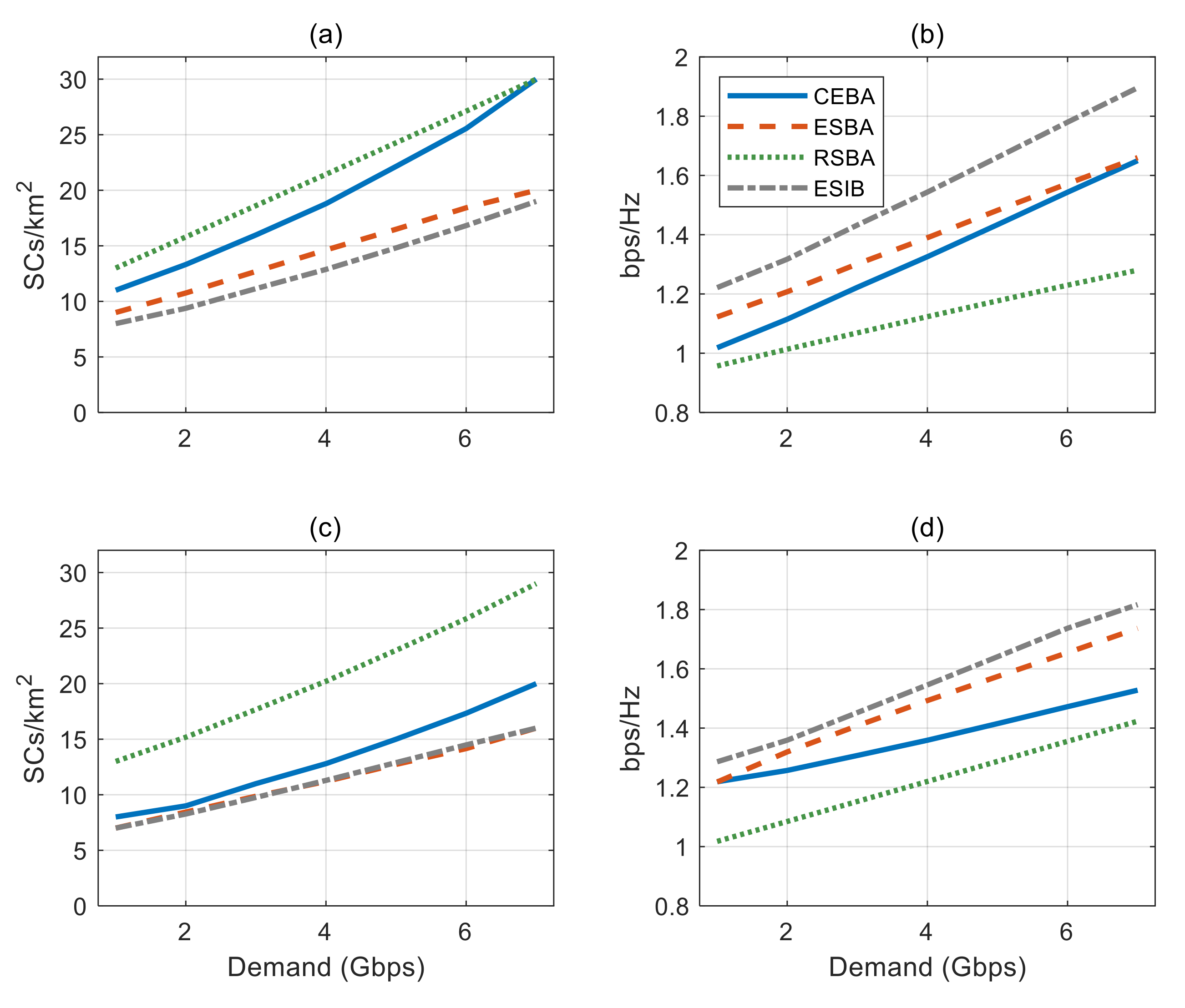
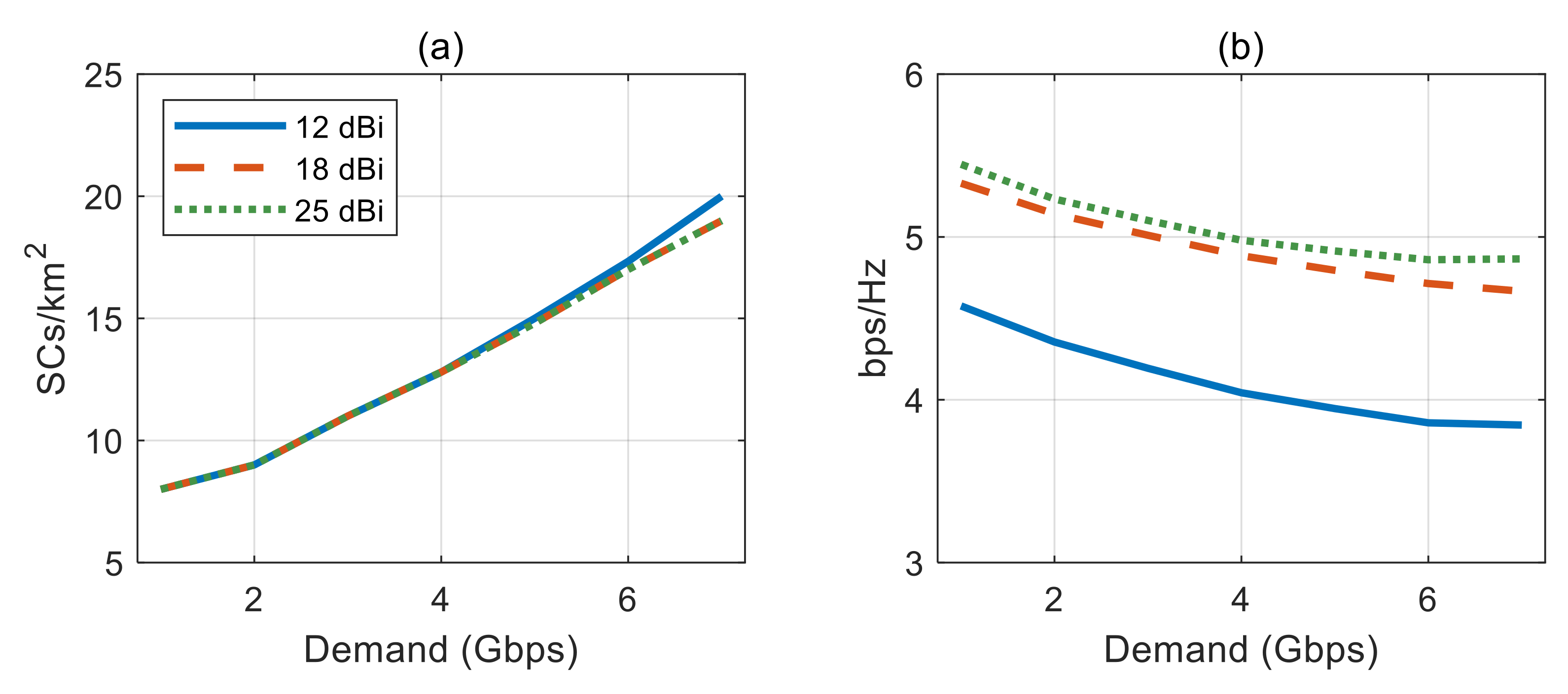
4.2. Simulation Results and Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mitra, R.N.; Agrawal, D.P. 5G mobile technology: A survey. Ict Express 2015, 1, 132–137. [Google Scholar] [CrossRef]
- Siddiqi, M.A.; Yu, H.; Joung, J. 5G Ultra-Reliable Low-Latency Communication Implementation Challenges and Operational Issues with IoT Devices. Electronics 2019, 8, 981. [Google Scholar] [CrossRef]
- GSMA. Road to 5G Introduction and Migration. In White Paper; GSM Association: London, UK, 2018; Available online: https://www.gsma.com/futurenetworks/wp-content/uploads/2018/04/Road-to-5G-Introduction-and-Migration_FINAL.pdf (accessed on 23 August 2020).
- GSMA. Mobile backhaul options. Spectrum analysis and recommendations. In White Paper; GSM Association: London, UK, 2018; Available online: https://www.gsma.com/spectrum/wp-content/uploads/2019/04/Mobile-Backhaul-Options.pdf (accessed on 23 August 2020).
- Xiao, K.; Li, W.; Kadoch, M.; Li, C. On the Secrecy Capacity of 5G MmWave Small Cell Networks. IEEE Wirel. Commun. 2018, 25, 47–51. [Google Scholar] [CrossRef]
- Okasaka, S.; Weiler, R.J.; Keusgen, W.; Pudeyev, A.; Maltsev, A.; Karls, I.; Sakaguchi, K. Proof-of-Concept of a Millimeter-Wave Integrated Heterogeneous Network for 5G Cellular. Sensors 2016, 16, 1362. [Google Scholar] [CrossRef] [PubMed]
- Rezaabad, A.L.; Beyranvand, H.; Salehi, J.A.; Maier, M. Ultra-Dense 5G Small Cell Deployment for Fiber and Wireless Backhaul-Aware Infrastructures. IEEE Trans. Veh. Technol. 2018, 67, 12231–12243. [Google Scholar] [CrossRef]
- Feng, W.; Li, Y.; Jin, D.; Su, L.; Chen, S. Millimetre-Wave Backhaul for 5G Networks: Challenges and Solutions. Sensors 2016, 16, 892. [Google Scholar] [CrossRef] [PubMed]
- Saha, C.; Dhillon, H.S. Millimeter Wave Integrated Access and Backhaul in 5G: Performance Analysis and Design Insights. IEEE J. Sel. Areas Commun. 2019, 37, 2669–2684. [Google Scholar] [CrossRef]
- Song, X.; Hälsig, T.; Cvetkovski, D.; Rave, W.; Lankl, B.; Grass, E.; Fettweis, G. Design and Experimental Evaluation of Equalization Algorithms for Line-of-Sight Spatial Multiplexing at 60 GHz. IEEE J. Sel. Areas Commun. 2018, 36, 2570–2580. [Google Scholar] [CrossRef]
- Chataut, R.; Akl, R. Massive MIMO Systems for 5G and beyond Networks—Overview, Recent Trends, Challenges, and Future Research Direction. Sensors 2020, 20, 2753. [Google Scholar] [CrossRef] [PubMed]
- Gkonis, P.K.; Trakadas, P.T.; Kaklamani, D.I. A Comprehensive Study on Simulation Techniques for 5G Networks: State of the Art Results, Analysis, and Future Challenges. Electronics 2020, 9, 468. [Google Scholar] [CrossRef]
- Busari, S.A.; Huq, K.M.S.; Mumtaz, S.; Dai, L.; Rodriguez, J. Millimeter-Wave Massive MIMO Communication for Future Wireless Systems: A Survey. IEEE Commun. Surv. Tutor. 2018, 20, 836–869. [Google Scholar] [CrossRef]
- Ghazzai, H.; Yaacoub, E.; Alouini, M.S.; Dawy, Z.; Abu-Dayya, A. Optimized LTE cell planning with varying spatial and temporal user densities. IEEE Trans. Veh. Technol. 2016, 65, 1575–1589. [Google Scholar] [CrossRef]
- Yaacoub, E.; Dawy, Z. LTE radio network planning with HetNets: BS placement optimization using simulated annealing. In Proceedings of the 17th IEEE Mediterranean Electrotechnical Conference, Beirut, Lebanon, 13–16 April 2014; pp. 327–333. [Google Scholar] [CrossRef]
- Son, K.; Oh, E.; Krishnamachari, B. Energy-efficient design of heterogeneous cellular networks from deployment to operation. Comput. Netw. 2015, 78, 95–106. [Google Scholar] [CrossRef]
- Ganame, H.; Yingzhuang, L.; Ghazzai, H.; Kamissoko, D. 5G Base Station Deployment Perspectives in Millimeter Wave Frequencies Using Meta-Heuristic Algorithms. Electronics 2019, 8, 1318. [Google Scholar] [CrossRef]
- Athanasiadou, G.E.; Fytampanis, P.; Zarbouti, D.A.; Tsoulos, G.V.; Gkonis, P.K.; Kaklamani, D.I. Radio Network Planning towards 5G mmWave Standalone Small-Cell Architectures. Electronics 2020, 9, 339. [Google Scholar] [CrossRef]
- Soorki, M.N.; Saad, W.; Bennis, M. Optimized Deployment of Millimeter Wave Networks for In-Venue Regions with Stochastic Users’ Orientation. IEEE Trans. Wirel. Commun. 2019, 18, 5037–5049. [Google Scholar] [CrossRef]
- Tonini, F.; Fiorani, M.; Raffaelli, C.; Wosinska, L.; Monti, P. Benefits of joint planning of small cells and fiber backhaul in 5G dense cellular networks. In Proceedings of the IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, X.; Saad, W.; Zhang, X.; Xu, X.; Zhou, S. Joint Deployment of Small Cells and Wireless Backhaul Links in Next-Generation Networks. IEEE Commun. Lett. 2015, 19, 2250–2253. [Google Scholar] [CrossRef]
- Mesodiakaki, A.; Kassler, A.; Zola, E.; Ferndahl, M.; Cai, T. Energy efficient line-of-sight millimeter wave small cell backhaul: 60, 70, 80 or 140 GHz? In Proceedings of the IEEE 17th International Symposium on A World of Wireless, Mobile and Multimedia Networks (WoWMoM), Coimbra, Portugal, 21–24 June 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Bonfante, A.; Giordano, L.G.; López-Pérez, D.; Garcia-Rodriguez, A.; Geraci, G.; Baracca, P.; Butt, M.M.; Marchetti, N. 5G Massive MIMO Architectures: Self-Backhauled Small Cells Versus Direct Access. IEEE Trans. Veh. Technol. 2019, 68, 10003–10017. [Google Scholar] [CrossRef]
- Kwon, G.; Park, H. Joint User Association and Beamforming Design for Millimeter Wave UDN with Wireless Backhaul. IEEE J. Sel. Areas Commun. 2019, 37, 2653–2668. [Google Scholar] [CrossRef]
- Łukowa, A.; Venkatasubramanian, V. Dynamic In-band Self-backhauling for 5G Systems with Inter-Cell Resource Coordination. Int. J. Wirel. Inf. Netw. 2019, 26, 319–330. [Google Scholar] [CrossRef]
- Saadat, S.; Chen, D.; Jiang, T. Multipath multihop mmWave backhaul in ultra-dense small-cell network. Digit. Commun. Netw. 2018, 4, 111–117. [Google Scholar] [CrossRef]
- Tran, G.K.; Santos, R.; Ogawa, H.; Nakamura, M.; Sakaguchi, K.; Kassler, A. Context-Based Dynamic Meshed Backhaul Construction for 5G Heterogeneous Networks. J. Sens. Actuator Netw. 2018, 7, 43. [Google Scholar] [CrossRef]
- Marabissi, D.; Fantacci, R.; Simoncini, L. SDN-Based Routing for Backhauling in Ultra-Dense Networks. J. Sens. Actuator Netw. 2019, 8, 23. [Google Scholar] [CrossRef]
- Semiari, O.; Saad, W.; Bennis, M.; Dawy, Z. Inter-Operator Resource Management for Millimeter Wave Multi-Hop Backhaul Networks. IEEE Trans. Wirel. Commun. 2017, 16, 5258–5272. [Google Scholar] [CrossRef]
- Almohamad, A.; Hasna, M.O.; Khattab, T.; Haouari, M. An Efficient Algorithm for Dense Network Flow Maximization with Multihop Backhauling and NFPs. In Proceedings of the IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Hong, J.; Park, J.; Beak, S. Millimeter-Wave-Based Cooperative Backhaul for a Mobile Station in an X-Haul Network. IEEE Syst. J. 2019, 13, 2500–2506. [Google Scholar] [CrossRef]
- Muñoz, P.; Sallent, O.; Pérez-Romero, J. Self-Dimensioning and Planning of Small Cell Capacity in Multitenant 5G Networks. IEEE Trans. Veh. Technol. 2018, 67, 4552–4564. [Google Scholar] [CrossRef]
- Quadri, C.; Premoli, M.; Ceselli, A.; Gaito, S.; Rossi, G.P. Optimal Assignment Plan in Sliced Backhaul Networks. IEEE Access 2020, 8, 68983–69002. [Google Scholar] [CrossRef]
- 3GPP. Study on New Radio Access Technology: Radio Frequency (RF) and Co-existence Aspects, version 14.2.0; TR 38.803; European Telecommunications Standards Institute: Valbonne, France, 2017. [Google Scholar]
- Singh, S.; Kulkarni, M.N.; Ghosh, A.; Andrews, J.G. Tractable Model for Rate in Self-Backhauled Millimeter Wave Cellular Networks. IEEE J. Sel. Areas Commun. 2015, 33, 2196–2211. [Google Scholar] [CrossRef]
- 3GPP. Study on Channel Model for Frequencies from 0.5 to 100 GHz, version 15.0.0; TR 38.901; European Telecommunications Standards Institute: Valbonne, France, 2018. [Google Scholar]
- Yuan, Y. LTE-Advanced Relay Technology and Standardization; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ju, S.; Rappaport, T.S. Simulating Motion–Incorporating Spatial Consistency into NYUSIM Channel Model. In Proceedings of the IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Hilt, A. Availability and Fade Margin Calculations for 5G Microwave and Millimeter-Wave Anyhaul Links. Appl. Sci. 2019, 9, 5240. [Google Scholar] [CrossRef]
| Parameter | Access | BH |
|---|---|---|
| Operating frequency (GHz) | MC: 5 SC: 60 | 60 |
| Cell bandwidth (MHz) | MC: 100 SC: 250–1000 | 1000 |
| Propagation—path loss | 3GPP model [36] | 3GPP model [36] |
| MC antenna gain (dBi) | 12 | [12,13,14,15,16,17,18,19,20,21,22,23,24,25] |
| SC antenna gain (dBi) | 10 | [12,13,14,15,16,17,18,19,20,21,22,23,24,25] |
| MC transmit power (dBm) | 43 | 33 |
| SC transmit power (dBm) | 25–33 | 30 |
| Antenna height (m) | UE: 1.5, MC: 25, SC: 12 | MC: 25, SC: 12 |
| UE service demand (Mbps) | 20 | - |
| Number of demand realizations | 100 | 100 |
| Method | Traffic Demand [Gbps] | |||
|---|---|---|---|---|
| 1.0 | 3.0 | 5.0 | 7.0 | |
| CEBA | 13.6 | 41.0 | 56.3 | 197.5 |
| ESBA | 123.1 | 381.7 | 813.2 | 1444.3 |
| RSBA | 4.1 | 12.3 | 30.5 | 53.9 |
| ESIB | 150.0 | 419.4 | 771.1 | 1709.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz, P.; Adamuz-Hinojosa, O.; Ameigeiras, P.; Navarro-Ortiz, J.; Ramos-Muñoz, J.J. Backhaul-Aware Dimensioning and Planning of Millimeter-Wave Small Cell Networks. Electronics 2020, 9, 1429. https://doi.org/10.3390/electronics9091429
Muñoz P, Adamuz-Hinojosa O, Ameigeiras P, Navarro-Ortiz J, Ramos-Muñoz JJ. Backhaul-Aware Dimensioning and Planning of Millimeter-Wave Small Cell Networks. Electronics. 2020; 9(9):1429. https://doi.org/10.3390/electronics9091429
Chicago/Turabian StyleMuñoz, Pablo, Oscar Adamuz-Hinojosa, Pablo Ameigeiras, Jorge Navarro-Ortiz, and Juan J. Ramos-Muñoz. 2020. "Backhaul-Aware Dimensioning and Planning of Millimeter-Wave Small Cell Networks" Electronics 9, no. 9: 1429. https://doi.org/10.3390/electronics9091429
APA StyleMuñoz, P., Adamuz-Hinojosa, O., Ameigeiras, P., Navarro-Ortiz, J., & Ramos-Muñoz, J. J. (2020). Backhaul-Aware Dimensioning and Planning of Millimeter-Wave Small Cell Networks. Electronics, 9(9), 1429. https://doi.org/10.3390/electronics9091429







