1. Introduction
The study, development, and applications of bidirectional power converters are gaining a lot of attention due to their vital role in areas like renewable energy systems, DC microgrids, hybrid energy storage systems, smart mobility, etc. A bidirectional DC-DC converter (BDC) allows power flow in both directions. This functionality is not available in a traditional unidirectional DC-DC converter. Because of this flexibility, BDCs are widely used in several applications, such as battery-powered electric vehicles (BEVs) or hybrid electric vehicles (HEVs), power trains, uninterruptable power supplies (UPS), smart grids, charging stations for BEVs and plug-in hybrid electric vehicles (PHEV), aerospace, defense, aerospace, and non-conventional energy sources such as photovoltaic (PV) arrays, fuel cells (FCs), and wind turbines. Specifically, BDCs are widely adopted by the electric vehicle industry to achieve objectives, such as battery charging/discharging and energy recovery during regeneration modes of operation in electric vehicles. In case of the BEVs, electric energy needs to flow in both directions, i.e., from the motor to the battery and vice versa in regenerative mode. To avoid pollutant emissions, the electric vehicle must be powered only by batteries or other electrical sources (fuel cells, solar panels, etc.) [
1,
2,
3,
4]. In all the above-mentioned applications, a BDC is preferred for saving space by eliminating a separate boost and buck converter. A BDC can offer some benefits, like cost reduction, improved power density, and effective utilization of the converter [
4].
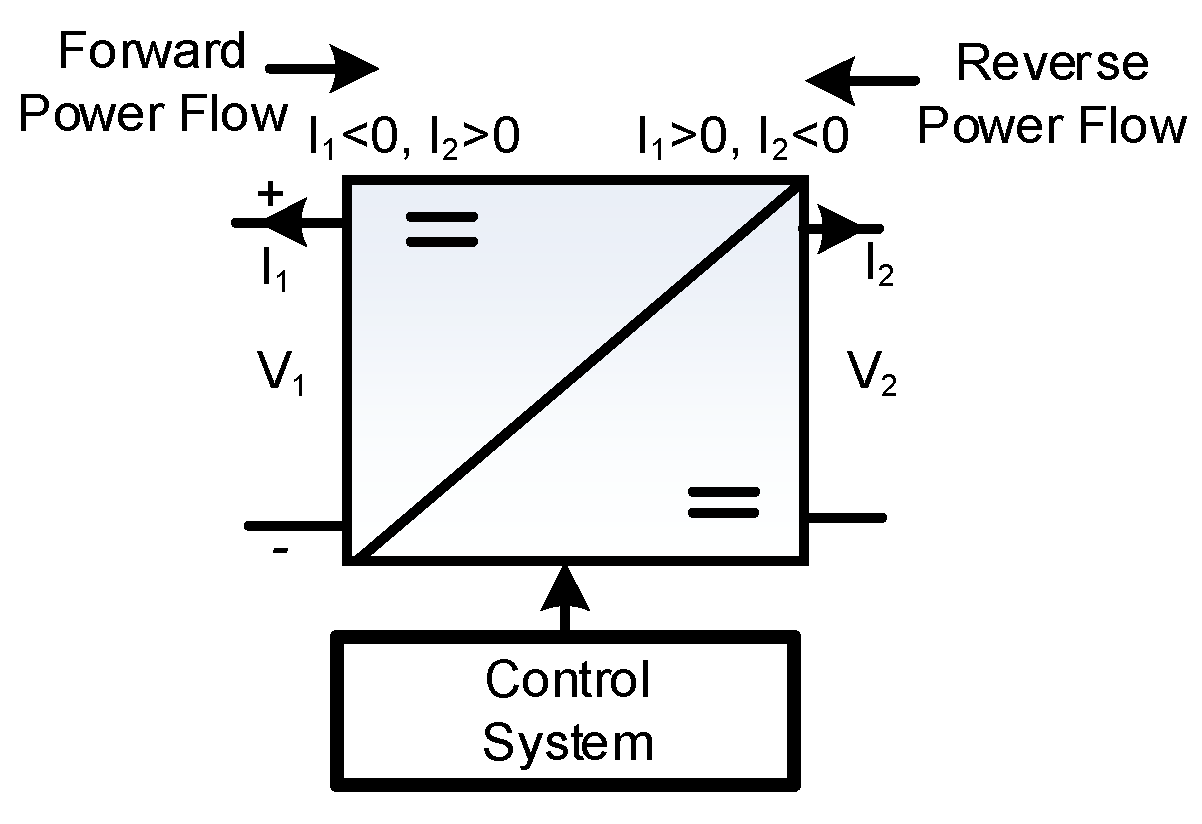
Figure 1 shows the typical structure of the bidirectional DC–DC converters. The BDC, shown in
Figure 2, helps to enhance the system efficiency and performance by interfacing with power and energy storage devices [
5]. It also avoids a couple of individual unidirectional converters for achieving bidirectional power flow. The BDC’s mode of operation (buck or boost) is mainly decided by power flow direction and voltage levels of sources/energy storage elements. Accordingly, the controller must be designed to regulate the voltage/current of the system. While designing DC–DC converters, the main functional objectives are high power density and high efficiency. The high density can be achieved by increasing the switching frequency [
6] due to the reduction in reactive components size. However, the problem is that increasing the switching frequency increases the switching losses, which leads to efficiency reduction. This problem can be addressed by adopting wide-bandgap power devices along with suitable gate drivers instead of conventional Si devices.
In general, conventional step-up DC–DC converters are classified into isolated and non-isolated converters. Isolated converters like fly-back, push–pull, forward, half-bridge, and full-bridge converters have a high voltage gain by keeping a high enough transformer turns ratio. However, there is a problem with voltage spikes due to transformer leakage inductance, which leads to high power losses across the switch. On the other hand, in non-isolated converters, a high duty cycle is required to get a high voltage gain, which leads to decreasing efficiency due to reverse recovery problems [
7]. In addition, non-isolated converters also have the problem of voltage stress nearly equal to the output voltage, causing a reduction of the device’s reliability. Many DC–DC converter topologies are introduced to mitigate the problems mentioned above, such as interleaving topologies for the reduction of current ripple [
8,
9], soft-switching techniques to mitigate voltage spikes and efficiency improvement [
10], and cascading boost converters [
11] and incorporating a coupled inductor [
12] in the conventional boost topology to get a high conversion gain. Input current ripples are reduced with the help of an interleaving concept, which leads to improving the source life. Additionally, it offers the flexibility of current sharing to enhance the power handling capacity [
8,
9].
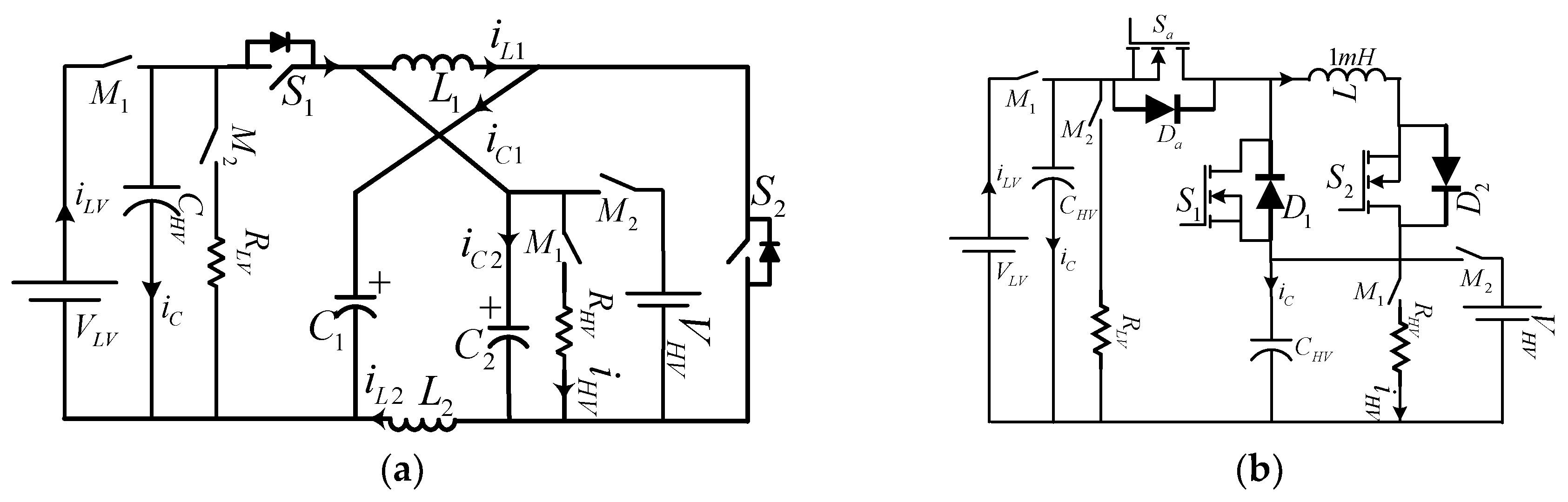
On the other hand, several other converter topologies are suggested in the literature; most of these are designed to meet the various objectives, such as reliability, capacitor voltage reduction, and input current ripple reductions, by placing an impedance network between input DC source and switching network in various fashions. An X-shaped LC impedance network, as shown in
Figure 3a, is placed to get the voltage boosting capability by operating a switching network in the shoot-through mode [
13]. As an alternative to the Z-source converter, the same authors proposed a quasi Z-source (qZS) converter in two variants based on input current, namely continuous input current q-ZS (qZS-CC) and discontinuous input current q-ZS (qZS-DC) [
14,
15] with a reduced current and capacitor voltage stresses, respectively. The main variation between these two topologies is the input side inductor connection with the supply. In case of qZS-CC, the inductor is placed directly in series with the source, and it tries to always maintain constant input current, whereas the source current is of discontinuous nature in the case of qZS-DC, which increases the stress on the source [
15]. Later, Yu Tang et al. proposed an improved Z-source (IZS) converter [
16] with reduced capacitor stresses. In this paper, the authors claim that the utilization of a low voltage capacitor reduces the inrush current, the resonance between the Z-source inductor and capacitors, and the cost and volume of the system compared to a conventional Z-source converter [
17]. The switched boost converter is proposed with a reduced passive components count, achieved by replacing one pair of LCs with power semi-conductor devices to have the same kind of buck-boost conversion, as shown in
Figure 3b [
18]. However, this topology uses more power semiconductor devices compared to the topologies mentioned above.
A SL-ZS converter is proposed with an enhanced gain by placing switched inductors instead of inductors in the impedance network [
19]. However, this topology suffers from a large component count (six power diodes and two inductors higher than the ZS converter) in the switching network. Alternatively, the SL-qZS converter proposed in [
20], consists of switched inductors in place of standard inductors in the qZS converter to reduce the capacitor voltage and startup inrush current compared to the SL-ZS converter. However, the downside of this topology is a higher component count. Hossein Fathi et al. [
21] proposed an enhanced boost ZS converter (EB-ZSC), achieved by replacing the impedance network with switched impedance to enhance the conversion gain further. Although this topology increases gain, it suffers from a higher component count (four inductors, four capacitors, and five power diodes). Additionally, this topology suffers from the usage of sophisticated control platforms to achieve smoother voltage control in the case of adjustable speed-controlled drive applications. Moreover, with a similar concept of variations in the impedance network either in ZS or qZS as discussed above, there are several other impedance source topologies, such as a diode-assisted qZS (DA-qZS) converter [
22], a capacitor-assisted qZS (CS-qZS) converter [
22], and an enhanced boost quasi ZS (EB-qZS) converter [
23], which are proposed in the literature. Though these topologies are mainly proposed for DC–AC power conversion applications due to high reliability (operation during shoot-through mode), they are equally applicable for bi-directional applications and are widely used in micro/nano-grid applications [
18,
23].
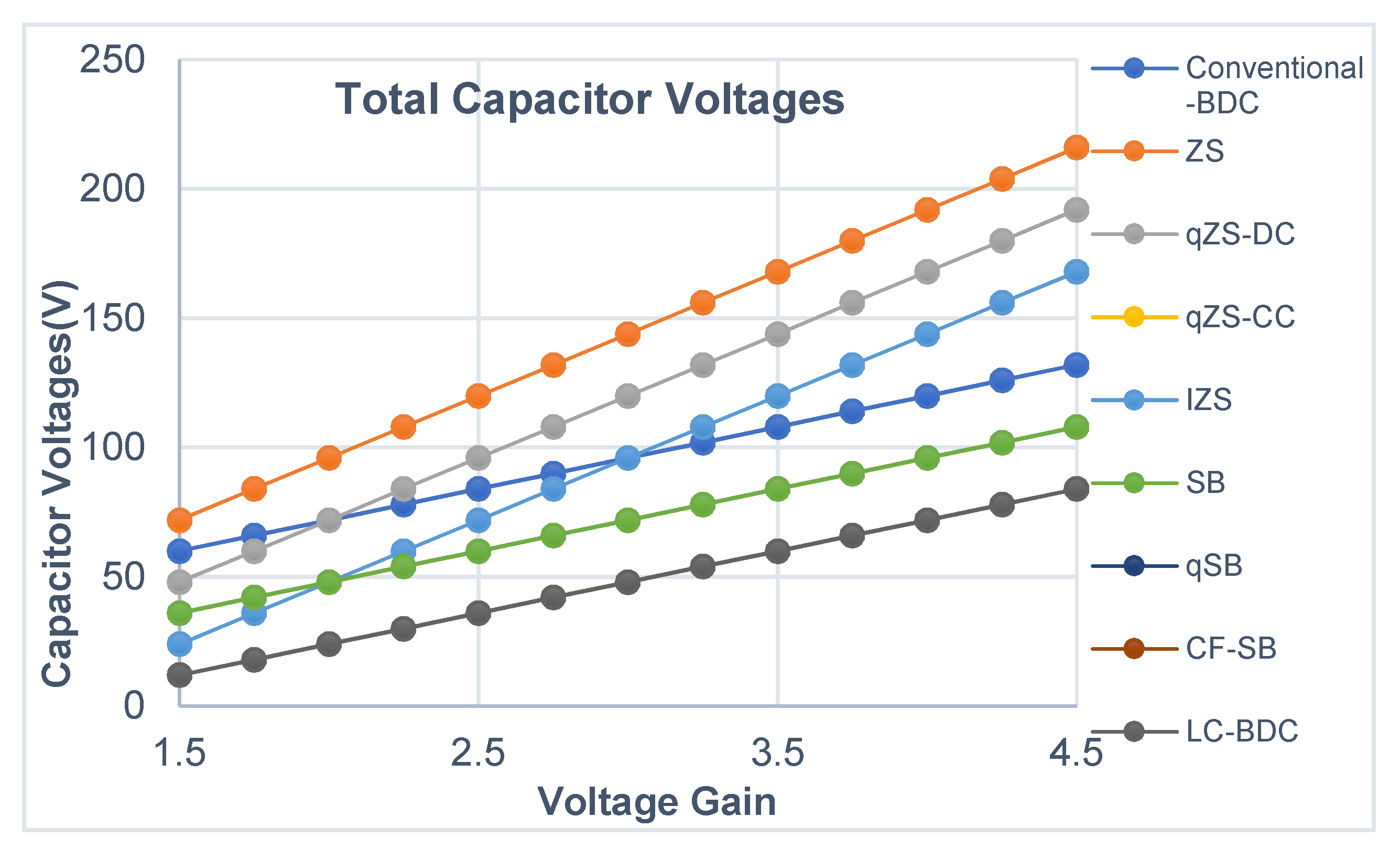
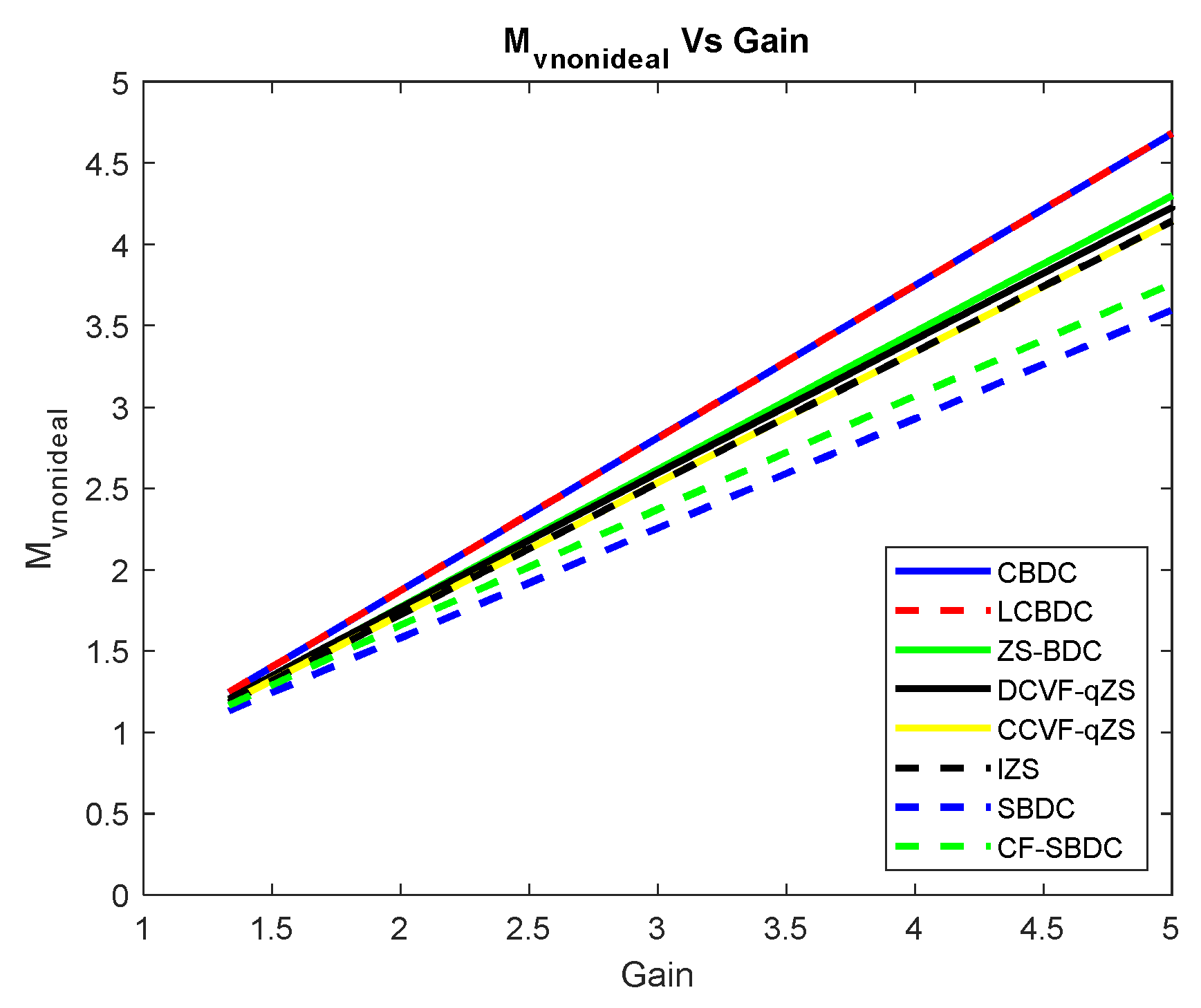
For most of these topologies, it has been suggested to incorporate switched-inductor, switched-capacitor, and hybrid switched-capacitor/switched-inductor structures resulting in high boosting factors. However, the effect of nonlinearity can be increased by increasing the energy storage elements in the circuit, which leads to a higher output current and voltage distortion [
24]. Additionally, introducing more energy storage elements in the circuit affects the control complexity, total cost, size, volume, losses, and weight of the converter [
25,
26]. Moreover, these topologies are suffering from the usage of more capacitors and higher capacitor voltage stresses. Additionally, the voltage across most of the capacitors is generally more than the supply voltage in the case of impedance source topologies in order to perform the voltage boost functionality. Hence, high-voltage Z-capacitors should be used, which may increase the volume and system cost. Capacitors are prone to failure in the field operation of power electronic converters [
27]. Hence, due to the stricter reliability constraints brought by aerospace, automotive, defense, space, and energy industries, the stresses and usage of capacitors should be reduced to enhance the converter’s reliability [
28]. Therefore, to enhance the life and converter reliability, either reduction in capacitors usage or voltage stresses on the capacitor is highly recommended [
29,
30].
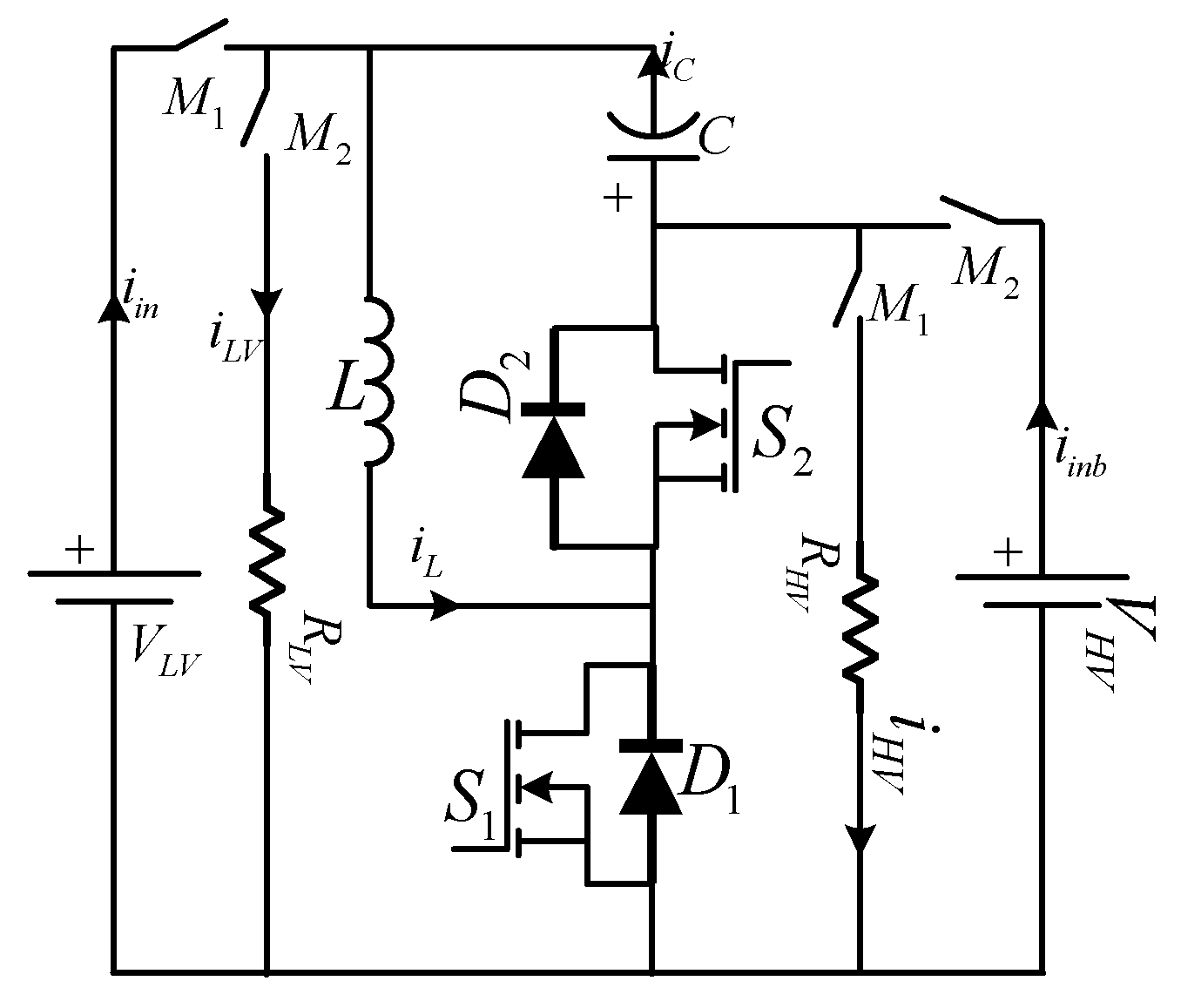
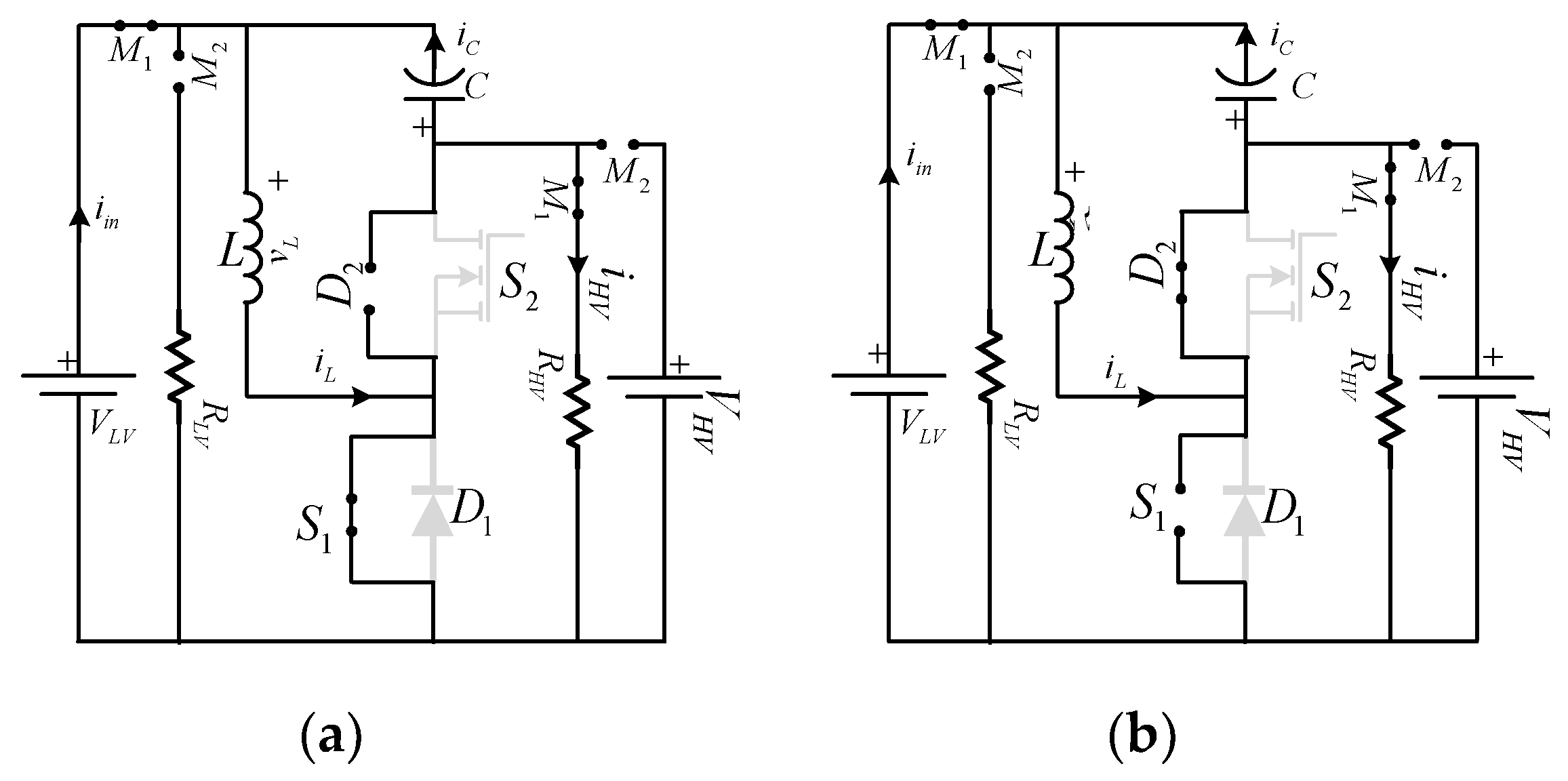
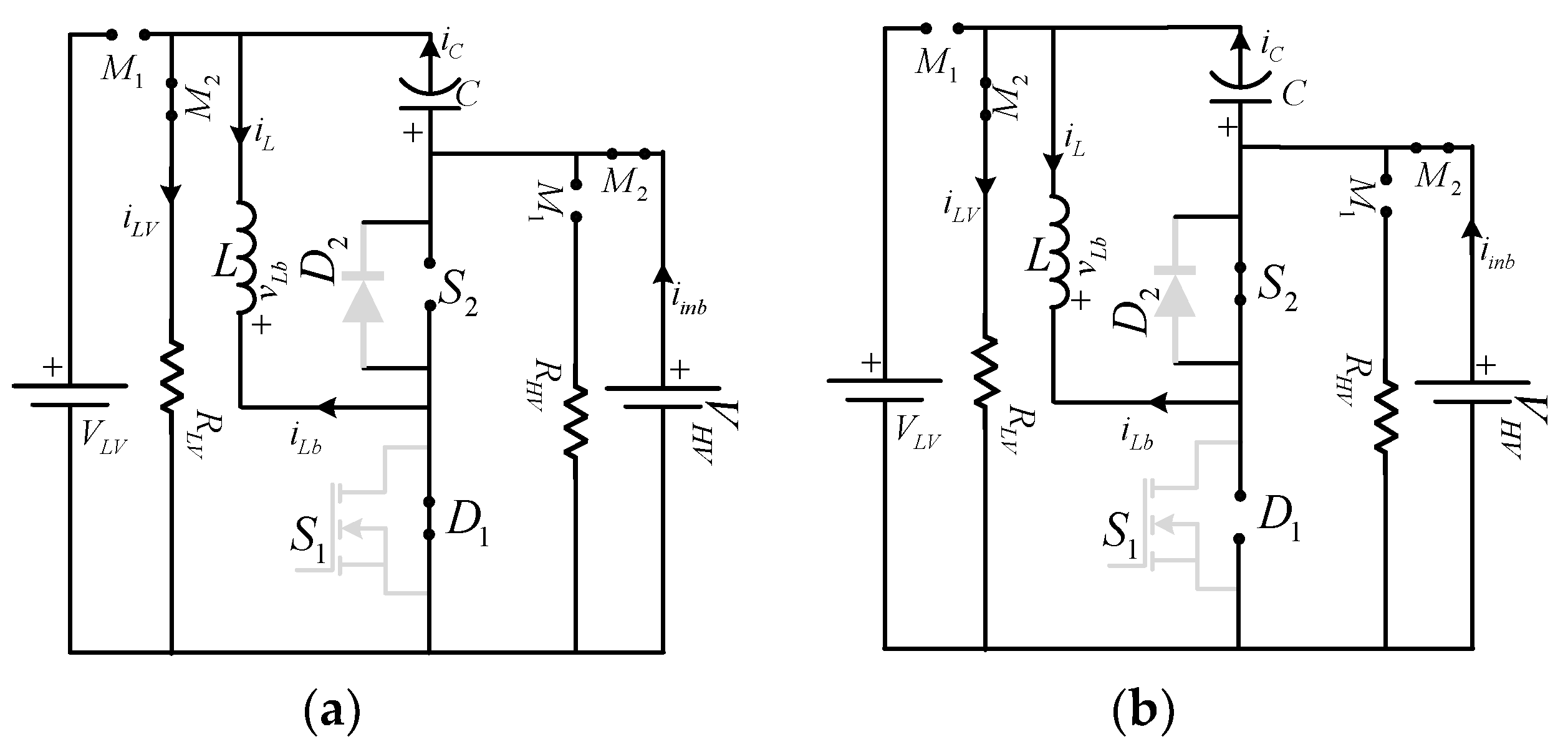
In this paper, the LC impedance bi-directional DC–DC converter (LC-BDC) is proposed by placing one inductor between source and half-bridge, and one capacitor between source and the load, as shown in
Figure 4 [
31]. These small passive components are arranged in such a way that the converter offers several features, such as lower capacitor voltages, which in turn reduces the cost, size, and volume of the converter and also increases the reliability while achieving the desired functionality. This topology reduces the voltage stresses on the device due to the usage of small passive components compared to existing converters in the case of SiC converters, which are less immune to parasitic components. The paper is organized as follows: the working principle, modes of operation, mathematical modeling, and state-space average models of the proposed topology are discussed in
Section 2. The concept validation using simulation and experimentation, along with the respective results, are presented in
Section 3. Additionally, to demonstrate the effectiveness of the proposed topology, a detailed comparative analysis of the proposed converter and conventional converter is carried out along with the results of the proposed converter. Moreover, a separate simulation-based comparative analysis of the proposed LC converter with eight similar boost/buck-boost converter topologies is presented in
Section 4. Finally, conclusions are presented in
Section 5 of this paper.
2. Proposed System
The LC bidirectional converter shown in
Figure 4 is an advanced version of a conventional bidirectional converter and switched boost bidirectional converter, designed to reduce the voltage stresses on the capacitor. The primary function of the inductor is to store energy during the converter “on” period and release the stored energy during the “off” period of the primary device. The inductor is also used to eliminate the current ripple. Another energy storage element, the capacitor, is used to eliminate the ripple in the output voltage in both cases, namely the conventional BDC and the proposed BDC. Switches
M1 and
M2 are unidirectional switches used to realize the bidirectional power flow in the test setup which operate in a complementary fashion. For the forward direction of power flow,
M1 must be in the “on” state, and
S1 acts as the main switch operating at switching frequency, while
D2 acts as a freewheeling diode. Similarly,
M2 must be in the “on” position for the reverse direction of power flow, and
S2 acts as the main switch, which operates at switching frequency, while
D1 acts as a freewheeling diode.
VLV and
RHV are source and load in boost mode, and
VHV and
RLV are source and load in buck mode. The gating signals for boost switch (
G1) and buck switch (
G2) complement each other. The duty cycle of boost switch (
S1) and buck switch (
S2) is denoted as
and
, respectively.
Ts represents the switching period of switches
S1 and
S2.
2.1. Boost Operation
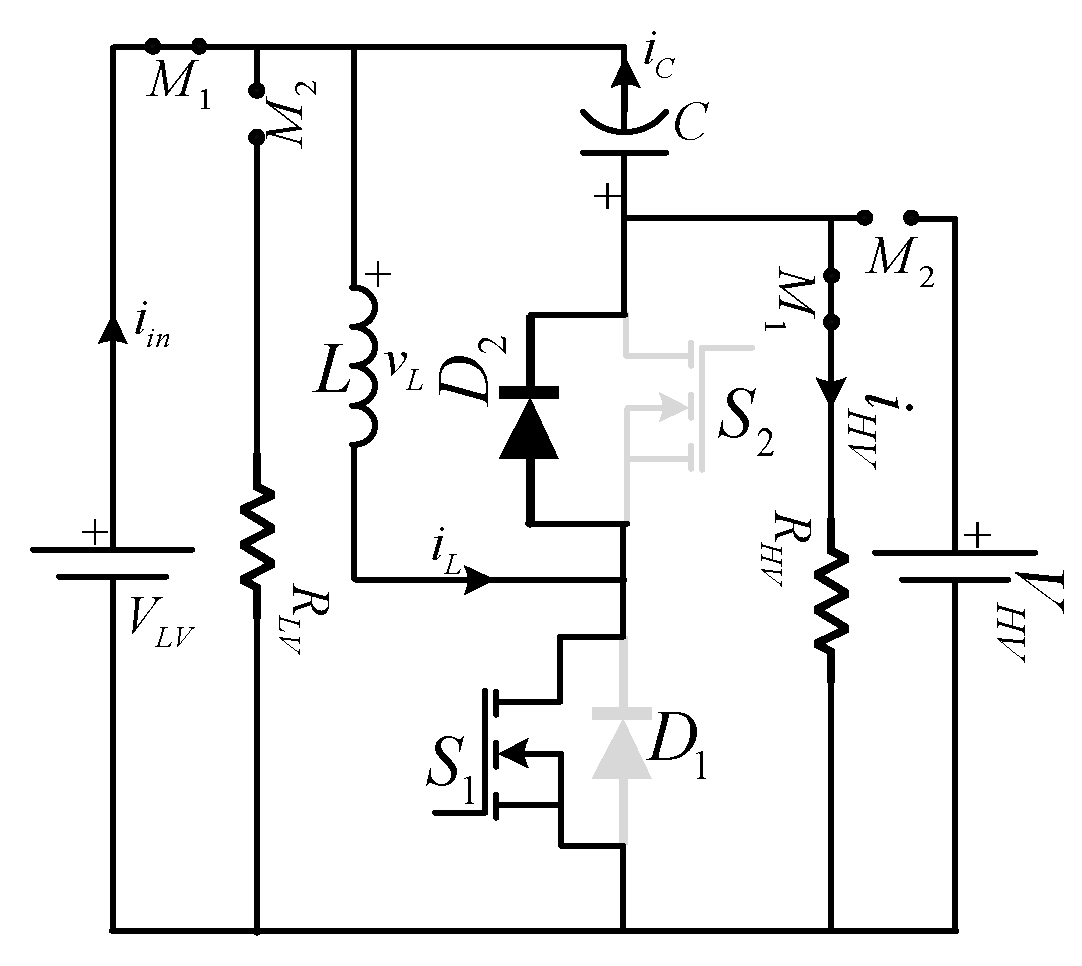
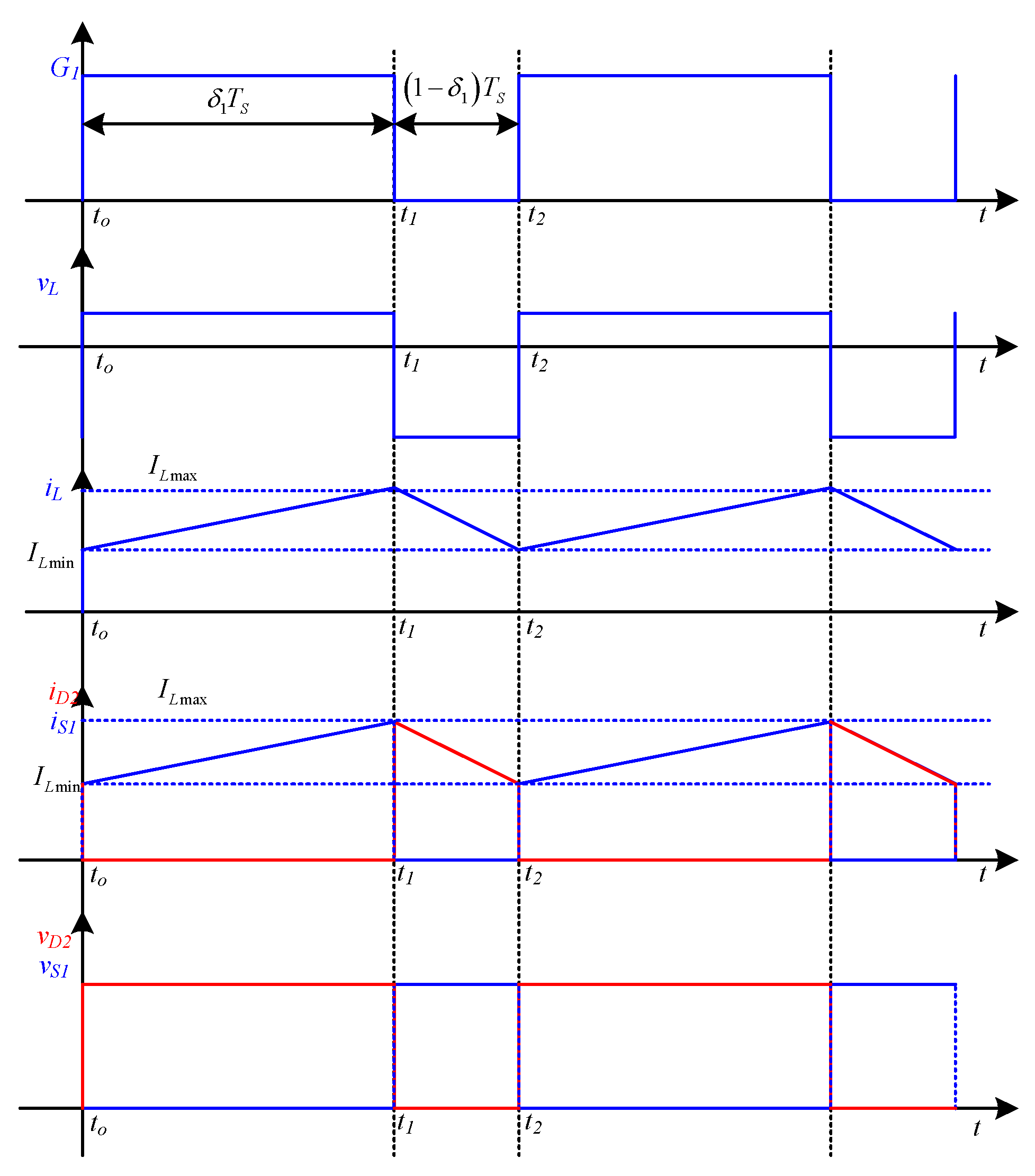
The equivalent circuit and idealized waveforms in boost mode of the LC-BDC converter are depicted in
Figure 5 and
Figure 6, respectively. The converter operation is considered to be in boost mode, during which the switch (
S1) is pulse-modulated and the diode
D2 freewheels. The boost mode operation is further categorized into two sub-modes of operation over a switching period, and the equivalent circuit of each sub-mode is depicted as shown in
Figure 7.
2.1.1. Mode 1 (t0 < t < t1): (S1 ON, D2 OFF)
In this mode, switch
S1 is turned on by applying a gate signal. The inductor
L starts charging linearly through switch
S1, and the capacitor
C will discharge through load
RHV. Hence, the diode
D2 goes into the “off” state. The equivalent circuit during this mode of operation is shown in
Figure 7a. The current through the inductor
L(
) and the voltage across the capacitor
C are given by
This mode of operation ends when the gate pulses to switch S1 are withdrawn.
2.1.2. Mode 2 (t1 < t < t2): (S1 OFF, D2 ON)
At the instant when the gate pulses of switch
S1 are removed, the switch
S1 goes into the “off” state due to which the voltage across the inductor brings the diode
D2 into the forward-biased state. The equivalent circuit during this mode is shown in
Figure 7b. In this mode, both inductor and source feed power to the load, and the inductor charges the capacitor. Hence, there is a formation of the
LC tank in this mode, which can offer zero voltage switching to the upper switch with the proper selection of the snubber capacitor. In this mode, the current through
L(
) reaches its minimum value. The current flowing through the inductor
L(
) and the voltage across the capacitor
C are given by
This mode ends at t = Ts when the gate signal is provided to S1 in the next switching cycle. Similar operation (Mode 1 and Mode 2) continues for several switching cycles until a power flow is required in the forward direction
2.2. Buck Mode of Operation of LC-BDC Converter
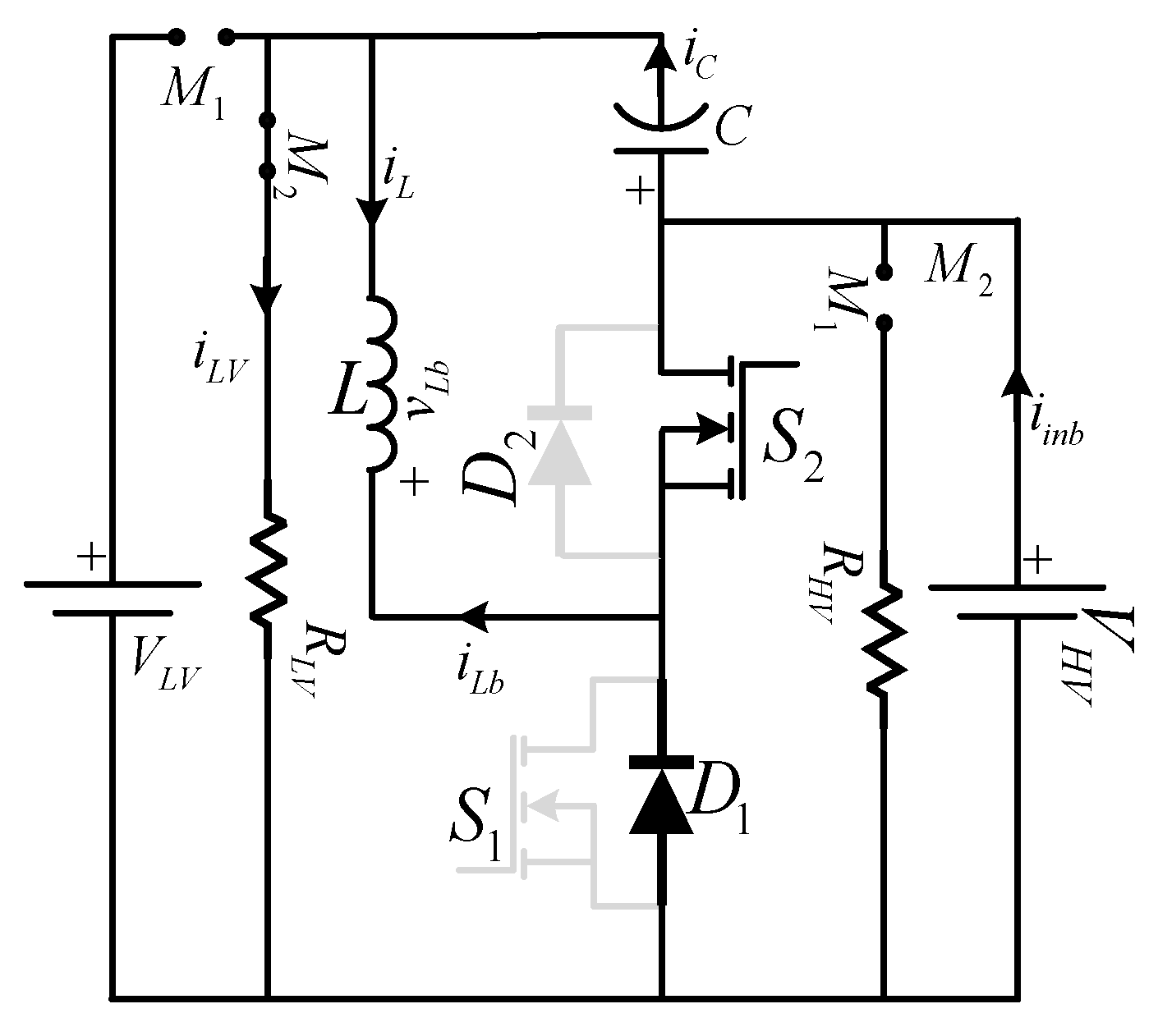
BDC operates in buck mode when there is a requirement of power flow in the reverse direction, and its equivalent circuit is shown in
Figure 8. The converter operation is considered to be in reverse buck mode, during which the switch
S2 is pulse-modulated and the diode
D1 in a freewheeling mode. The buck mode of operation is further categorized into two sub-modes (i.e., mode 3 and mode 4) of operation over a switching period. The operating mode from mode 3 to mode 4 in buck mode is similar to the mode 2 to mode 1 of the boost mode of operation, respectively.
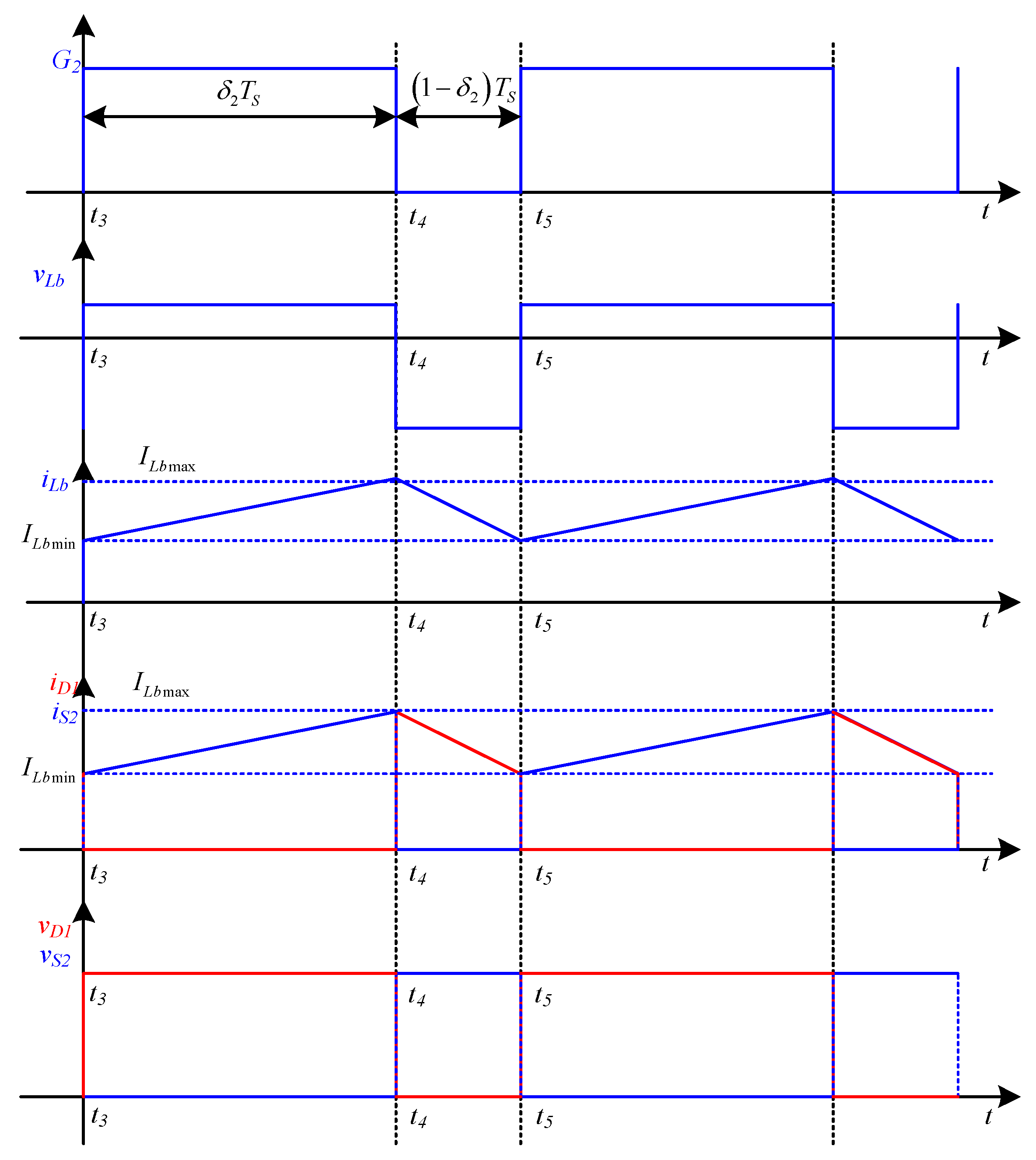
Figure 9 illustrates the characteristic waveforms of the converter in buck mode, and its equivalent circuits in each sub-mode are depicted as shown in
Figure 10.
2.2.1. Mode 3 (t3 < t < t4): (S2 ON, D1 OFF)
This mode starts at
t = t3 when the gate signal is given to
S2. At this instant, the main switch S
2 comes into conduction, and the diode
D1 goes into the “off” state. The supply
VHV then directly energizes the inductor
L. The capacitor is also discharged through the inductor. It leads to the formation of the
LC tank, as shown in
Figure 10a, similar to mode 2. This feature offers the resonating switching functionality to the upper switch. The current flowing through
L(
) and the voltage across capacitor
C (
) are given as
This mode continues until the gate pulse of S2 is withdrawn at t = t4.
2.2.2. Mode 4 (t4 < t < t5): (S2 OFF, D1 ON)
This mode starts at
t = t4 when the gate pulses to the main switch are removed. Hence
S2 goes into the “off” state. The voltage across the inductor brings diode
D1 into “on” state, and it continues until
t = t5. The energy stored in inductor L discharges through the load. The capacitor charges from the source. During this mode, the current flowing through the inductor
L and voltage across the capacitor
C can be expressed as
This mode ends at t = Ts when the gate signal is given to S2 in the next switching cycle. Similar operation of mode 3 and mode 4 continues, for several switching cycles, until power flow is required in the reverse direction.
2.3. State Space Analysis
This section presents the development of a small-signal AC model followed by the derivation of the state-space model equations for one complete switching cycle. For this analysis, few assumptions are considered; (i) the converter is operating in continuous conduction mode, and (ii) there is no trace resistance. For the proposed converter, the state variables are the current through the inductor
iL and the voltage across the coupling capacitor
VC. A complete derivation of the state-space model and small-signal analysis for boost mode is presented. A similar derivation method can also be used for buck mode. With the inclusion of the parasitic components during both “on” and “off” states, the system can be represented with the help of the state-space model as follows.
during “off” state:
Here, —on-state resistance of switching device, —the equivalent series resistance of the inductor, and —equivalent series resistance of the capacitor.
The state-space average model of the converter can be written as follows.
Here, , , , ,
,
The duty ratio of the main switch
S1 is defined as
The turn-off duty cycle of the main switch
S1 is
Substituting the duty ratio values from (20)–(22) in Equations (17)–(19) and then incorporating the perturbation effect into the state variables and other variables around the steady-state values gives
where
D1 is the duty ratio of the main switch under steady-state condition. After solving the above state-space equation, the steady-state gains of the converter can be obtained as
Comparing small-signal AC parameters while ignoring the considerably very small second-order quantities, and then solving the equations gives the following two transfer functions.
2.3.1. Control-to-Output Transfer Function
From the small-signal AC model, the control-to-output (output voltage to duty ratio) transfer function can be found under the condition of
, which is shown in Equation (25).
By neglecting parasitic components, it can be simplified as
2.3.2. Control-to-Input Transfer Function
From the small-signal AC model, the inductor current-to-control (input current to duty ratio) transfer function can be found under the condition of
, which is shown in Equation (27).
By neglecting parasitic components, it can be simplified as
2.3.3. Step and Bode Responses of LC-BDC
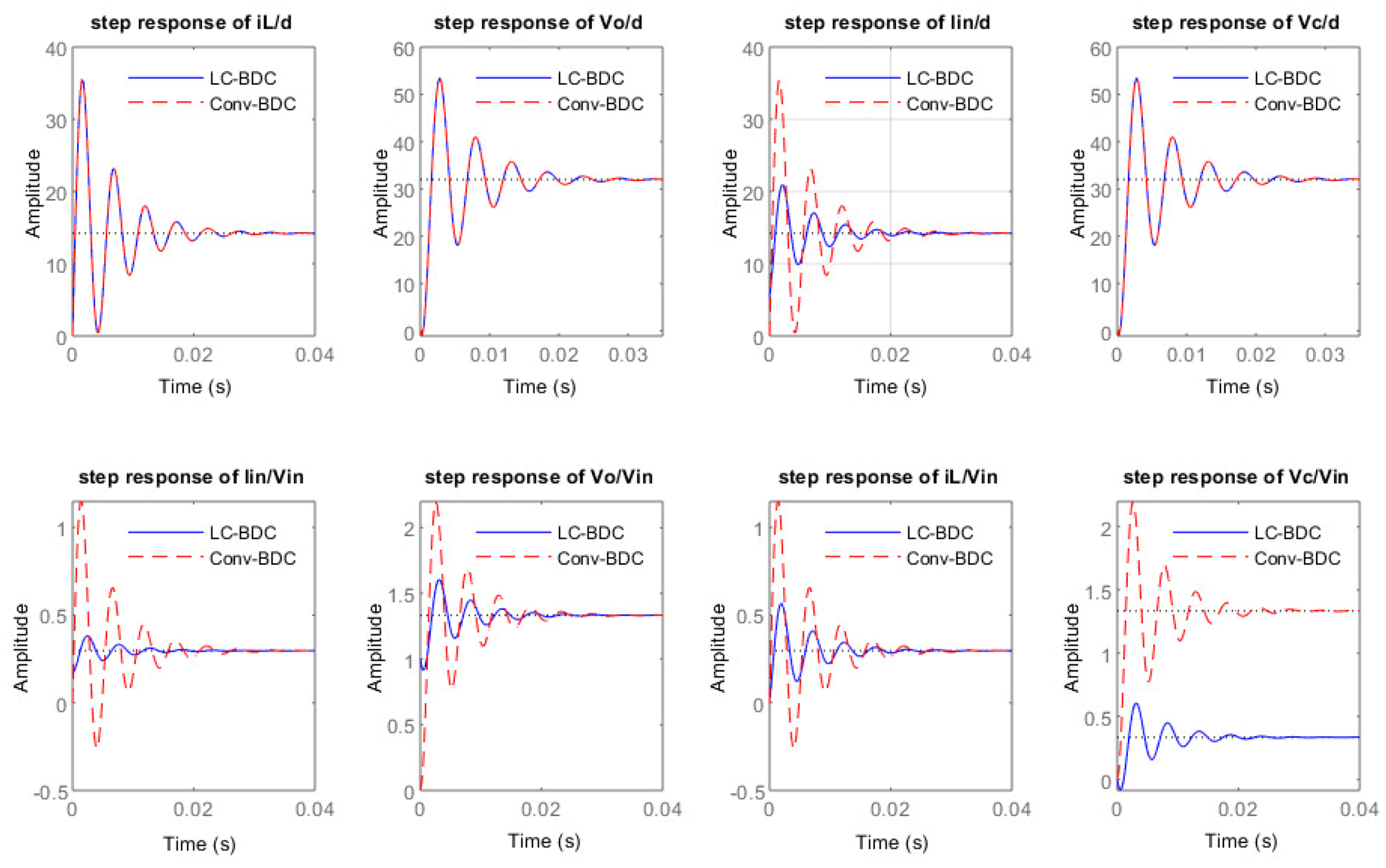
From the derived transfer functions, the step responses of various variables are presented in
Figure 11. From these results, it can be understood that the variations in input currents and capacitor voltages for both line and load disturbance are low in the case of the proposed converter compared to the existing converter. Moreover, the step responses reveal that the proposed LC-BDC converter response is the same for inductor current and capacitor current and capacitor voltage against the duty ratio, whereas input current transients against duty ratio variations are reduced in LC-BDC. It can also be noted that in the case of supply variations, the transient responses of the inductor current, output voltage, load current, and capacitor voltage are improved.
2.3.4. Ripple Capacitor Voltage
From the charge balance equation and further simplification of the above Equation (25) in the steady-state, the capacitor ripple voltage can be calculated as
From (29), the capacitor value can be sized to minimize the voltage ripple across the capacitor.
3. Experimental Results and Discussion
The proposed LC impedance bi-directional dc-dc converter has been successfully validated through experiments in both boost and buck modes. The parameters considered for the experimental validations are summarized in
Table 1. The experimental setup of the proposed converter is shown in
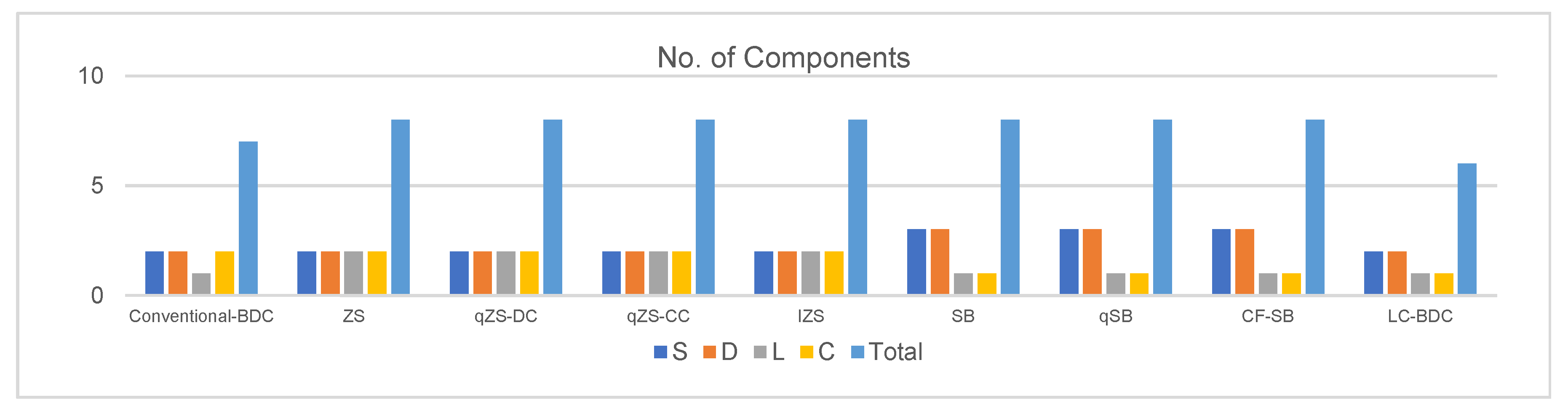
Figure 12. The system performance is evaluated in both steady-state and transient conditions while feeding power to two series-connected 12 V, 50 W lamp load under various test conditions for the 18 V DC to 24 V DC conversion in forwarding boost mode, and 24 V DC to 18 V DC conversion in reverse buck mode. The inductor current, load current, and capacitor voltage waveforms are captured in both boost and buck modes for both conventional and proposed converters. Comparative analysis through experimental results was carried out, as explained below. In the case of the conventional converter, there is a need for two capacitors (
CHV plays a vital role in boost mode, and
CLV plays a vital role in buck mode), whereas, in the case of the proposed converter, there is a need for only one capacitor
C, which can take care of the functionality of the above mentioned two capacitors in the respective modes. It can be observed that two capacitors are used in the realization of the conventional converter, whereas only one capacitor is used for the realization of the proposed LC-BDC, as shown in
Table 1.
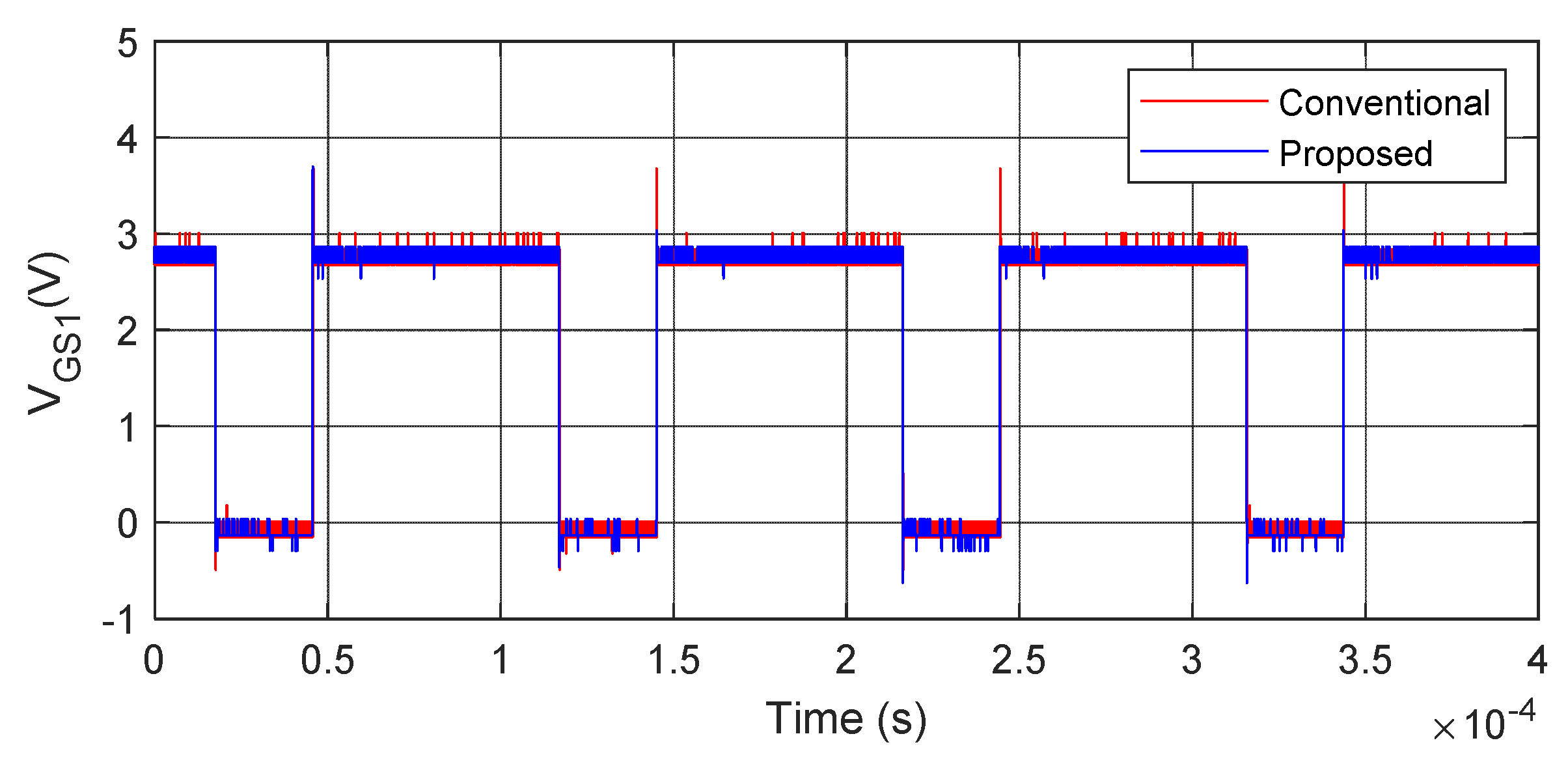
The gate signal of the lower switch, inductor current, load current, and capacitor voltage for four switching cycles are captured and presented in
Figure 13,
Figure 14,
Figure 15 and
Figure 16. From
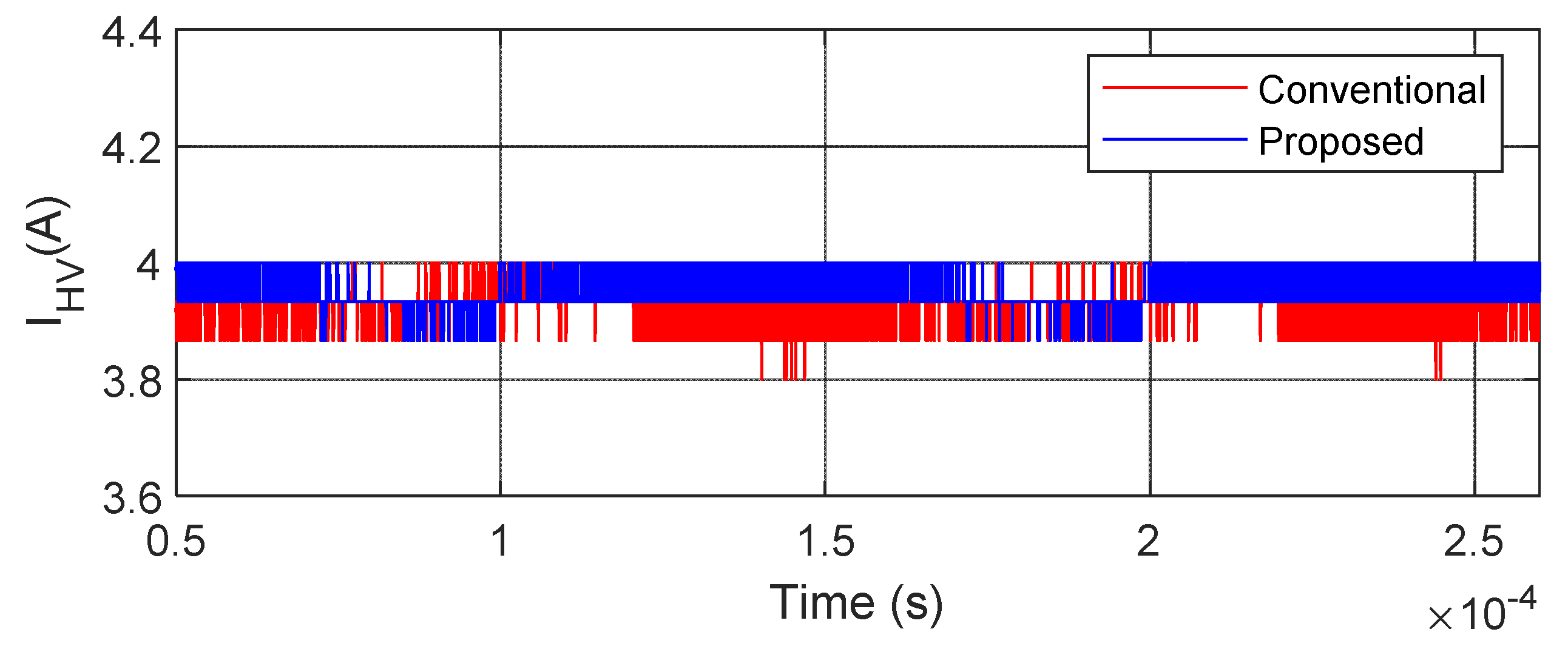
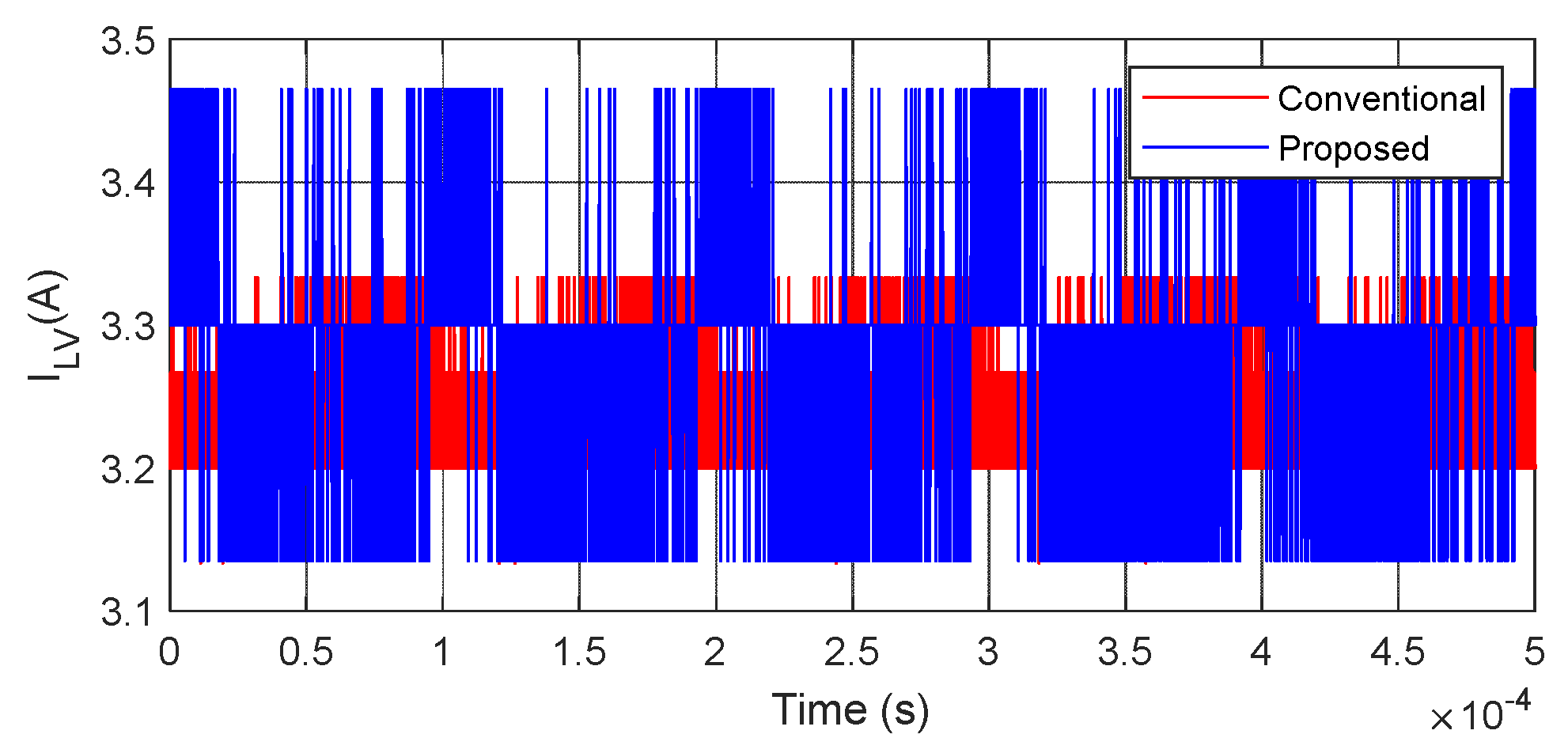
Figure 14, it can be seen that the peak value of the inductor current is 6.17 A in the conventional converter, whereas it is 6.07 A in the proposed converter for the same load current, as shown in
Figure 15. From
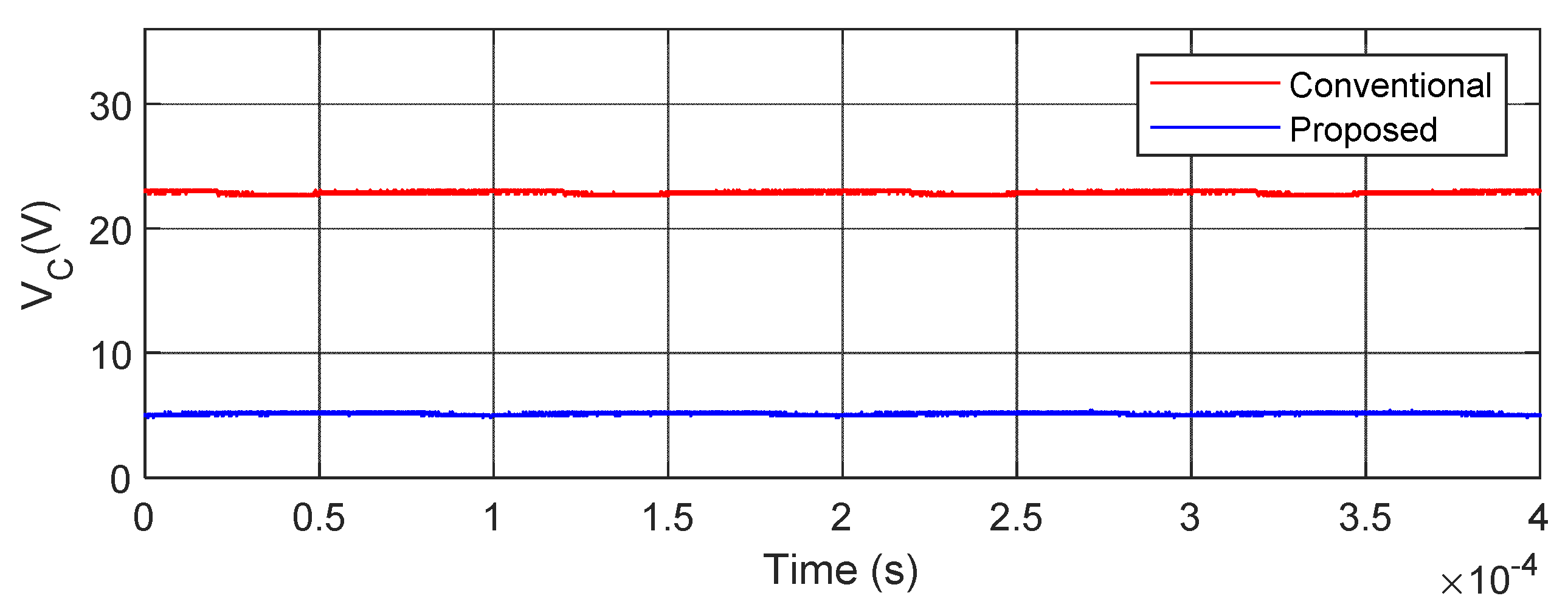
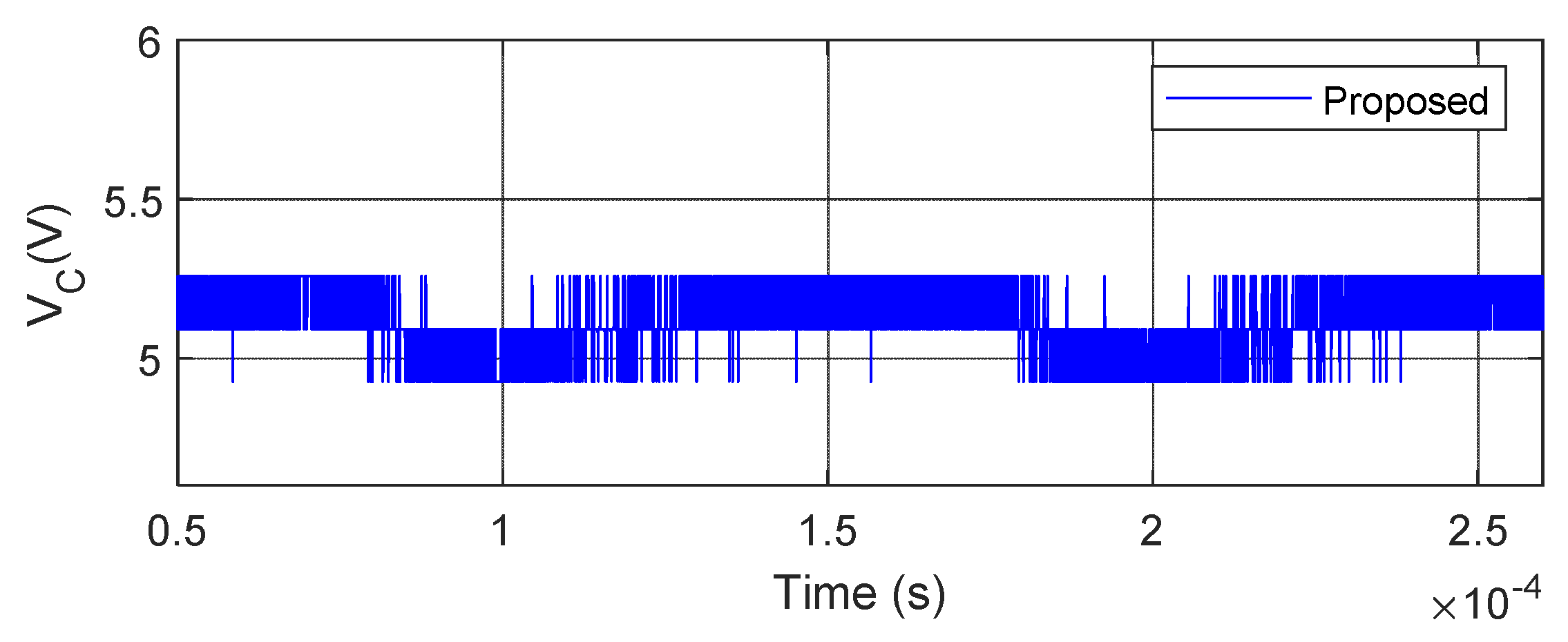
Figure 16, it can be seen that the voltage across the capacitor is 23.20 V in the case of the conventional converter, whereas it is 5.10 V in the case of the proposed converter. Hence, there is 78.02% of capacitor voltage reduction in the proposed converter as compared to the conventional converter for the same input/output voltage conversion.
In
Figure 17,
Figure 18 and
Figure 19, respectively, a zoomed view of respective parameters is presented during both “on” and “off” state. From these figures, peak values during both transient and steady-state can be measured as listed in
Table 2.
Form
Table 3, it can be observed that the proposed converter not only offer its best performance during steady-state conditions but also the exhibits same best performance during transient conditions in terms of capacitor voltage stresses.
For the ripple content investigation, a zoomed view of the inductor current, load current, and capacitor voltages are presented in
Figure 20,
Figure 21,
Figure 22 and
Figure 23, respectively. The summary of the ripple content for both converter topologies is tabulated in
Table 3. From this table, it can be understood that there is a 0.4% reduction of ripple content in capacitor voltages and inductor current for the same content of load current ripples.
For the reverse buck mode of operation, the gating signal of the upper switch, inductor current, load current, and capacitor voltage for four switching cycles have been captured, as presented in
Figure 24,
Figure 25,
Figure 26 and
Figure 27. From
Figure 25, it can be seen that the peak value of the inductor current is 3.61 A in the case of conventional converter, whereas it is 3.62 A in the case of the proposed converter for the same load current as shown in
Figure 26. From
Figure 27, it can be seen that the voltage across the capacitor is 16.40 V in the case of conventional converter, whereas it is 7.80 V in the case of the proposed converter. A capacitor voltage reduction of 35.80% can be witnessed in this mode of operation.
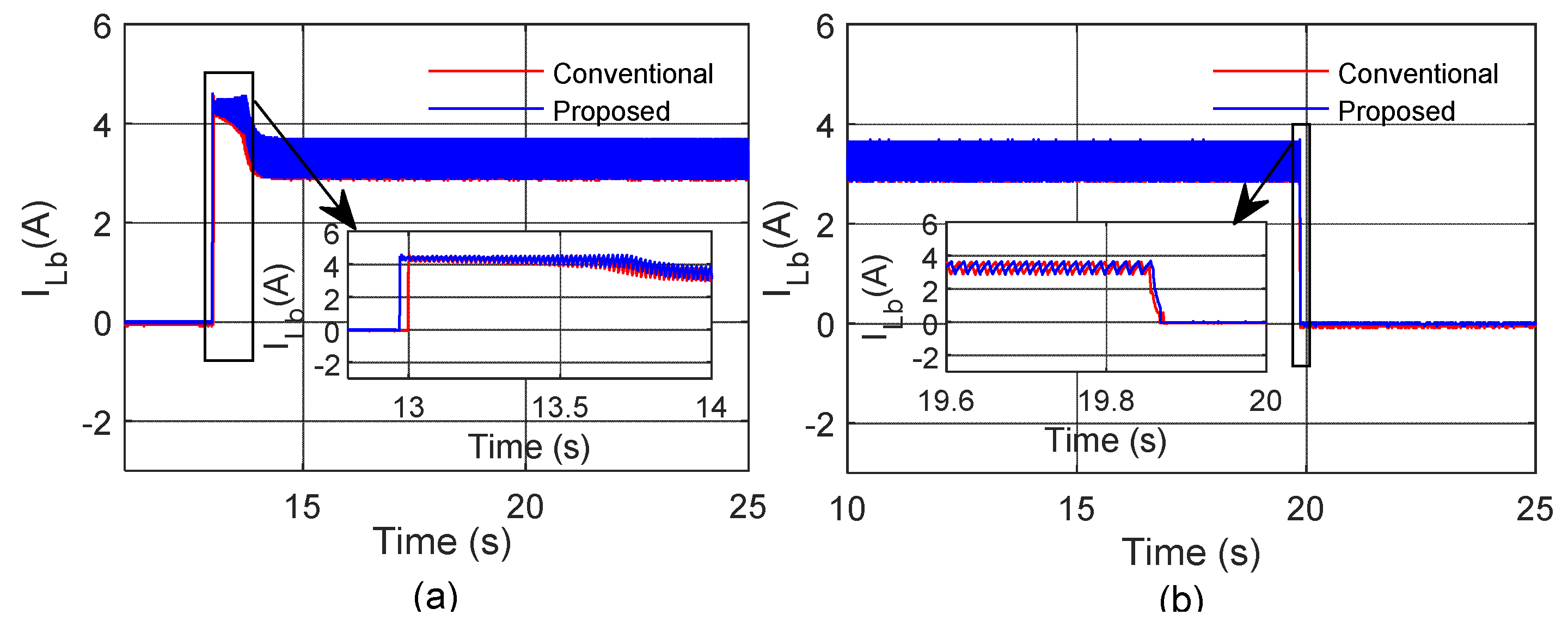
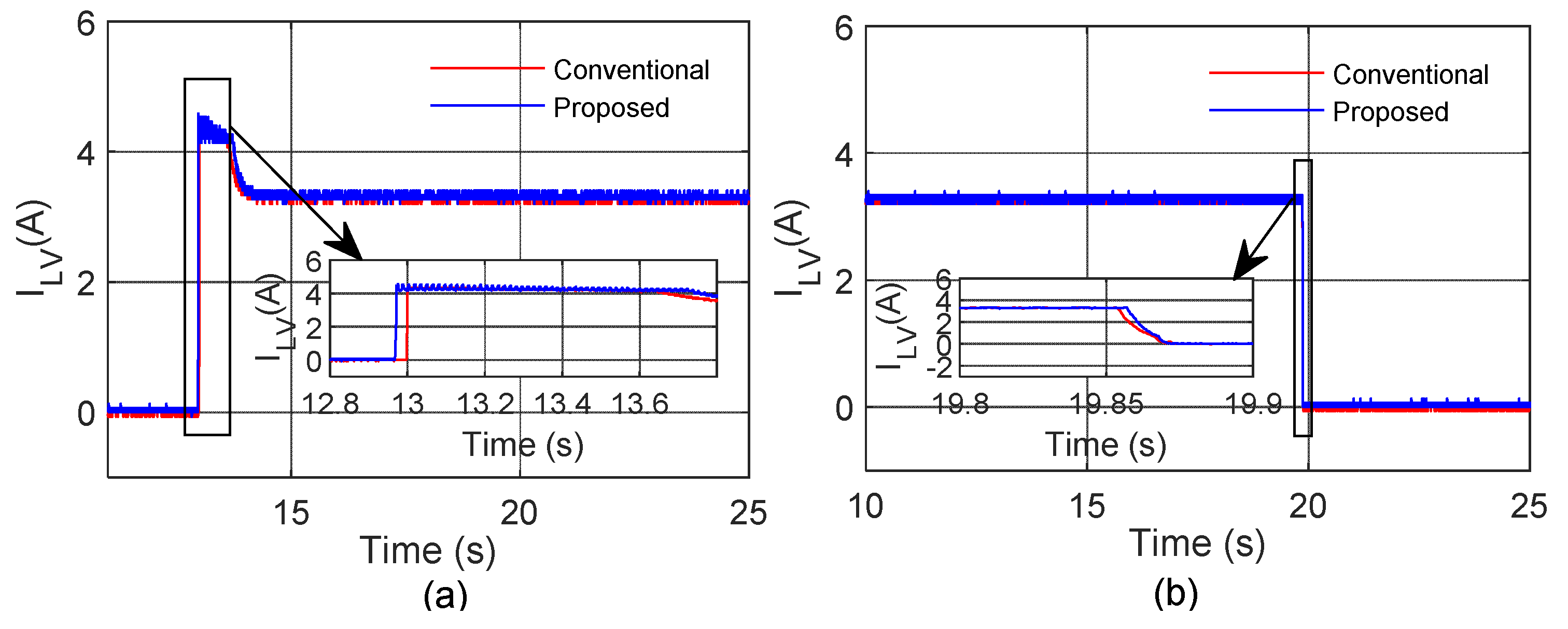
For the critical investigation, results have been captured under various test conditions to assess the proposed converter suitability for various applications like smooth turn-on, faster load turn-off, and converter on- and off-switching with variable duty. During these conditions, captured inductor current, load current, and capacitor voltage are shown in
Figure 28,
Figure 29 and
Figure 30, respectively. Moreover, in these figures, a zoomed view of respective parameters is presented during both turn-on and turn-off. From these figures, peak values during both transient and steady states can be measured as listed in
Table 4. Form the
Table 4, and it can be observed that the proposed converter not only offers its best performance during steady-state conditions but also exhibits the same best performance during transient conditions in terms of capacitor voltage stresses.
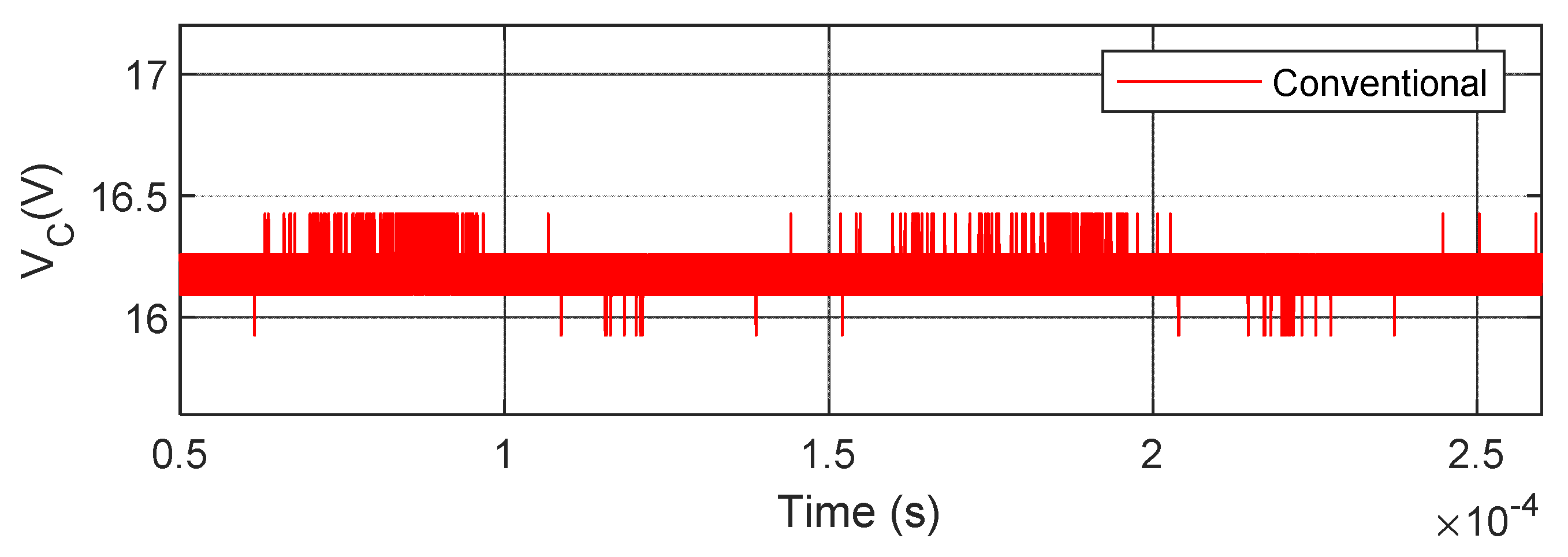
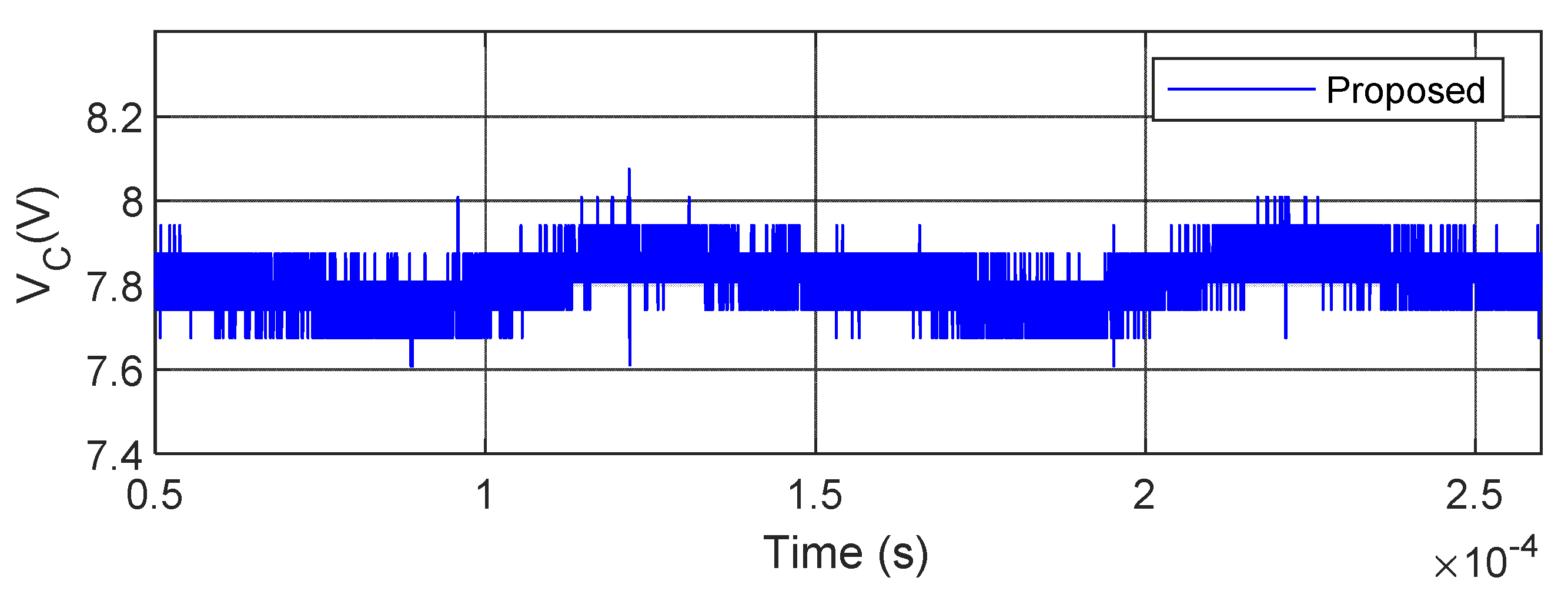
For the ripple content investigation, a zoomed view of the inductor current, load current, and capacitor voltages are presented in
Figure 31,
Figure 32,
Figure 33 and
Figure 34, respectively. The summary of the ripple content in both the converters is tabulated in
Table 5. From this table, it can be extracted that there is a 0.3% reduction of ripple content in capacitor voltages ripples for the same load current.