Towards Efficient Neuromorphic Hardware: Unsupervised Adaptive Neuron Pruning
Abstract
1. Introduction
- Three different strategies for pruning neurons are proposed by exploiting network dynamics in unsupervised SNNs. An adaptive neuron online pruning strategy can effectively reduce network size and maintain high classification accuracy.
- The adaptive neuron online pruning strategy outperforms post-training pruning, which shows significant potential for online training by improving both training energy efficiency and classification accuracy.
- A parallel digital implementation scheme is presented. The adaptive neuron pruning strategy enables significant memory size reduction and energy efficiency improvement.
- The proposed pruning strategies preserve the dense structure of the weight matrix. No additional compression technique is required for the implementation of pruned SNNs.
2. Pruning Strategies
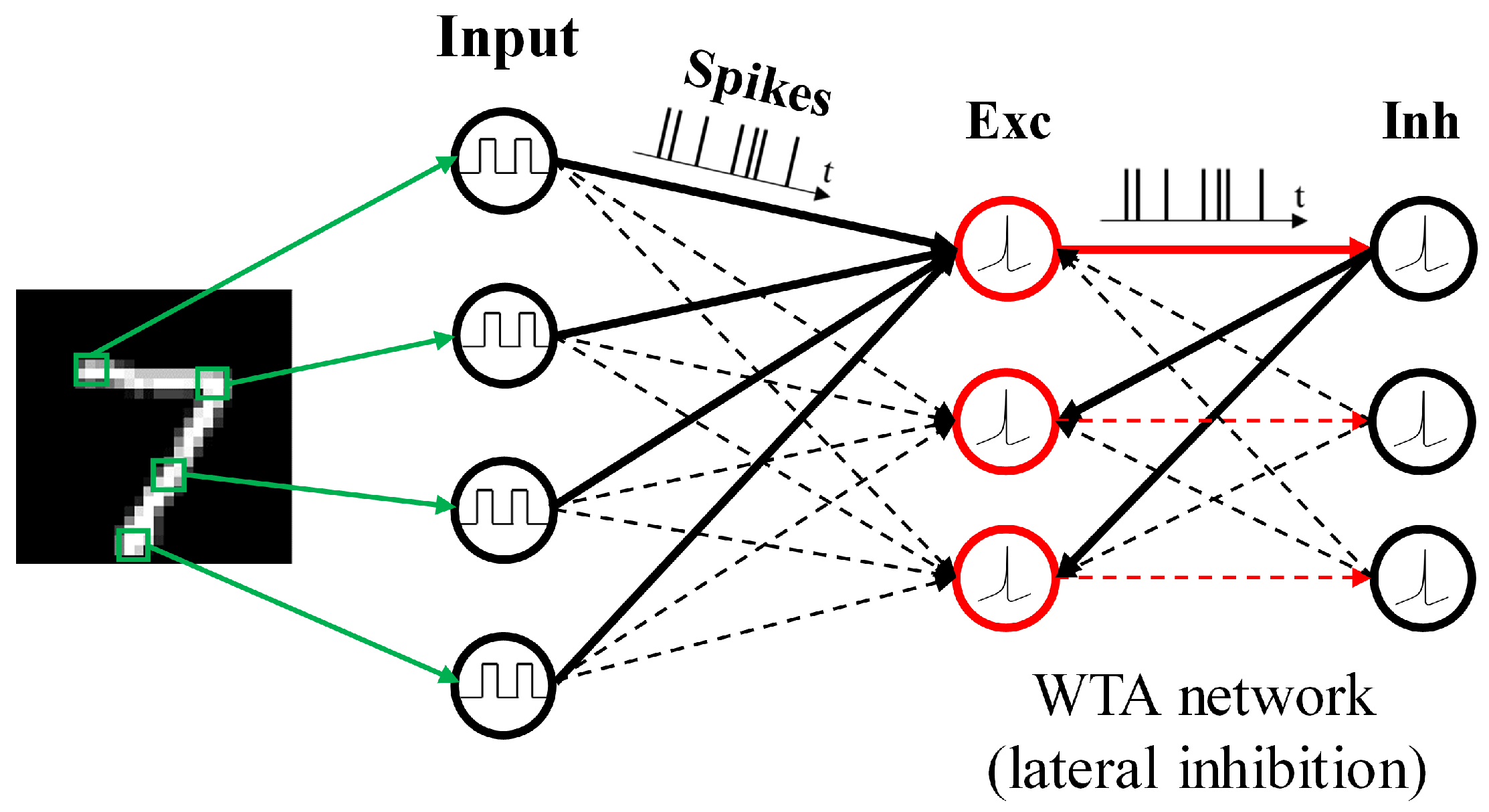
2.1. Network Architecture
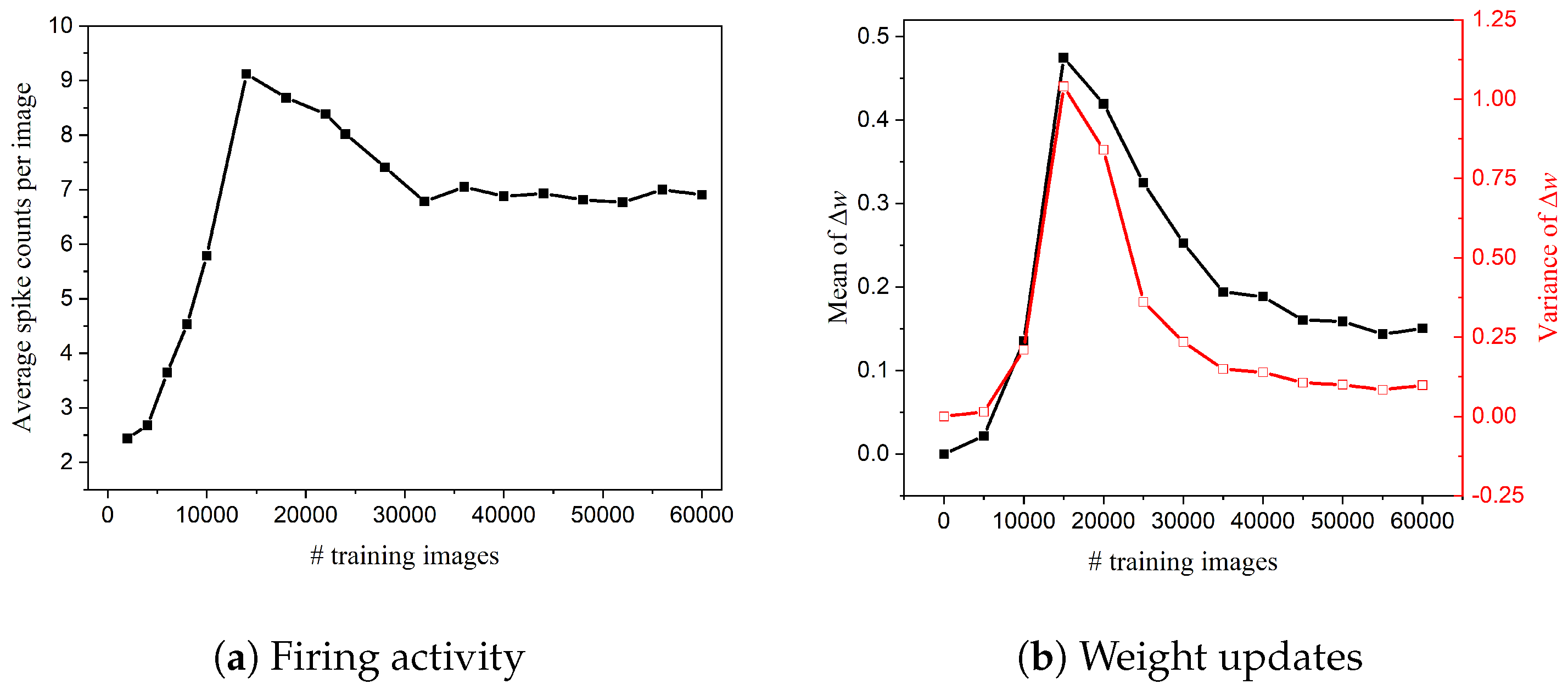
2.2. When to Start Neuron Pruning?
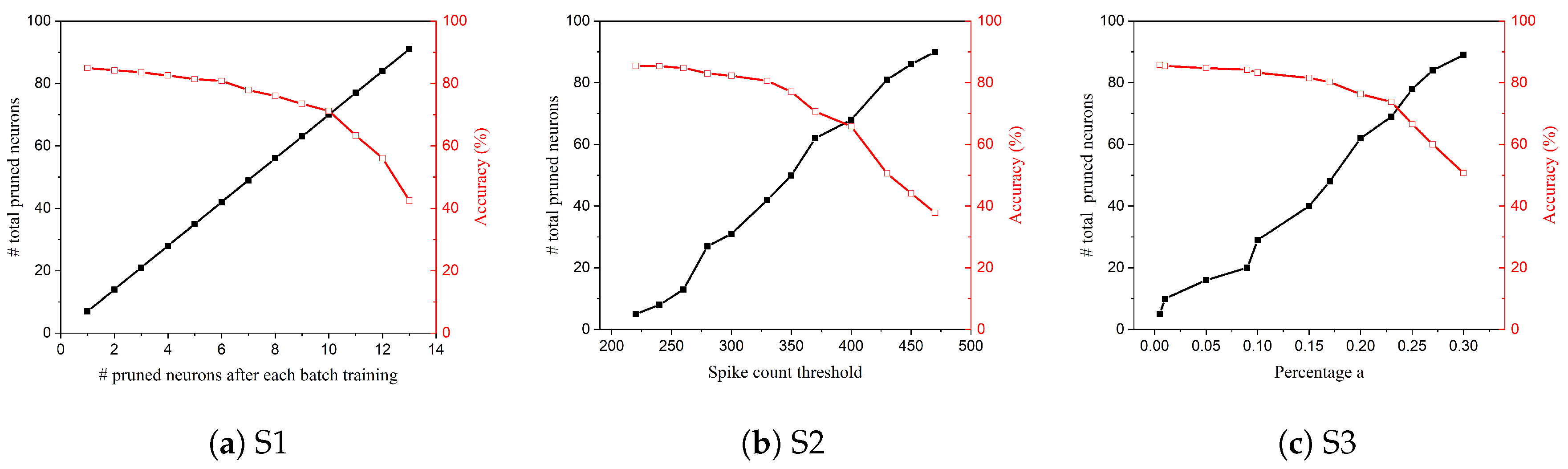
2.3. S1: Online Constant Pruning
2.4. S2: Online Constant-Threshold Pruning
2.5. S3: Online Adaptive Pruning
| Algorithm 1: Adaptive pruning algorithm |
 |
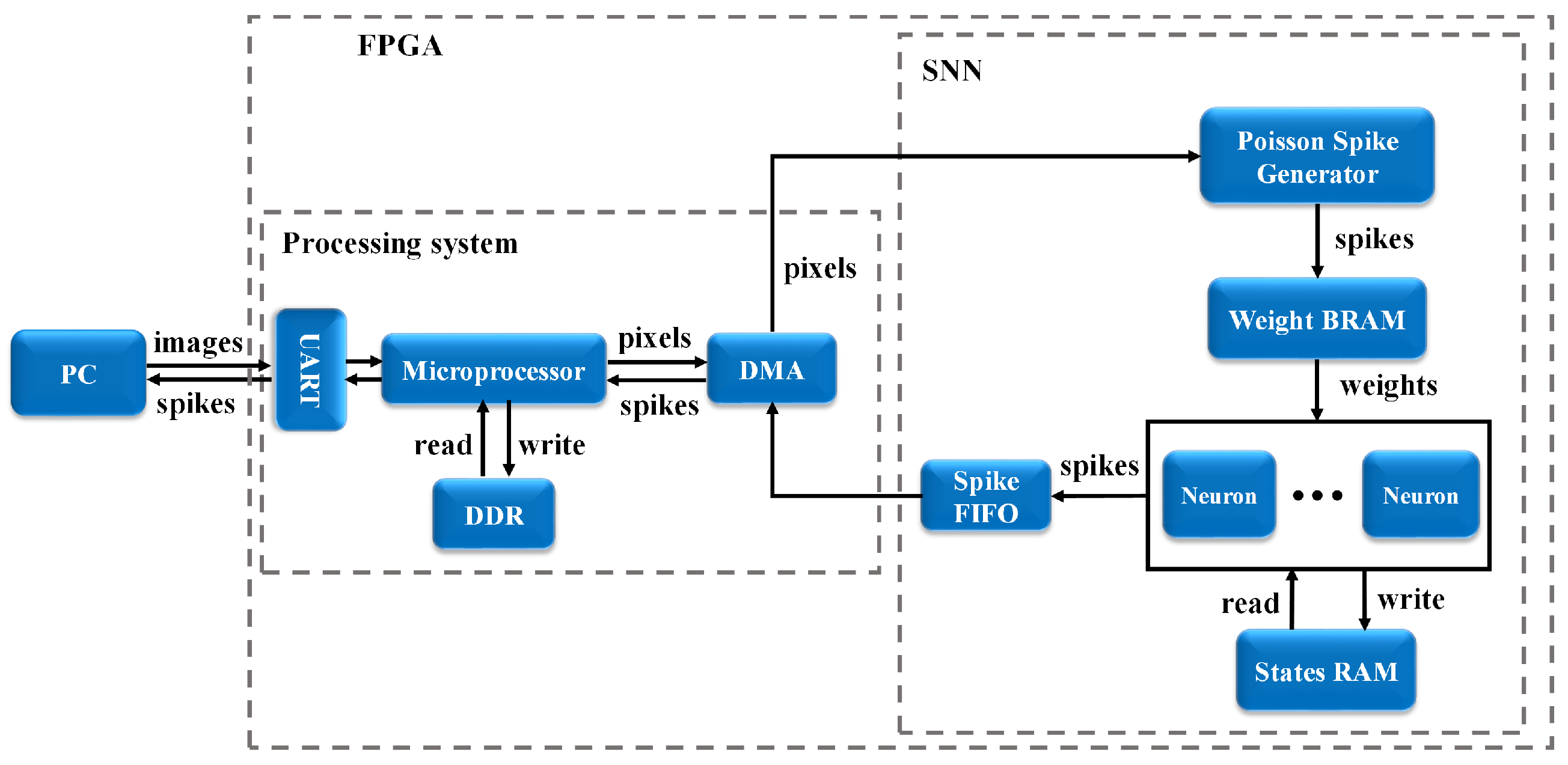
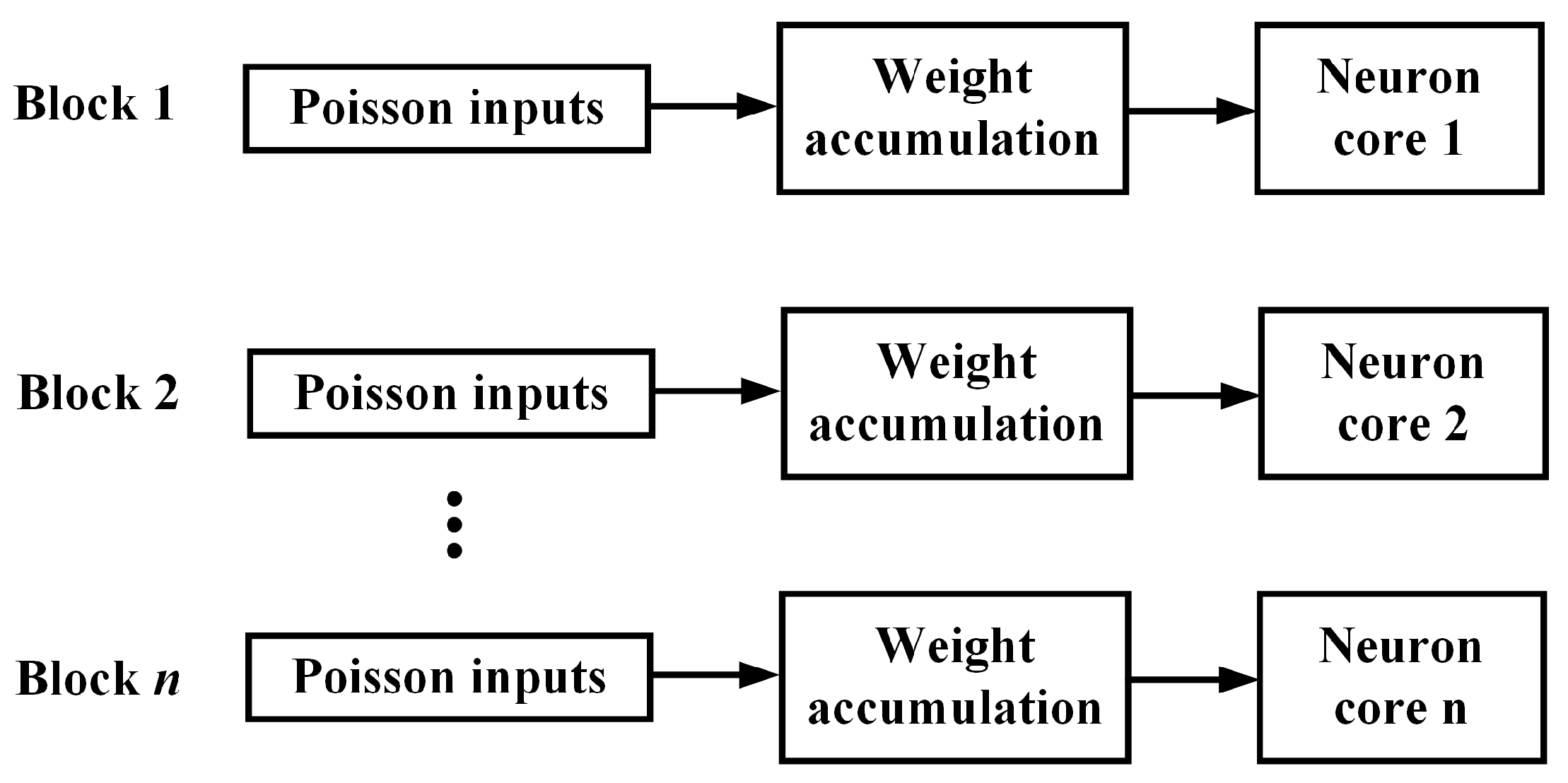
3. FPGA Implementation
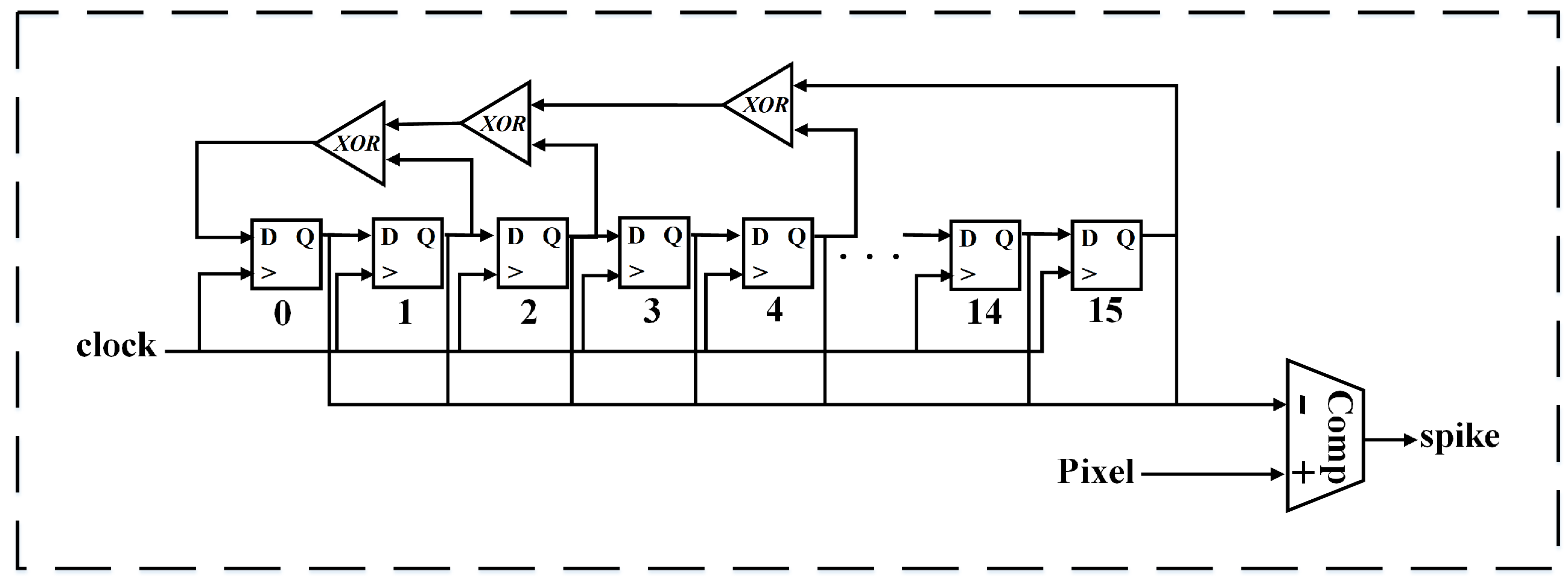
3.1. Poisson Spike Generator
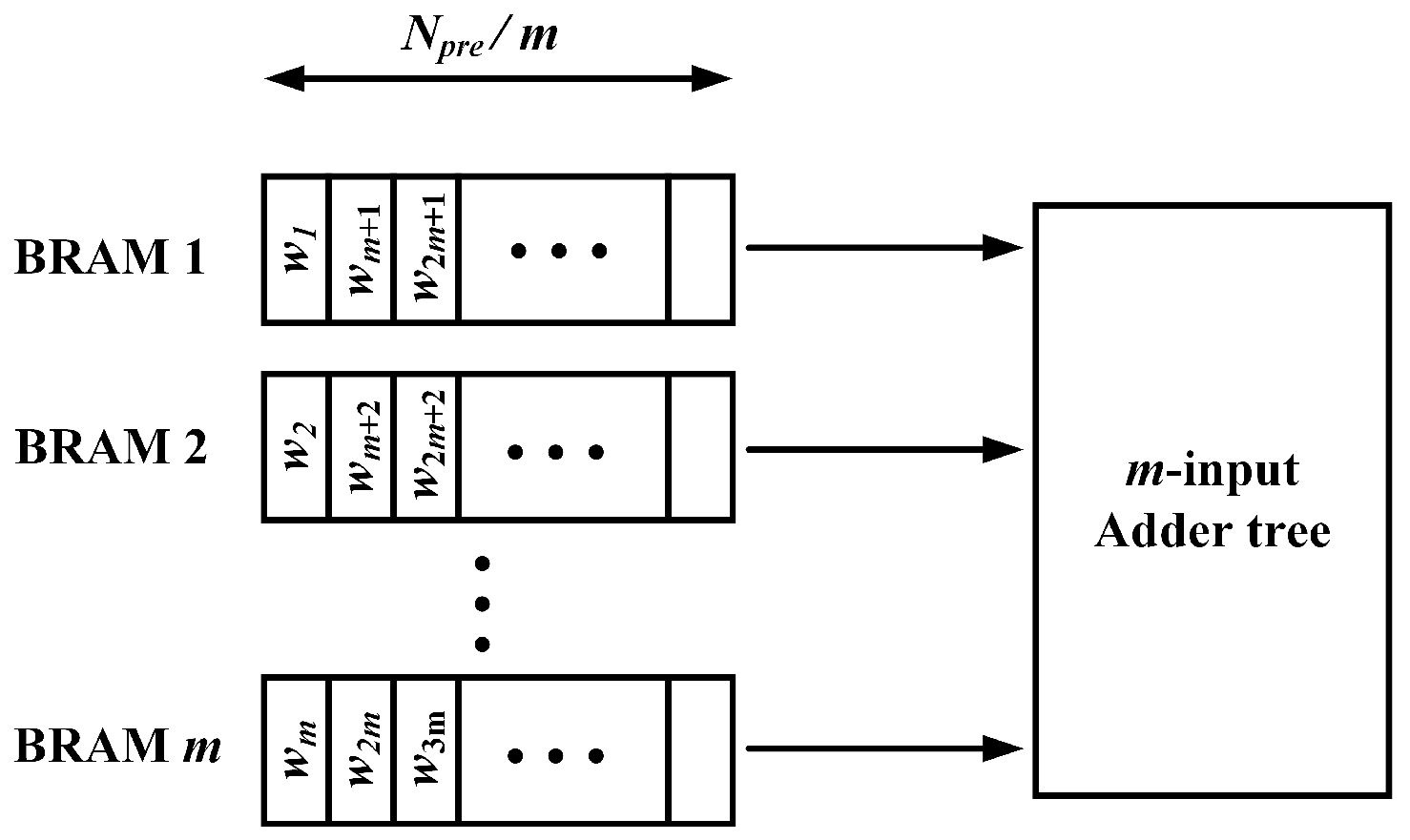
3.2. Memory Block
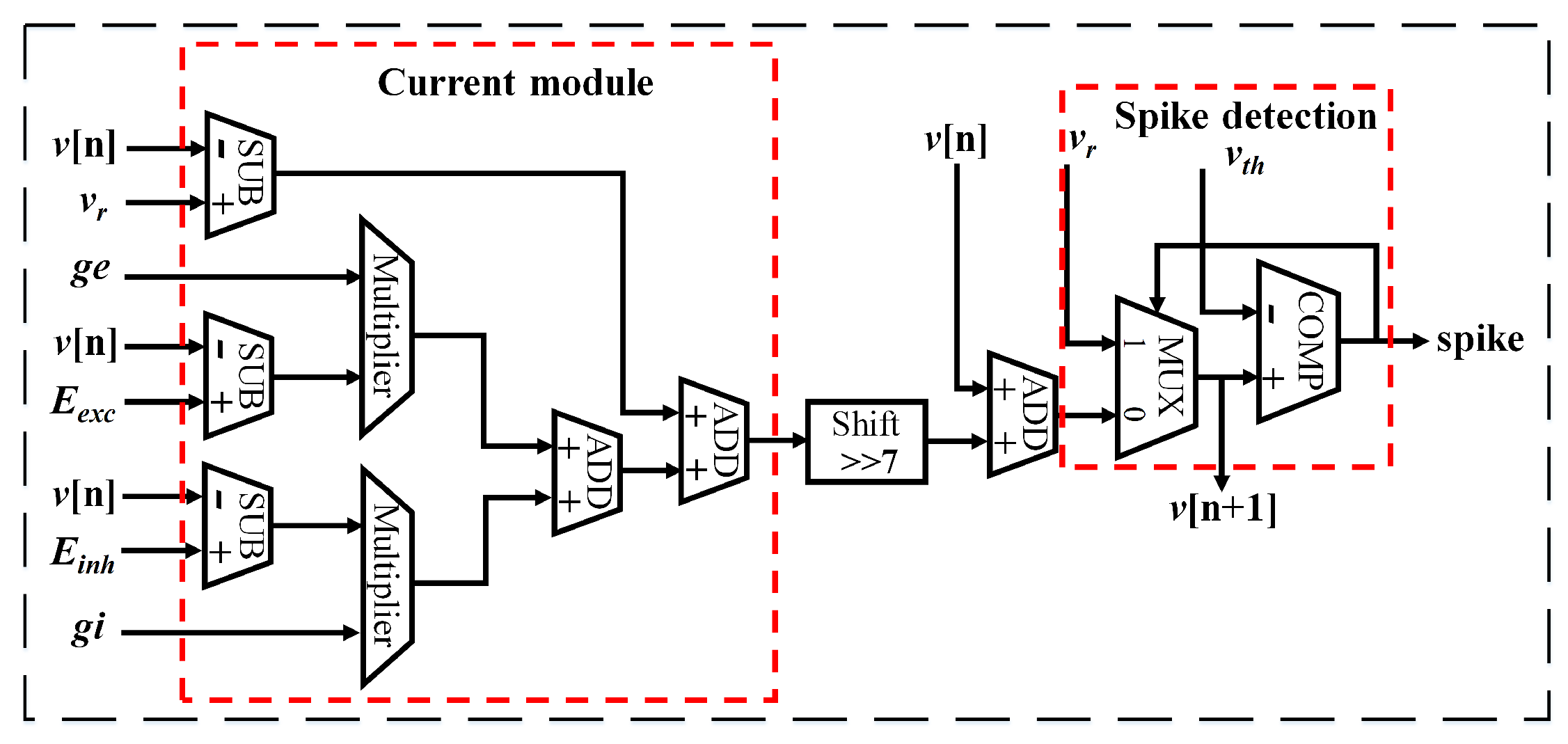
3.3. Neuron Processing Core
4. Results and Discussion
4.1. Network Performance
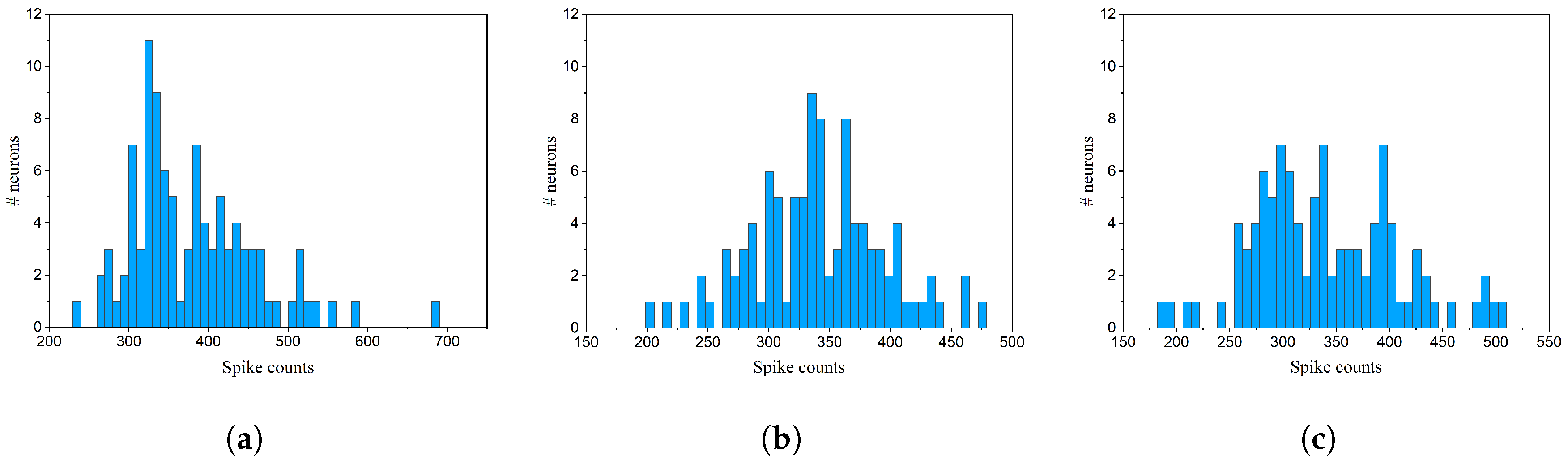
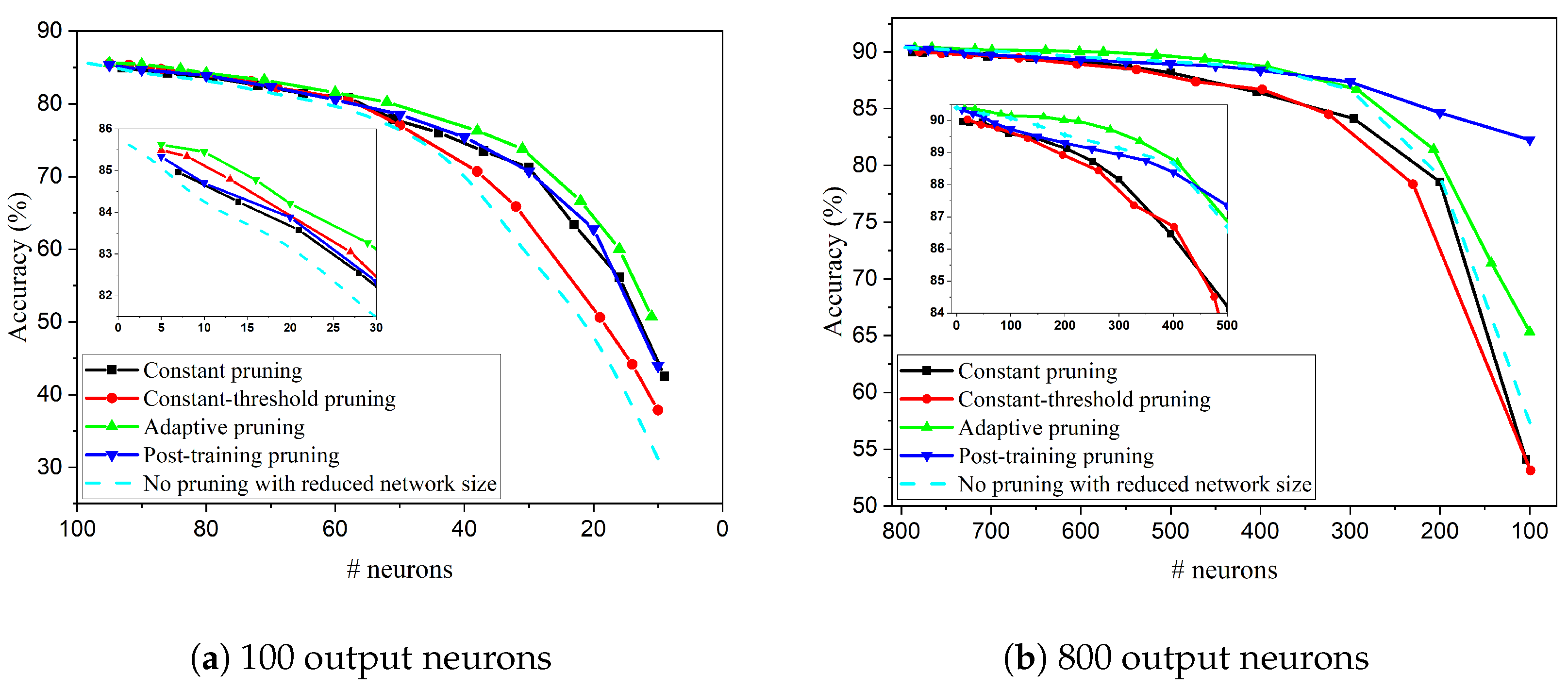
4.1.1. Online Pruning
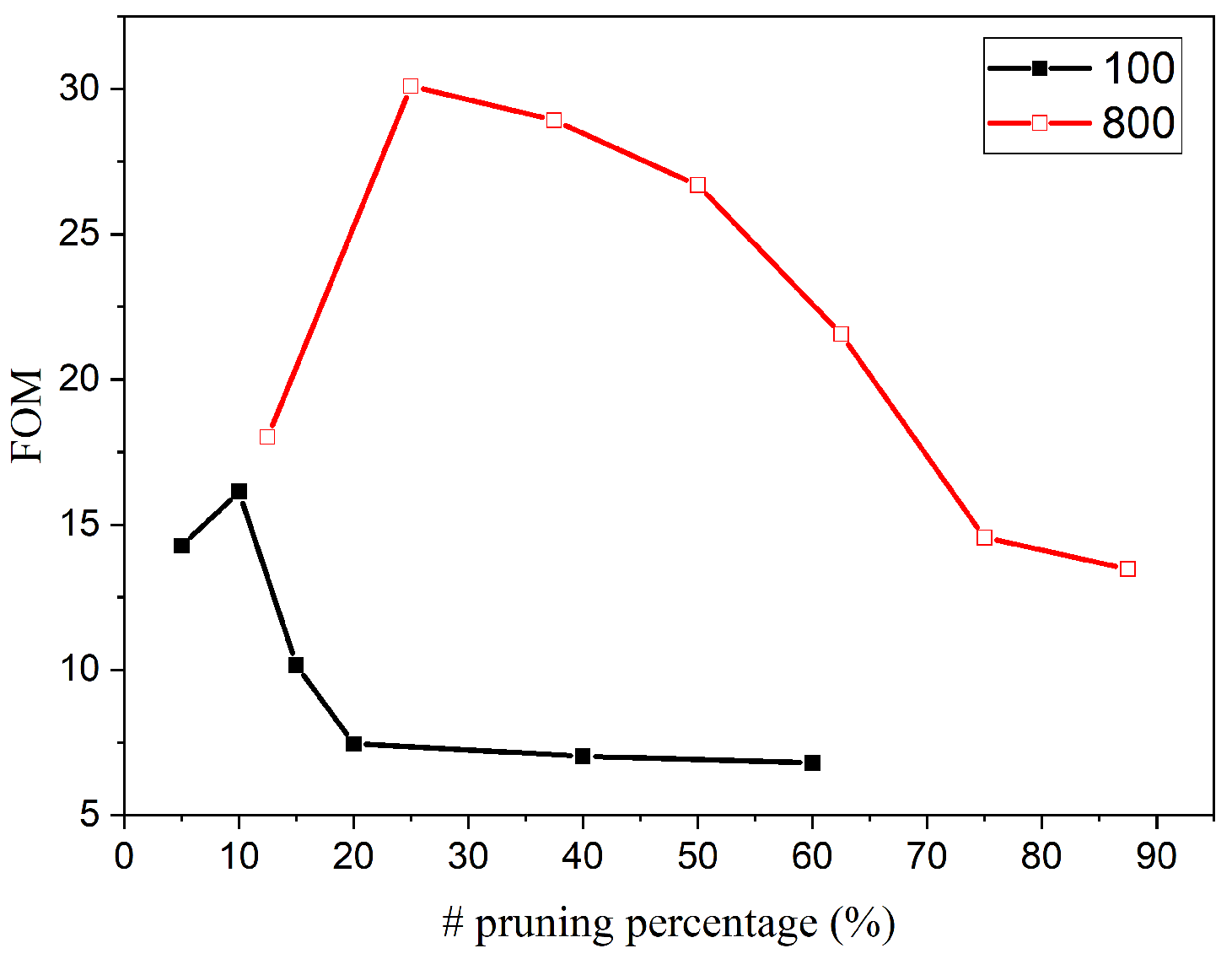
4.1.2. Comparison: 100 Output Neurons
4.1.3. Comparison: 800 Output Neurons
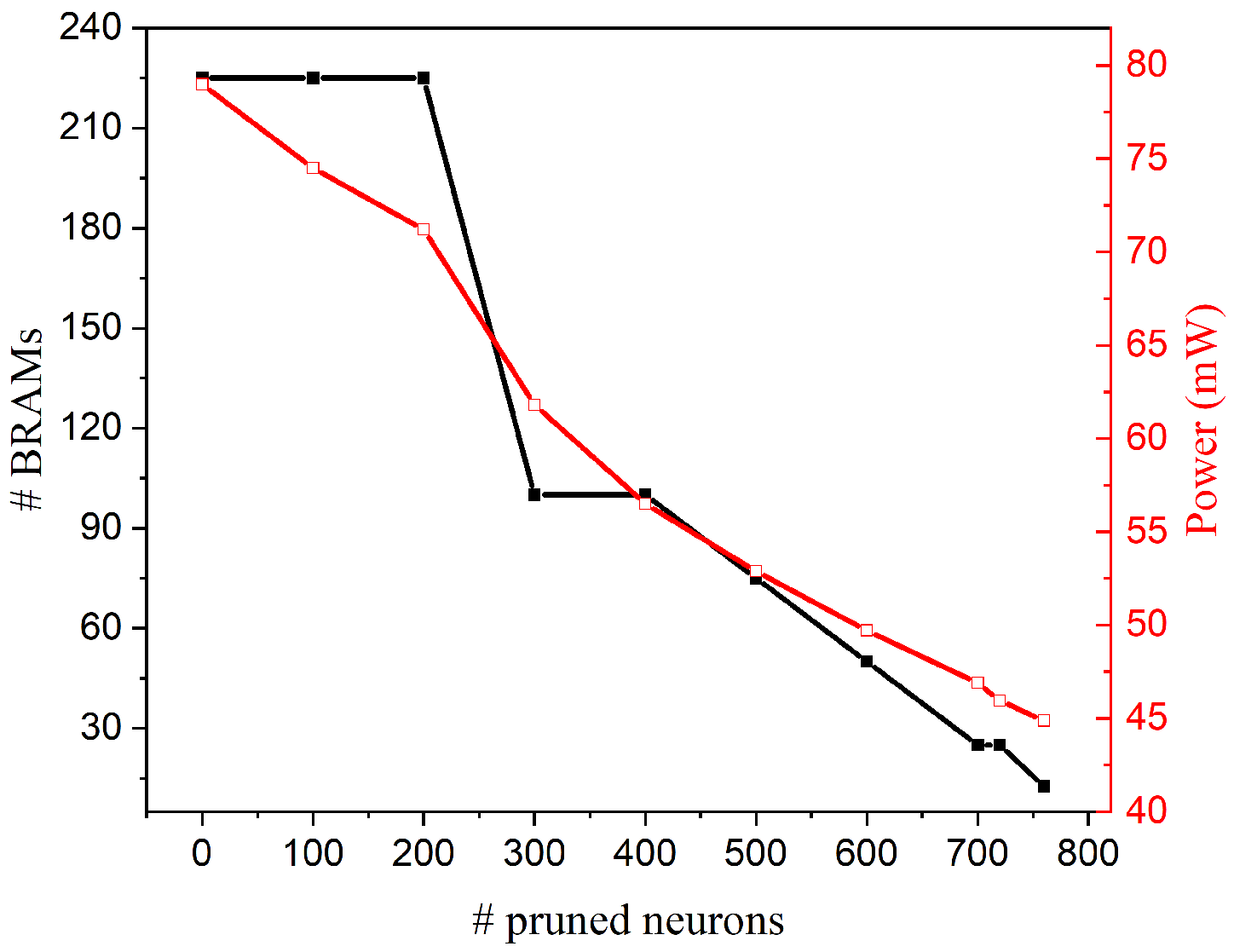
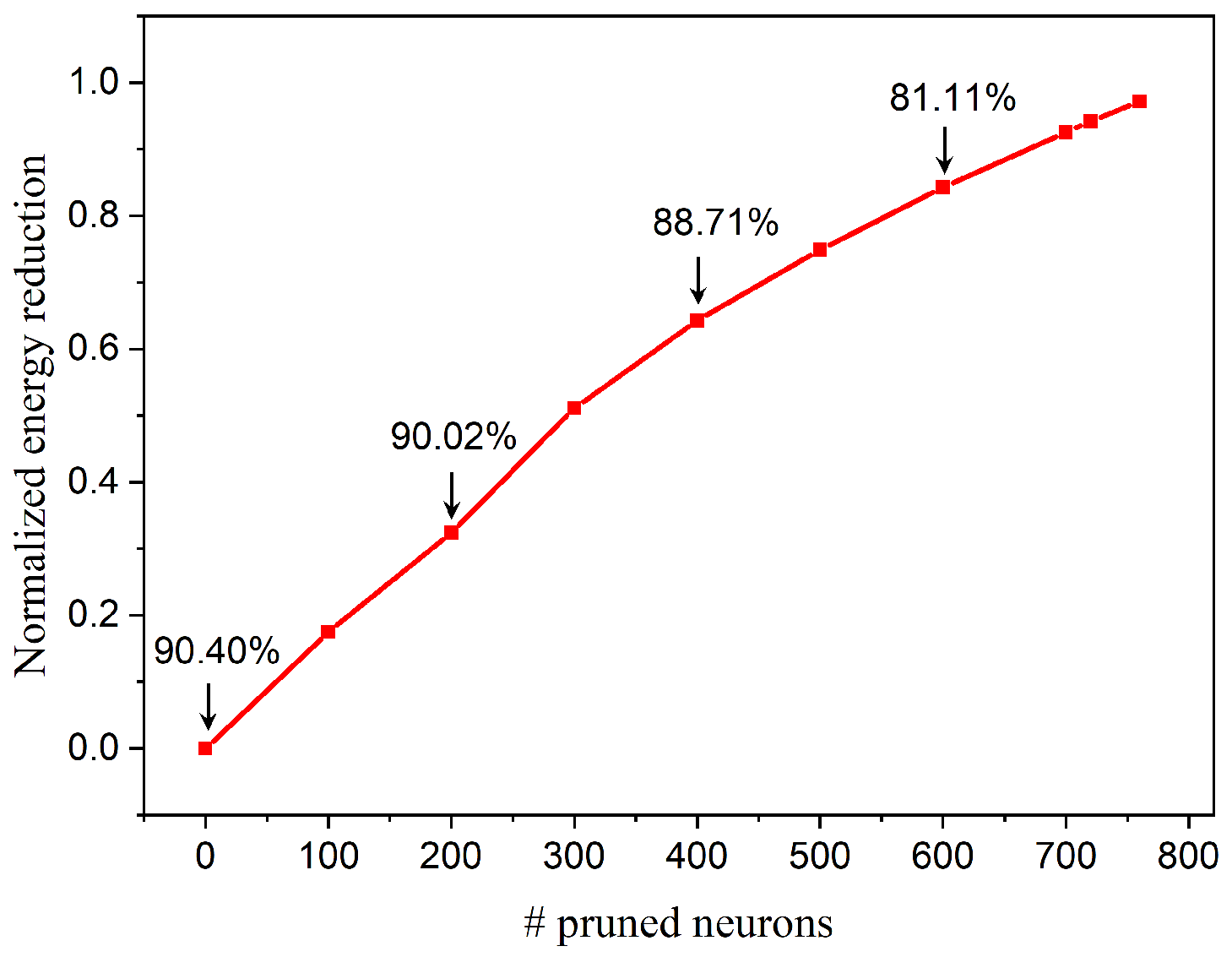
4.2. FPGA Implementation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grossfeld, R.M. An Introduction to Nervous Systems. Ralph J. Greenspan, editor. Integr. Comp. Biol. 2008, 48, 439–441. [Google Scholar] [CrossRef]
- Furber, S.B.; Galluppi, F.; Temple, S.; Plana, L.A. The SpiNNaker Project. Proc. IEEE 2014, 102, 652–665. [Google Scholar] [CrossRef]
- Davies, M.; Srinivasa, N.; Lin, T.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
- Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef] [PubMed]
- Tavanaei, A.; Ghodrati, M.; Kheradpisheh, S.R.; Masquelier, T.; Maida, A. Deep learning in spiking neural networks. Neural Netw. 2019, 111, 47–63. [Google Scholar] [CrossRef] [PubMed]
- Kolb, B.; Whishaw, I.Q. Fundamentals of Human Neuropsychology, 5th ed.; Worth Publishers: New York, NY, USA, 2003. [Google Scholar]
- Zillmer, E.; Spiers, M.; Culbertson, W. Principles of Neuropsychology; Thomson Wadsworth: Belmont, CA, USA, 2008. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning Both Weights and Connections for Efficient Neural Networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 1135–1143. [Google Scholar]
- Yu, J.; Lukefahr, A.; Palframan, D.; Dasika, G.; Das, R.; Mahlke, S. Scalpel: Customizing DNN pruning to the underlying hardware parallelism. In Proceedings of the 2017 ACM/IEEE 44th Annual International Symposium on Computer Architecture (ISCA), Toronto, ON, Canada, 24–28 June 2017; pp. 548–560. [Google Scholar] [CrossRef]
- Hu, H.; Peng, R.; Tai, Y.W.; Tang, C.K. Network Trimming: A Data-Driven Neuron Pruning Approach towards Efficient Deep Architectures. arXiv 2016, arXiv:1607.03250. [Google Scholar]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning Filters for Efficient ConvNets. arXiv 2016, arXiv:1608.08710. [Google Scholar]
- Moya Rueda, F.; Grzeszick, R.; Fink, G.A. Neuron Pruning for Compressing Deep Networks Using Maxout Architectures. In Pattern Recognition; Roth, V., Vetter, T., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 177–188. [Google Scholar] [CrossRef]
- Luo, J.H.; Wu, J.; Lin, W. ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5068–5076. [Google Scholar] [CrossRef]
- Molchanov, P.; Mallya, A.; Tyree, S.; Frosio, I.; Kautz, J. Importance Estimation for Neural Network Pruning. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–21 June 2019; pp. 11256–11264. [Google Scholar] [CrossRef]
- Dora, S.; Sundaram, S.; Sundararajan, N. A two stage learning algorithm for a Growing-Pruning Spiking Neural Network for pattern classification problems. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–16 July 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Chen, R.; Ma, H.; Xie, S.; Guo, P.; Li, P.; Wang, D. Fast and Efficient Deep Sparse Multi-Strength Spiking Neural Networks with Dynamic Pruning. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Dimovska, M.; Johnston, T.; Schuman, C.D.; Mitchell, J.P.; Potok, T.E. Multi-Objective Optimization for Size and Resilience of Spiking Neural Networks. In Proceedings of the 2019 IEEE 10th Annual Ubiquitous Computing, Electronics Mobile Communication Conference (UEMCON), New York, NY, USA, 10–12 October 2019; pp. 0433–0439. [Google Scholar] [CrossRef]
- Wu, D.; Lin, X.; Du, P. An Adaptive Structure Learning Algorithm for Multi-Layer Spiking Neural Networks. In Proceedings of the 2019 15th International Conference on Computational Intelligence and Security (CIS), Macau, China, 13–16 December 2019; pp. 98–102. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Diehl, P.; Cook, M. Unsupervised learning of digit recognition using spike-timing-dependent plasticity. Front. Comput. Neurosci. 2015, 9, 99. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, C.; Lefebvre, M.; Legat, J.; Bol, D. A 0.086-mm2 12.7-pJ/SOP 64k-Synapse 256-Neuron Online-Learning Digital Spiking Neuromorphic Processor in 28-nm CMOS. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 145–158. [Google Scholar] [CrossRef]
- Detorakis, G.; Sheik, S.; Augustine, C.; Paul, S.; Pedroni, B.U.; Dutt, N.; Krichmar, J.; Cauwenberghs, G.; Neftci, E. Neural and Synaptic Array Transceiver: A Brain-Inspired Computing Framework for Embedded Learning. Front. Neurosci. 2018, 12, 583. [Google Scholar] [CrossRef] [PubMed]
- Burkitt, N. A Review of the Integrate-and-Fire Neuron Model: I. Homogeneous Synaptic Input. Biol. Cybern. 2006, 95, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Pfister, J.P.; Gerstner, W. Triplets of spikes in a model of spike timing-dependent plasticity. J. Neurosci. 2006, 26, 9673–9682. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, K.E.; Han, W.; Stewart, D. Euler’s method. In Numerical Solution of Ordinary Differential Equations; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; Chapter 2; pp. 15–36. [Google Scholar] [CrossRef]
- Muslim, F.B.; Ma, L.; Roozmeh, M.; Lavagno, L. Efficient FPGA Implementation of OpenCL High-Performance Computing Applications via High-Level Synthesis. IEEE Access 2017, 5, 2747–2762. [Google Scholar] [CrossRef]
| Parameters | Value |
|---|---|
| The time constant for membrane potential update | 100 |
| The time constant for the presynaptic trace in the STDP model | 4 |
| The time constants for fast and slow postsynaptic traces in the STDP model respectively | 8, 16 |
| The time constant for the excitatory conductance | 1 |
| The time constant for the inhibitory conductance | 2 |
| The learning rates for presynaptic and postsynaptic update in the STDP model respectively | 0.0001, 0.01 |
| Threshold adaption constant | 0.01 |
| Methods | Accuracy (%) (100/800) | # Pruned Neurons (100/800) |
|---|---|---|
| No pruning | 85.78/90.4 | 0 |
| Constant pruning | 83.69/88.18 | 20/300 |
| Constant-threshold pruning | 83.89/87.89 | 20/300 |
| Adaptive pruning | 84.21/89.58 | 20/300 |
| Post-training pruning | 83.88/88.94 | 20/300 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Yantır, H.E.; Fouda, M.E.; Eltawil, A.M.; Salama, K.N. Towards Efficient Neuromorphic Hardware: Unsupervised Adaptive Neuron Pruning. Electronics 2020, 9, 1059. https://doi.org/10.3390/electronics9071059
Guo W, Yantır HE, Fouda ME, Eltawil AM, Salama KN. Towards Efficient Neuromorphic Hardware: Unsupervised Adaptive Neuron Pruning. Electronics. 2020; 9(7):1059. https://doi.org/10.3390/electronics9071059
Chicago/Turabian StyleGuo, Wenzhe, Hasan Erdem Yantır, Mohammed E. Fouda, Ahmed M. Eltawil, and Khaled Nabil Salama. 2020. "Towards Efficient Neuromorphic Hardware: Unsupervised Adaptive Neuron Pruning" Electronics 9, no. 7: 1059. https://doi.org/10.3390/electronics9071059
APA StyleGuo, W., Yantır, H. E., Fouda, M. E., Eltawil, A. M., & Salama, K. N. (2020). Towards Efficient Neuromorphic Hardware: Unsupervised Adaptive Neuron Pruning. Electronics, 9(7), 1059. https://doi.org/10.3390/electronics9071059






