A Spline Kernel-Based Approach for Nonlinear System Identification with Dimensionality Reduction
Abstract
1. Introduction
2. Related Work
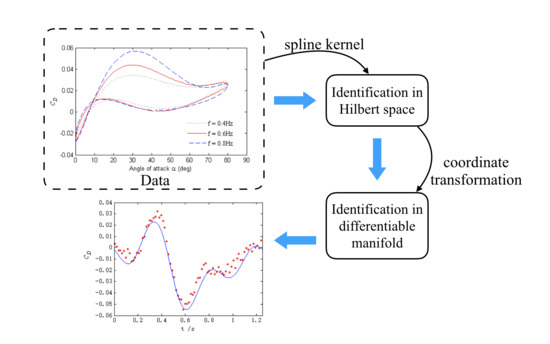
3. Proposed Framework
3.1. Problem Formulation
3.2. Spline Kernel-Based Identification Method
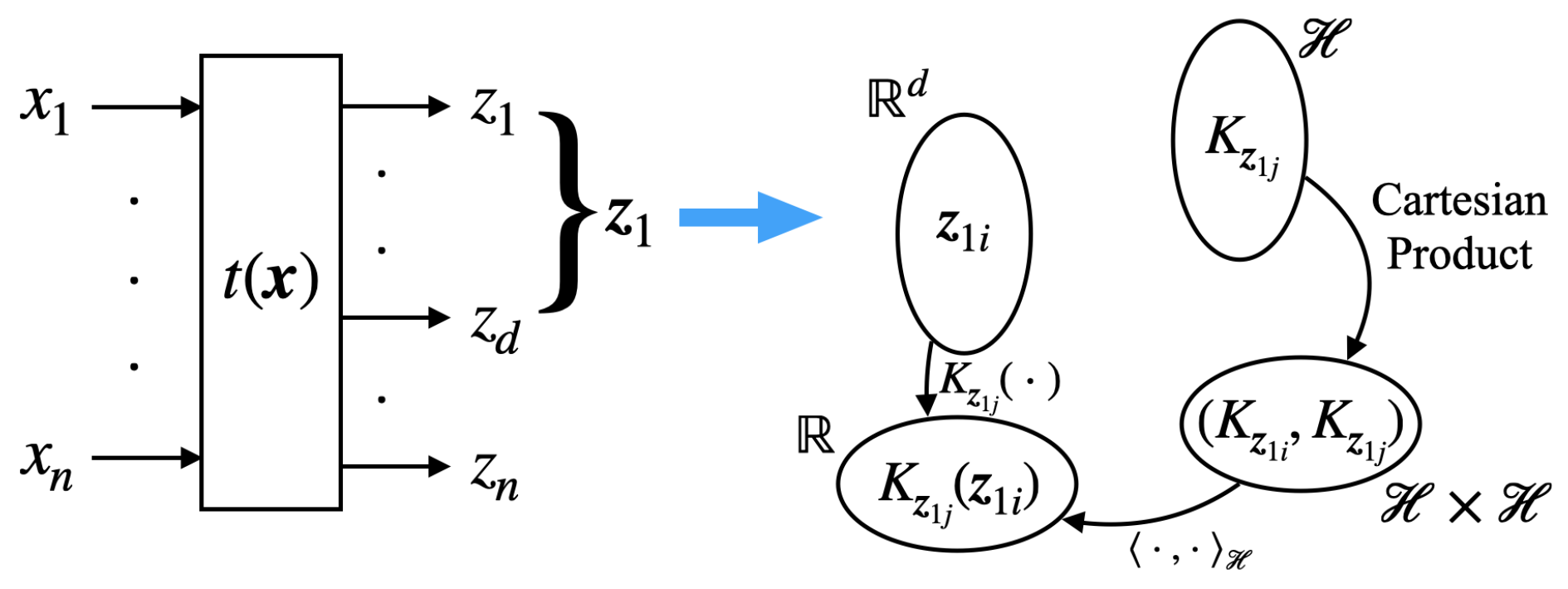
3.3. Dimensionality Reduction
4. Differential Manifold-Based Transformation
- The inverse function of can be found. For any in , .
- The functions and are both continuous and analytic on their domain of definition.
5. Simulation and Evaluation
5.1. Background Information
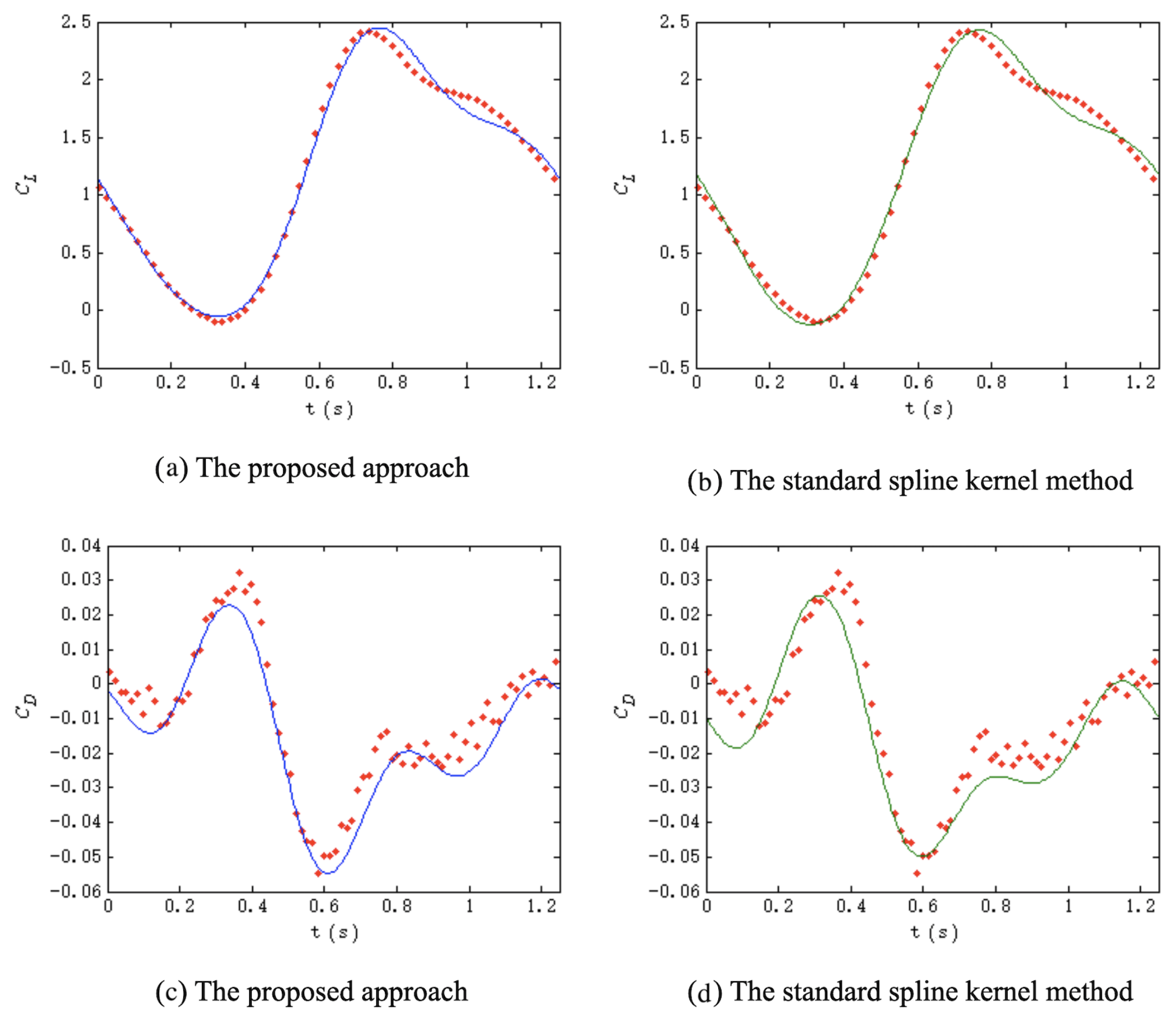
5.2. Comparison Results and Discussions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhu, M.; Feng, Z.; Zhou, X.; Xiao, R.; Qi, Y.; Zhang, X. Specific emitter identification based on synchrosqueezing transform for civil radar. Electronics 2020, 9, 658. [Google Scholar] [CrossRef]
- Guo, M.; Su, Y.; Gu, D. System identification of the quadrotor with inner loop stabilisation system. Int. J. Model. Identif. Control 2017, 28, 245–255. [Google Scholar] [CrossRef]
- Moreno, R.; Moreno-Salinas, D.; Aranda, J. Black-box marine vehicle identification with regression techniques for random manoeuvres. Electronics 2019, 8, 492. [Google Scholar] [CrossRef]
- Baldini, A.; Ciabattoni, L.; Felicetti, R.; Ferracuti, F.; Freddi, A.; Monteriù, A. Dynamic surface fault tolerant control for underwater remotely operated vehicles. ISA Trans. 2018, 78, 10–20. [Google Scholar] [CrossRef]
- He, W.; Ge, W.; Li, Y.; Liu, Y.J.; Yang, C.; Sun, C. Model identification and control design for a humanoid robot. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 45–57. [Google Scholar] [CrossRef]
- Veksler, A.; Johansen, T.A.; Borrelli, F.; Realfsen, B. Dynamic positioning with model predictive control. IEEE Trans. Control. Syst. Technol. 2016, 24, 1340–1353. [Google Scholar] [CrossRef]
- Haidegger, T.; Kovács, L.; Preitl, S.; Precup, R.E.; Benyo, B.; Benyó, Z. Controller design solutions for long distance telesurgical applications. Int. J. Artif. Intell. 2011, 6, 48–71. [Google Scholar]
- Ljung, L.; Wahlberg, B. Asymptotic properties of the least-squares method for estimating transfer functions and disturbance spectra. Adv. Appl. Probab. 1992, 24, 412–440. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, Y.; He, W.; Na, J.; Li, Z.; Xu, B. Adaptive parameter estimation and control design for robot manipulators with finite-time convergence. IEEE Trans. Ind. Electron. 2018, 65, 8112–8123. [Google Scholar] [CrossRef]
- Jasim, W.; Gu, D. Robust path tracking control for quadrotors with experimental validation. Int. J. Model. Identif. Control 2018, 29, 1–13. [Google Scholar] [CrossRef]
- Pillonetto, G.; De Nicolao, G. Pitfalls of the parametric approaches exploiting cross-validation for model order selection. IFAC Proc. Vol. 2012, 45, 215–220. [Google Scholar] [CrossRef]
- Fanesi, M.; Scaradozzi, D. Adaptive control for non-linear test bench dynamometer systems. In Proceedings of the 2019 IEEE 23rd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 9–11 October 2019; pp. 768–773. [Google Scholar]
- Sun, J.; Yang, Q. Research on least means squares adaptive control for automotive active suspension. In Proceedings of the 2008 IEEE International Conference on Industrial Technology, Chengdu, China, 21–24 April 2008; pp. 1–4. [Google Scholar]
- Yang, E.; Gu, D.; Hu, H. Performance improvement for formation-keeping control using a neural network HJI approach. In Trends in Neural Computation; Springer: Berlin, Germany, 2007; pp. 419–442. [Google Scholar]
- He, W.; Yan, Z.; Sun, Y.; Ou, Y.; Sun, C. Neural-learning-based control for a constrained robotic manipulator with flexible joints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5993–6003. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Jiang, T.; Li, S.; Yang, Y. Automated feature learning for nonlinear process monitoring—An approach using stacked denoising autoencoder and k-nearest neighbor rule. J. Process. Control 2018, 64, 49–61. [Google Scholar] [CrossRef]
- Zhou, X.; Jiang, P.; Wang, X. Recognition of control chart patterns using fuzzy SVM with a hybrid kernel function. J. Intell. Manuf. 2018, 29, 51–67. [Google Scholar] [CrossRef]
- Ai, Q.; Wang, A.; Zhang, A.; Wang, W.; Wang, Y. An effective multiclass twin hypersphere support vector machine and its practical engineering applications. Electronics 2019, 8, 1195. [Google Scholar] [CrossRef]
- Chodunaj, M.; Szcześniak, P.; Kaniewski, J. Mathematical modeling of current source matrix converter with Venturini and SVM. Electronics 2020, 9, 558. [Google Scholar] [CrossRef]
- Pillonetto, G.; De Nicolao, G. A new kernel-based approach for linear system identification. Automatica 2010, 46, 81–93. [Google Scholar] [CrossRef]
- Han, T.; Wang, L.; Wen, B. The kernel based multiple instances learning algorithm for object tracking. Electronics 2018, 7, 97. [Google Scholar] [CrossRef]
- Pillonetto, G.; Dinuzzo, F.; Chen, T.; De Nicolao, G.; Ljung, L. Kernel methods in system identification, machine learning and function estimation: A survey. Automatica 2014, 50, 657–682. [Google Scholar] [CrossRef]
- Chen, T. Continuous-time DC kernel-a stable generalized first-order spline kernel. IEEE Trans. Autom. Control 2018, 63, 4442–4447. [Google Scholar] [CrossRef]
- Dreano, D.; Tandeo, P.; Pulido, M.; Ait-El-Fquih, B.; Chonavel, T.; Hoteit, I. Estimating model-error covariances in nonlinear state-space models using Kalman smoothing and the expectation—Maximization algorithm. Q. J. R. Meteorol. Soc. 2017, 143, 1877–1885. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Prescribed performance fault-tolerant control of uncertain nonlinear systems with unknown control directions. IEEE Trans. Autom. Control 2017, 62, 6529–6535. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, H.; Xiao, G.; Su, H. Tracking control optimization scheme of continuous-time nonlinear system via online single network adaptive critic design method. Neurocomputing 2017, 251, 127–135. [Google Scholar] [CrossRef]
- Ding, F.; Xu, L.; Alsaadi, F.E.; Hayat, T. Iterative parameter identification for pseudo-linear systems with ARMA noise using the filtering technique. IET Control Theory Appl. 2018, 12, 892–899. [Google Scholar] [CrossRef]
- Esfahani, A.F.; Dreesen, P.; Tiels, K.; Noël, J.P.; Schoukens, J. Parameter reduction in nonlinear state-space identification of hysteresis. Mech. Syst. Signal Process. 2018, 104, 884–895. [Google Scholar] [CrossRef]
- Zanotti, C.; Rotiroti, M.; Sterlacchini, S.; Cappellini, G.; Fumagalli, L.; Stefania, G.A.; Nannucci, M.S.; Leoni, B.; Bonomi, T. Choosing between linear and nonlinear models and avoiding overfitting for short and long term groundwater level forecasting in a linear system. J. Hydrol. 2019, 578, 124015. [Google Scholar] [CrossRef]
- Schaefer, I.; Kosloff, R. Optimization of high-order harmonic generation by optimal control theory: Ascending a functional landscape in extreme conditions. Phys. Rev. A 2020, 101, 023407. [Google Scholar] [CrossRef]
- Mu, B.; Chen, T.; Ljung, L. On asymptotic properties of hyperparameter estimators for kernel-based regularization methods. Automatica 2018, 94, 381–395. [Google Scholar] [CrossRef]
- Steinwart, I.; Hush, D.; Scovel, C. An explicit description of the reproducing kernel Hilbert spaces of Gaussian RBF kernels. IEEE Trans. Inf. Theory 2006, 52, 4635–4643. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Fang, W.; Zhang, L.; Yang, S.; Sun, J.; Wu, X. A multiobjective evolutionary algorithm based on coordinate transformation. IEEE Trans. Cybern. 2019, 49, 2732–2743. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Qin, M.; Chen, X.; Meng, L.; Huang, Q.; Fu, C. Computationally efficient coordinate transformation for field-oriented control using phase shift of linear hall-effect sensor Signals. IEEE Trans. Ind. Electron. 2019, 67. [Google Scholar] [CrossRef]
- Isidori, A. Nonlinear Control Systems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Liu, C.; Zhao, Z.; Bu, C.; Wang, J.; Mu, W. Double degree-of-freedom large amplitude oscillation test technology in low speed wind tunnel. Acta Aeronaut. Astronaut. Sin. 2016, 37, 2417–2425. [Google Scholar]

| Physical Parameter | Value |
|---|---|
| Weight | ≤8 kg |
| Length | 1.1825 m |
| Wing Span | 0.8475 |
| Wing Area | 0.3047 m |
| Mean Aerodynamic Chord | 0.4269 m |
| Position of Aerodynamic Center | 0.6926 m |
| Algorithm | ||
|---|---|---|
| The Proposed Approach | 1.2996 | 0.0032 |
| The Standard Kernel Method | 1.6458 | 0.0102 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhu, J. A Spline Kernel-Based Approach for Nonlinear System Identification with Dimensionality Reduction. Electronics 2020, 9, 940. https://doi.org/10.3390/electronics9060940
Zhang W, Zhu J. A Spline Kernel-Based Approach for Nonlinear System Identification with Dimensionality Reduction. Electronics. 2020; 9(6):940. https://doi.org/10.3390/electronics9060940
Chicago/Turabian StyleZhang, Wanxin, and Jihong Zhu. 2020. "A Spline Kernel-Based Approach for Nonlinear System Identification with Dimensionality Reduction" Electronics 9, no. 6: 940. https://doi.org/10.3390/electronics9060940
APA StyleZhang, W., & Zhu, J. (2020). A Spline Kernel-Based Approach for Nonlinear System Identification with Dimensionality Reduction. Electronics, 9(6), 940. https://doi.org/10.3390/electronics9060940