Abstract
In recent years, the distribution of local and renewable generation plants has introduced significant challenges in the management of electrical energy. In order to increase the usage of renewable energy, the prosumers, i.e., the residential users that can act both as producers and consumers, can benefit from joining together and forming energy communities. The deployment of an energy community is based both on technological advancements and on a deep understanding of human decision-making, which in turn requires knowledge about the factors that influence the behavior of residential users. This new scenario calls for great research investigations aimed to improve the management of energy exchanges inside energy communities. An important role in this context is played by the Internet of Things (IoT) technology, as smart IoT objects are used both as a source of real-time information regarding the energy production and the users’ requirements, and as actuators that can help to regulate the distribution and use of energy. In this paper, an IoT-aware optimization model for the energy management in energy communities is presented. The main novelty consists in modeling the entire energy community as a whole, rather than each prosumer separately, with the goal of optimizing the energy sharing and balance at the community level. Experimental results, performed in an university campus, show the advantages of the approach and its capability of reducing the energy costs and increasing the community’s energy autonomy.
1. Introduction
The entire energy chain is in the midst of a major global transformation fueled by multilateral efforts focused on the shift towards an increasingly clean, intelligent, mobile, and distributed energy ecosystem. The rapid diffusion of renewable energy production plants, and the opening of national energy markets, have encouraged end-users to form energy communities, in which the producers can sell energy directly to consumers at advantageous local market prices [1,2].
The European Parliament has published a Renewable Energy Directive (RED II) [3] that defines an energy community as a legal autonomous entity that is based on open and voluntary participation and is effectively controlled by its members. As underlined in [4], the members of energy communities are entitled to: (i) produce, consume, store, and sell renewable energy; (ii) share, within the community, renewable energy that is produced locally; (iii) access and negotiate directly with the energy provider that applies wholesaler energy prices. The main advantages are the increase of energy self-consumption, the reduction of energy costs for the consumers and the increase of revenues for the producers. To achieve these advantages, appropriate models for the management of energy communities need to be envisioned.
The efficient management of energy needs to be assisted by a massive use of information and communication technology (ICT), in order to integrate the distributed energy systems with the Internet of Things (IoT). Indeed, smart IoT objects are used both as a precious source of real-time information, for example regarding the energy production and the users’ requirements, and as actuators that can help to regulate the distribution and use of energy. In this context, the new term Internet of Energy (IoE) [5] is used to identify the research area that aims to understand how the increasingly prominent market of the Internet of Things technology can be applied to energy management and smart grids.
In [6], the authors have proposed an energy management model for residential users. The model solves the so-called prosumer problem, and is capable of satisfying the user needs with minimum energy costs, by optimally managing local loads, storage systems, and controllable plants. Common goals are shared in the two-stage approach proposed in [7], which enables the redistribution of the amount of renewable energy, produced within a community, which is in excess after the solution of the prosumer problem in the first stage. The model minimizes the costs and maximizes the revenues both for single prosumers and for the community as a whole.
This paper in an extended and revised version of the conference paper [8]. We present a new optimization approach that applies the concept of energy community to a set of individual prosumers. Starting from input information about energy tariffs, energy needs, and energy production forecasts obtained by means of IoT devices, the model computes the scheduling plan of the electrical loads, and the amounts of energy exchanges, which minimize the overall cost. The objective function forces the minimization of the global energy cost obtained by summing the energy costs/revenues incurred by all the users of the community. The prosumers are enabled and encouraged to exchange energy with the other prosumers, as such energy is priced at a more convenient tariff, and are induced to limit energy exchanges outside the community, priced at a worse tariff. To clarify the novel contribution, in the following, we describe the main peculiarities of the approach evaluated in [6] and [7]—referred to as “Separated”—and of the approach assessed here–referred to as “Unified”—and illustrate the most important aspects:
- Separated. In [6,7], the optimization problem is solved separately for each prosumer, taking into accounts his/her energy needs and production. Therefore, the solution of the problem for a prosumer cannot consider the demand and production of all the other prosumers.
- Unified. With the new approach presented here, the optimization problem takes into account the energy needs and production profiles of all the prosumers, by considering not only the energy exchanges of each prosumer with the grid, but also the exchanges between the prosumers.
The main advantages of the Unified model are: (i) the optimal solution minimizes the energy cost of the community as a whole; (ii) the fraction of self-consumption i.e., of the amount of energy that is produced and consumed locally, is increased; (iii) it is possible to reduce the peaks of power demand, which is beneficial for the system management.
The paper is organized as follows: Section 2 discusses related work regarding both the technological advancements that enable energy communities and the factors that influence the user behavior; Section 3 presents the Internet of Things architecture that supports the energy management approach discussed in this paper; Section 4 illustrates the optimization model that computes the daily scheduling plan of energy loads that optimizes the energy exchanges and minimizes the energy cost incurred by the community; Section 5 evaluates the effectiveness of the proposed model in a specific scenario, i.e., the University of Calabria Campus, in Italy. Finally, Section 6 concludes the paper and suggests some possible avenues for future work.
2. Related Work
As mentioned in the introductory section, the Internet of Energy paradigm provides the digital foundation for transforming the traditional energy system, in order to improve its efficiency and its ability to exploit the diffusion of local energy communities that are willing to share the energy produced by local renewable sources. The change to the IoE model is already underway thanks to the availability of smart meters and new communications networks, and is stimulated by huge investments in the area of energy distribution automation [9]. Indeed, the integration of smart meters within the distributed energy systems allows for monitoring the physical state of loads and production systems, and for collecting data that is useful to forecast energy needs and energy production, as required by several optimization models for energy communities.
In [10], the authors propose an IoT-based framework for Energy Communities that enables the optimization of networked micro-grids, where each micro-grid is managed as a single consumer/producer from both electrical and market perspectives. A real-world practical application of energy community management is presented in [11], in which the implementation of the ICT architecture and other enabling technologies are discussed in detail.
The authors of [12] consider peer-to-peer (P2P) energy trading as a next-generation energy management mechanism for the smart grid that enables each prosumer of the network to participate in energy trading with one another and the grid. The principles and mechanisms for P2P cost and energy sharing are also presented in [13,14,15,16]. In [17], a coalition-based optimization problem is introduced to coordinate the operations of energy management systems in multiple households. The works presented in [18,19] propose real-time cooperative models for the energy management among grid-connected micro-grids. In the former paper, a cooperative logarithmic-barrier method is used to solve the predictive control problem in a distributed fashion, while, in the latter paper, a greedy search algorithm is adopted to match the energy needs of the prosumers.
Numerous recent studies have focused on energy management systems with energy storage devices. In [20], the authors aim to understand the potential of energy storage devices for residential energy management, and the ability of these devices to address intermittent nature of renewable energy generation. Innovative enabling IoT technologies and systems, such as smart meters, energy controllers, and communication systems, are also described. In [21], the exchange of energy among the house in a community is investigated by adopting a cooperative game theory model that aims to reduce the overall battery usage and prolong the life of batteries. An analytical framework is developed in [22] to define optimal mutual goals for prosumer communities using multiple-criteria goal programming techniques.
The deployment of an energy community is based not only on technological advancements, but also on a deep understanding of human decision-making, which in turn requires knowledge about the factors that influence human behavior. Identifying these factors provides a basis for theoretical and empirical work related to energy behavior. A large amount of research work have analyzed the consumption behavior [23,24,25,26]. However, the shift from a pure consumption role to a mixed role that includes production, storage, and consumption is dramatically changing both the electricity market and the user behavior. In this context, the need emerges for approaching the more human-centric electricity system shaped by active prosumers.
In [27], the authors identified a number of parameters, both quantitative and qualitative, which directly or indirectly influence the prosumers’ energy sharing behaviors. The quantitative effect of these parameters can be assessed as an increase or decrease in the amount of energy shared by a prosumer. The authors analyze two types of parameters: internal and external. Internal parameters can be captured within the prosumer’s operating domain and directly influence the amount of shared energy. Such parameters include the user’s energy consumption and the energy generation activities. Internal parameters also include contextual factors that add positive or negative weights to the final amount of energy shared with the grid. Some of those factors are the prosumer’s socio-cultural views, the financial ability to afford the cost of the technical infrastructures needed to energy sharing, the user’s availability to be involved in the energy sharing process, the educational knowledge on energy sharing concepts and benefits, and the living and residential conditions (urban or rural). Unlike the internal parameters, the external parameters are captured from various different domains other than the prosumer’s environment. They include energy market conditions, energy trading possibilities, electricity price, incentives, contracts, government jurisdiction, technical infrastructures, and weather forecasts. All of these factors indirectly influence the energy sharing activities of prosumers.
In [28], the authors analyzed the prosumers’ energy profiles in terms of energy generation, energy consumption, and energy sharing, using a dataset of 500 prosumers. They deduced that the energy sharing profiles of prosumers are not static, as they can vary both within a day and along an entire year. Therefore, the research contributions that aim to investigate the prosumer behavior should consider this variable nature of energy profiles. In [29], the authors introduced the concept of a goal-oriented Prosumer Community Group (PCG) as an improved method of grouping prosumers, which consists in the aggregation of the prosumers that present similar energy behaviors. Each prosumer community group is associated with a set of prequalification criteria that a new prosumer should match in order to join the group. Two key parameters are the upper and lower energy boundaries of the PCG: to receive the membership within the group, the prosumer’s energy sharing capacity should lie within those boundaries.
In [30], the authors present a framework that provides a basis for understanding and forecasting the prosumer behavior in an energy community. The framework focuses on the roles of different prosumer acts, such as consuming, storing, sharing, and selling. Different factors, related to both personal and contextual domains, influence the individual prosumer’s preferences, the decision-making processes and the selection of one or more of the mentioned prosumer acts. A prosumer operates to achieve not only individual goals, but also collective values, beliefs, norms, and goals.
In addition to the human behavior, public policies also influence the deployment of energy communities. Public policies can operate directly, with interventions that affect the deployment of smart grids, or indirectly, by altering the economic and regulatory landscapes that influence grid and end-user interactions. To be effective, policies should address the key barriers that hinder the deployment of smart grids, and should be designed to leverage the drivers that promote investments in smart-grid technologies [31]. Policy and regulatory drivers include, for example, feed-in tariffs and net-metering rules that provide incentives to deepen the aggregation in energy communities, policies that aim to minimize carbon emissions, incentives or requirements for green building practices, participation in demand-response programs, incentives for metering at on-site renewable energy systems, etc. Policies can also stimulate the development of new platforms for delivering energy services, reduce the financing costs for infrastructure investments, and offer tax advantages for smart grid assets and renewable sources [32]. Public procurement rules can help smart energy communities to diffuse widely, and reach critical mass in the market in the next few years [33].
3. IoT Architecture for the Energy Community
In order to optimize the energy exchange inside the energy community, this latter needs to be purposely instrumented by IoT devices that are able to interact with the physical components and inject smartness into the management of the whole energy community.
IoT devices, together with the communication network and data management system, constitute the Advanced Metering Infrastructure (AMI), which plays a vital role in energy community and power delivery systems by recording the consumption and production profiles and facilitating bi-directional information flows. IoT devices for residential users include state-of-the-art hardware and software devices, capable of measuring and collecting data in real time or at desired time intervals. These devices transmit information to a remote data center with which they have an established Internet connection. Communication in an AMI is bidirectional, as IoT and smart devices can accept command signals and act accordingly. Common IoT devices used in this context are electronic platforms such as the Arduino, with a limited computing capacity, and the Raspberry Pi, which is more powerful. In both cases, communication is established on an Internet connection.
In this section, we introduce the Internet of Things architecture, also referred to as energy district, which enables the application to the energy community of the optimization model described in the rest of the paper. The energy district comprises a number of prosumers that join together and form an energy community. Each prosumer is equipped with the following components:
- a nanogrid system, which manages the energy exchange between the prosumer and the distribution grid, the local energy production plants, and the storage system;
- a home automation system, which manages the activation and deactivation of the loads hosted inside the dwellings.
All the prosumers of the community communicate with a centralized component that is in charge of managing the whole community. Each prosumer hosts a software system, the Smart Energy Aware Gateway (SEAG), which manages both the nanogrid and the home automation system, and interacts with the centralized component.
In particular, the SEAG is designed to cope with the heterogeneity of devices that are built by different vendors with different technologies. The SEAG is an IoT system which intelligently controls the physical devices included in the nanogrid and in the home automation system, and interacts with the local smart meters to build a detailed and comprehensive profile of the user’s energy production and consumption. In addition, the SEAG is in charge of interacting with the centralized component that includes the aggregator of the district and a service provider that supplies to the SEAGs high-level information needed for their local optimization tasks. Figure 1 shows the whole IoT architecture, including the prosumers and the centralized component.
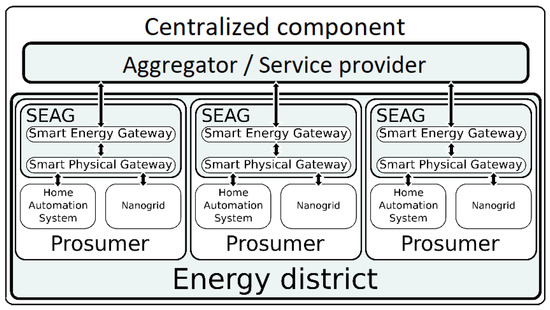
Figure 1.
The energy district.
As mentioned before, the centralized component is composed of two entities: (i) the aggregator and (ii) the service provider. The former is in charge of managing the energy exchanges among the prosumers and between the whole community and the main grid. The latter executes a set of algorithms on a daily basis with the goal of obtaining information concerning:
- the hour-by-hour energy production forecasts based on the weather forecast and the physical characteristics of the generation plants;
- the hour-by-hour prices of energy, which are determined by the conditions of the energy market.
This information is retrieved every day for the following day and is taken into account by the aggregator in order to elaborate a proper working plan for the nanogrid and the home automation system for all the prosumers with the aim of optimizing the energy consumption and reduces costs. In particular, the aggregator solves the optimization model presented in the next section, which takes the energy production forecasts and the electrical energy prices as input and computes the optimal schedule for: (i) the activation/deactivation of the loads, (ii) the use of the storage systems, and (iii) the amount of energy exchanged by the prosumers or imported/exported from/to the grid.
The prosumer SEAG is composed of two layers, as shown in Figure 1: the Smart Energy Gateway, devoted to the communications with the centralized component, and the Smart Physical Gateway which is in charge of interacting with the physical component, namely the nanogrid and the home automation system. Several technologies can be used to implement a home automation system. We adopted one of the most popular, i.e., Konnex, a standard developed by the KNX Association, which is open, platform-independent and approved as an European Standard (EN 50090 - EN 13321-1).
In the experimental testbed described in this paper, the SEAG is installed on a Raspberry Pi 3 single-board computer [34]. The Raspberry Pi is a general-purpose computer that represents a good solution since its performances are adequate to the goal, and at the same time it has a low energy consumption and a small size, which allows it to be deployed in a domestic environment.
In order to communicate with the home automation system, an Arduino Mega micro-controller is adopted since it is a small and inexpensive electronic board that allows for connecting to various external accessories (such as sensors) and create applications to use the collected data. In particular, an actuation on a load is managed through the Arduino Mega by operating an on/off command. The energy consumption and the state of loads can be monitored through the same micro-controller.
Nanogrid systems are instead conceived for managing the usage of energy in a dwelling, which is especially useful when the dwelling is equipped with local renewable energy generation plants or storage devices. Low-level information such as the values of energies and the state of battery charge are regularly monitored by an Atmel board and sent to the SEAG.
All the interactions among the physical components are managed by a software IoT platform [35], written in Java that includes several layers. The core component, in particular, contains two layers that provide the essential abstractions and functionalities: an agent layer and a virtual object layer.
A set of agent servers, ubiquitously located in the system, form the the agent layer on which a set of agents execute and interact with each other. Agents are computational entities able to pursue their goals in a flexible and autonomous fashion by interacting with each other and with the environment. A peculiar property of the multi-agent systems [36] is the so-called emergent behavior, i.e., a complex behavior that emerges from the interaction of simple individual behaviors. The emergent behavior paradigm is able to ensure important properties such as adaptivity, resilience, and fault tolerance.
The virtual object layer is used as the container of the so-called virtual objects, which are software abstractions of the actual physical components. Virtual objects hide the heterogeneity of the hardware by supplying a standardized and flexible interface for abstracting the functionalities of the physical IoT devices. In particular, the virtual object interface generalizes the read and actuation operations that allow the applications to retrieve information and control the physical devices. The virtual object interface also provides an event-based mechanism that allows the agents to be asynchronously notified about some event occurrences, i.e., when a resource state changes. Moreover, agents can subscribe to complex events defined by boolean rules over groups of functionalities.
The two layers, the agent and the virtual object layer, are co-located in the same process in order to speed up the execution and cope with real-time scenarios. Instead of transferring data to a central processing unit (the cloud component), agents are enabled to execute locally on the SEAG that is directly connected to the physical devices. As a consequence, less data need to be transferred towards remote hosts and local access and computation are fostered in order to achieve better performance and scalability.
4. A Model for the Optimal Energy Sharing in an Energy Community
This section describes the Unified optimization model for the optimal energy sharing in an energy community. The optimization problem can be classified as a mixed integer linear programming problem, in which some variables are constrained to be integer or binary, and some others can assume real values. The model takes as input the user energy needs, the energy production forecasts (obtained by analyzing the data acquired by means of IoT devices), and the energy tariffs related to the following day and then computes the optimal daily scheduling plan for controllable loads, local plants, and storage systems located at the users’ dwellings. The optimal solution also gives information about the energy values that the users exchange during the day. The definition of the objective function, presented in the following, forces the model to minimize the global energy cost obtained by summing the energy costs/revenues of the users that join the community. As mentioned before, the model encourages the energy sharing within the community and limits energy exchanges with the external grid, which are priced at a worse tariff. The unified model allows for increasing self-consumption and fosters the energy autonomy of the community.
The next subsection focuses on the electrical tariffs applied to compute the energy cost. Then, we provide a description of the sets, the variables, the objective function, and the constraints of the proposed model, emphasizing the differences between the Separated and the Unified models. The temporal granularity for all the quantities is the hour, e.g., the power consumed by the loads as well as the power produced by the plants or exchanged with the storage systems at a given hour h (say, 9:00) are assumed to be constant within a one-hour interval (between 9:00 and 10:00).
4.1. Electrical Energy Tariffs
The electrical energy tariffs are defined by the daily trend of the energy market. In our scenario, the Italian energy market defines the wholesaler energy prices: the zone price () and the single national price (), i.e., the selling price and the basic buying cost applied at hour h when importing/exporting energy from/to the external grid. Conversely, the selling price and the buying cost applied to exchange energy inside the community are denoted, respectively, by , . To ensure that users are encouraged to share energy among them, it must hold that and .
To be more specific, the values of and should be set depending whether an economical gain is to be guaranteed to the community manager, for example to incur the maintenance costs. In such a case, the value of should be lower than the value of . On the other hand, if the objective is to maximize exclusively the profit of the prosumers, the two values must be set equal to each other, i.e., to a single value . Figure 2 shows an example of the trend of the prices and costs for a specific day, i.e., 18 February 2020. In the following, we consider the general case in which and can assume different values.
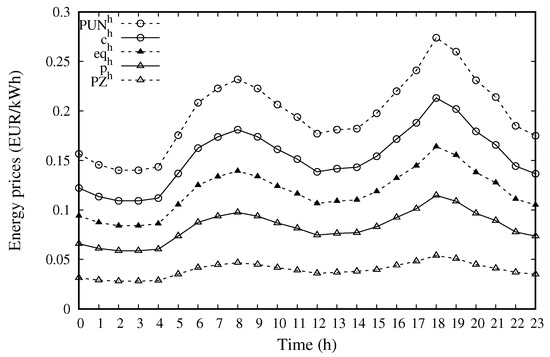
Figure 2.
Example of daily trends for the costs and prices of electrical energy.
4.2. Definition of Sets and Variables
In the following, we report the sets and variables that are used in the optimization model. The quantities that are used exclusively in the Unified model, i.e., which are not present in the Separated model, are reported in bold:
4.2.1. Sets
- set of the hours of a day
- set of users joining the community
- set of schedulable loads of user
- set of schedulable and non-interruptible loads of user
- set of non-schedulable loads of user
4.2.2. Variables
- electrical energy imported from the community at hour by user []
- electrical energy exported to the community at hour by user []
- electrical energy imported from the grid at hour by user []
- electrical energy exported to the grid at hour by user []
- state of the schedulable load at hour by user []
- electrical energy stored in the energy storage system during hour by user []
- electrical energy drawn from the energy storage system during hour by user []
4.3. Objective Function
The objective function of the optimization model aims to minimize the global energy cost obtained by summing the energy costs (positive values) and the revenues (negative values) of the community users. The expression in Label (1) is defined as the sum of four terms for each user :
- , the cost incurred by user u at hour h to import energy from the community;
- , the revenue obtained by user u at hour h by selling energy to the community;
- , the cost incurred by user u at hour h to import energy from the external grid;
- , the revenue obtained by user u at hour h by selling energy to the external grid:
The terms and are present only in the Unified model.
4.4. Constraints
The optimization model comprises a set of constraints, which are discussed in the following. In particular, Equations (2), (5)–(10) hold in both the Separated and the Unified model, while Equations (3) and (4) hold only for the Unified model, as they constrain the energy exchanges among the community users.
In detail, Equation (2) describes the energy balancing for each user and at each hour :
In the balance, the following energy components are considered: the energy produced from other prosumers of the community (), the energy imported from the grid (), the energy supplied by u to the community (), the energy injected to the grid (), the energy supplied by the storage system of u (, where is the discharging efficiency factor), the energy charged in the storage system of u (, where is the charging efficiency factor), the sum of the energy quantities consumed by the schedulable loads (), computed as the products of the variables and the rated powers (the rated power, expressed as energy/hour, can be considered as an amount of energy since the time interval is equal to an hour) , the sum of the forecast energy quantities consumed by non-schedulable loads () and the forecast energy produced by the local photovoltaic (PV) generators ().
Equation (3) balances the energy exchanges within the community:
The inequality (4) forces the total amount of imported energy, i.e., from the community () or from the external grid (), not to exceed the maximum operation power (the maximum operation power, expressed as energy/hour, can be considered as an amount of energy since the time interval is equal to an hour) of the Point Of Delivery (POD), :
For each user u, and for each schedulable load , let us introduce the duration in hours of the working time and the range of hours to which the working time must belong. The auxiliary variable is set to 1 at the hour h at which the schedulable load a is activated, and is set to 0 at any other hour. Equations (5) and (6) force the activation of load a to occur at a single hour . The upper bound of the latter interval is set to , instead of , in order to ensure that the working time of the load a ends before :
Inequalities (8) force every non-interruptible load to operate during its working time, without interruptions. Indeed, for all h where is 1, the variables can assume values greater or equal than 1. On the other hand, Equation (7) forces the same variables to assume values lower or equal than 1. As a consequence, the variables are equal to 1 for each hour , where is the activation hour of the load a, i.e., the hour at which :
With reference to users that hold electric storage systems, inequalities (9) and (10) express the fact that the total stored energy at each hour is within the allowed minimum and maximum states of charge ( and ). As introduced, is the stored energy and is the energy supplied by the storage system of user u during the hour i. The constant is defined as the amount of electrical energy stored at the end of the previous day, while is the maximum capacity of each electrical storage system:
4.5. Upper and Lower Bounds of Variables
Inequalities (11) and (12) force the hourly energy exported by user u to the community () and to the grid () to be positive values:
5. Numerical Results and Discussion
In this section, we evaluate the effectiveness of the Unified optimization model in a specific scenario: the Unical (University of Calabria) Campus, in Italy. The analysis is related to a specific day, i.e., 18 February 2020. The optimization problem was solved with the Branch and Bound technique, in particular we exploited the implementation provided by the CPLEX Library (https://www.ibm.com/us-en/marketplace/ibm-ilog-cplex). We computed the energy exchanges and the costs/revenues for a community of three grid-connected prosumers. With reference to Figure 2, we considered the case in which the selling price is equal to the buying cost, and both are denoted as . and are prosumers equipped with PV systems and storage systems, while is a simple consumer, devoid of local generation and storage systems. More details about the peak PV power, the grid operation power and the storage capacity are reported in Table 1.

Table 1.
Local PV, grid connection, and storage systems for the three prosumers.
Table 2, Table 3 and Table 4 show the user preferences and the details of the schedulable loads, i.e., of electrical appliances such as washing machines, dishwashers, electric ovens, for the three prosumers, respectively. We recall that, for each schedulable load, is the duration in hours of the working time, and is the range of hours to which the working time must belong; one or more interruptions of the working time are allowed for interruptible loads, while non-interruptible loads cannot be interrupted.

Table 2.
Schedulable loads of .

Table 3.
Schedulable loads of .

Table 4.
Schedulable loads of .
In addition to the schedulable loads, a fixed daily profile is considered (given by the sum of all non-schedulable electrical loads).
The results are compared to those obtained with the Separated model presented in [6], which does not take into account the energy sharing among the users, as specified in the introductory section. The comparison between the two models, Unified and Separated, provides important results, useful to highlight economic and energy advantages achieved when adopting the Unified model.
Figure 3 and Figure 4 show the profiles of the three prosumers with the Separated and the Unified model, respectively. In the figures, positive values correspond to the injection of energy by the user (either to the community or to the external grid), while negative values correspond to the withdrawal of energy from the community or from the grid.
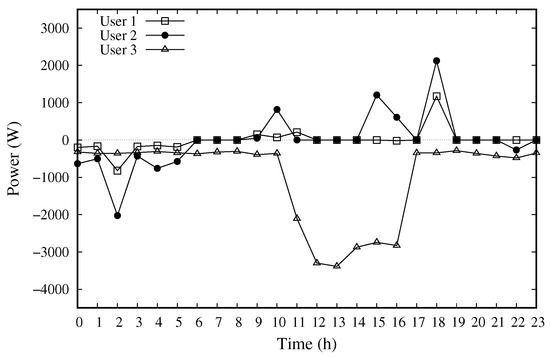
Figure 3.
Daily profile of the three users with the Separated model.
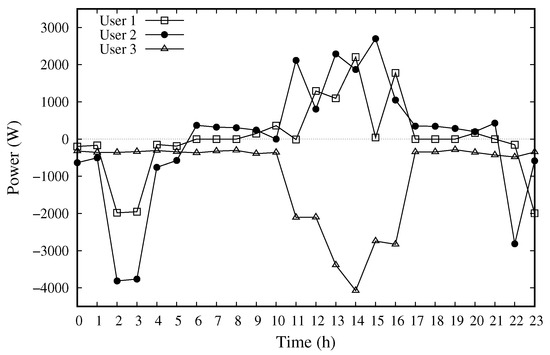
Figure 4.
Daily profile of the three users with the Unified model.
Figure 3 shows that, when adopting the Separated model, and make limited energy exchanges with the external grid. These two users own renewable energy plants that are able to match their energy needs, and therefore are nearly autonomous: they withdraw energy only in the earliest and last hours of the day, when the local PV plants are not productive, while they inject energy to the grid mainly in the hours between 15:00 and 19:00, when the selling price is higher. does not own a local plant, so it withdraws energy from the grid during the whole day, and mostly between 11:00 and 17:00. When compared to Figure 3, Figure 4 confirms a better usage of the available energy produced locally when using the Unified model, and a better coordination between production and demand among the users. The profiles appear to be complementary, i.e., the local producers ( and ) supply energy at the hours when needs such energy for its loads. Moreover, and are equipped with storage systems, so they find it convenient to buy energy from the grid, and charge their batteries, in the hours in which the energy is cheaper, i.e., between 02:00 and 04:00. Later in the day, the storage systems will be discharged to match the energy requirements of .
The energy sharing among the users of the community, enabled with the Unified model, ensures the optimal use of local energy sources. To show this, Figure 5 reports the total amount of energy produced by the PV plants, and the aggregated demand profile of the three users, i.e., the sum of the energy amounts required by the loads and accumulated in the storage systems, with the Separated and the Unified model. A comparison between the two models confirms that the Unified model ensures a better coordination between demand and production profiles, as can be noticed in the figure. In more detail, with the Separated model, the loads are scheduled and the storage systems are charged when the PV plants are productive, i.e., between 08:00 and 17:00. However, the curve of the demand profile is higher than the production curve, meaning that the a portion of the energy required by the loads—the area between the two curves—is bought from the grid. Conversely, the Unified model schedules some loads in the hours when the energy can be bought at a low cost, i.e., between 01:00 and 05:00 and between 22:00 and 24:00. Moreover, the storage systems are partially charged in the same hours. In this way, the community is able to exploit all the energy produced locally to fulfill its loads in the hours when the external energy is more expensive. Indeed, the curves of production and demand are nearly coincident.
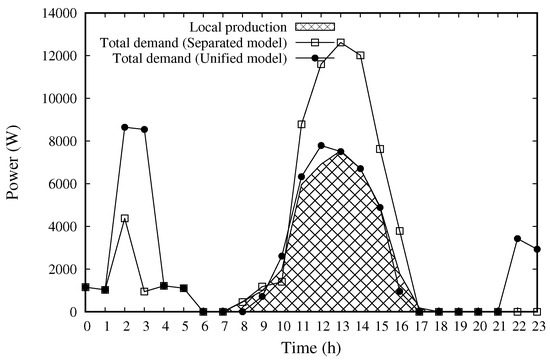
Figure 5.
Local production and aggregated demand profile with Separated and Unified models.
In detail, the “self-consumed” energy (i.e., the amount of energy produced locally and consumed by the prosumers of the community) is equal to 31.53 kWh with the Separated model, while it increases to 37.45 kWh when adopting the Unified model. On the other hand, the energy withdrawn from the grid is equal to 30.53 kWh with the Separated model, while it is reduced to 23.10 kWh when adopting the Unified model.
Figure 6 compares the energy profile of the whole community (obtained by summing the profiles of , , and ), for the Separated and Unified models. Positive values of the profile correspond to the injection of energy from the community to the grid, while negative values correspond to the withdrawal of energy from the grid. We observe that the Unified model enables a significant reduction of the time interval in which energy is withdrawn from the grid, meaning that the community becomes more autonomous: in particular, it does not need external energy between 06:00 and 22:00.
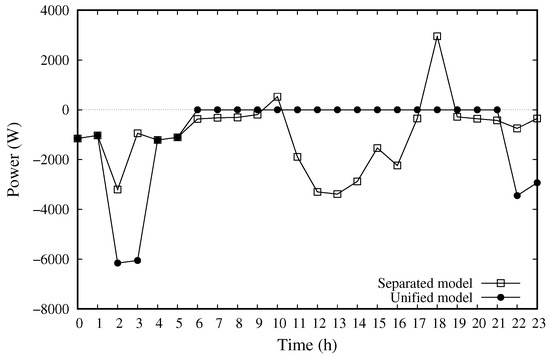
Figure 6.
Daily profile of the community for Separated and Unified models.
Figure 7 shows the values of the objective function during the considered day, i.e., the costs/revenues of the whole community obtained with the Separated and the Unified model. In the figure, negative values correspond to the purchase of energy while positive values correspond to the sale of energy. The Unified model allows the community to obtain significant cost savings with respect to the Separated model, especially in the second half of the day, when the energy produced by internal renewable sources can be exploited by other prosumers of the community. In particular, with the Unified model, no cost is incurred between 06:00 and 22:00, when the community is completely autonomous. Overall, the energy cost decreases from € 5.281 with the Separated model to € 3.584 with the Unified model.
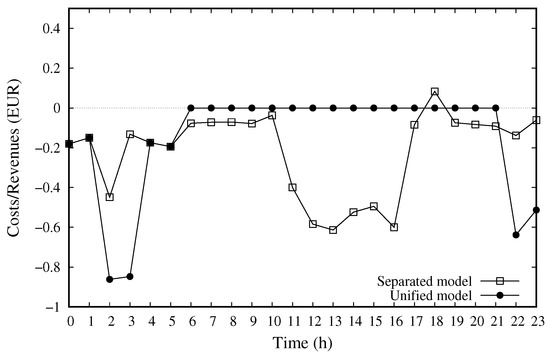
Figure 7.
Daily cost/saving for Separated and Unified models.
Table 5 reports the costs/revenues of the three users with the Separated and the Unified model, detailed both for the energy exchanges with the grid and for the energy exchanges within the community.

Table 5.
Costs/revenues for the Separated and Unified model.
Figure 8 shows the economical gain achieved when using the Unified model with respect to the Separated model, computed as the difference between the values of the objective function obtained by solving the two models. This analysis is made by varying the overall storage capacity and the total PV size, in order to assess the impact of these parameters. The figure confirms that the Unified model always ensures a gain, whose value depends on the storage capacity and the PV size. To be more specific, the value of the gain increases with the total PV size: indeed, a larger availability of energy produced by local sources allows the users of the community to share a larger amount of energy and therefore to reduce the energy costs. The figure also shows that the economical gain is very low for values of the total PV size between 0 kW and 3 kW: the reason is that the energy produced locally is not sufficient to match the energy demand of the users, who need to withdraw energy from the grid with both the Separated and the Unified model. Another interesting insight is that the economical gain saturates to about € 1.772 when the total PV size exceeds 10 kW, i.e., the Unified model does not ensure further gains: the local sources produce an over-generation of energy that cannot be used by the community and is directly sold to the external grid, and the corresponding revenue is the same with both of the models. Finally, it can be seen that, with values of the total PV size between 3 kW and 10 kW, the economical gain increases when the total storage capacity decreases. In particular, with small values of the total capacity, the autonomy of users is limited: in such a case, a great advantage derives from sharing the available energy, which is only possible with the Unified model. On the other hand, with large values of the storage capacity, a large amount of energy can be stored and used at a later time, thus reducing the energy exchanges with the grid: in this case, the Separated model provides a solution of the optimization problem that is very close to that ensured by the Unified model. Figure 8 also shows the value of the gain for the specific case study considered so far, and detailed in Table 1: when the total capacity is 23 kWh and the total PV size is 14 kWp, the gain is equal to € 1.697. From the plot, it can be observed that this scenario corresponds to a nearly optimal sizing of the PV size and storage capacity, as the gain is close to the maximum value, also shown in the plot, and equal to € 1.789.
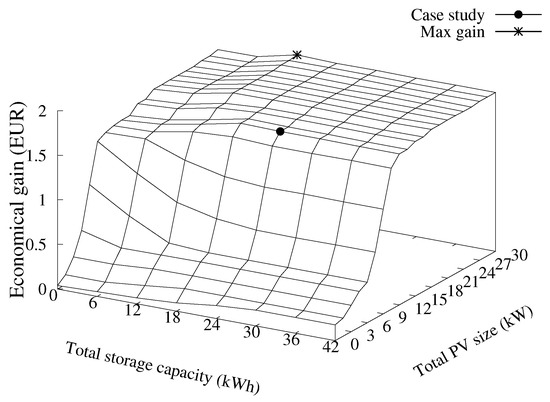
Figure 8.
Economical gain of the Unified model when varying the total storage capacity and the total PV size.
As a conclusive remark, the Unified approach is applicable and leads to the optimal solution when the number of prosumers is limited, but it is not fully scalable, as the size of the optimization problem increases quadratically with the number of prosumers, and so does the computation burden needed to solve the problem. To improve the scalability behavior, an efficient strategy can adopt a hierarchical approach, in which the problem is first solved for single groups of prosumers, using the model presented here, and then the energy exchanges among these groups are computed. This strategy is currently under assessment.
6. Conclusions and Future Work
This paper has presented a novel approach for the optimal management of energy communities, in which some of the prosumers are equipped with renewable energy plants. Differently from other approaches proposed in the literature, where each prosumer is modelled separately, a unique model of an entire energy community is developed here, with the goal of fostering the energy exchanges among the prosumers of the community. Experimental results, performed on the University of Calabria Campus, show the advantages of the approach and its capability of matching the production availability of some prosumers with the energy requirements of other prosumers. This matching allows the prosumers to reduce the need for external energy, or to withdraw such energy at hours when it is cheaper, store the energy in local accumulators and provide it to other users at a later time, thus leading to significant cost savings for the whole community. The presented model exploits the Internet of Energy paradigm, which integrates the distributed energy systems with the Internet of Things (IoT) technologies. Indeed, the energy community is instrumented by hardware and software devices that are able to interact with the physical components and inject smartness into the management of the energy community. The main limitation of the approach is that computational complexity costs can become excessive as the number of prosumers increases. Consequently, future work will be geared at improving the scalability of the approach, using swarm intelligence techniques that allow energy exchanges to be optimized and not determined at a unique central point, but in parallel among subsets of prosumers.
Author Contributions
Conceptualization, C.M.; Data curation, L.S.; Methodology, A.G.; Software, A.G. and L.G.; Validation, C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the “COGITO” project, funded by the Italian Government (ARS01_00836).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ICT | Information and Communication Technology |
| IoT | Internet of Things |
| IoE | Internet of Energy |
| P2P | Peer-To-Peer |
| PCG | Prosumer Community Group |
| AMI | Advanced Metering Infrastructure |
| SEAG | Smart Energy Aware Gateway |
| PZ | Zone Price |
| PUN | Single National Price |
| PV | Photovoltaic |
| POD | Point Of Delivery |
| SOC | States Of Charge |
References
- Alanne, K.; Saari, A. Distributed energy generation and sustainable development. Renew. Sustain. Energy Rev. 2006, 10, 539–558. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Staudt, P.; Garttner, J.; Weinhardt, C. Trading on local energy markets: A comparison of market designs and bidding strategies. In Proceedings of the 14th IEEE International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Union, E. Directive (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the promotion of the use of energy from renewable sources. Off. J. Eur. Union 2018, 5, 82–209. [Google Scholar]
- Tounquet, F.; De Vos, L.; Abada, I.; Kielichowska, I.; Klessmann, C. Energy Communities in the European Union. Revised Final Report of the ASSET Project (Advanced System Studies for Energy Transition). Available online: https://asset-ec.eu/wp-content/uploads/2019/07/ASSET-Energy-Comminities-Revised-final-report.pdf (accessed on 25 May 2020).
- Bui, N.; Castellani, A.P.; Casari, P.; Zorzi, M. The internet of energy: A web-enabled smart grid system. IEEE Netw. 2012, 26, 39–45. [Google Scholar] [CrossRef]
- Belli, G.; Giordano, A.; Mastroianni, C.; Menniti, D.; Pinnarelli, A.; Scarcello, L.; Sorrentino, N.; Stillo, M. A unified model for the optimal management of electrical and thermal equipment of a prosumer in a DR environment. IEEE Trans. Smart Grid 2017, 10, 1791–1800. [Google Scholar] [CrossRef]
- Giordano, A.; Mastroianni, C.; Menniti, D.; Pinnarelli, A.; Scarcello, L.; Sorrentino, N. A Two-Stage Approach for Efficient Power Sharing Within Energy Districts. In Transactions on Systems, Man, and Cybernetics: Systems; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Giordano, A.; Mastroianni, C.; Scarcello, L.; Spezzano, G. An Optimization Model for Efficient Energy Exchange in Energy Communities. In Proceedings of the 4th International Workshop on Smart Cities Systems Engineering (IEEE SCE 2020), Paris, France, 30 June–3 July 2020. [Google Scholar]
- Navigant. ENERGY CLOUD 4.0—Capturing Business Value through Disruptive Energy Platforms; Technical Report; Navigant Consulting: Chicago, IL, USA, 2018. [Google Scholar]
- Harmon, E.; Ozgur, U.; Cintuglu, M.H.; de Azevedo, R.; Akkaya, K.; Mohammed, O.A. The internet of microgrids: A cloud-based framework for wide area networked microgrids. IEEE Trans. Ind. Inform. 2017, 14, 1262–1274. [Google Scholar] [CrossRef]
- Giordano, A.; Mastroianni, C.; Menniti, D.; Pinnarelli, A.; Sorrentino, N. An Energy Community Implementation: The Unical Energy Cloud. Electronics 2019, 8, 1517. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Mohsenian-Rad, H.; Saha, T.; Poor, H.V.; Wood, K.L. Transforming energy networks via peer to peer energy trading: Potential of game theoretic approaches. arXiv 2018, arXiv:1804.00962. [Google Scholar] [CrossRef]
- Chau, S.C.K.; Xu, J.; Bow, W.; Elbassioni, K. Peer-to-Peer Energy Sharing: Effective Cost-Sharing Mechanisms and Social Efficiency. In Proceedings of the Tenth ACM International Conference on Future Energy Systems, Phoenix, AZ, USA, 25–28 June 2019; pp. 215–225. [Google Scholar]
- Lee, W.; Xiang, L.; Schober, R.; Wong, V.W. Direct electricity trading in smart grid: A coalitional game analysis. IEEE J. Sel. Areas Commun. 2014, 32, 1398–1411. [Google Scholar] [CrossRef]
- Tushar, W.; Chai, B.; Yuen, C.; Huang, S.; Smith, D.B.; Poor, H.V.; Yang, Z. Energy storage sharing in smart grid: A modified auction-based approach. IEEE Trans. Smart Grid 2016, 7, 1462–1475. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Cheng, M.; Zhou, Y.; Long, C. A bidding system for peer-to-peer energy trading in a grid-connected microgrid. Energy Procedia 2016, 103, 147–152. [Google Scholar] [CrossRef]
- Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy-sharing model with price-based demand response for microgrids of peer-to-peer prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
- Xing, X.; Xie, L.; Meng, H. Cooperative energy management optimization based on distributed MPC in grid-connected microgrids community. Int. J. Electr. Power Energy Syst. 2019, 107, 186–199. [Google Scholar] [CrossRef]
- Zhu, T.; Huang, Z.; Sharma, A.; Su, J.; Irwin, D.; Mishra, A.; Menasche, D.; Shenoy, P. Sharing renewable energy in smart microgrids. In Proceedings of the 2013 ACM/IEEE International Conference on Cyber-Physical Systems (ICCPS), Philadelphia, PA, USA, 8–11 April 2013; pp. 219–228. [Google Scholar]
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Alam, M.; Ramchurn, S.D.; Rogers, A. Cooperative energy exchange for the efficient use of energy and resources in remote communities. In Proceedings of the 2013 International Conference on Autonomous Agents and Multi-Agent Systems, St. Paul, MN, USA, 6–10 May 2013; pp. 731–738. [Google Scholar]
- Rathnayaka, A.D.; Potdar, V.M.; Dillon, T.; Kuruppu, S. Framework to manage multiple goals in community-based energy sharing network in smart grid. Int. J. Electr. Power Energy Syst. 2015, 73, 615–624. [Google Scholar] [CrossRef]
- Kowsari, R.; Zerriffi, H. Three dimensional energy profile: A conceptual framework for assessing household energy use. Energy Policy 2011, 39, 7505–7517. [Google Scholar] [CrossRef]
- Pothitou, M.; Varga, L.; Kolios, A.J.; Gu, S. Linking energy behavior, attitude and habits with environmental predisposition and knowledge. Int. J. Sustain. Energy 2017, 36, 398–414. [Google Scholar] [CrossRef]
- Stephenson, J.; Barton, B.; Carrington, G.; Gnoth, D.; Lawson, R.; Thorsnes, P. Energy cultures: A framework for understanding energy behaviors. Energy Policy 2010, 38, 6120–6129. [Google Scholar] [CrossRef]
- Wilson, C.; Dowlatabadi, H. Models of decision-making and residential energy use. Annu. Rev. Environ. Resour. 2007, 32, 169–203. [Google Scholar] [CrossRef]
- Rathnayaka, A.D.; Potdar, V.M.; Hussain, O.; Dillon, T. Identifying prosumer’s energy sharing behaviors for forming optimal prosumer-communities. In 2011 International Conference on Cloud and Service Computing; IEEE: Piscataway, NJ, USA, 2011; pp. 199–206. [Google Scholar]
- Rathnayaka, A.D.; Potdar, V.M.; Dillon, T.; Hussain, O.; Kuruppu, S. Analysis of energy behavior profiles of prosumers. In Proceedings of the IEEE 10th International Conference on Industrial Informatics, Beijing, China, 25–27 July 2012; pp. 236–241. [Google Scholar]
- Rathnayaka, A.D.; Potdar, V.M.; Dillon, T.S.; Hussain, O.K.; Chang, E. A methodology to find influential prosumers in prosumer community groups. IEEE Trans. Ind. Inform. 2013, 10, 706–713. [Google Scholar] [CrossRef]
- Hertig, Y.; Teufel, S. Prosumer involvement in smart grids: The relevance of energy prosumer behavior. In Proceedings of the 35th International Conference on Organizational Science Development, Portorož, Slovenia, 16–18 March 2016; pp. 30–41. [Google Scholar]
- Brown, M.A.; Zhou, S. Smart-grid policies: An international review. Wiley Interdiscip. Rev. Energy Environ. 2013, 2, 121–139. [Google Scholar] [CrossRef]
- Lawrence, T.M.; Boudreau, M.C.; Helsen, L.; Henze, G.; Mohammadpour, J.; Noonan, D.; Patteeuw, D.; Pless, S.; Watson, R.T. Ten questions concerning integrating smart buildings into the smart grid. Build. Environ. 2016, 108, 273–283. [Google Scholar] [CrossRef]
- Simcoe, T.; Toffel, M.W. Government green procurement spillovers: Evidence from municipal building policies in California. J. Environ. Econ. Manag. 2014, 68, 411–434. [Google Scholar] [CrossRef]
- Raspberry, P. Available online: http://www.raspberrypi.org/ (accessed on 25 May 2020).
- Giordano, A.; Spezzano, G.; Vinci, A. Rainbow: An Intelligent Platform for Large-Scale Networked Cyber-Physical Systems. In Proceedings of the 5th International Workshop on Networks of Cooperating Objects for Smart Cities 2014, UBICITEC 2014, Rome, Italy, 5–6 May 2014; pp. 70–85. [Google Scholar]
- Wooldridge, M. An Introduction to Multi-Agent Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).