A Pipeline for Adaptive Filtering and Transformation of Noisy Left-Arm ECG to Its Surrogate Chest Signal
Abstract
1. Introduction
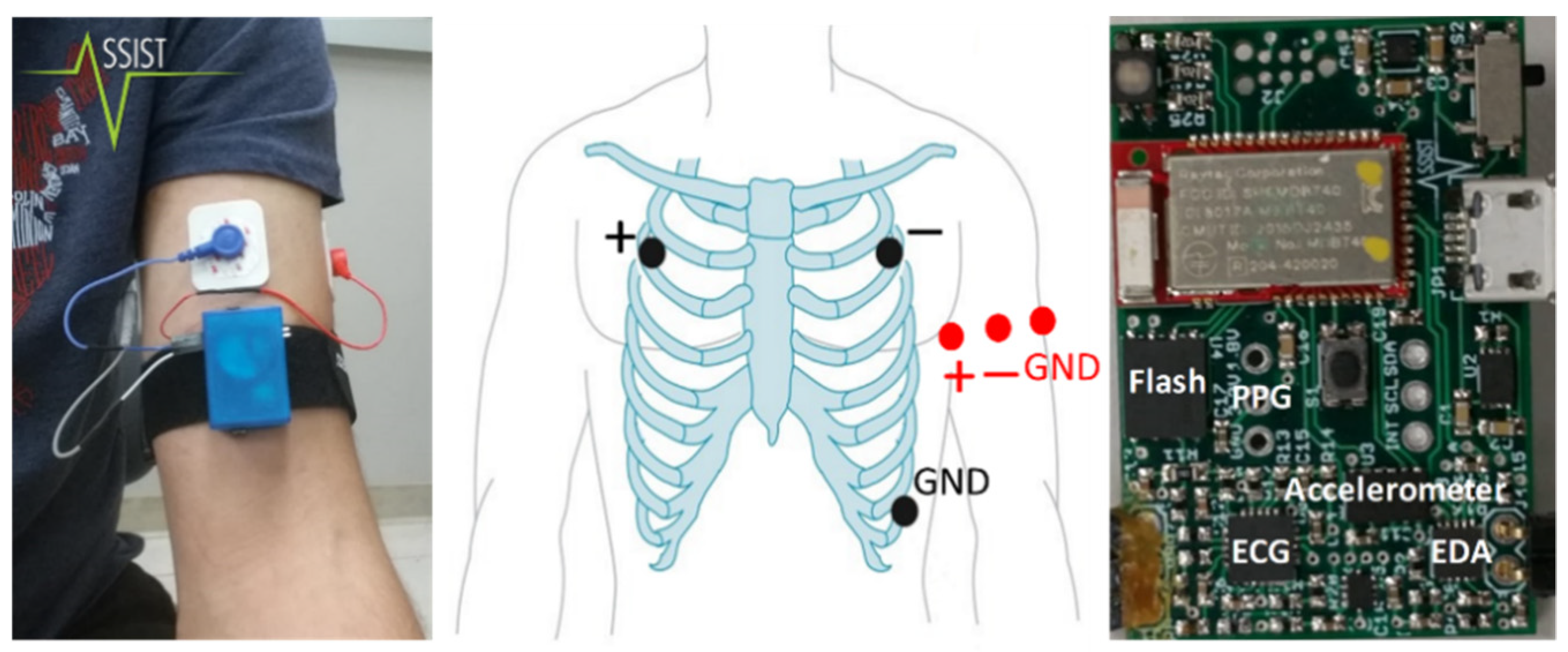
2. Hardware
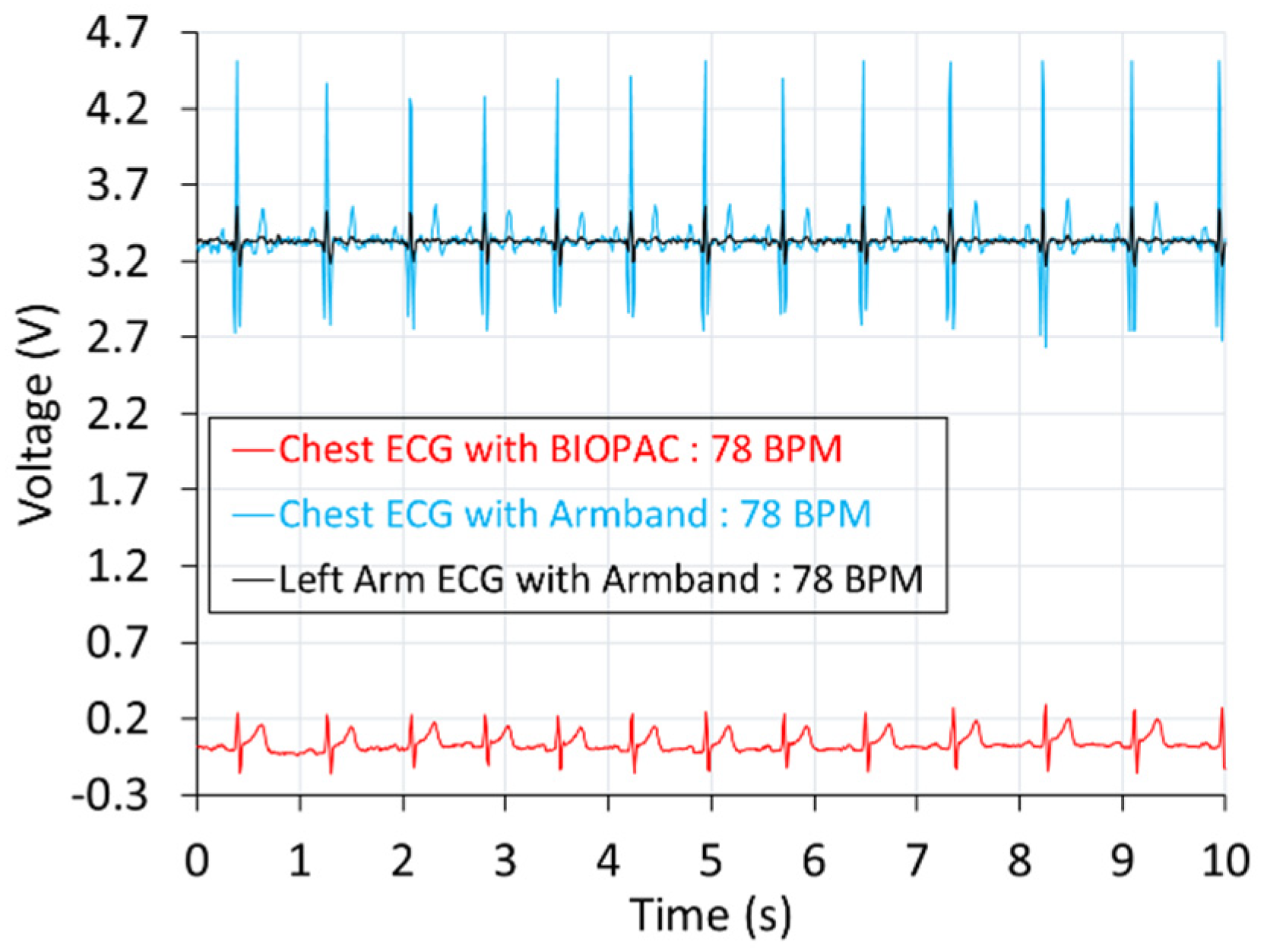
3. ECG Data Acquisitions
4. Modeling of ECG Noises
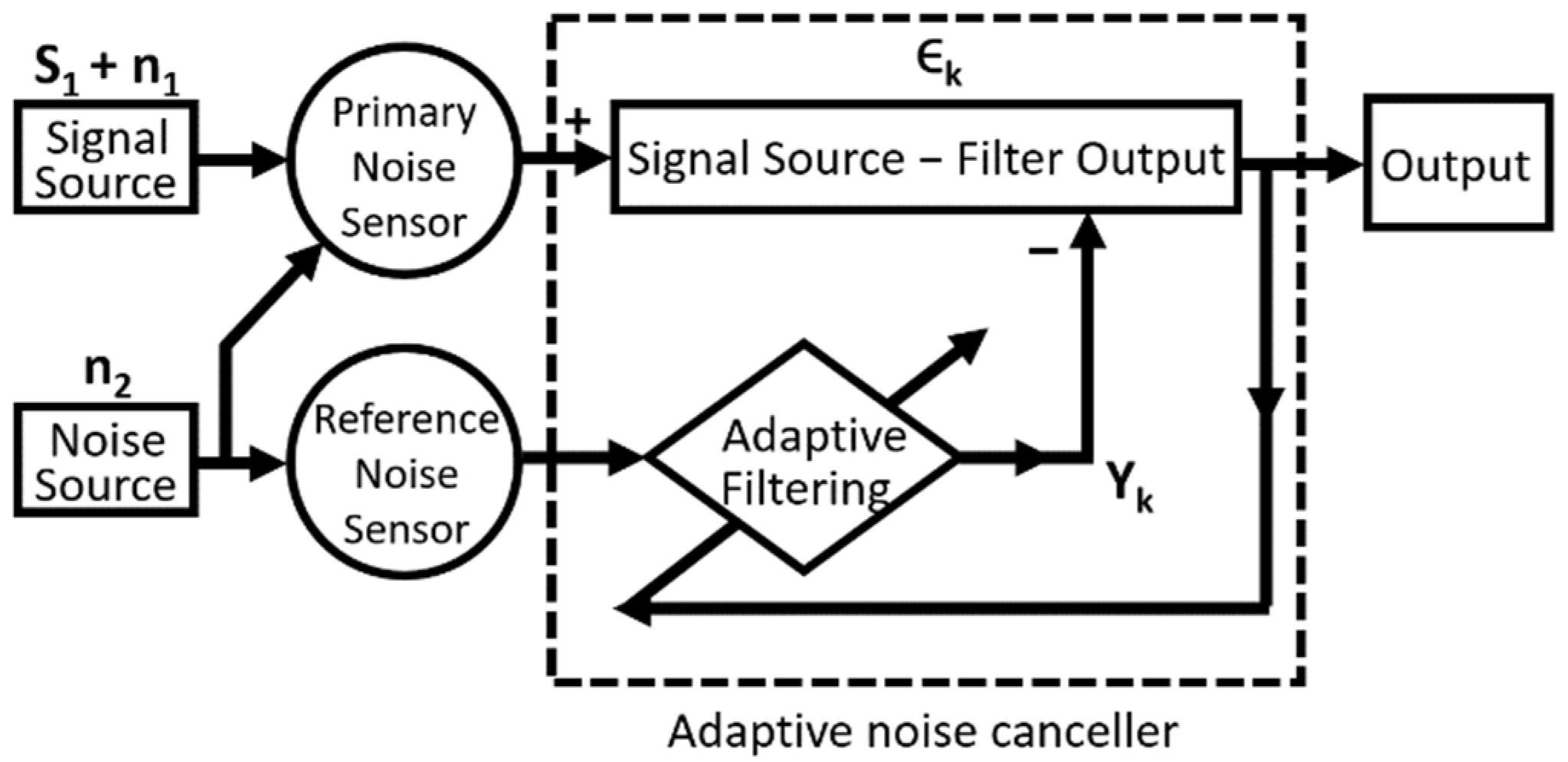
5. Adaptive Filtering Algorithms
5.1. LMS Algorithm
5.2. RLS Algorithm
5.3. EKRLS Algorithm
6. Transformation of Denoised ECG Signals
- Transformation of denoised LA-ECG into a T-ECG;
- Transformation of denoised C-ECG into a T-ECG.
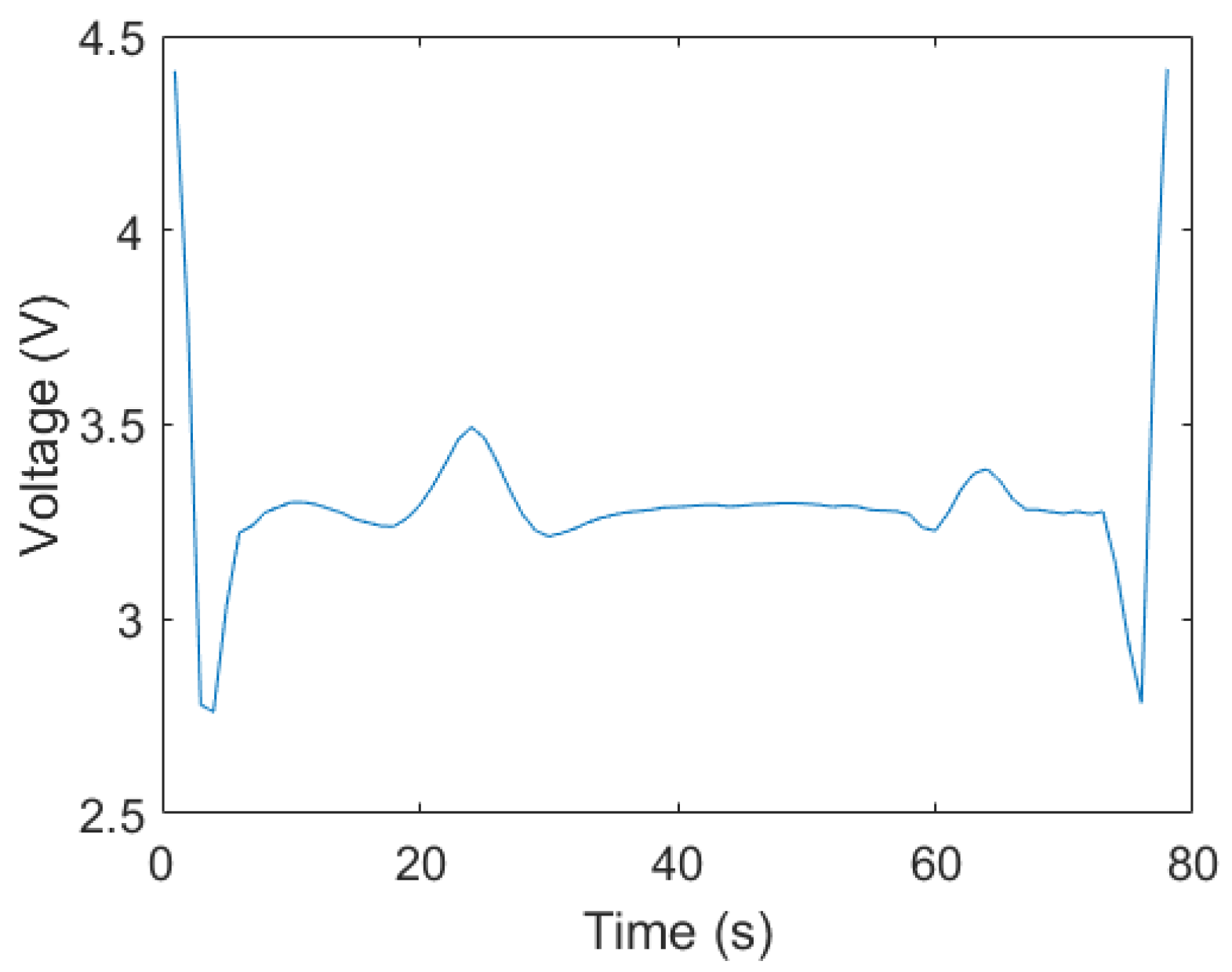
- Creation of the reference C-ECG template from the original C-ECG with an averaged RR interval (Figure 5);
- Creation of the LA-ECG template from the filtered LA-ECG with an averaged RR interval;
- Resampling of the averaged RR interval of the filtered LA-ECG with respect to the reference C-ECG template (upsampling or downsampling is implemented if required);
- Obtaining the transformation function through dividing the chest ECG template by the LA-ECG template;
- Resampling of the transformation function according to individual RR intervals of the filtered LA-ECG;
- Transformation of the filtered LA-ECG to C-ECG through multiplying the resampled transformation function by the original RR intervals of the filtered LA-ECG.
6.1. Creating the Averaged Templates
6.2. Constructing the Transformation Signal
6.3. Computing Customized MSE and SNR
7. Results and Discussion
7.1. Optimization of Filter Parameters
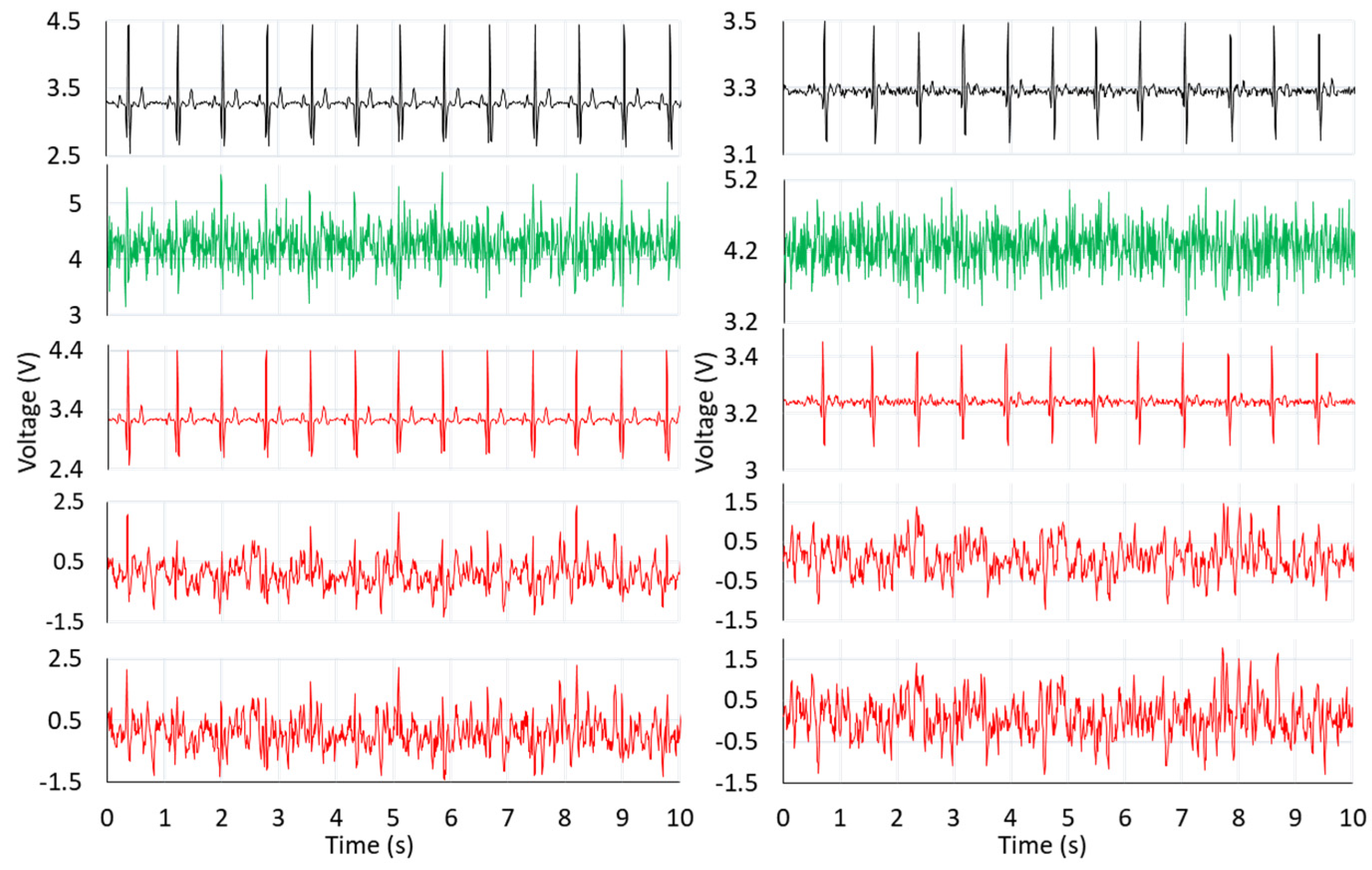
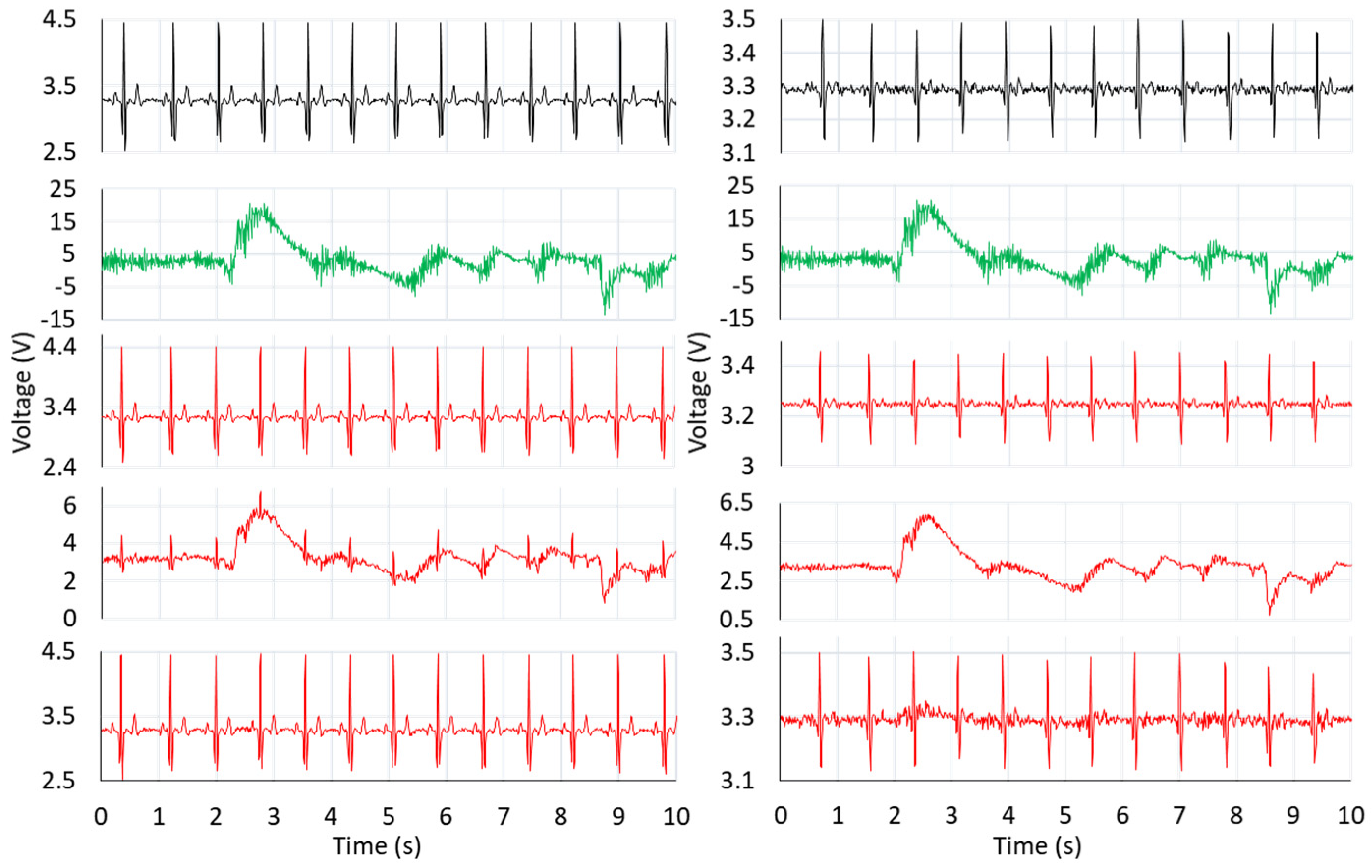
7.2. Evaluation of Adaptive Filtering Algorithms
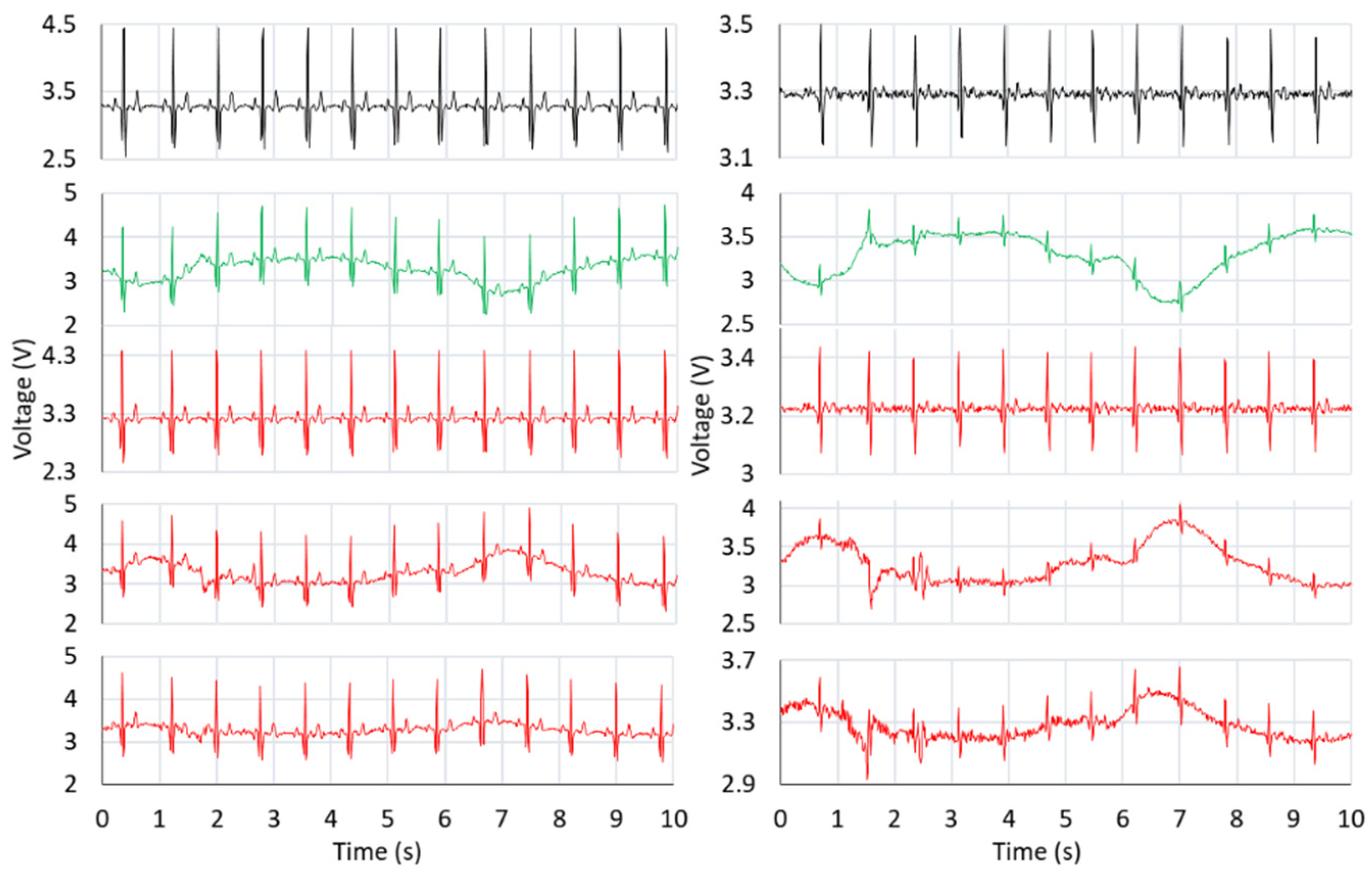
7.3. Evaluation of Transformation
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gross Domestic Product | Fourth Quarter and Annual 2018 (Initial Estimate). Available online: https://www.bea.gov/news/2019/initial-gross-domestic-product-4th-quarter-and-annual-2018 (accessed on 25 June 2019).
- NHE-Fact-Sheet. Available online: https://www.cms.gov/research-statistics-data-and-systems/statistics-trends-and-reports/nationalhealthexpenddata/nhe-fact-sheet.html (accessed on 25 June 2019).
- National Health Accounts Historical. Available online: https://www.cms.gov/research-statistics-data-and-systems/statistics-trends-and-reports/nationalhealthexpenddata/nationalhealthaccountshistorical.html (accessed on 25 June 2019).
- Medical Technology Industry Spotlight. Available online: https://www.selectusa.gov/medical-technology-industry-united-states (accessed on 25 June 2019).
- Heart Disease Fact Sheet | Centers for Disease Control and Prevention. Available online: https://www.cdc.gov/dhdsp/data_statistics/fact_sheets/fs_heart_disease.htm (accessed on 25 June 2019).
- Alghatrif, M.; Lindsay, J. A brief review: History to understand fundamentals of electrocardiography. JCHIMP 2012, 2, 14383. [Google Scholar] [CrossRef] [PubMed]
- Ogura, R.; Hiasa, Y.; Takahashi, T.; Yamaguchi, K.; Fujiwara, K.; Ohara, Y.; Nada, N.; Ogata, T.; Kusunoki, K.; Yuba, K.; et al. Specific Findings of the Standard 12-Lead ECG in Patients with Takotsubo Cardiomyopathy. Circulation 2003, 67, 687–690. [Google Scholar] [CrossRef] [PubMed]
- Klootwijk, P.; Meij, S.; Es, G.V.; Müller, E.J.; Umans, V.A.W.M.; Lenderink, T.; Simoons, M.L. Comparison of usefulness of computer assisted continuous 48-h 3-lead with 12-lead ECG ischaemia monitoring for detection and quantitation of ischaemia in patients with unstable angina. Eur. Heart J. 1997, 18, 931–940. [Google Scholar] [CrossRef] [PubMed]
- Moody, G.B.; Mark, R.G. Development and evaluation of a 2-lead ECG analysis program. Comput. Cardiol. 1982, 9, 39–44. [Google Scholar]
- Kardia Clinical Research Updated September 2019 00MKT0004.10. Available online: https://www.alivecor.com/research (accessed on 8 April 2020).
- Skordalakis, E. Syntactic ECG processing: A review. Pattern Recognit. 1986, 19, 305–313. [Google Scholar] [CrossRef]
- Raj, P.S.; Hatzinakos, D. Feasibility of single-arm single-lead ECG biometrics. In Proceedings of the 22nd EUSIPCO, Lisbon, Portugal, 1–5 September 2014; pp. 2525–2529. [Google Scholar]
- Villegas, A.; McEneaney, D.; Escalon, O. Arm-ECG Wireless Sensor System for Wearable Long-Term Surveillance of Heart Arrhythmias. Electronics 2019, 8, 1300. [Google Scholar] [CrossRef]
- Akbulut, F.P.; Lawless, K.; Tanneeru, A.; Rao, S.; Lee, B.; Misra, V. Estimation of Beat-to-Beat Interval from Wearable Photoplethysmography Sensor on Different Measurement Sites During Daily Activities. In Proceedings of the IEEE Sensors, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar]
- QRS AMPLITIUDE & RESPIRATORY MODULATION. Available online: https://www.biopac.com/knowledge-base/qrs-amplitiude-respiratory-modulation/ (accessed on 8 April 2020).
- Venkatesan, C.; Karthigaikumar, P.; Varatharajan, R. FPGA implementation of modified error normalized LMS adaptive filter for ECG noise removal. Clust. Comput. 2018, 22, 12233–12241. [Google Scholar] [CrossRef]
- Venkatesan, C.; Karthigaikumar, P.; Varatharajan, R. A novel LMS algorithm for ECG signal preprocessing and KNN classifier based abnormality detection. Multimed. Tools Appl. 2018, 77, 10365–10374. [Google Scholar] [CrossRef]
- Misra, V.; Bozkurt, A.; Calhoun, B.; Jackson, T.; Jur, J.S.; Lach, J.; Lee, B.; Muth, J.; Oralkan, Ö.; Öztürk, M.; et al. Flexible Technologies for Self-Powered Wearable Health and Environmental Sensing. Proc. IEEE 2015, 103, 665–681. [Google Scholar] [CrossRef]
- Mugdha, A.C.; Rawnaque, F.S.; Ahmed, M.U. A study of recursive least squares (RLS) adaptive filter algorithm in noise removal from ECG signals. In Proceedings of the ICIEV, Fukuoka, Japan, 15–18 June 2015; pp. 1–6. [Google Scholar]
- Jonas, D.E.; Kahwati, L.C.; Yun, J.D.Y.; Middleton, J.C.; Coker-Schwimmer, M.; Asher, G.N. Screening for Atrial Fibrillation with Electrocardiography: Evidence Report and Systematic Review for the US Preventive Services Task Force. JAMA 2018, 320, 485–498. [Google Scholar] [CrossRef] [PubMed]
- Baakek, Y.N.; Hadj Slimane, Z.E.; Bereksi Reguig, F. The Quantification of the QT-RR Interaction in ECG Signal Using the Detrended Fluctuation Analysis and ARARX Modelling. J. Med. Syst. 2014, 38, 62. [Google Scholar] [CrossRef] [PubMed]
- Clifford, G.D.; Azuaje, F.; Mcsharry, P. ECG statistics, noise, artifacts, and missing data. In Advanced Methods and Tools for ECG Data Analysis; Artech House: Boston, MA, USA, 2006; Volume 6, p. 18. [Google Scholar]
- Gonzalez, L.; Paniagua, T.; Starliper, N.; Lobaton, E. Signal Quality for RR Interval Prediction on Wearable Sensors. In Proceedings of the IEEE Engineering in Medicine and Biology Conference (EMBC), Berlin, Germany, 23–27 July 2019. [Google Scholar]
- Mohammadzadeh, F.; Nam, C.S.; Lobaton, E. Prediction of Physiological Response over Varying Forecast Lengths with a Wearable Health Monitoring Platform. In Proceedings of the IEEE Engineering in Medicine and Biology Conference (EMBC), Honolulu, HI, USA, 18–21 July 2018. [Google Scholar]
- Gonzalez, L.; Zhong, B.; Lobaton, E. A Framework for Physiological Response Prediction with Joint Activity State Optimization. In Proceedings of the IEEE Engineering in Medicine and Biology Conference (EMBC), Honolulu, HI, USA, 18–21 July 2018. [Google Scholar]
- Zhong, B.; Qin, Z.; Yang, S.; Chen, J.; Mudrick, N.; Taub, M.; Azevedo, R.; Lobaton, E. Emotion Recognition with Facial Expressions and Physiological Signals. In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017. [Google Scholar]
- Lokare, N.; Gonzalez, L.; Lobaton, E. Comparing the Effect of Muscle Activation in Wearable Devices using Wet and Textile Electrodes. In Proceedings of the IEEE Engineering in Medicine and Biology Conference (EMBC), Orlando, FL, USA, 16–20 August 2016. [Google Scholar]
- Starliper, N.; Mohammadzadeh, F.; Songkakul, T.; Hernandez, M.; Bozkurt, A.; Lobaton, E. Activity-Aware Wearable System for Power-Efficient Prediction of Physiological Responses. Sensors 2019, 19, 441. [Google Scholar] [CrossRef] [PubMed]
- Dogrusoz, Y.S.; Bear, L.R.; Svehlikova, J.; Coll-Font, J.; Good, W.; Dubois, R. Reduction of Effects of Noise on the Inverse Problem of Electrocardiography with Bayesian Estimation. Computing 2018, 45, 1. [Google Scholar]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Sameni, R.; Shamsollahi, M.B.; Jutten, C.; Babaie-Zade, M. Filtering noisy ECG signals using the extended Kalman filter based on a modified dynamic ECG model. In Proceedings of the IEEE: Computers in Cardiology, Leon, France, 25–28 September 2005; pp. 1017–1020. [Google Scholar]
- Zhao, Z.D.; Chen, Y.Q. A new method for removal of baseline wander and power line interference in ECG signals. In Proceedings of the IEEE: International Conference on Machine Learning and Cybernetics, Dalian, China, 16–18 August 2006; pp. 4342–4347. [Google Scholar]
- Thakor, N.V.; Zhu, Y.-S. Applications of adaptive filtering to ECG analysis: noise cancellation and arrhythmia detection. IEEE Trans. Biomed. Eng. 1991, 38, 785–794. [Google Scholar] [CrossRef] [PubMed]
- Widrow, B.; Weiss, S. Adaptive Signal Processing; Prentice-Hall Inc.: Saddle River, NJ, USA, 1985. [Google Scholar]
- Sankar, A.B.; Kumar, D.; Seethalakshmi, K. Performance study of various adaptive filters algorithms for noise cancellation in respiratory signals. Signal Process. Int. J. 2010, 4, 267–278. [Google Scholar]
- Zhao, S. Performance Analysis and Enhancements of Adaptive Algorithms and Their Applications. Ph.D. Thesis, Nanyang Technological University, Singapore, 2009. [Google Scholar]
- Sayed, A.H. Adaptive Filters; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Sultana, N.; Kamatham, Y.; Kinnara, B. Performance analysis of adaptive filtering algorithms for denoising of ECG signals. In Proceedings of the Institute of Electrical and Electronics Engineers, Inc. (IEEE) Conference, Coimbatore, India, 5–7 March 2015; pp. 297–302. [Google Scholar]
- Haykin, S. Adaptive Filter Theory; Prentice-Hall Inc: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Dhiman, J.; Ahmad, S.; Gulia, K. Comparison between Adaptive filter Algorithms (LMS, NLMS and RLS). International Journal of Science. Eng. Technol. Res. 2013, 2, 1100–1103. [Google Scholar]
- Li, G.-Q.; Yang, J.-M.; Li, X.-C. An improved RLS adaptive filter algorithm used to process human body balance signal. Comput. Sci. Educ. 2011, 275–278. [Google Scholar] [CrossRef]
- Liu, W.; Park, I.; Wang, Y.; Principe, J.C. Extended Kernel Recursive Least Squares Algorithm. IEEE Trans. Signal Process. 2009, 57, 3801–3814. [Google Scholar]

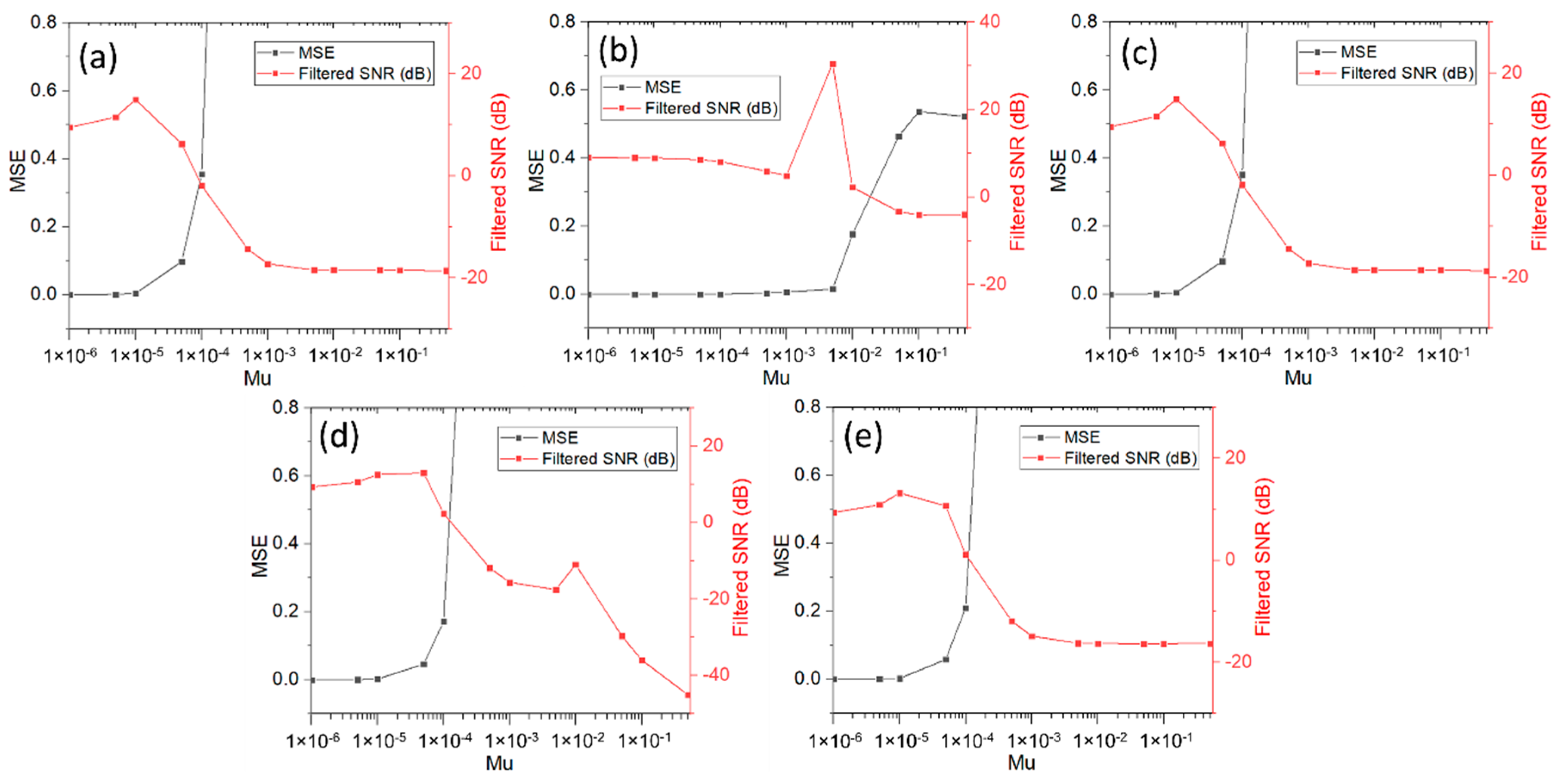



| Mu | BLW | EM | PLI | MA | W | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MSE | SNR (dB) | MSE | SNR (dB) | MSE | SNR (dB) | MSE | SNR (dB) | MSE | SNR (dB) | |
| 1 × 10−6 | 4.30 × 10−5 | 9.4674 | 2.51 × 10−8 | 9.0130 | 4.27 × 10−5 | 9.4660 | 1.98 × 10−5 | 9.3220 | 2.54 × 10−5 | 9.3627 |
| 5 × 10−6 | 1.07 × 10−3 | 11.5000 | 6.25 × 10−7 | 8.9714 | 1.06 × 0−3 | 11.4910 | 4.91 × 10−4 | 10.6252 | 6.31 × 10−4 | 10.8616 |
| 1 × 10−5 | 4.23 × 10−3 | 14.9306 | 2.49 × 10−6 | 8.9200 | 4.20 × 10−3 | 14.9041 | 1.95 × 10−3 | 12.5732 | 2.50 × 10−3 | 13.1680 |
| 5 × 10−5 | 9.76 × 10−2 | 6.2452 | 5.90 × 10−5 | 8.5305 | 9.70 × 10−2 | 6.2893 | 4.60 × 10−2 | 12.9927 | 5.77 × 10−2 | 10.6586 |
| 1 × 10−4 | 3.54 × 10−1 | −1.9147 | 2.21 × 10−4 | 8.0931 | 3.52 × 10−1 | −1.8844 | 1.71 × 10−1 | 2.3991 | 2.10 × 10−1 | 1.1424 |
| 5 × 10−4 | 4.31 | −14.3759 | 3.25 × 10−3 | 5.8949 | 4.31 | −14.3669 | 2.51 | −11.8337 | 2.56 | −11.9311 |
| 1 × 10−3 | 8.07 | −17.2542 | 6.45 × 10−3 | 4.8812 | 8.09 | −17.2633 | 5.64 | −15.6134 | 4.81 | −14.8776 |
| 5 × 10−3 | 1.06 × 10 | −18.4976 | 1.51 × 10−2 | 30.5555 | 1.09 × 10 | −18.6031 | 8.57 | −17.5296 | 6.50 | −16.2656 |
| 1 × 10−2 | 1.05 × 10 | −18.4373 | 1.76 × 10−1 | 2.2408 | 1.09 × 10 | −18.6037 | 2.08 | −10.9612 | 6.55 | −16.2992 |
| 5 × 10−2 | 1.06 × 10 | −18.4813 | 4.64 × 10−1 | −3.3502 | 1.09 × 10 | −18.6002 | 1.24 × 102 | −29.6458 | 6.70 | −16.4053 |
| 1 × 10−1 | 1.07 × 10 | −18.5448 | 5.37 × 10−1 | −4.1204 | 1.08 × 10 | −18.5957 | 5.35 × 102 | −35.9268 | 6.65 | −16.3671 |
| 5 × 10−1 | 1.09 × 10 | −18.6220 | 5.22 × 10−1 | −3.987 | 1.12 × 10 | −18.7387 | 4.38 × 103 | −45.0319 | 6.55 | −16.3029 |
| Noise | Algorithm | Filtered ECG MSE | |
|---|---|---|---|
| L.A. | Chest | ||
| BLW | LMS | 4.25 × 10−3 | 4.22 × 10−3 |
| RLS | 2.51 | 2.50 | |
| EKRLS | 1.25 | 1.24 | |
| EM * | LMS | 1.41 × 10−2 | 1.51 × 10−2 |
| RLS | 6.75 | 6.70 | |
| EKRLS | 1.22 × 10 | 1.21 × 10 | |
| PLI | LMS | 4.22 × 10−3 | 4.20 × 10−3 |
| RLS | 6.01 × 10−4 | 7.84 × 10−4 | |
| EKRLS | 1.03 × 10−2 | 1.04 × 10−2 | |
| MA | LMS | 1.91 × 10−3 | 1.95 × 10−3 |
| RLS | 2.94 | 2.93 | |
| EKRLS | 1.75 | 1.75 | |
| W | LMS | 2.50 × 10−3 | 2.50 × 10−3 |
| RLS | 1.02 × 10 | 1.02 × 10 | |
| EKRLS | 1.07 × 10 | 1.07 × 10 | |
| ECG Type | Noise Type | Noisy Signal SNR (dB) * | Transformed Signal SNR (dB) ** | Original C-ECG SNR (dB) | MSEc of T-ECG and Original C-ECG *** |
|---|---|---|---|---|---|
| C | BLW | −18.55 | 9.41 | 9.39 | 0.31 |
| EM | −31.51 | 10.34 | 0.31 | ||
| MA | −20.97 | 7.10 | 0.31 | ||
| PLI | −18.52 | 10.38 | 0.31 | ||
| W | −20.86 | 11.12 | 0.31 | ||
| LA | BLW | −18.40 | 7.97 | 9.10 | 0.75 |
| EM | −34.14 | 10.25 | 0.75 | ||
| MA | −20.99 | 8.13 | 0.75 | ||
| PLI | −18.39 | 10.94 | 0.75 | ||
| W | −18.39 | 8.09 | 0.75 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohaddes, F.; da Silva, R.L.; Akbulut, F.P.; Zhou, Y.; Tanneeru, A.; Lobaton, E.; Lee, B.; Misra, V. A Pipeline for Adaptive Filtering and Transformation of Noisy Left-Arm ECG to Its Surrogate Chest Signal. Electronics 2020, 9, 866. https://doi.org/10.3390/electronics9050866
Mohaddes F, da Silva RL, Akbulut FP, Zhou Y, Tanneeru A, Lobaton E, Lee B, Misra V. A Pipeline for Adaptive Filtering and Transformation of Noisy Left-Arm ECG to Its Surrogate Chest Signal. Electronics. 2020; 9(5):866. https://doi.org/10.3390/electronics9050866
Chicago/Turabian StyleMohaddes, Farzad, Rafael Luiz da Silva, Fatma Patlar Akbulut, Yilu Zhou, Akhilesh Tanneeru, Edgar Lobaton, Bongmook Lee, and Veena Misra. 2020. "A Pipeline for Adaptive Filtering and Transformation of Noisy Left-Arm ECG to Its Surrogate Chest Signal" Electronics 9, no. 5: 866. https://doi.org/10.3390/electronics9050866
APA StyleMohaddes, F., da Silva, R. L., Akbulut, F. P., Zhou, Y., Tanneeru, A., Lobaton, E., Lee, B., & Misra, V. (2020). A Pipeline for Adaptive Filtering and Transformation of Noisy Left-Arm ECG to Its Surrogate Chest Signal. Electronics, 9(5), 866. https://doi.org/10.3390/electronics9050866








