Abstract
Extreme learning machines (ELMs) are efficient for classification, regression, and time series prediction, as well as being a clear solution to backpropagation structures to determine values in intermediate layers of the learning model. One of the problems that an ELM may face is due to a large number of neurons in the hidden layer, making the expert model a specific data set. With a large number of neurons in the hidden layer, overfitting is more likely and thus unnecessary information can deterioriate the performance of the neural network. To solve this problem, a pruning method is proposed, called Pruning ELM Using Bootstrapped Lasso BR-ELM, which is based on regularization and resampling techniques, to select the most representative neurons for the model response. This method is based on an ensembled variant of Lasso (achieved through bootstrap replications) and aims to shrink the output weight parameters of the neurons to 0 as many and as much as possible. According to a subset of candidate regressors having significant coefficient values (greater than 0), it is possible to select the best neurons in the hidden layer of the ELM. Finally, pattern classification tests and benchmark regression tests of complex real-world problems are performed by comparing the proposed approach to other pruning models for ELMs. It can be seen that statistically BR-ELM can outperform several related state-of-the-art methods in terms of classification accuracies and model errors (while performing equally to Pruning-ELM P-ELM), and this with a significantly reduced number of finally selected neurons.
1. Introduction
The idea of randomly selecting hidden neurons for neural networks has been known for a few decades [1], and the Random Vector Functional-Link proposed by Pao et al. [2] introduces the idea of random weight assignment. Later, the concept was popularized by Huang et al. [3] who proposed and named the Extreme Learning Machine (ELM), which is a learning algorithm for single-hidden layer feedforward network (SLFNs) with low computational complexity, suitable for training with high-level datasets. The ELM algorithm allows models to be trained in a single interaction: the random definition of the hidden layer parameters is followed by the least-squares calculation (using the pseudoinverse matrix) of the linear output weights. This ensures rapid convergence and proper performance of the trained neural network.
However, ELM may suffer from a loss of generalization capability when the amount of neurons in the hidden layer is too high, incurring in a situation known as overfitting. Several approaches to deal with overfitting were proposed in the literature, typically based on trial and error runs to eliminate elements of the ELM architecture [4,5].
Thus, pruning methods have been designed in the past which have to identify how relevant each neuron is to the model and thus which neurons can be eliminated. For instance, Miche et al. [4] proposed a pruning technique in which neurons are ranked by the Multi-Response Sparse Regression (MRSR) algorithm [6] and then selected for elimination after leave-one-out cross validation. In the work of Rong et al. [5], a measure of mutual information between hidden neurons is used for pruning. More related work with a detailed description will be presented in the subsequent section.
This paper presents a new methodology for pruning the architecture of an ELM using regression and re-sampling techniques to select the most relevant neurons to the output of the model. For this purpose, a method proposed by Reference [7] called LARS (Least Angle Regression), which is a multi-variate regression algorithm, will be used in order to robustly estimate the regression coefficients and to shrink the subset of candidate regressors to be included in the final model. Therefore, we will demonstrate the usage of Bolasso method (as proposed in Reference [8]) to select the most relevant neurons in the hidden layer of ELMs. The main contribution to science that this paper proposes is to perform a reliable statistical evaluation in a practical way to define the optimal amount of neurons in the hidden layer of ELMs, allowing the training to be assertive and to improve the final model accuracy on separate test data due to more compact models, decreasing the likelihood of overfitting. The optimal amount is thereby steered by the outcome of LARS in combination with several bootstrap replications, which makes neuron selection more robust against noise in the data and a small amount of training samples (due to the consideration made in Reference [9] regarding the purpose and aims of boot-strapping in general). Based on extensive evaluations carried out on several complex real-world pattern classification and regression problems, we can clearly demonstrate a statistical significant improvement in model performance with a lower number neurons, compared to conventional ELMs, but also compared to several related pruning methods for ELMs.
The remainder of the article is organized as follows. Section 2 presents the theoretical concepts involved in extreme learning machines, pruning methods proposed in the literature, and the idea of simple linear regression. Section 3 describes the methodologies used for the construction of the proposed algorithm. In Section 4, the tests performed in the proposed pruning methodology to verify the efficiency in finding the ELM architecture in combination with various statistical tests are exposed to the reader, also by comparison of BR-ELM with related SoA techniques. Finally, Section 5 provides conclusions and future works.
2. Related Work
2.1. Extreme Learning Machines
The ELM (Extreme Learning Machine) is a training algorithm developed for a single hidden layer feedforward network (SLFN), in which random values are assigned to hidden layer weights, and output layer weights are estimated analytically [3,10].
For N given arbitrary training samples, with m features and associated outputs, composing pairs of type , an SLFN with k hidden nodes and activation functions f can be defined as follows: [3]:
where is the randomly assigned weight vector of the connections between the m inputs and the hidden j-th neuron, is the vector of weights of the connections between the j-th hidden neuron and the neurons of the network output, and is the bias of the j-hidden neuron. is the activation function applied to the scalar product of the input vector and the hidden weights. The activation function can be sigmoidal, sine, hyperbolic or Gaussian tangent [3,10]. Using the model defined in (1), the output vector y can be written as *h. G is defined as [2,3]:
The columns of the matrix G, defined in (2), correspond to the outputs of the hidden neurons of the network with respect to the input . The ELM algorithm proposes the initialization of the weights of the hidden layer, , at random. Then, the weights of the output layer are obtained through the Moore-Penrose pseudoinverse of G according to the expression [3,11]:
with .
The output weights obtained in (3) correspond to the minimum norm solution of the least squares problem defined as , in which represent the predicted outputs [12]. The number of hidden neurons affects the performance of the ELMs, especially regularization algorithms have been proposed to improve accuracy.
2.2. Pruning and Regularized Methods for Extreme Learning Machines
A neural network may suffer from lack or excess of hidden layer neurons, which can considerably damage model performance. When too many neurons are used, the model may present poor testing results despite a very good (sometimes perfect) training performance, a situation which is known as overfitting [13]. Therefore, the definition of its architecture is critical in obtaining a stable model. Two approaches have been followed when dealing with this subject: Tikhonov’s regularization theory [14] that allows the resolution of ill-posed problems and the technique of stabilization of structures, which consists of identifying the ideal structure for each problem by reducing the influence of unnecessary regressors (= columns of G in our case) towards 0.
The approach based on Tikhonov’s regularization theory [14] consists of treating the learning problem as an ill-posed inverse problem, and then inserting prior knowledge in order to make the problem well-posed. This prior knowledge corresponds to a smoothing term with I the identity matrix and a regularization parameter that balances the complexity and fit of the model to the data (also known as the bias-variance tradeoff [13]). The main difficulty with this kind of approach is finding the optimal balance. Therefore, various regularization parameter choice techniques have been proposed in the past, see Reference [15] for a comprehensive survey.
The techniques for stabilizing structures are based on problems that seek to approximate or interpolate a continuous function defined by a parameter vector. The theory of approximation [16] defines that models that have a single hidden layer, which has the ideal amount of neurons in the hidden layer, can act efficiently as a universal approximator. Therefore, the architecture stabilization theory of intelligent models is based on obtaining optimal neurons so that models that work with regression and classification of patterns can perform tasks with adequate responses. To find this structure, we aim to compare structures with different amounts of neurons in the hidden layer and compare their results. This approach can become very time-consuming if the number of neurons and statistical techniques to the aid decision making are huge. Another variant is to assign a high value to the neurons of the hidden layer and to eliminate unnecessary neurons through statistical approaches. Finally, the last approach is the opposite of the previous one, since the model starts with a simple structure and new neurons are added to find the best answer (bottom-up versus top-down). Both approaches may lead to inadequate responses when, in the top-down variant, pruning is rigid or very restricted, or when, in the bottom-up variant, the inclusion of neurons does not have a well-established stopping criterion.
Several training strategies employing those two approaches (theory of regularization and definition of architectures) were proposed in order to solve the problem of finding the optimal number of hidden ELM neurons. Concepts such as Lasso, Ridge Regression, and elastic net [11], Chi-Squared statistics, and information gain criteria [5], LARS and Tikhonov regularization [17] were used, as well as linear and quadratic regularization methods for ELM with incomplete data [18]. A new version of the original ELM was also formulated using the LARS regression method [4].
The algorithm developed by Reference [4] attempts to increase the robustness of the ELM by eliminating irrelevant neurons. Pruning is achieved with Multiresponse Sparse Regression (MRSR), along with Leave-One-Out (LOO) cross-validation.
A disadvantage of MRSR, however, may be a possibly too optimistic selection achieved through LOO-error, because this considers only one left out sample in each run for which then prediction often leads to a too optimistic error close to the training error, see Reference [19] (Chapter 7) for a detailed analysis of this issue.
In Rong et al. [5], an algorithm was proposed, which identifies the importance of each of the hidden neurons of the extreme learning machine to the class labels using statistical techniques that allow the removal of unnecessary information.
The main idea proposed by Reference [11] is to identify the degree of relevance of the weight that links the k-th hidden element with the ELM output layer through regression methods, in particular, the regularized least squares regression method is used that applies penalties to the coefficient vector. Less relevant neurons can be identified and removed from the model, allowing for better generalization capability of the neural network. This method is applied to ELM models that contain several neurons in the hidden layer whose number is greater than or equal to the number of training samples [11] (leading to an over-determined equation system to solve → no unique stable solution).
Another method for regularizing ELM based on ridge, lasso, and elastic net regression was developed by Reference [20], but this process is based on the formation of a committee (an ensemble) of extreme learning machines. This methodology deals with the problem that some parameters remain unchanged after their values are chosen at random because, in many cases, they do not translate an optimal value for the operations that will be performed by the ELM. The proposal to solve this problem rests on using a set of ELM networks in which their parameters are initialized autonomously, and the combination of their predictions is responsible for the final output of the model (with various combination techniques possible, see Reference [21]). This work makes use of regularization methods to automatically select the members who will be part of the committee [20].
Recently, studies have been conducted to improve the internal architecture of the ELM. Reference [22] has proposed a new sparse extreme learning machine (SPI-ELM) based on the condition number of the regression matrix and found a lemma to relate the condition number with the number of hidden neurons. SPI-ELM exhibits better generalization performance and lower run-time complexity compared with ELM and also demonstrates a beneficial relationship between the condition number in the ELM design matrix and the number of hidden neurons. This relationship helps to understand the random weights and non-linear activation functions in ELMs.
In Reference [23], two greedy learning algorithms are proposed: the forward feature selection algorithm (FFS-GELM) and a backward feature selection algorithm (BFS-GELM), which are meant to tackle the problem of the number of neurons in the hidden layer of ELMs. To reduce the computational complexity, an iterative strategy is used in FFS-GELM, and its convergence is proven. In BFS-GELM, the decreasing iteration is applied to decay this model, and in this process, the accelerating scheme was proposed to speed up the computation of removing the insignificant or redundant features.
Finally, DELM proposed by Reference [24] uses an online learning mechanism to train ELM as a primary classifier and train a double hidden layer structure to improve the performance of ELM. When an alert about concept drift is set, more hidden layer nodes are added to ELM to improve the generalization ability of the classifier. If the value measuring concept drift exceeds the upper limit, or the accuracy of ELM is at a low level, the current classifier will be deleted, and the algorithm will use new data to train a new classifier to learn the new concept.
2.3. Extreme Learning Machine and Pattern Recognition Problems
When the extreme learning machine acts on classification problems, it can also be regularized. Peng et al. [25] developed a method that is based on the idea that similar samples in an ELM should share similar properties, forming a regularized discriminative graph for extreme learning machines. In this method, to regularize ELM-based models for facial recognition, the constraint imposed on the output weights forces the output of the samples from the same class to be similar. This constraint is formulated with a regularization term that is added to the fundamental objective of an ELM model, causing the output layer weights to be solved analytically [25].
The work of Huang et al. [26] uses regularized ELM for problems of pattern classification and regression using semi-supervised and unsupervised learning. In a different way to the other related works, they introduce a form of regularization called manifold regularization [27], allowing its use in multiclass classification or multicluster grouping. The semi-supervised ELM proposal incorporates multiple regularizations to take advantage of unlabeled data to improve classification accuracy when they are scarce. In the unsupervised training scenario, the target is to find the data structure adjacent to the original data [26].
The model proposed by Silvestre et al. [28] uses a priori spatial information expressed by an affinity matrix to carry out the regularization, performed without any need for parameter tuning of the ELM. In Pinto et al. [29], the regularization is based on ranking and selection of best values of a priori information expressed by affinity matrices of the hidden neurons of ELM in pattern recognition in classification problems. Mohammed et al. proposed intelligent models based on the concepts of ELM and Bidirectional Principal Component Analysis [30] to act in the curvelet image decomposition of human faces. A subband that exhibits the maximum standard deviation is dimensionally reduced.
The variety of pattern identification tasks that can be performed with models trained by extreme learning machine is wide. In the Cao et al. model [31], the concept of sparse representation classification (SRC) in the area of image classification is applied in areas such as handwritten digit classification, landmark recognition and face recognition with satisfactory pattern identification results. The definition of the ELM space based on low classification decomposition is used for the treatment of data that are inserted into an intelligent model in the work proposed by Iosifidis et al. [32]. In the proposal of Jin et al. [33], ELM is adapted to work in conjunction with the MapReduce framework to classify patterns in Big Data problems. As in the Musikawan et al. [34] model, a parallelized metaheuristic proposal is used to identify existing patterns in regression problems.
The work proposed by Liangjun et al. [35] seeks to reduce the sensitivity of outliers and impulsive noises in the intelligent models through the correntropy. To confirm the results obtained by the model, datasets were submitted to standard classification tests with a significant improvement in the accuracy of the results obtained. The same concept of correntropy is also applied for robust ELM training in the model of Chen et al. [36] to act in function approximation and regression problems. Cybersecurity is also aided by models trained with ELM and feature selection methods. In the Gao et al. [37] model, an ELM incremental model combined with Adaptive Principal Component Analysis concepts is used to determine patterns of intrusions and intruders in computer networks. In the context of models using ELMs, Campos Souza et al. [38] built a model that performs pruning of less significant neurons using the concepts of Automatic Relevance Determination. There a strategy was suggested which is capable of defining the ELM hidden layer neurons that best contribute to the model with the usage of partial least squares regression [39]. The proposal in this paper differs from this approach due to the methodology of selection for the identification and construction of hidden layer neurons. In particular, the use of the LARS method in concomittance with bootstrap replications ensures the use of statistical techniques with various simulation scenarios. This technique seeks solid training to define the best subgroup of neurons capable of optimizing the model’s outputs through a combination of replications, statistical techniques, and selection of characteristics. In the Partial Least Squares (PLS) technique, only a single evaluation is used, which can be efficient in improving the performance of the model, but not in the selection of the best neuron selection group.
Recent work indeed also addresses pruning techniques using -regularization in neural networks (see, e.g., He et al. [40], Fan et al. [41], Chang et al. [42], and Alemu et al. [43]) together with their benefit to shrink as much regression coefficients as possible to 0, but unlike the approach suggested in this paper, they do not apply bootstrapping, neither any resampling technique [44] to elicit the hidden neurons actually needed. Such replications should make the selection more stable, especially in the case of a low amount of samples and/or significant noise in the data. This is because in the case of noisy data samples, regression fits may often provide instable solutions, even though regularization may be involved [45] (such as based on -norm, which is used in our approach for neuron selection). That is, the regression fits tend to over-fit due to fitting more the noise than the real underlying functional approximation trends, increasing the variance error much more than reducing the bias error [19]. Bagging short for Boostrap aggregating, invented by Leo Breiman in the 1990s [9], is a well-known and widely used method for reducing over-fitting effect due to noisy data samples [9,46]. Here, we use the bootstraps for providing a ’best of’ selection rather than combining various (ELM) models trained on bags, but the spirit of variance reduction and thus overall stability increase remains the same when conducting lasso regression on the various bootstrap samples (and combining their outputs, afterwards).
2.4. Determining Coefficients of Linear Regression in a Robust Manner with L1-Regularization
LARS [7] is a regression algorithm for high-dimensional data which estimates the regression coefficients and the subset of candidate regressors to be included in the final model. When we evaluate a set of N distinct samples , where where d is the dimension of and for , the cost function of this regression algorithm can be defined as:
where is a regularization parameter usually estimated using cross-validation [47]. The first term (4) corresponds to the residual sum of squares (RSS). This term decreases as the training error decreases. The second is the regularization term. First, it improves network generalization, avoiding overfitting [48]. Second, it can be used to generate sparse models [47], as it aims to force as much regression coefficients to 0 [49]. To understand why LARS can be used as a variable selection algorithm, Equation (4) can be rewritten as:
where B is an upper-bound on the -norm of the weights. A small value of B corresponds to a high value of , and vice versa. This equation is known as “least absolute shrinkage and selection operator” [19], or lasso. Figure 1 illustrates the contours of the RSS objective function, as well as the constraint surface. It is well known from the theory of constrained optimization that the optimal solution corresponds to the point where the lowest level of the objective function intersects the constraint surface. Thus, one should note that, when B grows until it meets the objective function, the points in the corners of the surface (i.e., the points on the coordinate axes) are more likely to intersect the RSS ellipse than those of the sides [47].
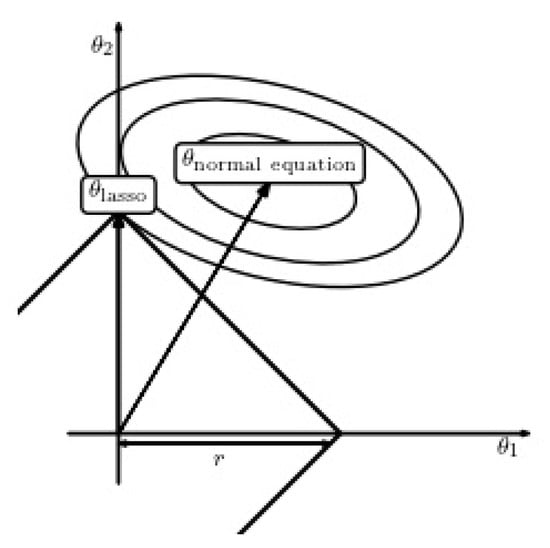
Figure 1.
Visualization of the effect of regularization: solution provided by lasso versus the unconstrained (regular) solution .
3. Pruning ELM Using Bootstrapped Lasso (BR-ELM)
When analyzing the behavior of ELM, we propose a method to choose the more significant neurons that actually contribute to the structure of the neural network for the actual learning problem at hand and thus to improve the prediction performance of the model due to reducing the likelihood of overfitting by more compact models. In this context, we will use regularization techniques to identify those elements which have a greater relevance to the hidden layer of the ELM and later apply a pruning technique to optimize the architecture of the network with the chosen neurons. Therefore, this approach is based on the choice of a large number of neurons in the hidden layer, and based on regularization and resampling techniques, we find the optimal set of neurons to solve the actual learning problem. In other words, the final network architecture in ELM is defined through a neuron shrinkage technique based on a combination of regularization and bootstrap replications.
For the problem considered in this paper, the regressors are the activation levels of the neurons, where each column of G can be associated with the activation level of one neuron on all training samples (rows). Thus, the LARS algorithm can be used to select an optimal subset of the significant neurons () that minimize Equation (4) for a given value of . This is because LARS tries to shrink as many coefficients as possible to 0, where one coefficient can be directly associated with a neuron (and its activation levels). Thus, all neurons leading to coefficients with value of 0 can be finally neglected in the final structure of the model. The amount of shrinkage thereby depends on the regularization parameter : the higher it becomes, the more coefficients will be shrinked to 0. In order to select an optimal , cross-validation (CV) based tuning (in a grid) can be applied, for instance, or also different direct choice techniques as proposed in Reference [15], circumventing time-intensive CV operations—for example, the method of hardened-balancing could be shown that it approximates the outcome of CV pretty well and often comes even closer to the optimal value of by avoiding distinct grid points. A final remark is that the application of LARS results in an embedded selection approach, which is closely linked to the supervised learning problem at hand, much more than a filter-based selection approach is (which usually relies on some information-theoretic measures, which are usually carried out in advance and not handled in combination with the current model and its learning method under investigation).
The approach used to increase the stability of the model selection algorithm is the use of re-sampling through bootstrapping, in combination with lasso regression also termed as Bolasso. Its principal procedure is summarized in Algorithm 1 [8].
| Algorithm 1 Bolasso-bootstrap-enhanced least absolute shrinkage operator |
| (1) Let n be the number of examples, (lines) in X and Y: (2) Draw n examples from , uniformly and with replacement, termed as (, ). (3) Perform LARS on (, ) with a given value of to estimate the regression coefficients . (4) Determine which coefficients are nonzero. (5) Repeat steps (2) to (4) for a specified number of bootstraps . (6) Take the intersection of the non-zero coefficients from all bootstrap replications as significant variables to be selected (100% consensus). (7) Revise using the variables selected via non-regularized least squares regression (if requested). (8) Calculate the expected error of the model on a separate validation set. (9) Repeat the procedure for each value of bootstraps and (actually done more efficiently by collecting interim results). (10) Determine “optimal” values for and b through eliciting the minimal expected error of the model on a separate validation set. |
In this procedure, the LARS algorithm runs on several bootstrap replications of the training data set and thus enjoys the benefits of bootstrap replications (noise reduction, sample significance increase and so forth [9]). For each repetition, a distinct subset of regressors is selected. The regressors to be included in the final model are defined according to the frequency with which each of them is chosen through different tests. In a more realistic variant, a consensus threshold smaller than may be determined, say , and a regressor is then included, if selected in at least of the assays. X can be set according to statistical significance level considerations, thus being typically in the range (e.g., 95 would belong to a significance level of 0.05). This means that a neuron has to be selected in most of the bootstrap replications such that it can be safely accepted that it is significantly important for the model structure to explain the modeling target.
Consider n independent and identically distributed observations ()∈ × , i = 1, …, n, provided by the matrices and Y∈, admit bootstrap replications of n data points [8,50]; that is, for , we suppose an auxiliary sample , i = 1, …, n, given by the matrices ∈ and ∈. The n pairs (, ), i = 1, …, n, are randomly drawn from the original n pairs in (X, Y) with replacement, subtracting the evaluations not to be biased. Thus, we determine the distribution of the auxiliary sample () by sampling n points with the substitution of (X, Y) and, given (X, Y), the auxiliary samples are independently sampled of () [8].
It is suggested to estimate the supports = j, of the Lasso estimates for the bootstrap samples, k = 1, …, , and to cross them to define the estimate of the support: J = , for A ∈ is the weight. Since J is selected, we estimate by the unregulated least-squares adjustment restricted to variables in J. This estimation can be computed simultaneously for a large number of regularization parameters due to the efficiency of the LARS algorithm, which allows us to find the whole regularization path for the Lasso at the empirical cost of a single matrix inversion [7]. Even with an order of high complexity, the bootstrapped lasso may be able to use the training samples and define the relevance of that evaluated neuron to the set of final responses by using resampling. As replications are random, the results are free of tendencies, and the pruning of less relevant neurons according to the consensus threshold can be performed in the following way:
with the coefficient (output weight) of neuron i estimated through LARS on the b-th bootstrap replication and the consensus threshold (X% belongs to . If this condition holds, then variable i is selected. Thus, the finally selected set of neurons becomes
with .
In our case, the learning algorithm assumes that the output hidden layer composed of the candidate neurons can be written as:
where is the weight vector of the output layer and the output vector of the second layer, for . In this context, is considered as the non-linear mapping of the input space for a feature space of dimension . Since the weights connecting the first two layers are randomly assigned, the only parameters to be estimated are the weights of the output layer. Thus, the problem of network parameter estimation can be seen as a linear regression problem, allowing the use of regression techniques [19] for estimating parameters and selecting candidate neurons. The benefit of using a bootstrap approach combined with the LARS procedure is the more coherent choice of a subset capable of better representing a problem’s data, due to the set of combinations that can be generated in order to validate the efficiency of an analyzed neuron. Despite several combinations, the impacts on the model’s outputs are considerable, as they are more assertive, even with a substantial increase in the complexity of the model’s training. The proposed method then consists of computing the matrix of the activation functions of the hidden layer G and then calculating the regression coefficients using the Lasso method on different bootstrap replications, and finally selecting the most significant number of neurons through consensus threshold (see above). The combined procedure for pruning ELMs is summarized in Algorithm 2 and should be self-explainable. The algorithm has three parameters:
- The number of bootstrap replicates, ;
- The consensus threshold, .
- The initial amount of hidden neurons, k
| Algorithm 2 Pruning algorithm for Extreme Learning Machines |
| (1) Define number of bootstrap replicates. (2) Define the consensus threshold . (3) Create initial hidden neurons k following the conventional strategy used in ELMs. (4) Assign random values to and , for j = 1, …, k. (5) For : (6) Draw n examples from , uniformly and with replacement, termed as (, ). (7) Compute using Equation (2). (8) Perform LARS algorithm in order to solve (4) for yielding (internally, apply regularization parameter choice technique to elicit the optimal ). (9) EndFor (10) Select the final neurons using (7) through (6) with consensus threshold . (11) Construct matrix from the selected neurons. (11) Estimate the final output layer weights by applying (3) using instead of G. (12) Define the output hidden layer using (8). |
For the initial amount of neurons we can assume any high value (>100) sufficiently covering the degree of non-linearity contained in a learning problem. As LARS is a regularized procedure and thus able to deal with weakly-determined equation systems, this initial amount can be expected to be not really sensitive. The ideal number of bootstrap replicates could be estimated through the out-of-bag error (OOB) [8] by varying and taking the minimal OOB value for final model training and pruning. The consensus threshold is typically set according statistical significance considerations (as discussed above).
4. Experiments
4.1. Synthetic Database Classification
To perform the following tests, four synthetic two-dimensional data sets were used to simulate the pattern classification for this type of hypothetical situations. The four data sets have 500 samples each and . Consider further the initial number of hidden neurons, , the number of bootstrap replicates, b = 8 and the pessimistic consensus threshold = 90% (thus, for all replications the estimated output weight of a neuron has to be non-zero to be selected).
In all the tests performed for the synthetic bases consider that the inputs were normalized, the outputs fall within the range of [−1, 1] and the initial number of neurons is equal to the number of samples of each of the bases used in the test (which in this case was 500). The organization of the data sets in space is presented below. The data sets are shown as geometric outlines to evaluate the ability of the models to find those labels. Figure 2 shows the triangulation of Delaunay [x] for the bases; Figure 3 shows the separation between positive and negative classes. Table 1 presents the characteristics of each base and the percentage of ELM training (70%) and the test value (30%).
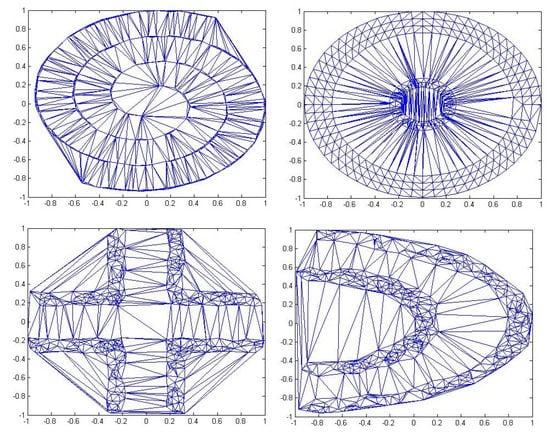
Figure 2.
Bases of Delaunay triangulation.
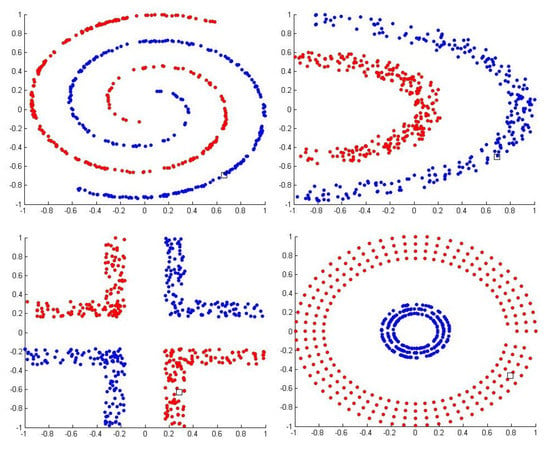
Figure 3.
Positive and negative samples in each data set.

Table 1.
Synthetic data set used in the experiments.
In Table 2 and Table 3, the average values of 30 repetitions were presented for each of the evaluated models. The highlighted values refer to the mean accuracy of the pattern classification for the first frame and the mean number of neurons used in the final architecture of the network. The values in parentheses represent the standard deviations of the tests performed.

Table 2.
Accuracies of the model in the tests performed.

Table 3.
Number of neurons selected in the test.
It can be verified by the synthetic bases test that the conventional ELM approach has a very high amount of neurons in the hidden layer, which does not necessarily lead to better accuracies (most probably it suffers from overfitting issues). Thus, pruning methods, especially our proposed algorithm BR-ELM, but also the related approach OP-ELM) help in the elimination of neurons that undermined the accuracy of the model in accomplishing the pattern classification.
The model proposed in the paper (BR-ELM) and the related state-of-the-art method OP-ELM in pruning of neurons had a statistically equivalent performance when dealing with accuracy, besides being superior to the P-ELM model and the original ELM, but our new approach used fewer neurons in three of the four tests performed. That emphasizes that the model of ELM based on regularization resampling allows a more efficient adaptation of the ELM architecture because it uses fewer neurons, reducing complexity and underlining the useability of the model in pattern classification. Figure 4 and Figure 5 identify the classifier response for the classes used in each of the tests. Also, the separation of classes in space is presented. For all the figures shown, the accuracy of the test was 100% (also compared with Table 2).
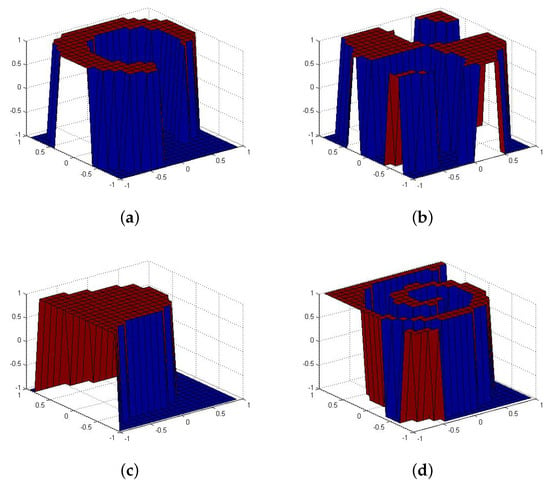
Figure 4.
(a) Data set Cluster. (b) Data set Corners. (c) Data set Half Kernel (d) Data set Spiral.
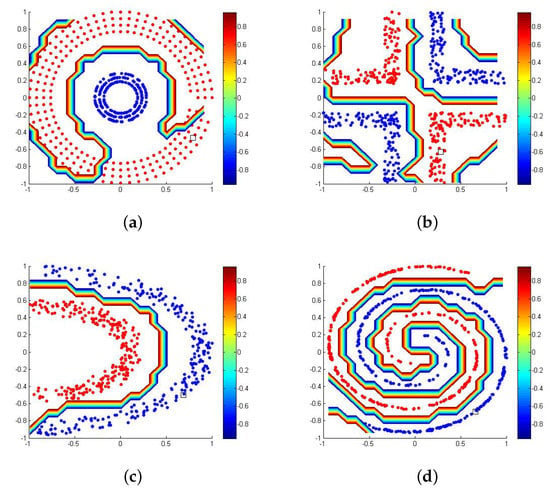
Figure 5.
(a) Data set Cluster Classification. (b) Data set Corners Classification. (c) Data set Half Kernel Classification. (d) Data set Spiral Classification.
4.2. Evaluation Measures Used for Tests on Real-World Data Sets
The proposed pruning algorithm described in the previous section is evaluated using binary pattern classification problems and regression problems. The performance analysis was performed based on data sets with small and high dimensions.The data sets also included a low number (<1000), a mean number (between 1001 and 5000), and a high number (above 5001) of samples.
The evaluation measures in the pattern classification problems were as follows:
where, true positives, true negatives, false negatives and false positives.
In regression tests, the methods were evaluated through the root-mean-square error (RMSE) as defined by:
where y is the target, is the estimation from the model, and N is the number of samples. That is a frequently used measure of the differences between values (sample or population values) predicted by a model and the values observed.
The pruning method proposed in this article (BR-ELM) was compared with other classifiers to verify their accuracies. In all tables, the principal value is the accuracy, and the highlighted value in the parentheses is the respective standard deviation. The comparison was done with conventional ELM method (without using any pruning technique), and with the recently proposed pruning-based approaches P-ELM [5] and OP-ELM [4], which are closely related to ours as also performing LARS algorithm for neuron selection (but without bootstrap replications).
The data samples were randomly selected. We collected 30 measurements of accuracy from each of the bases evaluated in each model analyzed. The variables involved in the process were normalized with mean zero and unit variance. All outputs of the model were normalized to the range . The initial parameters of the hidden layer were sampled from a uniform distribution . Hyperbolic tangent type sigmoidal activation functions were adopted for all neurons in all ELM models used in the test. The initial number of neurons k was set to the same value for all methods in order to achieve a fair comparison, typically to 500, except when the data set has less samples, then it was set to the number of samples
4.3. Benchmark Classification Datasets
The data sets used were obtained from the UCI machine learning repository [51] and in some standard-rank surveys performed by Reference [52,53]. Note the Iris class that had three types of classification was re-adapted to have only two outputs. Here is some relevant information about the real bases used in the tests [51,52,53].
Table 4 details the basics including the number of samples used for training and performance evaluation in addition to the number of initial neurons in the hidden layer .

Table 4.
Data sets used in the Classification experiments.
Table 5 shows the accuracy Equation( 9) of results of the binary pattern classification problems methods, Table 6 the respective number of selected neurons. In Table 7 and Table 8, the AUC and the time of execution of the tests are represented, respectively.

Table 5.
Accuracies of the model in the tests performed.

Table 6.
Number of neurons selected in the test.

Table 7.
AUC .

Table 8.
Time.
When analyzing Table 5 and Table 6, it can be seen that the BR-ELM model obtained better results than the other models analyzed in the accuracy test while the number of neurons selected () was much lower for BR-ELM. Statistical analysis was performed on the datasets, and the accuracy as the only factor evaluated, where each of the classification bases can be seen as the blocking factor. Figure 6 shows the graphical organization of algorithm performance based on blocking factors. It presents the average behavior of the algorithms in solving all problems and the normal behavior of the models in the evaluated datasets. To perform the statistical tests, the analysis of variance (ANOVA) on the results for each of the groups (algorithm x block factor) is used in the test. In general, it is verified that the test has 68 groups (4 algorithms and 17 bases). As a null hypothesis, we will consider that the four algorithms have the same mean accuracy to perform the pattern classification. As an alternative hypothesis, we define that they have a distinct average accuracy in performing the classification task of the 17 data sets. Using this test, it is possible to conclude whether or not the performance of the algorithm proposed in this paper achieves an average performance higher than the state-of-the-art methods. After performing the ANOVA test with a significance level of , it turned out that the null hypothesis of equality of the performance of the algorithms has to be rejected due to a p-value of (p-value = ). This is also the case for the equality of performance of the algorithms by the blocking factor (p-value = ). In Figure 7, we can observe the characteristics resulting from the ANOVA test for the database set evaluated. The factors presented in the figure represent the validations of the assumptions of the ANOVA test, proving normality (Shapiro-Wilk normality test), homogeneity of variances (Fligner-Killeen test) and independence (Durbin-Watson test) [54].
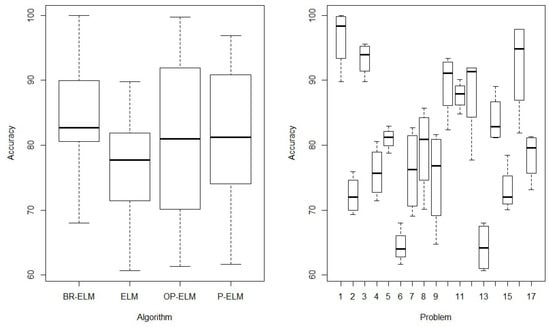
Figure 6.
Plot of the average behavior of the algorithms in solving all problems.
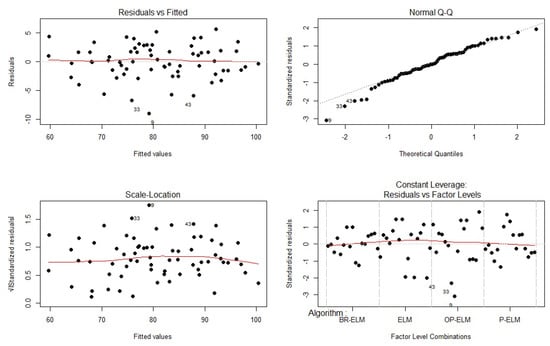
Figure 7.
Validation results of the ANOVA test.
Based on the results obtained by the ANOVA test and its due validations, we can conclude with 95% certainty that the algorithms evaluated in the test have different means to perform the block classification of these 17 databases (in this sense BR-ELM seems to be superior to the other methods as having the highest accuracy in most of the data sets and also having the highest one in average). We further verified the performance of the methods through statistical tests allowing multiple comparisons at the same time. Therefore, we performed a multiple comparisons post-hoc test called Tukey’s test [54] that makes two-to-two comparisons between all the algorithms involved. The numerous comparisons are presented in Table 9 and there is enough evidence in the results obtained to reject the equivalence between BR-ELM and ELM as well as BR-ELM and OP-ELM with a significance level of 0.05 (as both achieving a p-value smaller than 0.05), but not between BR-ELM and P-ELM. Significant differences are also identified between the performance of P-ELM and OP-ELM with ELM. Figure 8 and Table 9 presents a graphical evaluation of the Tukey test that can corroborate the statements presents in Table 9, especially in the demonstration of the lowest and highest values present in the comparison between the analyzed algorithms.

Table 9.
Tukey multiple comparisons of means. 95% family-wise confidence level.
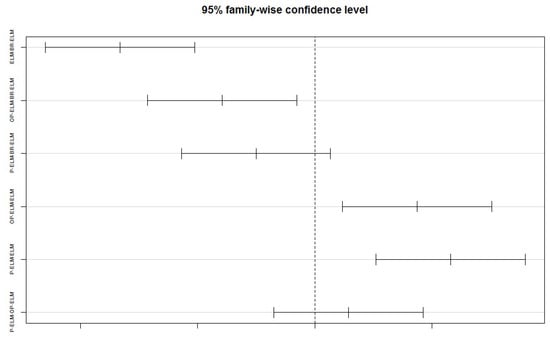
Figure 8.
Multiple comparisons of Tukey.
Another way to visualize the performance of the model proposed is to perform the multiple comparisons of Dunnett [54], where one of the algorithms is highlighted as reference, and all comparisons can be made with this reference. Table 10 shows the result of the comparisons of this test and Figure 9 is the graph result obtained by the multiple comparisons; again, a value of indicates statistical significance for rejecting the equal performance assumption. Thus, ELM and OP-ELM can be clearly outperformed by BR-ELM. Although P-ELM can be not outperformed it is remarkable the BR-ELM leads to a lower number of neurons than P-ELM in 13 out of 17 data sets and in average to a significantly lower number (54.69 vs. 143.42). Figure 9 showing the comparison of the values present in Table 10.

Table 10.
Multiple Comparisons of Means: Dunnett Contrasts.
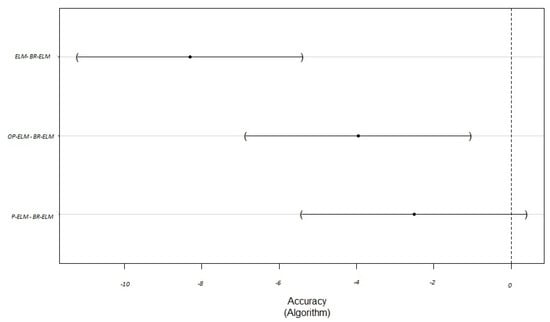
Figure 9.
Dunnett Contrasts.
Through this multiple comparison tests we can thus affirm with 95% confidence that ELM and OP-ELM can be clearly outperformed by BR-ELM. Although P-ELM cannot be outperformed, it is remarkable that BR-ELM leads to a lower number of neurons than P-ELM in 13 out of 17 data sets and in average to a significantly lower number (54.69 vs. 143.42).
4.4. Benchmark Regression Datasets
To verify the ability of the BR-ELM model in the regression tests, it was performed with bases commonly used in problems for this purpose. The model was again compared to the OP-ELM approach. The seven regression sets use in these tests (cf. Table 11) can be classified into three groups of data:

Table 11.
Data sets used in the experiments for regression problems.
- Datasets with relatively small size and low dimensions, for example, Cloud [55] and Container Crane Controller [56].
- Datasets with low size and low dimensions, for example, Carbon nanotubes [57].
- Datasets with relatively large size and low dimensions, for example, Quake [58], Abalone [55], Absenteeism at work [59] and Air Quality (Without features Date and Time.) [60] and Combined Cycle Power Plant [61]
In the regression test (Table 12), the BR-ELM results were the best in five of the seven bases evaluated. That shows that despite the longer time to solve problems, the approximation of the values is more consistent with the BR-ELM. In this context, it is possible to evaluate that the model, despite the time excess, presents a better presentation than the OP-ELM using a set of more significant neurons. In contrast, the number of neurons used in the models (Table 13) was much lower in BR-ELM in almost all experiments than the models were compared. This shows that the resampling technique can also identify the essential neurons, generating models with responses that are closer to what is intended to be evaluated.

Table 12.
Result of regression test—RMSE.

Table 13.
Result of regression test—number of neurons.
4.5. Pattern Classification Tests Using Complex Real Datasets
The BR-ELM model proposed in this paper will solve the real problems of various kinds. To this end, its performance will be compared with recent further approaches that also use techniques to select hidden layer neurons (statistical, bayesian, among others).
The models used for comparisons will be the correlation coefficient pruning (CE-ELM) [62], partial least squares regression in combination with ELMs (PS-ELM) [39], and Automatic Relevance Determination (ARD-ELM) [38] for pruning ELMs. All neurons in the hidden layer of all models are the same (sigmoidal). The number of hidden layer neurons for all models was set to 200 neurons, and the BR-ELM parameter values are the same as those elicited by cross-validation during the previous pattern classification experiments. These factors are essential to maintain the ability to evaluate improvement in resampling technique results along with regularization l1.
The evaluation criteria follow the same assumptions as in the standard classification or regression tests, and the machine configuration for the tests follows the same characteristics as listed above. Highlighted bold values represent the best values when comparing models. These models will act to solve complex problems of various kinds, as listed below.
4.5.1. Objectivity or Subjectivity of Sporting Articles
The dataset (sports articles) from this experiment represents 1000 English sports articles from 50 different sites. Professional journalists or sports blog fans wrote most of these articles. Articles ranged from 47 to 4283 words, with an average length of 697 words. For identification, we used Amazon’s Mechanical Turk tool [63]. 658 articles were labeled as objective (1), and 342 were labeled as subjective (−1). The database is unbalanced and made up of articles from various sources and authors. Therefore, the linguistic structures of the articles vary significantly, making the classification task difficult. Most features extracted from the text are linked to the frequency of specific terms. All features can be viewed in the paper by Hall et al. [63]. Table 14 presents the results obtained by the pruned ELM models to identify whether or not the evaluated articles are objective.

Table 14.
Objectivity or subjectivity of sporting articles.
The results of the BR-ELM model (Table 14) were superior in almost all evaluated items, except in its execution time. However, it should be noted that it was the model that used a simpler architecture to solve the problem and obtained the best results of correctness in the objectivity of sports articles. It is noteworthy that using all the features of the problem, the average results obtained by the BR-ELM model were superior to the state-of-the-art ([63]). That demonstrates that the model proposed in this paper has high accuracy in the evaluation of sports articles, with the lowest confusion rate between the possible variations between false positives and false negatives.
4.5.2. Suspicious Firm Classification
Companies that cheat markets are apparent these days. Therefore, databases for this purpose are relevant to be solved by intelligent models. The database uses a case study of an external audit firm that wants to improve its actions. Annual data were collected from 777 companies from 14 different sectors. The characteristics of the database can be viewed in the paper by Hooda et al. [64].
Table 15 presents the results of intelligent models in identifying companies with audit problems. The results presented by the BR-ELM were extremely satisfactory due to its high performance in the configurations defined in the fraud detection tests in companies. A relevant factor is that the model was immensely superior to state of the art for the subject increasing by approximately 4% the ability to detect fraud in company audits (94% accuracy in the paper by Hooda et al. Versus 98.72% in this paper.), and this with the lowest number of neurons.

Table 15.
Classification of fraud in companies.
5. Conclusions
After the tests were performed and the statistical evaluations completed, we can conclude that the pruning methods presented in this work maintain the average accuracy of data classification correctness when compared to an ELM structure with the complete neurons in the hidden layer, besides pruning methods commonly used in the literature. With fewer neurons, the probability of overfitting is lower, which in turn increases the likelihood that the model performs well new separate test data. Furthermore, it reduces the calculations of the data between the hidden layer and the output layer. The model proposed in this paper assertively acts on complex regression and pattern classification problems. Its main contribution to science is the use of resampling and LARS to define subgroups of neurons in the hidden layer of artificial neural networks. That allows the definition of neurons in the hidden layer of a model to be more consistent with the problems to be solved, ensuring assertive outputs. The model was confirmed as efficient in solving real complex problems, thus allowing its results to be better than those presented for the state of the art of the analyzed problems. The proposed methods and cut-off factors eliminate unnecessary neurons, whereas the BR-ELM method did so more efficiently than OP-ELM and P-ELM for most of the data sets, and this with achieving better model accuracies. It was verified in the course of the tests that pruning algorithms significantly improved the final response of the model, but some adjustments in the pruning variable can be performed to improve the algorithms further. Regarding the tests related to real and complex problems, the BR-ELM model was superior to the other pruning models used in the pattern classification tests, demonstrating that their results even surpass the state of the art of the problem. Bolasso’s approach brought stability and more efficient answers to solve problems of various specificities.
For future work, optimization methods can be used to evaluate each case of the data set used in the model, finding the best pruning factor for the neurons in the hidden layer. The use of optimization methods can find hyperparameters more efficiently and obtain optimal results in the construction of the internal structures of the model (weights, bias, the first number of neurons). Studies on weight restrictions or limitations [65,66,67,68,69] as an alternative approach to solving the problem of overfitting may be targets for future implementations.
Author Contributions
Conceptualization, P.V.d.C.S. and L.C.B.T.; methodology, G.R.L.S.; software, P.V.d.C.S. and G.R.L.S.; validation, A.d.P.B., L.C.B.T. and E.L.; formal analysis, P.V.d.C.S.; investigation, L.C.B.T.; resources, P.V.d.C.S.; data curation, P.V.d.C.S. and A.d.P.B.; writing—original draft preparation, P.V.d.C.S.; writing—review and editing, P.V.d.C.S. and L.C.B.T; visualization, G.R.L.S.; supervision, P.V.d.C.S.; project administration, P.V.d.C.S.; funding acquisition, P.V.d.C.S. and E.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Brazilian agency CAPES, in part by CNPq, and in part by FAPEMIG.
Acknowledgments
The fifth author acknowledges the support by the “LCM—K2 Center for Symbiotic Mechatronics” within the framework of the Austrian COMET-K2 program. Open Access Funding by the University of Linz.
Conflicts of Interest
The authors declare that there is no conflict of interest in the work.
References
- Broomhead, D.S.; Lowe, D. Radial Basis Functions, Multi-Variable Functional Interpolation and Adaptive Networks; Technical Report; Royal Signals and Radar Establishment Malvern: Malvern, UK, 1988. [Google Scholar]
- Pao, Y.H.; Park, G.H.; Sobajic, D.J. Learning and generalization characteristics of the random vector functional-link net. Neurocomputing 1994, 6, 163–180. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Miche, Y.; Sorjamaa, A.; Bas, P.; Simula, O.; Jutten, C.; Lendasse, A. OP-ELM: Optimally pruned extreme learning machine. IEEE Trans. Neural Netw. 2010, 21, 158–162. [Google Scholar] [CrossRef] [PubMed]
- Rong, H.J.; Ong, Y.S.; Tan, A.H.; Zhu, Z. A fast pruned-extreme learning machine for classification problem. Neurocomputing 2008, 72, 359–366. [Google Scholar] [CrossRef]
- Similä, T.; Tikka, J. Multiresponse Sparse Regression with Application to Multidimensional Scaling. In Artificial Neural Networks: Formal Models and Their Applications—ICANN 2005; Duch, W., Kacprzyk, J., Oja, E., Zadrożny, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 97–102. [Google Scholar]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Bach, F.R. Bolasso: Model Consistent Lasso Estimation Through the Bootstrap. In Proceedings of the 25th International Conference on Machine Learning; ACM: New York, NY, USA, 2008; pp. 33–40. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Pao, Y.H.; Takefuji, Y. Functional-link net computing: Theory, system architecture, and functionalities. Computer 1992, 25, 76–79. [Google Scholar] [CrossRef]
- Martínez-Martínez, J.M.; Escandell-Montero, P.; Soria-Olivas, E.; Martín-Guerrero, J.D.; Magdalena-Benedito, R.; Gómez-Sanchis, J. Regularized extreme learning machine for regression problems. Neurocomputing 2011, 74, 3716–3721. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User; Prentice Hall PTR, Prentic Hall Inc.: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Tikhonov, A.N. On the solution of ill-posed problems and the method of regularization. In Doklady Akademii Nauk; Russian Academy of Sciences: Moscow, Russia, 1963; Volume 151, pp. 501–504. [Google Scholar]
- Bauer, F.; Lukas, M. Comparing parameter choice methods for regularization of ill-posed problems. Math. Comput. Simul. 2011, 81, 1795–1841. [Google Scholar] [CrossRef]
- Csáji, B.C. Approximation with artificial neural networks. Fac. Sci. Etvs Lornd Univ. Hung. 2001, 24, 48. [Google Scholar]
- Miche, Y.; van Heeswijk, M.; Bas, P.; Simula, O.; Lendasse, A. TROP-ELM: A double-regularized ELM using LARS and Tikhonov regularization. Neurocomputing 2011, 74, 2413–2421. [Google Scholar] [CrossRef]
- Yu, Q.; Miche, Y.; Eirola, E.; van Heeswijk, M.; Séverin, E.; Lendasse, A. Regularized extreme learning machine for regression with missing data. Neurocomputing 2013, 102, 45–51. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.; Franklin, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction; Springer: Berlin/Heidelberg, Germany, 2005; Volume 27, pp. 83–85. [Google Scholar]
- Escandell-Montero, P.; Martínez-Martínez, J.M.; Soria-Olivas, E.; Guimerá-Tomás, J.; Martínez-Sober, M.; Serrano-López, A.J. Regularized Committee of Extreme Learning Machine for Regression Problems. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, ESANN 2012, Bruges, Belgium, 25–27 April 2012; pp. 251–256. [Google Scholar]
- Kuncheva, L. Combining Pattern Classifiers: Methods and Algorithms; Wiley-Interscience (John Wiley & Sons): Chichester, West Sussex, UK, 2004. [Google Scholar]
- Kassani, P.H.; Teoh, A.B.J.; Kim, E. Sparse pseudoinverse incremental extreme learning machine. Neurocomputing 2018, 287, 128–142. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Pan, Y.T.; Song, F.Q.; Sun, L.; Chen, T.H. Feature selection of generalized extreme learning machine for regression problems. Neurocomputing 2018, 275, 2810–2823. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J. Dynamic extreme learning machine for data stream classification. Neurocomputing 2017, 238, 433–449. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, S.; Long, X.; Lu, B.L. Discriminative graph regularized extreme learning machine and its application to face recognition. Neurocomputing 2015, 149, 340–353. [Google Scholar] [CrossRef]
- Huang, G.; Song, S.; Gupta, J.N.D.; Wu, C. Semi-Supervised and Unsupervised Extreme Learning Machines. IEEE Trans. Cybern. 2014, 44, 2405–2417. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Silvestre, L.J.; Lemos, A.P.; Braga, J.P.; Braga, A.P. Dataset structure as prior information for parameter-free regularization of extreme learning machines. Neurocomputing 2015, 169, 288–294. [Google Scholar] [CrossRef]
- Pinto, D.; Lemos, A.P.; Braga, A.P.; Horizonte, B.; Gerais-Brazil, M. An affinity matrix approach for structure selection of extreme learning machines. In Proceedings; Presses universitaires de Louvain: Louvain-la-Neuve, Belgium, 2015; p. 343. [Google Scholar]
- Mohammed, A.A.; Minhas, R.; Wu, Q.J.; Sid-Ahmed, M.A. Human face recognition based on multidimensional PCA and extreme learning machine. Pattern Recognit. 2011, 44, 2588–2597. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, K.; Luo, M.; Yin, C.; Lai, X. Extreme learning machine and adaptive sparse representation for image classification. Neural Netw. 2016, 81, 91–102. [Google Scholar] [CrossRef] [PubMed]
- Iosifidis, A.; Tefas, A.; Pitas, I. On the kernel extreme learning machine classifier. Pattern Recognit. Lett. 2015, 54, 11–17. [Google Scholar] [CrossRef]
- Xin, J.; Wang, Z.; Qu, L.; Wang, G. Elastic extreme learning machine for big data classification. Neurocomputing 2015, 149, 464–471. [Google Scholar] [CrossRef]
- Musikawan, P.; Sunat, K.; Kongsorot, Y.; Horata, P.; Chiewchanwattana, S. Parallelized Metaheuristic-Ensemble of Heterogeneous Feedforward Neural Networks for Regression Problems. IEEE Access 2019, 7, 26909–26932. [Google Scholar] [CrossRef]
- Liangjun, C.; Honeine, P.; Hua, Q.; Jihong, Z.; Xia, S. Correntropy-based robust multilayer extreme learning machines. Pattern Recognit. 2018, 84, 357–370. [Google Scholar] [CrossRef]
- Chen, B.; Wang, X.; Lu, N.; Wang, S.; Cao, J.; Qin, J. Mixture correntropy for robust learning. Pattern Recognit. 2018, 79, 318–327. [Google Scholar] [CrossRef]
- Gao, J.; Chai, S.; Zhang, B.; Xia, Y. Research on Network Intrusion Detection Based on Incremental Extreme Learning Machine and Adaptive Principal Component Analysis. Energies 2019, 12, 1223. [Google Scholar] [CrossRef]
- de Campos Souza, P.V.; Araujo, V.J.S.; Araujo, V.S.; Batista, L.O.; Guimaraes, A.J. Pruning Extreme Wavelets Learning Machine by Automatic Relevance Determination. In Engineering Applications of Neural Networks; Macintyre, J., Iliadis, L., Maglogiannis, I., Jayne, C., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 208–220. [Google Scholar]
- de Campos Souza, P.V. Pruning method in the architecture of extreme learning machines based on partial least squares regression. IEEE Lat. Am. Trans. 2018, 16, 2864–2871. [Google Scholar] [CrossRef]
- He, B.; Sun, T.; Yan, T.; Shen, Y.; Nian, R. A pruning ensemble model of extreme learning machine with L_{1/2} regularizer. Multidimens. Syst. Signal Process. 2017, 28, 1051–1069. [Google Scholar] [CrossRef]
- Fan, Y.T.; Wu, W.; Yang, W.Y.; Fan, Q.W.; Wang, J. A pruning algorithm with L 1/2 regularizer for extreme learning machine. J. Zhejiang Univ. Sci. C 2014, 15, 119–125. [Google Scholar] [CrossRef]
- Chang, J.; Sha, J. Prune Deep Neural Networks With the Modified L_{1/2} Penalty. IEEE Access 2018, 7, 2273–2280. [Google Scholar] [CrossRef]
- Alemu, H.Z.; Zhao, J.; Li, F.; Wu, W. Group L_{1/2} regularization for pruning hidden layer nodes of feedforward neural networks. IEEE Access 2019, 7, 9540–9557. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, H.; Wang, J.; Chang, Q.; Wang, J.; Pal, N.R. Learning Optimized Structure of Neural Networks by Hidden Node Pruning With L1 Regularization. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef]
- Schaffer, C. Overfitting Avoidance as Bias. Mach. Learn. 1993, 10, 153–178. [Google Scholar] [CrossRef]
- Islam, M.; Yao, X.; Nirjon, S.; Islam, M.; Murase, K. Bagging and Boosting Negatively Correlated Neural Networks. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2008, 38, 771–784. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Girosi, F.; Jones, M.; Poggio, T. Regularization Theory and Neural Networks Architectures. Neural Comput. 1995, 7, 219–269. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 1996, 58B, 267–288. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Lichman, M. UCI Machine Learning Repository; University of California: Irvine, CA, USA, 2013. [Google Scholar]
- Ho, T.K.; Kleinberg, E.M. Building projectable classifiers of arbitrary complexity. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; Volume 2, pp. 880–885. [Google Scholar]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification. 2003. Available online: http://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide (accessed on 15 April 2010).
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Blake, C. UCI Repository of Machine Learning Databases; University of California: Irvine, CA, USA, 1998. [Google Scholar]
- Ferreira, R.P.; Martiniano, A.; Ferreira, A.; Romero, M.; Sassi, R.J. Container crane controller with the use of a NeuroFuzzy Network. In IFIP International Conference on Advances in Production Management Systems; Springer: Berlin/Heidelberg, Germany, 2016; pp. 122–129. [Google Scholar]
- Acı, M.; Avcı, M. Artificial neural network approach for atomic coordinate prediction of carbon nanotubes. Appl. Phys. A 2016, 122, 631. [Google Scholar] [CrossRef]
- Mike, M. Statistical Datasets; Carnegie Mellon University Department of Statistics and Data Science: Pittsburgh, PA, USA, 1989. [Google Scholar]
- Martiniano, A.; Ferreira, R.; Sassi, R.; Affonso, C. Application of a neuro fuzzy network in prediction of absenteeism at work. In Proceedings of the 7th Iberian Conference on Information Systems and Technologies (CISTI 2012), Madrid, Spain, 20–23 June 2012; pp. 1–4. [Google Scholar]
- De Vito, S.; Massera, E.; Piga, M.; Martinotto, L.; Di Francia, G. On field calibration of an electronic nose for benzene estimation in an urban pollution monitoring scenario. Sens. Actuators B Chem. 2008, 129, 750–757. [Google Scholar] [CrossRef]
- Tüfekci, P. Prediction of full load electrical power output of a base load operated combined cycle power plant using machine learning methods. Int. J. Electr. Power Energy Syst. 2014, 60, 126–140. [Google Scholar] [CrossRef]
- de Campos Souza, P.V.; Araujo, V.S.; Guimaraes, A.J.; Araujo, V.J.S.; Rezende, T.S. Method of pruning the hidden layer of the extreme learning machine based on correlation coefficient. In Proceedings of the 2018 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Gudalajara, Mexico, 7–9 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Hajj, N.; Rizk, Y.; Awad, M. A subjectivity classification framework for sports articles using improved cortical algorithms. Neural Comput. Appl. 2018, 31, 8069–8085. [Google Scholar] [CrossRef]
- Hooda, N.; Bawa, S.; Rana, P.S. Fraudulent Firm Classification: A Case Study of an External Audit. Appl. Artif. Intell. 2018, 32, 48–64. [Google Scholar] [CrossRef]
- Hagiwara, K.; Fukumizu, K. Relation between weight size and degree of over-fitting in neural network regression. Neural Netw. 2008, 21, 48–58. [Google Scholar] [CrossRef] [PubMed]
- Livieris, I.E.; Iliadis, L.; Pintelas, P. On ensemble techniques of weight-constrained neural networks. Evol. Syst. 2020. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, P. An improved weight-constrained neural network training algorithm. Neural Comput. Appl. 2019, 32, 4177–4185. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, P. An adaptive nonmonotone active set–weight constrained–neural network training algorithm. Neurocomputing 2019, 360, 294–303. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, E.; Kotsilieris, T.; Stavroyiannis, S.; Pintelas, P. Weight-constrained neural networks in forecasting tourist volumes: A case study. Electronics 2019, 8, 1005. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).