Open-Loop Switched-Capacitor Integrator for Low Voltage Applications

Abstract

An architecture of a switched-capacitor integrator that includes a charge buffer operating in an open-loop is hereby proposed. As for the switched-capacitor filters, the gain of the proposed integrator, which is given by the input/output capacitor ratio, ensures desensitization to process, voltage, and temperature variations. The proposed circuit is suitable for low voltage supplies. It enables a significant power saving compared to a traditional switched-capacitor integrator. This was demonstrated through an analytical comparison between the proposed integrator and a traditional switched-capacitor integrator. The mathematical results were supported and verified by simulations performed on a circuit prototype designed in 16 nm finFET technology with 0.95 V supply. The proposed switched-capacitor integrator consumes 76 µW, resulting in more than twice the efficiency for the traditional closed-loop switched-capacitor filter as an input voltage equal to 31.25 mV at 7 ns clock period is considered. The comparison of architectures was led among the proposed integrator and the state-of-the-art technology in terms of the figure of merit.

1. Introduction

Switched-capacitor filters are used in a variety of applications like sensors interfaces [1], audio applications [2], RF front-ends [3], analog-to-digital converters [4], etc. The high accuracy, comparable to the capacitors mismatch and the ease of reprogramming, makes this topology preferable. Such filters require high-performance operational transconductance amplifiers (OTAs). Using modern IC technologies helps to reach high-frequency operation. However, obtaining high DC-gain becomes more challenging for two main reasons: the low supply voltage of the modern IC technologies that limit the number of stackable devices, generally used to obtain high DC-gain OTAs; the reduced length of the transistors that reduces the output resistances and limits the transistor intrinsic gain. On the other hand, the required high-DC gain is obtainable, increasing the number of gain stages of the OTA at the cost of higher power consumption.

In this paper, an open-loop switched-capacitor filter as a building block for the design of a higher-order switched-capacitor filter is presented. Despite its open-loop architecture, the integrator gain depends on the capacitor ratio whose accuracy is related to the capacitor mismatch as it is usually done in closed-loop switched-capacitor integrators. Furthermore, the proposed switched-capacitor integrator enables low voltage operation and relaxes the power requirement compared to the closed-loop counterpart. The paper is organized as follows: Section 2 starts with the analysis from the conventional switched-capacitor integrator used as a benchmark. Section 3 extends the analysis to the proposed open-loop integrator. Section 4 reports the simulation results and Section 5 concludes the paper.

2. The Closed Loop Switched-Capacitor Integrator

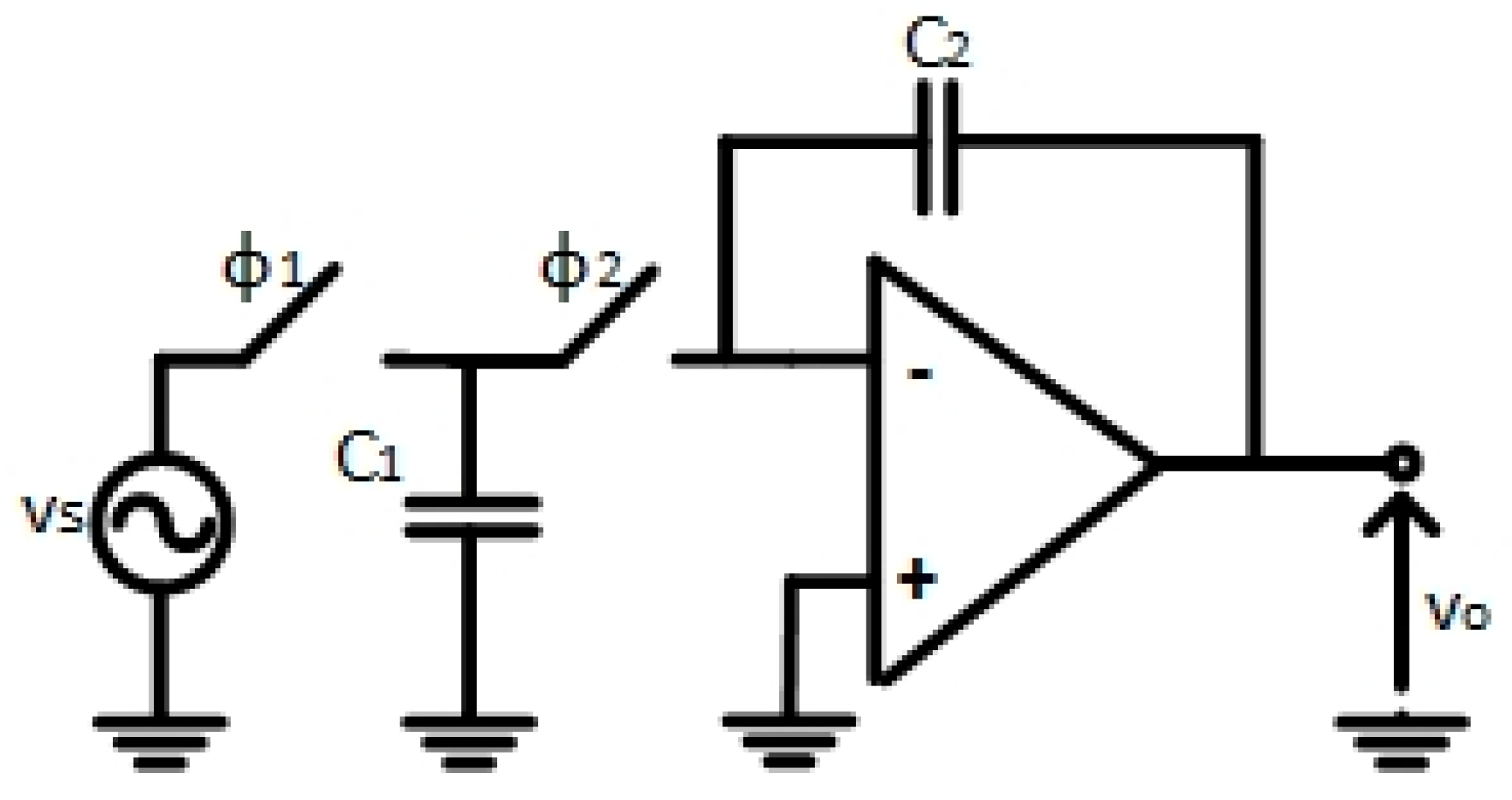
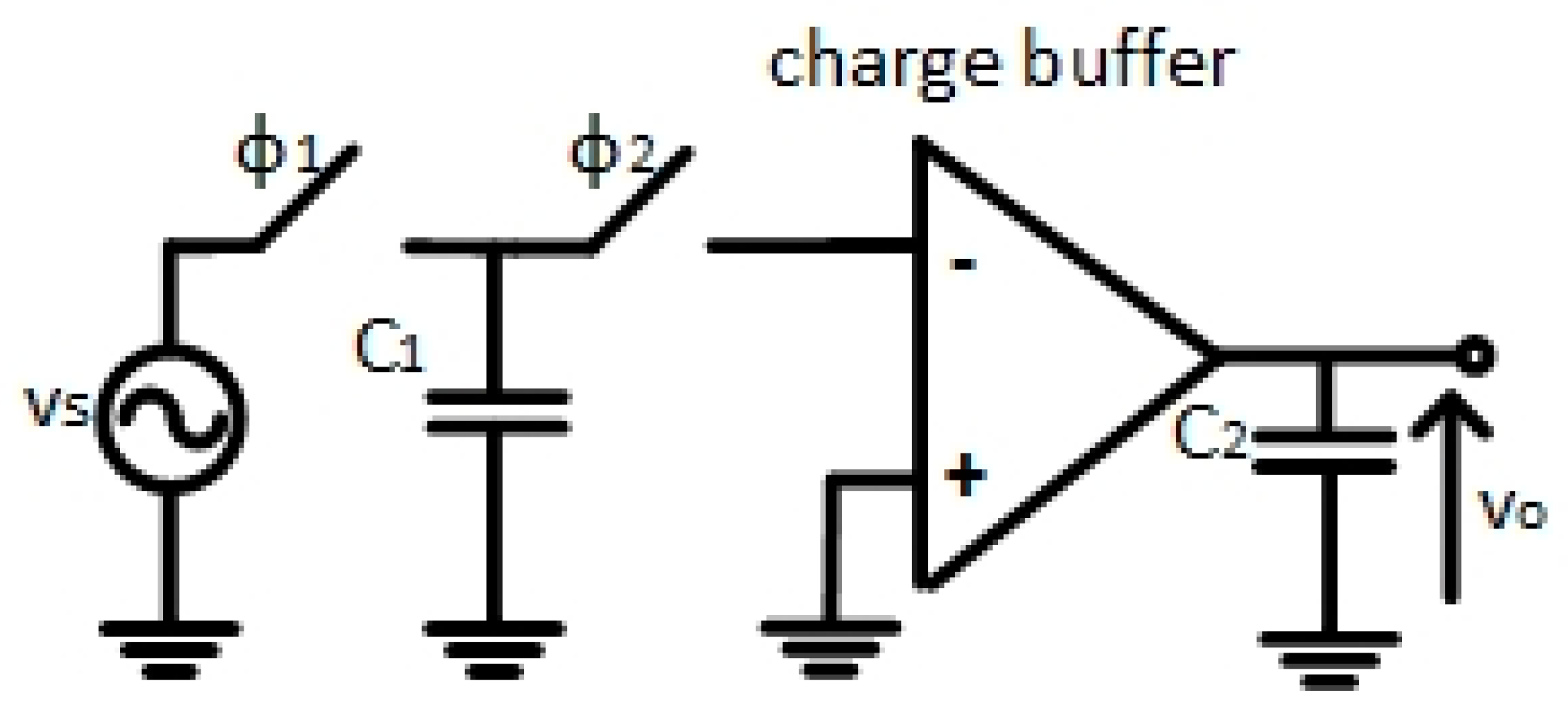
Figure 1 shows the conventional architecture of a switched capacitor integrator.

The switching scheme of this architecture is defined by two complementary clock phases, ϕ₁ and ϕ₂. During ϕ₁ phase, the input signal, v_s, is sampled with the input capacitor, C₁. During ϕ₂ phase the charge collected by C₁ is transferred to the feedback capacitor C₂, assuming an ideal virtual ground at the input of the OTA. The overall transfer function in Z-domain is the following

$$\frac{v_o}{v_s}\left(z\right)=-\frac{C_1}{C_2}·\frac{z^{-1}}{1-z^{-1}}$$

(1)

As in many other electronic systems, the feedback in this circuit serves two main functions:

▪

mitigate the impact of nonlinearities in the OTA;

▪

desensitize the overall transfer function to process, voltage, and temperature (PVT) variations.

The cost of these desirable features is an excessive OTA requirement.

2.1. Analysis of the Requirements of the Single Stage OTA

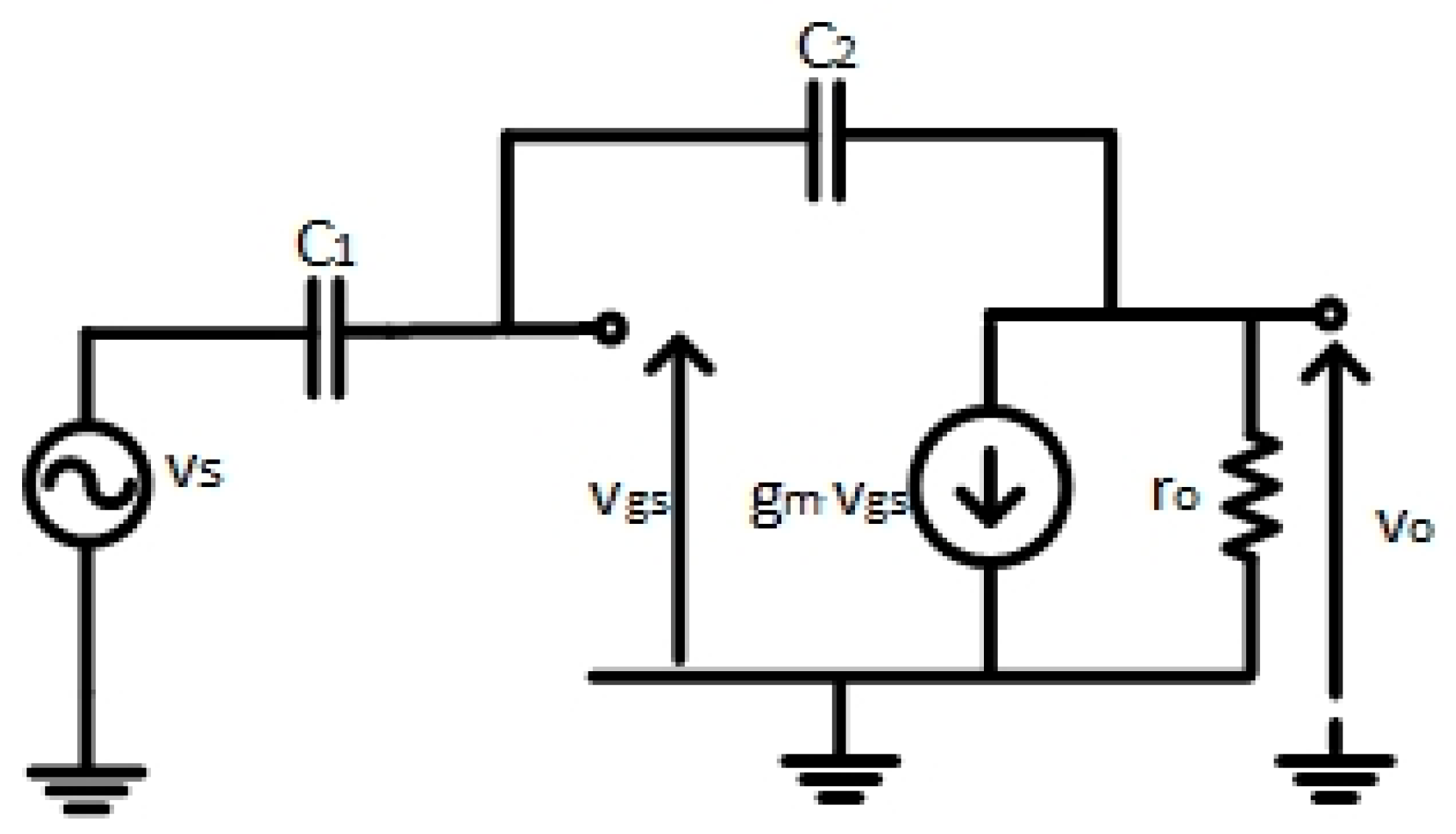
To evaluate the OTA requirements, a single-stage architecture was considered. The linear model of the OTA includes a transconductance g_m and an output resistance r_o. Figure 2 reports the linear model of the integrator including the model of the OTA.

In a switched-capacitor integrator, the input signal, v_s, changes suddenly at each clock hit. Therefore, v_s can be assimilated to a step signal whose a maximum amplitude is equal to V_i:

$$v_s\left(t\right)=V_i·u\left(t\right)$$

(2)

where u(t) is the unitary step signal.

The approach followed for this analysis is the following:

1

firstly, the transfer function $\frac{v_o}{v_s}$ is calculated;

2

the output voltage v_o(s) is calculated in s domain multiplying the transfer function $\frac{v_o}{v_s}$ and the Laplace transform of v_s(t);

3

v_o(s) is then inverse transformed to get the output voltage, v_o(t), in time domain.

The transfer function,$\frac{v_o}{v_s}$, is calculated as follows:

$$\frac{v_o}{v_s}=-\frac{C_1}{C_2·\left(1+\frac{1+\frac{C_1}{C_2}}{g_m·r_o}\right)}·\frac{1-\frac{s·C_2}{g_m}}{1+\frac{s·C_1}{g_m·\left(1+\frac{1+\frac{C_1}{C_2}}{g_m·r_o}\right)}}=-\frac{C_1}{C_2·\left(1+\frac{1+\frac{C_1}{C_2}}{A_o}\right)}·\frac{1-\frac{s·C_2}{g_m}}{1+\frac{s·C_1}{g_m·\left(1+\frac{1+\frac{C_1}{C_2}}{A_o}\right)}}$$

(3)

where A₀ (=g_m∙r_o) is the OTA DC-gain. Assuming that both r_o and g_m tend to infinite, $\frac{v_o}{v_s}$ can be approximate to the ideal value ${\frac{v_o}{v_s}|}_{ideal}$:

$${\frac{v_o}{v_s}|}_{ideal}={\frac{v_o}{v_s}|}_{\begin{array}{c}{r}_o\to \infty \\ g_m\to \infty \end{array}}=-\frac{C_1}{C_2}$$

(4)

The function v_s(t) reported in Equation (2) is transformed in s domain and combined with Equation (3), and then the inverse Laplace Transform is evaluated as follows:

$$v_o\left(t\right)=-\frac{C_1}{C_2\left(1+\frac{1+\frac{C_1}{C_2}}{A_o}\right)}·V_i·\left(1-\frac{{\tau }_z+{\tau }_p}{{\tau }_p}·e^{-\frac{t}{{\tau }_p}}\right)$$

(5)

where τ_p and τ_z are time constants calculated as reciprocal of pole and zero of the transfer function, i.e.,

$${\tau }_p=\frac{C_1}{g_m·\left(1+\frac{1+\frac{C_1}{C_2}}{A_o}\right)}\mathrm{and}{\tau }_z=\frac{C_2}{g_m}$$

(6)

Assuming $A_0\gg 1+\frac{C_1}{C_2}$, τ_p can be approximated as follows:

$${\tau }_p\cong \frac{C_1}{g_m}$$

(7)

The output voltage v_o(0) at t = 0, is defined as:

$$v_o\left(0\right)=-\frac{C_1}{C_2·\left(1+\frac{1+\frac{C_1}{C_2}}{A_o}\right)}·V_i·\left(1-\frac{{\tau }_z+{\tau }_p}{{\tau }_p}\right)\cong V_i$$

(8)

The discontinuity is due to the zero in the transfer function.

2.2. Requirements of the Single Stage OTA

A finite gain of the OTA, A₀, and the non-null time is required for settling introduced errors on the output voltage. The OTA finite gain determines an error in a steady state. This error is called static error, ε_stat:

$${\epsilon }_{stat}=\left|{\frac{v_o}{v_s}|}_{ideal}{V}_i-v_o\left(t\to \infty \right)\right|$$

(9)

On the base of Equations (4) and (5), the static error, ε_stat, is calculated as follows:

$${\epsilon }_{stat}=\left(\frac{C_1}{C_2}-\frac{C_1}{C_2\left(1+\frac{1+\frac{C_1}{C_2}}{A_o}\right)}\right)·V_i=\frac{\frac{C_1}{C_2}·\frac{1+\frac{C_1}{C_2}}{A_o}}{1+\frac{1+\frac{C_1}{C_2}}{A_o}}·V_i\cong \frac{C_1}{C_2}·\frac{1+\frac{C_1}{C_2}}{A_o}·V_i$$

(10)

where the last approximation is valid as $A_0\gg 1+\frac{C_1}{C_2}$.

The charging process of the feedback capacitance, C₁, has a finite duration. In the following calculations, it is assumed that the duration of the charging phase is half of the clock period, T_CLK. Furthermore, an incomplete settling of the output voltage produces an error, which is called dynamic error, ε_dyn, which is defined as follows:

$${\epsilon }_{dyn}=\left|v_o\left(t\to \infty \right)-v_o\left(\frac{T_{CLK}}{2}\right)\right|$$

(11)

By using the expression of v_o(t), reported in Equation (5), the dynamic error, ε_dyn, is calculated as follows:

$${\epsilon }_{dyn}=\frac{C_1}{C_2}·V_i·\frac{1}{1+\frac{1+\frac{C_1}{C_2}}{A_o}}·\frac{{\tau }_z+{\tau }_p}{{\tau }_p}·e^{-\frac{T_{CLK}}{2{\tau }_p}}$$

(12)

which can be simplified combining Equation (12) with Equations (6) and (7) that:

$${\epsilon }_{dyn}=\left(1+\frac{C_1}{C_2}\right)·V_i·\frac{1}{1+\frac{1+\frac{C_1}{C_2}}{A_o}}{e}^{-\frac{T_{CLK}}{2·{\tau }_p}}$$

(13)

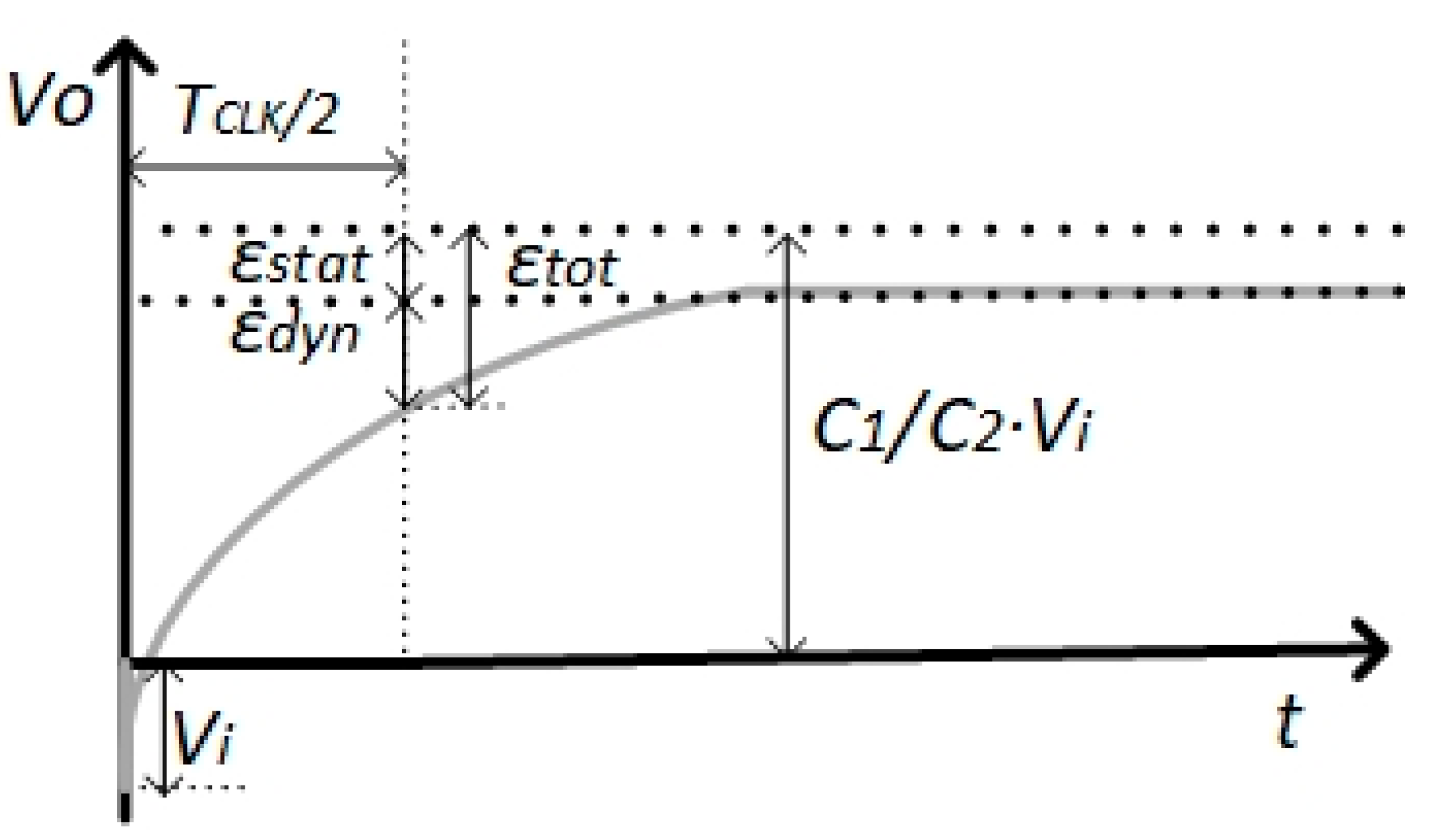
Figure 3 shows the qualitative behavior of the output voltage. Both static and dynamic errors are highlighted.

The overall error, ε_tot, evalueated on the output voltage, is defined as the difference between the ideal output voltage, C₂/C₁∙V_i, and the output voltage measured at T_CLK/2:

$${\epsilon }_{tot}=\left|\frac{C_2}{C_1}·V_i-v_o\left(\frac{T_{CLK}}{2}\right)\right|={\epsilon }_{stat}+{\epsilon }_{dyn}$$

(14)

As Equation (14) shows, ε_tot is calculated as the sum of ε_stat and ε_dyn.

2.2.1. DC-Gain Requirement of the Single-Stage OTA

The overall error must be less than the required accuracy, ξ, which is a parameter related to the application. According to the definition, both ε_stat and ε_dyn must be positive and smaller than the required accuracy, ξ.

To fulfill the DC-gain requirement, the accuracy of the static error, ε_stat, needs to be addressed as follows:

$${\epsilon }_{stat}<\xi$$

(15)

Combining Equations (10) and (15), the following is obtained:

$$\frac{C_1}{C_2}·\frac{1+\frac{C_1}{C_2}}{A_o}·V_i<\xi$$

(16)

Then, the following constraint on the DC-gain, A_o, is derived:

$$A_o>\frac{C_1^2}{C_2^2}·\frac{V_i}{\xi }-1\cong \frac{C_1^2}{C_2^2}·\frac{V_i}{\xi }$$

(17)

Since the DC-gain, A_o, undergoes process, voltage and temperature variations, the sensitivity of A_o, $S_{A_0}^{v_o\left(\frac{T_{CLK}}{2}\right)}$, of the output voltage at $t=\frac{T_{CLK}}{2}$, $v_o\left(\frac{T_{CLK}}{2}\right)$, is evaluated from Equation (5) as follows:

$$S_{A_0}^{v_o\left(\frac{T_{CLK}}{2}\right)}=\frac{A_0}{v_o\left(\frac{T_{CLK}}{2}\right)}·\frac{\partial v_o\left(\frac{T_{CLK}}{2}\right)}{\partial A_0}=A_0·\frac{1+\frac{C_1}{C_2}}{{\left(A_0+\frac{C_1}{C_2}+1\right)}^2}\cong \frac{1+\frac{C_1}{C_2}}{A_0}$$

(18)

where last approximation is valid as $A_0\gg 1+\frac{C_1}{C_2}$.

2.2.2. Transconductance Requirement of the Single Stage OTA

A transconductance constrain is determined through the relation between the accuracy specification and the dynamic error, ε_dyn, i.e.:

$${\epsilon }_{dyn}<\xi$$

(19)

Combining Equations (13) and (19), it is obtained:

$$\left(1+\frac{C_1}{C_2}\right)·V_i\frac{1}{1+\frac{1+\frac{C_1}{C_2}}{A_o}}·e^{-\frac{T_{CLK}}{2{\tau }_p}}\cong \left(1+\frac{C_1}{C_2}\right)·V_i·e^{-\frac{T_{CLK}}{2·{\tau }_p}}<\xi$$

(20)

The approximation contained in Equation (20) is justified as it is assumed that $A_0\gg 1+\frac{C_1}{C_2}$.

Combining Equations (7) and (20) the following constraint on g_m is set:

$$g_m>\frac{2·C_1}{T_{CLK}}·ln\left(\frac{V_i}{\xi }·\left(1+\frac{C_1}{C_2}\right)\right)$$

(21)

As for the DC-gain, A_o, the sensitivity of the output voltage, $S_{g_m}^{v_o\left(\frac{T_{CLK}}{2}\right)}$, at $\frac{T_{CLK}}{2}$, $v_o\left(\frac{T_{CLK}}{2}\right)$, with respect to g_m is derived from Equation (5) as follows:

$$S_{g_m}^{v_o\left(\frac{T_{CLK}}{2}\right)}=\frac{g_m}{v_o\left(\frac{T_{CLK}}{2}\right)}·\frac{\partial v_o\left(\frac{T_{CLK}}{2}\right)}{\partial g_m}=\frac{T_{CLK}}{2·{\tau }_p}·\frac{\left(1+\frac{2{\tau }_z}{T_{CLK}}+\frac{C_2}{C_1}\right)e^{-\frac{T_{CLK}}{2{\tau }_p}}}{1-\left(1+\frac{C_2}{C_1}\right)e^{\frac{-T_{CLK}}{2{\tau }_p}}}\cong \frac{T_{CLK}}{2·{\tau }_p}·\left(1+\frac{C_2}{C_1}\right)·e^{\frac{-T_{CLK}}{2{\tau }_p}}$$

(22)

where the last approximation is valid as $\left(1+\frac{C_2}{C_1}\right)·e^{\frac{-T_{CLK}}{2{\tau }_p}}\ll 1$ and ${\tau }_z\ll \frac{T_{CLK}}{2}$.

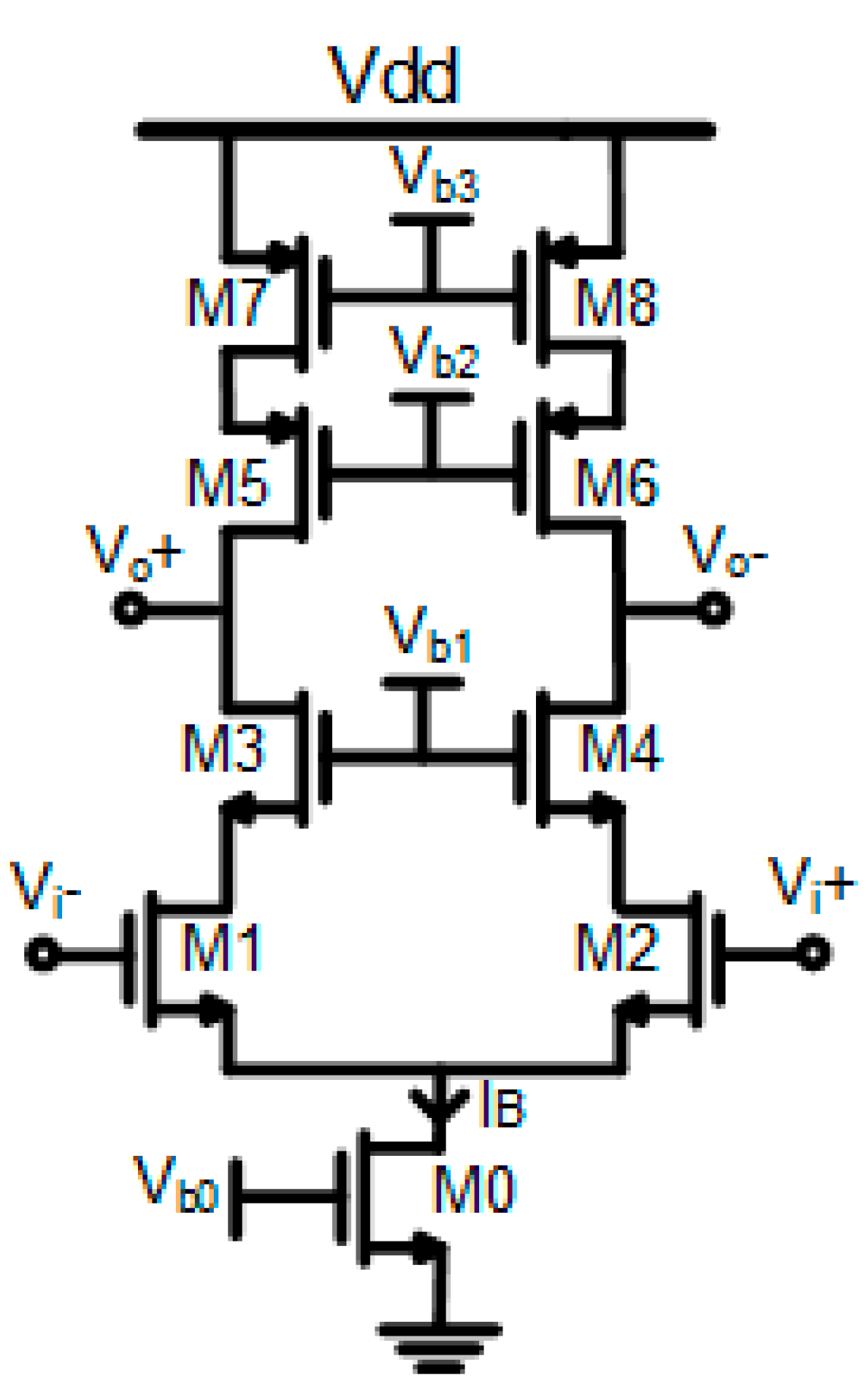
2.3. Circuit Implementation of the Single Stage OTA

A common circuit solution for the OTA is represented by the telescopic Cascode OTA, shown in Figure 4 [5,6]. As the DC-gain requirement is satisfied and the output signal swing is sufficient, the telescopic Cascode OTA reported in Figure 2 remains the most efficient and simplest OTA solution. Therefore, it was used as a benchmark in this paper.

The overdrive voltage of M₁-M₂ input transistors is limited by the available supply voltage, V_dd, and the NMOS transistor threshold, V_THN. Assuming a common mode, V_cm, equal to V_dd/2, by applying Kirchoff’s voltage law we obtain:

$$V_{cm}=\frac{V_{dd}}{2}=V_{GS1}+V_{DS0}$$

(23)

where V_GS1 is the gate-source voltage of M₁-M₂ input transistors, and V_DS0 is the drain-source voltage of the M₀ bias transistor.

The common mode, V_cm, must assure that M₁-M₂ and the M₀ transistors work in the saturation region. Therefore, assuming that all the overdrives of M₁-M₂ and M₀ transistors are equal to V_ov, from Equation (23) we derive:

$$\frac{V_{dd}}{2}>V_{THN}+2·V_{ov}$$

(24)

Thus:

$$V_{ov}<\frac{\frac{V_{dd}}{2}-V_{THN}}{2}$$

(25)

As seen in Equation (25), there is a strict limitation to the design of the overdrive of the input transistors at low supply voltage, which is typical of the modern CMOS IC technologies. For example, in finFET 16 nm technology, V_dd is 0.95 V, and V_THN is 0.275 V, therefore V_ov must be less than 100 mV.

2.4. Small Signal Analysis of the Single-Stage OTA

The transconductance g_m of the linear model of Figure 2 corresponds to the transconductance g_m1 of M₁-M₂ input transistors. The bias current, I_B, of the OTA is defined by the settling requirements, which mainly depends on M₁-M₂ input transistors.

The output resistance r_o of the linear model of Figure 2 is calculated as follows:

$$r_o=g_{m3}·r_{o3}·r_{o1}\Vert g_{m5}·r_{o5}·r_{o7}\cong \frac{1}{2}{g}_{m3}·r_{o3}·r_{o1}$$

(26)

where g_m3 and g_m⁵ are the transconductances of M₃ and M⁵ transistors, respectively, and r_o1, r_o³, and r_o⁵ are the output resistances of M₁, M₂, and M₃ transistors, respectively. The last approximation in Equation (24) is valid assuming g_m3 ≅ g_m⁵, r_o3 ≅ r_o5, and r_o1 ≅ r_o7. In practice, the output resistance of M₁-M₂ transistors, r_o1, is boosted by the intrinsic gain of transistor M₃, g_m3∙r_o3.

The voltage gain, A₀, can be calculated as follows:

$$A_0=g_{m1}·r_o\cong \frac{1}{2}{g}_{m1}·g_{m3}·r_{o3}·r_{o1}$$

(27)

Rearranging Equation (27), we obtain:

$$A_0\cong 2·\frac{V_{A3}·V_{A1}}{V_{ov3}·V_{ov1}}$$

(28)

where V_A3, V_A1, V_ov3, and V_ov1 are the early and the overdrive voltages of M₃ and M₁ transistors, respectively. As derived in Equation (28), the margins to increase the voltage gain A_o are limited. A possibility to increment the voltage gain consists of reducing V_ov3 and V_ov1. M₃ and M₁ transistors are then pushed to work in the subthreshold region, where the transconductance depends only on the bias current, while the transistor overdrives approach their inferior limit of about 50 mV [7]. Therefore, V_ov1 and V_ov3 have a strict range of variability between 50 mV and 100 mV. V_A³ and V_A1 can be increased by augmenting the length of M₃ and M₁. This solution degrades the frequency performance of the OTA since larger transistors introduce bigger parasitic capacitances. Moreover, every IC fabrication process has an intrinsic limit to the maximum allowable transistor length, which is lower and lower as the technology is scaled. For example, in FinFET 16 nm, the maximum allowable transistor length is 240 nm.

If the DC-gain requirement is not reachable by the telescopic Cascode OTA, it is necessary to modify the OTA architecture. An increment of r_o and, consequently, A_o is obtained by using a regulated Cascode OTA [8] or adding an output stage [9]. Both previous solutions imply a significant increase in power consumption. It is also possible to increase the gain by augmenting the number of stacked transistors. At low voltage supply, the last solution is not practicable because of the further reduction of the output signal swing.

2.5. Slew-Rate (SR) Analysis of the Single-Stage OTA

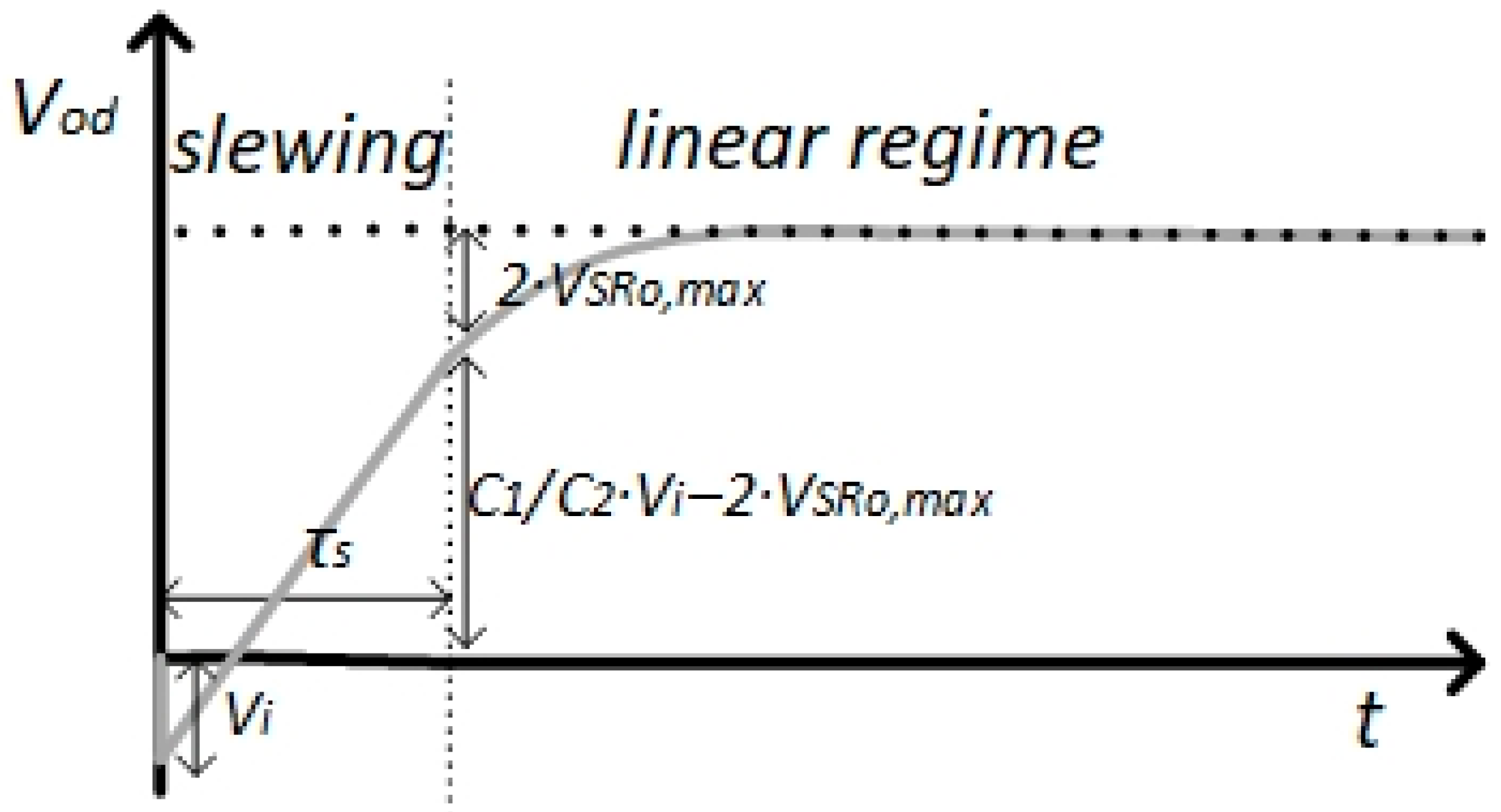
Due to the finite bias current, I_B, the OTA goes into a slew-rate regime at the beginning of the charging process.

According to Equation (5), the maximum rate of variation of the output voltage is obtained at t = 0 s.

$${\left|\frac{d{v}_o\left(t\right)}{dt}\right|}_{max}=\frac{C_1}{C_2·\left(1+\frac{1+\frac{C_1}{C_2}}{A_o}\right)}·V_{SRi,max}·\frac{{\tau }_z+{\tau }_p}{{\tau }_p^2}=\frac{V_{SRo,max}}{{\tau }_p}$$

(29)

where V_SRi,max is the maximum amplitude of the input voltage step that keeps the OTA in the linear region. The corresponding output voltage in steady state is given by V_SRo,max, which is calculated as follows:

$$V_{SRo,max}=\frac{C_1}{C_2·\left(1+\frac{1+\frac{C_1}{C_2}}{A_o}\right)}·\left(1+\frac{C_2}{C_1}\right)·V_{SRi,max}\cong \left(1+\frac{C_1}{C_2}\right)·V_{SRi,max}$$

(30)

where the last approximation is valid as A₀ >> 1 + C₁/C₂. In a single-stage OTA, the slew-rate depends on the bias current I_B and the feedback capacitance C₂, i.e.:

$$SR=\frac{I_B}{C_2}=\frac{I_B·g_{m1}}{C_2·g_{m1}}=\frac{V_{ov1}}{{\tau }_z}$$

(31)

where g_m1 and V_ov1 are the transconductance and the overdrive of the M₁-M₂ input transistors, respectively. Matching the SR formula in Equation (31) to the maximum rate of variation of the output voltage reported in Equation (29), the V_SRo,max calculation is obtained:

$$V_{SRo,max}=V_{ov1}·\frac{{\tau }_p}{{\tau }_z}\cong V_{ov1}·\frac{C_1}{C_2}$$

(32)

Due to its differential structure, the OTA starts slewing as the input differential voltage step, V_i, overcomes 2∙V_SRi,max. The value of V_SRi,max is calculated by combining Equations (30) and (32):

$$V_{SRi,max}\cong \frac{1}{\left(1+\frac{C_1}{C_2}\right)}·V_{SRo,max}=\frac{V_{ov1}}{\left(1+\frac{C_2}{C_1}\right)}$$

(33)

The OTA slews until the output voltage reaches the value $\frac{-C_1}{C_2}{V}_i+2V_{SRo,max}$:

$$V_i-\frac{2·V_{SRo,max}}{{\tau }_p}{t|}_{t={\tau }_s}=-\frac{C_1}{C_2}{V}_i+2·V_{SRo,max}$$

(34)

where the starting value of V_i depends on the fact that, at t = 0 s, the capacitances of the integrator behave like short circuits, transferring the input voltage directly to the output.

From the previous equation, it is possible to calculate the slewing time of the OTA, τ_s:

$${\tau }_s={\tau }_p·\left(\left(1+\frac{C_1}{C_2}\right)·\frac{V_i}{2·V_{SRo,max}}-1\right)={\tau }_p·\left(\frac{V_i}{2·V_{SRi,max}}-1\right)$$

(35)

During τ_s, the OTA output voltage evolves according to the linear law. Considering the slew-rate, the equation of the differential output voltage, v_od(t), is then calculated as follows:

$$\{\begin{array}{c}{v}_{od}\left(t\right)=V_i-\frac{2·V_{SRo,max}}{{\tau }_p}·t for 0<t<{\tau }_s\\ v_{od}\left(t\right)=-\frac{C_1}{C_2·\left(1+\frac{1+\frac{C_1}{C_2}}{A_o}\right)}·V_i+2·V_{SRo,max}·e^{-\frac{t-{\tau }_s}{{\tau }_p}}\cong -\frac{C_1}{C_2}·V_i+2·V_{SRo,max}{e}^{-\frac{t-{\tau }_s}{{\tau }_p}}for t>{\tau }_s\end{array}$$

(36)

Figure 5 shows the step response of the closed loop switched capacitor integrator including the slewing period.

2.6. Signal to Noise (SNR) Calculations of the Closed-Loop Switched-Capacitor Integrator

The telescopic Cascode OTA suffers from a reduced output swing. Indeed, both single-ended output voltages must guarantee that the Cascode transistors (M₃-M₄ and M₅-M₆) work in a saturation region even under the signal swing. The main limitation is the negative output swing since three transistors are stacked between the ground and the output nodes, while only two transistors are stacked between V_dd and the output nodes. Focusing the analysis on a single branch, V_o+ must satisfy the following inequation to guarantee that M₃ transistors operate in saturation region:

$$\begin{array}{c}{V}_{o+}>V_{DS,sat3}+V_{S3}=V_{ov}+V_{S3}\\ \end{array}$$

(37)

where V_S³ and V_DS,sat³ are the source and the saturation voltages of M₃ transistor, respectively. It is assumed that V_ds,sat³ is equal to V_ov. The bias voltage V_b1 is chosen to make M₁ transistor operating in saturation, i.e.:

$$V_{DS1}=V_{S3}-V_{S1}>V_{DS,sat1}=V_{ov}$$

(38)

where V_DS1, V_S¹, and V_DS,sat1 are the drain-source, the source, and the saturation voltages of M₁ transistor, respectively. In this case, it is assumed that V_ds,sat1 is equal to V_ov. V_S1 is derived from the input transistor common mode, V_cm, by dropping the gate-drain voltage of the M₁ transistors, V_GS1, i.e.:

$$V_{S1}=V_{cm}-V_{GS1}=V_{cm}-V_{TH}-V_{ov}$$

(39)

Combining Equations (38) and (39) we obtain the minimum source voltage of M₃ transistor, V_S3,min:

$$V_{S3}>V_{S1}+V_{ov}=V_{S3,min}$$

(40)

By replacing V_S3 in Equation (37) with the value of V_S3^,min calculated in Equation (40), the minimum value of V_o+, V_o+,min, is obtained:

$$V_{o+}>V_{ov}+V_{S3}=V_{cm}-V_{THN}=V_{o+,min}$$

(41)

As the output voltage starts swinging from the common-mode voltage, V_cm, down to V_o+,min, it is possible to calculate the maximum output voltage swing, V_swing:

$$V_{swing}=2·\left(V_{cm}-V_{o+,min}\right)=2·V_{THN}$$

(42)

where the 2 factor is due to the differential architecture.

The thermal noise due to the switches around C₁ is calculated as $2·\frac{K·T}{C_1}$, where the coefficient 2 takes into account both the sampling (ϕ₁) and the integration phase (ϕ₂). Assuming that the thermal noise $2·\frac{K·T}{C_1}$ is dominant, from Equation (42), the signal to noise ratio of the overall closed-loop switched-capacitor integrator, SNR_CL, is calculated as follows:

$$SN{R}_{CL}=\frac{1}{2}·\frac{V_{swing}^2}{\overline{v_{o,n}^2}}=\frac{1}{2}·\frac{4·V_{THN}^2}{2·\frac{K·T}{C_1}·{\left(\frac{C_1}{C_2}\right)}^2}=\frac{V_{THN}^2·C_2^2}{K·T·C_1}$$

(43)

where $\overline{v_{n,o}^2}$ is the total output noise, as a result of the thermal noise contribution due to the C₁ switched-capacitor multiplied by the square of the integrator gain ${\left(\frac{C_1}{C_2}\right)}^2$, furthermore, the $\frac{1}{2}$ factor takes into account that the input signal is a sinusoid.

2.7. Power Consumption Requirements

Regarding the telescopic Cascode shown in Figure 4, the power consumption is given by the product of the supply voltage, V_dd, and the bias current I_B:

$$P_{w,tot}=V_{dd}·I_B$$

(44)

Assuming dominant the thermal noise of C₁, the power consumption of the switched-capacitor integrator is determined by the settling time requirement. In fact, as the input transistor overdrive, V_ov1, is bonded to considerations on the DC-point at low voltage supply, the constraint on the input transistor transconductance, g_m1, expressed by in Equation (21), determines the minimum required bias current I_B,min:

$$I_{B,min}=\frac{2·C_1}{T_{CLK}}·V_{ov1}·ln\left(\frac{V_i}{\xi }·\left(1+\frac{C_1}{C_2}\right)\right)$$

(45)

Therefore, the minimum power consumption, P_w,min, is obtained as follows:

$$P_{w,min}=V_{dd}·I_{B,min}=V_{dd}·\frac{2·C_1}{T_{CLK}}·V_{ov1}·ln\left(\frac{V_i}{\xi }·\left(1+\frac{C_1}{C_2}\right)\right)$$

(46)

As the OTA starts slewing, the minimum bias current, I_B,min, is determined by taking into account a different calculation for the dynamic error, ε_dyn. Indeed, considering Equation (36) that assumes the slewing of the OTA, the differential output voltage at $t=\frac{T_{CLK}}{2}$ is calculated as follows:

$$v_{od}\left(\frac{T_{CLK}}{2}\right)\cong -\frac{C_1}{C_2}·V_i+2·V_{SRo,max}·e^{-\frac{\frac{T_{CLK}}{2}-{\tau }_s}{{\tau }_p}}$$

(47)

The dynamic error, ε_dyn, is, then, calculated as follows:

$${\epsilon }_{dyn}=\left|v_{od}\left(t\to \infty \right)-v_o\left(\frac{T_{CLK}}{2}\right)\right|=2·V_{SRo,max}{e}^{-\frac{\frac{T_{CLK}}{2}-{\tau }_s}{{\tau }_p}}$$

(48)

Since ε_dyn must be less than the required accuracy, ξ, as reported in Equation (19), we obtain:

$${\tau }_p<\frac{\frac{T_{CLK}}{2}-{\tau }_s}{ln\left(\frac{2V_{SRo,max}}{\xi }\right)}$$

(49)

Moreover, the minimum bias current I_B,min is evaluated considering τ_p reported in Equation (7), the transconductance of the input transistors, g_m1, determined as $\frac{I_{B,min}}{V_{ov1}}$, the formula of the slewing time, τ_s, in Equation (35), and the previous equation. As a result the minimum bias current I_B,min, is calculated as follows:

$$I_{B,min}=\frac{2·V_{ov1}·C_1}{T_{CLK}}·\left(ln\left(\frac{2·V_{SRo,max}}{\xi }\right)+\frac{V_i}{2·V_{SRi,max}}-1\right)$$

(50)

The minimum power consumption, P_w,min, is derived from the last equation as follows:

$$P_{w,min}=V_{dd}·I_{B,min}=\frac{2·V_{ov1}·V_{dd}·C_1}{T_{CLK}}·\left(ln\left(\frac{2·V_{SRo,max}}{\xi }\right)+\frac{V_i}{2·V_{SRi,max}}-1\right)$$

(51)

3. Proposed Open-Loop Integrator

As an alternative solution, an open-loop switched-capacitor integrator is presented (Figure 6).

The active element is an OTA, with a low input impedance, which is called charge buffer. Once the input capacitance, C₁, is connected to the charge buffer input, it is discharged and its charge is transferred to the output capacitance C₂. The proposed open-loop switched-capacitor integrator does not include two input nodes with high and low impedances, unlike the switched-capacitor integrator based on a current conveyor [10,11], but only low impedance input nodes. Therefore, the voltage buffer used at the input in the conveyor integrators is eliminated. These simplifications help to get a more efficient circuit implementation.

According to the operation mode aforementioned, C₁ is connected to the inverting input terminal, it is possible to write:

$$Q_1\left(n-1\right)=-Q_2\left(n\right)$$

(52)

where Q₁(n−1) and Q₂(n) are the charges stored in C₁ and C₂ capacitances, at n − 1 and n time steps, respectively. From Equation (52), it is obtained:

$$C_1·v_s\left(n-1\right)=-C_2·v_o\left(n\right)$$

(53)

where v_o and v_s are the output and the input voltages. Therefore, it is possible to calculate the integrator gain in the Z domain, $\frac{v_o}{v_s}\left(z\right)$:

$$\frac{v_o}{v_s}\left(z\right)=-\frac{C_1}{C_2}·\frac{z^{-1}}{1-z^{-1}}$$

(54)

By using the proposed approach, we obtain a gain expression, which is identical to the traditional closed-loop integrator reported in Equation (1). In both cases, the desensitization of the gain concerning the OTA parameters is reached as the gain depends only on the C₁ and C₂ capacitor ratio, in the ideal case.

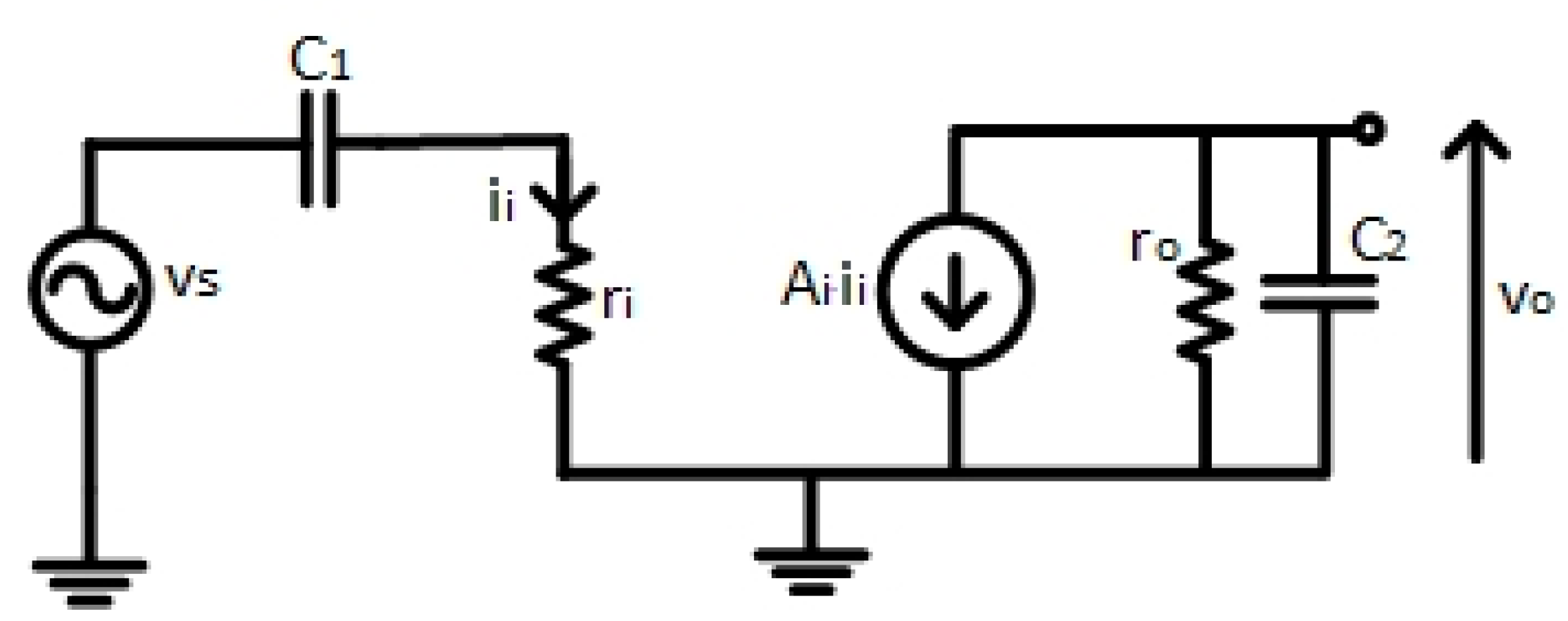
3.1. Small Signal Analysis of the Proposed Charge Buffer

To evaluate the impact of the non-null input resistance and the finite output resistance of the charge buffer, the linear model of the integrator reported in Figure 7 was considered.

In practice, the C₁ capacitance is discharged on input resistance r_i, producing the input current i_i. This current is amplified with a current gain A_i by the current amplifier that feds the output load made by the output resistance r_o and the output capacitance C₂.

First of all, the transfer function, $\frac{v_o}{v_s}\left(s\right)$, is calculated as previously done for the traditional closed-loop switched-capacitor integrator:

$$\frac{v_o}{v_s}\left(s\right)=-A_i·\frac{s·C_1}{1+s·r_i·C_1}·\frac{r_o}{1+s·r_o·C_2}$$

(55)

Compared to the transfer function of the closed-loop switched-capacitor integrator shown in Equation (3), the transfer function of the open-loop switched-capacitor integrator already is calculated, has an additional pole due to the finite output resistance r_o.

3.2. Transient Analysis of the Proposed Charge Buffer

Assuming a step signal at the input as reported in Equation (2), the output voltage becomes:

$$\begin{gathered} v_o\left(t\right)=-\frac{C_1}{C_2}·A_i·V_i·\frac{1}{1-\frac{r_i}{r_o}·\frac{C_1}{C_2}}\left(e^{-\frac{t}{{\tau }_{p2}}}-e^{-\frac{t}{{\tau }_{p1}}}\right) \\ =-\frac{C_1}{C_2}·A_i·V_i·\frac{1}{1-\frac{C_1}{A_v·C_2}}\left(e^{-\frac{t}{{\tau }_{p2}}}-e^{-\frac{t}{{\tau }_{p1}}}\right) \end{gathered}$$

(56)

where:

$${\tau }_{p1}=r_i·C_1, {\tau }_{p2}=r_o·C_2 A_v=\frac{r_o}{r_i}$$

(57)

A_v is the voltage gain. The error on the current gain, A_i, of the current mirror, directly affects the accuracy of the output voltage. This error mainly depends on the transistor mismatch, which can be minimized thanks to the appropriate design of the overdrive of the transistors forming the current mirror [12].

The output resistance r_o, partially drags the charge stored in C₂. Considering a first-order Taylor’s expansion for the e^−t/τp2 term, and assuming a unitary current gain, the output voltage, v_o(t), at t = T_CLK/2, is calculated as follows from Equation (56):

$$v_o\left(\frac{T_{CLK}}{2}\right)\cong -\frac{C_1}{C_2}·\frac{1}{1-\frac{C_1}{A_v·C_2}}·V_i·\left(1-\frac{T_{CLK}}{2·{\tau }_{p2}}-e^{-\frac{T_{CLK}}{2·{\tau }_{p1}}}\right)$$

(58)

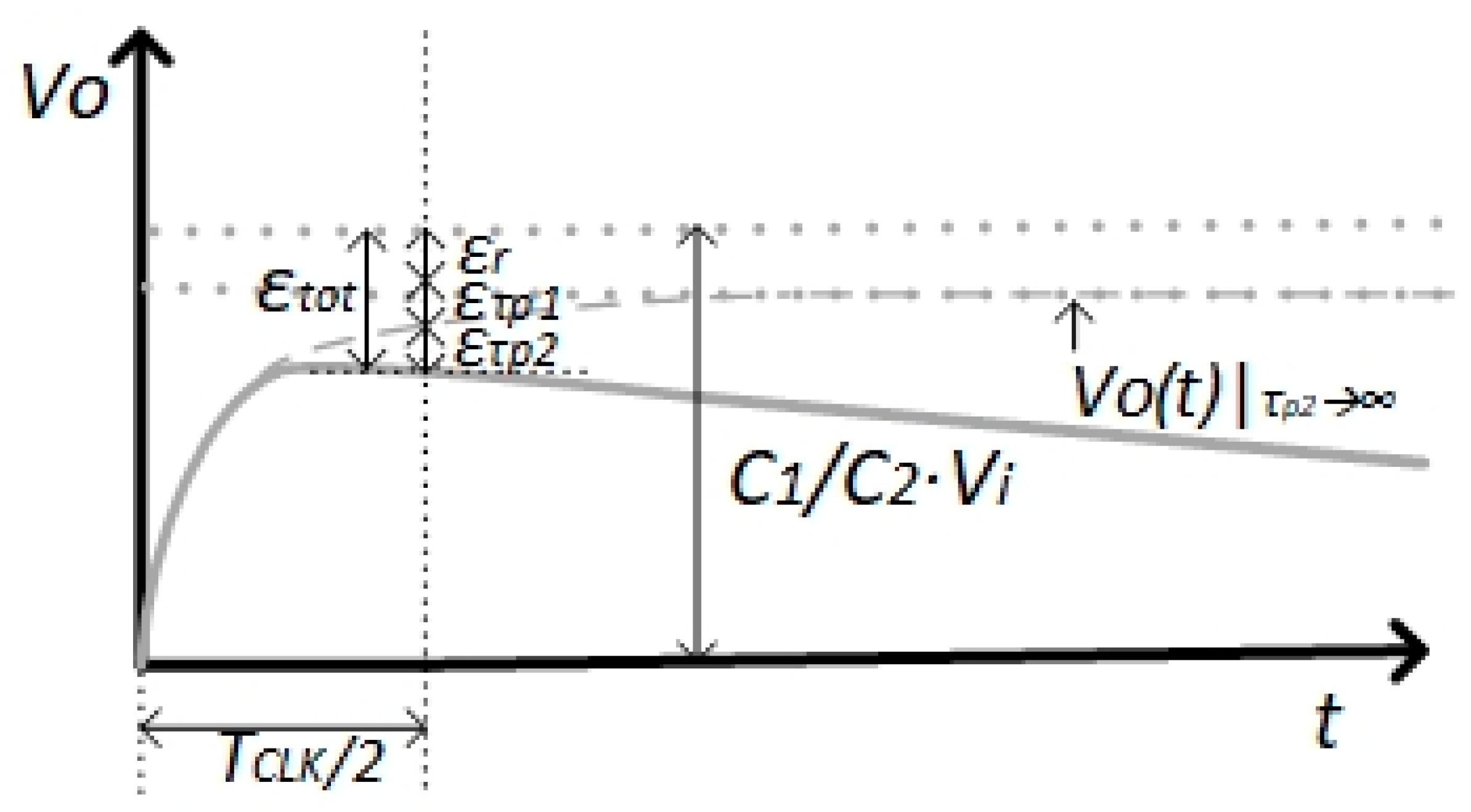
Three sources of error on the output voltage at $t=\frac{T_{CLK}}{2}$, $v_o\left(\frac{T_{CLK}}{2}\right)$, remain. They are due to:

▪

finite voltage gain A_v;

▪

non-null τ_p1;

▪

finite τ_p2.

The impact of each source of error is evaluated considering the remaining ones disabled.

To evaluate the error, ε_r, due to the finite voltage gain, A_v, it is assumed that τ_p1 tends to zero and τ_p2 tends to infinite. In these conditions, the output voltage can be approximated as follows:

$${v_o\left(\frac{T_{CLK}}{2}\right)|}_{\begin{array}{c}{\tau }_{p1}\to 0\\ {\tau }_{p2}\to \infty \end{array}}\cong -\frac{C_1}{C_2}·\frac{1}{1-\frac{C_1}{A_v·C_2}}·V_i$$

(59)

The corresponding error, ε_r, is calculated as the difference between the ideal voltage obtained using the ideal gain value shown in Equation (54), and the value of the voltage expressed in Equation (59), i.e.,

$${\epsilon }_r=\left|-\frac{C_1}{C_2}·V_i-{v_o\left(\frac{T_{CLK}}{2}\right)|}_{\begin{array}{c}{\tau }_{p1}\to 0\\ {\tau }_{p2}\to \infty \end{array}}\right|=\frac{C_1}{C_2}·\frac{\frac{C_1}{A_v·C_2}}{1-\frac{C_1}{A_v·C_2}}·V_i$$

(60)

To evaluate the error due to τ_p1, it is assumed that τ_p2 tends to infinite. In these conditions, the output voltage can be approximated as follows:

$${v_o\left(\frac{T_{CLK}}{2}\right)|}_{{\tau }_{p2}\to \infty }=-\frac{C_1}{C_2}·\frac{1}{1-\frac{C_1}{A_v·C_2}}·V_i·\left(e^{-\frac{T_{CLK}}{2·{\tau }_{p1}}}+1\right)$$

(61)

The error due to τ_p1, ε_τp1, is calculated as the difference between the output voltages expressed in Equations (50) and (52), i.e.:

$${\epsilon }_{\tau p1}=\left|{v_o\left(\frac{T_{CLK}}{2}\right)|}_{\begin{array}{c}{\tau }_{p1}\to 0\\ {\tau }_{p2}\to \infty \end{array}}-{v_o\left(\frac{T_{CLK}}{2}\right)|}_{{\tau }_{p2}\to \infty }\right|=\frac{C_1}{C_2}·\frac{1}{1-\frac{C_1}{A_v·C_2}}·V_i·e^{\frac{-T_{CLK}}{2·{\tau }_{p1}}}$$

(62)

The error due to τ_p2, ε_τp2, is calculated as the difference between the output voltages expressed in Equations (58) and (61), i.e.:

$${\epsilon }_{\tau p2}=\left|v_o\left(\frac{T_{CLK}}{2}\right)-{v_o\left(\frac{T_{CLK}}{2}\right)|}_{{\tau }_{p2}\to \infty }\right|=\frac{C_1}{C_2}·\frac{1}{1-\frac{C_1}{A_v·C_2}}·V_i·\frac{T_{CLK}}{2·{\tau }_{p2}}$$

(63)

Figure 8 shows the output voltage behavior.

The sum of the three error ε_r, ε_τp1, and ε_τp2, gives the total error ε_tot, which must be less than the required accuracy, ξ:

$${\epsilon }_{tot}={\epsilon }_r+{\epsilon }_{\tau p1}+{\epsilon }_{\tau p2}<\xi$$

(64)

Since the error terms ε_r, ε_τp1, and ε_τp2 are positive, each of them must be less than ξ.

3.3. Voltage Gain Requirement of the Proposed Charge Buffer

As calculated in Equation (60), ε_r is less than the ξ, therefore, we obtain

$$A_v>\frac{C_1}{C_2}·\left(1+\frac{V_i}{\xi }·\frac{C_1}{C_2}\right)\cong \frac{V_i}{\xi }·\frac{C_1^2}{C_2^2}$$

(65)

In Equation (65) is very similar to Equation (17), which defines the requirement of the OTA for the closed-loop switched-capacitor integrator. It can be concluded that the charge buffer of the proposed open-loop switched-capacitor integrator requires the same gain of the OTA in the traditional closed-loop solution.

From Equation (58), the sensitivity, $S_{A_v}^{v_o\left(\frac{T_{CLK}}{2}\right)}$, of the output voltage at $\frac{T_{CLK}}{2}$, $v_o\left(\frac{T_{CLK}}{2}\right)$, and A_v is evaluated as follows:

$$S_{A_v}^{v_o\left(\frac{T_{CLK}}{2}\right)}=\frac{A_v}{v_o\left(\frac{T_{CLK}}{2}\right)}·\frac{\partial v_o\left(\frac{T_{CLK}}{2}\right)}{\partial A_v}=\frac{A_v·\frac{C_1}{C_2}}{{\left(A_v-\frac{C_1}{C_2}\right)}^2}\cong \frac{A_v·\frac{C_1}{C_2}}{{\left(A_v-\frac{C_1}{C_2}\right)}^2}$$

(66)

where the last approximation is valid as $A_v\gg \frac{C_1}{C_2}$. The previous result is very similar to the one obtained for the Cascode OTA in the closed-loop switched-capacitor integrator in Equation (18).

3.4. Input and Output Resistances Requirements of the Proposed Charge Buffer

Assuming ε_τp1, calculated in Equation (62), less than ξ we obtain

$${\tau }_{p1}<\frac{T_{CLK}}{2·ln\left(\frac{V_i}{\xi ·\left(1-\frac{C_1}{A_v·C_2}\right)·\frac{C_2}{C_1}}\right)}\cong \frac{T_{CLK}}{2·ln\left(\frac{V_i}{\xi }·\frac{C_1}{C_2}\right)}$$

(67)

Last approximation in Equation (67) is valid as $A_v\gg \frac{C_1}{C_2}$.

Taking into account the expression of τ_p1 in Equation (57), the following constraint on the input resistance, r_i, is obtained:

$$r_i<\frac{T_{CLK}}{2·C_1·ln\left(\frac{V_i}{\xi }·\frac{C_1}{C_2}\right)}$$

(68)

Assuming ε_τp2, calculated in Equation (63), less than ξ we obtain

$${\tau }_{p2}>\frac{T_{CLK}}{2}·\frac{V_i}{\xi ·\left(1-\frac{C_1}{A_v·C_2}\right)}·\frac{C_1}{C_2}\cong \frac{T_{CLK}}{2}·\frac{V_i}{\xi }·\frac{C_1}{C_2}$$

(69)

In this case, last approximation is valid as $A_v\gg \frac{C_1}{C_2}$.

Considering τ_p2 in Equation (57), from Equation (69) it is derived the following constraint on the output resistance, r_o:

$$r_o>\frac{T_{CLK}}{2}·\frac{V_i}{\xi }·\frac{C_1}{C_2^2}$$

(70)

As already done for the voltage gain, A_v, from Equation (58) the sensitivity, $S_{r_i}^{v_o\left(\frac{T_{CLK}}{2}\right)}$, of the output voltage at $\frac{T_{CLK}}{2}$, $v_o\left(\frac{T_{CLK}}{2}\right)$, and r_i is evaluated as follows:

$$S_{r_i}^{v_o\left(\frac{T_{CLK}}{2}\right)}=\frac{r_i}{v_o\left(\frac{T_{CLK}}{2}\right)}·\frac{\partial v_o\left(\frac{T_{CLK}}{2}\right)}{\partial r_i}=\frac{T_{CLK}}{2·{\tau }_{p1}}·\frac{e^{\frac{-T_{CLK}}{2{\tau }_{p1}}}}{1-\frac{T_{CLK}}{2·{\tau }_{p2}}-e^{\frac{-T_{CLK}}{2·{\tau }_{p1}}}}\cong \frac{T_{CLK}}{2·{\tau }_{p1}}{e}^{\frac{-T_{CLK}}{2·{\tau }_{p1}}}$$

(71)

where last approximation is valid as $\frac{T_{CLK}}{2·{\tau }_{p2}}-e^{\frac{-T_{CLK}}{2·{\tau }_{p1}}}\ll 1$. This inequation is verified as the condition imposed by Equations (67) and (69) are satisfied, since, generally, $V_i\gg \xi$ and $\frac{C_1}{C_2}\ge 1$. It can be seen that the result of the calculation of the sensitivity of the output voltage compared to r_i is very similar to the one obtained for the calculation of the output voltage sensitivity for g_m of the Cascode OTA in the closed-loop switched-capacitor integrator in Equation (22).

Regarding the sensitivity, it can be concluded that the proposed switched-capacitor integrator, despite working in an open-loop configuration, has a robustness to PVT variations similar to the closed-loop switched-capacitor integrator.

However, since the performance of the proposed open-loop switched-capacitor integrator depends on the output resistance of the charge buffer, r_o, the sensitivity, $S_{r_o}^{v_o\left(\frac{T_{CLK}}{2}\right)}$, of the output voltage at $\frac{T_{CLK}}{2}$, $v_o\left(\frac{T_{CLK}}{2}\right)$, and r_o is calculated as:

$$S_{r_o}^{v_o\left(\frac{T_{CLK}}{2}\right)}=\frac{r_i}{v_o\left(\frac{T_{CLK}}{2}\right)}·\frac{\partial v_o\left(\frac{T_{CLK}}{2}\right)}{\partial r_i}=\frac{T_{CLK}}{2·{\tau }_{p2}}·\frac{1}{1-\frac{T_{CLK}}{2·{\tau }_{p2}}-e^{\frac{-T_{CLK}}{2·{\tau }_{p2}}}}\cong \frac{T_{CLK}}{2·{\tau }_{p2}}$$

(72)

According to Equation (69) and considering that $\frac{V_i}{\xi }\gg 1$ and $\frac{C_1}{C_2}\ge 1$, it can be assumed that $S_{r_o}^{v_o\left(\frac{T_{CLK}}{2}\right)}$ is quite less than 1. Therefore, the impact of the r_o variation on the integrator performance is limited.

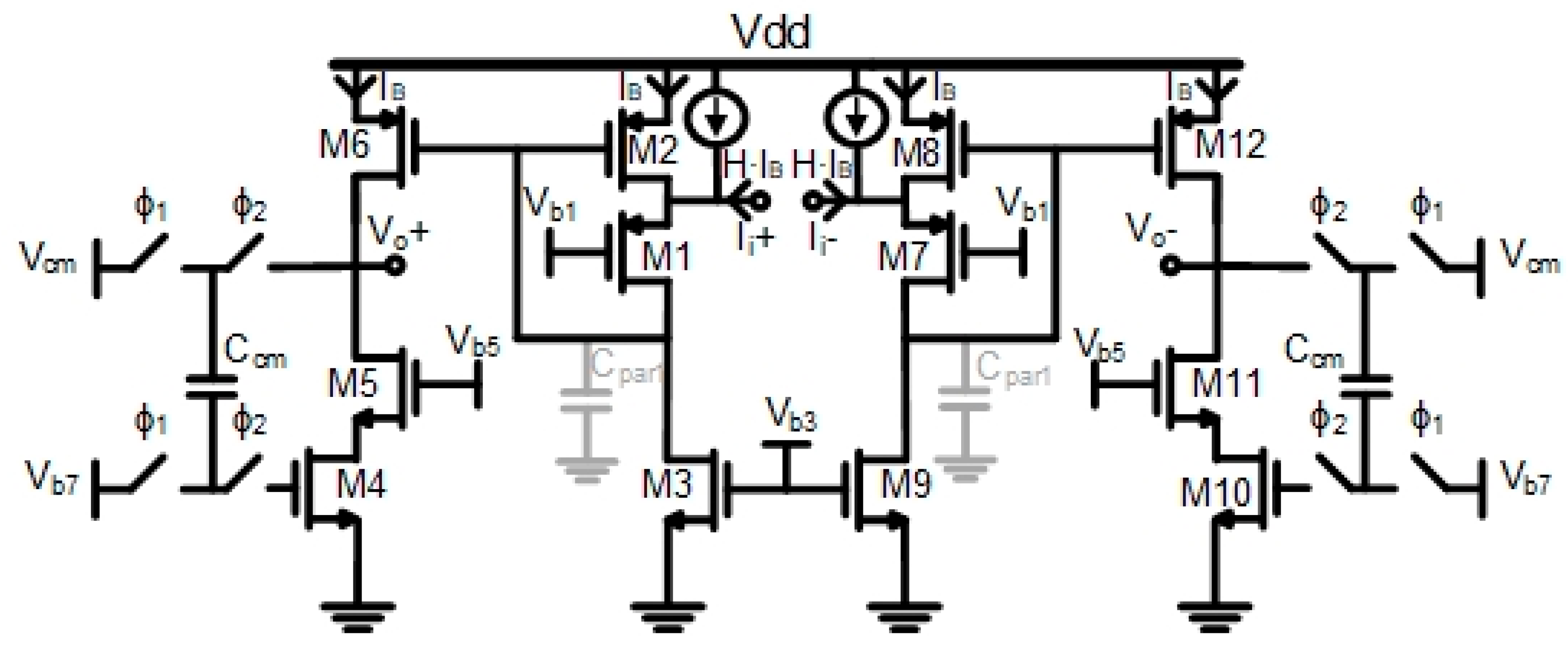
3.5. Circuit Implementation of the Proposed Charge Buffer

Figure 9 shows a possible circuit implementation of the charge buffer. The switched capacitors network at the output nodes is used to set the output common-mode voltage at V_cm. Reference V_b1 is designed to set the input common-mode voltage at V_cm. To keep M₂ and M₈ transistors in the saturation region, their source-drain voltage must be more than their saturation voltage, i.e.:

$$V_{SD2}=V_{dd}-V_{cm}>V_{SD2,sat}$$

(73)

It is supposed that V_cm is equal to half supply voltage and the saturation voltages correspond to the transistor overdrive, V_ov2, from Equation (73) we derive

$$V_{ov2}<\frac{V_{dd}}{2}$$

(74)

To bias the M₁ transistor in the saturation region, it must be guaranteed that its source-drain voltage, V_SD1, overcomes its saturation voltage, corresponding to the transistor overdrive, V_ov1, i.e.:

$$V_{SD1}>V_{ov1}$$

(75)

From the last equation, we obtain

$$V_{SD1}=V_{cm}-V_{dd}+\left|V_{THP}\right|+V_{ov2}>V_{ov1}$$

(76)

Assuming V_cm = V_dd/2, the last equation can be rearranged to obtain a constraint on the difference between the M₁ and M₂ transistors overdrives, ΔV_ov2−1, i.e.:

$$\Delta V_{ov2-1}=V_{ov2}-V_{ov1}>\frac{V_{dd}}{2}-\left|V_{THP}\right|$$

(77)

Using the finFET 16 nm we obtain the result V_dd = 0.95 V, V_THP = 0.4 V. Consequently, ΔV_ov2−1 must be higher than 75 mV.

According to Equations (74) and (77), using a charge buffer in open-loop configuration gives more flexibility to the design since larger overdrives can be defined for the transistors, to employing an OTA in a closed-loop fashion. This is extremely important at low voltage supply.

The input and the output resistances, r_i and r_o, are calculated as follows:

$$r_i\cong \frac{1}{g_{m1}·g_{m2}·r_{ds3}}=\frac{V_{ov1}·V_{ov2}}{4·V_{A3}·I_B}; r_o\cong r_{ds6}=\frac{V_{A6}}{I_B}$$

(78)

where g_m1 and g_m2 are the transconductance of M₁ and M₂ transistors, respectively, while r_ds3 and r_ds6 are the output resistance of M₃ and M₆ transistors, respectively.

The voltage gain, A_v, is calculated as follows:

$$A_v=\frac{r_o}{r_i}=\frac{4·V_{A3}·V_{A6}}{V_{ov1}·V_{ov2}}$$

(79)

The telescopic Cascode OTA reported in Figure 4 implements the boost of the output resistance, r_o. On the other end, the proposed charge buffer circuit enables the boosting of the transconductance of the input transistors, g_m1, by a g_m2∙r_ds3 factor, lowering the input resistance, r_i. The impact on the final voltage gain is similar as demonstrated by the similitude of the voltage gain expressions reported in Equations (79) and (27), even if the voltage gain, A_v, of the proposed charge buffer results the double with respect to the telescopic Cascode OTA.

In both cases, the power consumption is determined by the settling requirements, i.e., both the time constants τ_p and τ_p1 for the closed-loop and the proposed open-loop switched-capacitor integrator, respectively. The time constant, τ_p, depends on 1/g_m1. In this case, the only possibility to increase g_m1 is to increase the bias current I_B of the telescopic Cascode OTA, since the input transistor overdrive is bound to bias constraints. For the proposed integrator, the time constant τ_p1 is proportional to r_i. However, in the last case, as the boost on the input transistor transconductance lowers the input resistance, r_i, a significant power saving is obtained.

3.6. Slew-Rate Analysis of the Proposed Charge Buffer

According to Equation (56), the maximum rate of variation of the output voltage, i.e., the slew-rate, is obtained at the initial instant, t = 0 s:

$${SR=\frac{d{v}_o\left(t\right)}{dt}|}_{max}=\frac{C_1}{C_2}·\frac{1}{1-\frac{C_1}{A_v·C_2}}·V_{SRi,max}·\left(\frac{1}{{\tau }_{p1}}-\frac{1}{{\tau }_{p2}}\right)\cong \frac{V_{SRo,max}}{{\tau }_{p1}}$$

(80)

where:

$$V_{SRo,max}=\frac{C_1}{C_2}·\frac{1}{1-\frac{C_1}{A_v{C}_2}}·V_{SRi,max}\cong \frac{C_1}{C_2}·V_{SRi,max}$$

(81)

The last approximation in Equation (81) is valid assuming ${\tau }_{p1}\ll {\tau }_{p2}$.

The slew-rate depends on the bias current I_B and the output capacitance C₂, i.e.:

$$SR=\frac{I_B}{C_2}$$

(82)

where I_B is the bias current of each branches composing the charge buffer drawn in Figure 9.

Combining Equations (80) and (82) and considering the expression of τ_p1 and r_i reported in Equations (57) and (78), respectively, we derive:

$$V_{SRo,max}=\frac{I_B}{C_2}·{\tau }_{p1}=\frac{C_1}{C_2}·\frac{V_{ov1}·V_{ov2}}{4·V_{A3}}$$

(83)

where V_ov1 and V_ov2 are the overdrive voltage of M₁ and M₂ transistors, respectively, and V_A³ is the early voltage of M₃ transistor.

Combining Equations (81) and (84), the value of V_SRi,max is obtained:

$$V_{SRi,max}=\frac{V_{ov1}·V_{ov2}}{4·V_{A3}}\frac{1}{1-\frac{C_1}{A_v·C_2}}\cong \frac{V_{ov1}·V_{ov2}}{4·V_{A3}}$$

(84)

The output voltage range where the charge buffer operates in the linear regime, V_SRo,max, has been reduced by a factor equal to $\frac{4·V_{A3}}{V_{ov2}}$ concerning the traditional closed-loop switched-capacitor integrator with the OTA.

Due to its differential structure, the charge buffer starts slewing as V_i > 2∙V_SRi,max. If a slewing period is considered, the differential output voltage, v_od(t), can be calculated as follows:

$$\{\begin{array}{c}{v}_{od}\left(t\right)=-2·\frac{V_{SRo,max}}{{\tau }_{p1}}·t for 0<t<{\tau }_s\\ v_{od}\left(t\right)=\left(-\frac{C_1}{C_2}·\frac{1}{1-\frac{C_1}{A_{v·}{C}_2}}·V_i+2·V_{SRo,max}\right)\left(1-\frac{t-{\tau }_s}{{\tau }_{p2}}\right)-2·V_{SRo,max}·\left(1-\frac{t-{\tau }_s}{{\tau }_{p2}}-e^{-\frac{t-{\tau }_s}{{\tau }_{p1}}}\right)for t>{\tau }_s\end{array}$$

(85)

where τ_s is the duration of the slewing period. The charge buffer slews until the output differential voltage, v_od(t), is less than 2·V_SRo,max concerning the final value in steady-state, neglecting the losses due to the output resistance (i.e., τ_p2→∞):

$$-2·\frac{V_{SRo,max}}{{\tau }_{p1}}·{\tau }_s=-\frac{C_1}{C_2}·\frac{1}{1-\frac{C_1}{A_v·C_2}}·V_i+2·V_{SRo,max}\cong -\frac{C_1}{C_2}·V_i+2·V_{SRo,max}$$

(86)

From the combination of the last equation and Equation (83), the expression of τ_s is derived:

$${\tau }_s={\tau }_{p1}·\left(\frac{C_1}{C_2}·\frac{V_i}{2·V_{SRo,max}}-1\right)={\tau }_{p1}·\left(\frac{V_i}{2·V_{SRi,max}}-1\right)$$

(87)

3.7. SNR Analysis of the Proposed Open-Loop Switched-Capacitor Integrator

By focusing the analysis on a single branch, V_o+ must satisfy the following inequation to guarantee that M⁴ transistors operate in saturation region:

$$V_{o+}>V_{DS,sat4}+V_{S4}=V_{ov}+V_{S4}$$

(88)

where V_S⁴ and V_DS,sat⁴ are the source and the saturation voltages of M⁴ transistor, respectively. It is assumed that V_ds,sat⁴ is equal to V_ov. The bias voltage V_b⁵ was chosen to make M₅ transistor operating in saturation, i.e.,

$$V_{ds5}=V_{S4}>V_{DS,sat5}=V_{ov}$$

(89)

where V_DS⁵, and V_DS,sat⁵ are the drain-source, and the saturation voltages of M⁴ transistor, respectively. In this case, it is assumed that V_ds,sat1 is equal to V_ov. V_S1 is derived from the V_b⁵ bias voltage, by dropping the gate-drain voltage of the M⁴ transistors, V_GS⁴, i.e.:

$$V_{S4}=V_{b1}-V_{GS4}=V_{b1}-V_{TH}-V_{ov}$$

(90)

V_b1 can be designed to make V_S⁴, and, hence, V_DS⁵ equal to V_DS5,sat, i.e., V_ov. If so, from Equation (88) we derive the minimum output voltage, V_o+,min:

$$V_{o+}>V_{ov}+V_{DS5,sat}=2·V_{ov}=V_{o+,min}$$

(91)

As the output voltage starts swinging from the common-mode voltage, V_cm, down to V_o,min, it is possible to calculate the maximum output voltage swing, V_swing:

$$V_{swing}=2·\left(V_{cm}-V_{o+,min}\right)=2·\left(\frac{V_{dd}}{2}-2·V_{ov}\right)=V_{dd}-4·V_{ov}$$

(92)

where the 2 factor is due to the differential architecture. It is assumed that V_cm is equal to half V_dd.

Assuming that the thermal noise due to the switches around C₁, $2·\frac{KT}{C_1}$ is dominant, from Equation (92), the signal to noise ratio of the overall open loop switched capacitor integrator, SNR_OL, is calculated as follows:

$$SN{R}_{OL}=\frac{1}{2}·\frac{V_{swing}^2}{\overline{v_{n,o}^2}}=\frac{1}{2}·\frac{{\left(V_{dd}-4·V_{ov}\right)}^2}{2·\frac{K·T}{C_1}·{\left(\frac{C_1}{C_2}\right)}^2}=\frac{{\left(V_{dd}-4·V_{ov}\right)}^2·C_2^2}{4·K·T·C_1}$$

(93)

where $\overline{v_{n,o}^2}$ is the total output noise, which is given by the thermal noise contribution due to the C₁ switched-capacitor multiplied by the square of the integrator gain ${\left(\frac{C_1}{C_2}\right)}^2$, and the $\frac{1}{2}$ factor takes into account that the input signal is a sinusoid.

The resulting SNR_OL is slightly higher than the SNR_CL calculated by Equation (43). The output noise is about the same since the noise contribution of C₁ is assumed dominant. However, assuming V_TH = 0.275 V and V_dd = 0.95 V as for the finFET technology and V_ov = 0.1 V, due to bias constraint as defined by Equation (43), the output voltage swing for the proposed switched-capacitor integrator is higher.

3.8. Power Consumption Requirement of the Proposed Charge Buffer

The minimum power consumption, P_w,min, is given by the product of the supply voltage V_dd, by the minimum total bias current I_BTOT.min:

$$P_{w,min}=V_{dd}·I_{BTOT,min}·4·\left(1+\frac{H}{2}\right)·V_{dd}·I_{B,min}$$

(94)

where I_B,min is the minimum I_B bias current. The power requirement is calculated according to the settling time requirement. In practice, the minimum bias current I_B,min is derived assuming that the ε_τp1 error must be less than the required accuracy ξ, i.e.:

$${\epsilon }_{\tau p1}<\xi$$

(95)

As V_i < 2·V_SRi,max, the charge buffer is in the linear regime, where the expression of I_B,min is derived from Equation (62):

$$I_{B,min}=\frac{2·C_1·V_{SRi,max}}{T_{CLK}}·ln\left(\frac{C_1}{C_2}·\frac{V_i}{\xi }\right)$$

(96)

Combining Equations (94) and (96), the minimum required power consumption, P_w,min, is calculated as follows:

$$P_{w,min}=\frac{8·V_{dd}·\left(1+\frac{H}{2}\right)·C_1·V_{SRi,max}}{T_{CLK}}·ln\left(\frac{C_1}{C_2}·\frac{V_i}{\xi }\right)$$

(97)

As V_i > 2∙V_SRi,max, the charge buffer starts slewing. Considering the expression of the differential output voltage v_od(t), including the slewing period reported in Equation (85), the calculation of the error due to τ_p1, ε_τp1, is updated as follows:

$${\epsilon }_{\tau p1}=\left|{v_o\left(\frac{T_{CLK}}{2}\right)|}_{\begin{array}{c}{\tau }_{p1}\to 0\\ {\tau }_{p2}\to \infty \end{array}}-{v_o\left(\frac{T_{CLK}}{2}\right)|}_{{\tau }_{p2}\to \infty }\right|=2·V_{SRo,max}·e^{-\frac{\frac{T_{CLK}}{2}-{\tau }_s}{{\tau }_{p1}}}$$

(98)

Considering ε_τp1 as reported in the previous equation, the constraint on τ_p1 is derived from Equation (95):

$${\tau }_{p1}<\frac{T_{CLK}}{2\left(ln\left(\frac{2·V_{SRo,max}}{\xi }\right)+\frac{V_i}{2·V_{SRi,max}}-1\right)}$$

(99)

Looking at τ_p1 and r_i in Equations (57) and (78), respectively, the minimum bias current that satisfies Equation (99), I_B,min is calculated as follows:

$$I_{B,min}=\frac{2·C_1·V_{SRi,max}}{T_{CLK}}·\left(ln\left(\frac{2·V_{SRo,max}}{\xi }\right)+\frac{V_i}{2·V_{SRi,max}}-1\right)$$

(100)

Combining Equations (97) and (100), the minimum required power consumption is calculated as follows:

$$P_{w,min}=\frac{8·V_{dd}·C_1·\left(1+\frac{H}{2}\right)·V_{SRi,max}}{T_{CLK}}·\left(ln\left(\frac{2·V_{SRo,max}}{\xi }\right)+\frac{V_i}{2·V_{SRi,max}}-1\right)$$

(101)

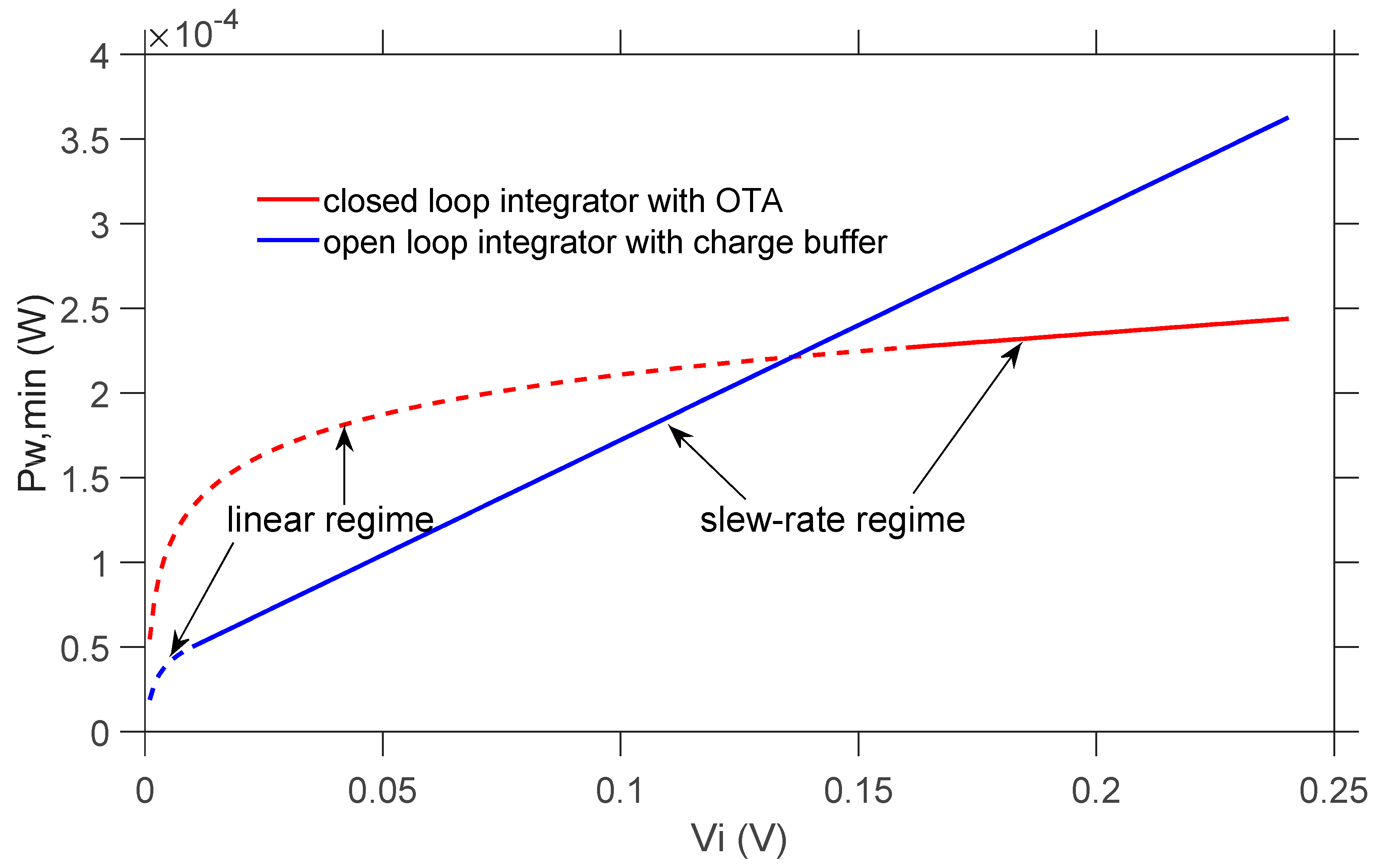
Figure 10 shows the power consumption of the proposed switched-capacitor integrator and the closed-loop switched-capacitor integrator plotted as a function of V_i.

The two curves in Figure 10 are obtained plotting the Equations (97) and (101) for the proposed design, and Equations (46) and (51) for the closed-loop switched-capacitor integrator. The common design parameters are reported in

Table 1. Design parameters of the switched capacitor integrator.

Design Parameter	Value
Vov	0.1 V
Vov2	0.2 V
Vdd	0.95 V
Vi	31.25 mV
ξ (accuracy)	1 mV
TCLK	7 ns
C1	1.25 pF
C2	312.5 fF
C1/C2	4
Cpar1	27 fF
VA3	1 V
VA6	18 V

.

The transistors overdrives have been defined according to the constraints derived from Equations (25), (74), and (77). The values of C_par1, V_A3, and V_A6 are estimated from the simulation results. The H factor was set to 2 for the proposed design.

The minimum power required by the closed-loop switched-capacitor integrator is higher than the proposed open loop integrator for an input signal up to 140 mV large. For V_i = 31.25 mV, the proposed circuit requires a minimum power of 76 µW, while the closed-loop switched-capacitor integrator requires about 173 µW, i.e., more than the double.

3.9. Small Signal Analysis of the Charge Buffer Considering the Parasitic Capacitance C_par1

The small-signal equivalent circuit shown in Figure 7 is a first-order approximation of the small-signal behavior of the proposed transistor-level open-loop switched-capacitor integrator. Considering also the C_par1 as a parasitic capacitance shown in Figure 9, a more accurate transfer function is obtained:

$$\frac{v_o}{v_s}=-\frac{s·C_1·\left(1+\frac{s·C_{par1}}{g_{m2}}\right)}{1+s·\left(\frac{C_{par1}}{g_{m2}}+\frac{C_1}{g_{m1}·g_{m2}·r_{ds3}}\right)+s^2·\frac{C_1·C_{par1}}{g_{m1}·g_{m2}}}·\frac{r_o}{1+s·r_o·C_2}$$

(102)

where r_ds³ is the output resistances of M₃ transistor. The parasitic capacitance, C_par1, mainly depends on the gate capacitances of M₂ and M₆ transistors. Therefore, it can be approximated as follows:

$$C_{par1}\cong \frac{2}{3}·W_2·L_2·C_{ox}+\frac{2}{3}·W_6·L_6·C_{ox}=\frac{4}{3}·W_2·L_2·C_{ox}$$

(103)

where W₂ and L₂, and W₆ and L₆, are the width and the length of M₂ and M₆ transistors.

Concerning the transfer function reported in Equation (55), the transfer function in Equation (84) includes a further zero, z₁:

$$z_1=-\frac{g_{m2}}{C_{par1}}$$

(104)

This zero is considered to be at a very high frequency and it does not produce significant effects on the step response of the proposed circuit.

Moreover, two complex poles appear in the transfer function. Their frequency, ω_o, and quality factor, Q, are calculated as follows:

$$\begin{gathered} {\omega }_0=\sqrt{\frac{g_{m1}·g_{m2}}{C_1·C_{par1}}}=2·I_B·\sqrt{\frac{H+1}{V_{ov1}{V}_{ov2}{C}_1{C}_{par1}}}\mathrm{and} \\ Q=\frac{1}{\sqrt{\frac{g_{m1}·C_{par1}}{g_{m2}·C_1}}+\sqrt{\frac{C_1}{r_{ds3}^2·g_{m1}·g_{m2}·C_{par1}}}}=\frac{1}{\left(\sqrt{H+1}\right)·\left(\sqrt{\frac{V_{ov2}·C_{par1}}{V_{ov1}·C_1}}+\sqrt{\frac{V_{ov1}·V_{ov2}·C_1}{4·V_{A3}^2·C_{par1}}}\right)} \end{gathered}$$

(105)

A high Q factor determines a large overshoot, OS, on the step response of the proposed circuit, and wide oscillations, which can have a severe impact on the accuracy of the output voltage. Otherwise, as the circuit is excessively dumped, the step response slows significantly. The criterion here adopted is to limit the overshoot to the required accuracy, ξ, i.e.:

$$OS=\frac{C_1}{C_2}·V_i·e^{\frac{-\frac{\pi }{2·Q}}{\sqrt{1-\frac{1}{4·Q^2}}}}=\xi$$

(106)

The previous equation is valid in linear regime; otherwise, in case of slewing of the charge buffer, the overshot is calculated as follows:

$$OS=V_{SRo,max}·e^{\frac{-\frac{\pi }{2·Q}}{\sqrt{1-\frac{1}{4·Q^2}}}}=\xi$$

(107)

For the proposed design, the last equation is satisfied for a Q value of about to 0.75. The Q factor can be reduced by operating on V_ov2 and V_ov1, or, by acting on the H factor, which gives a further degree of freedom to the design.

The desired value of Q is reached by designing an H factor of 2.

4. Simulation Results

A transistor-level design of the proposed switched-capacitor circuit was performed in finFET 16 nm CMOS technology. The design parameter reported in Table 1 were considered. The input signal, V_i, was assumed equal to 31.25 mV. The bias current, I_B, set to 10 µA, corresponds to the minimum value, I_B,min, as predicted by Equation (100). The H factor was set to 2 as derived from Equation (107). The minimum power consumption of the core circuit was 76 µA, as predicted by Equation (83).

According to Equation (65), the required voltage gain is 56 dB, while a voltage gain of 71 dB results from simulations. Similarly, the required output resistance obtained from Equation (70) was 1.4 MΩ, while the value obtained through simulations was 1.85 MΩ. Therefore, we can conclude that the voltage gain and the output resistance requirements were largely satisfied.

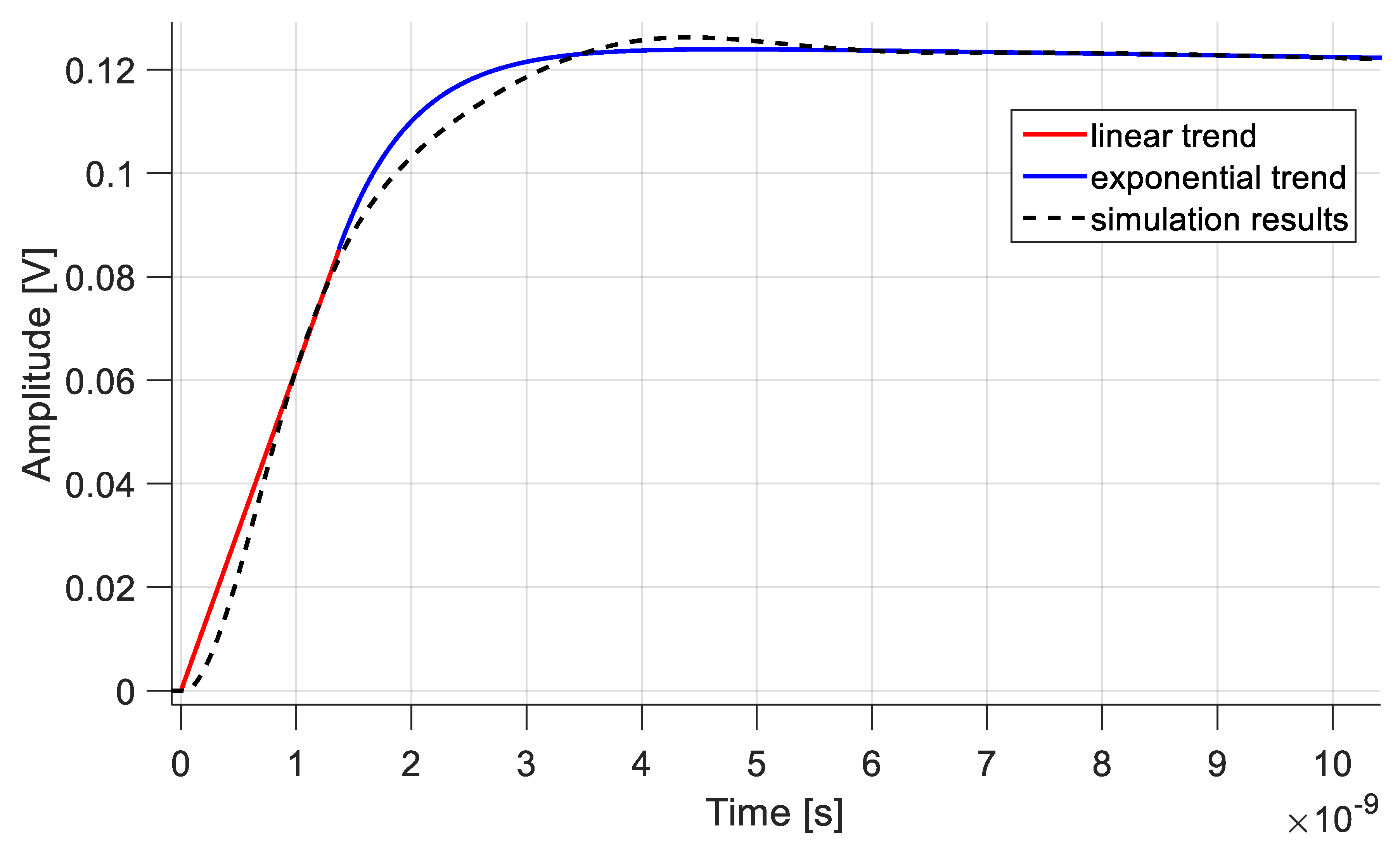
Figure 11 shows the response of the circuit to an input step of 31.25 mV for the theoretical model and simulations. The two curves are very close, proving the validity of the proposed circuit model. Based on the design parameters, the expected error on the output voltage at T_CLK/2 was 1 mV. This results from both the model prediction and the simulations.

The simulation results show a slightly marked overshot due to the complex poles generated by the internal loop including M₁ and M₂ transistors, as predicted in paragraph 3.9. However, the first-order model gives a valid approximation of the circuit behavior especially in the steady-state regime.

Table 2. Required and simulated design parameters for the open-loop switched-capacitor integrator.

Design Parameter	Required Value	Simulated Value
Av	>56 dB	71 dB
ro	>1.4 MΩ	1.85 MΩ
IB,min	10 µA	10 µA
ξ (accuracy)	1 mV	1 mV

summarizes the required values of the design parameters and their values obtained through simulations.

Table 3. Performance summary and state-of-the-art comparison.

Parameter	This work	[13]	[14]
Supply	0.95 V	1.8 V	1.2 V
Power	76 µW	4.3 mW	8.4 mW
Technology	16 nm FinFET	180 nm	65 nm
Number of poles	1	4	12
fCLK	143 MHz	300 MHz	430 MHz
OSR	1.57	11.3	9.23
SNR	61.5 dB	74.9 dB	45 dB
FoM	179.3 dB	175.8 dB	150.6 dB

reports the performance summary of the proposed switched-capacitor integrator and compares it to the state-of-the-art approach. The following figure of merit (FoM) is introduced for a fast comparison

$$FoM=\frac{SNR}{\frac{Pw}{N}·\frac{f_{CLK}}{2·OSR}}$$

(108)

where N is the number of poles of the switched-capacitor filter under consideration, P_w is its power, f_CLK is the clock frequency and OSR is the oversampling ratio, i.e., the ratio between half clock frequency and the maximum signal bandwidth.

As can be seen in Table 3, the proposed work is well compared to the state of the art in terms of FoM.

5. Conclusions

An architecture of a switched-capacitor integrator including a charge buffer operating in open-loop have been proposed and designed in finFET 16 nm technology. As for the switched capacitor filters, the gain of the proposed integrator is given by the capacitor ratio, guarantying desensitization concerning the PVT variations. Furthermore, the proposed circuit is more suitable for low voltage supplies. Moreover, the analytical study demonstrated that the proposed integrator is more efficient than the traditional closed-loop switched-capacitor integrator for input signal amplitude less than 140 mV. The proposed switched-capacitor integrator results were more than twice the efficiency when compared to the traditional closed-loop switched-capacitor filter, as it consumes 76 µW from the 0.95 V supply, assuming an input voltage of 31.25 mV and a clock period of 7 ns. The proposed work results were satisfactory when compared to the state-of-the-art in terms of the figure of merit.