1. Introduction
There is no doubt that antenna arrays, thanks to their capability to provide a dynamical manipulation of the received and radiated field, have a strong potential for most communication applications. Antenna arrays have been studied for half of the last century, and all crucial high-performance applications, (radar [
1], satellite communication [
2], and astronomical observation [
3]), have made use of them.
In the last decades, we have also seen the extension of antenna arrays to civil, low-cost applications (Wi-Fi networks, 4G [
4] and 5G [
5,
6] networks); as a matter of fact, the achievement of the demands of modern communication systems (in terms of the number of terminals served, band, latency) require the aforementioned potential [
7].
This trend is not going to stop, particularly now that we are moving towards the use of mm-wave frequencies for communications [
8], which require the use of arrays to obtain electronically focusable beams with good directivity.
Roughly speaking, the more radiating elements, the more directivity is possible to achieve. Unfortunately, antenna arrays have a non-trivial cost, usually not related to the antenna itself, but to all the amplifiers, phase shifters, beam forming networks that are required to operate the array. All these devices have a weight, occupy a volume, and require maintenance. In some applications, like satellite ones, payload reduction is a mandatory requirement; so, in general, the reduction of the elements’ number is fundamental to lower the overall cost [
9]. The choice of the number of radiators needs to be done with judiciousness.
Furthermore, in many applications, we need to verify specific constraints in terms of beam-width (BW) and side-lobe-level (SLL), but their realization requires a tapering of the source, which is known to reduce the directivity of the array [
10]. Moreover, the design of an antenna array capable of scanning the beam in a certain angular range requires particular care in the inter-elements distance otherwise grating lobes could appear in the visible range of the antenna. This could be a very negative effect for most of the application cases.
The difficulty of the array synthesis problem, particularly when non-regular lattices are used, is testified by a large number of papers on this topic that have been published in the last 60 years; many deterministic, evolutionary, and hybrid algorithms have been recently proposed [
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47,
48,
49,
50,
51].
Even if a large literature exists, the array dimensioning is still a non-trivial topic for antenna engineers; one may think that using the “right number” of radiators, half-wavelength equispaced, is the only thing to do, but this simplistic approach is not the best choice [
52,
53,
54].
So, an antenna engineer dealing with the synthesis of an array radiating a pencil beam needs to take into account at least five parameters: the number of radiating elements that is possible to use, the required beam-width and side-lobe level, the necessary scanning range of the beam, and the desired directivity. Obviously, those five parameters are not the only ones that could be taken into account in the synthesis, but a more general analysis would be beyond the scope of these notes.
In this paper, in particular, the issue of the directivity decrease in sparse arrays will be analyzed, showing that with a novel approach to the synthesis it is possible to achieve sparse layouts that can challenge with equispaced lattices in terms of directivity, with a significant reduction of the number of radiators.
To achieve this task, the present manuscript is structured in the following way. In the first part (
Section 2), the relationship between the relevant parameters is reviewed and simple ready-to-use formulas for the preliminary dimensioning of equispaced planar arrays are provided. In the second part (
Section 3), we then focus on the synthesis of sparse arrays, showing that the reduction in the number of radiating elements is usually paid in terms of a reduction of the directivity, in particular when beams out of the broadside direction are considered. In the third part (
Section 4), a novel design strategy, for achieving very high directivity is introduced and discussed through numerical examples. Conclusions follow.
2. Planar Arrays with Regular Lattices
For the sake of simplicity, in the following sections we will focus on the radiation of planar arrays of isotropic elements: we will deal with the synthesis of the “array factor” (AF) [
10]:
where
is the free-space wavenumber,
N is the number of radiating elements,
is the excitation of the
th element,
are the coordinates of the
th radiating element,
and
, with (
,
) the spherical coordinates with respect to the broadside direction.
It must be recalled that the use of the AF for pattern synthesis is convenient also when dealing with “real”, non-isotropic, radiating elements. In this case, we could apply the approach proposed in [
40] to properly modify the power pattern mask guaranteeing the satisfaction of the side-lobe level specification for any direction within the maximum scanning angle.
Let us now consider the synthesis of a pencil beam with prescribed side-lobe level employing a regular lattice array. If we require that the beam scanning is performed using a linear phase shift of the excitations, the synthesis problem can be written as:
where
, SLL is the desired side-lobe level, and
defines the circular footprint of the pencil beam, which establishes the beam-width, and
with
, the angle defining the scanning cone for the beam. Roughly speaking, we are increasing the region of the
plane where we impose the pattern constraints, to take into account the scanning of the beam.
2.1. The Choice of the Lattice
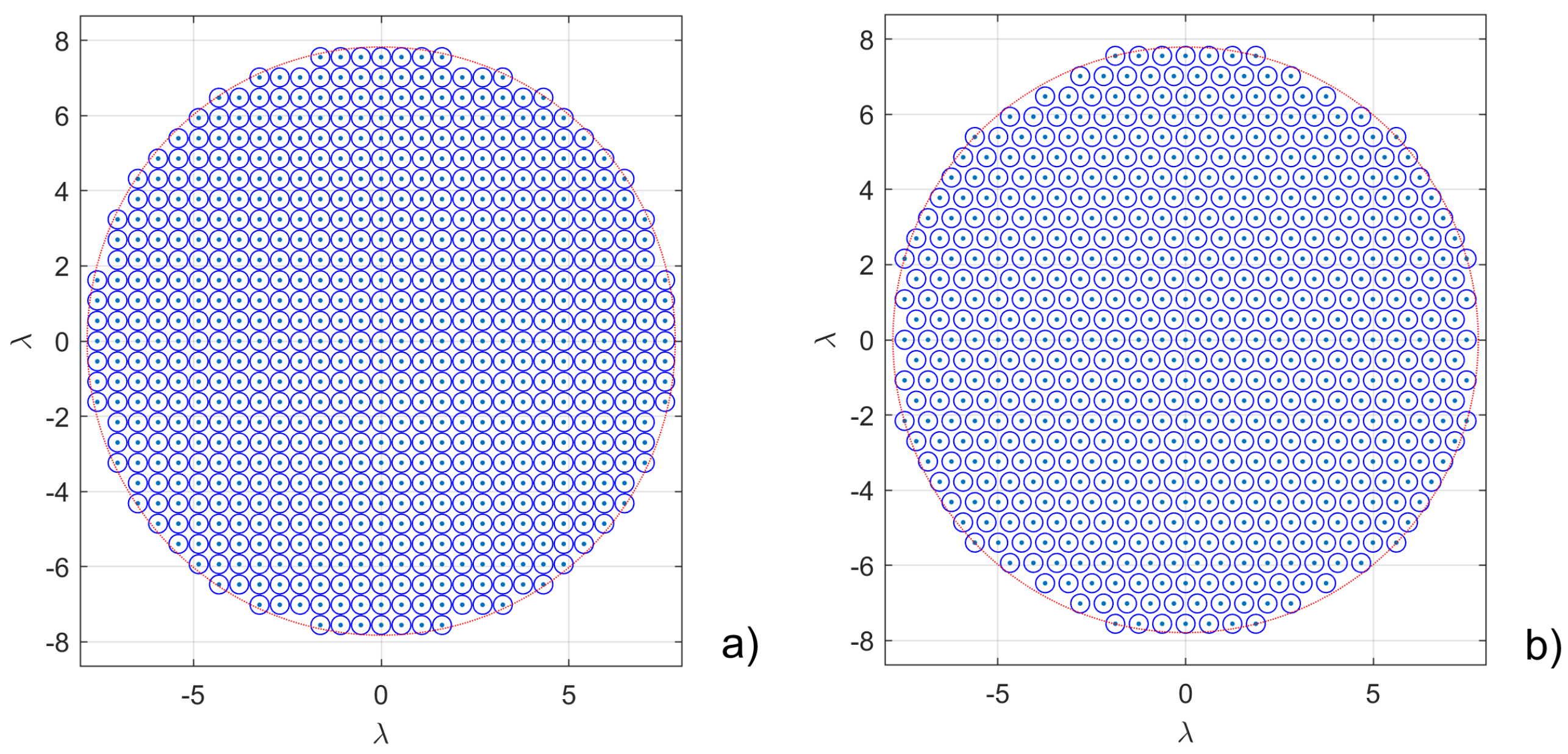
Once the synthesis problem is defined, the first question we do have to answer is: how many antennas do we need? For square lattices (
Figure 1a) we could use a Tchebyshev-based approach used in [
55] for linear arrays, finding that the maximum inter-element distance between elements must be:
It is also possible to use a triangular lattice (
Figure 1b) for the placing of elements on the plane; in this case, the required maximum distance must be:
It is interesting to note that is about lager than .
The inter-element distances and are such to have the grating lobes focused just outside the region () that could be in the visible range when scanning the beam.
In the case of a square lattice with
, we could use a grid of
elements, with
where
approximates
x to the smallest integer larger than
x.
It turns out that to radiate a beam with a circular footprint, the entire
elements square array is not necessary, so we could take only the elements of the rectangular lattice that fall into the circle of radius
(see
Figure 1a). The approximate overall number of elements to use would be equal to
but the exact effective number of radiators to use needs to be found numerically.
Similarly, with the triangular lattice, we could start from a grid of
radiators, with
and then taking only the elements of the lattice that fall into the circle of radius
(see
Figure 1b). The approximate overall number of radiators to use would be equal to
but, even in this case, the exact number of radiators to use needs to be found numerically.
It is, again, interesting to observe that the triangular lattice allows a reduction of the number of radiating elements of about with respect to the square lattice.
The relationships shown above allow us to make a first dimensioning of the parameters for two types of regular lattice arrays.
Given the beam-width, the SLL, and the scanning range, the found element number is the minimum that a regular lattice would require. As it will be shown later, this is not true for sparse or thinned arrays, but the number of elements of the regular lattices will represent a benchmark for the “sparsification” of the algorithm: it is possible to claim a reduction of the number of radiators only if the obtained layout uses fewer elements than the triangular equispaced lattice.
2.2. Calculation of the Excitations
Once the lattice has been chosen, it is possible to calculate the excitations of the elements.
It is worth recalling that there could be many different set of excitations, satisfying the same pattern specifications with the same elements’ positions, so we are going to choose the excitations to maximize the broadside directivity of the array of isotropic elements:
where
is the vector of the elements’ excitations, and
is a square matrix in which the entries are:
with
the distance between two elements, and we have applied Equation (
2). The relationship in Equation (
11) can be obtained, exploiting the symmetry of isotropic radiators, from the well-known formula for linear arrays [
10], through a simple rotation of the coordinate system.
According to Equation (
10), the maximization of the directivity requires the minimization of the term
. The pencil beam synthesis, with the maximization of the directivity in Equation (
10) and constraints on BW and SLL (Equations (
2) and (
3)), turns out to be a convex problem, which can be efficiently solved by one of the efficient convex programming packages, like CVX for Matlab [
56].
2.3. Comparing Directivities
Let us now apply the aforementioned procedure to the synthesis of a specific pattern. We want to radiate a pencil beam with SLL lower than −20 dB for
, and we want to have the SLL specification met for any beam focused in the conical region
(deg). Using the aforementioned rules for the creation of the two lattices, it is possible to achieve a layout with a square lattice of 665 elements, and a layout with a triangular lattice of 571 elements (which are the ones depicted in
Figure 1).
In
Figure 2, we can see the result of the pattern synthesis with the square lattice (the pink/cyan colormap is chosen to emphasize violation of the SLL constraint). The distance between elements is
, and the directivity of the broadside beam is
dBi. The grating lobes are outside the
plane region
, so they will not appear when scanning the beam up to
(deg).
In
Figure 3, we can see the result of the synthesis with the triangular lattice. The distance between elements is
, and the directivity of the broadside beam is
dBi. Even in this case, the grating lobes are outside the
plane region
, so they will not appear when scanning the beam up to
(deg).
Let us discuss the results of the two lattices. The higher directivity of the former compared to the latter is mostly due to the larger number of radiating elements of the square lattice; it is worth noting that the difference in directivity can be also inferred from the different power pattern imagemaps of
Figure 2 and
Figure 3, since the former shows slightly darker tones of cyan.
It is worth underlining that the employed inter-element distances in Equations (
4) and (
5) are only the maximum ones, to avoid the appearance of grating lobes when focusing the beam in the angular region of interest. Smaller distances can be used for achieving a better aperture efficiency and, hence, directivity. This choice would imply using many more radiating elements, so it will be not considered in these notes.
The use of a regular grid of radiators allows a very high directivity, but the number of employed elements is also huge: for many applications, the number of radiators should be reduced as much as possible to obtain a reasonable system cost, space occupation, and weight. For this reason, it could be convenient to use sparse, non-regular lattices.
3. Sparse Array Synthesis
As stated in the introduction, the synthesis of sparse arrays is a much more complex than the synthesis of a regular lattice ones, since the array factor (
1) is a non-linear function of the position of the sources: we are not allowed to directly use convex programming techniques as in the case of fixed, regular lattices.
To solve this problem, as stated in the introduction, many synthesis methods have been developed. For the present manuscript, we will employ IDEA [
49], a powerful algorithm, the working principle of which will be briefly recalled in the following.
IDEA requires a preliminary solution that will be locally optimized using two iterative steps. Let us suppose that as a starting solution we use one of the regular lattices described in the previous section; in this way, we can obtain the positions and excitations of radiating elements (the apex and subscript “1” has the meaning of “first iteration” of the algorithm).
3.1. The Two Steps of IDEA
In the first step, for each iteration
k, the new excitation vector
is obtained solving the problem:
where
and
with
and
is the Hadamard entry-wise product of the two vectors
and
,
stands for
norm of
vector, given by
,
is column vector sampling the upper mask in the aforementioned directions,
is a matrix sampling the array factor (
1),
is a row vector, sampling the radiation operator in the direction of the desired maximum of the focused beam, and
is a constant, usually chosen equal to a small fraction of the maximum of
, to limit the weighting for entries close to zero.
The problem in Equations (
12)–(
14) is a re-weighted L1 minimization where the weighting in Equation (
15) is similar to the one proposed in Reference [
48], and it is used because it tends to force the lower entries of the unknown vector
to zero. Its choice has shown excellent sparsification capabilities: when the algorithm has converged, the
norm of the vector
tends to the number of radiators with an excitation greater than the chosen threshold [
48].
The second step of IDEA is the one in which “inflation” and “deflation” actually occur. Each one of the
sources obtained from the previous step, is split into a set of
P sources of coordinates
, placed at the vertexes of a regular polygon of radius
with the centre in
:
where
and
is an offset angle, which can be chosen randomly.
The output of this inflation is an increased number of sources, from to . These new sources can well approximate the field of the starting sources, and it is possible to demonstrate that the approximation error is proportional to .
Once the sources have been inflated, we can solve the following problem for each one of them:
where
is the vector of the
excitations,
is the radiation operator for the sources of coordinates
,
is a row vector, sampling the radiation operator in the direction of the maximum of the focused beam and
where
Once we have solved the problem in Equations(
17)–(
19), we can “deflate” the
polygons: we can find the positions and excitations of the new
sources, of coordinates
and excitation
, that best approximate each set of
P sources obtained by Equations (
17)–(
19).
This “deflation” can be performed numerically, looking for the coordinates
and excitations
that minimize:
The minimization of Equation (
21) has to be computed for the
values of interest and is fast to calculate since it can be solved as a local optimization, the starting point of which is given by the excitation obtained from the first step.
3.2. The Sparsification Effect
The weighted minimizations make the relative excitation of some of the points to be very small; by choosing a threshold , we can start the first step of the successive iteration with only the excitations with an amplitude larger than .
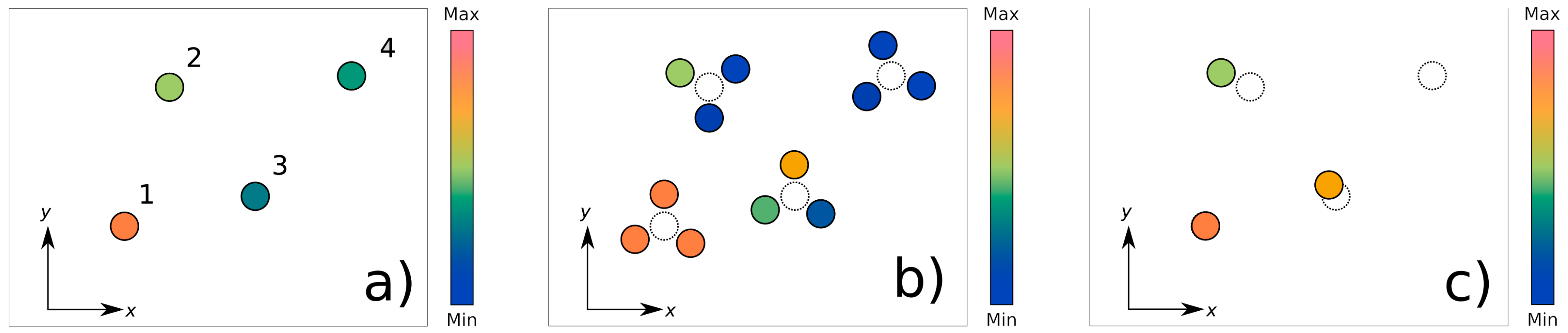
Now we are going to focus on a single iteration for a test case of
Figure 4. In the left subplot, marked (a), we see four excitations in the
plane; their amplitude is calculated solving Equations (
12)–(
14). In the middle subplot, marked (b), we can see the inflation of the sources with
, and the amplitude of these is calculated using Equations (
17)–(
19). Finally in the right subplot, marked (c), each set of sources is substituted by a new source obtained by the minimization of Equation (
21).
Summarizing, at each iteration, the sources can be modified in two possible ways: they can be moved, or they can be removed. This means that the overall number of sources can only be reduced during the process of optimization, and the sparsification of the antenna can only increase. Then the algorithm can be stopped when the solution found does not change anymore, or when a chosen number of iterations has been performed.
3.3. A Synthesis Example
Now, let us consider the synthesis of a sparse array with the same specifications, beam-width, side-lobe level and scanning range, used for the regular lattices (all the layouts presented in the following will comply with the same constraints to simplify the comparisons): SLL lower than −20 dB for .
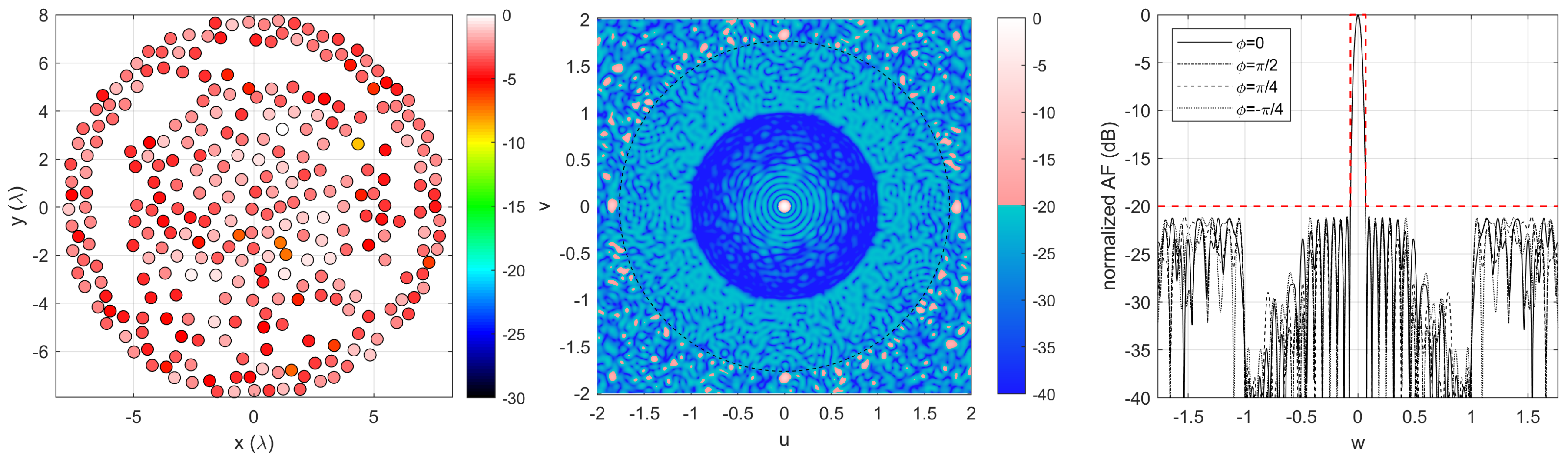
Using IDEA, it is possible to find a layout employing 213 elements only (see
Figure 5). All the data (elements’ positions and excitations) necessary to reproduce this layout, as well as the data for the layouts that will be presented in the following, are given in
Appendix A. The achieved layout shows an excitation dynamic
dB, the minimum inter-element distance is
. The overall computation time, on an Intel i7-8700 k 4.7 GHz processor, required about 50 min, and was performed using
,
,
,
; some computational remarks are discussed in
Appendix B.
Undoubtedly, the sparsification allows a huge reduction of the number of elements to the number of radiators a regular lattice, from 665 to 213 radiators (a reduction of about 68%), but such a reduction has a cost: the very low directivity of the obtained pattern, which is 23.6 dB only.
3.4. Directivity Constraint
A possibility to achieve a better sparse array consists of adding a directivity constraint during the synthesis.
It has been recalled that the directivity can be written as Equation (
10). Since the form
is a quadratic form, a constraint like
turns out to be a convex constraint that can be added with minimum effort to minimizations Equations (
12) and (
17).
As an example, we could start from the higher directivity layout of
Figure 2, which presents 665 elements, and impose as a constraint that the broadside directivity is always not lower than the directivity of the fully populated starting array.
The result of this synthesis is provided in
Figure 6; the achieved layout employs 310 elements and shows an excitation dynamic
dB, the minimum inter-element distance is
, and the computation time was about eight hours. The beam-width and side-lobe level specifications are perfectly verified, even for the most scanned beam, and the directivity of the broadside beam is 29 dB, like the directivity of the fully populated array.
It is also worth underlining that the number of radiators is much larger than the previous sparse layout, but we are indeed using a much lower number of radiating elements than the fully populated array, 310 instead of 665 (a reduction of more than 53%).
3.5. The Directivity of the Scanned Beams
The previous result seems to be excellent: the same directivity of a fully populated array using less than 50% of its radiators. Unfortunately, all that glitters is not gold.
If we look at the normalized array factor in the
plane, we can see a reduction of the side lobes in the region
, which is the region that is taken into account for the calculation of the broadside directivity of Equation (
10). We can see that the side-lobe level increases in the
region: the side lobes are lower than the specification threshold, but we should expect a reduction in directivity when scanning the beam.
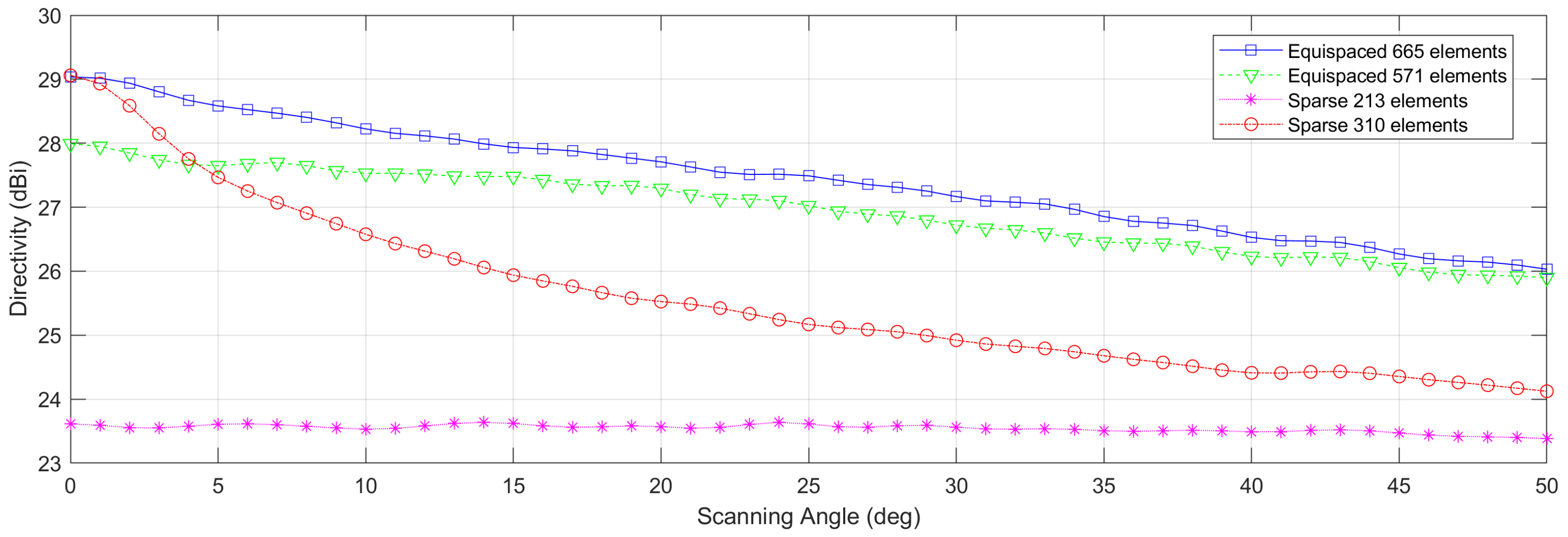
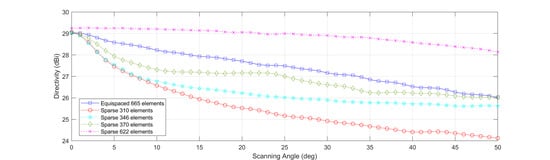
In
Figure 7, we have represented the variation of the directivity for the four arrays that we have considered up to this point. As expected, the performances of the 310 elements sparse array are very good but rapidly decrease as soon as the beam is focused in a direction different than the broadside one.
This effect represents one of the main issues of sparse arrays: since the position of the elements is optimized for a particular beam, focusing in a direction different from the optimized one results in a reduction of the performances.
It is worth underlining that this decrease does not occur, or is very limited, in equispaced arrays: because of the periodicity introduced by the lattice, the side-lobes are automatically lowered in the region.
In sparse arrays we have, instead, to perform the synthesis taking into account the desired reconfiguration of the beam, like in [
42]; the scanning of the beam for large angular ranges must be explicitly managed.
A first choice, could be to manually increase the side-lobe level requirements for the region, but this choice should be avoided since imposing such a constraint would require the use of a larger starting array. Furthermore, lowering the threshold to a not-needed level could make us avoid some good solutions.
A second possibility could be to explicitly optimize for a discrete set of scanning angles, but this choice would increase the computational effort of the synthesis algorithm since we could not use simple formulas like Equation (
10).
Fortunately, it is possible to use a smart approach to this problem, which will be described in the next section.
4. Improving the Scanning Performance of Sparse Arrays
If we look at
Figure 6, we can see that the threshold on the directivity has lowered the side-lobes in the region
compared to the sidelobes of the layout of
Figure 5. This happens because the compact formula
is the result of the integration of the array factor in the visible range.
Imagine now to perform a “scaling” of the positions of the radiating elements of a factor , so that the scaled coordinates of the radiating elements are . If we chose , without changing the excitation of the radiators, we will obtain an array that radiates a “scaled” array factor, that is shrunk of the same factor : the pattern radiated by the starting array in the angular region will be radiated by the scaled array in the angular region .
Let us now introduce a “dummy directivity”
with
is a square matrix, the entries of which are:
and obviously,
.
It turns out that the equation of dummy directivity has a form as simple as the directivity in Equation (
10), but allows a significant improvement of the scanning performances.
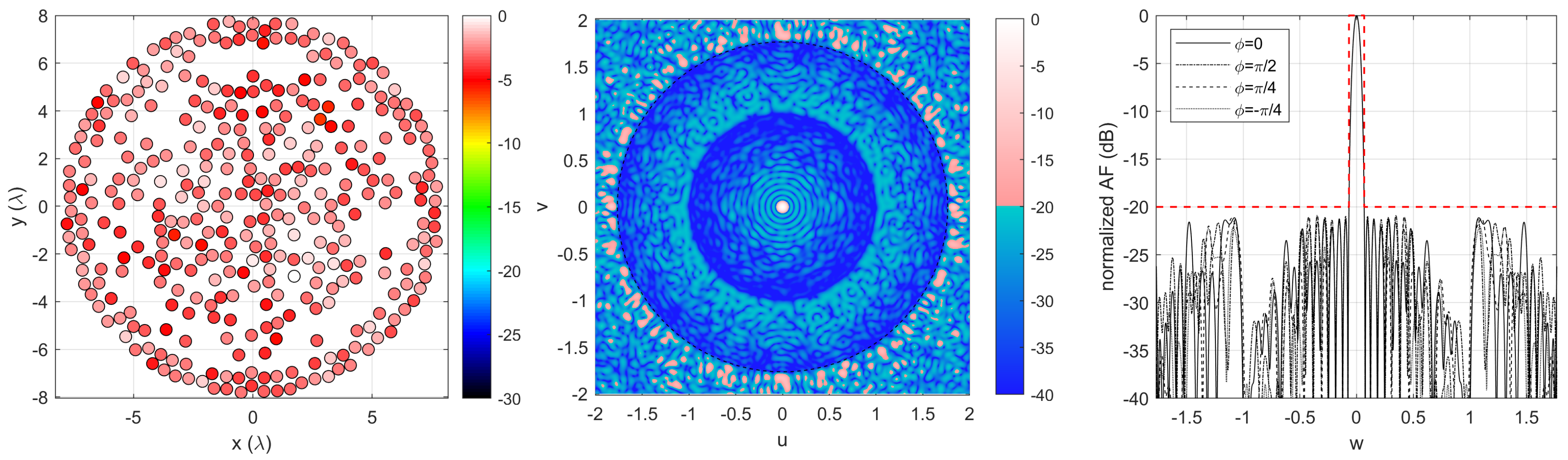
To show this improvement, we will consider the synthesis of a new sparse array, in which we add two further convex thresholds to the original IDEA. The first is , the second is .
The obtained layout is shown in
Figure 8; the achieved layout employs 346 elements and shows an excitation dynamic
dB, the minimum inter-element distance is
, and the computation time was about six hours; again, the beam-width and side-lobe level constraints are perfectly verified.
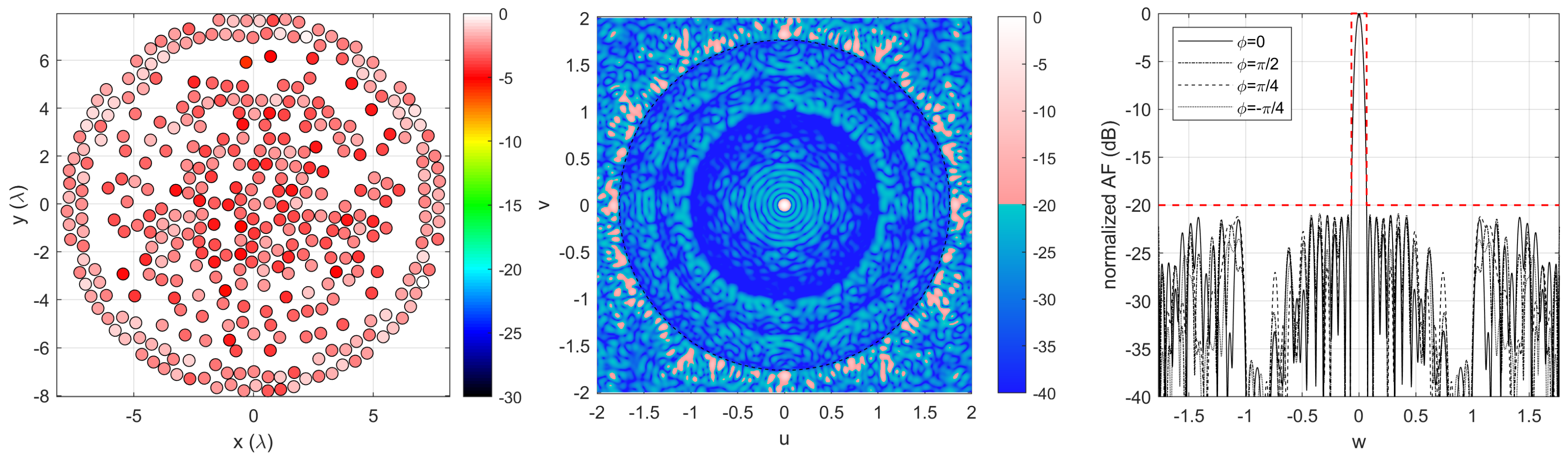
It is also possible to introduce further convex constraints using Equation (
22). We can consider the synthesis with the thresholds
,
and
.
The obtained layout is shown in
Figure 9; it employs 370 elements and shows an excitation dynamic
dB, the minimum inter-element distance is
, and the computation time was about four hours; even in this case, the beam-width and side-lobe level constraints are perfectly verified.
In
Figure 10, we can see the comparison of the scanning performances of all the sparse layouts synthesized up to this point. The use of the constraints on the dummy directivity allows to create arrays that have a much lower number of radiating elements than the fully populated array, but the directivity performance is very good.
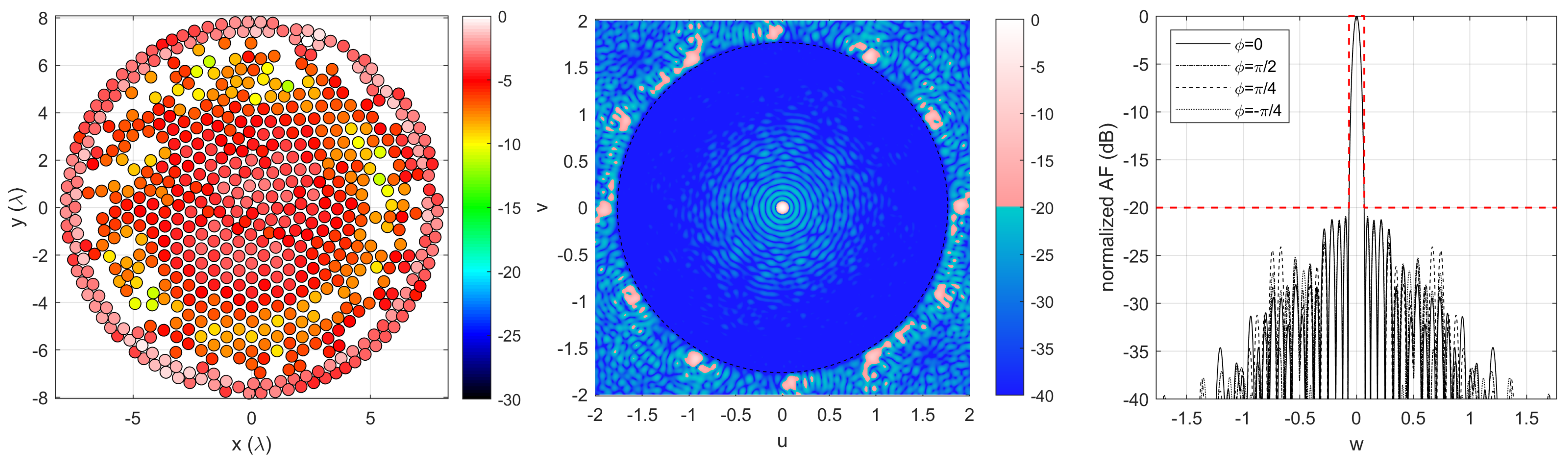
The previous layouts were aimed to reduce the number of radiating elements as much as possible. In other applications, the number of radiators may not be the key parameter in the design, but we could be interested in maximizing the directivity.
In this case, we could perform the synthesis maximizing the dummy directivity of the array
, instead of performing the minimizations of (
12) and (
17). Applying this approach to the same pattern specifications of the previous cases, it is possible to obtain an array of 622 elements (
Figure 11), which shows an excitation dynamic
dB and a minimum inter-element distance of
; the computation time was about sixteen hours. Even in this case, the beam-width and side-lobe level constraints are perfectly verified. The maximum directivity achieved is 29.3 dB, and such good performance is maintained for a very large scanning region since, for the most scanned angle, we have a directivity of 28.1 dB, about 2 dB better than the equispaced lattice of 665 elements (see
Figure 10).
It is worth underlining that all the synthesized sparse layouts have the same size (the same of the equispaced lattices), so there are no variations of the occupation of the arrays. The fact that the arrays share the same area occupation has been obtained by simply restricting the inflated set of sources of Equation (
16) to have a maximum distance from the origin equal to
(in this case the polygon of the inflation may not be a regular one).
Last but not least, it must be recalled that the use of the dummy directivity in Equation (
22) to improve the scanning performances of the sparse arrays does not necessarily require the use of IDEA, which can be substituted by any synthesis algorithm that can manage convex constraints.
5. Conclusions
In this contribution, the trade-off between the main parameters of planar antenna arrays has been reviewed and a technique to overcome directivity issues in sparse arrays has been proposed.
More in detail, the synthesis of pencil-beam planar arrays has been reviewed, and formulas relating the beam-width, the side-lobe level, the scanning range and the minimum number of radiators, have been provided.
After focusing on the sparse array synthesis, the problem of directivity reduction has been analyzed. It has been shown that, without directivity constraints, it is possible to have a huge reduction in the number of radiators. This reduction is paid with a fall of the array directivity, which can be even 5–6 dB lower than that of equispaced lattices.
It has also been shown that, using conventional optimization techniques, it is possible to synthesize array layouts that are able to radiate a pencil beam that has a good directivity in the broadside direction, with a limited number of antennas. Unfortunately, these layouts show a rapid fall of the performances when the beam is scanned far from broadside direction.
Finally, a novel, yet simple, dummy directivity formula that also allows optimizing the scanned beams has been introduced. This new formula is convex as the conventional directivity constraint, so the overall synthesis algorithm remains convex and efficient.
Using the proposed approach, we can synthesize arrays that have a minimum directivity reduction compared to an equispaced array but use a smaller number of radiators (a reduction of 30%–40%). It is also possible to exploit the aforementioned formula to synthesize arrays that exhibit an excellent directivity, significantly better than that of equispaced lattices employing a similar number of radiators.
As a future development, the discussed approach will be applied to the synthesis of shaped beams, and the synthesis of isophoric arrays.