Abstract
Position information is essential for an underwater vehicle that can affect the performance of many other applications. Vehicle motion during the two-way travel time (TWTT) using an acoustic positioning system can affect the localization accuracy of the estimators based on the traditional static model. A new time measurement model for moving vehicle localization is presented, which compensates for the vehicle motion. The Cramér–Rao lower bounds (CRLBs) of the proposed model are derived for two different cases, where the depth of the underwater vehicle is unknown or known. Then, closed-form solutions for the two cases using the proposed model are derived and the solutions are shown analytically to reach the CRLBs. Simulations collaborate the theoretical performance of the proposed estimators and the moving model significantly improves the localization accuracy in comparison with the static model.
1. Introduction
Accurate localization and navigation of autonomous underwater vehicle (AUV) is a critical focus area to a number of applications, such as underwater search and rescue, seafloor mapping, shallow water mine countermeasures, and oceanographic surveys [1,2,3,4,5,6,7,8,9,10]. Accurate localization is vital to ensure the accuracy of navigation and other applications.
The techniques of AUV localization usually can be classified to two categories, i.e., inertial/dead reckoning system and the acoustic transponders and modem system. The inertial/dead reckoning system uses inertial measurement unit (IMU) or Doppler Velocity Logs (DVL) to estimate the vehicle position [11]. However, all of the methods in this category have position error growth that is unbounded. Since they have accumulated error, their localization error will continue to increase if it is not corrected by other techniques for a long time. Therefore, location resets are necessary during some long-duration mission scenarios and these position resets of AUV are typically obtained by Global Positioning System (GPS) updates [12]. However, due to the strong attenuation of electromagnetic waves by water, GPS signal is not practically feasible except for distances of a few meters. AUV has to transit to the surface to access GPS satellites. This operation is always time consuming especially for deep-ocean scenarios. Another technique is the use of the acoustic transponders and modem system such as long baseline (LBL) system [1] and moving LBL system [13]. In this system, AUV is designed to measure the time of flight (TOF) of signals from acoustic beacons or transponders at known positions to perform localization. These methods based on the acoustic positioning system can provide bounded, long-term localization precision.
Many methods have been proposed in this area to find the position of an AUV using the acoustic positioning system [14,15,16,17,18,19,20,21,22]. The simultaneous localization and mapping (SLAM) methods proposed in [15,16] simultaneously estimate the position of an AUV and the positions of stationary beacons using range-only data. In their experiments, an AUV would send out an interrogation signal, and the beacons would reply in a predefined sequence. The two-way travel time (TWTT) of the acoustic signals is usually used to determine the ranges. When enough measurements and samples are obtained during the trajectory of the moving AUV, their proposed navigation filters will estimate all the unknown positions. However, they assume the value of AUV speed is small and the vehicle motion during interrogation and reception is ignored to simplify their algorithm. Actually, the travel times from AUV to beacons and back are not the same. Some different AUV localization systems using one-way travel time (OWTT) were proposed in [17,18,19] to avoid the problem of vehicle motion in TWTT. Refenence [17] used a ship (precisely localized via GPS) and transponders to localize the AUV. In this system, the AUV only sends out an interrogation signal and the ship receives all the signals: the direct propagation from AUV and the reflections by all the transponders. The time difference of arrivals between the reflection paths and the direct path along with depth measurements are used to locate the AUV. In [18,19], the acoustic data packets containing the state information are broadcast from a single, moving reference beacon and can be received by multiple AUVs within an acoustic range. The synchronous clocks enable range measurements based on OWTT measurements between the beacon and the AUVs. Every AUV can estimate its position when enough range measurements are obtained from the moving beacon.
The aforementioned localization methods mainly focus on Kalman filter (KF), which is a widely used recursive, self-correcting model-based estimator. The KF requires range measurements at different times, and an initial transient period is needed before it produces a good source location estimate [23]. In addition, an initial guess closed to the true value is also required to initialize the filter. Another kind of localization methods are nonlinear estimation, such as maximum likelihood estimation (MLE) [24] and the closed-form solutions [20,25,26] based on least squares (LS) or weighted LS. However, often only the measurement error is considered in causing the errors on the location estimate [27,28]. The extension of localization algorithms to account for inaccurate sensor positions [20,29,30] or spatiotemporal variation of sound speed [31,32] has also been investigated. Nevertheless, the AUV motion effect is ignored in most existing research to simplify their methods. [20] proposed a closed-form solution using the LS method for the TWTT measurements by considering the calibration error of deployed beacons, where the vehicle motion is still ignored. The vehicle motion is compensated in [21] to obtain a better solution by developing a Bayesian inference algorithm. [33] determines the vehicle position using TWTT together with the information of the angle measurements and orientation (pitch angle and yaw angle) of AUV. Feng [25] accounted for the AUV motion in the method and proposed an approximate solution by solving the circular equations constructed from the nonlinear equations of the time measurements. Although [21,25,33] improve the localization performance by including the AUV motion effect in their methods, their works lack analysis of the optimality property.
In AUV localization, the depth information can be normally measured by the pressure sensor mounted on AUV [5]. Only two position coordinate values need to be estimated by the localization system in a 3D scenario if the depth measurement is accurately obtained. However, when the pressure sensor is broken or there is a large error with the depth measurement, the known depth localization will be invalid or inaccurate. Therefore, the unknown depth localization shall be a complement of the known depth localization, and will also increase the robustness of the localization system. Thus, we will focus on these two localization cases.
This paper will propose a time measurement moving model for range-only AUV localization which compensates for vehicle motion during the TWTT interval. The Cramér–Rao lower bound (CRLB) is derived for the proposed moving model in two different cases: unknown depth localization and known depth localization. We also prove that the AUV localization accuracy can be improved by measuring the AUV depth. Then, an accurate closed-form solution is derived for the proposed model in these two cases. The closed-form solution does not require initial solution guess, and so it is computationally attractive. Finally, results from the Monte Carlo (MC) simulation show that applying the proposed moving model significantly improves the localization accuracy in comparison with the static model. More importantly, the proposed closed-form solution can reach the accuracy set by the CRLB. The main contributions of this work are highlighted as follows:
- a new time delay measurement model that accounts for the AUV motion during the TWTT is proposed in the paper. it is unbiased and accurate for the moving AUV localization.
- the CRLBs are derived using the proposed model for the two cases in range-only AUV localization. it is proved that the AUV localization accuracy can be improved by measuring the AUV depth.
- a set of closed-form solutions are constructed using time delay measurement for the two cases in range-only AUV localization. The proposed solutions are computationally efficient and can achieve the CRLB analytically. Simulations validate the performance of the proposed solutions.
The paper is organized as follows: Section 2 provides a new time measurement moving model as well as the traditional static model for a moving AUV localization scenario. Section 3 derives the CRLB for the proposed moving model in two different cases and compares the CRLBs theoretically. Section 4 presents the proposed closed-form solution and compares analytically the proposed estimator with the CRLB. Section 5 shows the simulation results, and Section 6 provides the conclusions.
The following notation will be adopted throughout the paper. Bold face uppercase letters represent matrices and lowercase bold letters represent vectors. is the true value and is its noisy version with additive noise . The symbols and represent the identity matrix and zero matrix with appropriate dimension. For a given matrix , , and denote the positive eigenvalues, the trace, and the rank of . For a given vector , or is the norm. is the mathematical expectation.
2. Models for AUV Localization
2.1. Moving Model
We first consider a moving AUV localization system with N sensors (transponders and/or beacons) fixed at , as shown in Figure 1. The moving AUV with known velocity sends out an interrogation signal at position and will receive all the replied signals from the sensors. We suppose the signals received by AUV do not interfere with each other, and the processing delay of every sensor is assumed to be zero. The true signal travel distance from the moving AUV to the ith sensor and finally back to the moving AUV can be obtained as
where c is acoustic signal propagation speed. The model describes the relationship between the true signal travel distance and the true AUV position value. However, when the time delay is estimated from the received signals, there will be noise in the time delay measurement [34]. Therefore, the two-way travel time (TWTT) measurement is modeled as
where is the time measurement noise that is assumed to be zero-mean Gaussian. Finally, the moving measurement model in vector form is expressed as
where and . The noise vector is modeled as a zero-mean Gaussian with covariance matrix .
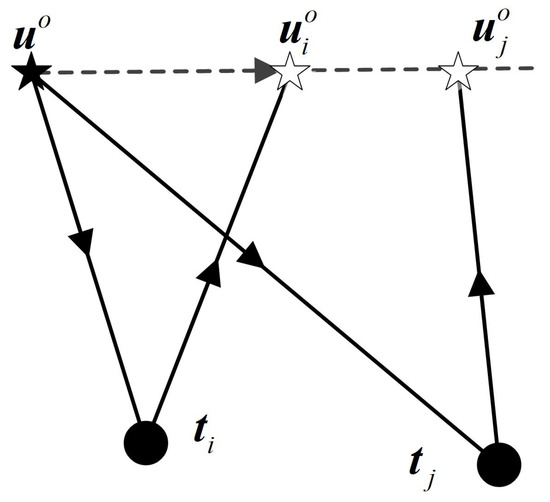
Figure 1.
Localization scenario for moving AUV.
This paper is to find the AUV position from the TWTT measurement , the known sensor positions , the signal propagation speed c, and the noise covariance matrix . According to whether AUV depth is known or not, we will focus on two different cases: AUV localization with unknown depth and AUV localization with known depth.
2.2. AUV Motion Effect and Static Model
The original new model in Equation (1) is recursive and we would like to gain some insights about the effect of AUV motion after transformation of the recursive model. In Equation (1), after moving to the left, squaring both sides and expanding the Euclidean norms give
where . Substituting it in (4) gives
Because is positive and cannot be zero, cancelling on both sides and solving for yield
Defining as the angle between and , we have
We can see from (8) that, if the AUV motion effect during the interrogation is ignored and can be set to zero, will be approximated by
which is also known as the two-way time of arrival (TW-TOA) measurement [35,36,37]. It is simple and accurate for static AUV localization. Actually, the moving model (1) is a natural generalization of the static model (9) for moving AUV localization, which compensates the AUV motion effect. When the static model is used for moving AUV localization, the error in the two-way distance is
We can see that the error caused by the AUV motion is nonlinear with respect to the speed normalized by the propagation speed, with leading order one. It has a sinusoidal relationship with the angle between the AUV-movement and AUV-sensor directions. Figure 2 gives an example of the model error related to and where m, m and m/s. The model error of the two-way distance becomes significant when increases.
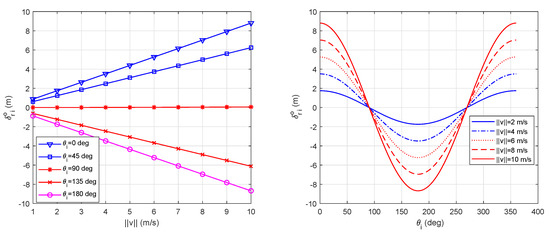
Figure 2.
The effect of and on .
Therefore, for moving AUV localization, the static model ignores the AUV motion effect and the position estimate based on (9) shall be inaccurate. In other words, the static model will introduce estimation error in localization.
We illustrate this aspect visually in Figure 3 where the blue square symbol represents the true position of the moving AUV in the instant of interrogation. The use of static model to locate a moving AUV will lead to a biased estimate, and the optimal position of the likelihood function is away from the true value. In contrast, the true position value is on the peak of the likelihood surface using moving model. Thus, the corresponding ML estimator is unbiased. We would like to show the loss of localization performance when using the static model compared with the moving model.
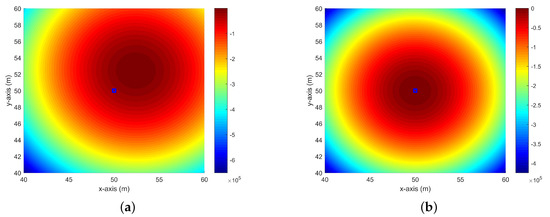
Figure 3.
Log-likelihood surface of moving AUV localization. The blue square symbol represents the true position of AUV in the instant of interrogation. The true position is m and the speed is m. This scenario has four sensors located at m, m, m and . (a) likelihood under the static model: biased estimator; (b) likelihood surface under the moving model: unbiased estimator.
3. CRLB
This section will evaluate the CRLB for moving AUV localization problem. The CRLB is the lowest bound of the covariance matrix of an unbiased estimate. Roughly speaking, the CRLB defines the best estimation accuracy that an unbiased estimator can achieve in terms of mean square error. The CRLB is always used as a benchmark for comparison of the localization methods although some of them may not be unbiased. Because the AUV may have the information of its depth, the CRLB focuses on the two cases: AUV localization with unknown depth and AUV localization with known depth.
3.1. AUV Localization with Unknown Depth
Assume that the time measurement vector satisfies the measurement model in (3) and define the CRLB matrix of an unbiased estimate as . Based on the equations in [23,38], we have
where is the Fisher information matrix and it is
is concretely expressed as
where is the partial derivative of with respect to the unknown vector . This term is given by
where
3.2. AUV Localization with Known Depth
If the depth of AUV is known, the z-axis coordinate value is a known parameter. Supposing that , the CRLB of using model (3) has the similar expression as (11) by replacing with . Hence, the related vector that represents the partial derivative of with respect to the unknown vector is
where , and . We can obtain by solving (17), which is
3.3. Comparisons of the CRLBs of Proposed Cases
We claim that
when the covariance matrix of the measurement noise in the two cases is the same. The detailed derivation is shown in Appendix A. This implies the CRLB of AUV localization with known depth is less than that of unknown depth localization. In other words, the AUV localization accuracy can be improved by measuring the AUV depth.
The following simulation compares the CRLBs of the proposed two cases using the moving AUV localization scenario in [21], with one additional sensor. The positions of sensors are shown in Table 1 in Section 5. The AUV moving tracks are shown as blue lines in Figure 4a. The AUV starts at m, moves from left to right with m/s, and then turns back on a opposite direction with the same speed. The AUV performs this operation until it covers the preset region. The localization cycle period is eight seconds. In each cycle, the AUV first interrogates the sensors and sends out a signal, and the sensors would reply a predefined sequence once they receive the signal. The AUV estimates its position every cycle. The acoustic signal speed m/s and the covariance matrix of time measurement noise is . The standard deviation s.

Table 1.
The positions of sensors.
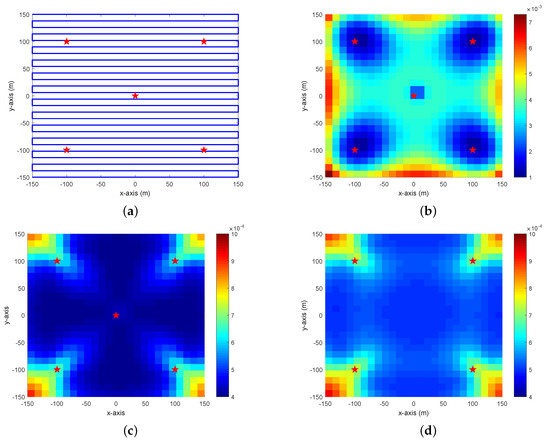
Figure 4.
AUV localization scenario and the comparisons of the CRLBs in different cases. The red star symbol represents the sensor position and pixel colors indicate the values of CRLB at the corresponding positions. (a) AUV moving tracks and the sensor positions. The blue lines are the moving tracks and there are five sensors in total; (b) CRLB of unknown depth localization using five sensors; (c) CRLB of known depth localization using five sensors; (d) CRLB of known depth localization using four sensors.
The CRLB establishes the theoretical lower bound for the variance of the position error. Figure 4b–c show the comparisons of CRLBs in different cases. The simulation settings in Figure 4b,c are the same except if the AUV depth is unknown. Figure 4b is the CRLB for AUV localization with unknown depth. The CRLB of the position error is between and and the large values occur at the beginning and end of each row in the tracks. The CRLB values for known depth localization shown in Figure 4c are generally less than the CRLB values in the corresponding positions of Figure 4b. Furthermore, the large values only occur in the corners of the region. This result also validates the previous claim that the AUV localization accuracy can be improved by measuring the AUV depth. The known depth localization in Figure 4d only uses four co-plane sensors which usually become invalid in unknown depth localization. However, the CRLB is also less than the result in Figure 4b.
4. Closed-Form Solution
The closed-form solution for localization using a static model has been derived in [26,39]. This section will propose a close-form solution using the accurate model (3) for moving AUV localization. We first find an initial solution using the static model, and then we use the moving model to refine the initial estimate. The proposed solution has three stages. The first and second stages aim to provide a position estimation from the traditional static model as accurate as possible so that the refinement in the third stage can work well. the first stage introduces a nuisance variable to transform the nonlinear static measurement model to a pseudo linear equation. The second stage is to estimate the amount of correction to refine the estimate from the first stage solution. Finally, in the third stage, the moving model is to used to refine the solution by using Taylor-series expansions [23,40]. The closed-form solutions are proposed in this section for two cases: moving AUV localization with unknown depth and moving AUV localization with known depth.
4.1. AUV Localization with Unknown Depth
In this case, we shall estimate from (2) using , , and . The proposed closed-form solution has three stages.
4.1.1. First Stage
In this stage, a nuisance variable is introduced to transform the nonlinear static measurement model to a pseudo linear equation that can be solved directly by weighted least squares (WLS). We start with the static model in (9). Squaring on both sides yields the nonlinear TOA equation
where and . Substituting and rearranging yield
where the second-order error terms have been ignored. Define and Equation (21) can be written in matrix form and finally we get the linear system of equations
where
The WLS solution to (22) is
where is the weighting matrix.
4.1.2. Second Stage
Because the first stage neglects the relevance between and , this stage improves the accuracy of position estimate by computing the amounts of corrections. Supposing that , and, based on , we have
where is considered as a unknown vector and it can be used to correct the solution in the first stage. We can construct a system of equations
where
The left-side is pretended as a random error vector and on the right side is the unknown. The WLS solution of (25) is
where is the weighting matrix. Finally, the estimate of this stage is
4.1.3. Third Stage
In this stage, we will refine the estimate using the moving model (1). Squaring (1) after putting to the left side,
Suppose and we have the first-order Taylor-series expansion
Then, substituting , and (29) in (28), and neglecting the high-order noise terms yield
where is unknown. This is another set of linear equations with respect to and the matrix form is
where the i-th row vector of is , the i-th element of is , and is a diagonal matrix. The i-th diagonal element is .
The WLS solution of (31) is
where the weighting matrix is . By refining the estimate in the second stage, the solution in this stage is finally updated as
4.2. AUV Localization with Known Depth
In this case, we shall estimate from the moving measurement model (1) using , , and .
4.2.1. First Stage
When the depth is known ( is known), (20) can be transformed as
where is a nonlinear term, and it is supposed to be independent unknown variable with in the first step. Substituting into (34) and rearranging yield
where . Define , and Equation (35) can be written in a matrix form as
where and is
The WLS solution is
where is the weighting matrix. Under small noise conditions, we have .
4.2.2. Second Stage
The second stage will estimate the amounts of corrections to the estimate from the first stage solution . Supposing and , we have
where is the unknown to be estimated. (39) can be written in a matrix form as
where
is pretended as a noise vector and . The unknown vector can be solved using an WLS method
where is the weighting matrix. Finally, the estimate of this stage is
4.2.3. Third Stage
Suppose , and we have the first-order Taylor-series expansion
4.3. Performance Analysis
We shall estimate the theoretical covariance matrix of the proposed solution, and compare it with the CRLB. We first consider the known depth localization. When the noise is small, both the bias of the final estimate and the bias of the third step estimate are negligible, and so the covariance of is
This implies that the covariance of the final estimate is equal to the covariance matrix of the third step estimate . After subtracting both sides of (32) by the value and applying (31) yield the estimation error
When the noise is small so that the noise in the related matrices can be ignored, it can be shown that
Substitute below (32), and can be expressed as
Note that (52) has the same form as the CRLB of (11). If we substitute the true values and for the estimated ones and in and , we have
and the ith column of is
After some straightforward matrix manipulation, we have
As a result, based on (11) and (52) and for sufficient small noise, we have
and the proposed closed-form solution can reach the CRLB.
The same analysis can also obtained for the AUV localization case with known depth. The estimated theoretical covariance matrix is
if the noise effect in or is insignificant. Therefore, the proposed solution can attain the corresponding CRLB for sufficient small noise.
5. Simulation
In this section, the numerical simulations are carried out to examine the performance of the proposed closed-form solution for the moving model. the existing Feng’s method in [25] for moving AUV localization and the two-step WLS method in [26] for solving the static model are included for comparison. In addition, the first stage solution and second stage solution are evaluated to show the performance improvement in different stages. the localization accuracy is examined in terms of mean square error (MSE) and bias,
where denotes a position estimate of a given method at ensemble l and is the ensemble runs.
The sensor positions shown in Table 1 are based on the moving AUV localization scenario in [21], with one additional sensor. The acoustic signal speed m/s and the covariance matrix of time measurement noise is . is the standard deviation of . For simplicity, we define range measurement standard deviation m.
5.1. AUV Localization with Unknown Depth
Figure 5 compares the MSE of the proposed solution for a moving model and the two-step WLS solution for a static model. The localization scenario and noise setting are the same as in Figure 4b, and Figure 4b is also the corresponding CRLB of this scenario. Figure 5a shows the MSE using the static model. The MSE values of the static model are large and far away from the CRLB. In contrast, the proposed solution shown in Figure 5b can improve the estimation accuracy and reach the CRLB.
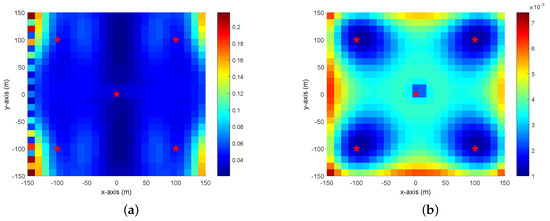
Figure 5.
Comparisons of the MSE in unknown depth localization. The red star symbol represents the sensor and pixel colors indicate the localization MSE at the corresponding position. The scenario is the same as that in Figure 4b where the pixel colors represent the values of CRLB. (a) MSE using the static model; (b) MSE using the moving model.
Figure 6a is the result for a moving AUV located at m with velocity m/s. The sensor positions correspond to those in Figure 4b and there are five sensors. The value of measurement noise varies from dB to 0 dB. The localization performance of the static model is generally worse for a moving AUV. There is a definite performance improvement in the three stages and the performance of second stage solution is almost the same as that of the two-step WLS. the bias of the proposed closed-form method for moving model is near zero, while the two-step WLS solution of the static model has a steady bias. Although the bias of Feng’s method is also close to zero, the corresponding MSE can not reach the CRLB and there is a steady gap between them that is about dB. As expected, the MSE values of static model are far away from CRLB, especially when the noise is small. The MSE of the proposed method can attain the CRLB and is lower than Feng’s method by dB. For example, when m, the MSE of the proposed method is less than that of Feng’s method by m.
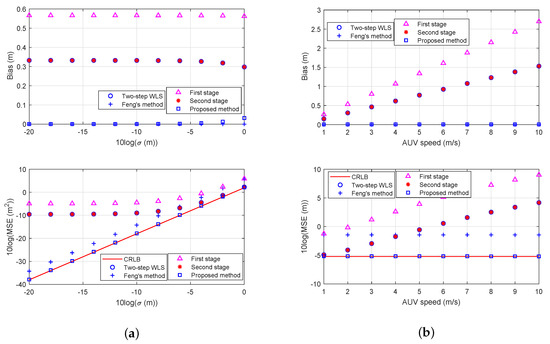
Figure 6.
Comparisons of the MSE and bias in unknown depth localization. (a) comparisons of the performance for unknown depth localization with different noise power; (b) comparisons of the performance for unknown depth localization with different AUV speed.
Figure 6b shows the result of the proposed method for moving AUV localization with different values of speed. The same localization geometry is utilized as in Figure 6a, except that the AUV speed is normalized to be a unit vector and then is multiplied by a scale value, and the standard deviation s ( m). Both the bias and the MSE of the static model increase as the AUV speed increases. On the contrary, the AUV speed has less effect on the performance of the proposed solution and Feng’s method. However, the observation validates again that the proposed method is better than Feng’s method in terms of MSE. in general, the proposed method using the moving model outperforms the other two methods.
5.2. AUV Localization with Known Depth
Figure 7 shows the result for known depth localization. The localization scenario and noise setting are the same as in Figure 4d which also shows the CRLB of this case. It is evident that the proposed method in Figure 7b is able to attain the accuracy set by the CRLB. However, the MSE of the two-step WLS solution using the static model is not satisfying.
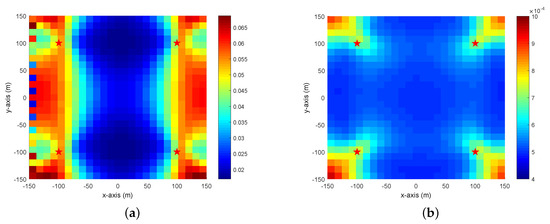
Figure 7.
Comparisons of the MSE in unknown depth localization. The red star symbol represents the sensor and pixel colors indicate the localization MSE at the corresponding position. The scenario is the same as that in Figure 4d where the pixel colors represent the values of CRLB. (a) MSE using a static model; (b) MSE using a moving model.
Figure 8a,b are for the known depth localization as in Figure 4d and there are four sensors. The AUV is located at m with velocity m/s. Figure 8a shows the effect of noise to bias and MSE. The proposed solution performs better than the two-step WLS using the static model and it can reach the CRLB when the measurement noise is small. The performance improvement in MSE is about dB when using the proposed method compared with Feng’s method. Figure 8b shows the performance of the mentioned methods with different values of speed. The observations are consistent with those in Figure 8b. The performance improvement of the proposed method using the moving model is significant.
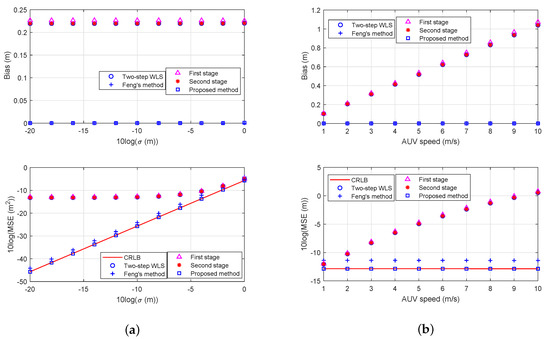
Figure 8.
Comparisons of the MSE and bias in known depth localization. (a) Comparisons of the performance for known depth localization with different noise power. (b) Comparisons of the performance for known depth localization with different AUV speed.
5.3. AUV Localization Performance When Error Occurring in Depth
This subsection investigates the effect of depth error on AUV localization. The AUV depth is assumed to be exactly known in the known depth localization. However, there is an error with the depth measurement in the real situation besides the TWTT measurement noise. In this subsection, the available depth measurement is contaminated by noise and it is modeled as . is zero mean Gaussian and is the standard deviation that changes from 0.2 m to 2 m. The other settings are the same as Figure 6 except .
Figure 9 demonstrates the performance of the proposed methods when depth error increases where “UD” denotes “Unknown Depth” and “KD” denotes “Known Depth”. Apparently, the observation shows that the depth error cannot affect the performance of unknown depth localization. Figure 9a shows that depth error effect is not significant in the known depth localization when TWTT measurement noise is relatively large ( s). The proposed known depth localization can still reach the CRLB. However, the depth error effect becomes significant in Figure 9b when TWTT measurement noise is relatively small ( s). Therefore, the known depth localization methods are sensitive to depth error when the TWTT measurement noise is small.
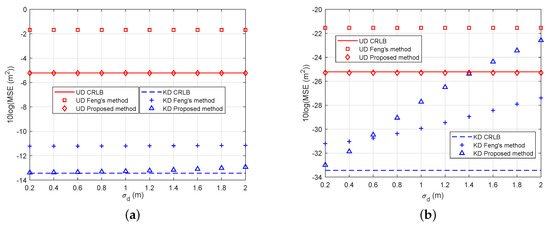
Figure 9.
The effect of depth error on localization. “UD” denotes “Unknown Depth” and “KD” denotes “Known Depth”. (a) comparisons of the performance with different depth error where sets as 300 s; (b) comparisons of the performance with different depth error where sets as 30 s.
5.4. AUV Localization Performance When Error Occurring in Velocity
Similar to the depth measurement, there is an error with the AUV velocity in the real situation besides the TWTT measurement noise. This subsection investigates the effect of AUV velocity error on the localization. The available velocity is instead of and is assumed to be zero-mean Gaussian. In the simulation, the covariance of is set as and is the standard deviation that changes from 0.1 m/s to 1 m/s. The other settings are the same as Figure 6 except .
Figure 10 demonstrates the performance of the proposed methods when velocity error increases. The performance is affected by the velocity error. Figure 10a shows that velocity error effect is not significant when TWTT measurement noise is relatively large ( s). The proposed methods can still reach the CRLB when m/s. However, the velocity error effect becomes significant in Figure 10b when TWTT measurement noise is relatively small ( s). Therefore, the localization methods are sensitive to velocity error when the TWTT measurement noise is small.
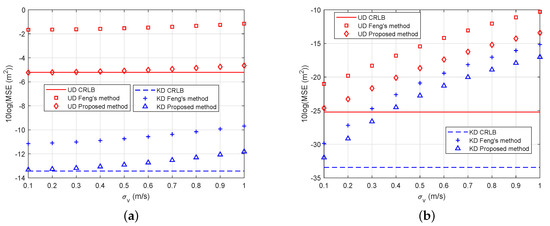
Figure 10.
The effect of AUV velocity error on localization. “UD” denotes “Unknown Depth” and “KD” denotes “Known Depth”. (a) comparisons of the performance with different velocity error where sets as 300 s; (b) comparisons of the performance with different velocity error where sets as 30 s.
5.5. AUV Localization Performance with Randomly Generated Scenarios
It is widely known that the localization performance depends greatly on the AUV-sensor geometry, such as sensor positions, number of sensors, AUV positions, AUV moving direction, and so on. These factors are fixed in the above experiments. Therefore, in this subsection, the localization performance is examined using the randomly generated scenarios. The sensors and AUV are placed randomly at uniformly distributed positions inside a 3D cube ( m m m). The AUV moving direction is generated randomly in each direction and AUV speed is generated randomly from the interval m/s. We randomly generate 200 scenarios each with different geometries, and the results are the average over them. The number of ensemble runs is 5000 for each given geometry realization. There is no depth error or velocity error and TWTT noise s.
Figure 11 and Figure 12 show the performance with randomly generated scenarios using different number of sensors. The introduction of the auxiliary variable (or ) in the first stage requires a minimum of four (or three) TWTT measurements for the unknown (or known) depth localization. However, the minimum required measurements are not enough to ensure the localization performance in the randomly generated scenarios because an improper geometry with less sensors can appear. This phenomenon can be alleviated dramatically if we increase the number of sensors by two (or one) for unknown (or known) depth localization. The proposed solutions can reach the CRLBs when there are enough sensors. In addition, it should be noted that extensive simulations show that the performance of the second stage solution is almost the same as that of the two-step WLS. Hence, the proposed first and second stage solution can be replaced by the two-step WLS in most cases.
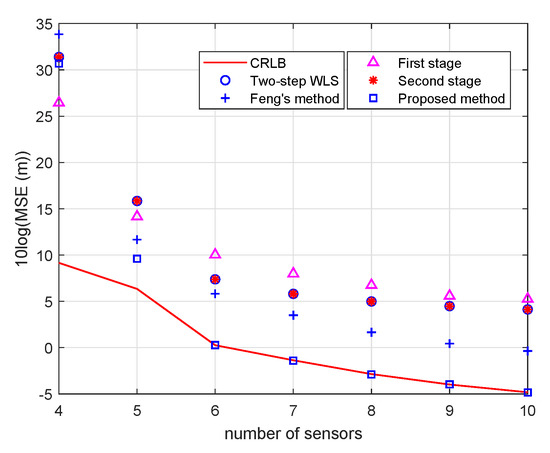
Figure 11.
Unknown depth localization performance with randomly generated scenarios.
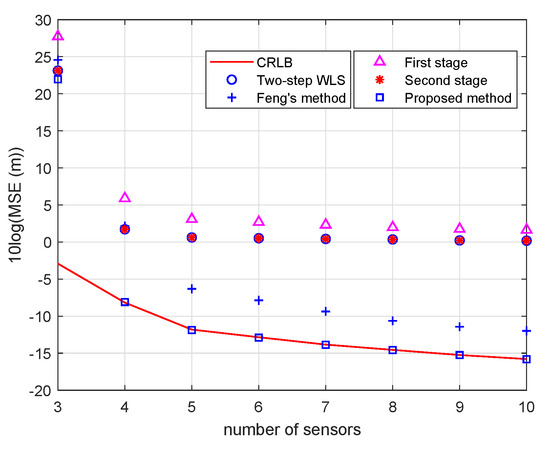
Figure 12.
Known depth localization performance with randomly generated scenarios.
6. Conclusions
In this paper, we studied the accurate closed-form solution for moving AUV localization with range-only data. First, a new time measurement model for moving AUV localization was presented, which compensates for vehicle motion. Then, the CRLB of the proposed model was derived in two different cases. We also proved that accurately measuring the AUV depth can improve the AUV localization accuracy. Next, we derived a closed-form solution for the proposed model in two cases. Moreover, the proposed solution was shown analytically to reach the CRLB. Finally simulations collaborate the theoretical performance of the proposed estimators and the moving model significantly improves the localization accuracy in comparison with the static model.
The AUV localization accuracy can be affected by the accuracy of parameters in the measurement model, including the TWTT measurement noise, the depth error, the AUV velocity error, the sensor position error, and the sound speed error. When the TWTT measurement noise is significant compared with the other errors, the proposed solutions are accurate enough to reach the CRLB. However, when the other errors are comparable with the TWTT measurement noise, the errors that are significant should also be accounted for in the method to improve the localization accuracy. Some errors, such as the sensor position error and the sound speed error, have been studied by the previous research [20,29,30,31,32], while the other errors, such as depth error and AUV velocity error, should be studied further in the future research.
Author Contributions
Conceptualization, H.W. and X.S.; Formal analysis, H.W.; Methodology, T.J.; Software, T.J.; Validation, Y.Y.; Writing original draft, T.J.; Writing—review and editing, T.J., H.W., X.S., and Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported in part by the National Key Research and Development Program of China under Grant 2016YFC1400200, the National Natural Science Foundation of China under Grants 61571365 and 61671386 and the Innovation Foundation for Doctor Dissertation of Northwestern Polytechnical University under Grant CX201939.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| TWTT | Two-Way Travel Time |
| OWTT | One-Way Travel Time |
| AUV | Autonomous Underwater Vehicle |
| LBL | Long Baseline |
| CRLB | Cramér–Rao Lower Bounds |
| MSE | Mean Square Error |
Appendix A
Based on the expressions in (13), can be expressed as
Then, substituting this in (12), is equal to
Using the block matrix inversion formula, we have the CRLB of
where is a vector and Z is a scalar. They are expressed as
Therefore,
It is clear that and , which means . The next part is the details. It can be shown that
The positive-definite matrices and have invertible lower triangular matrices, such that and . Defining a vector and a matrix , Z becomes
It can be shown that
where denotes all the positive eigenvalues of a matrix. Note that all the eigenvalues of are greater than or equal to 0. Therefore, there are only two nonzero eigenvalues that are equal to and let be an eigendecomposition of the symmetric real matrix , where . We have
where . Clearly, is a positive semidefinite matrix and, as a result, . In addition, , and this is because, if , is a singular matrix and does not exist. References
References
- Chen, L.; Wang, S.; McDonald-Maier, K.; Hu, H. Towards autonomous localization and mapping of AUVs: A survey. Int. J. Intell. Unmanned Syst. 2013, 1, 97–120. [Google Scholar] [CrossRef]
- Fang, J.; He, Z. Robust modified newton algorithms using tikhonov regularization for TDOA source localization. Circuits Syst. Signal Process. 2019, 38, 5342–5359. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D.; Liu, R.; Yin, J.; Wu, Y. Structural total least squares algorithm for locating multiple disjoint sources based on AOA/TOA/FOA in the presence of system error. Front. Inf. Technol. Electron. Eng. 2018, 19, 917–936. [Google Scholar] [CrossRef]
- Yan, Y.; Shen, X.; Hua, F.; Zhong, X. On the Semidefinite Programming Algorithm for Energy-Based Acoustic Source Localization in Sensor Networks. IEEE Sens. J. 2018, 18, 8835–8846. [Google Scholar] [CrossRef]
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV navigation and localization: A review. IEEE J. Ocean. Eng. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Jia, T.; Wang, H.; Shen, X.; Liu, X.; Jing, H. Bearing-only multiple sources localization and the spatial spectrum. In Proceedings of the IEEE Oceans Conference, Aberdeen, UK, 19–22 June 2017; pp. 1–5. [Google Scholar]
- Gao, J.; Shen, X.; Mei, H.; Jia, T.; Wang, L.; Wang, H. A range-angle based self-localization scheme for MUANS. In Proceedings of the IEEE Oceans Conference, Aberdeen, UK, 19–22 June 2017; pp. 1–4. [Google Scholar]
- Gao, J.; Shen, X.; Mei, H.; Zhang, Z. Dynamic Reference Selection-Based Self-Localization Algorithm for Drifted Underwater Acoustic Networks. Sensors 2019, 19, 3920. [Google Scholar] [CrossRef]
- Zhong, X.; Premkumar, A.; Wang, H. Multiple wideband acoustic source tracking in 3-D space using a distributed acoustic vector sensor array. IEEE Sens. J. 2014, 14, 2502–2513. [Google Scholar] [CrossRef]
- Renner, C. Packet-based ranging with a low-power, low-cost acoustic modem for micro AUVs. In Proceedings of the International ITG Conference on Systems, Communications, and Coding, Hamburg, Germany, 6–9 February 2017; pp. 1–6. [Google Scholar]
- Sabet, M.T.; Sarhadi, P.; Zarini, M. Extended and Unscented Kalman filters for parameter estimation of an autonomous underwater vehicle. Ocean Eng. 2014, 91, 329–339. [Google Scholar] [CrossRef]
- Donovan, G.T. Position error correction for an autonomous underwater vehicle inertial navigation system (INS) using a particle filter. IEEE J. Ocean. Eng. 2012, 37, 431–445. [Google Scholar] [CrossRef]
- Yan, W.; Fang, X.; Li, J. Formation optimization for AUV localization with range-dependent measurements noise. IEEE Commun. Lett. 2014, 18, 1579–1582. [Google Scholar] [CrossRef]
- Jia, T.; Shen, X.; Wang, H. Multistatic Sonar Localization With a Transmitter. IEEE Access 2019, 7, 111192–111203. [Google Scholar] [CrossRef]
- Newman, P.; Leonard, J. Pure range-only sub-sea SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; Volume 2, pp. 1921–1926. [Google Scholar]
- Olson, E.; Leonard, J.J.; Teller, S. Robust range-only beacon localization. IEEE J. Ocean. Eng. 2006, 31, 949–958. [Google Scholar] [CrossRef]
- Kussat, N.H.; Chadwell, C.D.; Zimmerman, R. Absolute positioning of an autonomous underwater vehicle using GPS and acoustic measurements. IEEE J. Ocean. Eng. 2005, 30, 153–164. [Google Scholar] [CrossRef]
- Webster, S.E.; Eustice, R.M.; Singh, H.; Whitcomb, L.L. Advances in single-beacon one-way-travel-time acoustic navigation for underwater vehicles. Int. J. Robot. Res. 2012, 31, 935–950. [Google Scholar] [CrossRef]
- Webster, S.E.; Walls, J.M.; Whitcomb, L.L.; Eustice, R.M. Decentralized extended information filter for single-beacon cooperative acoustic navigation: Theory and experiments. IEEE Trans. Robot. 2013, 29, 957–974. [Google Scholar] [CrossRef]
- Zhang, J.; Han, Y.; Zheng, C.; Sun, D. Underwater target localization using long baseline positioning system. Appl. Acoust. 2016, 111, 129–134. [Google Scholar] [CrossRef]
- Li, Z.; Dosso, S.E.; Sun, D. Motion-compensated acoustic localization for underwater vehicles. IEEE J. Ocean. Eng. 2016, 41, 840–851. [Google Scholar] [CrossRef]
- Jia, T.; Ho, K.C.; Wang, H.; Shen, X. Effect of Sensor Motion on Time Delay and Doppler Shift Localization: Analysis and Solution. IEEE Trans. Signal Process. 2019, 67, 5881–5895. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; PTR Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Chan, Y.T.; Hang, H.Y.C.; Ching, P.C. Exact and approximate maximum likelihood localization algorithms. IEEE Trans. Veh. Technol. 2006, 55, 10–16. [Google Scholar] [CrossRef]
- Feng, J.; Ding, S.; Hui, J. A solution of locating a moving object using long-base line acoustic system. Acta Acust. 1996, 21, 832–837. [Google Scholar]
- Chan, Y.T.; Ho, K.C. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Yang, L.; Yang, L.; Ho, K.C. Moving target localization in multistatic sonar by differential delays and Doppler shifts. IEEE Signal Process. Lett. 2016, 23, 1160–1164. [Google Scholar] [CrossRef]
- Beck, A.; Stoica, P.; Li, J. Exact and approximate solutions of source localization problems. IEEE Trans. Signal Process. 2008, 56, 1770–1778. [Google Scholar] [CrossRef]
- Ho, K.C.; Lu, X.; Kovavisaruch, L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution. IEEE Trans. Signal Process. 2007, 55, 684–696. [Google Scholar] [CrossRef]
- Simakov, S. Localization in airborne multistatic sonars. IEEE J. Ocean. Eng. 2008, 33, 278–288. [Google Scholar] [CrossRef]
- Diamant, R.; Lampe, L. Underwater localization with time synchronization and propagation speed uncertainties. IEEE Trans. Mob. Comput. 2013, 12, 1257–1269. [Google Scholar] [CrossRef]
- Rui, L.; Ho, K.C. Efficient closed-form estimators for multistatic sonar localization. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 600–614. [Google Scholar] [CrossRef]
- Li, J.; Gao, H.; Zhang, S.; Chang, S.; Chen, J.; Liu, Z. Self-localization of autonomous underwater vehicles with accurate sound travel time solution. Comput. Electr. Eng. 2016, 50, 26–38. [Google Scholar] [CrossRef]
- Carter, G. Time delay estimation for passive sonar signal processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 463–470. [Google Scholar] [CrossRef]
- Gholami, M.R.; Gezici, S.; Strom, E.G. Improved position estimation using hybrid TW-TOA and TDOA in cooperative networks. IEEE Trans. Signal Process. 2012, 60, 3770–3785. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, S.; Wang, G.; Li, Y. Robust second-order cone relaxation for TW-TOA-based localization with clock imperfection. IEEE Signal Process. Lett. 2016, 23, 1047–1051. [Google Scholar] [CrossRef]
- Sahinoglu, Z. Improving range accuracy of IEEE 802.15. 4a radios in the presence of clock frequency offsets. IEEE Commun. Lett. 2011, 15, 244–246. [Google Scholar] [CrossRef]
- Jia, T.; Wang, H.; Shen, X.; Jiang, Z.; He, K. Target localization based on structured total least squares with hybrid TDOA-AOA measurements. Signal Process. 2018, 143, 211–221. [Google Scholar] [CrossRef]
- Wei, H.; Wan, Q.; Chen, Z.; Ye, S. A novel weighted multidimensional scaling analysis for time-of-arrival-based mobile location. IEEE Trans. Signal Process. 2008, 56, 3018–3022. [Google Scholar] [CrossRef]
- Foy, W.H. Position-location solutions by Taylor-series estimation. IEEE Trans. Aerosp. Electron. Syst. 1976, 12, 187–194. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).