1. Introduction
In commercial wireless standards, protection against eavesdropping attacks has been provided by cryptographic protocols [
1,
2]. Despite the large-scale proliferation of these protocols, confidentiality is only achieved when the processing capabilities of the attacker are not sufficient to solve the mathematical problems underlying these protocols. However, with the recent progress in the field of quantum processing, some of these difficult mathematical problems will be solvable [
3], making the current cryptographic techniques less secure. A research line that has been followed to address these new threats focuses on exploiting the random properties of the wireless channel with the aim of developing advanced security functionalities at the physical layer [
4,
5,
6]. Contrary to what happens with commercial cryptosystems, in physical layer security, the secrecy performance is quantified from an information theoretical perspective, not relying on any type of technological limitation at the eavesdropper.
1.1. Motivation and Related Work
The exploitation of the wireless medium as a source of secrecy can be carried out in two different ways. In the first, the internal dynamics of the channel can be used as a source of entropy to extract secret keys [
7,
8]. A second approach involves the use of cooperative jamming to force the degradation of the eavesdropper channel. In relation to cooperative jamming, a typical approach considers artificial noise (AN) generation to impair the eavesdropper channel with continuous Gaussian signals. The work in [
9] shows that a positive secrecy rate can be achieved by sending AN in the null space (NS) direction of the legitimate receiver. Although the solution in [
9] does not require eavesdropper channel state information (CSI) at the legitimate nodes, an advantage on the number of antennas is required at the transmitting side to create a null space. The impairment of the channel training phase with the execution of pilot contamination attacks carried out by active eavesdroppers can be used to increase the capacity of the wiretap channel. To address the secrecy capacity reduction caused by contaminated channel estimations, the work in [
10] explores the additional degrees of freedom of a massive multiple-input-multiple-output (MIMO) system to impair the eavesdropper with AN. The authors of [
10] analyzed the tradeoff between performance and complexity of NS-based precoding and random shaping precoding, concluding that the latter offers a good solution for AN generation. Considering a scenario where the cooperative jammer is also the information source of a second receiver, the authors of [
11] designed an AN jamming solution to protect the first receiver, ensuring at the same time a specific quality-of-service at the second. The integration of wireless powered communications with cooperative jamming was proposed in [
12]. Using first the base station as a power source and then as a cooperative jammer, a secrecy rate maximization was performed in [
12], computing optimal parameters for the jamming and energy harvesting phases.
The development of cooperative secure communications to protect two-hop relay networks has also been one of the most active research topics in the field of physical layer security. The authors of [
13] evaluated several precoding schemes to secure a MIMO relay network considering two cooperative jamming configurations. In the full cooperative jamming configuration, both inactive and active nodes transmit jamming signals; in the partial jamming configuration, only the inactive nodes are used as jammers. An optimal relay selection algorithm was designed in [
14] to secure a two-hop wireless network in a scenario where an adaptive eavesdropper can also act as a malicious jammer. Similarly to [
14], protection against passive eavesdropping attacks is provided in [
15] by selecting a pair of nodes to perform the jamming and relaying functions. While [
13,
14,
15] focus on decode-and-forward (DF) relaying techniques, the authors of [
16,
17] considered the use of amplify-and-forward (AF) relays.
Following the theoretical insights of the real interference alignment framework defined in [
18,
19], another important line of research was established with the results obtained in [
20,
21]. In real interference alignment, the rational dimensions available in single antenna systems are used to set alignment directions for data and interference. These directions are defined using rationally independent scalars as precoding coefficients. By making a proper selection of these coefficients, different alignment conditions between the jamming and information signals can be exploited to secure the system. According to the findings of [
20,
21], positive secure degrees of freedom (DoF) are obtained if the jamming process is designed with some structure. Through the alignment of discrete jamming signals with the information signals at the eavesdropper, the work in [
20] showed that positive secure DoF are achievable if the eavesdropper CSI is available at the legitimate terminals. The same authors of [
20] considered a more realistic scenario in [
21] where eavesdropper CSI is not available. In this second scenario, the authors proposed a blind cooperative jamming solution, demonstrating that positive secure DoF can still be achieved by spreading the jamming components across the signal space of the eavesdropper.
1.2. Contribution
The authors of [
20,
21] analyzed several network structures, including the wiretap channel, the interference channel and the multiple access channel. The broadcast channel was solely evaluated in [
20] by considering a scenario where information leakage only occurs among legitimate users, i.e., not taking into account the presence of external eavesdroppers. In this type of channel, the interference generated by the information sent to the other users must always be decoded by the receiver in order to allow a correct acquisition of the intended data. Additionally, because this interference could represent valuable information, it should remain confidential even among the terminals registered as legitimate users inside the network. Please note that an eavesdropper could connect to the network as a fake legitimate user only for the purpose of tapping the information sent to the other users. Therefore, a robust secrecy solution should provide protection not only against attacks carried out by external eavesdroppers, but also against attacks executed by terminals registered in the network as legitimate users. To the best of the authors’ knowledge, securing a broadcast channel against eavesdropping attacks carried out simultaneously by internal users and external eavesdroppers is an open problem that remains untreated in the literature. To address this issue, the present work extends [
20] by providing a cooperative jamming solution that also protects a two-user broadcast channel against passive eavesdropping attacks carried out by external terminals. To achieve this goal, the developed scheme combines real interference alignment with the concept of blind cooperative jamming defined in [
21]. An information theoretical analysis shows that positive secure DoF are achievable with the proposed solution.
1.3. Organization
The remainder of this paper is organized as follows:
Section 2 presents the system model, while
Section 3 defines some preliminaries on real interference alignment. The cooperative jamming solution proposed in this manuscript is formulated in
Section 4 and evaluated in
Section 5. Some practical challenges are discussed in
Section 6. The main conclusions are outlined in
Section 7.
Notation: The discrete entropy of the random variable X is denoted by , and the continuous differential entropy by . The notation refers to the mutual information between and , while the expected value of is represented by . A vector comprising n realizations of is denoted by Xn, and defines the little-o notation.
2. System Model
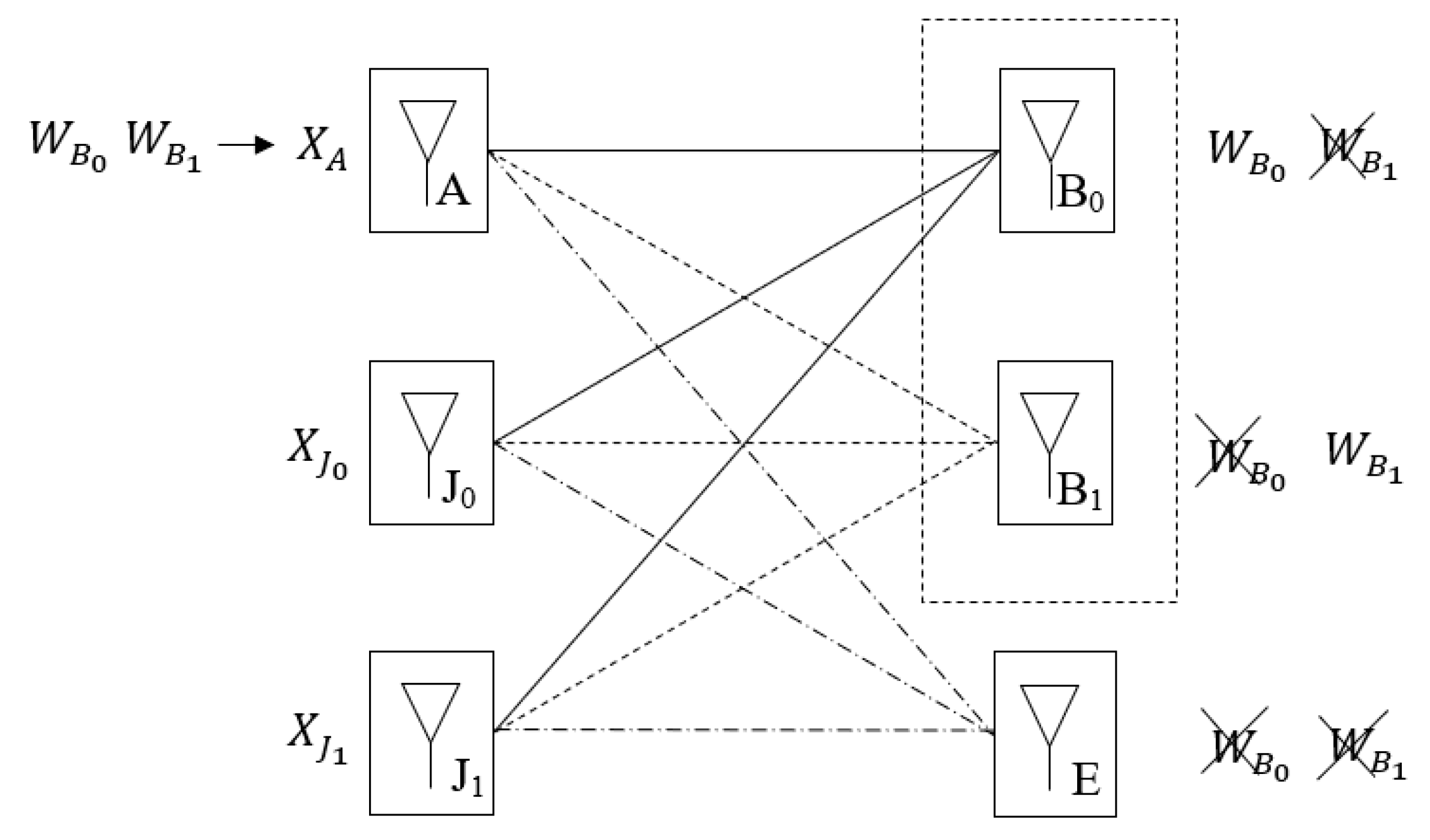
The communication model considered in this work is illustrated in
Figure 1. Node “A” pretends to transmit two confidential messages to users “B
0” and “B
1”. Additionally, a passive eavesdropper denoted by “E” tries to obtain the information sent to both users. This work also assumes that “B
0” and “B
1” are eavesdroppers of each other. To enhance the security level of the system, two jammers represented by “J
0” and “J
1” cooperate with “A”, generating two independent jamming signals. All the terminals have a single antenna. The channel gains are real and remain static during the entire communication phase. Furthermore, this work also assumes that the channels of the different users are independently sampled from a continuous known distribution. Finally, this model assumes that the channel of the eavesdropper “E” is the only one that is not known by the remaining terminals.
Defining
as the channel input of transmitter
, and assuming an average power constraint
, the signals observed at the receiving nodes
are formulated as
The channel gain between terminal and is denoted by the coefficient , while noise at the receiving node is defined by random variable , which follows a zero-mean Gaussian distribution with variance . In this work, node “A” wants to transmit, in secrecy, message to node “B0”, and message to node “B1”. In the case of , secrecy implies that the message is either protected against eavesdropping attacks carried out by “E” or “B1”. Similarly, the message is secured if neither node “E” nor node “B0” is capable of decoding the respective information. The messages are independent and chosen uniformly from the sets and .
Before the transmission, each message is mapped into a codeword of length
using the encoding functions
and
. In each channel use,
is computed combining the codeword elements
and
with a jamming component
, resulting in the following transmitted signal
At nodes “J0” and “J1”, two jamming components
and
are also generated and transmitted using the signals
The coefficient
,
denotes a channel dependent precoder that is specified in
Section 4. After the encoding phase, each message is transmitted across
channel uses at the following rates
where
and
define the cardinality of the sets
and
, respectively. After sampling the channel output
times, “B
0” decodes
and obtains an estimation of
, which is denoted by
. In a similar way, “B
1” computes
after decoding
. The rate pair
is achievable if for any
there exists an
-length code such that the probability of decoding error is given by
Furthermore, at the same time,
and
are transmitted in perfect secrecy if
The conditions in (9)–(12) can be mutually achieved if the rate pair belongs to the capacity region of the system. The proof of achievability can be performed using random code constructions featuring codeword lengths with . In the remainder of this work, it is assumed that the codebooks and encoding functions and at all terminals are known.
3. Preliminaries
This section presents a lemma that has been applied in the DoF analysis of different network structures. This lemma is a fundamental tool in the field of real interference alignment [
18,
19], being used to demonstrate that the fractional dimensions offered by single antenna systems can be exploited to manage interference. In this work, this lemma is applied in the DoF analysis of the proposed cooperative jamming solution. The considered lemma was used in [
20] to derive an upper bound on the probability of error of the following multi-layer constellation
where
denotes a set composed by
rationally independent real numbers, and
defines
information streams independently sampled from
The ensemble
represents a set of
real numbers, where parameter
defines the distance between consecutive points. The probability of decoding error is derived for an additive noise channel
where
denotes Gaussian noise with variance
, and
defines a set of
real points featuring an average power constraint
. The considered lemma states the following:
Lemma 1. For any small enough , there exists a positive constant , which is independent of , such that if we select the parametersthen the average power constraint is satisfied, and for almost all , except for a set of Lebesgue measure zero (probability of the event arbitrarily close to zero), the probability of error is upper bounded bywhere is a positive constant independent of , and the condition is always verified for . Lemma 1 is supported by the Khintchine–Groshev theorem [
18,
19], which defines a lower bound on the minimal distance between consecutive points of (13). The theorem states that when the information streams
are drawn from the set
, there exists a constant
such that for any
, the minimal distance between the
points of
can be lower bounded by
The Khintchine–Groshev theorem can be extended to the case where the terms of
are drawn from different sets
. In this case, the minimal distance between the
points of
is lower bounded in the following way:
The result formulated in Lemma 1 is applied in the DoF analysis of the cooperative jamming solution proposed in this work. In the real domain, a DoF pair is formulated as
where
denotes a channel input power constraint, and the pair
comprises achievable secrecy rates for nodes “B
0” and “B
1”.
4. Security Scheme
The cooperative jamming solution proposed in this work is developed in the context of the theoretical framework described in
Section 3. Accordingly, in the following, we assume that the signals
are mutually independent and are sampled from
in (14), applying the parameters
After the encoding phase, the jamming and the information signals are linearly precoded and transmitted using the following signals:
Please note that in (22)–(24), the precoding coefficients
,
are designed without using the channel gains of the external eavesdropper “E”, which complies with the passive condition defined for this terminal. For the channel model formulated in (1)–(3), the signals observed at the channel output are defined as
The developed solution protects “B
0” from the eavesdropping attacks of “B
1”, forcing the alignment of
with
at the channel output of “B
1”. At node “B
0”, the information intended for “B
1” is also secured with the alignment of
with
. In the case of node “E”, it is not possible to explicitly align
and
with any jamming signal. However, as demonstrated in [
21], secrecy against node “E” is still achievable by filling the signal space of node “E” with enough jamming signals. As it is demonstrated in
Section 5, positive secure DoF are achievable using the secrecy solution proposed in this work.
5. Secrecy Analysis
The secrecy analysis of the proposed scheme is presented in the following using the limits formulated in (20) as the evaluation metric. For the reliability and secrecy constraints defined in equations (9)–(12), the following secrecy rates
are achievable using the random encoding schemes defined in [
22]. In order to derive an achievable DoF pair, all the mutual information terms in (28) and (29) are computed in this section. The main result of the theoretical analysis performed in this work is formalized in the following theorem:
Theorem 1. The secure DoF pairis achievable using the cooperative jamming scheme formulated in Section 4. As stated above, in the asymptotical power regime of (20), fractional secure DoF can be reached by applying the cooperative jamming scheme developed in this work. The demonstration of Theorem 1 is provided in
Section 5.1 and
Section 5.2.
5.1. DoF Characterization at “B0”
The derivation of the achievable DoF at node “B0” is presented in this subsection. To accomplish this, theoretical bounds on the mutual information terms of (28) are defined in Lemmas 2–4.
Introducing Lemma 2 first, a lower bound on the amount of legitimate information obtained by node “B0” is formalized as follows:
Lemma 2. For any , the amount of information that node “B0” obtains from the observation of is lower bounded by Lemma 2 was computed applying the theoretical tools provided by the real interference alignment framework described in
Section 3, namely, Lemma 1. The amount of information intended for node “B
0” that is eavesdropped by “B
1” is quantified in Lemma 3.
Lemma 3. The amount of information that node “B1” obtains from the observation of is given by Proof. Because
is aligned with
in (26), “B
0” can only obtain information about
from the observation of
. Therefore, the following upper bound
can be computed assuming a noiseless and non-interference regime in (26). As demonstrated in [
23],
bits, leading to the result in (31). □
To complete the secure DoF characterization at “B
0”, an upper bound on the amount of information
obtained by node “E” is formulated in Lemma 4. As in Lemma 2, the computation of Lemma 4 was performed using the theoretical framework defined in
Section 3.
Lemma 4. For any , the amount of information that node “E” obtains from the observation of is defined by According to Lemma 1, the value of in (30) and (33) can be made arbitrarily close to zero. Therefore, applying Lemmas 2–4 to (28) and (20), it is possible to conclude that is achievable at node “B0”.
5.2. DoF Characterization at “B1”
The DoF characterization at node “B
1” is presented in the following. As demonstrated in
Section 5.1, all the mutual information terms of (29) are analyzed in this subsection. Again using the framework described in
Section 3, a lower bound on the amount of information
obtained by node “B1” is defined in Lemma 5.
Lemma 5. For any , the amount of information that node “B1” obtains from the observation of is lower bounded by Proof. Similar to the proof of Lemma 2 in
Section 5.1, only the equivalent channel gains are different. □
Lemma 6 quantifies an upper bound on the total information acquired by “B0” when the channel output in (25) is observed.
Lemma 6. The amount of information that node “B0” obtains from the observation of is given by Proof. Because
is aligned with
in (25), “B
0” only obtains information about
from the observation of
. Therefore, the following upper bound
can be computed assuming a noiseless and non-interference regime in (25). As demonstrated in [
23],
bits, leading to the result in (35). □
The leakage of information
at node “E” is upper bounded in Lemma 7. As shown in Lemma 4, the theoretical framework defined in
Section 3 was again applied to build Lemma 7.
Lemma 7. For any , the amount of information that node “E” obtains from the observation of is upper bounded by The achievability of follows from Lemmas 5–7, (29) and (20). After this final step, the proof of Theorem 1 is completed.
6. Discussion
Although this work considers a static channel environment, in a real scenario, the channel is always dynamic and therefore must be measured periodically. In a dynamic channel context, a practical execution of the proposed scheme would require the implementation of a channel training phase for each new realization of the channel. This channel training phase would comprise an initial stage for pilot transmission, which would be carried out by all the terminals with the exception of node “E”. Then, a channel feedback stage would be performed in order to provide each node with the necessary information to set the alignment conditions and to allow the decoding process at “B0” and “B1”. Due to the large number of channel gains that must be known at each terminal, one of the main challenges associated with the practical implementation of the proposed scheme is related to the complexity and overhead associated with the channel training phase. These requirements stem from the alignment conditions that need to be met to ensure the security requirements. We should point out that this issue is not specific to the proposed scheme, being widely recognized as a general problem in the field of real interference alignment, particularly when these types of techniques are applied to large multiuser networks. To address the practical constraints mentioned above, efficient channel training methods must be designed to enable the practical implementation of such technology.