Cooperative Secure Transmission in MISO-NOMA Networks

Abstract

In this paper, we investigate cooperative secure transmission in non-orthogonal multiple access (NOMA) networks where a source (Alice) intends to transmit confidential messages to one legitimate user with high-level security requirement (LU1), and serve another normal one (LU2) simultaneously. In order to enhance the transmission security, a cooperative jammer (Charlie) is employed to confuse multiple non-colluding eavesdroppers (Eves). Taking both secrecy outage restriction of LU1 and the desired quality of service (QoS) requirement of LU2 into consideration, we propose an adaptive power allocation strategy for maximizing secrecy rate. Numerical results are provided to validate that our proposed scheme significantly outperforms the conventional NOMA secure transmission scheme.

1. Introduction

Non-orthogonal multiple access (NOMA), which has shown the potential to significantly improve spectral efficiency, is envisaged as a promising technique for the 5G wireless networks [1,2]. In contrast to the conventional orthogonal multiple access (OMA), NOMA exploits the power domain to serve multiple users simultaneously [3]. Based on multi-antenna techniques, cooperative communication techniques have become attractive strategies to further enhance the performance of wireless systems for the noticeable properties of achieving spatial degrees of freedom and diversity gains [4,5]. The cooperative nodes mainly play two roles including cooperative relaying (CR) [4] and cooperative jamming (CJ) [5]. Specifically, thanks to their benefit of easy deployment, the helper nodes can be adaptively selected to play different roles based on their location [6]. Inspired by its superior performance in improving spectrum efficiency and realizing larger coverage, intensive efforts have been devoted to investigating cooperative NOMA recently for further transmission reliability improvement [7,8,9,10,11]. In [7], users with better channel conditions acted as relays to forward messages for users with low link quality. The authors in [8] have derived the exact expression of the average achievable rate in cooperative NOMA systems. The primary long-distance transceivers were able to achieve spectrum sharing via a NOMA relay in [9]. In the work of [10], the impact of the number of transmit antennas at the base station on outage performance in a multiple-antenna NOMA system has been studied. In [11], aiming to provide FD relaying operation by relying only on low-complexity single antenna relays, a novel buffer-aided algorithm has been presented for two-hop NOMA networks.

Due to the open nature of wireless channels, cooperative NOMA systems offer new possibilities and opportunities for security challenge. Recently, emerging as promising solutions to against eavesdropping and guarantee secure transmission, physical layer security techniques have attracted considerable attention and applied in cooperative NOMA systems [12,13,14,15,16,17,18]. In [12], the authors considered both amplify-and-forward (AF) and decode-and-forward (DF) protocols, and derived analytical expressions for secrecy outage probability (SOP) and secrecy capacity. To maximize the capacity of the systems, a secure two-way relay selection method was proposed for multiple relays networks with two pairs of cellular users [13]. In the work of [14], a novel NOMA-inspired jamming and relaying scheme has been developed to enhance the physical layer security of untrusted relay networks. In [15], an artificial noise (AN)-aided cooperative jamming scheme for multi-input single-output NOMA Cognitive radio networks (CRNs) using simultaneous wireless information and power transfer technology has been proposed to improve the security of the primary network. The works in [16] analyzed analytical and asymptotical expressions of SOP under both random and max-min relay selection schemes for jammer-aided cooperative NOMA networks. In [17], a multi-antenna full-duplex (FD) relay has been introduced in a cooperative NOMA system with two users, and a full-duplex-jamming (FDJam) scheme has been proposed to guarantee the secure transmission for the user with a weak channel. To increase secrecy rate and reduce information leakage, a new cooperative non-orthogonal jamming decode-and-forward (JDF) scheme has been proposed where the source actively sends jamming signals while the relay is forwarding [18].

To the best of our knowledge, there is a lack of research focused on the robust secrecy rate maximization (SRM) problem subject to secrecy outage constraint in jammer-aided cooperative NOMA systems. In this paper, we study cooperative secure transmission in two-user MISO-NOMA networks where one user (LU1) desires a high data rate with security requirement, while the other one (LU2) only subject to a predefined quality of service (QoS) requirement. This scenario commonly exists in many practical applications. For example, some users with high secrecy priority (bank staffs, government officers, etc) will pay more attention to security while others may have low or no secrecy requirements (e.g., a public weather alert). Different from [19,20], a friendly jammer exploiting AN beamforming is employed to disturb multiple eavesdroppers in these considered networks. Specifically, in [16,17,18], the power allocation factor is considered to be fixed in jammer-aided cooperative NOMA networks, while, in this paper, taking both security and performance guarantee into account, an efficient adaptive approach has been developed to obtain the optimal power allocation factor for the secrecy rate maximization. In addition, we define the effective sum rate as the sum rate of the secrecy rate at LU1 and the transmission rate at LU2. Then, the ratio of the effective sum rate to the total power consumption can be defined as effective energy efficiency (EE) accordingly. Simulation results are provided to indicate significant improvements in secrecy performance and effective EE by the proposed scheme compared with the conventional NOMA secure scheme.

Our specific contributions of this paper are summarized as follows:

• Taking multiple eavesdroppers into consideration, we investigate physical layer security in cooperative MISO-NOMA networks. We first derive an accurate closed form expression for SOP. Then, we transform the objective function in the SRM problem under certain SOP into a strictly concave function through strict mathematical proofs.
• Different from the work of [21] in which only one user was served by Alice, in this paper, we investigate cooperative secure transmission in NOMA networks where a source (Alice) intends to transmit confidential messages to one legitimate user with high-level security requirement (LU1), and serve another normal one (LU2) simultaneously. In particular, we consider the upper bound of the power Alice allocates to LU2 to guarantee the QoS constraint at LU2. In addition, we have made a comprehensive discussion and developed an adaptive approach based on different cases to obtain the optimal power allocation factor for solving the SRM problem under certain SOP.
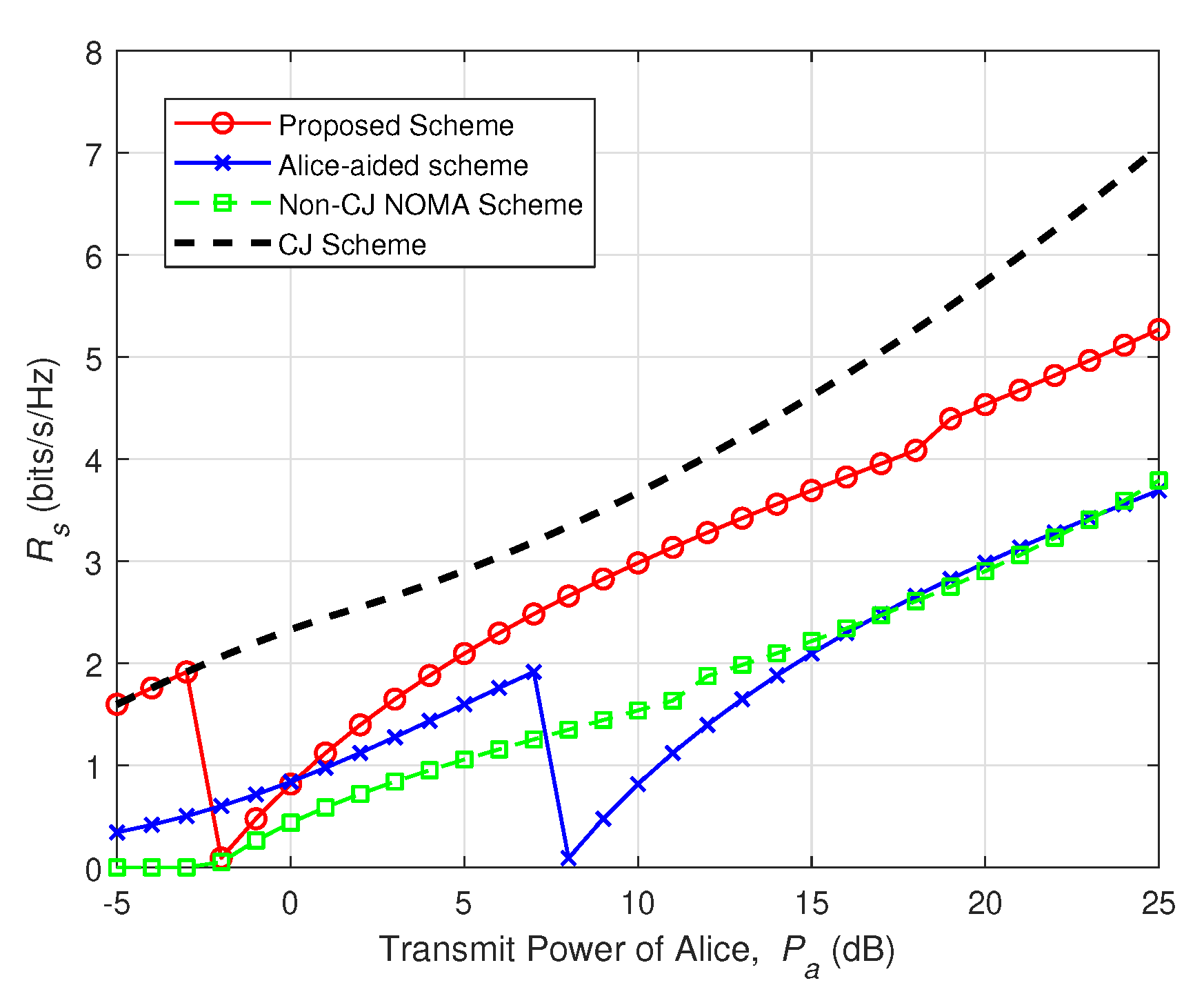
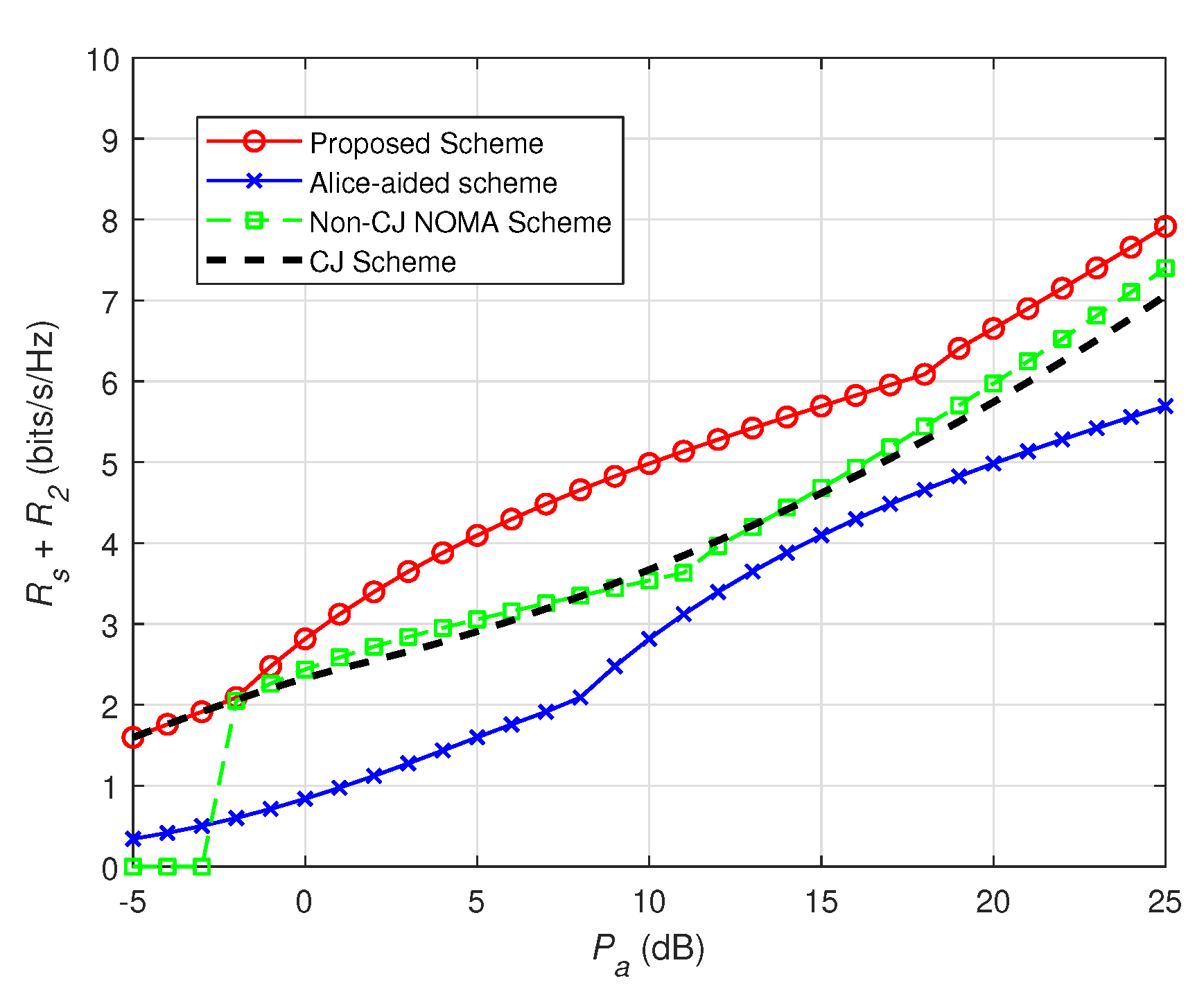
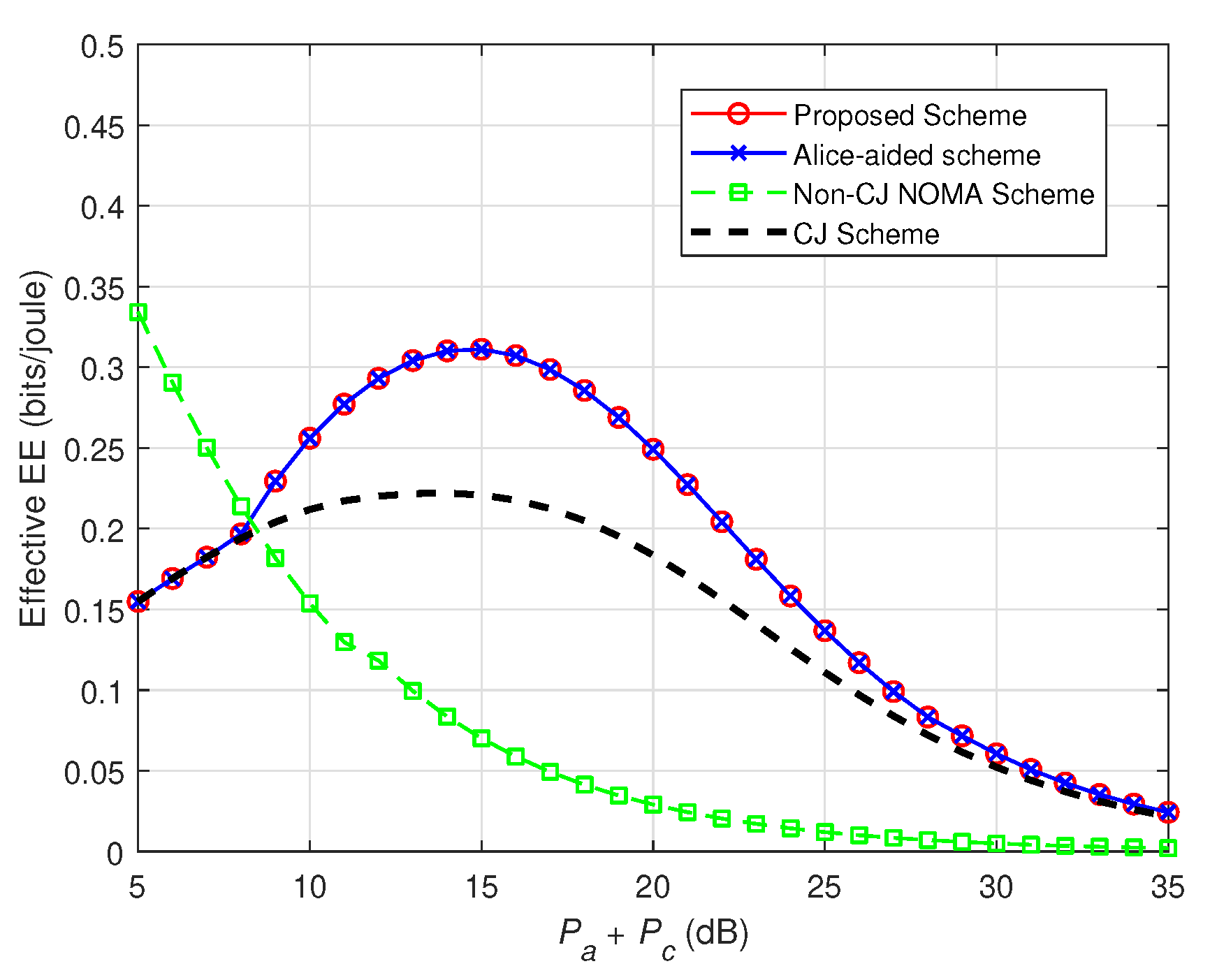
• Numerical results are provided to verify that the proposed scheme enables dynamic transmission. Both the effectiveness and flexibility of our scheme in achieving higher secrecy performance and effective EE have also been demonstrated.

The rest of this paper is organized as follows. The system model and problem formulation is described in Section 2. The proposed scheme is presented in Section 3. Numerical results are provided in Section 4. Finally, the paper is concluded in Section 5.

Notations: Boldface upper and lower cases denote matrices and vectors, respectively. ${\mathbf{I}}_N$ represents $N\times N$ identity matrix. ${\mathbb{C}}^n$ denotes the n-dimensional complex space and circularly symmetric complex Gaussian random vector submits to $\mathcal{CN}(\mu ,\mathsf{\Lambda })$, with mean $\mu$ and covariance matrix $\mathsf{\Lambda }$. null(X) is the null space of X. Subscripts ${[·]}^{+}$ stands for max-function max$(·,0)$. $\mathbf{Pr}(·)$ is the probability measure. Exponential distribution with parameter $\lambda$ and Gamma distribution with shape parameter $\alpha$ and rate parameter $\beta$ is denoted as $\mathrm{Exp}\left(\lambda \right)$ and $\mathsf{\Gamma }(\alpha ,\beta )$, respectively.

2. System Model and Problem Formulation

2.1. System Model

A MISO-NOMA wireless network is considered as shown in Figure 1, in which the source (Alice) intends to serve two single-antenna legitimate users (e.g., LU1 and LU2) in the presence of non-colluding single-antenna eavesdroppers (Eves). Meanwhile, a cooperative jammer (Charlie) is employed to enhance the secrecy performance of the system. Alice and Charlie are assumed to be equipped with $N_a$ and $N_c$ ($N_c>2$) antennas, respectively. In addition, the set of Eves is defined as $\mathcal{M}\triangleq \{1,\dots ,M\}$.

The channels from Alice to the legitimate users and the m-th Eve are denoted by ${\mathbf{h}}_{ak}\in {\mathbb{C}}^{1\times N_a},k\in \{1,2\}$ and ${\mathbf{h}}_{ae,m}\in {\mathbb{C}}^{1\times N_a}$, respectively, and we also denote the channels from Charlie to the legitimate users and the m-th Eve by ${\mathbf{h}}_{ck}\in {\mathbb{C}}^{1\times N_c},k\in \{1,2\}$ and ${\mathbf{h}}_{ce,m}\in {\mathbb{C}}^{1\times N_c}$, respectively. All the channels involved are modeled as quasi-static independent and identically distributed (i.i.d) Rayleigh fading channels. Since the eavesdroppers are passive, we further assume that the perfect knowledge of all the legitimate channels is known at all nodes, while only the statistical CSIs of Eves’ channels are available. Without loss of generality, it is assumed that the channels between Alice and the legitimate users follow the order of $|{\mathbf{h}}_{a2}{|}^2\le {\left|{\mathbf{h}}_{a1}\right|}^2$ [19,22].

For the implementation of NOMA, Alice transmits two information signals $x_1$ and $x_2$ to LU1 and LU2, respectively. We denote $\mathbf{t}\in {\mathbb{C}}^{N_a\times 1}$ as the signals transmitted by Alice, and $\mathbf{t}$ can be constructed as

$$\mathbf{t}=\sqrt{P_a{a}_1}{\mathbf{w}}_s{x}_1+\sqrt{P_a{a}_2}{\mathbf{w}}_s{x}_2,$$

(1)

where $P_a$ stands for the transmit power budget of Alice and $x_k\sim \mathcal{CN}(0,1),k\in \{1,2\}$. We denote $a_1$ and $a_2$ as the fraction of the power allocated for $x_1$ and $x_2$, respectively. Following the NOMA protocol, $x_2$ are allocated with more power, thus the power allocation coefficients satisfy the conditions that $a_1\le a_2$ and $a_1+a_2=1$ [3]. In addition, aiming to guarantee the effective channel gain of LU1, Alice adopts maximal ratio transmission (MRT), and the beamforming vector is given by ${\mathbf{w}}_s=\frac{{\mathbf{h}}_{a1}}{\Vert {\mathbf{h}}_{a1}\Vert }$ [20].

Specifically, in this considered systems, Charlie is employed as an auxiliary node to enhance secrecy performance by generating AN. To eliminate the additional interference at the legitimate users and confuse Eves at the same time, i.e., ${\mathbf{h}}_{ck}{\mathbf{t}}_c=0,k\in \{1,2\}$ [23], the transmitted signal at Charlie can be designed as

$${\mathbf{t}}_c=\sqrt{\frac{P_c}{N_c-2}}\mathbf{V}\mathbf{s},$$

(2)

where $P_c$ represents the transmit power constraint at Charlie, $\mathbf{V}\in {\mathbb{C}}^{N_c\times (N_c-2)}$ is an orthonormal basis for null(${\mathbf{h}}_{a1},{\mathbf{h}}_{a2}$), and $\mathbf{s}$ denotes the Gaussian jamming signal with distribution $\mathcal{CN}(0,{\mathbf{I}}_{N_c-2})$.

From Equations (1) and (2), the observed signals at the k-th user and the m-th Eve can be expressed as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill y_k& ={\mathbf{h}}_{ak}\mathbf{t}+{\mathbf{h}}_{ck}{\mathbf{t}}_c+n_k,\hfill \\ \hfill & =\sqrt{P_a{a}_1}{\mathbf{h}}_{ak}{\mathbf{w}}_s{x}_1+\sqrt{P_a{a}_2}{\mathbf{h}}_{ak}{\mathbf{w}}_s{x}_2+n_k,\hfill \end{array}\end{array}$$

(3)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill y_{e,m}& ={\mathbf{h}}_{ae,m}\mathbf{t}+{\mathbf{h}}_{ce,m}{\mathbf{t}}_c+n_{e,m},\hfill \\ \hfill & =\sqrt{P_a{a}_1}{\mathbf{h}}_{ae,m}{\mathbf{w}}_s{x}_1+\sqrt{P_a{a}_2}{\mathbf{h}}_{ae,m}{\mathbf{w}}_s{x}_2\hfill \\ \hfill & +\sqrt{\frac{P_c}{N_c-2}}{\mathbf{h}}_{ae,m}\mathbf{V}\mathbf{s}+n_{e,m}\hfill \end{array}\end{array}$$

(4)

where $n_k$ and $n_{e,m}\in \mathcal{CN}(0,1)$ denote additive complex white Gaussian noise (AWGN) at the k-th user and the m-th Eve, respectively.

In NOMA systems, the legitimate users employ successive interference cancellation (SIC) to detect received signals. Accordingly, LU1 firstly decodes $x_2$ by treating $x_1$ as interference and then applies SIC to decode its intended information $x_1$. As a result, the signal-to-interference-plus-noise ratio (SINR) at LU1 and LU2 can be described as

$$\begin{array}{cc}\hfill {\zeta }_1& =P_a{a}_1{\Vert {\mathbf{h}}_{a1}\Vert }^2,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\zeta }_2& =\frac{P_a(1-a_1){\Vert {\mathbf{h}}_{a2}{\mathbf{w}}_s\Vert }^2}{P_a{a}_1{\Vert {\mathbf{h}}_{a2}{\mathbf{w}}_s\Vert }^2+1}.\hfill \end{array}$$

(6)

In the work of [19], the eavesdropper’s interception capability has been overestimated, while, in this paper, we extend this assumption to a more general case that the eavesdroppers are regarded as ordinary users, which owe no decoding ability [24,25]. Hence, the received SINR of $x_1$ at the m-th Eve can be given by

$${\zeta }_{e,m}=\frac{P_a{a}_1{\Vert {\mathbf{h}}_{ae,m}{\mathbf{w}}_s\Vert }^2}{1+P_a(1-a_1){\Vert {\mathbf{h}}_{ae,m}{\mathbf{w}}_s\Vert }^2+\frac{P_c}{N_c-2}{\Vert {\mathbf{h}}_{ce,m}\mathbf{V}\Vert }^2}.$$

(7)

In order to guarantee secure transmission, the Wyner’s encoding scheme is adopted by Alice, and the transmission rate at users and secrecy rate are denoted as $R_k={log}_2(1+{\zeta }_k),k\in \{1,2\}$ [26] and $R_s$, respectively. The redundancy rate $R_k-R_s$ can be utilized for anti-eavesdropping. According to [5,13,21], in non-colluding Eves scenario, the maximal eavesdropped information is determined by the maximal SNR among all the Eves, thus $C_e={log}_2(1+{max}_{m\in \mathcal{M}}{\zeta }_{e,m})$, and the secrecy outage occurs when $C_e>R_e$. Therefore, the secrecy outage probability (SOP) of LU1 can be described as [5]

$$\begin{array}{cc}\hfill P_{out}(R_s,a_1)& =\mathbf{Pr}(R_s>C_s)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & =\mathbf{Pr}(C_e>R_e).\hfill \end{array}$$

(9)

Since $R_e=R_1-R_s$ represents the redundant rate that can be utilized for anti-eavesdropping at LU1, finally, we can rewrite the expression of SOP as

$$P_{out}(R_s,a_1)=\mathbf{Pr}(\underset{m\in \mathcal{M}}{max}{\zeta }_{e,m}>2^{R_1-R_s}-1).$$

(10)

2.2. Problem Formulation

First, we denote the minimum transmission rate required by LU2 as $R_{th}$. Hence, the SRM problem under certain SOP can be written as

$$\begin{array}{cc}\hfill \underset{0<a_1\le 0.5}{max}& {\left[R_s\right]}^{+};\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& P_{out}(R_s,a_1)\le \epsilon ;\hfill \\ \hfill & {log}_2(1+{\zeta }_2)\ge R_{th},\hfill \end{array}$$

(11)

where $\epsilon \in (0,1)$ represents the maximum allowable SOP. To simplify our analysis, we define $\delta =2^{R_1-R_s}-1$ and denote the maximum achievable SINR at LU1 as $\zeta =P_a{\Vert {\mathbf{h}}_{a1}\Vert }^2$. Consequently, problem (11) can be equivalently reformulated as

$$\begin{array}{cc}\hfill \underset{0<a_1\le 0.5}{max}& R_s={log}_2\left(\frac{1+\zeta a_1}{1+\delta }\right);\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \epsilon =\mathbf{Pr}(\underset{m\in \mathcal{M}}{max}{\zeta }_{e,m}>\delta );\hfill \\ \hfill & {log}_2(1+{\zeta }_2)\ge R_{th}.\hfill \end{array}$$

(12)

3. Proposed Solution for SRM Problem under Certain SOP Constraint

In this section, we develop an efficient adaptive approach to maximize $R_s$ in (12). Particularly, notice from (12) that a threshold in terms of $a_1$ should be provided to meet the desired QoS requirement at LU2. Otherwise, the CJ scheme in [21] is exploited in our considered systems to satisfy secure transmission for LU1.

3.1. Solution for SOP Constraint

Firstly, we assume the QoS requirement at LU2 is satisfied and focus on deriving a more general analysis for the expression of SOP in (12). For simplifying our analysis, we denote ${\epsilon }_m=\mathbf{Pr}({\zeta }_{e,m}>\delta ),m\in \mathcal{M}$, and define new variables as follows:

$$\begin{array}{cc}\hfill T_{1,m}& =P_a{a}_1{\Vert {\mathbf{h}}_{ae,m}{\mathbf{w}}_s\Vert }^2,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill T_{2,m}& =P_a(1-a_1){\Vert {\mathbf{h}}_{ae,m}\Vert }^2,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill T_{3,m}& =\frac{P_c}{N_c-2}{\Vert {\mathbf{h}}_{ce,m}\mathbf{V}\Vert }^2,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill U_m& =T_{2,m}+T_{3,m}.\hfill \end{array}$$

(16)

With the aid of stochastic theory knowledge, $T_{1,m}\sim \mathrm{Exp}\left({\kappa }_{1,m}\right)$, $T_{2,m}\sim \mathrm{Exp}\left({\kappa }_{2,m}\right)$, where ${\kappa }_{1,m}=\frac{1}{P_a{a}_1}$, ${\kappa }_{2,m}=\frac{1}{P_a(1-a_1)}$ can be easily verified, respectively. According to [5,21,27], due to the fact that the entries of ${\mathbf{h}}_{ce,m}$ follow independent $\mathcal{CN}(0,1)$, the square of each entry’s modulus follows exponential distribution with mean 1, hence we have ${\Vert {\mathbf{h}}_{ce,m}\mathbf{V}\Vert }^2\sim \mathsf{\Gamma }(N_c-2,1)$ [28]. Finally, $T_{3,m}\sim \mathsf{\Gamma }(N_c-2,{\kappa }_{3,m})$, where ${\kappa }_{3,m}=\frac{N_c-2}{P_c}$ can be obtained. As such, the SOP expression in (12) can be rewritten as

$$\begin{array}{cc}\hfill {\epsilon }_m& =\mathbf{Pr}\left\{{\zeta }_{e,m}>\delta \right\}\hfill \\ \hfill & =\mathbf{Pr}\left\{T_{1,m}>\delta +\delta U_m\right\}.\hfill \end{array}$$

(17)

From Equations (13)–(17), a closed form expression of ${\epsilon }_m$ can be achieved by referring to [21], and we omit the detailed calculation here for simplicity. Then, ${\epsilon }_m$ can be re-expressed as

$${\epsilon }_m=\frac{1}{e^{{\kappa }_{1,m}\delta }}\left(\frac{{\kappa }_{2,m}}{{\kappa }_{2,m}+{\kappa }_{1,m}\delta }\right){\left(\frac{{\kappa }_{3,m}}{{\kappa }_{3,m}+{\kappa }_{1,m}\delta }\right)}^{N_c-2}.$$

(18)

Proposition 1.

A closed form expression for the SOP constraint in the SRM problem (12) can be described as

$$ln\left(\frac{1}{1-{\left(1-\epsilon \right)}^{\frac{1}{M}}}\right)=\frac{\rho \left(a_1\right)}{P_a}+ln\left[A\left(a_1\right)\right]+\left(N_c-2\right)ln\left[B\left(a_1\right)\right],$$

(19)

where $\rho \left(a_1\right)=\frac{\delta }{a_1}$, $A\left(a_1\right)=1+\left(1-a_1\right)\rho \left(a_1\right)$ and $B\left(a_1\right)=1+\frac{P_c}{P_a(N_c-2)}\rho \left(a_1\right)$.

Proof. 

Since multiple non-colluding Eves are considered in this paper, the SINR at each Eve is independent of each other due to the fact that the functions of independent random variables are independent [5,21]. Thus, the SOP constraint in (12) can be rewritten as

$$\begin{array}{cc}\hfill \epsilon & =1-\mathbf{Pr}(\underset{m\in \mathcal{M}}{max}{\zeta }_{e,m}\le \delta )\hfill \\ \hfill & =1-{\left[\mathbf{Pr}({\zeta }_{e,m}\le \delta )\right]}^M\hfill \\ \hfill & =1-{(1-{\epsilon }_m)}^M\hfill \end{array}$$

(20)

Then, substituting (18) into (20) and doing some transformation, we can obtain Proposition 1. □

3.2. Power Allocation Optimization for LU1

Analyzing Proposition 1, the following results can be obtained and utilized to facilitate our analysis.

Lemma 1.

$\rho \left(a_1\right)$ is a monotonically increasing function of $a_1$.

Proof. 

According to (19), it can be easily verified that $\rho \left(a_1\right)>0$. Taking the derivatives on both sides of (17), we have

$$0=\frac{{\rho }^{\prime }\left(a_1\right)}{P_a}+\frac{(1-a_1){\rho }^{\prime }\left(a_1\right)}{A\left(a_1\right)}+\frac{P_c{\rho }^{\prime }\left(a_1\right)}{P_{a}B\left(a_1\right)}.$$

(21)

Thus, the first derivative of $\rho \left(a_1\right)$ can be given by

$${\rho }^{\prime }\left(a_1\right)=\frac{P_{a}B\left(a_1\right)\rho \left(a_1\right)}{A\left(a_1\right)B\left(a_1\right)+P_{a}B\left(a_1\right)(1-a_1)+A\left(a_1\right)P_c}.$$

(22)

Hence, ${\rho }^{\prime }\left(a_1\right)>0$. Lemma 1 is established. □

Lemma 2.

$\frac{{\rho }^{\prime }\left(a_1\right)}{\rho \left(a_1\right)}$ is a monotonically increasing function of $a_1$.

Proof. 

From (22), $\frac{{\rho }^{\prime }\left(a_1\right)}{\rho \left(a_1\right)}$ can be calculated as

$$\frac{{\rho }^{\prime }\left(a_1\right)}{\rho \left(a_1\right)}=\frac{P_{a}B\left(a_1\right)}{A\left(a_1\right)B\left(a_1\right)+P_{a}B\left(a_1\right)(1-a_1)+A\left(a_1\right)P_c},$$

(23)

and it is obvious that the numerator of (23) strictly increases with respect to $a_1$, while the denominator strictly decreases with respect to $a_1$. This completes the proof of Lemma 2. □

Proposition 2.

$R_s$ is a strictly concave function of $a_1$.

Proof. 

According to (12), $R_s^{\prime }\left(a_1\right)$ can be given by

$$\begin{array}{cc}\hfill R_s^{\prime }\left(a_1\right)& =\frac{1}{ln2}\left[\frac{\zeta }{1+\zeta a_1}-\frac{\rho \left(a_1\right)+a_1{\rho }^{\prime }\left(a_1\right)}{1+a_1\rho \left(a_1\right)}\right]\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & =\frac{\zeta -\rho \left(a_1\right)}{(1+\zeta a_1)[1+a_1\rho \left(a_1\right)]ln2}-\frac{\frac{{\rho }^{\prime }\left(a_1\right)}{\rho \left(a_1\right)}}{\left[1+\frac{1}{a_1\rho \left(a_1\right)}\right]ln2}.\hfill \end{array}$$

(25)

Note that the first term on the right-hand side of (25) is shown to be a strictly decreasing function of $a_1$, and increasing function of $a_1$ for the second one, respectively. Hence, $R_s^{″}\left(a_1\right)<0$ can be obtained. Based on convex optimization theory [29], we can conclude Proposition 2. □

Recalling the transmission rate constraint of LU2 in problem (12), the upper bound of $a_1$ can be calculated by

$$a_1^U=\frac{P_a{\Vert {\mathbf{h}}_{a2}{\mathbf{w}}_s\Vert }^2-\left(2^{R_{th}}-1\right)}{2^{R_{th}}{P}_a{\Vert {\mathbf{h}}_{a2}{\mathbf{w}}_s\Vert }^2}.$$

(26)

Then, taking $a_1^U$ into account, we utilize the aforementioned results to derive an efficient approach for solving (10). The details are discussed in the following different cases.

(1) Case 1: $a_1^U\le 0$. The given QoS requirement at LU2 can not be satisfied. Thus, Alice stops serving LU2, and adopts the conventional orthogonal multiple access (OMA) CJ scheme in [21] to guarantee secure transmission for LU1. Note that the restriction of $a_1$ will be replaced by $a_1\in [0,1]$.

(2) Case 2: $a_1^U>0.5$. From (12), the required transmission rate of LU2 will always be established if $a_1^U>0.5$. Hence, (10) can be simplified as

$$\begin{array}{cc}\hfill \underset{0<a_1\le 0.5}{max}& R_s={log}_2\left(\frac{1+\zeta a_1}{1+\delta }\right);\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \epsilon =\mathbf{Pr}(\underset{m\in \mathcal{M}}{max}{\zeta }_{e,m}>\delta ),\hfill \end{array}$$

(27)

and the CJ scheme in [21] is implemented to solve the SRM problem in (12). Specifically, in this situation, $x_2$ can be regarded as artificial noise generated by Alice to strengthen the secrecy performance of LU1.

(3) Case 3: $0<a_1^U\le 0.5$. There must be a trade-off between secrecy rate and QoS. We denote $a_{1,opt}\in (0,0.5]$ and $R_s^{*}\left(a_1\right)$ as the unique optimal solution that satisfies $R_s^{\prime }\left(a_{1,opt}\right)=0$ and the corresponding maximum secrecy rate, respectively. Next, different cases are characterized below:

(a)

$R_s^{\prime }\left(0.5\right)\ge 0$. $\zeta >\rho \left(0.5\right)$ can be easily verified. Thus, we have $a_1^{*}=0.5,R_s^{*}\left(a_1\right)=R_s\left(0.5\right)$, if $a_1^U=0.5$; otherwise, $a_1^{*}=a_1^U,R_s^{*}\left(a_1\right)=R_s\left(a_1^U\right)$.

(b)

$R_s^{\prime }\left(0.5\right)<0\&R_s^{\prime }\left(0\right)>0$. Based on the characteristics of the concave function, there must exist a unique $a_{1,opt}$. Hence, if $a_{1,opt}\le a_1^U$, we have $a_1^{*}=a_{1,opt},R_s^{*}\left(a_1\right)=R_s\left(a_{1,opt}\right)$; otherwise, $a_1^{*}=a_1^U,R_s^{*}\left(a_1\right)=R_s\left(a_1^U\right)$.

(c)

$R_s^{\prime }\left(0\right)\le 0$. According to (25), we have $\zeta <\rho \left(0\right)$, and it is optimal for Alice to stop secure transmission, which leads to $a_1^{*}=0^{+}$ and $R_s^{*}\left(a_1\right)=R_s\left(0^{+}\right)$.

In the light of the above conclusion, we summarize the details of the overall algorithm in Algorithm 1.

Algorithm 1 Solution to the SRM problem in (12).
Input:$\epsilon$, $P_a$, $P_c$, $N_a$, $N_c$, $h_{a1}$, $h_{a2}$, $h_{ae}$, $h_{ce}$, $R_{th}$;
Output:$R_s^{*}\left(a_1\right)=R_s\left(a_1^{*}\right)$;
1:	calculate $a_1^U$ according to (26);
2:	if $a_1^U\le 0$,
	Alice stops serving LU2. In addition, the CJ scheme in [21] is carried out at Alice to guarantee secure transmission for LU1;
3:	else if $a_1^U>0.5$,
	the CJ scheme in [21] is implemented to solve the SRM problem in (12);
4:	else
	the solution to obtain $a_1^{*}$ has been discussed in Case 3;
5:	end if
6:	return$a_1^{*}$;

4. Numerical Results

Numerical simulations are presented in this section to compare the proposed scheme with the proposed adaptive scheme with Alice-aided AN beamforming (without relying on Charlie), the Non-CJ-NOMA scheme in [19] and the CJ-OMA scheme (only for LU1) in [21]. We adopt the basic setting $N_a=4$, $N_c=4$, $M=4$, $\epsilon =0.01$, $P_c=10$ dB, ${\Vert {\mathbf{h}}_{a1}\Vert }^2=10$ dB, ${\Vert {\mathbf{h}}_{a2}\Vert }^2=5$ dB, and $R_{th}=2$ bit/s/Hz. Note that the aforementioned second scheme is named the Alice-aided scheme, in which AN beamforming is exploited by Alice but not Charlie, and Alice allocates $P_c$ to generate AN for fairness. Here, all the simulation results are averaged over 200 channel realizations.

Figure 2 and Figure 3 compare the secrecy rates and the transmission rates at LU2 achieved by different schemes, respectively. It can be shown that the proposed scheme suffers an inevitable loss of secrecy performance for providing service to LU2 by the NOMA principle compared with the CJ-OMA scheme. From Figure 2, obviously, the secrecy rate of the proposed scheme outperforms the Non-CJ-NOMA scheme, especially when $P_a<-3$ dB and $a_1^U<0$. This is mainly due to the fact that the proposed scheme consists of adaptive strategy adjustment while the NON-CJ-NOMA scheme fails to work in this case. In addition, we can observe from Figure 2 that, thanks to the external jamming signal from Charlie for anti eavesdropping, a much higher secrecy rate can be achieved by the proposed scheme against the Alice-aided scheme when $P_a\ge 0$ dB. Specifically, when $P_a<-3$ dB, the desired QoS constraint at LU2 can not be satisfied, Alice stops serving LU2 and the CJ scheme in [21] is carried out. When $P_a\ge -2$ dB, Alice begins to provide service to Rx2 by NOMA principle, and the $R_s$ at LU1 first decreases to zero when $P_a=-2$ dB then increases as $P_a$ increases. Similar results are provided by the adaptive Alice-aided scheme that the QoS requirement at LU2 can not be met when $P_a<-8$ dB, and in this case Alice only provides service to LU1 by adopting the CJ scheme in [21]. Then, the secrecy rate decreases to zero when $P_a=8$ dB due to the transmit strategy adjustment, and Alice begins to serve both LU1 and LU2 simultaneously when $P_a\ge -8$ dB. Figure 3 validates the effectiveness of the proposed power allocation strategy that, as $P_a$ increases from −3 dB to 19 dB, $a_1^{*}$ is set to be $a_1^U$ and $R_2$ remains at $R_{th}$. Compared with the Non-CJ scheme, when the required QoS at LU2 is satisfied, more power could be allocated to LU1 thanks to the jamming signals generated by Charlie in the proposed scheme. In addition, although both the proposed scheme and the Alice-aided scheme consist of adaptive power allocation adjustment, it can be observed that the first scheme outperforms the second one in a wide range of $P_a$. The reason is that, compared to the Alice-aided scheme, in the systems exploiting the proposed scheme, the SOP constraint can be satisfied much more easily with the aid of external jamming from Charlie, thus more power could be allocated to serve both LU1 and LU2.

Figure 4 and Figure 5 demonstrate the effective sum rate and the effective EE performance of all the four schemes, respectively. As shown in Figure 4 and Figure 5, we observe that significantly higher performance of both effective sum rate and effective EE can be achieved by the proposed scheme in a wide range of the total transmit power. Specifically, it can be observed from Figure 5 that there exists a close match between the curves of the proposed scheme and the Alice-aided scheme. This observation indicates that though introducing a cooperative jammer in our considered systems may lead to higher total power consumption, a relatively sufficient effective EE can be achieved by the proposed scheme.

5. Conclusions

In this paper, we investigate secure transmission in cooperative MISO-NOMA networks. An efficient adaptive scheme has been developed to solve the SRM problem under certain SOP for the user with high-level security requirement and meanwhile guarantee the predefined transmission rate for another user. Numerical results have been provided to confirm the effectiveness and flexibility of the proposed scheme in enhancing secrecy performance and effective EE. In our future work, imperfect CSI will be further considered to study the secrecy performance of cooperative NOMA networks.