Classification of Transition Human Activities in IoT Environments via Memory-Based Neural Networks
Abstract
1. Introduction
2. Related Works
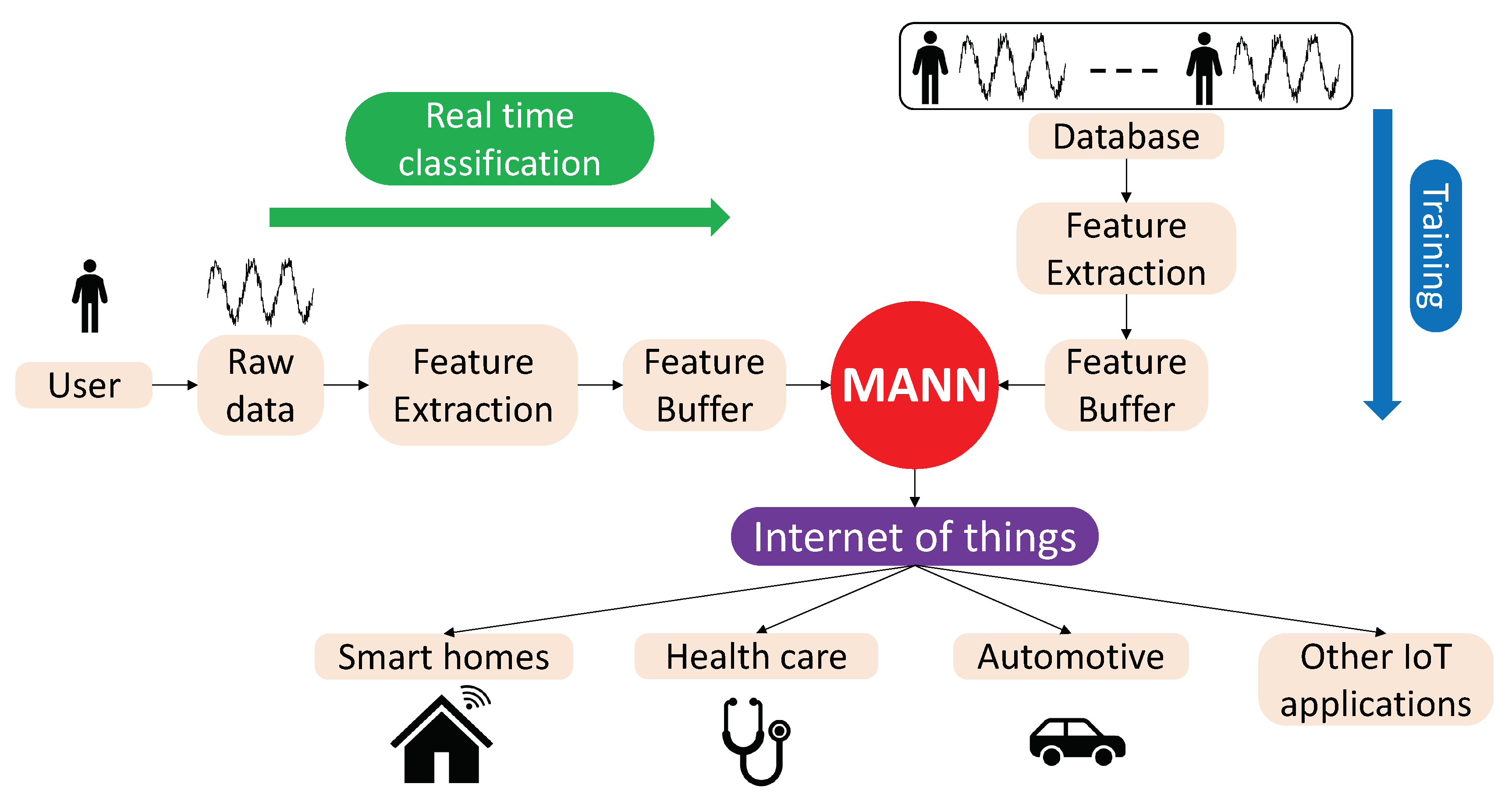
3. The Proposed Architecture
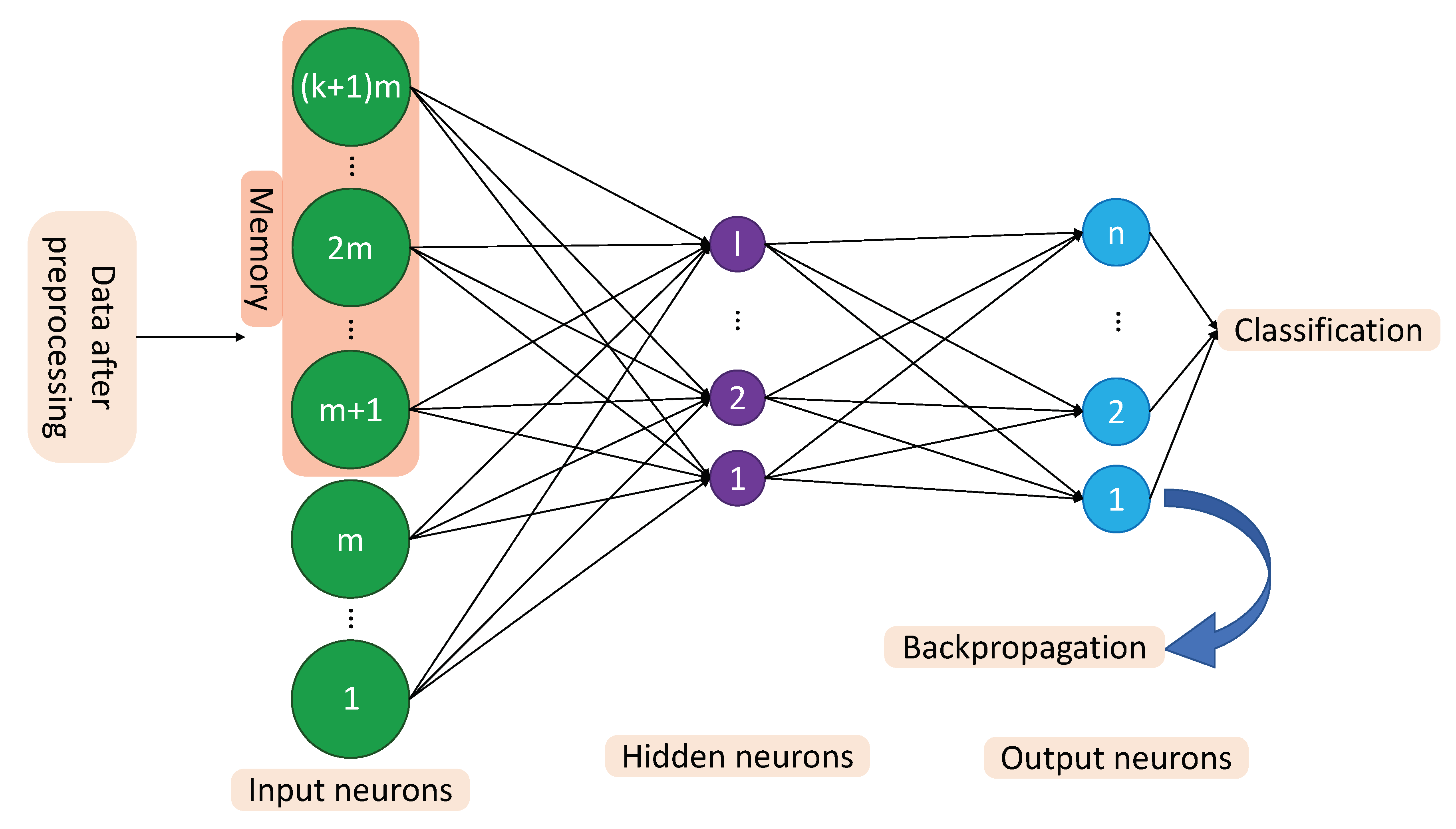
3.1. MANN
3.2. Data Acquisition and Feature Extraction for HAR
4. Experiments
4.1. SBHAR Dataset
4.2. Comparison of MANN Results to Other Studies on the SBHAR Dataset
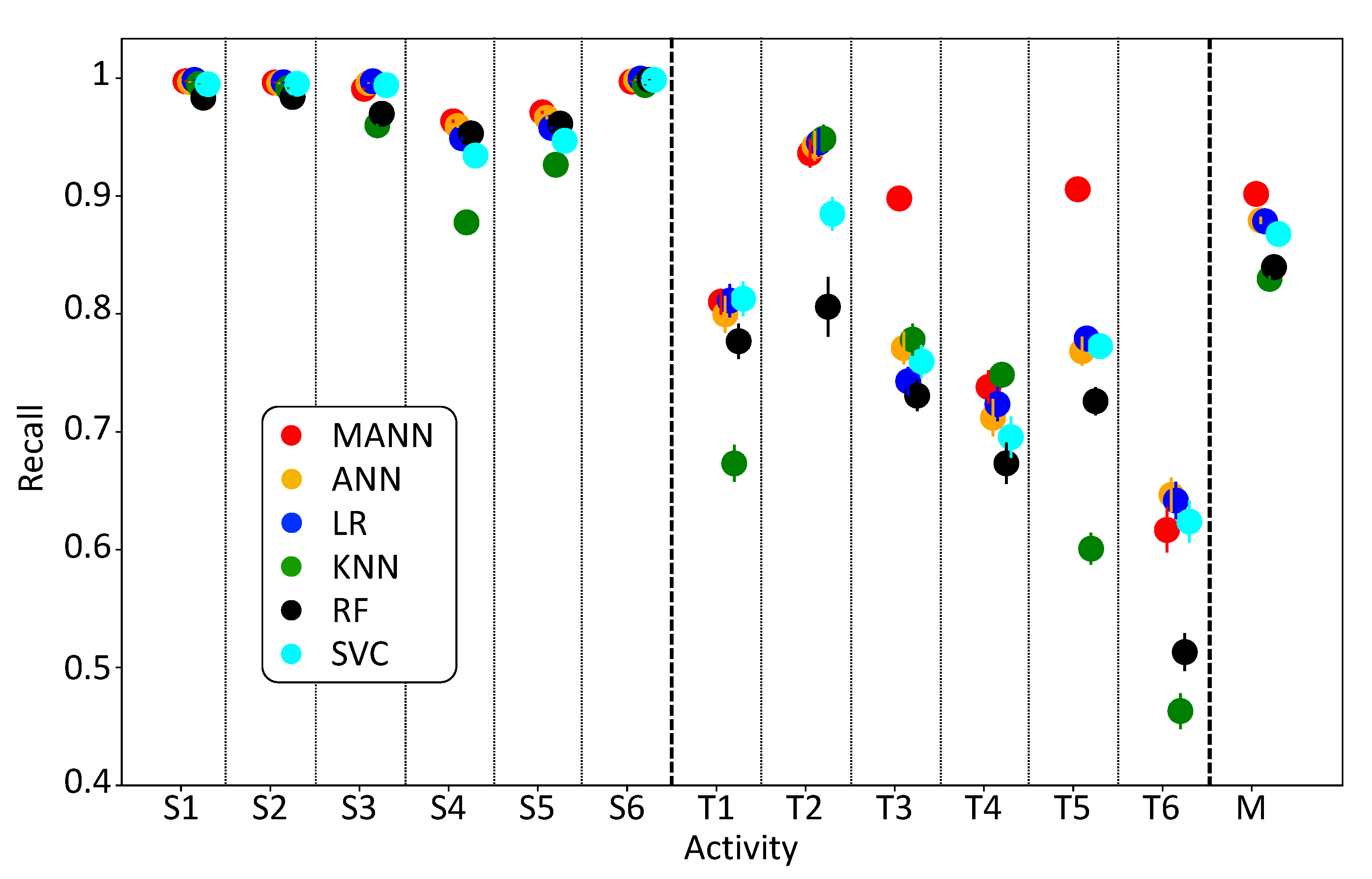
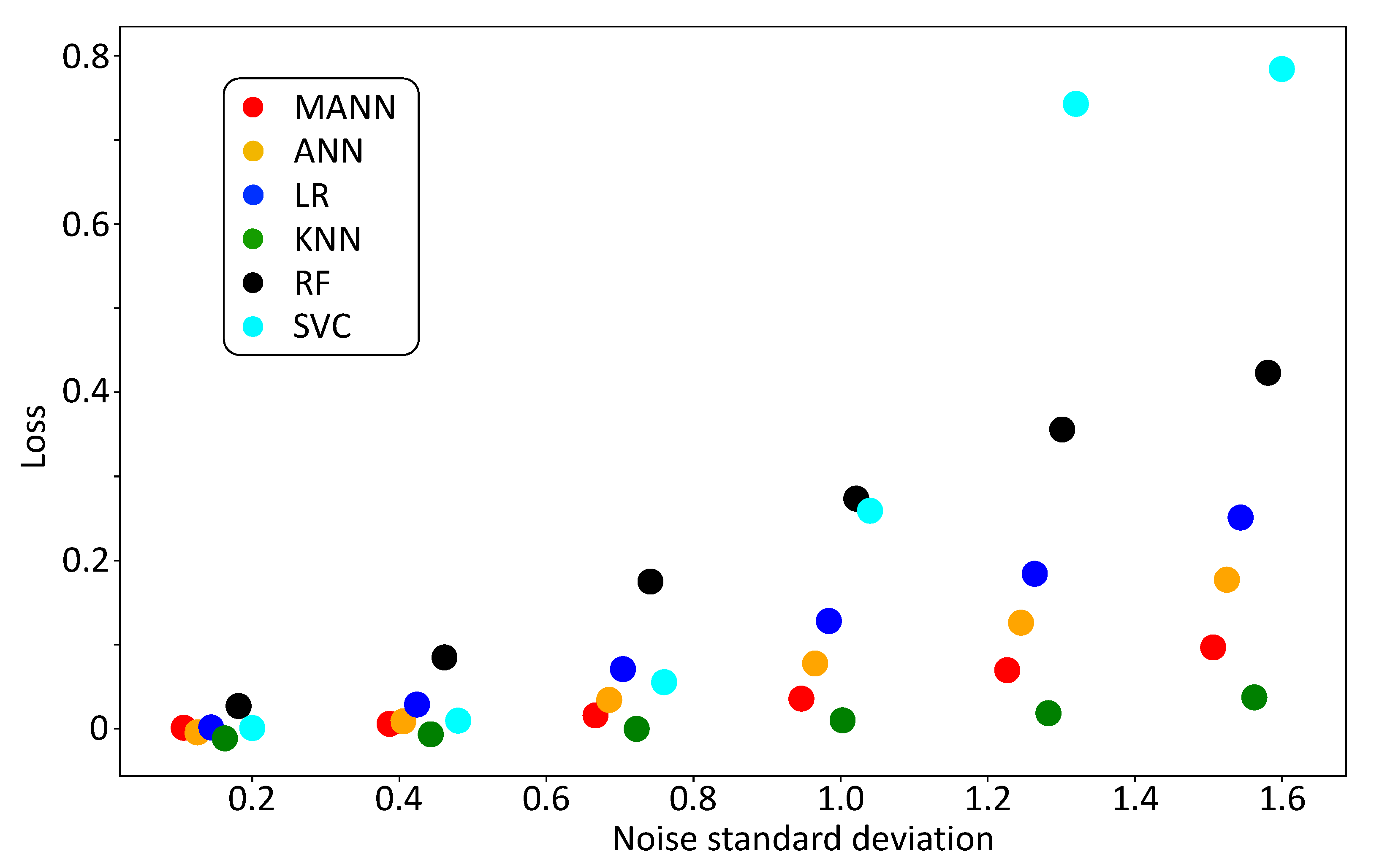
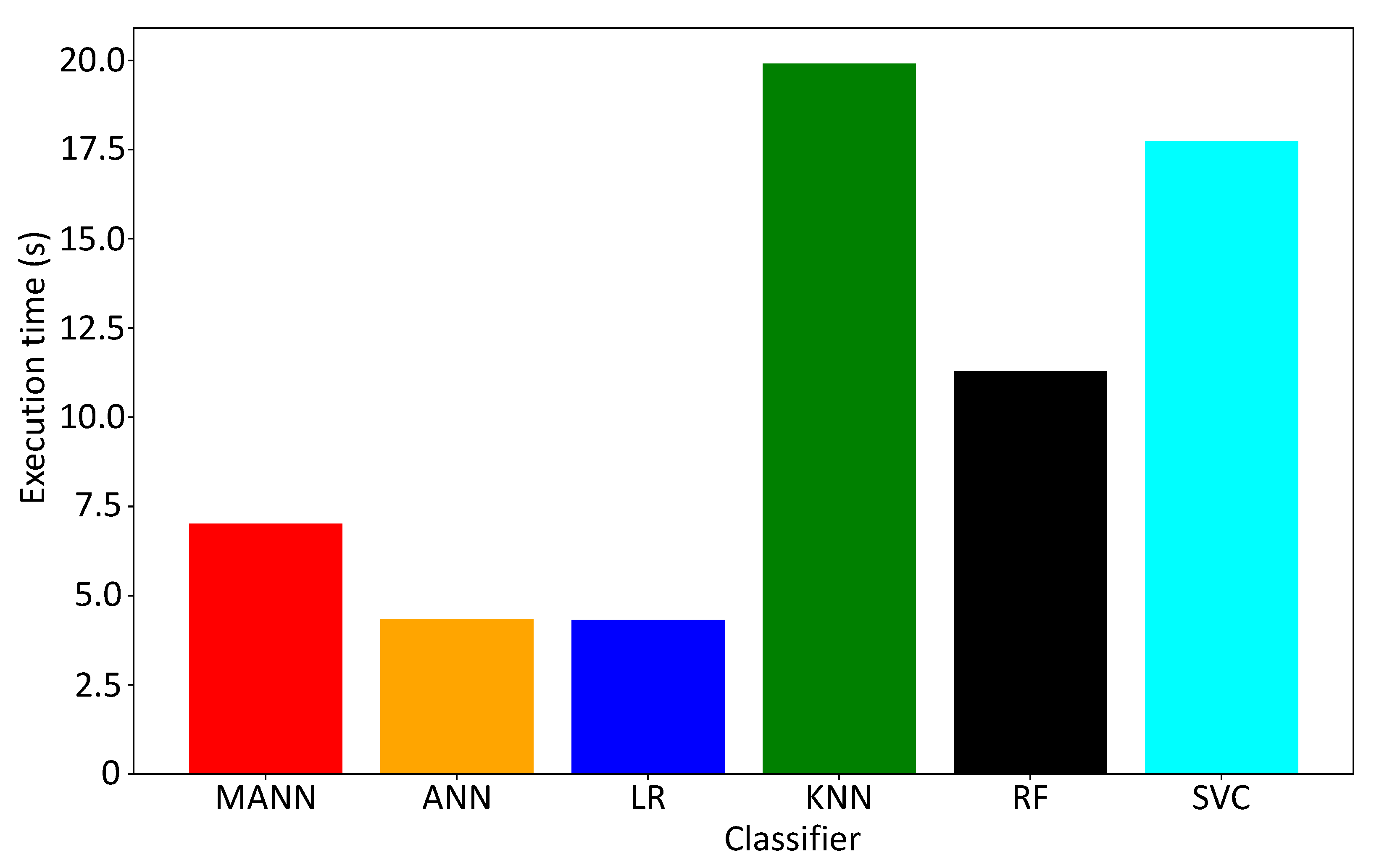
4.3. Comparison of MANN to Standard Methodologies in HAR
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HAR | Human Activity Recognition |
| TA | Transitional Activity |
| NTA | Non-Transitional Activity |
| NN | Neural Networks |
| ANN | Artificial Neural Networks |
| MANN | Memory Artificial Neural Networks |
| LR | Logistic Regressor |
| SVC | Support Vector Classifier |
| RF | Random Forest |
| KNN | K-Nearest Neighbor |
References
- Bisio, I.; Lavagetto, F.; Marchese, M.; Sciarrone, A. Comparison of situation awareness algorithms for remote health monitoring with smartphones. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 2454–2459. [Google Scholar]
- Rossi, S.; Capasso, R.; Acampora, G.; Staffa, M. A Multimodal Deep Learning Network for Group Activity Recognition. In Proceedings of the International Joint Conference on Neural Networks, Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- Vitiello, A.; Acampora, G.; Staffa, M.; Siciliano, B.; Rossi, S. A neuro-fuzzy-Bayesian approach for the adaptive control of robot proxemics behavior. In Proceedings of the IEEE International Conference on Fuzzy Systems, Naples, Italy, 9–12 July 2017. [Google Scholar] [CrossRef]
- Rossi, S.; Staffa, M.; Bove, L.; Capasso, R.; Ercolano, G. User’s Personality and Activity Influence on HRI Comfortable Distances. In Social Robotics. ICSR 2017; Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2017; pp. 167–177. [Google Scholar] [CrossRef]
- Amroun, H.; Ouarti, N.; Ammi, M. Recognition of human activity using Internet of Things in a non-controlled environment. In Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), Phuket, Thailand, 13–15 November 2016; pp. 1–6. [Google Scholar]
- Batool, S.; Saqib, N.A.; Khan, M.A. Internet of Things data analytics for user authentication and activity recognition. In Proceedings of the 2017 Second International Conference on Fog and Mobile Edge Computing (FMEC), Valencia, Spain, 8–11 May 2017; pp. 183–187. [Google Scholar]
- Osmani, V.; Balasubramaniam, S.; Botvich, D. Human activity recognition in pervasive health-care: Supporting efficient remote collaboration. J. Netw. Comput. Appl. 2008, 31, 628–655. [Google Scholar] [CrossRef]
- Ronao, C.A.; Cho, S.B. Recognizing human activities from smartphone sensors using hierarchical continuous hidden Markov models. Int. J. Distrib. Sens. Netw. 2017, 13. [Google Scholar] [CrossRef]
- Ronao, C.; Cho, S.B. Human activity recognition with smartphone sensors using deep learning neural networks. Expert Syst. Appl. 2016, 59, 235–244. [Google Scholar] [CrossRef]
- Jiang, W.; Yin, Z. Human Activity Recognition Using Wearable Sensors by Deep Convolutional Neural Networks. In Proceedings of the 23rd ACM International Conference on Multimedia, Brisbane, Australia, 26–30 October 2015; ACM: New York, NY, USA, 2015; pp. 1307–1310. [Google Scholar] [CrossRef]
- Anguita, D.; Ghio, A.; Oneto, L.; Parra, X.; Reyes-Ortiz, J.L. A Public Domain Dataset for Human Activity Recognition using Smartphones. In Proceedings of the ESANN, Bruges, Belgium, 24–26 April 2013. [Google Scholar]
- Acampora, G.; Foggia, P.; Saggese, A.; Vento, M. A hierarchical neuro-fuzzy architecture for human behavior analysis. Inf. Sci. 2015, 310, 130–148. [Google Scholar] [CrossRef]
- Ronao, C.A.; Cho, S.B. Human activity recognition using smartphone sensors with two-stage continuous hidden Markov models. In Proceedings of the 2014 10th International Conference on Natural Computation (ICNC), Xiamen, China, 19–21 August 2014; pp. 681–686. [Google Scholar]
- Kozina, S.; Gjoreski, H.; Gams, M.; Lustrek, M. Three-layer Activity Recognition Combining Domain Knowledge and Meta-classification. J. Med. Biol. Eng. 2013, 33, 406–414. [Google Scholar] [CrossRef]
- Hammerla, N.Y.; Halloran, S.; Plötz, T. Deep, Convolutional, and Recurrent Models for Human Activity Recognition Using Wearables. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI-16), New York, NY, USA, 9–15 July 2016; pp. 1533–1540. [Google Scholar]
- Zhao, Y.; Yang, R.; Chevalier, G.; Gong, M. Deep Residual Bidir-LSTM for Human Activity Recognition Using Wearable Sensors. Math. Probl. Eng. 2018, 2018, 7316954. [Google Scholar] [CrossRef]
- Frank, J.; Mannor, S.; Precup, D. Activity and Gait Recognition with Time-Delay Embeddings. In Twenty-Fourth AAAI Conference on Artificial Intelligence; Fox, M., Poole, D., Eds.; AAAI Press: Palo Alto, CA, USA, 2010. [Google Scholar]
- Bulling, A.; Blanke, U.; Schiele, B. A tutorial on human activity recognition using body-worn inertial sensors. ACM Comput. Surv. 2014, 46, 33:1–33:33. [Google Scholar] [CrossRef]
- Salarian, A.; Russmann, H.; Vingerhoets, F.J.G.; Burkhard, P.R.; Aminian, K. Ambulatory Monitoring of Physical Activities in Patients With Parkinson’s Disease. IEEE Trans. Biomed. Eng. 2007, 54, 2296–2299. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, B.; Chen, C.W. A two-layer and multi-strategy framework for human activity recognition using smartphone. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lampur, Malaysia, 23–27 May 2016; pp. 1–6. [Google Scholar]
- Abdullah, M.F.A.; Negara, A.F.P.; Sayeed, S.; Choi, D.; Anbananthen, K. Classification algorithms in human activity recognition using smartphones. Int. J. Comput. Inf. Eng. 2012, 6, 415–432. [Google Scholar]
- Capela, N.A.; Lemaire, E.D.; Baddour, N. Improving classification of sit, stand, and lie in a smartphone human activity recognition system. In Proceedings of the 2015 IEEE International Symposium on Medical Measurements and Applications (MeMeA) Proceedings, Turin, Italy, 7–9 May 2015; pp. 473–478. [Google Scholar] [CrossRef]
- Najafi, B.; Aminian, K.; Loew, F.; Blanc, Y.; Robert, P.A. Measurement of stand-sit and sit-stand transitions using a miniature gyroscope and its application in fall risk evaluation in the elderly. IEEE Trans. Biomed. Eng. 2002, 49, 843–851. [Google Scholar] [CrossRef]
- Reyes-Ortiz, J.L.; Oneto, L.; Samà, A.; Parra, X.; Anguita, D. Transition-Aware Human Activity Recognition Using Smartphones. Neurocomputing 2016, 171, 754–767. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. LSTM can solve hard long time lag problems. In Advances in Neural Information Processing Systems; NeurIPS Press: San Diego, CA, USA, 1996; pp. 473–479. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2018, 6, 1662–1669. [Google Scholar] [CrossRef]
- Martinez, J.; Black, M.J.; Romero, J. On human motion prediction using recurrent neural networks. arXiv 2017, arXiv:1705.02445. [Google Scholar]
- Waibel, A.; Hanazawa, T.; Hinton, G.; Shikano, K.; Lang, K.J. Phoneme recognition using time-delay neural networks. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 328–339. [Google Scholar] [CrossRef]
- Peddinti, V.; Povey, D.; Khudanpur, S. A time delay neural network architecture for efficient modeling of long temporal contexts. In Proceedings of the INTERSPEECH, Dresden, Germany, 6–10 September 2015. [Google Scholar]
- Huang, X.; Zhang, W.; Xu, X.; Yin, R.; Chen, D. Deeper Time Delay Neural Networks for Effective Acoustic Modelling. J. Phys. Conf. Ser. 2019, 1229, 012076. [Google Scholar] [CrossRef]
- Micucci, D.; Mobilio, M.; Napoletano, P. UniMiB SHAR: a new dataset for human activity recognition using acceleration data from smartphones. Appl. Sci. 2017, 7, 1101. [Google Scholar] [CrossRef]
- Xu, H.; Liu, J.; Hu, H.; Zhang, Y. Wearable Sensor-Based Human Activity Recognition Method with Multi-Features Extracted from Hilbert-Huang Transform. Sensors 2016, 16, 2048. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Kwapisz, J.R.; Weiss, G.M.; Moore, S. Activity recognition using cell phone accelerometers. SIGKDD Explor. 2010, 12, 74–82. [Google Scholar] [CrossRef]
- Lee, Y.; Cho, S.B. Activity Recognition Using Hierarchical Hidden Markov Models on a Smartphone with 3D Accelerometer. In Hybrid Artificial Intelligent Systems. HAIS 2011; Lecture Notes in Computer Science; Corchado, E., Kurzynski, M., Wozniak, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6678, pp. 460–467. [Google Scholar]
- Wu, W.; Dasgupta, S.; Ramirez, E.E.; Peterson, C.; Norman, G.J. Classification accuracies of physical activities using smartphone motion sensors. J. Med. Internet Res. 2012, 14. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Ronao, C.; Cho, S. Evaluation of Deep Convolutional Neural Network Architectures for Human Activity Recognition with Smartphone Sensors. In Proceedings of the KIISE Korea Computer Congress, Jeju Island, Korea, 24–26 June 2015; pp. 858–860. [Google Scholar]
- Andrey, I. Real-time human activity recognition from accelerometer data using Convolutional Neural Networks. Appl. Soft Comput. 2017, 62. [Google Scholar] [CrossRef]
- Pires, I.M.; Garcia, N.M.; Pombo, N.; Flórez-Revuelta, F.; Spinsante, S.; Teixeira, M.C.C.; Zdravevski, E. Pattern recognition techniques for the identification of Activities of Daily Living using mobile device accelerometer. PeerJ Prepr. 2018, 6, e27225. [Google Scholar]
- Seto, S.; Zhang, W.; Zhou, Y. Multivariate Time Series Classification Using Dynamic Time Warping Template Selection for Human Activity Recognition. In Proceedings of the 2015 IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015. [Google Scholar]
- Anguita, D.; Ghio, A.; Oneto, L.; Parra, X.; Reyes-Ortiz, J.L. Human Activity Recognition on Smartphones Using a Multiclass Hardware-Friendly Support Vector Machine. In Ambient Assisted Living and Home Care; Bravo, J., Hervás, R., Rodríguez, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 216–223. [Google Scholar]
- Li, Y.; Shi, D.; Ding, B.; Liu, D. Unsupervised Feature Learning for Human Activity Recognition Using Smartphone Sensors. In Mining Intelligence and Knowledge Exploration; Prasath, R., O’Reilly, P., Kathirvalavakumar, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 99–107. [Google Scholar]

| Activities | Number of Terms | |||
|---|---|---|---|---|
| NTAs | Walking | 1722 | 10,411 | 10,929 |
| Walking upstairs | 1544 | |||
| Walking downstairs | 1407 | |||
| Sitting | 1801 | |||
| Standing | 1979 | |||
| Laying | 1958 | |||
| TAs | Stand to sit | 70 | 518 | |
| Sit-to-stand | 33 | |||
| Sit-to-lie | 107 | |||
| Lie-to-sit | 85 | |||
| Stand-to-lie | 139 | |||
| Lie-to-stand | 84 | |||
| Paper | Method | Accuracy |
|---|---|---|
| [40] | Hidden Markov Models | 83.51 |
| [41] | Dynamic Time Warping | 89.00 |
| [42] | Handcrafted Features + SVM | 89.00 |
| [38] | Convolutional Neural Network | 90.89 |
| [13] | Hidden Markov Models | 91.76 |
| [43] | PCA + SVM | 91.82 |
| [43] | Stacked Autoencoders + SVM | 92.16 |
| [8] | Hierarchical Continuous HMM | 93.18 |
| [9] | Convolutional Neural Network | 94.79 |
| [10] | Convolutional Neural Network | 95.18 |
| [9] | FFT + CNN Features | 95.75 |
| MANN | 96.24 | |
| [11] | Handcrafted Features + SVM | 96.37 |
| [39] | Convolutional Neural Networks | 97.63 |
| S1 | S2 | S3 | S4 | S5 | S6 | T1 | T2 | T3 | T4 | T5 | T6 | Recall | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 491 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 98.99% |
| S2 | 17 | 450 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 95.54% |
| S3 | 5 | 7 | 408 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 97.14% |
| S4 | 0 | 1 | 0 | 455 | 50 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 89.57% |
| S5 | 0 | 0 | 0 | 11 | 527 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 97.96% |
| S6 | 0 | 0 | 0 | 0 | 4 | 540 | 1 | 0 | 0 | 0 | 0 | 0 | 99.08% |
| T1 | 0 | 0 | 0 | 2 | 2 | 0 | 19 | 0 | 0 | 0 | 0 | 0 | 82.61% |
| T2 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 8 | 0 | 0 | 0 | 0 | 80.00% |
| T3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 31 | 0 | 1 | 0 | 96.88% |
| T4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 16 | 0 | 8 | 64.00% |
| T5 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 4 | 0 | 41 | 0 | 83.67% |
| T6 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 9 | 1 | 16 | 59.26% |
| Precision | 95.53% | 98.25% | 97.84% | 96.60% | 90.24% | 99.63% | 86.36% | 100% | 88.57% | 64.00% | 93.18% | 66.67% | 95.48% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acampora, G.; Minopoli, G.; Musella, F.; Staffa, M. Classification of Transition Human Activities in IoT Environments via Memory-Based Neural Networks. Electronics 2020, 9, 409. https://doi.org/10.3390/electronics9030409
Acampora G, Minopoli G, Musella F, Staffa M. Classification of Transition Human Activities in IoT Environments via Memory-Based Neural Networks. Electronics. 2020; 9(3):409. https://doi.org/10.3390/electronics9030409
Chicago/Turabian StyleAcampora, Giovanni, Gianluca Minopoli, Francesco Musella, and Mariacarla Staffa. 2020. "Classification of Transition Human Activities in IoT Environments via Memory-Based Neural Networks" Electronics 9, no. 3: 409. https://doi.org/10.3390/electronics9030409
APA StyleAcampora, G., Minopoli, G., Musella, F., & Staffa, M. (2020). Classification of Transition Human Activities in IoT Environments via Memory-Based Neural Networks. Electronics, 9(3), 409. https://doi.org/10.3390/electronics9030409






