A Low Cross-Polarization Configuration Method for Phased Array Radar Antenna

1. Introduction

Thanks to the beam flexibility and the polarization capability of the polarimetric phased array radar (PPAR), it has attracted a lot of attention in weather observation, air traffic control, and air surveillance [1,2,3]. However, as one of the major obstacles, the requirement of high accuracy for polarimetric measurement still slow the use of the PPAR technology [3,4,5]. Specifically, the significant cross-polarization component is produced for the PPAR, which is caused by beam steering off the principal plane [1]. Hence, the polarization measurement bias is generated, while resulting in the bias of the polarization variables including the differential reflectivity ($Z_{DR}$), the linear depolarization ratio ($LDR$), and the differential phase ${\Phi }_{dp}$. Therefore, it is crucial to mitigate the bias resulting from the cross-polar or the cross-polar itself, thereby realizing the potential of the PPAR.

The sequential enthusiasm and efforts are poured into the bias correction methods. The bias correction technique for polarization measurement in PPAR was firstly suggested in [1], simulated in [5,6,7,8], and further updated in [9], and demonstrated in [2,10] using the large-scale testbeds. To be specific, the bias correction is done either to the measured polarization scattering matrix (PSM) or to polarimetric variables [1]. Nonetheless, most of the bias correction methods focus on the narrow-band issue. An iterative frequency division method is proposed for the wideband PPAR in [11], which expands the projection matrix correction method in [1]. Moreover, the correction matrix based on the theoretical pattern is not necessarily feasible due to the distortion of the radiation pattern, which results from mutual coupling and the edge diffraction between antenna elements. To reduce the effect of non-ideality, a reconstruction technique for the antenna pattern is proposed to correct the polarization measurement bias [12,13]. However, the source of bias still exists, and the bias increases with the larger of the beam scanning angle deviation.

To address the problem, the polarization state configuration (PSC) technique is an alternative strategy to reduce the cross-polarization level. The polarization state can be described with the Poincaré sphere [14,15]. Each point on the surface of a unit sphere represents each polarization state. The magnitude ratio and phase difference of two orthogonal components of electromagnetic field vectors are mapped to the sphere’s surface. In the practical application, the agile beam of the PPAR will be scanned to a wide steering direction. The polarization state with lower cross-polarization is superior for a given direction, so the characteristics of amplitude and phase in the dual-polarization antenna should be modulated appropriately. Moreover, the requirement of the cross-polarization level for the accurate polarimetric measurement is strict for the Alternate Transmission and Simultaneous Reception (ATSR) mode ($-25$ dB). In addition, the parameter requirement is $-45$ dB for the Simultaneous Transmission and Simultaneous Reception (STSR) mode [10,16]. Therefore, the polarization state is necessary to be modulated optimally to reduce the cross-polarization level, especially for the polarization measurement applications.

To suppress the cross-polar component, a PSC method is proposed to obtain the desired polarization state. The motivation is to reduce the cross-polarization level dramatically and make the co-polarization at an acceptable level. Each beam direction corresponds to a type of configured polarization state. The modulation operation depends on the beam direction and is equivalent to finding the optimal point on the Poincaré sphere. Therefore, the problem is formulated as a minimum problem under some parameter constraints, while achieving the lower cross-polarization. The magnitude and phase of two polarized ports are modulated, thereby denoting that the radiated wave is not the linearly polarized wave but the elliptically polarized wave, including the right-hand elliptical polarization (RHEP) and left-hand elliptical polarization (LHEP). We assume that the RHEP is the co-polarization component, and the LHEP is the cross-polarization component. This pair of orthogonal vectors are antipodal points on the surface of a unit sphere. The structured polarization states are achieved according to the CPI requirement. The simulated results and comparisons illustrate the priority of PSC with respect to the fixed linear polarization (LP) and circular polarization (CP). Furthermore, the polarization variables are used to assess the performance of the PSC method on the polarization measurement application. The results reveal that the value of $Z_{DR}$ and $LDR$ could meet the accuracy requirement for the polarization measurement.

In Section 2, the radiation model with elliptical polarization (EP) wave is developed. The corresponding radiation model is deduced based on the crossed dipoles antenna, and the constrained nonlinear multivariable function is formulated. In Section 3, the comparisons between radiation patterns of the linear, circular, and elliptical polarization waves are illustrated. The performance and priority of the elliptical polarization are analyzed based on the radiation pattern and polarization variables. Conclusions and discussions are presented in Section 4.

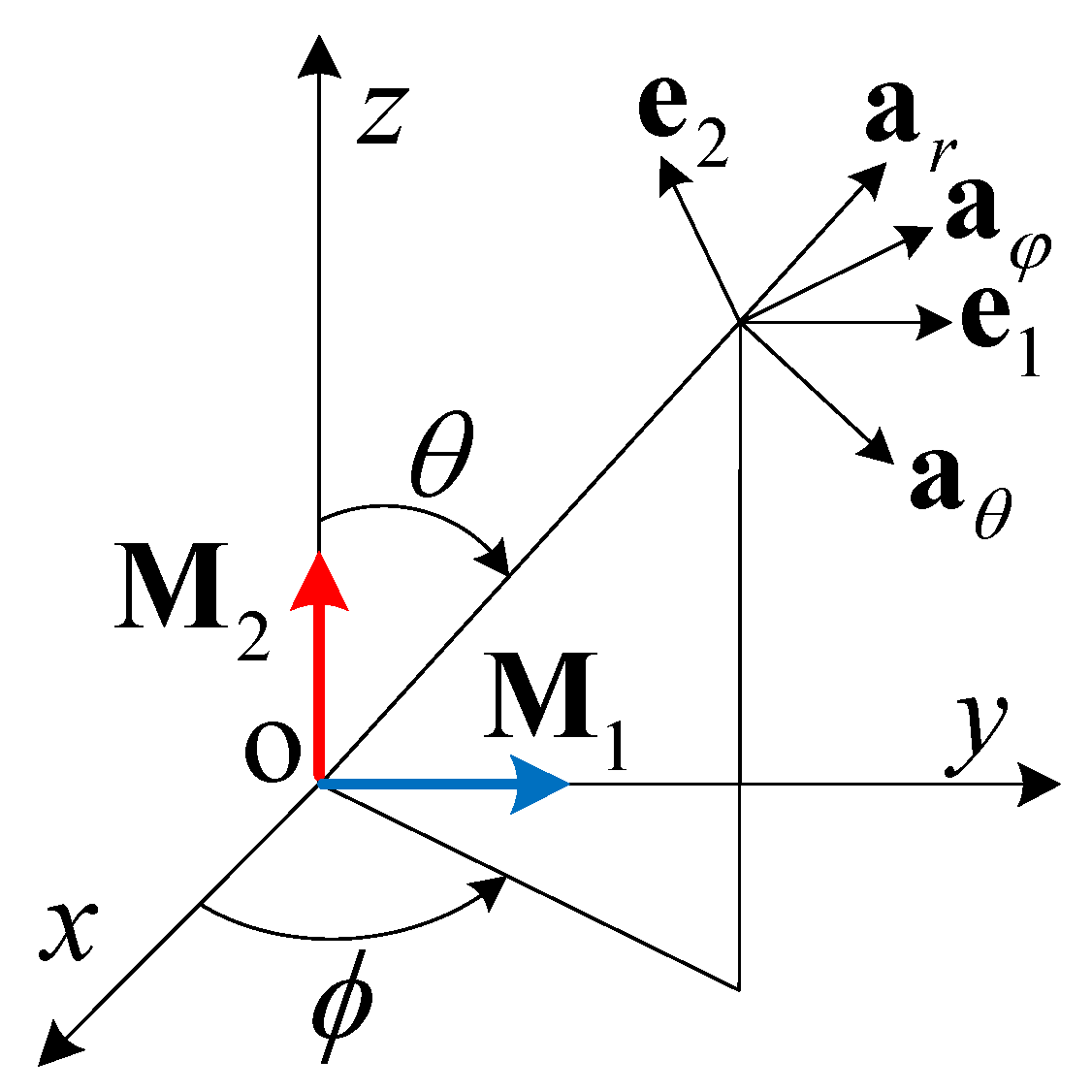
2. Formulation

A theoretical formula is derived using the radiated electric field at the antenna element. The coordinate system is chosen with the dual-polarization radiating element located at the origin, and the antenna plane is in the $yz$ plane as shown in Figure 1. We develop the radiation model and solve the solution of the CPI objective function based on a pair of crossed dipoles.

2.1. Radiation Model with Elliptical Polarization

If the 1st and 2nd port of the dual-polarization element are energized respectively, the radiated electric field amplitudes of two ports can be written by

$${\mathbf{E}}_q=E_q{\mathbf{e}}_q=E_{q\theta }{\mathbf{a}}_{\theta }+E_{q\varphi }{\mathbf{a}}_{\varphi }$$

(1)

where the subscript q (1 or 2) denotes the qth element. The definitions of the unit vectors ${\mathbf{e}}_q$, ${\mathbf{a}}_{\varphi }$, and ${\mathbf{a}}_{\theta }$ are consistent with that [1,7,17]. ${\mathbf{E}}_q$ is the vector form of $E_q$.

If the phase of excitation voltage in qth port is ${\phi }_q$, the phase difference is defined as $\phi$, where $\phi ={\phi }_1-{\phi }_2$. Without loss of generality, the RHEP radiated from this pair of elements can be expressed as

$$\begin{array}{ccc}\hfill {\mathbf{E}}_R& =E_R{\mathbf{e}}_R={\mathbf{E}}_1+e^{-j\phi }{\mathbf{E}}_2\hfill & \hfill =\left(E_{1\theta }+e^{-j\phi }{E}_{2\theta }\right){\mathbf{a}}_{\theta }+\left(E_{1\varphi }+e^{-j\phi }{E}_{2\varphi }\right){\mathbf{a}}_{\varphi }\end{array}$$

(2)

Similarly, the LHEP radiated from this pair of elements can be given by

$$\begin{array}{ccc}\hfill {\mathbf{E}}_L& =E_L{\mathbf{e}}_L={\mathbf{E}}_1+e^{j\phi }{\mathbf{E}}_2\hfill & \hfill =\left(E_{1\theta }+e^{j\phi }{E}_{2\theta }\right){\mathbf{a}}_{\theta }+\left(E_{1\varphi }+e^{j\phi }{E}_{2\varphi }\right){\mathbf{a}}_{\varphi }\end{array}$$

(3)

The orthonormal elliptical polarization basis $\left\{{\mathbf{e}}_R,{\mathbf{e}}_L\right\}$ is defined,

$$\left\{\begin{array}{l}{\mathbf{e}}_R=\frac{1}{\sqrt{1+p^2}}\left({\mathbf{a}}_h+e^{-j\phi }p{\mathbf{a}}_v\right)=\frac{1}{\sqrt{1+p^2}}\left({\mathbf{a}}_{\varphi }-e^{-j\phi }p{\mathbf{a}}_{\theta }\right)\\ {\mathbf{e}}_L=\frac{1}{\sqrt{1+p^2}}\left({\mathbf{a}}_h+e^{j\phi }p{\mathbf{a}}_v\right)=\frac{1}{\sqrt{1+p^2}}\left({\mathbf{a}}_{\varphi }-e^{j\phi }p{\mathbf{a}}_{\theta }\right)\end{array}\right.$$

(4)

where p is the ratio of amplitude of excitation voltage between ports 1 and 2, $p=\left|E_2\right|/\left|E_1\right|$. The polarization parameter $\left(\phi ,p\right)$ is equivalent to the Jones vector representation of polarization states [14]. ${\mathbf{a}}_h$ and ${\mathbf{a}}_v$ are the horizontal and vertical unit vectors in local orthogonal system, respectively. In addition, we assume ${\mathbf{a}}_h={\mathbf{a}}_{\varphi }$, ${\mathbf{a}}_v=-{\mathbf{a}}_{\theta }$.

If the activated port produces an RHEP wave, the projections of radiated electric fields onto the defined elliptical polarization basis yield

$$\left\{\begin{array}{ll}{E}_{RR}& =〈{\mathbf{e}}_R,{\mathbf{E}}_R〉={\mathbf{e}}_R^H{\mathbf{E}}_R\\ E_{LR}& =〈{\mathbf{e}}_L,{\mathbf{E}}_R〉={\mathbf{e}}_L^H{\mathbf{E}}_R\end{array}\right.$$

(5)

where $E_{RR}$ and $E_{LR}$ are the co- and cross-polarization components, respectively.

Similarly, when the activated port produces an LHEP wave, the projections of radiated electric fields onto the defined elliptical polarization basis yield

$$\left\{\begin{array}{ll}{E}_{LL}& =〈{\mathbf{e}}_L,{\mathbf{E}}_L〉={\mathbf{e}}_L^H{\mathbf{E}}_L\\ E_{RL}& =〈{\mathbf{e}}_R,{\mathbf{E}}_L〉={\mathbf{e}}_R^H{\mathbf{E}}_L\end{array}\right.$$

(6)

where $E_{LL}$ and $E_{RL}$ are the co-polarization and cross-polarization components separately.

Let $0\le \phi \le \pi$, so the rotation direction of the elliptical polarization wave keeps unchanged. In addition, the axial ratio of elliptical polarization is constrained within $\pm 3$ dB, i.e., $0.5\le p\le 2$.

The cross-polarization isolation (CPI) indicates the ratio of the two orthogonally polarized components including the co-polarization and the cross-polarization. Hence, when the radiated wave is RHEP, the CPI is given by

$${\mathrm{CPI}}_R=20\log \left(\frac{E_{RR}}{E_{LR}}\right)$$

(7)

For simplicity of calculation, let ${\mathrm{CPI}}_R=20\log \left(1/\rho \right)$, where

$$\rho =\frac{-e^{-j\phi }p{E}_{1\theta }-e^{-j2\phi }p{E}_{2\theta }+E_{1\varphi }+e^{-j\phi }{E}_{2\varphi }}{-e^{j\phi }p{E}_{1\theta }-p{E}_{2\theta }+E_{1\varphi }+e^{-j\phi }{E}_{2\varphi }}$$

(8)

The cross-polar level $\rho$ is represented by the ratio of co- and cross-polarization components, which is equivalent to formula (7). The co- and cross-polarization fields are functions of polarization parameters $\left(\phi ,p\right)$, so the cross-polar reduction issue can be formulated as a constrained minimum problem. The objective function subject to a set of constraints is

$$\begin{array}{l}\underset{\phi ,p}{\min }\rho \left(\phi ,p\right)\\ s.t.\left\{\begin{array}{c}0\le \phi \le \pi \\ 0.5\le p\le 2\end{array}\right.\end{array}$$

(9)

2.2. Radiation Model of Crossed Dipoles

A PPAR antenna is composed of elements whereby each is treated as a pair of dipoles placed orthogonally as displayed in Figure 1. The dipole moment is given by

$${\mathbf{M}}_q={\mathbf{a}}_q{A}_q{e}^{j{\phi }_q}$$

(10)

where $A_q$ is the excitation amplitude, ${\phi }_q$ excitation phase, and ${\mathbf{a}}_q$ the unit vector along the dipole direction.

The radiated electric field is

$${\mathbf{E}}_q=-\frac{k^2{e}^{-jkr}}{4\pi \epsilon r}\left\{{\mathbf{a}}_r\times \left[{\mathbf{a}}_r\times {\mathbf{M}}_q\right]\right\}$$

(11)

where r is the distance from the antenna, k the wavenumber $\left(k=2\pi /\lambda \right)$, $\lambda$ the radar wavelength, and $\epsilon$ the permittivity for an assumed uniform precipitation-free atmosphere.

Based on formula (10) and formula (11), the radiated electric fields of ports 1 and 2 are

$$\left\{\begin{array}{l}{\mathbf{E}}_1=\left({\mathbf{a}}_{\theta }\cos \theta \sin \varphi +{\mathbf{a}}_{\varphi }\cos \varphi \right)E_1\\ {\mathbf{E}}_2=-{\mathbf{a}}_{\theta }\sin \theta E_2\end{array}\right.$$

(12)

formula (2) and formula (3) are rewritten as

$$\left\{\begin{array}{l}{\mathbf{E}}_R=E_1\left({\mathbf{a}}_{\theta }\cos \theta \sin \varphi +{\mathbf{a}}_{\varphi }\cos \varphi -{\mathbf{a}}_{\theta }p{e}^{-j\phi }\sin \theta \right)\\ {\mathbf{E}}_L=E_1\left({\mathbf{a}}_{\theta }\cos \theta \sin \varphi +{\mathbf{a}}_{\varphi }\cos \varphi -{\mathbf{a}}_{\theta }p{e}^{j\phi }\sin \theta \right)\end{array}\right.$$

(13)

where $0\le \theta \le \pi$, $-\pi /2\le \varphi \le \pi /2$, that is, the radiation characteristics on the hemisphere pointing to the positive x-axis.

On the basis of formula (5) and formula (6), when the activated ports radiate the RHEP wave, the co-polarization and cross-polarization components are

$$\left\{\begin{array}{l}{E}_{RR}=\frac{E_1}{\sqrt{1+p^2}}\left(-e^{j\phi }p\cos \theta \sin \varphi +\cos \varphi +p^2\sin \theta \right)\\ E_{LR}=\frac{E_1}{\sqrt{1+p^2}}\left(-e^{-j\phi }p\cos \theta \sin \varphi +\cos \varphi +p^2{e}^{-j2\phi }\sin \theta \right)\end{array}\right.$$

(14)

Similarly, when the activated ports product LHEP wave, the co- and cross-polarization components are

$$\left\{\begin{array}{l}{E}_{LL}=\frac{E_1}{\sqrt{1+p^2}}\left(-e^{-j\phi }p\cos \theta \sin \varphi +\cos \varphi +p^2\sin \theta \right)\\ E_{RL}=\frac{E_1}{\sqrt{1+p^2}}\left(-e^{j\phi }p\cos \theta \sin \varphi +\cos \varphi +p^2{e}^{j2\phi }\sin \theta \right)\end{array}\right.$$

(15)

Therefore, formula (8) is rewritten as

$$\rho =\frac{-e^{-j\phi }p\cos \theta \sin \varphi +\cos \varphi +p^2{e}^{-j2\phi }\sin \theta }{-e^{j\phi }p\cos \theta \sin \varphi +\cos \varphi +p^2\sin \theta }$$

(16)

For the given beam direction, the optimal polarization state is calculated. Specifically speaking, a set of polarization parameters $\left(\phi ,p\right)$ is obtained for each set of beam angle $\left(\theta ,\varphi \right)$, minimizing the ratio $\rho$. The expression is given by

$${\rho }_{min}=\underset{\begin{array}{c}0\le \phi \le \pi \\ 0.5\le p\le 2\end{array}}{min}\rho \left(\theta ,\varphi \right)$$

(17)

In our experiments, a standard constrained nonlinear multivariable function fmincon in MATLAB 2017b (MathWorks, Natick, MA, USA) is used to find the minimum of $\rho$. The nonlinear programming solver can find the minimum of formula (17), thereby calculating $\phi$ and p for the given $\theta$ and $\varphi$.

2.3. PSM Using Elliptically Polarized Wave

The dual-polarization antenna could acquire the four components of the scattering matrix alternately or simultaneously, that is, STSR and ATSR mode. The latter can estimate all four components of the backscattering covariance matrix during two or more pulses. Through the process of radiation, scattering, and propagation of the electromagnetic wave, the PSM measured by the receiver can be written as

$${\mathbf{S}}^{\left(p\right)}={\mathbf{P}}^T{\mathbf{S}}^{\left(b\right)}\mathbf{P}.$$

(18)

Consistent with the polarization definition and expression in [1,7], ${\mathbf{S}}^{\left(b\right)}$ is the intrinsic backscatter matrix of the target, while ${\mathbf{S}}^{\left(p\right)}$ is the measured backscatter matrix. $\mathbf{P}$ is the projection matrix and represents projections of radiated fields onto the defined polarization basis. Its definition and formula are consistent with that in [1], and the superscript T is the transpose operator. In this paper, we assume that the observed object is a metallic sphere.

In order to evaluate the superiority of the configured polarization state for the polarization measurement application, we use the polarimetric variables including $Z_{DR}$ and $LDR$ [18]. The bias of differential reflectivity is denoted as $\Delta Z_{DR}$. The expected requirement of $\Delta Z_{DR}$ for accurate polarization measurement is less than 0.1 dB for the PPAR system [10]. Similarly, the bias of the linear depolarization ratio is described as $\Delta LDR$. We assume that the constraint condition to $\Delta LDR$ is less than $-40$ dB for accurate polarization measurement:

$$\Delta Z_{DR}=Z_{DR}^{\left(p\right)}-Z_{DR}^{\left(b\right)}$$

(19)

$$\Delta LDR=LD{R}^{\left(p\right)}-LD{R}^{\left(b\right)}$$

(20)

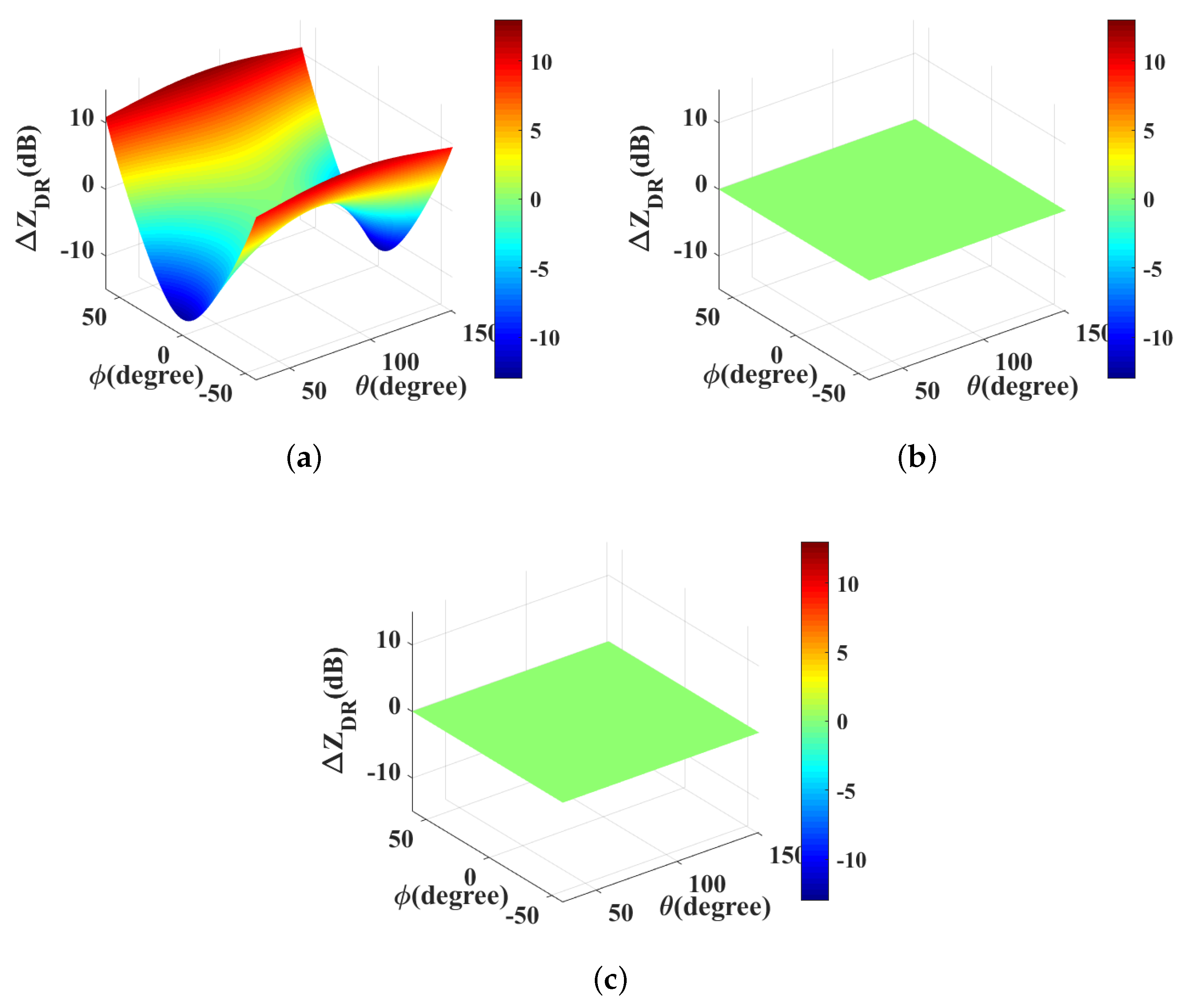
3. Simulation Results and Analyses

The dual-polarization radiation element of the PPAR herein is composed of a pair of crossed dipoles. In this section, the comparison is made among the antenna patterns by radiating the linear, circular, and elliptical polarization wave, including the co-polarization and cross-polarization components.

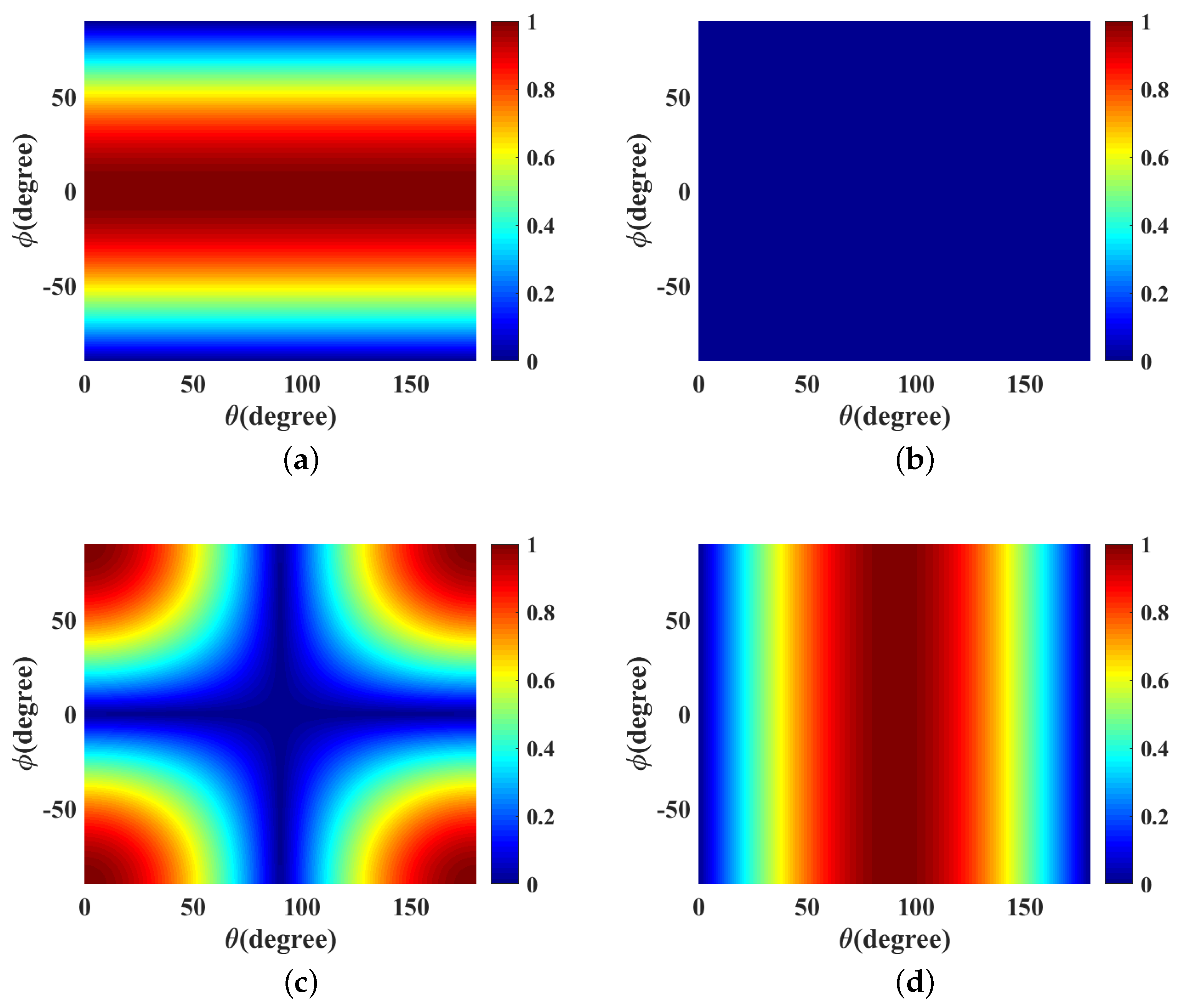
3.1. Linear Polarization

The patterns of the electric field given by [1] are plotted in Figure 2. If the linear polarization basis $\left\{{\mathbf{a}}_{\varphi },{\mathbf{a}}_{\theta }\right\}$ is used, the co-polarization and cross-polarization patterns of horizontally polarized dipole (${\mathbf{M}}_1$) are shown in Figure 2a,c, and the co-polarization and cross-polarization patterns of vertically polarized dipole (${\mathbf{M}}_2$) are shown in Figure 2b,d. As displayed in Figure 2a,c, the co-polarization pattern of the horizontal dipole is the highest along the vertical principal plane, i.e., $\varphi =0$ for each elevation angle, and the corresponding cross-polarization pattern is the lowest. For the horizontally polarized dipole, the copolar pattern decreases and the cross-polar pattern increases with an increased angle declining away from the principal plane, respectively. For the vertical dipole, the co-polarization pattern is the highest along the horizontal principal plane, i.e., $\theta =90°$ for each azimuth angle, and the corresponding cross-polarization component is constantly equal to zero.

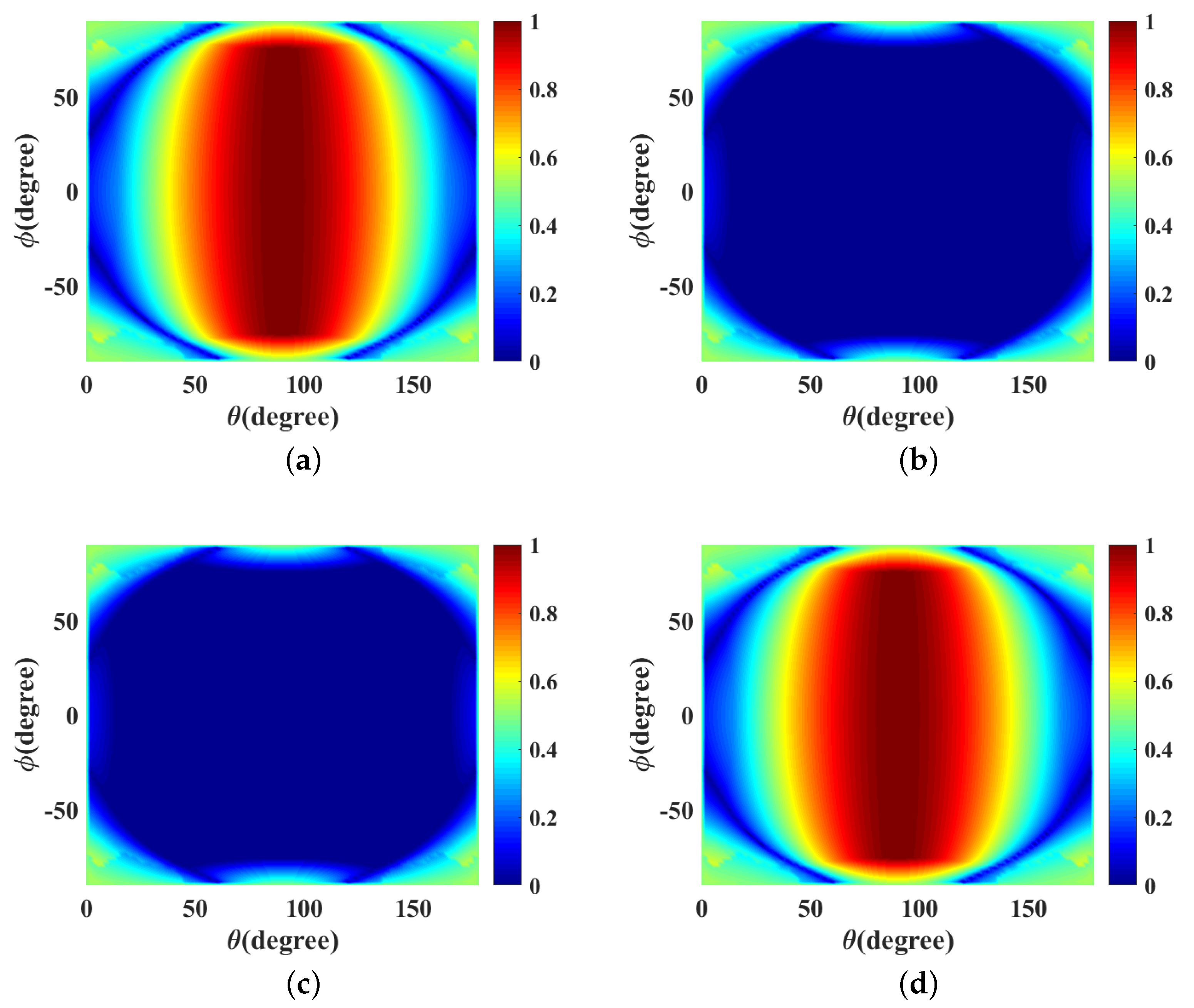
3.2. Circular Polarization

If the circular polarization antenna is used, the RHCP and LHCP unit vectors are defined as the circular polarization basis. As shown in Figure 3, the co-polarization and cross-polarization patterns vary with the azimuth and elevation angle. Figure 3a,c depict the copolar and cross-polar electric fields when the radiated circularly polarized wave is LHCP state. The co-polarization pattern is the largest in the normal direction of the beam, i.e., $(\theta ,\varphi )=(90°,0°)$, where the cross-polarization pattern is the lowest. When the direction is pointed off the broadside, the copolar pattern decreases and the cross-polar pattern increases simultaneously. Thus, the CPI decreases with the increasing angle away from the principal plane. Figure 3b,d illustrate the copolar and cross-polar electric fields when the radiated polarized wave is RHCP state. The conclusion of LHCP radiation is also suitable for the RHCP issue.

3.3. Elliptical Polarization

The polarization state of the radiated electric field can be configured by using the proposed PSC method to modulate the amplitude and phase of two dipoles. The modulation is implemented in each direction while obtaining the optimal amplitude and phase. The co-polarization and cross-polarization patterns of the antenna after configuring are shown in Figure 4. Figure 4a,c depict the copolar and cross-polar electric fields when the radiated wave is LHEP state. Similar to the linear and circular polarization, the copolar pattern of the elliptical polarization wave decreases if the beam direction is pointed off the positive x-axis herein. However, the cross-polar pattern does not increase significantly but remains at a lower level in a wider angle range. This will not lead to the deterioration of CPI considerably. Figure 4b,d depict the copolar and cross-polar electric fields when the radiated wave is RHEP state. The pattern characteristic of the RHEP dipoles is approximate to that of LHEP dipoles, having a low cross-polarization level.

For the horizontally polarized dipole, the copolar pattern decreases and the cross-polar pattern increases for the beam directions away from the principal plane, respectively. This results in the reduction of CPI, thereby restricting the beam scanning range of PPAR antenna. The issue of CPI has been previously proved to be crucial to the accuracy of polarization measurement [19]. Figure 5a depicts the available angle range when CPI is greater than 40 dB. The available elevation angle is from $52.7°$ to $127.3°$, and the available azimuth angle from $-31.82°$ to $31.82°$. However, the usable angle range is not uniform and restricted. The peak value of CPI is $71.98$ dB.

With respect to the LP wave, the CPI of the CP wave has better symmetry. As shown in Figure 5b, the angle range meeting the CPI requirement (40 dB) is approximately a circle throughout about $20°$ in the azimuth and elevation direction. The range is relatively uniform, but it is not broadened compared with that of the linearly polarized wave, which still troubles the available beam scanning range of the PPAR antenna. The peak value of CPI is 78 dB, which is greater than that of the LP issue.

The improved CPI when using the configurated elliptical polarization is shown in Figure 5c, and the angle range meeting the CPI requirement is broadened considerably. When the CPI is greater than 40 dB, the available elevation angle spans from $10.91°$ to $169.1°$, and the available azimuth angle from $-79.09°$ to $79.09°$. CPI is greater than 160 dB in most of the available angles described above. Compared with the CPI of linear and circular polarization, the CPI of the elliptical polarization wave not only has a wider considerable angle range but also a greater value. For the phased array antenna, the accurate polarization measurement can be met in most of the angles within $\pm 75°$. The superiority of the modulated EP wave is verified intuitively.

The modulation of the amplitude and phase can change the polarization state of the radiated electric field. The polarization state can be described by the point on the Poincaré sphere as shown in Figure 6. The discrete distribution represents the various polarization states corresponding to different beam directions. Figure 6a depicts the polarization states distribution along with the azimuth angle when $\theta =60°$, and Figure 6b depicts that along with the elevation angle when $\varphi =-30°$.

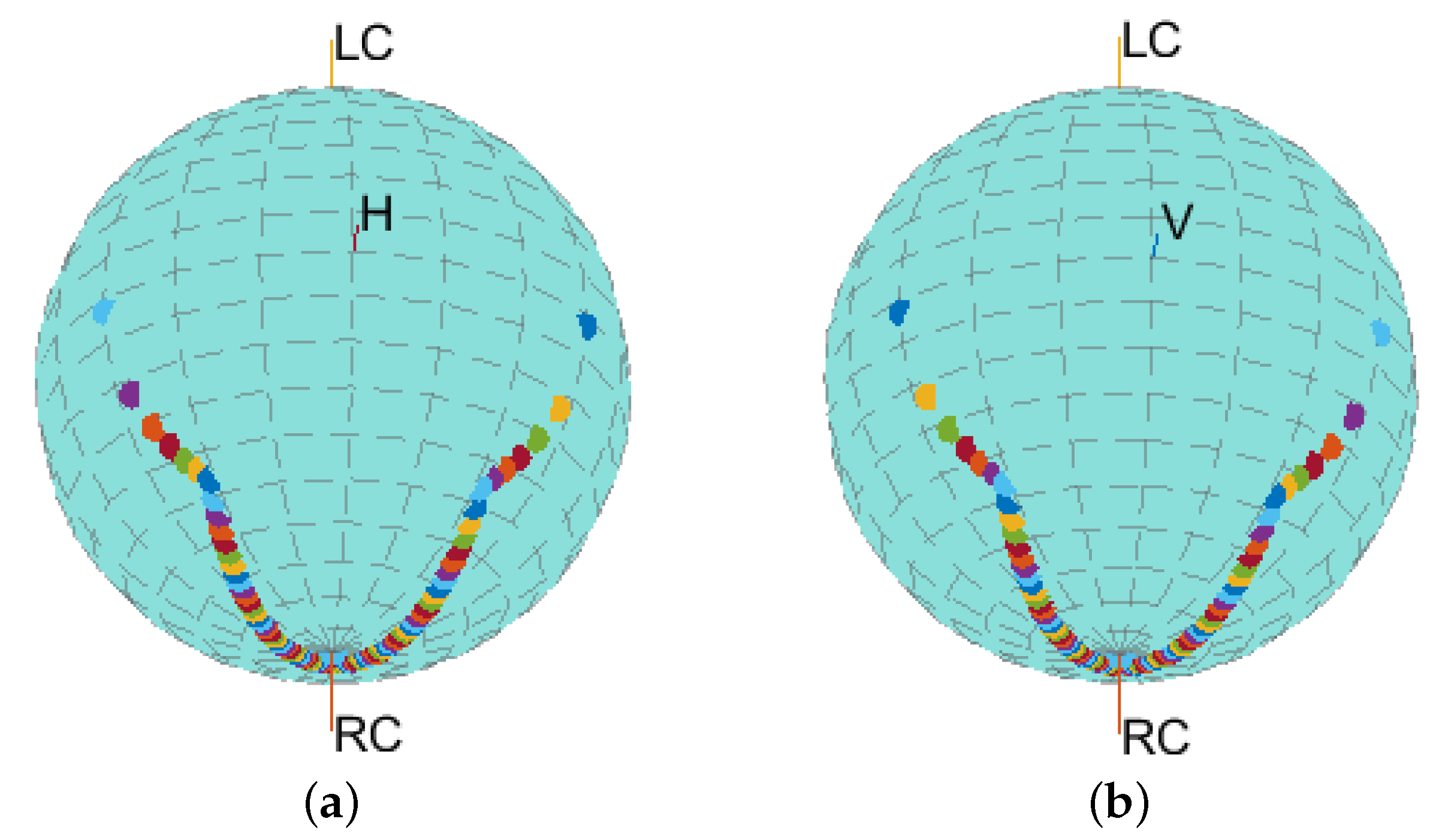
3.4. Polarization Measurement Using the Elliptically Polarized Wave

The polarization measurement is implemented using a PPAR antenna composed of eight elements. It is worth noting that the magnitude weighting factor is obtained by a 40 dB Taylor. To evaluate the performance of the polarization measurement, the polarimetric variables including $Z_{DR}$ and $LDR$ are investigated. Numerical simulations show the bias profile of the polarization measurement results. From the comparisons, the configured elliptical polarized wave could achieve the lower polarimetric variable bias, which is conformed well to the above CPI results. The biases of $Z_{DR}$ and $LDR$ are expressed as $\Delta Z_{DR}$ and $\Delta LDR$, respectively, which are shown in the following Figure 7 and Figure 8.

For the constructed array plane, $(\theta ,\varphi )=(90°,0°)$ is the normal direction. Generally speaking, the expected beam scanning range is $\pm 60°$ from the normal that is, $\theta$ varies from $30°$ to $150°$, $\varphi$ from $-{60}^{°}$ to $60°$. As shown in Figure 7a, the absolute value of bias of $Z_{DR}$ increases once the beam is scanned away from the normal direction when the radiated wave is the LP. $\Delta Z_{DR}$ in most of the directions is far greater than the expected 0.1 dB. The increasing bias not only results in the considerable deterioration of polarization measurement performance, but also reduces the available scanning range of the phased array. In contrast, the $\Delta Z_{DR}$ using the CP and EP wave reduces considerably, as shown in Figure 7b,c. In the whole angle range, $\Delta Z_{DR}$ is around 0 dB which is less than $0.1$ dB. Hence, the LP wave is suitable for the polarization measurement without beam scanning. The CP and EP waves have superiority in the polarization measurement using the PPAR antenna.

Figure 8 displays the bias of the linear depolarization ratio, that is, $\Delta LDR$, when using different polarized waves. If the LP wave is used, the minimum of $\Delta LDR$ is $-70.32$ dB as shown in Figure 8a. The angle range that meets the $-40$ dB requirement is limited. The distribution of the available angle is along or approaching the y- and z-axis. Other angle range floats within $\pm 5°$ from the normal of the antenna plane. Similarly, the usable angle range is less than $\pm 7°$ from the normal of the antenna plane when the antenna is configured with CP wave, and the minimum of $\Delta LDR$ is also $-70.32$ dB as shown in Figure 8b. In view of the bias of polarization measurement, the restricted available angle range is in conflict with the wide scanning range of the phased array. Thus, the LP and CP wave would introduce an unexpected bias of $LDR$. If the configured EP is used, the situation improves dramatically as shown in Figure 8c. On the one hand, $\Delta LDR$ is less than $-40$ dB in most of the beam directions within $\pm 60°$, which is consistent with the conventional scanning range of the phased array. On the other hand, $\Delta LDR$ is decreased considerably, while meeting the requirement of the polarization measurement well.

Therefore, the EP wave could improve the CPI and reduce the polarization measurement bias in a wider scanning range as well.

4. Conclusions

In this paper, an effective polarization state configuration method has been proposed to reduce the cross-polarization level and enhance the CPI in a wide beam scan range of the PPAR antenna. The amplitude and phase of the dual-polarization elements are modulated for each beam direction according to the CPI requirement. In contrast to the LP and CP state, the radiated polarization wave is EP state, and it is received by using a set of elliptical polarization basis. For the defined co-polarization and cross-polarization components, the PSC technique is formulated as a minimum problem of CPI, thereby achieving the available amplitude ratio and phase difference. This method is beneficial for reducing the polarization measurement bias even in a wide scan angle. Moreover, we take a dual-polarization dipole antenna, for example, to test the priority of the proposed method. The biases of the polarization variables $Z_{DR}$ and $LDR$ are less than $0.1$ dB and $-40$ dB, respectively, in most of the beam directions within $\pm 60°$. Numerical simulations reveal that the obtained CPI could meet the requirement of the polarization measurement for PPAR.