Contact Resistance Parallel Model for Edge-Contacted 2D Material Back-Gate FET

Abstract

Because 2D materials have adjust band gap, high mobility ratio, bipolar, anisotropy and flexibility characters, they have become the new direction for FET’s channel materials. According to the characteristics of the layers of 2D materials, the current transport characteristics can be improved by using the edge-contacted electrode. Moreover, the research on the current transfer mechanism between channel layers is the basis of the practical application of 2D transistors. In the research, the 2D material-MoS₂ is used as the channel material, the back-gate transistors with different layers are prepared by dry etching and edge-contacted electrode structure. We also discuss the current transport mechanism of channel and established the channel resistance parallel transport model. The parallel model and TLM are used to analyze the contact resistance of the edge-contacted structure, and the total resistance, total contact resistance, and single-layer contact resistance of different layers are calculated. The parallel model is verified by dc test data. The number of channel layers is closely related to contact resistance, total resistance, and mobility. In addition, the of single MoS₂ is about 7.27 kΩ·um. This contact resistance parallel model can also be applied to other 2D materials edge-contacted FET.

1. Introduction

Since graphene was discovered, more and more 2D (two-dimensional) materials have been found, such as TMDs (Transition Metal Dichalcogenides), BP (Black Phosphorus), etc. [1,2,3,4]. Like graphene, few layered 2D materials can be obtained by mechanical exfoliation [5]. At present, there are mainly four types of 2D layered materials. The first type is the graphene-like family, including graphene, boron nitride, etc. The second type is the 2D transition metal dichalcogenides family, including the semiconductor dichalcogenides and the metal dichalcogenides. The third type is the 2D oxide family, which mainly consists of some layered oxides. Finally, there are some layered materials of other structures, like as black phosphorus [6]. These 2D materials have different properties, such as graphene, which is a Dirac semi-metal, and transition metal dichalcogenides, which is an excellent semiconductor, while boron nitride is an excellent insulator. These transition metal dichalcogenides not only have the mechanical, electrical, and optical advantages of graphene, but also have the natural optical band gap that graphene does not have. Therefore, they have been the research hotspots in the field of materials science in the past few years. With the rapid development of the semiconductor industry, the high integration of electronic components is further increased. Because of the approximation to the limit of Moore’s law, the application of traditional semiconductor has become increasingly restricted. At the same time, the varied physical properties of 2D materials displayed superior performance, and 2D materials are expected to instead of some traditional semiconductor materials (Figure 1). In the post-Moore circuit era, 2D materials will create a new path for the development of photoelectric applications [7,8,9].

Figure 1. Application based on 2D materials.

Because of the layer properties of 2D materials [10], their transport characteristics are significantly different from the conventional semiconductor transistors. When 2D materials are used for transistor channel material, the current transport in the transistor channel is no longer mainly concentrated on the surface of the channel. The charge is transported along every layer in the channel [11,12]. According to characteristics of 2D materials, many new techniques have been developed for transistor fabrication, such as edge-contacted [12,13,14,15] (Figure 2b) or one-dimensional contacted [16,17], sandwich/combined-contacted structure [18] (Figure 2c), and so on.

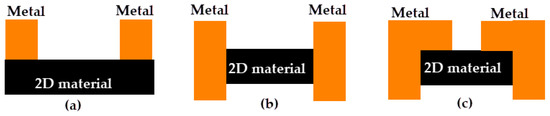
Figure 2. (a) traditional top-contacted; (b) edge/one dimensional-contacted; (c) sandwich/combined-contacted.

As shown in Table 1, the mobility of edge-conducted and sandwich-contacted structure is more than that of the top-contacted structure. Because no additional etching is required, the structure that is sandwich-contacted is simpler than that which is edge-conducted in the process. However, due to the overall encapsulation in sandwich-contacted structure, some of the electrodes are in contact with the top layer of the channel material. It can easily lead to tunneling resistance effect, increase the transport impedance, and reduce the mobility of FET (Field Effect Transistor). Thus, in the three structures, the order of difficult process is: edge-conducted > sandwich-contacted > top-contacted, and the order of performance is: edge-conducted > combined-contacted > top-contacted. Due to 2D materials’ special properties, the edge-conducted structure has becoming new direction of FET’s channel investigation.

Table 1. Mobility comparison of different electrode structure.

Paper	Channel Thickness	Mobility (cm2/Vs)	Electrode Structure
[19]	8 L	54	edge
[20]	multilayer	71.8	combined
[21]	1 L	35	top
[22]	30 nm	104	edge
This work	31 L	107	edge

Before the emergence of 2D materials, the research on transistor channel was limited to simple circuit model analysis, and the channel material was regarded as a whole semiconductor. With the further study of 2D material physical properties and transport characteristics, the current transport mechanisms obviously different from that of ordinary materials due to their layer characteristics [11]. The traditional channel circuit model was not able to accurately analyze the working mechanism of the 2D materials transistor. The correct description of channel current transport mechanism is the basis of the application of 2D semiconductor materials, so a new channel circuit model must be established for 2D material FET. In recent years, the channel current of 2D semiconductor transistors has been analyzed and studied [23,24,25,26]. A lot of work has been done from the aspects of charge flow between layers [12] and channel resistance mode [27]. It lays the foundation for the application of 2D materials.

In this paper, a 2D semiconductor back gate FET with edge-contacted was prepared by dry etching. The channel material was used by MoS₂ of different layers (11 L, 14 L, 23 L, 31 L). From the aspect of layered transport, the current transport mechanism of channel was discussed. We established the channel resistance parallel transport model, and the current transport mechanism of 2D channel material was studied. In a certain layer range, the more layers, the lower the total channel resistance. For transistors with different channel layers, the channel resistance parallel model and TLM (transfer-length method) were used to calculate the per-layer channel contact resistance, and results of various channel layers MoS₂ FET tended to be consistent (about 7.27 kΩ·um).

2. Fabrication

MoS₂, which was used as the channel material, is a member of the TMDC family and has emerged as the prototypical 2D semiconductor. It has great potential for improvement, particularly from the perspective of device transport.

Figure 3 shows the fabrication process flow and the cross-sectional schematic of our device structure. MoS₂ samples were exfoliated from a bulk MoS₂ crystal using the conventional mechanical exfoliation method. The samples were transferred on a clean SiO₂ (285 nm) highly doped Si substrate (Figure 3a), and the thickness as identified by AFM (atomic force microscopy) (Figure 4a). We used 7 nm, 9 nm, 15 nm, 20 nm varied thickness of MoS₂ for 2D material FETs channel. During the fabrication process, the MoS₂ samples were covered HfO₂ (30 nm) by ALD (atomic layer deposition) equipment, in order to avoid any possible degradation upon longer exposure to air. We used resist AR-P6200/PMMA as the etch mask. The top layer was coated with AR-P 6200 of layer thickness ≈220 nm and the sample was pre-baked at 150 °C for 3 min. The mask was defined on the top lay by EBL (electron-beam lithography). The etching was performed in ICP380 with a gas Ar. Suitable etching times for the desired grating depths were found out during the process. In the etching process, through adjusting ICP power, RF power, air flow and pressure, we were able to make the side wall of the electrode more inclined and were able to make MoS₂ more fully contact the electrode, to ensure good contact. Figure 4b shows that after the sputter process, the electrodes are in close contact with the lateral wall of the channel. Finally, electrodes consisted of 10 nm Ti/100 nm Au were fabricated on edge of channel by sputter and lift-off techniques (Figure 4c).

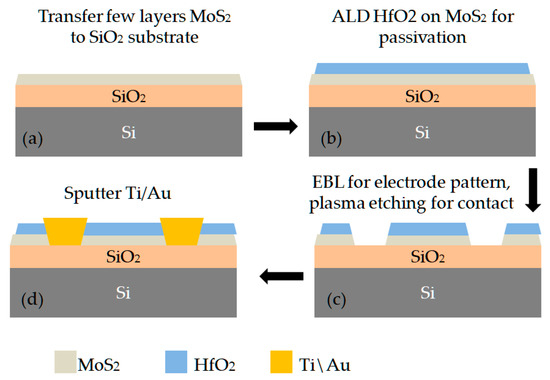
Figure 3. Fabrication process of edge-contacted 2D material back-gate FET (a) Transfer MoS2 to substrate; (b) ALD HfO2 for passivation; (c) Etching for contact; (d) Sputter Ti/Au.

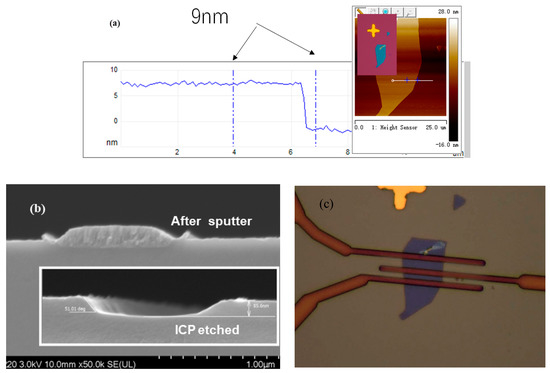
Figure 4. (a) AFM image of MoS₂ thickness; (b) SEM image of channel cross sectional surface after the Sputter; (c)optical images of edge-contacted MoS₂ back-gate FET.

3. Results and Discussion

The relationship of current of drain (I_d) with voltage of gate (V_g), drain (V_d) is the key for research on FET’s DC characteristic to build a resistance model. Electrical measurements were performed in an air environment at room temperature using an Keithley 4200 semiconductor parameter analyzer. In the measurements, V_g ranged from −80 V to 80 V and V_d from 0 V to 4 V. For different channel thickness MoS₂, each layer MoS₂ had a thickness of ∼0.65 nm, the corresponding layer numbers are about 11 L (11 layers), 14 L (14 layers), 23 L (23 layers), 31 L (31 layers).

Mobility ratio is one of the key indexes to estimate FET’s transfer performance; it decides the operating frequency and speed of the semiconductor device. We obtained edge contacted MoS₂ FET’s hole mobility ratio in room temperature, from transconductance curve in Figure 5c using the classic formula of mobility ratio:

$$\mu =g_m·\frac{L}{W}·\frac{1}{C_{ox}·V_d}$$

(1)

where g_m is transconductance, L is channel length of MoS₂ FET, W is channel width of MoS₂ FET, $C_{ox}={\epsilon }_{ox}/d_{ox}$(${\epsilon }_{ox}$ is dielectric constant of insulation materials, $d_{ox}$ is thickness of insulation materials).

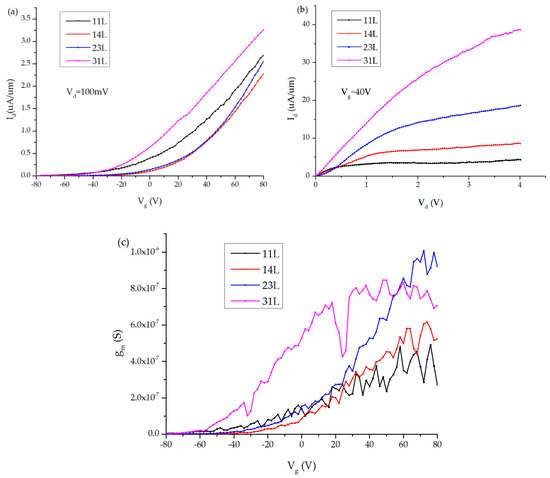
Figure 5. (a) I_d-V_g curves of 11 L, 14 L, 23 L, 31 L MoS₂ FET; (b) I_d-V_d curves of 11 L, 14 L, 23 L, 31 L MoS₂ FET; (c) g_m-V_g curves of 11 L, 14 L, 23 L, 31 L MoS₂ FET.

According to the above formula calculation of mobility ratio, we get the hole mobility of various channel layers MoS₂ FET. Figure 6a further compares different channel layers, hole mobility of around 31 layers MoS₂ FET get maximum. When channel thickness comprises of more than 11 layers, hole mobility showed an upward trend. The hole mobility of few-layer MoS₂ FET shows a strong thickness dependence in Figure 5b.

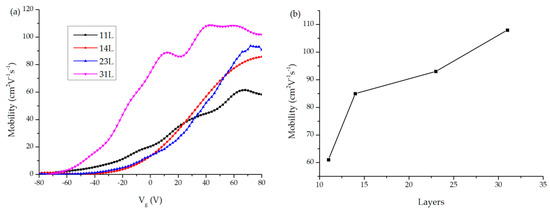
Figure 6. (a) FET’s mobility of varying layers versus gate bias; (b) mobility with varying layers.

Unlike top-contacted structure (Figure 7a), edge-contacted MoS₂ FET (Figure 7c) fabrication uses dry etch and electron-beam evaporation. In the procession, it avoids MoS₂ polluted by chemical liquid and O₂ to the most extent. Because electrodes of edge-contacted structure contact every lay of MoS₂ directly, drain current is not influenced by interlayer resistance, like Figure 7c. From the experimentation, compared to the published literature, the maximum hole mobility ratio of edge-contacted MoS₂ FET is much larger than top-contacted FET’s. The edge-contacted electrode process is adopted. According to the layer structure characteristics of 2D material and the current transport mode in channel, we use parallel structure to describe the current transport mechanism in the channel, and build the associated resistance parallel model, as in Figure 7d.

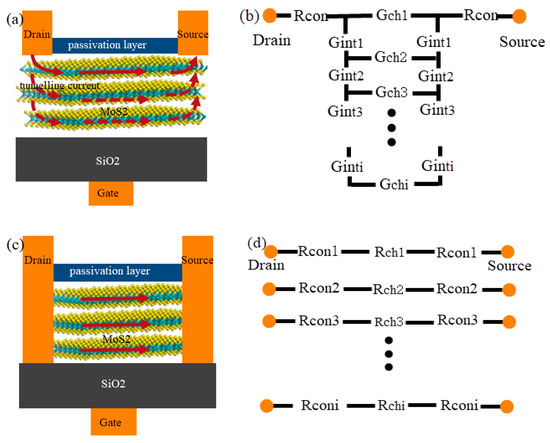
Figure 7. (a) current flow in top-contact structure MoS₂ FET; (b) channel resistance model of top-contacted structure MoS₂ FET; (c) current flow in edge-contacted structure MoS₂ FET; (d) channel resistance model of edge-contacted structure MoS₂ FET.

In the channel resistance model, contact resistance (R_con) plays an important role in FET performance. Understanding metal with MoS₂ contact is of great scientific and technological importance. In top-contacted structure, because of tunneling resistance, resistance equation becomes nonlinear. In Figure 7b, total channel resistance is:

$$R_{total}=2R_{con}+\frac{1}{{{\displaystyle \sum }}_{n=1}^i\frac{2}{G_{intn}}+\frac{1}{G_{chn}}}$$

(2)

In order to simplify the calculation, the concept of electrical conductance is led into the calculation. G_chn (n = 1, …, i, i is the number of layers) is semiconductor transport conductance of each channel layer, G_intn (n = 1, …, i) is tunneling conductance between different channel layers. R_con is the resistance due to the contact mental, R_total is the total transport resistance. Thus, the TLM will no longer be suit for calculate total channel resistance and contact resistance in the top-contacted structure.

In the edge-contacted structure, the electrode is contact with each layer of MoS₂ directly, bypass the tunneling resistance. Charge transmit between each layer uniformly. The channel resistance model of charge transport in MoS₂ FET (Figure 7d), can be derived from the mechanism of charge transfer in 2D material channels. The total transport resistance of each layer is R_totali = 2R_coni + R_chi. Becauseof the use of the edge-contacted structure, the charge transmitted parallel in the layers. The MoS₂ FET’s total transport resistance is the sum of the transport resistances in parallel for each layer. To simplify the calculation, we assume that R_coni, R_chi of each layer is the same resistance R_conper, R_chper. Then, MoS₂ back gate FET’s total channel transport resistance is:

$$R_{totali}=2R_{conper}+R_{chper}$$

(3)

$$R_{total}=||R_{totali}=\raisebox{1ex}{$\left(2R_{conper}+R_{chper}\right)$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$$

(4)

Through the transistor DC test, V_d and I_d are obtained under different V_g. R_total can be get from V_d/I_d. From Figure 8a, it can be seen that R_total decreases and tends to be stable as V_g increased. In Figure 8a,b, the more the channel layers, the smaller the total resistance will be. The result fully accords with the parallel structure characteristics of resistance in the channel.

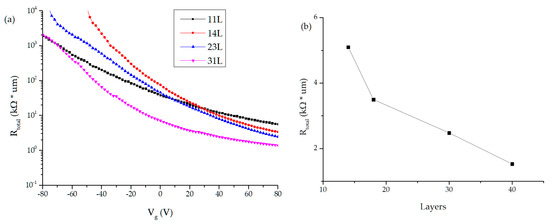
Figure 8. (a) FET’s R_total of varying layers versus voltage gate; (b) R_toral versus different layers.

From the formula of total channel resistance, the resistance model is still a linear equation, we also can use TLM method to calculate the contact resistance of edge contacted MoS₂ FET. The contact resistance per layer (R_conper) was extracted by:

$$R_{conper}=\raisebox{1ex}{$(n{R}_{total}-R_{chper})$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$$

(5)

As seen from Equation (5), in the edge-contacted electrode structure, different from the classical TLM method, R_conper is not only related to channel length, but also related to the number of layers of MoS₂ in the channel. Finally, R_con is the total parallel contact resistance of each layer MoS₂ to the electrode.

From Figure 9a R_conper of each layer can be calculated by TLM, then the total R_con of the side wall can be calculated as follows:

$$R_{con}=R_{conper}/n$$

(6)

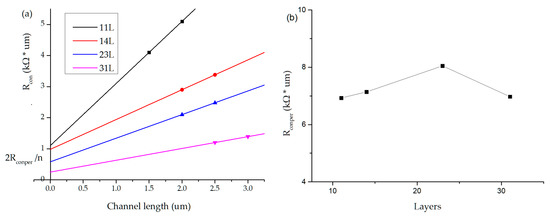
Figure 9. (a) use TLM Solve the per contact resistance (R_conper) of different layers; (b) per contact resistance vs. different layers.

For edge-contacted MoS₂ back gate transistors with different layers, the R_conper of each layer can be calculated according to the TLM method and the Equations (4) and (5). As can be seen from Figure 9b, use the same process (etched, sputter, Ti/Au), each layer of R_conper is consistent, and contact resistance is about 7.27 kΩ·um. According to Equation (6), we get R_con of different layers. From Table 2, the more layers of MoS₂ in the channel, the smaller R_con will be, therefore, the lower total transport resistance.

Table 2. R_con of different layers from Equation (6).

Layers	Rcon (kΩ∙um)
11	0.632
14	0.511
23	0.350
31	0.225

From Table 3, the contact resistance of the edge-contacted structure is better than the combined- contacted and top-contacted. Although the top-contacted structure can reduce the contact resistance through additional process (Ultra-High Vacuum Metal Deposition), it increased the complexity of the process. Thus, it shows that the edge-contacted structure has obvious advantages.

Table 3. R_con comparison of different electrode structure.

Paper	Channel Thickness	Rcon (kΩ∙um)	Electrode Structure
[28]	6–13 nm	0.9	combined
[29]	8 L	2.5	top
[30]	4.5 nm	0.74	top
This work	11 L	0.63	edge

4. Conclusions

In summary, we report a contact resistance model of edge-contacted MoS₂ back-gate FET. According to the characteristics of 2D materials, the edge-contacted structure transistors with different layers (11 L, 14 L, 23 L, 31 L) were prepared by dry etching. Direct contact between metal electrodes to each layer of 2D material in the channel improved the current transport of transistors. Dc characteristics of transistors with different layers are analyzed by using Keithley 4200 in an air environment at room temperature. According to the measured I_d-V_g and I_d-V_d of the transistors with different layers, the mobility was calculated. The current characteristics of transistors with different thickness were studied and their mechanism was analyzed by the models. On the basis of the analysis, combined with contact resistance parallel model, TLM method was adopted, and the contact resistance of MoS₂ per-layer of different layers thickness FET were calculated and compared.

From the above analysis, it can be seen that the test results are in line with the model expectations. In addition, according to the characteristics of 2D materials, this model can also be used in other 2D materials, such as TMDs, BP, etc.